
A Two-step Bidding Price Decision Algorithm under Limited
Man-Hours in EPC Projects
Nobuaki Ishii
1
, Yuichi Takano
2
and Masaaki Muraki
2
1
Faculty of Information and Communications, Bunkyo University, 1100, Namegaya, Chigasaki, Kanagawa, Japan
2
Graduate School of Decision Science and Technology, Tokyo Institute of Technology, Tokyo, Japan
Keywords: Competitive Bidding, Cost Estimation Accuracy, EPC Contract, Project Management, Project Selection.
Abstract: In Engineering-Procurement-Construction (EPC) projects, the contractor accepts an order through a
competitive bidding process. If the contractor’s bidding price is set higher than that of a competitor due to
cost estimation error, the contractor could fail to receive the order. Conversely, if the cost estimation error
results in an underestimation of the cost, the contractor would be granted the order; however, he would
eventually suffer a loss on this order. Thus, a bidding price decision in consideration of the cost estimation
accuracy and the deficit order probability is essential for the contractor in EPC projects. In this paper, we
develop a two-step bidding price decision algorithm. It allocates MH (Man-Hour) for cost estimation, which
determines the cost estimation accuracy, to each order under the limited volume of MH, and then
determines the bidding price for maximizing the expected profit under the deficit order probability
constraint. Numerical examples show that the bidding price decision in consideration of the cost estimation
accuracy and the deficit order probability is essential for the contractor to make a stable profit in EPC
projects, and that the developed algorithm is effective for making such bidding price decision.
1 INTRODUCTION
Among various types of project contracts, the
importance of Engineering, Procurement,
Construction (EPC) projects (Ranjan, 2009), where
contractors design and build unique products or
services based on the client requirements, is widely
recognized in practice in the field of construction,
civil engineering, plant engineering, and so on. In
EPC projects, the contractor has a single
responsibility for project cost, quality, and schedule
under a fixed-price that is determined before the
start of the project as a lump-sum contract. Thus, a
reduced project cost and shorter schedule are
expected (Jinru, 2011).
Although several shortcomings, for instance,
decisions on relatively detailed issues have to be
made early on in the project delivery process, have
been pointed out e.g., in Elfving et al. (2005),
competitive bidding is widely used for selecting a
contractor who carries out the project. In the
competitive bidding, the client usually evaluates
contractors on the basis of the multi-attribute bid
evaluation criteria, such as bidding price, past
experience, past performance, company reputation,
and the proposed method of delivery and technical
solutions (Watt et al., 2009). Then, the client
basically selects the contractor who proposes the
lowest price if there is not much difference in other
criteria.
In EPC projects, accordingly, it is necessary for
any contractor to determine the bidding price based
on precise cost estimation. If the contractor’s
bidding price, which is obtained as a sum of the
estimated cost and the target profit, is higher than
that of the competitor due to cost estimation error,
then the contractor could not accept the order and
hence obtain no profit. In contrast, the contractor
would increase the chance of accepting the order if
the estimated cost is low due to cost estimation
error. In this case, however, the profit could be
below the contractor’s expectation because of being
over-budget, and he possibly suffers a loss on this
order.
Namely, for stable profit from EPC projects, the
contractor must determine the bidding price in
consideration of cost estimation accuracy and deficit
order probability. Cost estimation, however, is a
highly intellectual task of predicting the costs of
products or services to be provided in the future
393
Ishii N., Takano Y. and Muraki M..
A Two-step Bidding Price Decision Algorithm under Limited Man-Hours in EPC Projects.
DOI: 10.5220/0004418903930403
In Proceedings of the 3rd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2013),
pages 393-403
ISBN: 978-989-8565-69-3
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

based on the analysis of the client’s requirements
and his tacit knowledge. Thus, experienced and
skilled human resources, i.e., MH (Man-Hour), are
required for accurate cost estimation. Those
resources, however, are limited for any contractor.
For these reasons, it is important to realize
appropriate allocation of MH for cost estimation to
each order to maximize the profits under the
constraints on the volume of total MH. In addition,
contractors should consider the possibility of
realizing a loss due to cost estimation error and a
competitive relationship with bidders. For example,
the bidding price needs to be cut to some extent to
accept the order successfully under a severe
competitive environment; however, a low bidding
price would reduce profit, or even worse, would
create a large loss. Moreover, just a few deficit
orders would result in the significant reduction of
realized profits when the number of accepted orders
is limited. (Note, in this paper, that we refer to the
order creating an eventual loss as a deficit order.)
In this paper, we develop a two-step bidding
price decision algorithm in consideration of the cost
estimation accuracy and the deficit order probability
under limited MH in EPC projects. The algorithm
assumes that the costs are estimated at the same time
for all orders. At the first step, the algorithm
allocates MH for cost estimation to each order
according to the ranking of orders under the
constraints on the volume of total MH. The MH
allocation determines the cost estimation accuracy of
each order. At the second step, it determines the
bidding price for maximizing the expected profit
under the deficit order probability constraint.
We develop a mathematical model for simulating
competitive bidding. Through the numerical results
obtained by using this model, we show that the
bidding price decision in consideration of the cost
estimation accuracy and the deficit order probability
is essential for the contractor to make a stable profit
in EPC projects, and that our two-step bidding price
decision algorithm is effective for making such
bidding price decisions.
2 RELATED WORK
Among the research related to the bidding price
decision, there are order acceptance and project
selection problems.
Order acceptance is basically the problem of
making a decision to accept each order or not in
Make-To-Order (MTO) manufacturing (Kolisch,
2001), and its objective is to maximize profits with
capacity limitations. As literature surveys done by
Slotnick and Morton (2007), Herbots et al. (2007),
and Rom and Slotnick (2009) have shown, there
exists a variety of related research topics. Project
selection, on the other hand, is the problem of
creating a mix of projects from candidate projects to
help achieve an organization’s goals within its
resource constraints. Research and development
(R&D), information technology, and capital
budgeting are typical application fields of the project
selection. Researchers have applied various kinds of
methods to these problems (Dey, 2006; Medaglia et
al., 2007; Wang et al., 2009).
Most of the literature dealing with the order
acceptance and the project selection problems has
assumed that the contractor can select orders or
projects according to the contractor’s own criteria
and by the contractor’s own initiative. In
competitive bidding, however, the contractor
basically offers a bidding price and accepts the order
based on the client’s decision.
A variety of studies, such as bidding theory,
bidding model, and auction design, have been
conducted on competitive bidding (see Ballesteros-
Pérez et al., 2012 for detailed references). In
particular, a number of papers regarding the
competitive bidding strategy date back to Friedman
(1956), who presented a method to determine an
optimal bidding price based on the distribution of
the ratio of the bidding price to cost estimate.
However, little attention has been paid to profit
volatility risk, which cannot be ignored in EPC
projects. When, for instance, the number of accepted
orders is limited, the realized total profit from the
projects might be sharply lower than expected
because the profit is significantly affected by a few
deficit orders. Accordingly, the deficit order
probability should be considered in the bidding price
decision.
In addition to the profit volatility risk, we
consider the allocation of MH for cost estimation to
each order when making a decision on the bidding
because certain MH is necessary to estimate cost
accurately in EPC projects. Several papers have
analysed the problem of allocating scarce resources
in competitive bidding (see Rothkopf and Harstad,
1994 for detailed references). Among them,
Kortanek et al. (1973) considered sequential bidding
models where the obtained contracts require the use
of restricted resources, such as production capacity,
at the time of actual production. Ishii et al. (2012)
develop a mathematical model where bidding prices
are determined in consideration of the MH allocation
for cost estimation to maximize the expected profit
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
394
from the projects. Their model assumes that the
contractor has no preference orders for bidding,
although the contractor usually ranks the orders
according to the multi-criteria, such as technical
feasibility, relationship with clients, and so on, in
addition to the expected profits.
Regarding cost estimation accuracy, various
types of research have been performed. Oberlender
and Trost (2001) studied determinants of cost
estimation accuracy and developed a system for
predicting cost estimation accuracy. Bertisen and
Davis (2008) analysed costs of 63 projects and
evaluated the accuracy of capital cost estimation
statistically. In addition, several researchers have
studied cost estimation methods and their accuracy.
For example, Towler and Sinnott (2008) studied
relations among cost estimation methods, cost
estimation data, and their accuracy in the field of
plant engineering. More crucially, they suggested
that the cost estimation accuracy is positively
correlated with the volume of MH for cost
estimation.
In EPC projects, the bidding price decision
affects the expected profit and the deficit order
probability. Since the bidding price is determined
based on the project cost estimated before starting
the project, cost estimation accuracy is clearly a
major factor to lead an EPC project to a successful
conclusion. Nevertheless, as stated above, few
studies have ever attempted to analyse the bidding
price decision problem in terms of cost estimation
accuracy and deficit order probability under limited
MH in EPC projects.
3 FEATURES OF THE BIDDING
PRICE DECISION PROBLEM
IN EPC PROJECT
There are several ways to select a contractor from
bidders in competitive bidding (Steel, 2004; Elfving
et al., 2005; Helmus, 2008; Wang et al., 2009). In a
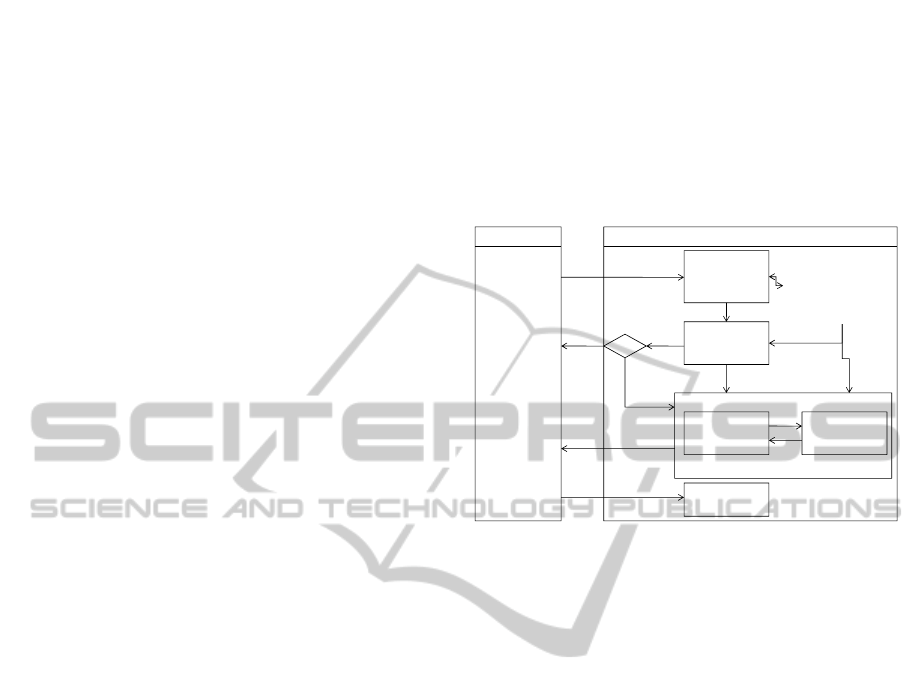
generic competitive bidding process shown in Figure
1 (Ishii and Muraki, 2011), the client prepares a
Request For Proposal (RFP) and invites several
potential contractors to the bidding. The contractor
first carries out the preliminary evaluation followed
by the bid or no-bid decision. In the preliminary
evaluation, the contractor evaluates the RFP and
estimates the preliminary cost based on limited
information, such as the order information provided
by the RFP and the past project data of the
contractor. In the bid or no-bid decision, the
contractor evaluates the order from the viewpoints of
profitability, technical feasibility and so on, and
makes a decision whether to bid or not. If the
contractor decides to place the bid, he then starts the
bidding price decision process, that is, he estimates
the cost more accurately and determines the bidding
price. At the end of the competitive bidding, the
client assesses the proposals offered by contractors
and selects one contractor as a successful bidder.
Figure 1: An overview of contractor’s activities of
competitive bidding.
The preliminary evaluation and bid or no-bid
decision are usually made by senior managers based
on the RFP, past project data, competitive
environment, target profit rate, and so on.
As shown in Figure 1, the bidding price decision,
for which this paper develops an algorithm in
Section 4.2, is made based on order information,
such as estimated cost, target profit rate, and
competitive environment, so that the contractor can
accept profit-making orders successfully. As Ishii et
al. (2012) pointed out, since the contractor must
determine the bidding price using the limited
information above, he should consider the following
features of the competitive bidding.
The first feature is relevant to the accuracy of
cost estimation. The bidding price is basically
determined by adding the target profit to the
estimated cost. However, the contractor cannot
estimate the precise cost in the process of
determining the bidding price because of limited
information and restricted time. Thus the bidding
price, which is affected by estimation errors, has a
probability distribution. We define the cost
estimation accuracy as the standard deviation of the
estimated cost or the bidding price depending on the
context. A lower deviation indicates a higher
accuracy.
The bidding price with the lower cost estimation
- Preparation of
Request For
Quotation
(RFQ)
-Bid
Evaluation
- Contractor
Selection
Preliminary
Evaluation
Bid or No-Bid
Decision
Bidding Price
Decision
Declination
of bid
- Past project data
- Competitive
environment
- Target total expected
orders
- Target profit rate
Preliminary cost
Bid
No-Bid
Bid reply
Accepted
Order
Contractor selection
result
Preliminary cost
Contractor (Bidder)
Client
Request For Proposal
(RFP)
Preparation of
Proposal &
Cost Estimation
Cost Estimation
MH
Estimated
Cost
ATwo-stepBiddingPriceDecisionAlgorithmunderLimitedMan-HoursinEPCProjects
395
accuracy is likely to be accepted as the deficit order,
from which the contractor suffers an eventual loss.
The bidding price with the low accuracy also has a
tendency to be very high compared to the other;
however, the chance of the order being accepted
becomes smaller as the bidding price increases under
a competitive environment where many competitors
would offer low bidding prices. Based on these
observations, it can be seen that consideration of the
cost estimation accuracy and deficit order
probability is essential for the contractor to make a
stable profit in EPC projects, and the bidding price
decision process needs to include all these factors.
The second feature is the MH allocation for cost
estimation. Cost estimation is a series of activities
where experienced engineers analyse requirements
of clients, thus the MH for cost estimation affects its
accuracy significantly. However, although the
contractor often has more than one order at the same
time, the number of MH of experienced engineers is
limited. Namely, the contractor needs to allocate
MH to each order effectively. Since the bidding
conditions are different in each order, the contractor
needs to prioritize orders and allocate more MH to
the potential orders to improve the expected profits.
The third feature is the effectiveness of adjusting
the bidding price. The contractor’s profit increases
as the bidding price rises. On the other hand, the
probability of accepting the order increases as the
bidding price goes down. This is because the
contractor can basically accept the order when the
contractor’s bidding price is lower than that of the
competitor. However, the contractor would accept
the deficit order when the bidding price is very low.
Namely, we can see that there is a bidding price that
maximizes the contractor’s expected profit under a
competitive environment.
Based on the above observations, we introduce a
parameter for adjusting the bidding price in view of
the cost estimation accuracy of one’s own company
and that of a competitor’s, as well as the deficit
order probability.
4 A BIDDING PRICE DECISION
PROCESS MODEL
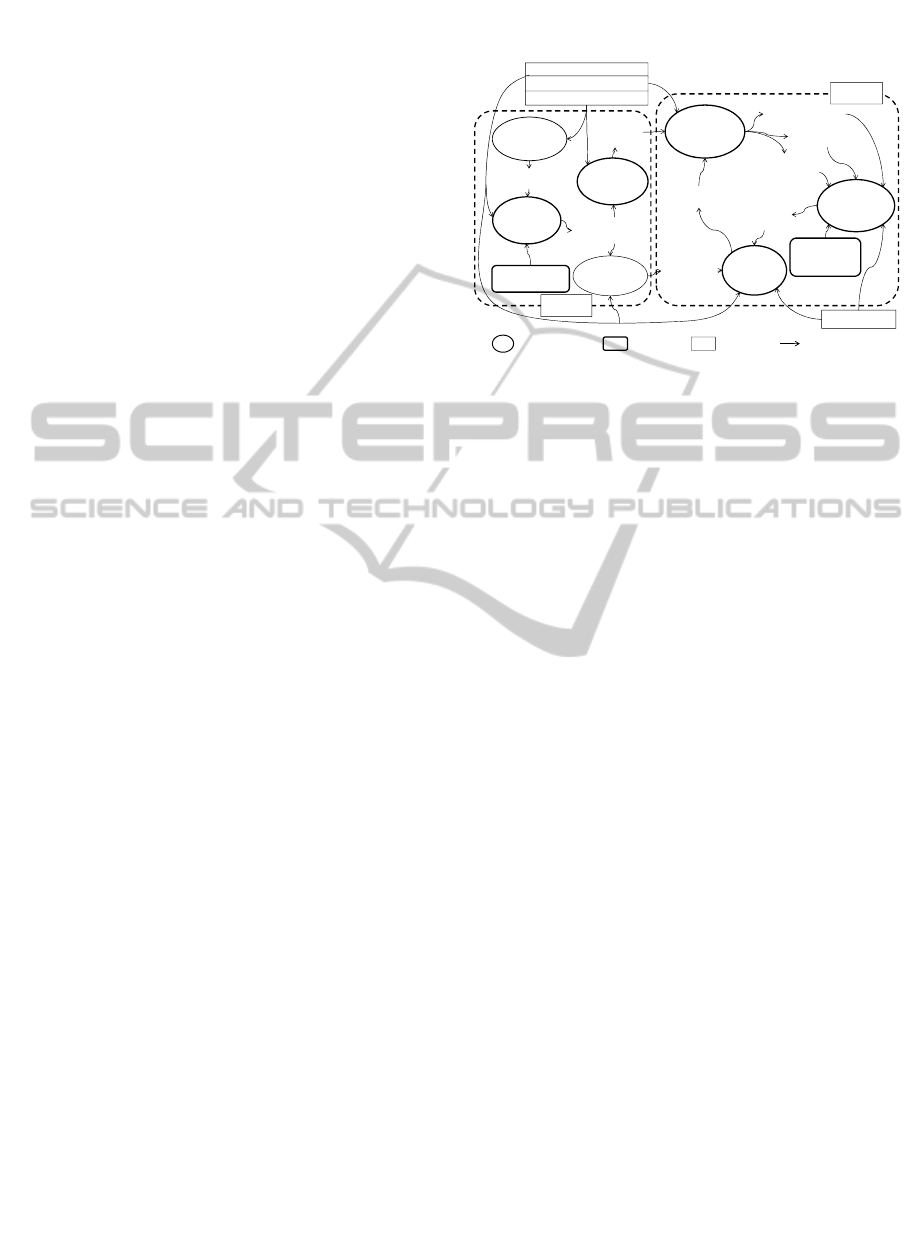
Figure 2 shows a bidding price decision process
model (Ishii et al., 2012), which represents
fundamental factors and their interactive processes,
to determine the bidding price in EPC projects based
on the observations in the previous section. The
model consists of three kinds of factors, i.e.,
decision processes, constraints, and given
conditions.
Figure 2: A bidding price decision process model in EPC
projects.
The model enables us to evaluate the expected
orders, the expected profits, and the deficit order
probability, based on the bidding price, the cost
estimation accuracy, and the information on
competitive environment. The bidding price is
determined based on the estimated cost, the target
profit rate, and the risk parameter for adjusting the
bidding price. The estimated cost and the cost
estimation accuracy are both determined depending
on the MH allocated to each order for cost
estimation. The MH allocation is determined
according to the ranking of orders provided by the
pre-evaluation of orders processed under the total
MH constraint as shown in Figure 2.
4.1 A Mathematical Model on Bidding
Price Decision
4.1.1 Evaluation of Cost Estimation
Accuracy
Since cost estimation requires a detailed analysis
conducted by experienced engineers, it can be seen
that the MH for cost estimation significantly affects
the cost estimation accuracy. In fact, Towler and
Sinnott (2008) suggest that the cost estimation
accuracy is positively correlated with the volume of
MH for cost estimation. It is also clear that the
marginal rate of cost estimation accuracy approaches
zero according to the increase of the volume of MH.
Thus, in this paper, we define the cost estimation
accuracy (σ) as the function of the MH for cost
estimation per order (PMH) based on the logistic
curve (Ishii and Muraki, 2011) as follows:
:Decision process :Constraint :Condition :Information flow
MH
allocation
for cost
estimation
Pre
evaluation
of orders
Bidding
price
decision
Setting
risk
parameter
Evaluation
of bidding
price
Deficit order
probability
Expected orders
Expected profit
Bidding price
Cost
Estimation
Evaluation
of cost
estimation
accuracy
Cost estimation
MH of each order
Estimated
cost
Risk
Parameter
Ranking of orders
Cost
estimation
accuracy
Target profit rate
Total MH for
cost estimation
Upper limit of
deficit order
probability
Preliminary cost
Past project data
Competitive environment
Step One
Step Two
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
396

})(/{)(
maxminmaxmaxmin
PMHC
ePMH
(PMH > 0.0) (1)
where σ
min
and σ
max
are the minimum and the
maximum value of the standard deviation of the
bidding price, and C is a parameter of the logistic
curve. In practice, the contractor could determine
these parameters from past project data.
4.1.2 Evaluation of Bidding Price
In the model, we consider n contractors (k=1,2,…,n)
and the bidding for L orders (i=1,2,…,L).
Particularly, k=1 represents one’s own company,
and k>=2 are its competitors. In the model, based on
standard order cost (STD), each contractor (k) sets a
tentative bidding price (TBP) of the order (i) in
consideration of the relative cost difference from
STD (RC) and target profit rate (e_profit) as follows:
(1 ) (1 _ )
iiii
ki k kk
TBP STD RC e profit rp
(2)
where TBP can be adjusted by changing the value of
risk parameter (rp). If there is no difference in cost-
competitiveness among contractors, RC is set to 0.
The expected volume of order (i) in one’s own
company (k=1) is as follows:
(3)
where
),,(
ii
k
i
k
kk
TBPxp
is the probability density
function of the bidding price (
i
k
x
) of the contractor
(k) for order (i), and its average value and standard
deviation are
i
k
TBP
and
i
k
, respectively. As shown
in Eq. (3), the expected order is the average value of
one’s own bidding price falling below those of all
other contractors (k>=2).
As shown in Eq. (4), the expected profit is the
average excess of the bidding price over the standard
order cost with the relative cost difference (STDR)
as defined in Eq. (5).
(4)
(1 )
ii
ki k
STDR STD RC
(5)
In addition, as shown in Eq. (6), the deficit
order probability is the probability of accepting the
order whose bidding price is lower than STDR.
n
k
x
ii
k
i
k
i
k
i
kk
STDR
iii
i
i
dxdxTBPxpTBPxp
2
1
0
1111
1
1
),,(),,(
(6)
We also assume that the data used in the above
equations, such as the number of competitors (n-1),
standard order cost (STD), relative cost difference
over STD (RC), probability density function of
bidding price (p
k
), and so on, can be provided from
RFP, past project data, several departments of the
contractor, and published data. For example, STD
can be specified in reference to the preliminary cost,
which is estimated by scaling it from the cost data of
past projects, which used similar technology
(Kerzner, 2009). Although a project is a temporary
endeavour undertaken to create a unique product,
similar parts can be found in functional units of past
projects. Accordingly, even if the cost data of
similar projects are not available, the preliminary
cost estimate can be made by breaking down the
project into functional units, and adding up the cost
data of similar functional units in past projects. The
cost data, the number of competitors, and so on, can
also be estimated based on published data in many
industries. For example, magazines related to the
EPC business, such as Chemical Engineering,
Hydrocarbon Processing, publish plant cost indexes,
cost engineering data, EPC project news and surveys,
periodically.
4.2 A Two-step Bidding Price Decision
Algorithm
In this section, we develop a two-step algorithm for
bidding price decision. As shown in Figure 2, this
algorithm determines the allocation of MH for cost
estimation according to the ranking of orders at the
first step, and searches the value of rp for
maximizing the expected profit of each order under
the deficit order probability constraint at the second
step.
4.2.1 Step One: Ranking of Orders and MH
Allocation
There are several procedures to rank orders. For
example, pair-wise comparisons, scoring models,
and analytical hierarchy process (AHP) are
commonly used (Martino, 1995).
In this paper, we shall rank orders based only on
the expected profit so as to assess the effectiveness
of our algorithm from the perspective of profits.
Specifically, we define the ranking score (Score) of
the order (i) as the expected profit based on the
tentative bidding price (TBPF) estimated for the
ranking at rp =1 as follows:
1
1
2
(, , )
i
n
iiiii
i
kk k k k
TBPF
k
Score TBPF p x TBPF dx
(7)
(
1
)(
1
_)
iii
ki k k
TBPF STD RC e
p
ro
f
it
(8)
ii
n
k
x
iii
k
iiii
dxdxTBPxpTBPxpx
k
i
kkk 1
1
1111
0
2
1
),,(),,(
ii
n
k
x
iii
k
iiiii
dxdxTBPxpTBPxpSTDRx
k
i
kkk 1
1
1111
0
2
11
),,(),,()(
ATwo-stepBiddingPriceDecisionAlgorithmunderLimitedMan-HoursinEPCProjects
397

Note that we can modify the ranking score in
consideration of multiple criteria besides the
expected profit, such as technical feasibility,
relationship with clients, and so on.
In the following MH allocation procedure, the
order with the high Score is ranked high because
such an order is expected to generate a large profit.
As described in the procedure below, we
consider three grades of accuracy, A (high
accuracy), B (average), and C (low accuracy), and
we assign one of them to each order. The expected
profit increases according to the increase of cost
estimation accuracy, and hence, the following
procedure results in the grade of high accuracy to
high-ranking orders, and the grade of low accuracy
to low-ranking orders in view of the allowable total
MH.
MH Allocation Procedure
Step 0 [Parameter Setting]: Set the range of
allowable total MH for cost estimation, and set
the accuracy level from (σ
min
, σ
max
) to each
grade; A (high accuracy), B (average), and C
(low accuracy).
Step 1 [Initial MH Allocation]: Set all the orders to
grade B, and allocate the corresponding MH
for cost estimation to each order based on Eq.
(1).
Step 2 [Termination Condition]: Calculate the total
MH required (TMR) by summing up all the
MH allocated to each order. If TMR is within
the range of allowable total MH, stop the
procedure with the current MH allocation. If
TMR is above the allowable range, go to Step
3. If TMR is below the allowable range, go to
Step 4.
Step 3 [Downgrading]: Choose the lowest-ranked
one from grade B orders, and set it to grade C.
If the grades of orders are all C, stop the
procedure with the current MH allocation.
Otherwise, go to Step 5.
Step 4 [Upgrading]: Choose the highest-ranked
one from grade B orders, and set it to grade A.
If the grades of orders are all A, stop the
procedure with the current MH allocation.
Otherwise, go to Step 5.
Step 5 [MH Reallocation]: According to the given
grades, reallocate the MH for cost estimation to
each order based on Eq. (1). Return to Step 2.
4.2.2 Step Two: Searching Risk Parameter
Value for Profit Maximization
Given the MH allocation determined by the
procedure described above, we search the value of
rp by solving the following optimization problem:
Maximize
1
111111 1
0
1
2
()(,,) (,,)
i
n
L
iiiii iiiii
kk k k k
x
i
k
x
STDR p x TBP p x TBP dx dx
(9)
subject to
(1 ) (1 _ )
iiii
i
kkkk
TBP STD RC e profit rp
(i=1,2,…,L; k=1,2,…,n)
(10)
1
1
11 1 1 1
0
2
(, , ) ( , , )
i
i
n
STDR
iii i iiii
kk k k k i
x
k
p
x TBP p x TBP dx dx rprob
i=1,2,….L)
(11)
where
i
rprob is the upper limit of the deficit order
probability of the order (i).
In the above optimization problem, the objective
is to maximize the total expected profit from orders.
Eq. (10) defines TBP, and Eq. (11) is the upper limit
constraint of the deficit order probability. Note that
Eq. (10) can be eliminated from the problem by
substituting Eq. (10) into Eq. (9) and (11).
Moreover, the problem can be separated into L
problems (i=1,2,…,L). As a result, rp of one’s own
company (k=1) is the single decision variable of
each problem. In this paper, we use a simple
iterative algorithm to search for a solution by
gradually eliminating search space.
Given the MH allocation for cost estimation and
the value of rp, the final bidding price is determined
as follows:
11
(1 _ )
ii
i
N
ET e profit rp
(12)
where NET, as shown in Figure 2, is the estimated
cost that is calculated by the allocated MH after the
bid or no-bid decision.
5 NUMERICAL EXAMPLES
In this section, we analyse and discuss the
performance of the two-step bidding price decision
algorithm in EPC projects based on the numerical
examples from the following perspectives: relations
between cost estimation accuracy and expected
profit, effectiveness of bidding price adjustment, and
effect of the upper limit constraint of the deficit
order probability.
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
398

5.1 Problem Setting
5.1.1 Setting of Cases
In this paper, we use the cases shown in Table 1 for
numerical examples. Cases 0 and 1 are set to show
the effectiveness of bidding price adjustment by the
risk parameter. Cases 2 and 3 are set to show the
effects of the competitors’ cost estimation accuracy
on the expected profit and deficit order probability
of one’s own company. The competitors’ cost
estimation accuracy
i
k
(k>=2) in Table 1 are set
based on the expected accuracy for bidding
(Oberlender, 2000).
Table 1: Cases for numerical examples.
Case
i
rp
1
i
k
(k>=2)
Case 0 1.0 8% of STD
i
Case 1 To be searched 8% of STD
i
Case 2 To be searched 6% of STD
i
Case 3 To be searched 10% of STD
i
Table 2: Conditions of orders. (NBR: number of bidders).
We set other parameter values through all the
cases as follows:
0.1
i
k
rp
(k >= 2),
0.0
i
k
RC
(k >=
1), rprob
i
=1.0, and
1.0_
i
k
profite
. We set rprob
i
to 1.0 (100%) to maximize the expected profit
without the upper limit constraint of the deficit order
probability. The effect of the constraint is shown in
section 5.2.4.
Note that the value of
i
1
is determined by Eq.
(1) and the allocated MH. We suppose that the
bidding price follows a normal distribution.
Furthermore, we consider four conditions for the
range of allowable total MH for cost estimation, i.e.,
(A) 70-80, (B) 80-90, (C) 90-100, and (D) 100-110
[M MH].
5.1.2 Setting of Orders
In this paper, we assume a midsize EPC contractor
in the chemical plant engineering business, and
consider the conditions of 16 orders in each case as
shown in Table 2.
Regarding the cost estimation accuracy of one’s own
company (see Eq. (1)), we set C to 0.25*100/STD
i
,
and σ
min
and σ
max
to 0.5% and 30% of STD
i
,
respectively. In addition, we set the cost estimation
accuracy level to 5% of STD
i
for grade A, 8% of
STD
i
for grade B, and 15% of STD
i
for grade C
when performing the MH allocation procedure.
5.2 Results of Numerical Calculations
5.2.1 Cost Estimation Accuracy
and Expected Profit
As shown in Table 3, the significant difference in
the total expected profits is caused by the total MH
for cost estimation for all the cases. For example, the
expected profits in Case 0.A (70-80 [M MH]), Case
0.B (80-90 [M MH]), Case 0.C (90-100 [M MH]),
and Case 0.D (100-110 [M MH]) are 28.6, 46.3,
51.7, and 61.5 [MM$], respectively.
Since the cost estimation accuracy depends on
the MH for cost estimation as shown in Eq. (1), the
results indicate that the cost estimation accuracy
affects the expected profit significantly. Namely, the
contractor can expect a higher profit by increasing
the cost estimation accuracy in EPC projects.
However, there is usually a limit to the available
MH for cost estimation. Thus we can conclude that
an effective mechanism to allocate the MH for cost
estimation to each order under the constraint of the
volume of total MH is necessary in the bidding price
decision process.
5.2.2 Effectiveness of Bidding Price
Adjustment by Risk Parameter
Based on the results of Case 0 and Case 1, we
analyse the effect of the bidding price adjustment on
the expected profit. The bidding price is adjusted by
rp to attain the maximum expected profits in Case 1,
and the value of rp is fixed in Case 0.
As shown in Table 3, there is a significant
difference in the expected profits between Case 0
and Case 1. For example, the total expected profits
in Case 0.A and Case 1.A are 28.6 and 53.3 [MM$],
respectively. The bidding price adjustment also
affects the expected orders and profit rate. In Case
0.A, for instance, the expected orders and profits are
1858.2 and 28.6; therefore the expected profit rate is
1.54%. In contrast, in Case 1.A, the expected orders
and profits are 1141.6 and 53.3; therefore the
expected profit rate is 4.67%, which is about three
times as high as that in Case 0.A.
Order id (i) 1 2 3 4 5 6 7 8
STD
i
100.0 200.0 300.0
N
BR (n) 2 3 4 2 3 4 2 3
Order id (i) 9 10 11 12 13 14 15 16
STD
i
400.0 500.0 600.0
N
BR (n) 4 2 3 4 3 4 3 4
ATwo-stepBiddingPriceDecisionAlgorithmunderLimitedMan-HoursinEPCProjects
399
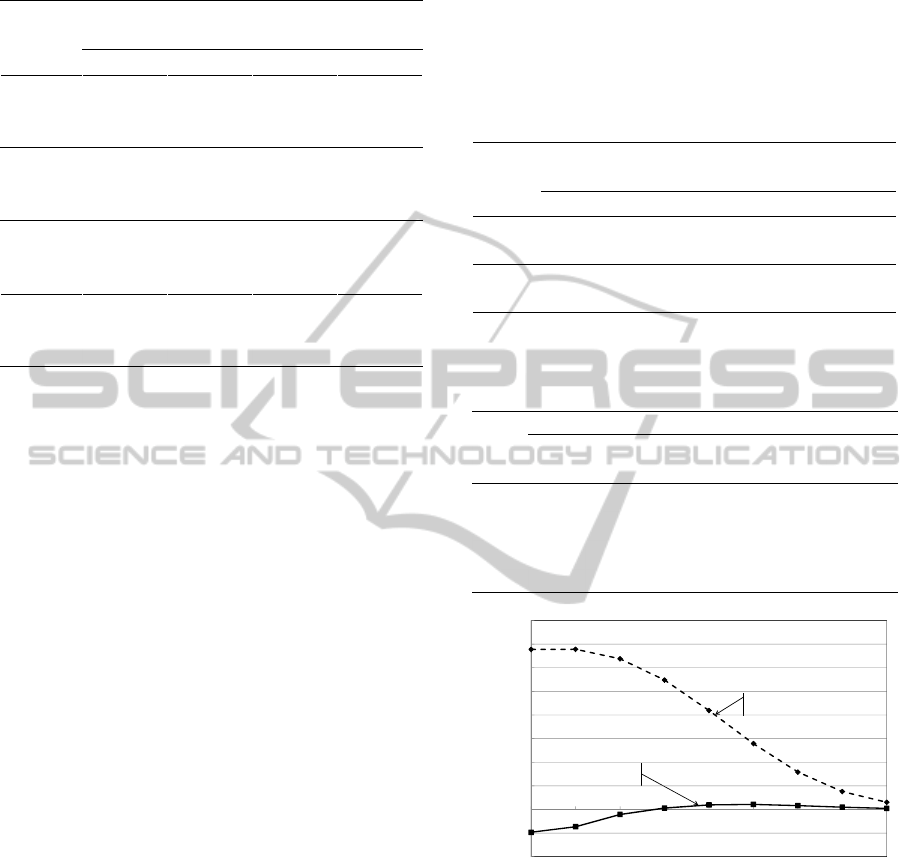
Table 3: Expected orders (EO; Eq. (3)) and Expected
profits (EP; Eq. (4)).
[MM$]
The Range of Allowable Total MH for Cost
Estimation [M MH]
70-80 80-90 90-100 100-110
Case 0 Case 0.A Case 0.B Case 0.C Case 0.D
EO 1858.2 1817.9 1823.3 1809.0
EP 28.6 46.3 51.7 61.5
Case 1 Case 1.A Case 1.B Case 1.C Case 1.D
EO 1141.6 1238.1 1269.5 1357.2
EP 53.3 56.4 60.9 69.1
Case 2 Case 2.A Case 2.B Case 2.C Case 2.D
EO 1275.2 1395.2 1437.6 1547.3
EP 48.0 51.3 56.3 65.5
Case 3 Case 3.A Case 3.B Case 3.C Case 3.D
EO 1061.6 1143.7 1168.1 1236.6
EP 60.2 63.5 67.5 74.8
The deficit order probability is significantly
decreased by the adjustment of the bidding price as
shown in Table 4. For example, the range of deficit
order probability in the orders is between 11.0% and
25.8% in Case 0.A, and between 0.777% and 5.81%
in Case 1.A. In Case 0.A, the MH allocation
procedure results in the low cost estimation accuracy
level (grade C) to the orders 2, 3, 6, and 9, and these
orders result in negative earnings as shown in Table
5. However, in Case 1.A, the bidding price
adjustment decreases the deficit order probabilities
of these orders and improves the expected profits.
Table 6 shows the effects of the competitors’
cost estimation accuracy on the value of rp, the
expected profit, and the deficit order probability of
each order. Note that the competitors’ cost
estimation accuracy of Case 2.B, Case 1.B, and Case
3.B is 6%, 8%, and 10% of
i
STD
, respectively. As
shown in Table 6, as the competitors’ cost
estimation accuracy increases, the value of rp
searched for by the algorithm decreases and the
deficit order probability of each order increases.
This is because the high accuracy of the
competitors’ cost estimation reduces the chance of
accepting the orders at high prices, and
consequently, a small rp is chosen to accept such
orders.
Figure 3 depicts the relation of the expected
order and profit of the order id 10 with the value of
rp in Case 1.B. In addition, Figure 4 depicts the
relation of the expected profits of the order id 10
with the value of rp in Case 1.B and Case 1.C, each
of which corresponds to a different range of
allowable total MH. Figure 3 shows that the
expected order decreases as the value of rp
increases. However, it is found from Figures 3 and 4
that there is a value of rp that attains the maximum
expected profit. Furthermore, Figure 4 tells us the
higher cost estimation accuracy, i.e., more MH for
cost estimation, makes the maximum expected profit
higher.
Table 4: Range of deficit order probability (Eq. (6)) [%].
The range of allowable total MH for cost
estimation [M MH]
70-80 80-90 90-100 100-110
Case 0 Case 0.A Case 0.B Case 0.C Case 0.D
11.0-25.8 11.0-12.1 3.20-12.1 2.98-12.1
Case 1 Case 1.A Case 1.B Case 1.C Case 1.D
0.777-5.81 4.33-5.81 1.77-5.81 1.77-5.81
Table 5: Effectiveness of bidding price adjustment by risk
parameter. (EP: Expected Profit, DOP: Deficit Order
Probability).
Order
id (i)
Case 0.A Case 1.A
i
rp
1
EP
[MM$]
DOP
[%]
i
rp
1
EP
[MM$]
DOP
[%]
2 1.0 -1.92 25.8 1.20 0.155 2.32
3 1.0 -2.25 25.2 1.26 0.0290 0.777
6 1.0 -4.50 25.2 1.26 0.0581 0.777
9 1.0 -6.75 25.2 1.26 0.0871 0.777
Figure 3: Relations among expected order, expected profit,
and risk parameter. (Case 1.B; Order id = 10).
We can see that the higher cost estimation
accuracy reduces the chance of accepting orders at
very low price and thus increases the expected
profit. However, the higher cost estimation accuracy
also reduces chance of accepting profitable orders
when the value of rp is high. In Figure 4, for
instance, the expected profit in Case 1.C is lower
than that in Case 1.B when rp is 1.15 or more.
Expected order
Expected profit
-100.0
-50.0
0.0
50.0
100.0
150.0
200.0
250.0
300.0
350.0
400.0
0.8 0.85 0.9 0.95 1 1.05 1.1 1.15 1.2
Expected order and profit [MM$]
Risk parameter (rp)
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
400

Table 6: Bidding price adjustment with different competitors’ accuracy (80-90 [M MH]). (EP: Expected Profit, DOP:
Deficit Order Probability).
Order id
(i)
Case 2.B Case 1.B Case 3.B
i
rp
1
EP
[MM$]
DOP
[%]
i
rp
1
EP
[MM$]
DOP
[%]
i
rp
1
EP
[MM$]
DOP
[%]
1 1.026 2.27 7.12 1.035 2.70 5.44 1.045 3.14 4.09
2 1.026 0.916 6.99 1.030 0.983 5.81 1.035 1.09 4.73
3 1.035 0.444 5.44 1.040 0.418 4.32 1.042 0.436 3.63
4 1.026 4.54 7.12 1.035 5.40 5.44 1.045 6.29 4.09
5 1.026 1.83 6.99 1.030 1.97 5.81 1.035 2.18 4.73
6 1.035 0.888 5.44 1.040 0.836 4.32 1.042 0.872 3.63
7 1.026 6.81 7.12 1.035 8.11 5.44 1.045 9.43 4.09
8 1.026 2.75 6.99 1.030 2.95 5.81 1.035 3.27 4.73
9 1.035 1.33 5.44 1.040 1.25 4.32 1.042 1.31 3.63
10 1.026 9.08 7.06 1.035 10.8 5.54 1.044 12.6 4.13
11 1.026 3.67 6.99 1.030 3.93 5.81 1.035 4.36 4.73
12 1.035 1.78 5.44 1.040 1.67 4.32 1.042 1.74 3.63
13 1.026 4.58 6.99 1.030 4.91 5.81 1.035 5.45 4.73
14 1.035 2.22 5.44 1.040 2.09 4.32 1.042 2.18 3.63
15 1.026 5.50 6.99 1.030 5.90 5.81 1.035 6.54 4.73
16 1.035 2.66 5.44 1.040 2.51 4.32 1.042 2.62 3.63
Figure 4: Relations among expected profit, total MH for
cost estimation, and risk parameter. (Case 1.B, Order id
=10, Total MH for cost estimation: 80-90 [M MH]; and
Case 1.C, Order id =10, Total MH for cost estimation 90-
100 [M MH]).
5.2.3 Effect of the Number of Bidders
Figure 5 depicts the relation of the expected profit
and the deficit order probability of the order id 1, 2
and 3 in Cases 2.B, 1.B, and 3.B. Note that the
number of bidders is set to two, three, and four for
the order id 1, 2 and 3, respectively. Also, in Cases
2.B, 1.B, and 3.B, the competitors’ cost estimation
accuracy is set to 6%, 8%, and 10% of STD
i
. As
shown in Figure 5, the effect of the competitors’ cost
estimation accuracy on the expected profit and the
deficit order probability becomes smaller as the
number of bidders increases.
Figure 5: Relations among expected profits and deficit
order probability. (Case 2B, 1B, and 3B; Order id 1, 2, and
3) (CCEA: Competitors’ Cost Estimation Accuracy).
For instance, in Order id 1, i.e., when the number
of bidders is two, the difference of the expected
profit between Case 3.B and Case 2.B is 0.87
[MM$]. In contrast, in Order id 3, i.e., when the
number of bidders is four, the difference of the
expected profit between Case 3.B and Case 2.B is
0.008 [MM$]. The difference in the deficit order
probability between Case 3.B and Case 2.B is also
reduced from 3.03 [%] (in the case of Order id 1) to
1.81 [%] (in the case of Order id 3).
High degree of competition significantly reduces
the chance of accepting orders at high prices as well
as at low prices regardless of the competitors’ cost
estimation accuracy. Consequently, it reduces the
-60.0
-50.0
-40.0
-30.0
-20.0
-10.0
0.0
10.0
20.0
0.8 0.85 0.9 0.95 1 1.05 1.1 1.15 1.2
Expected profit [MM$]
Risk
p
aramete
r
(rp)
Total MH for cost estimation: 90-100 [M MH]
Case 1.C, Order id =10
Cost estimation accuracy (σ): 21 [MM$]
Total MH for cost estimation : 80-90 [M MH]
Case 1.B, Order id =10
Cost estimation accuracy (σ): 35.2 [MM$]
0
0.5
1
1.5
2
2.5
3
3.5
3.04.05.06.07.08.0
Expected profit [MM$]
Deficit order probability [%]
Order id 1
(No of bidders: 2)
Order id 2
(No of bidders: 3)
Order id 3
(No of bidders: 4)
Case 2.B
CCEA: 6% of STD
i
Case 1.B
CCEA: 8% of STD
i
Case 3.B
CCEA: 10% of STD
i
ATwo-stepBiddingPriceDecisionAlgorithmunderLimitedMan-HoursinEPCProjects
401

effect of the competitors’ cost estimation accuracy
on the expected profit and the deficit order
probability.
5.2.4 Effect of Upper Limit Constraint
of the Deficit Order Probability
We examine how the upper limit constraint of the
deficit order probability shown in Eq. (11) affects
the expected profit. Figure 6 depicts the relation of
the upper limit of the deficit order probability and
the total expected profit in Case 1. As explained in
Sections 2 and 3, the risk of unexpected loss from
the deficit orders should be avoided especially when
only a small number of orders can be accepted. As
shown in Figure 6, the small upper limit of the
deficit order probability decreases the total expected
profit; however, it is found that the deficit order
probability can be reduced from 5.0% to 1.0% at the
expense of the total expected profits of 10 to 15
[MM$].
Bidding for a large-scale EPC project involves a
substantial risk. Our framework developed for EPC
projects will certainly be helpful for any contractor
to avoid large deficit from accepted orders.
Figure 6: Relations among expected profits, total MH for
cost estimation, and upper limit of deficit order probability
(Case 1).
6 CONCLUSIONS
In this paper, we develop a two-step bidding price
decision algorithm under limited MH in EPC
projects. The algorithm allocates MH for cost
estimation to each order under the limited volume of
MH, and then determines the bidding price to
maximize the expected profit under the deficit order
probability constraint.
We develop a mathematical model for simulating
competitive bidding. Through the numerical results
obtained by using the model, we show that the
bidding price decision in consideration of the cost
estimation accuracy and the deficit order probability
is essential for the contractor to make a stable profit
in EPC projects, and that the two-step bidding price
decision algorithm developed in this paper is
effective for making such bidding price decisions.
There are several issues which require further
research. For example, the procedure for modifying
the MH allocation and adjusting the bidding price
dynamically in response to each order arrival is
required for practical application. In addition, our
two-step algorithm does not consider the duration
for estimating cost and for carrying out the project.
The MH allocation procedure should consider the
time cost-trade-off and its implication on the cost
estimation accuracy and profit. It is also necessary to
compare the performance of our procedure with
other project scheduling methods dealing with the
optimum allocation of resources for multiple
projects.
ACKNOWLEDGEMENTS
The authors would like to thank all the reviewers for
their valuable comments.
REFERENCES
Ballesteros-Pérez, P., González-Cruz, M
a
. C., Cañavate-
Grimal, a., 2012. on Competitive Bidding: Scoring and
Position Probability Graphs. International Journal of
Project Management, in Press.
Bertisen, J., Davis, G. a., 2008. Bias and Error in Mine
Project Capital Cost Estimation. the Engineering
Economist. 53, 118-139.
Dey, P. K., 2006. Integrated Project Evaluation and
Selection using Multiple-Attribute Decision-Making
Technique. International Journal of Production
Economics. 103, 90-103.
Elfving, J. a., Tommelein, I. D., Ballard, G., 2005.
Consequences of Competitive Bidding in Project-
based Production. Journal of Purchasing & Supply
Management. 11, 173-181.
Friedman, L., 1956. a Competitive-Bidding Strategy. the
Journal of the Operations Research Society of
America. 4, 104-112.
Helmus, F. P., 2008. Process Plant Design: Project
Management from Inquiry to Acceptance. Wiley-
VCH, Weinheim.
Herbots, J., Herroelen, W., Leus, R., 2007. Dynamic Order
Acceptance and Capacity Planning on a Single
Bottleneck Resource. Naval Research Logistics.
54, 874-889.
Total MH for cost estimation: 100-110 [M MH]
Total MH for cost estimation: 90-100 [M MH]
Total MH for cost estimation: 80-90 [M MH]
Total MH for cost estimation: 70-80 [M MH]
30.0
40.0
50.0
60.0
70.0
80.0
1.0% 2.0% 3.0% 4.0% 5.0% 6.0% 7.0% 8.0% 9.0% 10.0%
Expected profit [MM$]
Upper limit of deficit order probability
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
402

Ishii, N., Muraki, M., 2011. a Strategy for Accepting
Orders in ETO Manufacturing with Competitive
Bidding. Proceedings of 1st International Conference
on Simulation and Modeling Methodologies,
Technologies and Applications (SIMULTECH 2011).
380-385.
Ishii, N., Takano, Y., Muraki, M., 2012. Decision on
Bidding Prices under Limited Man-Hours in EPC
Projects. Submitted to Computers & Industrial
Engineering.
Jinru, Z., 2011. Study on Cost Management under EPC
General Contracting Model. Advanced Materials
Research, 181/182, 49-53.
Kerzner, H., 2009. Project Management: a Systems
Approach to Planning, Scheduling, and Controlling.
John Wiley & Sons, New Jersey.
Kolisch, R., 2001. Make-to-Order Assembly Management.
Springer-Verlag, Berlin.
Kortanek, K. O., Soden, J. V., Sodaro, D., 1973. Profit
Analyses and Sequential Bid Pricing Models.
Management Science, 20, 396-417.
Martino, J. P., 1995. Research and Development Project
Selection. John Wiley & Sons, New York.
Medaglia, a. L., Graves, S. B., Ringuest, J. L., 2007. a
Multiobjective Evolutionary Approach for Linearly
Constrained Project Selection under Uncertainty.
European Journal of Operational Research. 179, 869-
894.
Oberlender, G. D., 2000. Project Management for
Engineering and Construction. Mcgraw-Hill, New
York.
Oberlender, G. D., Trost, S. M., 2001. Predicting
Accuracy of Early Cost Estimates based on Estimate
Quality. Journal of Construction Engineering and
Management. May/June, 173-182.
Ranjan, M., 2009. EPC: a Better Approach, Chemical
Engineering World. 44, 7, 46-49.
Rom, W. O., Slotnick, S. a., 2009. Order Acceptance using
Genetic Algorithms. Computers & Operations
Research. 36, 1758-1767.
Rothkopf, M. H., Harstad R. M., 1994. Modeling
Competitive Bidding: a Critical Essay. Management
Science. 40, 364-384.
Slotnick, S., Morton, T. E., 2007. Order Acceptance with
Weighted Tardiness. Computers & Operations
Research. 34, 3029-3042.
Steel, G., 2004. Tender Management, in: Morris, P. W. G.,
Pinto, J. K., (Eds.). the Wiley Guide to Managing
Projects. John Wiley & Sons, New Jersey.
Towler, G., Sinnott, R., 2008, Chemical Engineering
Design Principles, Practice and Economics of Plant
and Process Design. Elsevier, Burlington.
Wang, J., Xu, Y., Li, Z., 2009. Research on Project
Selection System of Pre-Evaluation of Engineering
Design Project Bidding. International Journal of
Project Management. 27, 584-599.
Watt, D. J, Kayis, B., Willey, K., 2009. Identifying Key
Factors in the Evaluation of Tenders for Projects and
Services. International Journal of Project
Management, 27, 250-260.
ATwo-stepBiddingPriceDecisionAlgorithmunderLimitedMan-HoursinEPCProjects
403
