Semi-centralized Reconstruction of Robot Swarm Topologies
The Largest Laplacian Eigenvalue and High Frequency Noise are used to
Calculate the Adjacency Matrix of an Underwater Swarm from Time-series
Vincenzo Fioriti, Stefano Chiesa and Fabio Fratichini
ENEA C. R. Casaccia, Laboratory of Robotics, Via Anguillarese 301, S. Maria in Galeria, Roma, Italy
Keywords: Swarm Intelligence, Underwater Autonomous Vehicle, Topology Reconstruction, Eigenvalue Spectrum.
Abstract: An important task in underwater autonomous vehicle swarm management is the knowledge of the graph
topology, to be obtained with the minimum possible communication exchanges and amid heavy
interferences and background noises. Despite the importance of the task, this problem is still partially
unsolved. Recently, the Fast Fourier Transform and the addition of white noise to consensus signals have
been proposed independently to determine respectively the laplacian spectrum and the adjacency matrix of
the graph of interacting agents from consensus time series, but both methodologies suffer technical
difficulties. In this paper, we combine them in order to simplify calculations, save energy and avoid
topological reconstruction errors using only the largest eigenvalue of the spectrum and instead of white
noise, a high frequency, low amplitude noise. Numerical simulations of several swarms (random, small-
world, pipeline, grid) show an exact reconstruction of the configuration topologies.
1 INTRODUCTION
Monitoring the marine environment is acquiring
more and more importance because of scientific and
economic reasons. Just to name some of them, we
could indicate the search for natural resources,
fishery, sea pollution mapping, maintenance
activities.
In this paper we describe a methodology able to
reconstruct exactly the graph from time series (the
network inverse problem), using recently developed
signal analysis and algebraic graph theory
techniques.
Although our methodology depends on a semi-
centralized data elaboration, there are particular
situations when the noises, disturbances and
interferences reach very high levels that may require
such approach, as the last resort.
2 PROBLEM DESCRIPTION
Autonomous underwater vehicle systems (AUV)
have moved from the prototype stage to scientific,
and commercial uses (Nawaz et al., 2009).
An AUV must be considered (Dell’Erba, 2012)
as a real cost alternative to other available
technologies, such as manned submersibles,
remotely operated vehicles and towed instruments
led by ships. However, many problems are still to be
solved to make AUV competitive especially for the
issues relevant to power availability, information
processing, navigation, and control. Communication
channels are a major concern, as the acoustic
underwater transmission is very slow and bandwidth
limited, but, in the future, optical, high power
transmission devices will be available for a number
of different approaches integrating the acoustical
data channel.
Nevertheless, a swarm could be advantageous
compared to a single vessel, if high communication
rate were available to reduce the dead reckoning
errors. It can collect together all the data of all the
vessels to minimize the errors in estimating position.
Therefore, in some cases, a centralized formation
analysis may be helpful, although economic costs
rise (Pompili and Melodia, 2005). For example when
the swarm size is large, since multi-hop paths are
needed to reach every node causing delays in several
ways.
This means that information about the
configuration cannot be transmitted inside the
swarm in the form of simple link look-up table
74
Fioriti V., Chiesa S. and Fratichini F..
Semi-centralized Reconstruction of Robot Swarm Topologies - The Largest Laplacian Eigenvalue and High Frequency Noise are used to Calculate the
Adjacency Matrix of an Underwater Swarm from Time-series.
DOI: 10.5220/0004421800740081
In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2013), pages 74-81
ISBN: 978-989-8565-70-9
Copyright
c
 2013 SCITEPRESS (Science and Technology Publications, Lda.)

because large delays are prone to cause instability.
To be more precise, consider a large swarm and a
consensus control protocol (see Paragraph 3).
According to (Olfati-Saber and Murray, 2004) the
stability of a fixed configuration is guaranteed iff:
τ ≤ π / 2λ
max
where τ is the uniform delay experienced by the
consensus distributed computations. Similar
constraints may be set for non uniform switching
topologies.
The delay τ depends on a number of factors:
CPU power, data transmission bandwidth, MAC
protocols, the number of AUV N, the inter-symbol
interference and finally the time necessary to acquire
the largest eigenvalue of the Laplacian, T
λ
.
If we calculate λ
max
by means of a look-up table
simply verifying the existence of an
acoustical/optical link between two AUV and
passing the information to other nodes, it is to be
expected a relatively large amount of time T
λ
. Then
we have:
τ = T
λ
+ τ
1
+ τ
2
+ ... τ
n
≤ π / 2λ
max
Now, for a large swarm over a wide area it turns out
that:
τ ≈ T
λ
≤ π / 2λ
max
therefore T
λ
is a sort of time-horizon beyond which
the swarm configuration looses stability, i.e. the
consensus solutions diverge.
Another situation that prevents from using multi-
hop paths is the marine background noise (Traverso
et al., 2012) together to the inter-symbol interference
(ISI) (Dousse et al., 2005).
ISI is a signal in which one symbol interferes
with subsequent symbols. The phenomenon is
enhanced by multiple reflections of the signal and as
has an effect similar to a non-gaussian noise.
The problem is produced by a number of
emitting nodes (AUV) towards the receiver and by
the background noise. Dousse has demonstrated that
above a critical value of ISI the network of reliably
communicating nodes splits into small isolated
components, and as a consequence, the connectivity
is lost (Dousse et al., 2005).
This result is true in general and even more so in
the marine environment. Difficulties are exacerbate
if a CDMA (Code Division Multiple Access), the
transmission of multiple digital signals
simultaneously over the same carrier frequency, is to
be used (Appala Raju et al., 2012). As a
consequence, data packets arrive deteriorated to the
receiver node.
Nevertheless, there are many reasons to know the
swarm topology. To name only two of them: the
second largest laplacian eigenvalue (the Fiedler or
algebraic eigenvalue) is relevant to the swarm
connectivity and the maximum eigenvalue is
relevant to the tolerable delay. Moreover, according
to (Camperi et al., 2012); (Ballerini et al., 2008) in
biological swarms maintaining a certain topology is
preferred to maintain a metric graph, i.e. metric
distances. It seems that topological interactions are
more robust to predatory attacks, facilitating the
group cohesion.
Then a solution may be to implement a semi-
centralized scheme, taking advantage of the noise
resilient procedure of (Ren et al., 2010) and of the
spectrum distributed computation (Franceschelli et
al., 2012), (Yang et al., 2008).
3.1 The proposed Scheme
We come to envision a large AUV swarm
monitoring a very wide area. A Gausssian noise
codifies the information about the topology and is
transmitted on the consensus channel. Thus,
provided the power of the added noise is large
enough, the transmission inside the swarm is robust.
The centralized data collection/elaboration task is
carried out by one or more ships. A ship covers a
part of the monitored area as shown in the pictorial
representation of Figure 1. The radius r of the
circumference covered by the ship depends on the
inter vehicle distance, the number of AUV (Chiesa
and Taraglio, 2012), the topology, and the maximum
allowable delay. Ships exchange data each other by
means of RF devices and with the swarm by optical
transmitters. When the maximum extension D of the
area is D >> r, it would be unfeasible to implement a
multi-hop inter-swarm data transmission to control
the configuration because delays would prevent any
synchronization.
Clearly, this scheme is based on a centralized
approach; instead the consensus control of
position/velocity is completely distributed (Olfati-
Saber and Murray, 2004). An appropriate position
prediction algorithm may also alleviate consensus
errors due to delays (Joordens and Ponds, 2010).
It should be noted that the consensus protocol is
necessary to the swarm stabilization, thus no
calculation encumbrance is the required to the
system at least with respect to control tasks.
Another distributed procedure we use in this
work is the determination of the laplacian spectrum
of the swarm network. Since also the spectrum is
determinate locally, we have two distributed
Semi-centralizedReconstructionofRobotSwarmTopologies-TheLargestLaplacianEigenvalueandHighFrequency
NoiseareusedtoCalculatetheAdjacencyMatrixofanUnderwaterSwarmfromTime-series
75

calculations and a centralized one, i.e. a semi-
centralized scheme. If the swarm configuration is
fixed obviously the spectrum is known in advance.
Moreover, instead of a ship, the central
elaborations could take place in one or more AUV,
properly equipped and able to broadcast relevant
data to the whole swarm by a gossip protocol.
Figure 1: Ships receive information from the AUV inside
the dotted circles of radius r and from the other ships. The
small red circle is the transmission range of an AUV
towards the closest neighbours. The same functions of
ships could be fulfilled by one or more AUV properly
equipped.
3 METHODS
Recently, a method to recover the Laplacian matrix
of the a network of dynamical coupled systems has
been given (Ren 2010). Starting from the general
form of the i-th differential system:
x
i
’ = F
i
( x
i
)
i = 1, ... N, and adding couplings and noise we have:
x
i
’ = F
i
(x
i
) – c Σ
j
L
ij
H(x
j
) + η
i
(1)
i, j = 1, ... N , where c is the coupling coefficient
(here c = 1), H the coupling functions, x the state
variables, η the white gaussian noise with strength
σ
2
, L
ij
are the entries of the Laplacian matrix derived
from the undirected graph of the systems. Vectors
and matrices are in bold. The Laplacian matrix is:
L = D – A
where D is a diagonal matrix formed by the node
degrees and A is the adjacency matrix (1 if a link i-j
exists, 0 otherwise) of the graph.
The very interesting point here is that the noise
added enables the solution of the inverse problem:
given the time series, reconstruct the graph.
Because of the particular problem of the swarm
control, in our paper we focus on the standard
consensus form of (1):
x
i
’ = Σ
j
a
ij
(x
j
-x
i
) + ξ
i
, j = 1, ... N
(2)
where a
ij
are the entries of the adjacency matrix A,
but here we consider a high frequency (HF) noise ξ
instead of the white noise η, as it will be explained
later.
It is known that for a connected network, the
equilibrium point for (2) is globally exponentially
stable. Moreover, the consensus value is equal to the
average of the initial values; for small swarms the
average is easy to calculate. In compact form (2) is
written:
x’ = - Lx + η
Expression (2) and similar are utilized in the swarm
control to coordinate the states of the robots on a
common position/velocity agreement resilient to
disturbs (Tanner et al., 2003); (Bullo et al., 2009);
(Xi et al., 2012); (Olfati_Saber, 2007); (Cucker and
Smale, 2007).
Figure 2: Scheme of data elaboration in an AUV.
After long enough time-series have been collected, it
is demonstrated (Ren, 2010) that:
L = C
+
(σ
2
/2) (3)
where C is the correlation matrix among the time
series between node i and node j, C
+
is the Moore-
Penrose pseudoinverse. Note that (2) requires the
knowledge of all time series to calculate the
pseudoinverse, hence the reconstruction is
centralized. Authors of (Ren, 2010) find a one-to-
one correspondence between the correlation matrix
of time series from nodes and the Laplacian matrix;
albeit no physical explanation of the phenomenon is
clearly claimed, an analytical proof is sketched.
This remarkable, counterintuitive finding
actually allows to set a threshold for the entries of
C
+
: below it the entries are considered -1, above 0,
thus the Laplacian and consequently the adjacency
matrix, is reconstructed. The threshold procedure is
not immediate to implement, anyway in (Ren, 2010)
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
76

it is claimed a very good success rate. Nevertheless,
some errors are reported to remain. Since the AUV
has a non negligible economic value, any effort for
eliminating the residual error is reasonable.
Moreover, considering the energy saving
requirement of the signal transmission apparatus of
the AUV, the average degree (i.e. the number of
underwater communication links) should be kept as
low as possible. At the same time, the consensus
signals are needed also to control the swarm and in
this respect, noise is a disturb to keep as small as
possible. Therefore, bearing in mind these
considerations, we suggest a node to transmit
consensus signals added with HF noise and to low
pass the noisy signals received, as in Figure 2.
3.1 The Spectral Estimation
To reduce or eliminate the residual error in the graph
reconstruction we need extra information.
A relevant help could be the knowledge at least
of some eigenvalues of the laplacian spectrum.
In some cases the graph is fixed and there is no
need of topological variations, thus the desired
spectrum is known and only a periodic verification
is required, but usually the graph changes frequently
and demands an on-line check.
The spectral reconstruction has been studied in
(Franceschelli et al., 2012); (Yang et al., 2008).
Franceschelli calculates a distributed Fast
Fourier Transform (FFT) of signals derived from a
proper distributed protocol and received at a node i:
x
i
’ = z
i
+ ∑
j
( z
i
- z
j
)
z
i
’ = - x
i
- ∑
j
( x
i
- x
j
)
with j
∈ N
i
(nodes at one hop of distance from node
i). Thus, the state trajectory is a linear combination
of sinusoids oscillating only at frequencies function
of the eigenvalues of the Laplacian matrix λ
j
, and the
amplitude of the peaks in the spectrogram are related
to the eigenvalues:
|F (x
i
(t))| = 1/2∑
j
a
ij
δ (f ± (1+ λ
j
) / 2π )
|F (z
i
(t))| = 1/2∑
j
b
ij
δ (f ± (1+ λ
j
) / 2π )
This method has some drawbacks (Kibangou and
Commault, 2012): the multiplicities of the
eigenvalues cannot be calculated and the FFT suffers
from the presence of noise. Remember that
independently from the Ren’s procedure, underwater
communications are polluted by several sources of
noise.
On the other hand (Yang et al., 2008) provides
an estimation of the laplacian spectrum based on
matrix power iteration, but this way only an
approximate solution can be obtained.
Finally, it is worth noting that even if an exact
spectrum reconstruction was available, today is not
clear if, at least theoretically, is possible to
reconstruct univocally its adjacency matrix (Van
Dam and Haemers, 2003). Alternative combinatorial
optimization techniques such as the tabu search,
simulated annealing or graph theory methods are not
exact and some of them would anyway require a
long computation time.
In spite of these limitations, having available the
estimation of just a single eigenvalue, we show how
to eliminate completely or at least reduce the
estimation error in the graph reconstruction.
3.2 Error Reduction
Let us consider that only the largest lapalacian
eigenvalue λ
N
has been calculated by means of one
of the previously described methods. It is intuitive to
use it as a simple cost function, instead of the
threshold procedure, to determine the non null
entries of the adjacency matrix recovered by (3).
Therefore in our methodology the pseudoinverse
C
+
is calculated from noisy consensus time-series
and normalized. Then, starting from a convenient
value, an initial adjacency matrix A is produced, its
largest laplacian eigenvalue λ
*
N
calculated and
subtracted to the actual eigenvalue λ
N
:
min g(λ) = | λ
N
- λ
*
N
|
and when:
g(λ
N
) = 0 (4)
the actual matrix A is reconstructed (best results
have been obtained with the largest eigenvalue,
although other eigenvalus may be used). In Figure 3
it is shown how the zero estimation error of the
eigenvalue is reached jointly with the complete
reconstruction of the adjacency matrix.
If errors in the exact estimation of the maximum
laplacian eigenvalue were present, the exact
reconstruction as in Figure 2 is still possible for low
– moderate amounts of the error. Moreover,
accepting just a few errors in the link reconstruction,
the acceptable error in the eigenvalue estimation
increases quickly (see Table 2)
.
Semi-centralizedReconstructionofRobotSwarmTopologies-TheLargestLaplacianEigenvalueandHighFrequency
NoiseareusedtoCalculatetheAdjacencyMatrixofanUnderwaterSwarmfromTime-series
77

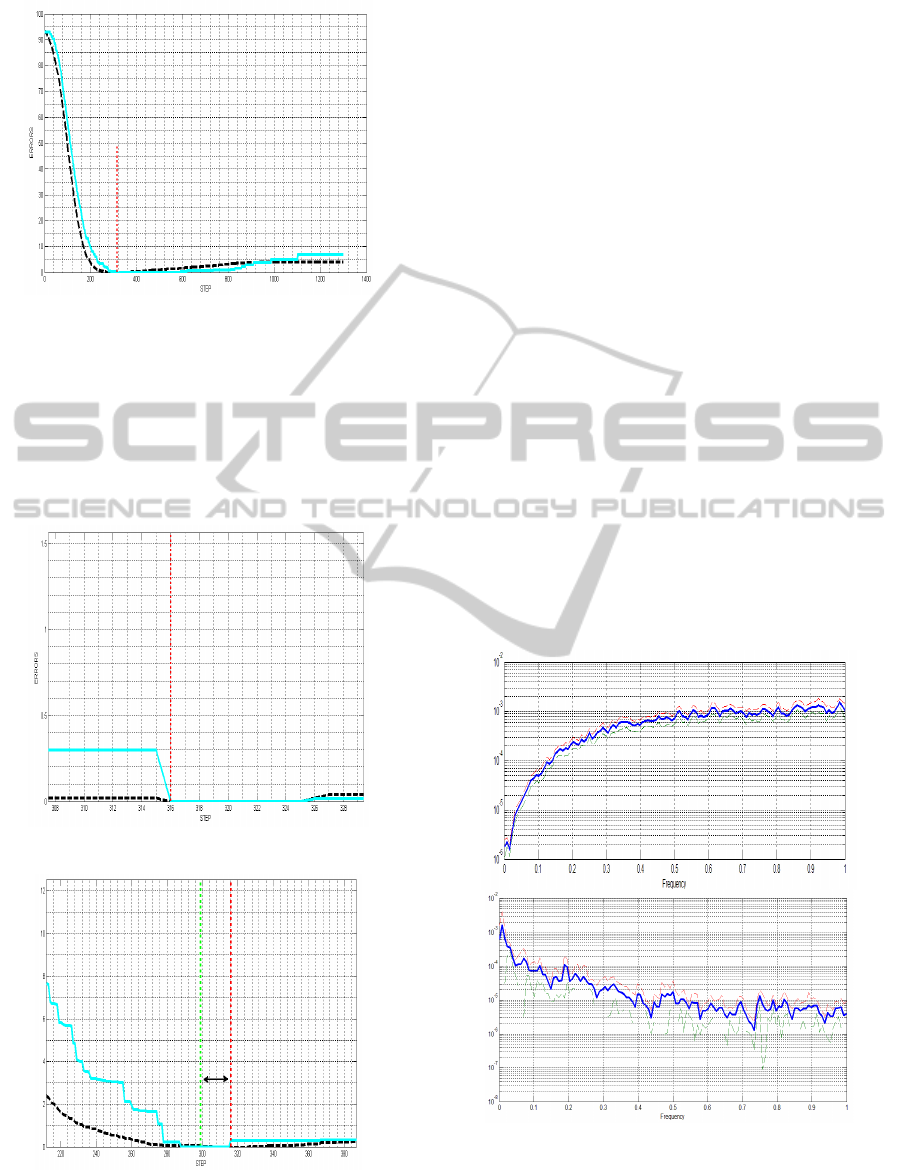
Figure 3a: Small World graph, 100 nodes (abscissa: time
steps, ordinate: errors). Black dotted curve: actual error
percentage of the adjacency matrix entries (not including
diagonal and symmetric elements), continuous blue curve:
the eigenvalue absolute error | λ
N
- λ
*
N
|. Vertical red and
green (green line is not visible because is coincident with
the red one) lines: exact reconstruction according to the
(4). The minimum value of the continuous blue curve
indicates the correct topology reconstruction, i.e. zero
errors.
Figure 3b: Enlargement of the minimum area.
Figure 3c: In this case two entries are wrong and the
minimum indicated by the largest eigenvalue (green dotted
line), is no more coincident with the actual zero
reconstruction error (dotted red line), see Table 2 also.
3.3 Noise Addition
For the methodology to work it is necessary the
addition of noise to the consensus protocol. As
pointed out in Paragraph 2, in a real environment it
is already present a background of natural or
artificial noise, then the previous noise level is
increased. This does not undermine the
methodology, provided the strength of the added
Gaussian noise is large enough.
In order to save energy and allow the consensus
signals to produce a proper control action on the
AUV swarm, we add a high frequency (HF), low
amplitude, zero mean, unitary variance Gaussian
noise to (1).
Noise strength in simulations is σ
2
= 0.01, one
order magnitude smaller with respect to (Ren, 2010).
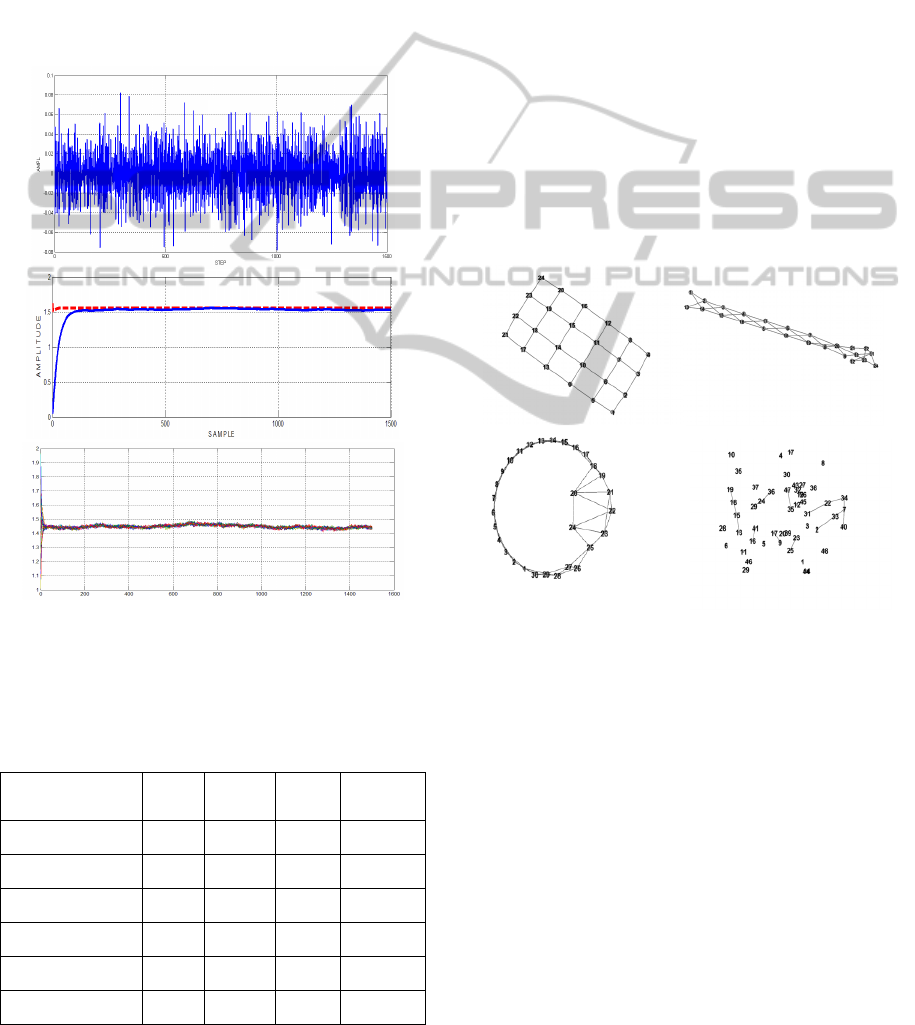
In Figure 4 is shown the HF noise and the signal
power spectral density (psd) spectrum (frequencies
are normalized).
In Figure 4 is shown a consensus signal, as it
appears after the low-pass filtering, once the signal
has been received in a node.
Aside the delay due to the low-pass filter, the
original signal is recovered. Anyway, even without
the low-pass filtering, the consensus solutions
converge all (Figure 5), but the Erdos-Renyi random
configuration that is not connected.
Figure 4: Top, psd of HF noise, middle, psd of the
consensus signal with HF noise. Last image: HF noise in
the time domain.
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
78

4 NUMERICAL SIMULATIONS
Numerical simulations have been conducted to
validate the methodology, results are shown in Table
1.
The task is to recovery exactly all of the
significant ( N
2
– N ) / 2 entries of the adjacency
matrix A of the swarm graph.
Four types of
topologies have been considered,
as relevant to underwater robot swarms: Erdos-
Renyi (random, p = 0.01), small-world (average
degree: 4, p = 0.1), pipeline (average degree: 4),
grid (average degree: 4), N = 24, see Figure 6.
Figure 5: Top, the noisy time series. Middle: consensus
time series after the low-pass filtering. The red dotted
curve is the original consensus. Bottom: noisy consensus
solutions for a SW (N = 24, average degree 4) before the
low-pass filtering.
Table: 1 Simulation results.
Graph
topology
Error Nodes Links
Integrati
on steps
Erdos-Renyi 0 48 16 ~150
Small-World 0 24 48 ~150
Small-World 0 100 200 ~370
Pipeline 0 24 43 ~150
Grid 0 24 38 ~150
Grid 0 100 180 ~370
The average degree 4 has been chosen because
biologically inspired investigations (Camperi et al.,
2012) indicates in the range 5-10 the optimal
number of neighbours in order to maintain the group
cohesion while saving an evenly space distribution.
In the simulations the centralized elaborations
are represented by the computation of the correlation
matrix C among all the time-series received from the
N nodes and by its pseudo inverse C
+
.
For each configuration a complete reconstruction
(zero errors) has been achieved, see Table 1.
In particular, SW networks are very interesting
for AUV configuration, as pointed out by
(Olfati_Saber, 2005), because of the high consensus
speed and connectedness properties.
The small-world consensus scheme seems to be
the fastest also for low number of nodes. In fact, it is
known (Olfati_Saber, 2005) that when a SW has a
number of nodes N > 100 the convergence is very
fast, but for N = 24, as in our case, there is no
guarantee.
Figure 6: Left to right graph topologies: regular grid,
pipe-line, small-world, random. Each node is an AUV,
links are inter-swarm acoustical or optical communication
channels. The grid topology is the most regular, the SW is
half-way between regularity and randomness. Note the
disconnected nodes of the ER topology.
All time series have a length of 150 simulation time-
steps (1500 samples) for N = 24; the first 30 samples
have been discarded because the transitory impair
the calculations. As the size (in nodes) increases,
longer time series are needed. As an example, when
the node size of a SW graph is 100, about 370 time-
steps are needed to recover the graph.
Note that an higher noise level reduces the time-
step length, bur increases the energy dissipation. The
trade-off should be analyzed on an ad hoc basis.
In Table 2 are shown the results for a large and a
Semi-centralizedReconstructionofRobotSwarmTopologies-TheLargestLaplacianEigenvalueandHighFrequency
NoiseareusedtoCalculatetheAdjacencyMatrixofanUnderwaterSwarmfromTime-series
79

small SW graph in presence of errors on the
estimation of the maximum laplacian eigenvalue,
obtained by the methods of (Yang et al., 2008) or
(Franceschelli et al., 2012).
The acceptable error on the maximum eigenvalue
estimation (meaning that the number of mistaken
entries of A is still zero) increases as N increases.
For example for N = 100, the 3.22% estimation error
means that the real value λ
N
= 4.0375 is altered as
much as: λ
N
± 0.13, but the reconstruction of the
matrix A remains exact.
Table 2: Stability of solutions.
Graph
Topo-
logy
Mista-
ken
entries
Nodes
Overall
Entries
Acceptable
error in the
λ
N
estimation
SW 0 100 4950 3.22%
SW 2 100 4950 7%
SW 0 24 276 0.22%
SW 2 24 276 15.2%
4 CONCLUSIONS
The control of an underwater robot swarm is a
complex task because of the particular environment,
especially when are present high levels of noises and
interferences. To this end, new biologically inspired
methodologies are currently under development.
One of the most important and unsolved control
problems in this field is the reconstruction of the
swarm topology. In fact, position sensors are often
inaccurate or unable to work properly. At the cost of
a semi- centralized elaboration of the consensus time
series, we have shown how it is possible to achieve a
complete topology reconstruction within the
technological framework suited to the marine
environment.
The methodology envisages the reconstruction of
the graph of the swarm using the noisy signals of the
consensus protocol. When received, signals are
correlated and the resulting correlation matrix is
elaborated according to a simple relation to obtain
the Laplacian matrix. Since the largest eigenvalue
of the Laplacian matrix can be estimated
independently, although not exactly, it is possible to
calculate the difference with the eigenvalue from the
reconstructed one at every step of the algorithm.
This information allows to decide the correct
adjacency matrix with zero or minimum
reconstruction error.
The original consensus signals necessary to
control the AUV are recovered by low-pass filtering,
as noise is allocated in the relatively high frequency
band.
ACKNOWLEDGEMENTS
This work has been supported by the HARNESS
Project, funded by the Italian Institute of
Technology (IIT).
REFERENCES
Ren, J., Wang, W.-X., Li, B., and Lai, Y.-C., 2010. Noise
Bridges Dynamical Correlation and Topology in
Coupled Oscillator Networks, Phys. Rev. Lett., 104 pp.
058701.
Olfati-Saber, R., and Murray, R. M., 2004. Consensus
Problem in Networks of Agents with Switching
Topology and Time-Delays, IEEE Trans. Aut. Contr.,
49 (9) pp. 1520-1531.
Olfati_Saber, R., 2005. Ultrafast Consensus, Proceedings
of the American Control Conference IEEE. pp. 2371-
2378, Los Alamitos, CA.
Olfati_Saber, R., Fax, J., Murray, R. M., 2007. Consensus
and Cooperation in Networked Multi-Agent Systems.
Proceedings of IEEE, 95, 1, Jan.2007.
Dousse, O., Baccelli, F., and Thiran, P., 2005. Impact of
Interferences on Connectivity in Ad Hoc Networks,
IEEE ACM Trans. Networking, 13 (2) 425.
Franceschelli, M., Gasparri, A., Giua, A., Seatzu, C.,2012.
Decentralized Estimation of Laplacian Eigenvalues in
Multi-Agent Systems, http://arxiv.org/pdf/1206.4509.
pdf.
Cucker, F. and Smale, S., 2007, On the mathematics of the
emergence, Jnp. J. Math., 2 (1) pp. 197-227.
Camperi, M., Cavagna, A., Giardina, I., Parisi, G., and
Silvestri, E., 2012, Spatially balanced topological
interaction grants optimal cohesion in flocking
models. http://rsfs.royalsocietypublishing.org/content/
early/2012/08/07/rsfs.2012.0026.
Yang, P., Freeman, R. A., Gordon, G., Lynch, K.,
Srinivasa, S., and Sukthankar, R, 2008. Decentralized
estimation and control of graph connectivity in mobile
sensor networks. American Control Conference.
Van Dam, E., and Haemers, W., 2003, Which graphs are
determined by their spectrum?, Linear Algebra and its
Applications, 373 pp.241–272.
Dell’Erba, R., and Moriconi, C., 2012. The Localization
problem for Harness: a Multipurpose Robotic Swarm.
SENSORCOMM 2012 Sixth International Conference
on Sensor Technologies and Applications.
Pompili, D. and Melodia, T., 2005. Three-dimensional
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
80

routing in under water acoustic sensor network. PE-
SWASUN ‘05 ACM Conference 1-59593, Montreal,
Quebec, Canada.
Ballerini, M., et al., 2008, Interaction ruling animal
collective behavior depends on topological rather than
metric distances: evidence from a field study, Proc.
Nat. Acad. Sci. USA, 105 pp. 1232-1237.
Chiesa, S. and Taraglio, S., 2012. Flock Formation
Control through Parameter Tuning in Underwater
Swarms. ICINCO’12 Conference Rome, pp. 313-316.
Kibangou, A., Commault, C., 2012. Decentralize
Laplacian Eigenvalues Estimation and Collaborative
Network Topology Identification. 3rd IFAC Workshop
on Distributed Estimation and Control in Networked
Systems, NecSys '12, Santa Barbara.
Wang, W. X., Ren, J., Lai, Y. C., Li. B., 2012. Reverse
engineering of complex dinamic networks in the
presence of time-delayed interaction based on time-
series. Chaos, 22 033131.
Nawaz, S., Hussain, M., Watson, S., Trigoni, N., and
Green, P. N., 2009. An Underwater Robotic Network
for Monitoring Nuclear Waste Storage Pools. 1st
International ICST Conference on Sensor Systems
and Software.
Joordens, M. And Ponds, W., 2010. Consensus Control for
a System of Underwater Swarm Robots. IEEE Systems
Journal, 4 (1).
Appala Raju, Y., Devee Prasan, U., 2012, Network Layer
Analysis & Novel Recommendations Regarding
Feasibility towards UWSN, Int. J. Eng. Res. Dev. 4
(10) pp. 1-7.
Traverso, F., Trucco, A. , Vernazza, G., 2012. Simulation
of non-White and non-Gaussian Underwater Ambient
Noise. OCEANS’12 MTS/IEEE Yeosu Conference,
Yeosu South Korea.
Tanner, H., Jadbabaie, A., and Pappas, 2003. G., Stable
flocking of mobile agents, part I: Fixed topology.
Proceedings of the 42nd IEEE Conference on
Decision and Control DC2003), vol. 2, Dec. 2003, pp.
2010–2015.
Bullo, F. Cortes, J., and Martınez, S. 2009. Distributed
Control of Robotic Networks, ser. Applied
Mathematics Series. Princeton University Press.
Xi, J., Shi, Z., Zhong, Y., 2012. Consensus and
consensualization of high-order swarm systems with
time delays and external disturbances, J. Dyn. Sys.
Meas. 134 4.
Semi-centralizedReconstructionofRobotSwarmTopologies-TheLargestLaplacianEigenvalueandHighFrequency
NoiseareusedtoCalculatetheAdjacencyMatrixofanUnderwaterSwarmfromTime-series
81