
The Optimal Quaternion Equilibrium Point
Using an Energy Function to Choose the Optimal Quaternion Equilibrium Point
Margrete Djupaa and Rune Schlanbusch
Department of Technology, Narvik University College, Narvik, Norway
Keywords:
Dual Equilibria, Quaternions, Rotational Energy, PD+ Controller.
Abstract:
By parameterizing the attitude of a rotating rigid body in a closed-loop system with unit quaternions, the
existence of dual equilibria leads to new challenges. In order to optimize the energy consumption due to
control effort, the choice of the cheapest equilibria, that is, the one which requires least energy to reach, is
essential. A new predicting solution of choosing the optimal equilibrium point for rotational maneuvers of
a rigid body is presented in this article. This new solution consists of an energy function which base its
prediction on the initial attitude on the rotational sphere, taking account for both potential and kinetic energy
of the rigid body. The equilibrium energy function is developed through a previously presented statistical
analysis for the system behaviour of a rigid body in closed loop attitude control.
1 INTRODUCTION
For controlling and steering an object there is a need
for a controller. New controllers have been evolved
during several years, with different focus. There are
different needs for different situations, and many of
the demands are in contrast to each other. Needs like
minimum energy consumption, robust stability, faster
and more accurate settling giving enhanced perfor-
mance and minimizing the control effort, can give the
developers some interesting tradeoffs. The develop-
ment of newtechniques for the controller to give more
optimal control of a rigid body is needed, especially
in spacecrafts and UAV’s where resources are sparse.
To control the attitude of a rotational rigid body
when the attitude is parameterized by unit quater-
nions, can be a challenging task. The existence of
dual equilibria and possibilities of the unwinding phe-
nomenon (Bhat and Bernstein, 2000) are the main is-
sues. (Kristiansen, 2008) presented a technique to
overcome the issue with two equilibria, where the
shortest rotational path was chosen initially and kept
throughout the maneuver. The technique uses two
state-feedback controllers in the development work,
one for each equilibrium point, the positive and the
negative one. These two controllers steer the rigid
body to each of the equilibrium points, and they both
give an uniformly asymptotically stable equilibrium
point for the chosen equilibrium, while the not cho-
sen equilibrium is rendered unstable. This control
strategy is called the initial choice of equilibrium, and
it bases it’s choice only on the initial attitude scalar
value called η(t
0
). With this method the shortest ro-
tational length towards equilibrium will always be the
chosen one, which will function well if the rigid body
is not rotating at initial time. This method is further
developed from the attitude error function presented
by (Fjellstad, 1994), where a signum function is con-
tinuously choosing the closest equilibrium. Later it
was proved that the signum function is not robust
against measurement noise, and that the function can
lead the closed-loop system stuck for infinite time,
never reaching it’s desired position (Mayhew et al.,
2009).
The disadvantage of using these mentioned meth-
ods of choosing the closest equilibrium is that it is
not taking account of rotational motion by the rigid
body at the initial time, thus it will only consider the
shortest distance. From a resource-consuming point
of view of the controller this is not appropriate, and
better methods are sought.
The goal is to predict the optimal equilibrium
point based on the rigid body’s attitude at the initial
time, in order to save energy consumed by the con-
trol solution. By taking account of both potential and
kinetic energy of the rotational sphere in the initial
phase, the need of control power can be reduced to
a minimum. This is done with a prediction of the
most optimal equilibrium based on the initial attitude
and angular velocity of the rigid body. The prediction
345
Djupaa M. and Schlanbusch R..
The Optimal Quaternion Equilibrium Point - Using an Energy Function to Choose the Optimal Quaternion Equilibrium Point.
DOI: 10.5220/0004422903450352
In Proceedings of the 3rd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2013),
pages 345-352
ISBN: 978-989-8565-69-3
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

method is based on an equilibrium energy function,
developed on the basis of the behaviours of the dy-
namical system seen by the statistical analysis done
by (Schlanbusch, 2012).
In Matlab a dynamical closed-loop model is de-
veloped of a rigid body having constant inertia ma-
trix. The rigid body could be anything, but its motion
can be viewed as a unit sphere. In real life no ob-
ject is perfectly rigid, but with this approximation the
study of attitude maneuvers is less complicated. The
control law used is based on the PD+ controller in-
troduced by (Paden and Panja, 1988). This controller
is a state-feedback controller which controls the rigid
body to a desired position. The only acting torque
in the closed-loop system in simulations are the con-
troller, no disturbance torques are accounted for in the
system model. The system model and simulations are
conducted in Matlab. The simulation results with the
use of a PD+-controller and randomized initial val-
ues shows that the presented equilibrium energy func-
tion is able to predict the optimal equilibrium point in
about 97% of the maneuvers. This prediction result
is a further improvement compared to previously pre-
sented results.
2 MATHEMATICAL
BACKGROUND
2.1 Quaternions
The attitude of a rigid object can according to (Fjell-
stad, 1994) be described by a rotation matrix R ∈
SO(3), where SO(3) is the special orthogonal group
of order three, which is the set of all rotation matrices
with the determinant equal to +1, defined as
SO(3) = {R ∈ R
3×3
: R
⊤
R = I, det(R) = 1} (1)
where I is the 3 × 3 identity matrix. The manifold
SO(3), which is the group of rotation matrices, is
closed and bounded, while the manifold called the
Euclidean space R
3×3
, is open and unbounded. This
difference in manifolds leads to the fact that there is
no homeomorphism between these two spaces.
The quaternion parameterization of SO(3) can be
done according to (Fjellstad, 1994) by four parame-
ters q = [η, ε
⊤
]
⊤
; the three-dimensional vector ε ∈ R
3
and the scalar component η ∈ R. The definition of an
unit quaternion is q ∈ S
3
= {x ∈ R
4
: x
⊤
x = 1}. The
rotation matrix can be rewritten as
R
η,ε
= I+ 2ηS(ε) + 2S
2
(ε) (2)
where S(ε) is the skew matrix of the ε vector, such
that S(x)y = x× y, ∀x, y ∈ R
3
.
With unit norm the quaternion’s conjugate
¯
q =
[η, −ε
⊤
]
⊤
and the inverse is the same.
q
−1
=
¯
q
||q||
2
. (3)
The manifold S
3
forms a group of quaternion mul-
tiplication, which is distributive and associative, but
not commutative. The quaternion product between
two quaternion vectors is defined by (Egeland and
Gravdahl, 2002) as
q
1
⊗ q
2
=
η
1
η
2
− ε
⊤
1
ε
2
η
1
ε
2
+ η
2
ε
1
+ S(ε
1
)ε
2
. (4)
S
3
is the set of unit quaternions and is the cov-
ering manifold for SO(3). According to (Bhat and
Bernstein, 2000) this situation with the covering map
provides a globally nonsingular parametrization of
SO(3). The covering map is onto and a locally dif-
feomorphism everywhere, but globally many to one.
Mentioned by (Fjellstad, 1994) that due to the redun-
dant fourth parameter there is a double coveringof the
space SO(3). This givesthe existence of the unwanted
phenomenon of two equilibria.
2.2 Kinematics and Dynamics
The angular velocity vector gives the rate of change
of the attitude of the rigid body with respect to time.
Given by (Egeland and Gravdahl, 2002) the defini-
tion of the angular velocity vector represents the time
derivative of the rotation matrix.
S(ω
a
a,b
) =
˙
R
a
b
(R
a
b
)
⊤
(5)
where ω
a
a,b
∈ R
3
is the angular velocity of F
b
relative
to F
a
represented in F
b
where F
(·)
denotes frame
(·). Furthermore, (5) can be expressed as (Egeland
and Gravdahl, 2002)
˙
R
a
b
= S(ω
a
a,b
)R
a
b
= R
a
b
S(ω
b
a,b
). (6)
The angular momentum vector h can be expressed
by the angular velocity ω and the rigid body’s inertia
matrix J∈ R
3×3
= diag{J
x
, J
y
, J
z
} about its center of
mass, as (Sidi, 1997)
h
b
= Jω
b
i,b
. (7)
The rotational kinematic of a rigid body which ro-
tates from F
b
to F
a
, can according to (Egeland and
Gravdahl, 2002) be described by the kinetic differen-
tial equations
˙
q =
˙
η
˙
ε
= T(q)ω ,
T(q) =
1
2
−ε
⊤
ηI+ S(ε)
∈ R
4×3
.
(8)
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
346

The dynamical model of the rotational rigid body
can be described by a differential equation for angular
velocity, deduced from the Euler’s moment equation
as described by (Sidi, 1997)
τ =
˙
h
i
=
˙
h
b
+ S(ω
b
i,b
)h
b
(9)
where F
i
is the inertial frame and F
b
is the body
frame. From (9) it can be seen how the applied torque
τ is affecting the rotational motion of the rigid body.
Through the angular momentum (7) and the as-
sumption that the inertia matrix J of the rigid body is
constant, the derivative of the angular momentum is
˙
h
b
= J
˙
ω
b
i,b
. (10)
By inserting the equations for the angular momen-
tum (7) and (10) within the Euler’s moment (9), we
obtain
τ = J
˙
ω
b
i,b
+ S(ω
b
i,b
)Jω
b
i,b
, (11)
and with some rearranging of the terms, the dynami-
cal model of the system is found to be
J
˙
ω
b
i,b
= −S(ω
b
i,b
)Jω
b
i,b
+ τ (12)
where the external torque τ is the sum of all forces
acting on the rigid body. For simplicity through this
article, the only force working in the closed-loop dy-
namical model is the controller τ
a
, there are no distur-
bance torques τ
d
.
τ = τ
a
+ τ
d
where τ
d
= 0 ⇒ τ = τ
a
.
(13)
3 CONTROLLER DESIGN
The controller is designed to control a rigid body from
it’s state q(t) towards a reference state q
d
(t) satisfy-
ing the kinematic equation
˙
q
d
= T(q
d
)ω
d
(14)
where ω
d
is the desired angular velocity.
Shown by (Schlanbusch, 2012) the quaternion er-
ror can be defined by using the quaternion product
˜
q =
¯
q
d
⊗ q =
ηη
d
− ε
⊤
ε
d
η
d
ε+ ηε
d
+ S(ε)ε
d
(15)
where
˜
q = [
˜
η,
˜
ε
⊤
]
⊤
. The angular velocity error can be
defined as
˜
ω = ω− ω
d
, (16)
and from (8) the error kinematics can be expressed as
˙
˜
q = T(
˜
q)
˜
ω , T(
˜
q) =
1
2
−
˜
ε
⊤
˜
ηI+ S(
˜
ε)
. (17)
The two equilibria represents the same physi-
cal orientation, there is a need to choose which
of the equilibrium point that is going to stabilized.
For stability reasons, the error functions are intro-
duced to make the equilibrium points from (
˜
q,
˜
ω) =
([±1, 0, 0, 0]
T
, [0, 0, 0]
T
) for the closed-loop system to
become (e
q±
, e
ω
) = ([0, 0, 0, 0]
T
, [0, 0, 0]
T
). The error
quaternion
˜
q is earlier found in (15), and the equilib-
ria can be moved to the origin according to
e
q±
= [1∓
˜
η,
˜
ε] (18)
and the definition of the angular velocity error is
found from (16) as
e
ω
= ω− ω
d
. (19)
The controllers goal is to steer the rigid body’s
attitude and angular velocity towards the origin,
[e
q±
, e
ω
]
⊤
→ 0 as t → ∞.
We start by analyzing the positive equilibrium,
thus define e
q
= e
q+
. The control law of the continu-
ous dynamical system can then be expressed as
τ
a
= J
˙
ω
d
− S(Jω)ω
d
− k
q
T
⊤
e
e
q
− k
ω
e
ω
. (20)
The closed-loop rotational dynamics is then obtained
by inserting (20) into (12) as
J
˙
e
ω
− S(Jω)e
ω
+ κ
q
T
⊤
e
e
q
+ κ
ω
e
ω
= 0. (21)
With the definition of a Lyapunov function candidate
which is radially unbounded and positive definitive,
the candidate is
V(e
q+
, e
ω
) =
1
2
e
⊤
ω
Je
ω
+
1
2
e
⊤
q
k
p
e
q
(22)
satisfying V > 0 ∀ e
ω
6= 0, e
q
6= 0. By differentiation
along closed loop trajectories we obtain
˙
V = e
⊤
q
k
q
T
e
e
ω
+ e
⊤
ω
S(Jω)e
ω
− e
⊤
ω
k
ω
e
ω
− e
⊤
ω
k
q
T
⊤
e
e
q
(23)
where it can be seen that the first term is canceled by
the last term and the second term is zero because S(·)
is skew-symmetric, thus yielding
˙
V = −e
⊤
ω
k
ω
e
ω
≤ 0. (24)
By (Khalil, 2002) we can conclude that the equilib-
rium point (e
q+
, e
ω
) = (0, 0) is uniformly stable.
To check the convergence properties of the tra-
jectories we make us of Matrosov’s theorem (Hahn,
1967) by defining an auxiliary function
W(e
q+
, e
ω
) = e
⊤
q
T
e
k
q
Je
ω
. (25)
which is continuous and bounded for any states in a
closed set. In the set E : {
˙
V = 0} = {e
ω
= 0} the
time derivative of (25) is non-zero definite and is neg-
ative definite in the attitude error
e
ω
= 0 ⇒
˙
W = −e
⊤
q
T
e
k
q
T
⊤
e
e
q
, (26)
TheOptimalQuaternionEquilibriumPoint-UsinganEnergyFunctiontoChoosetheOptimalQuaternionEquilibrium
Point
347

which concludes the proof of (Hahn, 1967), thus ren-
dering the equilibrium point of the closed-loop sys-
tem as uniformly asymptotically stable. The stability
proof for the negative equilibrium point e
q−
= [1 +
˜
η,
˜
ε
⊤
]
⊤
can be concluded by utilizing the same struc-
ture of the candidates V and W, thus the stability re-
sult holds for both of the equilibria (e
q±
, e
ω
) = (0, 0).
It is not possible to achieve a global result due to dual
equilibria and also because of the fact that V is not
radially unbounded in the attitude.
4 STATISTICAL CHOICE OF
EQUILIBRIUM
Due to the constant need of reducing the energy con-
sumption by the attitude controller, the idea of using
the rotational energy in the initial maneuver phase
took place. A prediction method was developed for
finding the optimal equilibrium based on statistical
analysis (Schlanbusch, 2012). Multiple simulations
with different initial angular velocities and initial atti-
tudes of the rigid body were conducted, and the sys-
tem behaviour of the attitude control was visualized
in plots. Through statistical analysis of the patterns
in these plots (Schlanbusch, 2012) found three dif-
ferent motion behaviours, and from these behaviours
there were developed three prediction formulas based
on the initial attitude and angular velocity. With these
statistical based formulas the prediction of which of
the two equilibria is cheapest to reach based on en-
ergy consumption, were correct in nearly 90% of the
maneuvers.
Through a minimum criteria of the controller’s
torque used to reach each of the equilibrium point,
the statistical solution was evolved. The criteria was
described as
J = min{J
p+
, J
p−
} (27)
is satisfied where J
p±
called a performance functional
is described with the integral of the applied control
torque
J
p±
=
Z
t
f
t
0
τ
⊤
a
(e
q±
)τ
a
(e
q±
)dt (28)
where e
q±
is defined in (18) and t
0
and t
f
denotes
the start and end time, respectively. Thus, J denotes
whether either the positive or the negativeequilibrium
is chosen based on the energy criteria.
If the rigid body is standing still in the initial
phase, it is obvious that the shortest rotation length is
the least resource-demanding. The situation is more
complex if the object is moving in the initial phase,
both the attitude and the angular velocity can affect
the need of the controller’s torque. If an object is near
the positive equilibrium, but the rigid body rotates in
a direction towards the negative equilibrium, the least
energy demanding can be to control the body towards
the negative equilibrium.
4.1 Simulations for the Statistical
Analysis
With use of the performance functional (28) and the
control law for the closed-loop system (20), the en-
ergy consumption for the controller to maneuver a
rigid body to one of the two equilibria from an initial
position can be calculated. In our setup we have plot-
ted each result in two different plots. Each dot indi-
cates the initial values for a given simulation, and the
distribution of dots between the plots is such that one
plot collects all initial values which gives cheapest ro-
tation for the positive equilibrium, and vice versa for
the negative equilibrium.
There are three simulation cases with respectively
three different standard deviation values for the ini-
tial angular velocity. Each of the simulation cases are
simulated 1000 times. The initial four element atti-
tude vector q(t
0
) is uniform random generated with
values from -1 to 1. The angular velocity is random
generated from a normal distribution with a mean
value as 0 rad/s, and the standard deviation of 0.01,
0.1 and 1 rad/s, respectively.
With the torque τ
a
, the controller is able to ma-
neuver the rigid body either to the positive or the neg-
ative equilibrium. In the following simulation results,
all other forces than the controller’s is set to zero, so
no external or noise induced disturbancesare accumu-
lated within the performance functional. The desired
states are the origin, which gives the desired attitude
q
d
= [±1, 0
⊤
]
⊤
and the desired angular velocity and
acceleration ω
d
=
˙
ω
d
= 0.
4.1.1 Simulation Case 1, Standard Deviation
0.01 rad/s
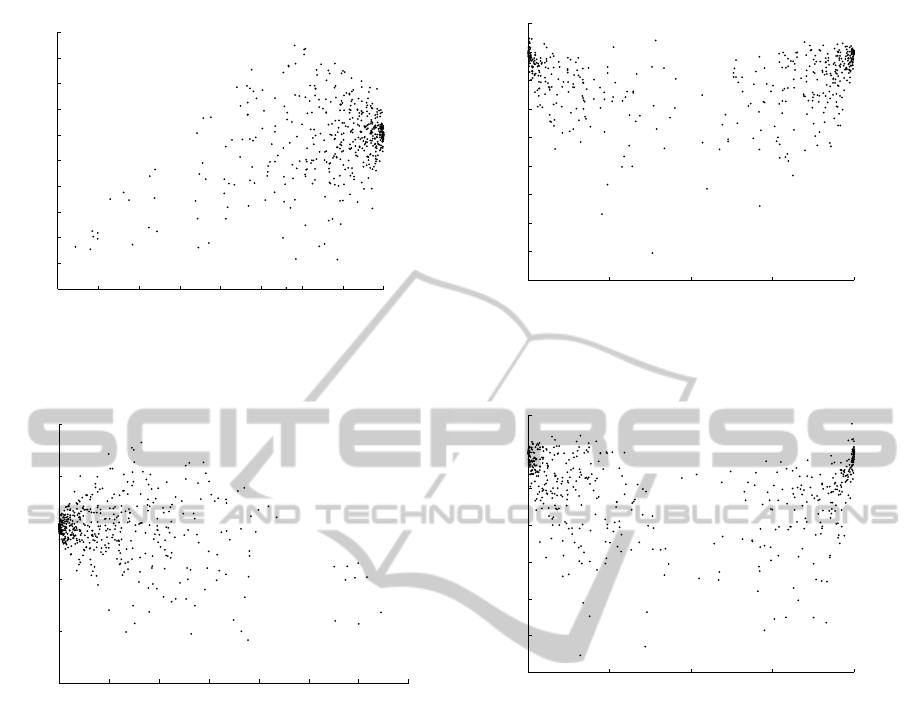
The plot of the simulations are presented in the Figure
1 and in Figure 2. They show the closed-loop system
behaviour for small initial angular velocities, given
standard deviation of 0.01 rad/s in the random initial
angular velocity vector.
Figure 1 shows scatter in the maneuvers where the
positive equilibrium is the cheapest rotational direc-
tion based on the given initial values. Figure 2 shows
the same for the negative equilibrium. As seen in the
scatter plots of the simulations runs, the initial scalar
part of the quaternion is the dominated part. The er-
ror value
˜
η(t
0
) gives the best solution for which of the
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
348
−0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1
−12
−10
−8
−6
−4
−2
0
2
4
6
8
x 10
−3
˜η
˙
˜η
Figure 1: Simulation results of the positive equilibrium
from random initial values with 0.01 rad/s standard devi-
ation for angular velocity.
−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4
−0.015
−0.01
−0.005
0
0.005
0.01
˜η
˙
˜η
Figure 2: Simulation results of the negative equilibrium
from random initial values with 0.01 rad/s standard devi-
ation for angular velocity.
equilibrium to choose. If
˜
η(t
0
) is negative, then ma-
neuvering to the negative equilibrium is least energy
consuming. A positive
˜
η(t
0
) indicates that the pos-
itive equilibrium is the optimal one. This result can
also be concluded by the fact that the kinetic energy
is nearly zero. The cheapest rotation path for rigid
bodies nearly standing still is the nearest equilibrium,
as expected.
The first rule is made for cases with small initial
angular velocities and is set up as
e
q
=
e
q+
if k
˜
η
˜
η(t
0
) + k
˙
˜
η
˙
˜
η(t
0
) ≥ 0
e
q−
if k
˜
η
˜
η(t
0
) + k
˙
˜
η
˙
˜
η(t
0
) < 0
(29)
with the initial
˜
η(t
0
) values, and k
˜
η
and k
˙
˜
η
which are
scaling constant. By tuning the k-constants through
trial/error or statistical methods, this first rule will
give a good estimation of which equilibrium point is
least energy demanding for the controller.
−1 −0.5 0 0.5 1
−0.16
−0.14
−0.12
−0.1
−0.08
−0.06
−0.04
−0.02
0
0.02
˜η
˙
˜η
Figure 3: Simulation results for the positive equilibrium
from random initial values with 0.1 rad/s standard deviation
for angular velocity.
−1 −0.5 0 0.5 1
−0.12
−0.1
−0.08
−0.06
−0.04
−0.02
0
0.02
˜η
˙
˜η
Figure 4: Simulation results for the negative equilibrium
from random initial values with 0.1 rad/s standard deviation
for angular velocity.
4.1.2 Simulation Case 2, Standard Deviation 0.1
rad/s
The second simulation case is performed with a stan-
dard deviation of 0.1 rad/s in the random angular ve-
locity vector, which gives larger initial velocity values
compared to the first simulation case.
The hit scatter for the positive equilibrium is lo-
cated in the Figure 3, while the results for the negative
equilibrium is located in Figure 4. From the plots it
can now be seen that
˙
˜
η(t
0
) is the dominant parameter.
The second rule found from this analysis can then be
expressed as
e
q
=
e
q+
if
˙
˜
η(t
0
) > 0
e
q−
if
˙
˜
η(t
0
) < 0
∀
˙
˜
η(t
0
) 6= 0 (30)
for cases where
˙
˜
η(t
0
) = 0 then
e
q
=
e
q+
if
˜
η(t
0
) ≥ 0
e
q−
if
˜
η(t
0
) < 0
. (31)
TheOptimalQuaternionEquilibriumPoint-UsinganEnergyFunctiontoChoosetheOptimalQuaternionEquilibrium
Point
349

−1 −0.5 0 0.5 1
−1
−0.5
0
0.5
1
1.5
˜η
˙
˜η
Figure 5: Simulation results for positive equilibrium from
random initial values with 1 rad/s standard deviation for an-
gular velocity.
−1 −0.5 0 0.5 1
−1.5
−1
−0.5
0
0.5
1
1.5
˜η
˙
˜η
Figure 6: Simulation results for negative equilibrium from
random initial values with 1 rad/s standard deviation for an-
gular velocity.
4.1.3 Simulation Case 3, Standard Deviation 1
rad/s
For the third simulation case the random values for
angular velocity have a standard deviation of 1 rad/s,
which can be considered as large initial angular ve-
locities.In Figure 5 we see the initial values which
are preferred for the positive equilibrium, and for the
negative equilibrium in Figure 6. The system is now
preferring the opposite equilibrium, than observed in
simulation case one, for small initial angular veloci-
ties (ω(t
0
) ≈ 0.01 rad/s). The system does not care
much for the sign of
˙
˜
η(t
0
as in simulation case two,
shown in Figures 3 - 4. The behavior can be described
by a third rule as
e
q
=
e
q+
if
˜
η(t
0
) < 0
e
q−
if
˜
η(t
0
) > 0
∀
˜
η(t
0
) 6= 0 (32)
for
˜
η = 0 following is set
e
q
=
e
q+
if
˙
˜
η(t
0
) ≥ 0
e
q−
if
˙
˜
η(t
0
) < 0
. (33)
With large initial angular velocity for a rigid body,
it seems that it can be more efficient not to stop at
the nearest equilibrium, thus demand fast and “hard”
maneuvers, but use the initial velocity to rotate to-
wards the opposite point, reducing the angular veloc-
ity more slowly. Also, stopping and reverse rotation
due to overshoot seems to be more energy consum-
ing, than instead continue in the initial rotational di-
rection. Stated by (Schlanbusch, 2012) it can be seen
that the opposite equilibrium compared to case one is
preferred by the system, even if the parameter
˙
˜
η ≈ 0.
This is due to the relation
˙
˜
η = −
1
2
˜
ε
⊤
e
ω
. If the vector
ε(t
0
) ≈ 0, that is, the rigid body is initially oriented
close to one of the equilibria, large angular velocities
e
ω
will not affect the resultant parameter
˙
˜
η.
5 EQUILIBRIUM ENERGY
FUNCTION
For the behavioural analysis presented in Section
4.1 three different behaviours were observed, leading
to three rules for choosing the cheapest equilibrium
based on size of the initial values. By taking these
three statistical rules and the initial angular velocity
value, it is possible to make a better prediction func-
tion which works for all maneuver situations. The
goal is to improve the accuracy in predicting the equi-
librium point which requires least energy to reach,
based on the initial value of the attitude and the angu-
lar velocity of the rigid body. If both the kinetic and
potential energy in the initial states are accounted for,
the energy usage for bringing the states of the dynam-
ical system to the equilibrium can be made as small
as possible.
If the rigid body is standing still in the initial
phase, it is obvious that the shortest rotational path
will be the least resource-demanding one. In situa-
tions with a rotational motion in the initial phase, then
an energy function predicting the equilibrium based
on the initial kinetic energy level is needed to predict
which is optimal equilibrium point to reach.
From the statistical analysis presented in Section
4, three behaviours were found for the dynamical sys-
tem. For small initial angular velocities |
˜
ω(t
0
)| ≈ 0
it can then be seen that the behaviour is dependant of
the initial value of
˜
η(t
0
). For large initial angular ve-
locities over 1 rad/s, it can be seen the behaviour of
the dynamical system is dependant on the same pa-
rameter, although with opposite behaviour, that is, the
preferable equilibrium point is the one which is most
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
350
far away from the initial attitude. For initial angular
velocities between 0 rad/s to 1 rad/s, the system’s be-
haviour is dependant of the
˙
˜
η(t
0
).
Following element of the equilibrium energy func-
tion
1
can be found for the first case - note that for
all energy functions it is implicit that for E ≥ 0 we
choose e
q+
and for E < 0 we choose e
q−
- where there
are small initial angular velocities
E
±
= k
1
˜
η(t
0
), (34)
thus the sign of η(t
0
) in the error quaternion decides
the prefered equilibrium. This can be related to an
object standing still, where it is “cheaper” to move to
the nearest equilibrium.
The energy function can be expanded with an ele-
ment from the second case
E
±
= k
1
˜
η(t
0
) + k
2
˙
˜
η(t
0
) (35)
for angular velocities up to 1 rad/s a comparison of
direction and speed of the rotation, where it can be
seen that the initial orientation is less significant, than
in the first case. As stated in Section 4.1.3 we have
that
˙
˜
η = −
1
2
˜
ε
⊤
e
ω
. (36)
where the initial kinetic energy disappears from the
energy function when the initial orientation is close
to either equilibria. To counter this effect we add a
new cross coupling term between initial potential and
kinetic energy according to
E
±
= k
1
˜
η(t
0
) + k
2
˙
˜
η(t
0
) − k
3
˜
η(t
0
)
˜
ω
⊤
(t
0
)
˜
ω(t
0
), (37)
where k
1
, k
2
andk
3
are scaling constants. It can be
seen that we propose to include
˜
η in the last term
of (37) in addition to
˜
ε as in the cross term intro-
duced in (35), to make the contributionalso hold close
to an equilibrium point. Also, we multiply with the
quadratic term
˜
ω
⊤
˜
ω because we consider large angu-
lar velocity as in the third case, and the negative sign
is used also in accordance with the third case, because
we want to move away from the closest initial equi-
librium point for large initial kinetic energy. The scal-
ing constants k
1
, k
2
andk
3
need be to tuned based on
the system parameters such as moment of inertia and
controller gains, to be able to do best possible predic-
tion of the preferable equilibrium. Optimizing these
constants can be done either manually, by trial and
error, or through statistical analysis with an optimiza-
tion tool. To sum up, we consider the first term in
(37) as the potential energy while the two other terms
as kinetic.
1
Note that we don’t consider the energy in this study to
be of a specific type of unit, e.g. joule.
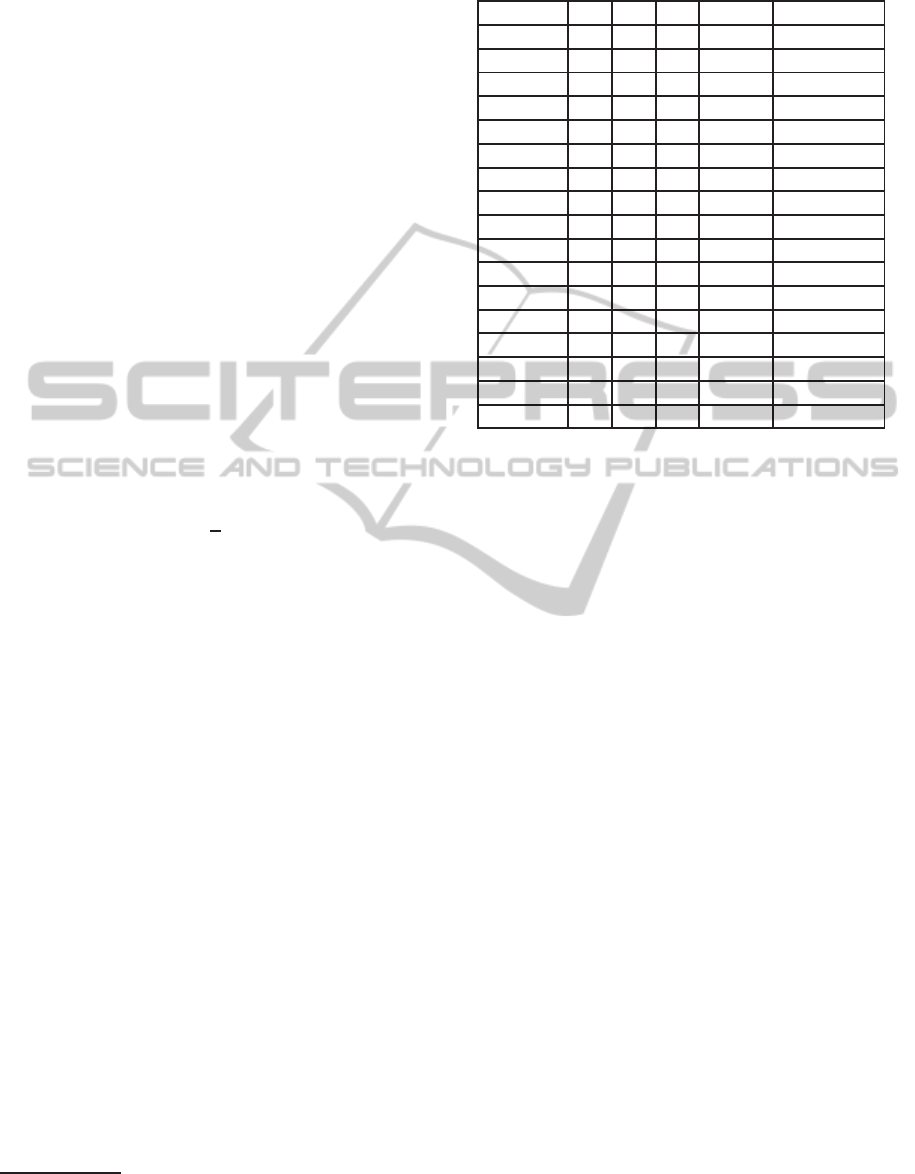
Table 1: Simulation results with different k values.
St.dev k1 k2 k3 Hits Percentage
0.01 1 61 56 9944 99.4 %
0.1 1 61 56 8832 88.3 %
1 1 61 56 9388 93.9 %
0.01 1 97 32 9838 98.4 %
0.1 1 97 32 9417 94.2 %
1 1 97 32 9806 98.1 %
0.01 2 51 17 9810 98.1 %
0.1 2 51 17 7246 72.5 %
1 2 51 17 9818 98.2 %
0.01 1 70 22 9963 99.6 %
0.1 1 70 22 9074 90.7 %
1 1 70 22 9823 98.2 %
0.01-1.5 1 70 22 9286 92.9 %
0.01 1 90 33 9878 98.8 %
0.1 1 90 33 9366 93.7 %
1 1 90 33 9784 97.8 %
0.01-1.5 1 90 33 96605 96.6 %
The optimized k-values are placed in Table 1 with
the related simulation results with 10,000 runs for
each row. The ”St.dev” column in the Table 1 indi-
cates which standard deviation is used when gener-
ating the randomized initial angular velocities. The
”Hits” column gives the number of times where the
energy function was able to predict the equilibrium
which required least energy to reach. The last row
contains 100,000 runs of simulations, which are con-
ducted with varying standard deviation in equal steps
from 0.01 to 1.5 rad/s in the initial angular velocities.
5.1 Error Analysis
Error analysis is done for the three methods;
”InitChoice” is the initial choice equilibrium method
introduced by (Kristiansen, 2008), ”StatScheme” is
the method called statistical scheme by (Schlanbusch,
2012) and the last one ”OpEquEnFunc” is the opti-
mized equilibrium energy function developed in this
paper. Through 10,000 maneuver situations Table 2
counts the incidents where the prediction is correct.
In the situations where the control solution is not lead-
ing the rigid body to the optimal equilibrium, the con-
troller will use extra energy. The column ”EnergyD-
iff” gives the percentage rate between the controller’s
actual used energy, and the energy used if the opti-
mal equilibrium point were chosen all the time. It can
be seen that the statistical scheme method and the op-
timized equilibrium energy function performs much
better than the initial choice method, the best method
is the one based of the equilibrium energy function.
In Table 3 the simulation results for maneuvers
with the use of the best optimized equilibrium energy
TheOptimalQuaternionEquilibriumPoint-UsinganEnergyFunctiontoChoosetheOptimalQuaternionEquilibrium
Point
351

Table 2: Energy Table Different methods.
St.dev Hit EnergyDiff% Pred.Method
0.01 9737 0.64%
InitChoice0.1 5410 31.94%
1 872 22.55%
0.01 9959 0.01%
StatScheme0.1 9089 1.70%
1 9209 0.62%
0.01 9888 0.07%
OpEquEnFunc0.1 9356 0.60%
1 9773 0.45%
Table 3: Average Energy Difference.
St.dev EnergyDiff Hit EnergyDiff Non-Hit
0.01 0.169 0.016
0.1 0.060 0.004
1 3.366 0.178
function are presented. With 1000 trials for each stan-
dard deviation three simulations runs were conducted.
The column ”EnergyDiff Hit” gives the difference in
the energy consumption of the controller rotating ei-
ther to the positive or the negative equilibrium in the
situations when the method chooses the optimal equi-
librium. ”EnergyDiff Non-Hit” is the energy differ-
ence when the prediction fails. The result indicates
that the prediction method struggles in the situations
where the difference in energy is small, thus it can be
concluded that in general there is a minimal use of ex-
tra energy when the wrong equilibrium is predicted.
6 CONCLUSIONS
In this paper a prediction function for choosing the
optimal equilibrium for a rotational sphere is pre-
sented. This function is called the equilibrium en-
ergy function, and through the initial attitude values
of the rotational object, the best equilibrium point is
chosen. Simulation results show that this prediction
function is able to predict the optimal equilibrium in
nearly 97% of the maneuvers.
The energy function is only simulated in a closed-
loop system with no perturbing torques, the only act-
ing force on the dynamical model is the controller’s
attitude torque. It is recommended to investigate how
perturbing forces will affect the prediction of the op-
timal equilibrium.
REFERENCES
Bhat, S. P. and Bernstein, D. S. (2000). A topological
obstruction to continuous global stabilization of rota-
tional motion and the unwinding phenomenon. Sys-
tems & Control Letters, 39(1):63–70.
Egeland, O. and Gravdahl, J. T. (2002). Modeling and Simu-
lation for Automatic Control. Marine Cybernetics AS.
ISBN: 82-92356-01-0.
Fjellstad, O.-E. (1994). Control of Unmanned Underwa-
ter Vehicles on Six Degrees of Freedom. A Quaternion
Feedback Approach. NTNU, Dep of Engineering Cy-
bernetics. Dr.ing thesis Report 94-92-W.
Hahn, W. (1967). Stability of Motion. Springer-Verlag.
ISBN: 9783540038290.
Khalil, H. K. (2002). Nonlinear Systems. Prentice Hall.
ISBN: 978-01-306-7389-3.
Kristiansen, R. (2008). Dynamic Synchronization of Space-
craft. Modeling and Coordinated Control of Leader-
Follower Spacecraft Formations. NTNU, Dep of En-
gineering Cybernetics. Dr.ing thesis 2008:115 ISBN:
978-82-471-8317-5.
Mayhew, C. G., Sanfelice, R. G., and Teel, A. R. (2009).
Robust global asymptotic attitude stabilization of a
rigid body by quaternion-based hybrid feedback. In
Proceedings of the 48th IEEE Conference on Deci-
sion and Control, held jointly with the 28th Chinese
Control Conference, pages 2522–2527, Shanghai, P.
R. China.
Paden, B. and Panja, R. (1988). Globally asymptotically
stable ’PD+’ controller for robot manipulators. Inter-
national Journal of Control, 47(6):1697–1712.
Schlanbusch, R. (2012). Control of Rigid Bodies with ap-
plications to leader-follower spacecraft formations.
NTNU, Dep of Engineering Cybernetics. Dr.ing thesis
2012:49 ISBN: 978-82-471-3365-1.
Sidi, M. J. (1997). Spacecraft Dynamics & Control. A prac-
tical engineering approach. Cambridge University
Press. ISBN: 0-521-78780-7.
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
352
