The Parameter Optimization in Multiple Layered Deduplication System

Mikito Ogata

and Norihisa Komoda

Hitachi Computer Peripherals Co., Ltd., 781 Sakai, Nakai-machi, Ashigarakami-gun, 259-0180, Kanagawa, Japan

Osaka University, 2-1 Yamadaoka, Suita, 565-0824, Osaka, Japan

Keywords:

Deduplication, Backup, Capacity Optimization, Enterprise Storage.

Abstract:

This paper proposes a multiple layered deduplication system for backup operation in IT environment. The

proposed system reduces the duplication in data by using a series of algorithms which are installed with

different chunk sizes in descendent order. Our research deﬁnes the models and formula for the cumulative

deduplication rate and processing time over multiple layers of the system, then, points out the efﬁciency is

heavily affected by how to assign the chunk sizes in each layer in order to achieve the optimal assignment.

Finally, the efﬁciency of the proposal is compared to a conventional single layer deduplication system to assure

the improvement.

1 INTRODUCTION

Due to the explosive increase of the data in IT sys-

tem, the resource usage, the processing time and the

managing cost for backup operation are becoming a

burden to the system, while it is recognized as an in-

dispensable operation to protect the data in case of

unpredictable disaster. Major requirements to backup

operations are to shorten the processing time and to

reduce the resource usage, especially storage capac-

ity. Recently, the technology called deduplication has

become popular to reduce the burden. This is a tech-

nology to eliminate the duplication of the backup tar-

get data and store only unique data in the storage. The

reduction of stored data reduces not only the backup

storage cost but also other resources running work-

load. Various techniques have been proposed so far

to provide more deduction with less processing time

from the point view of more cost-effective backup op-

eration(Y. Tan et al., 2010)(Y. Won et al., 2008)(B.

Zhu et al., 2008). However, the trade-off between the

improvement of the rate and the time makes it difﬁ-

cult to improve both rate and time simultaneously.

This paper points out the trade-off is hard to over-

come only by using single layer deduplication sys-

tem, then, proposes the multiple layered deduplica-

tion system breaks the trade-off and achieves higher

efﬁciency than the conventional one. We make the

formula to represent the efﬁciency, then, deﬁne Pareto

optimal solution and analyze the tendency of the af-

fection of chunk sizes of each layer in order to max-

imize the rate or minimize the processing time, ﬁ-

nally, show the improvement of our proposed method

in comparison to the conventional method.

2 CONVENTIONAL APPROACH

AND THE ISSUES

2.1 Single Layer Deduplication System

The conventional deduplication backup system con-

sists of single module, which has the associated dedu-

plication algorithm. The module analyzes the tar-

get data, identify the segments, distinguish the du-

plicated area from the unique or newly updated area,

then transfer and store only the unique data in the

storage. Backup target data includes various types of

ﬁles, such as imaging, documents, compressed ﬁles,

structured M2M data and so on. The duplication

level included in the data also depends on the environ-

ments, for example some are scarcely duplicated be-

cause it was much edited, changed or updated, some

are densely duplicated because it was rarely changed,

just replicated or copied, and so on.

Figure 1 shows the typical operational ﬂow of the

deduplicationprocess from reading the targetdata and

ﬁnalizing to store the unique data.

The size of the box is not to scale. A

module divides the target data in small segments

called ’Chunk’s which are the unit of reduce or

143

Ogata M. and Komoda N..

The Parameter Optimization in Multiple Layered Deduplication System.

DOI: 10.5220/0004423601430150

In Proceedings of the 15th International Conference on Enterprise Information Systems (ICEIS-2013), pages 143-150

ISBN: 978-989-8565-60-0

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Deduplication process.

store(Chunking). Commonly used dividing mech-

anism is ﬁxed length chunking or variable length

chunking. Fixed length chunking divides the data into

the same length chunks. Variable length chunking

divides into different length chunks. Typical imple-

mentation of variable length chunking scans the data

from the starting bytes to the end in sequence with

short length window using like Rabin’s algorithm(M.

O. Rabin, 1981), then a special value in the window

is recognized as a boundary of the chunks(U. Man-

ber, 1994)(A. Muthitacharoen et al., 2001). This pa-

per call the value ’anchor’. The average chunk size is

deﬁned from how many bits is taken in the window

bandwidth. Next, the module calculates the unique

code from the chunk data to analyze the similarity

of chunks(Fingerprinting). The codes are calculated

for example by SHA-1, SHA-256, MD5 algorithms(J.

Burrows and D. O. C. W. DC, 1995)(R. Rivest, 1992).

This paper call the codes ’ﬁngerprint’. Next the mod-

ule decides the uniqueness of each chunk using the

codes(Decision), such that the chunk is duplicated

that the same chunk has been stored or not duplicated

that all previous chunks are different. Finally, the

module write out only the unique data into the stor-

age(Writing).

Backup target data includes various types of ﬁles,

such as images, documents, compressed ﬁles, struc-

tured M2M data and so on(N. Park and D J. Lilj,

2010). The duplication level included in the data

also depends on the environments, for example some

are scarcely duplicated because it was much edited,

changed or updated, some are densely duplicated be-

cause it was rarely changed, just replicated or copied,

and so on.

2.2 Issues

Many approaches have been proposed and imple-

mented with the aim of increasing the deduplica-

tion rate and decreasing the processing time. These

approaches are applied only for the improvement

of single layer deduplication system. Some typical

techniques are to choose ﬁxed or variable chunking

method, use bloom ﬁlter, construct the layered index

table and become aware of the data contents and so

on(Y. Tan et al., 2010)(C. Liu et al., 2008)(Y. Won

et al., 2008)(B. Zhu et al., 2008). How to choose the

adequate chunk size in practice is a sensitive factor

of the algorithm, because that affects the total sys-

tem behavior. In many cases, it is determined based

on the reasonable balance of the performance and the

deduplication capability for a hypothetical environ-

ment(D. Meister and A. Brinkmann, 2009)(C. Dub-

nicki et al., 2009)(Quantum Corporation, 2009)(EMC

Corporation, 2010)(G. Wallace et al., 2012).

The trade-off between the chunk size and the pro-

cessing time is not easy to overcome. A smaller

chunk size provides more precise reduction of dupli-

cation, a bigger one provides more coarse. At the

same time, a smaller chunk size requires more CPU

and IO intensive processing time, a bigger one does

less time. Further, it is a non-linear correlation, that

is, for a smaller chunk size, the processing time in-

creases more steeply as the size decreases.

On the other hand, in typical user environment,

the time tolerance for backup operation is pre-deﬁned.

The time tolerance is decided to minimize the impact

by an operation for system continuity. One important

factor is a period of time during which backup are

permitted to run. It should be decided to assure the

least interference with normal operations. We call it

as Backup-window. In these cases, even if the system

desires more precise deduplication for reducing the

storing capacity and cost, the Backup-window cannot

allow to use the adequate small size. In practical en-

vironment, bigger chunk size is adapted to maintain

required performance as a compromise.

In addition, smaller chunk size causes disadvan-

tages as well as advantages, for example, the smaller

chunk works efﬁciently to reduce the duplication in

case that the duplicate area is adequately spread out

across the data, but works inefﬁciently when the du-

plicate area is heavily or sparsely localized. When the

duplication is heavy or sparse, smaller chunk wastes

the time of chunking and decision. The continuous

appearance of duplicate area or unique area cause less

productive chunking process. In this case, smaller

chunk size is not beneﬁcial in comparison with bigger

chunk size. In typical user environment, periodical

full backup scenario is popular to help a safe disas-

ter recovery, in this situation, the target data includes

a lot of duplicate area, therefore smaller chunk size

may be inefﬁcient. On the other hand, in the situation

when periodical differential backup scenario is used

to reduce a excessive cost, the target data includes du-

plicate area with less density, ex. a half. Thus, the ef-

ﬁciency of the chunk size depends on the amount and

locality of duplication embedded in the target data.

This makes it difﬁcult to choose the size uniformly

over all different environments.

ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems

144

3 MULTIPLE LAYERED

DEDUPLICATION SYSTEM

3.1 Overview

Analysis described above indicates it would be bene-

ﬁcial to the system if a new approach can increase the

deduplication rate with less penalty for the processing

time. In addition, if the implementation provides sta-

bility even in case of densely or sparsely duplicated

data, it is useful to conﬁgure universal backup sys-

tems over various environments. We propose a multi-

ple layered deduplication system that can reduce the

duplication by using bigger chunk size in case that the

duplication is heavier and by using smaller chunk size

in case that the duplication is lighter.

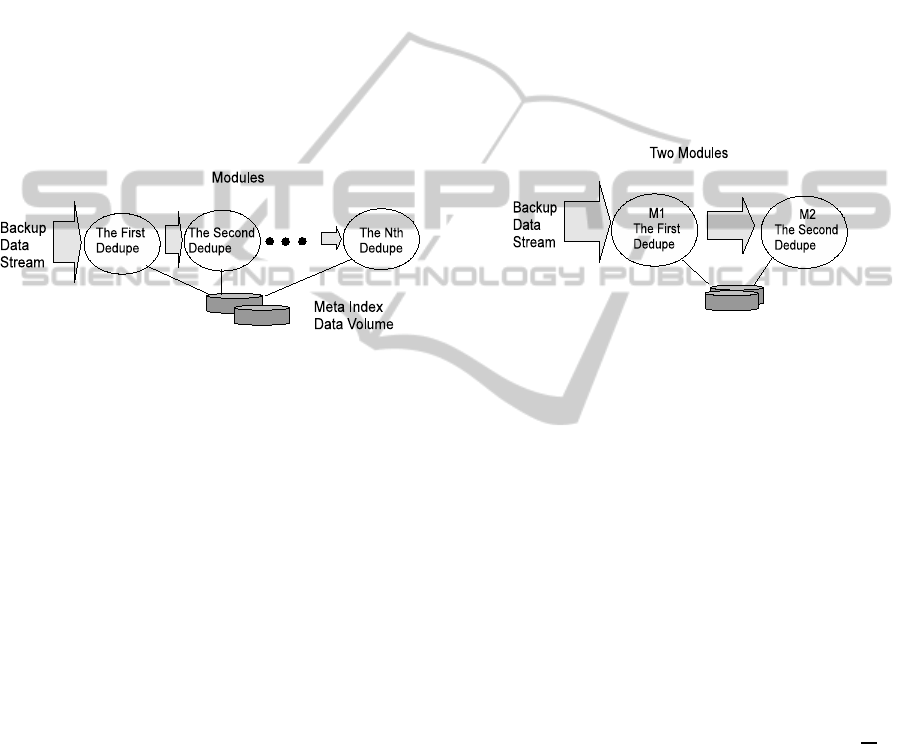
Figure 2: Multiple layered deduplication.

Figure 2 shows the system conﬁguration of multi-

ple layered deduplication system. Backup target data

are deduplicated by a series of modules. Each module

has an independent deduplication algorithm installed.

The data are ingested into the ﬁrst module for the ﬁrst

reduction, then the residual data are ingested from the

ﬁrst module into the second module for the second re-

duction, and the same shall apply hereafter.

Backup target data includes duplicated area,

which is equal to previously stored data, as well as

unique area, which does not match any previous one.

Here, the rate of amount of duplicated area to all of

data is called ’Duplication Rate’. How much data can

be reduced by a module depends on the algorithm in-

stalled in it, especially the chunk size. We implement

the chunk size in descending order over the layers.

The time tolerance is predeﬁned as Backup-window.

In practice, the implementation of multiple lay-

ered deduplication system happen to produce an ex-

cessive capacity tentatively during the process. The

story is that an original data is ingested, duplicated

portion are checked and removed while retaining new

chunks by the ﬁrst module, then the new chunks are

ingested into the second module. It divides the chunk

in smaller chunks and checks the duplication more

precisely. At ﬁrst changing timing, which is, the ﬁrst

time when a chunk is re-chunked by the second mod-

ule after the time when the chunk is stored by the ﬁrst

module, this may cause an excessive capacity due to

duplicate storing. However spacial locality character-

istic which is inherent in the data eliminate the excess

and recover the inefﬁciency through the consecutive

generated backup operations.

3.2 Process of Dual Layered

Deduplication System

Theoretically, our proposed system can be conﬁgured

with two layers, ex. three layers, four layers, and so

on, howeverfrom the implementation point view, dual

layered conﬁguration which consists of two layers is

practical. Hereafter, we focus on two layers conﬁgu-

ration, as a ’dual layered deduplication system’.

Figure 3: Dual layered deduplication.

Figure 3 shows the conﬁguration of dual layered

deduplication system.

is the ﬁrst module and M

is the second. Both

use variable length chunking method. The target data

is ingested into M

ﬁrst and reduced, then the residual

data after the M

reduction is ingested into M

and re-

duced. Only the residual data after M

are stored in

the ﬁnal storage as a deduplicated data.

Assuming M

has 32KB chunk size with 1ms of

processing time, M

has 8KB with 1.25ms. Fig-

ure 4 shows an example of the improvement. The

backup target data is 160KB length, is divided into

ﬁve chunks by M

variable size chunking and twenty

chunks by M

in average. Because the length of each

chunk generally differs due to the chunk boundaries

cut by anchor value, only the average length are as-

sumed. Target data has Duplication Rate of 0.9 (=

Three allocation of modules for target data, such

as M

-only, M

1,2

-combined, provide differ-

ent deduplication rate and processing time, which are

listed in Table 1.

The allocation of M

1,2

-combined provides the

maximum deduplication rate with shorter processing

time than M

-only. M

-only provides the shortest pro-

cessing time but with less deduplication rate. M

-only

has the maximum deduplication rate with the longest

processing time.

As a note for this example, the boundaries of

chunking by M

and M

do not always match when

TheParameterOptimizationinMultipleLayeredDeduplicationSystem

145

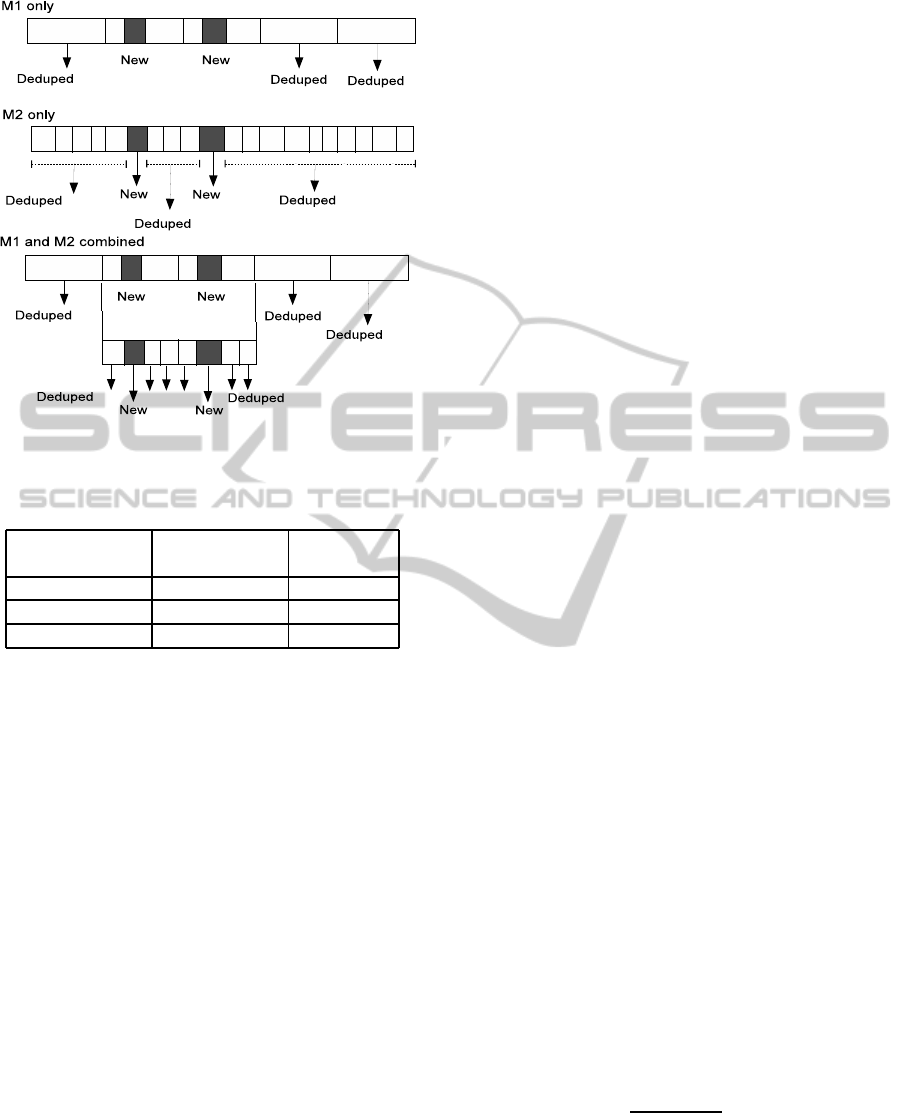
Figure 4: Example of deduplication by two layered method.

Table 1: Total processing time and deduplication ratio by

three allocation scenarios.

Allocation Deduplication Processing

scenario rate [%] time [ms.]

-only 60 5

-only 90 25

1,2

-combined 90 15

the system use anchor type variable chunkingmethod,

because it cannot assure the identical boundaries for

both.

In above system, the efﬁciency strongly depends

on the chunk sizes installed in M

, M

and Duplica-

tion Rate. If M

chunk size becomes bigger, M

pro-

cessing time is shortened but the deduplication rate

is also decreased. In addition, bigger chunk size in

causes heavier process in M

as a next layer. In

this case, bigger chunk size in M

may spoil the ben-

eﬁt of load distribution between the two layers. Con-

versely, if M

chunk size become smaller, M

pro-

cessing time is increased and the deduplication rate is

also increased. In this case, smaller chunk size in M

may spoil the beneﬁt of fast reduction in early layer.

There is the balanced combination of chunk sizes in-

stalled in both M

and M

. We propose how these

chunk sizes should be chosen to tune the efﬁciency,

considering the deduplication rate or the processing

time.

4 MODELING OF DUAL

LAYERED DEDUPLICATION

SYSTEM

4.1 System Deduplication Rate (SDR)

and System Processing Time Ratio

(SPT)

The system has two modules as M

(i=1,2). Modules

implement SHA type functions for FingerPrinting, a

bloom ﬁlter as an initial decision and index tables ma-

nipulating with binary search algorithm. Let D

(r) be

a rate of the amount of data that M

reduces in the

total amount, called Module Deduplication Rate, and

(r) be the processing time ratio that M

takes, called

Module Processing Time Ratio. For convenience, we

use here a ratio instead of an absolute time value for a

module processing time without losing generality, be-

cause the time varies depending on the data amount or

the system conﬁguration. The base of the ratio can be

chosen in many ways, here we use the value of a to-

tal processing time except a decision time, because all

processes other than decision are considered indepen-

dent from the chunk size and therefore takes relatively

constant time. On the other hand, the decision time is

heavily depends on the chunk size. We assign the ex-

act values of D

(r), T

(r) in the following evaluation

by measurement approach.

We generate the formula of the cumulative dedu-

plication rate and the processing time as a conjunction

of both M

and M

. The ratio of residual data by M

can be computed 1-D

) as a difference of reduced

amount of data from the total amount. These resid-

ual data still includes the duplication area as well as

unique area. The ratio r

, the Duplication Rate of the

residual data from M

ingesting into M

can be com-

puted as 1-(1-r

)/(1-D

))=(r

-D

))/(1-D

)).

As a conclusion, Eq. (1), Eq. (2) and Eq. (3) are

deﬁned as the cumulative deduplication rate, which is

D, and the processing time ratio, which is T. We call

D as System Deduplication Rate, or SDR in short, and

T as System Processing Time Ratio, or SPT.

D = D

) + (1− D

))D

) (1)

T = T

) + (1− D

))T

) (2)

− D

)

1− D

)

(3)

The condition that our dual layered deduplication

system provide higher SDR is deﬁned in Eq. (4).

SPT = T

) + (1− D

))T

)

< T

) (4)

ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems

146

In case of the single layer deduplication system,

the value which corresponds to SDR is D

) and to

SPT is T

4.2 Optimization of Chunk Sizes

Due to the negative correlation between Module

Deduplication Rate and Module Processing Time Ra-

tio, to attempt to maximize the improvement for one

of them decreases the other. This is the case of single

layer deduplication system. For dual layered dedupli-

cation system, two chunk sizes provide various values

of SDR and SPT depending on the combination. The

set of combination of a chunk size build a Pareto op-

timal solution for two objectives, such as maximizing

SDR or minimizing SPT. The choice of the unique

combination relies on the individual situation of each

system.

Let the chunk size of M

and M

be L

, L

respec-

tively, and (L

, L

) be a combination of chunk sizes.

In practical usage, the minimum value of chunk size

is 2KB, maximum is 128KB. Therefore, we assume

, L

are integers, 2 ≤ L

, L

≤ 128 and L

> L

from the deﬁnition. The Pareto optimal solution is

computed from the following equations. D of SDR

and T of SPT are functions of L1, L2 and r.

maximize D(L

, L

, r) (5)

minimize T(L

, L

, r) (6)

subject to D(L

, L

, r) ≥ SingleRate, (7)

T(L

, L

, r)V ≤ TimeConstraint, (8)

, L

) ∈ SetX

Here,

SetX = {(L

, L

) | L

, L

∈ N, 2 ≤ L

, L

≤ 128,

> L

}

D(L

, L

, r) : System Deduplication Rate (SDR)

T(L

, L

, r) : System Deduplication Processing

Time Ratio (SPT)

TimeConstraint : Backup-window

SingleRate : Deduplication Rate of single

deduplication system as a base.

V : Amount of backup target data

5 EVALUATION OF DUAL

LAYERED DEDUPLICATION

5.1 Module Deduplication Rate and

Module Processing Time Ratio

A sample of measurement of Module Deduplication

Rate and the Module Processing Time Ratio is shown

0.0 0.2 0.4 0.6 0.8 1.0

Duplication rate

Deduped rate (measurement)

8KB Chunk

32KB Chunk

0.0 0.2 0.4 0.6 0.8 1.0

1.0 1.5 2.0 2.5 3.0

Duplication rate

Processing time ratio (measurement)

8KB Chunk

32KB Chunk

Figure 5: Measured deduplication rates and processing time

ratios.

in ﬁgure 5. The curve indicates the case of chunk

size of 8KB and 32KB. In the following experiments,

Module Deduplication Rate and the Module Process-

ing Time Ratio for other chunk sizes are estimated

based on these values.

0.0 0.2 0.4 0.6 0.8

0 1 2 3 4 5

Duplication rate

Module Processing Time ratio

128KB 64KB

32KB

16KB

8KB

4KB

2KB

r=0.4

r=0.6

r=0.8

Figure 6: Single layer deduplication for r=0.4,0.6,0.8.

Figure 6 shows the correlation of a Module Pro-

cessing Time Ratio under varying chunk sizes with a

parameter of Duplication Rate ’r’. r is set to 0.4, 0.6

and 0.8. The chunk sizes are 2, 4, 8, 16, 32, 64 and

128KB. X axis means Duplication Rate, Y axis means

Module Processing Time Ratio. The smaller chunk

size is, because of their capability of more precise

deduplication, the higher the Module Deduplication

Rate is. That is asymptotic to the ideal deduplication

value of Duplication Rate itself. The ﬁgure clariﬁes

the heavy negative and nonlinear correlation.

5.2 Pareto Optimal Solution of Chunk

Sizes

The set of chunk sizes of a multiple layered dedu-

plication system generates a Pareto optimal solution.

Figure 7 shows the comparison of the single layer

deduplication system and the dual layered dedupli-

cation system in case of Duplication Rate equal to

0.7. X axis means SDR, Y axis means SPT. The dot-

ted line in the ﬁgure indicates the correlation over the

chunk sizes in the case of the single layer deduplica-

tion system, solid lines indicate in cases of dual lay-

TheParameterOptimizationinMultipleLayeredDeduplicationSystem

147

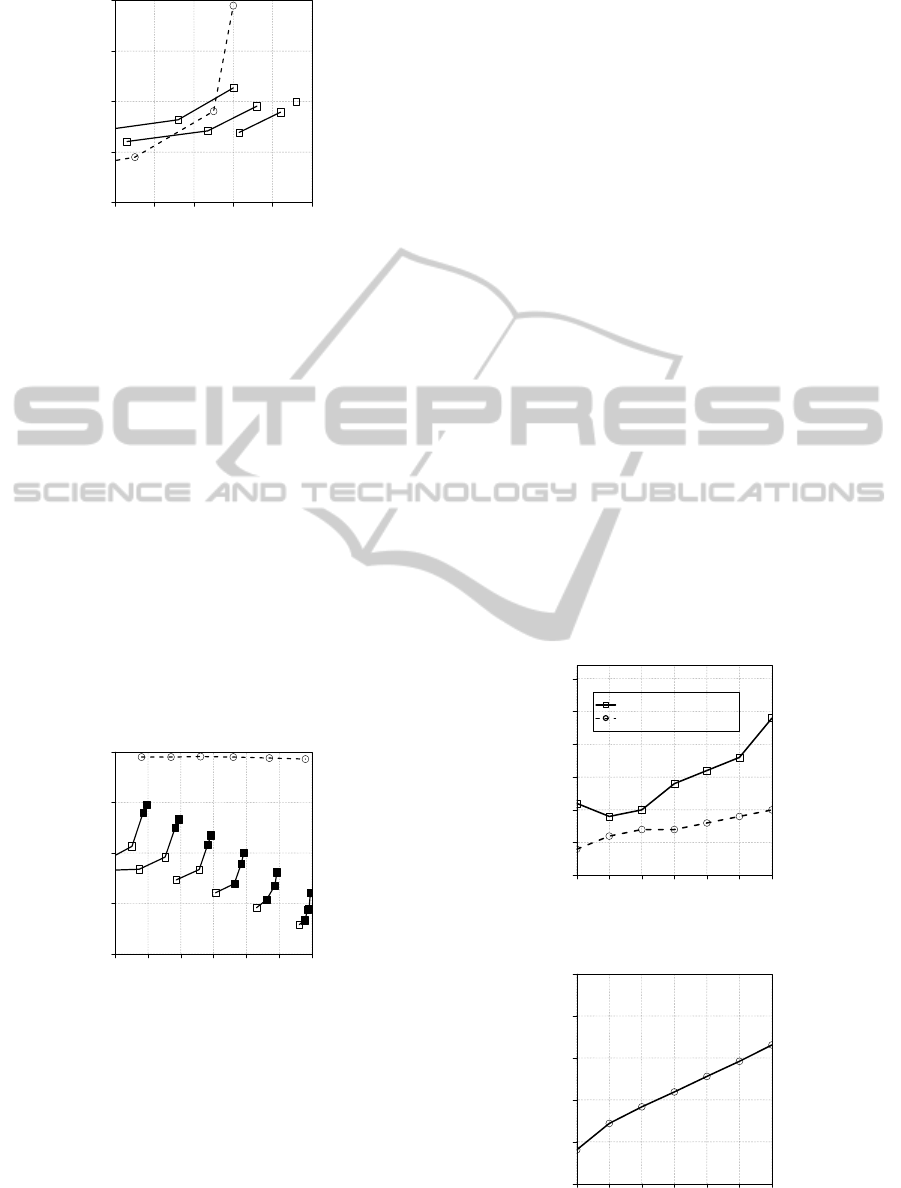
0.60 0.62 0.64 0.66 0.68 0.70

1 2 3 4 5

SDR

SPT

Single layer

Multiple layers

(64,8)

(64,4)

(8)

(4)

(2)

(32,8)

(32,4)

(16,8)

(16,4)

(8,4)

Figure 7: Dual layered deduplication for r=0.7.

ered deduplication system. The numbers and pairs

of numbers means the associated chunk sizes. As-

signment of smaller chunk size as the ﬁrst or second

module push the SDR increasing and conversing for

the ideal number of reduction. The SPT is increasing

by using smaller chunk sizes in both systems, how-

ever the increment is defused from steep degradation

in dual layered system.

When a base of chunk size is assumed in single

layer system, the set of combinations of chunk sizes

in dual layered system can be ﬁxed so that dual lay-

ered system provide the higher SDR and shorter SPT.

The set varies depending on which chunk size is as-

sumed as a base of the comparison. When the chunk

size of 2KB is assumed, it provides 0.66 as SDR and

4.90 as SPT. Then Set of { (16, 8), (16, 4), (8, 4) } is

Pareto optimal solution. Among the solutions, (16, 8)

is a speciﬁc to take the minimum SPT as well as (8,

4) take the maximum SDR.

0.3 0.4 0.5 0.6 0.7 0.8 0.9

1 2 3 4 5

SDR

SPT

Single layer (2KB chunk size)

Multiple layers

(Pareto optimal solution)

(8,4)

(32,16)

(16,8)

(16,4)

Figure 8: Pareto optimal solution by dual layered dedupli-

cation.

Figure 8 shows how the Pareto optimal solutions

varies depends on Duplication Rate of r. The dotted

line indicates the values of 2KB in the single layer

deduplication system as a comparison. The blacked

marks indicates subset of the Pareto optimal solution

whose elements has higher SDR and smaller SPT than

those of single layer deduplication system.

Because the choice of one of them depends on

the individual system requirement, we evaluate here

the aspects of them under changing the parameters

which are considered as a practical requirements in

the systems. The ﬁrst interesting combination is the

one which provides the higher SDR to the conven-

tional single deduplication system with the minimum

SPT. The second is the one which provides the maxi-

mum SDR under predeﬁned Backup-windows, in our

model, equivalent to TimeConstrains. The ﬁrst com-

bination is called ’Minimum Time combination’ and

the second ’Maximum Rate combination’.

5.3 Improvement of System Processing

Time Ratio (SPT)

Figure 9 shows a series of L1 and L2 of Minimum

Time combination under varying Duplication Rate r.

X and Y axis means the Duplication Rate and the

chunk size, respectively, which provide the minimum

SPT. The ﬁgure indicates the aspect that the bigger the

Duplication Rate increase, the bigger the chunk sizes

are. This comes from the reason why the efﬁciency of

ﬁrst layer reduction is higher in case of bigger chunk

size, in addition the efﬁciencyis more dominant while

r increases. Figure 10 shows the improvement. The

improvement increase depending on the Duplication

Rates, ex. 66% in case of 0.9 of r. This comes from

the facts that for the area of high Duplication Rate,

0.3 0.4 0.5 0.6 0.7 0.8 0.9

0 5 10 15 20 25 30

Duplication rate

Optimal chunk size [KB]

The first chunksize

The second chunksize

Figure 9: Minimum Time combination.

0.3 0.4 0.5 0.6 0.7 0.8 0.9

0 20 40 60 80 100

Duplication rate

Improvement of SPT [%]

Figure 10: Improvement of SPT.

ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems

148

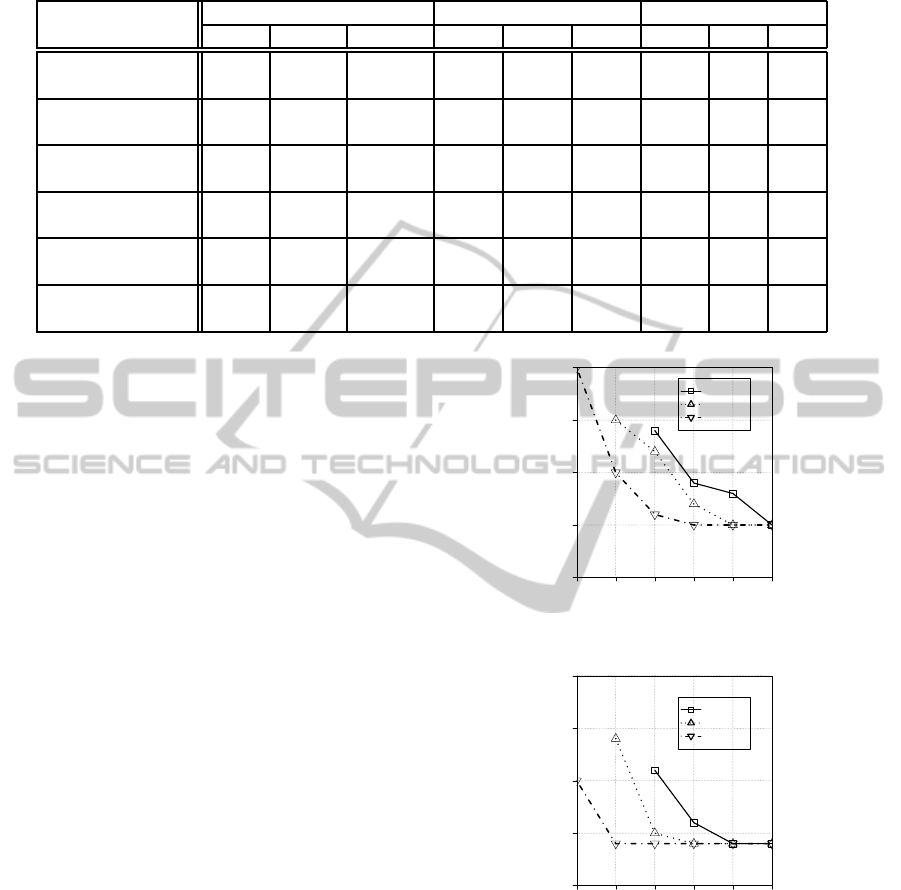
Table 2: Improvement by maximum rate chunk sizes.

Duplication Rate Multiple layered Single layer Improvement [%]

0.4 0.6 0.8 0.4 0.6 0.8 0.4 0.6 0.8

Constraints : 2 NA1 NA1 0.762 0.307 0.504 0.736 - - 3.53

(20, 10) (8) (8) (7)

Constraints : 2.5 NA1 NA1 0.791 0.330 0.533 0.748 - - 5.75

(10, 4) (6) (5) (5)

Constraints : 3 NA2 0.580 0.795 0.354 0.543 0.754 - 6.81 5.44

(12, 5) (6, 4) (4) (4) (4)

Constraints : 3.5 0.380 0.594 0.796 0.354 0.543 0.760 7.34 9.39 4.74

(9, 6) (7, 4) (5, 4) (4) (4) (4)

Constraints : 4 0.395 0.596 0.796 0.354 0.543 0.760 11.58 9.76 4.74

(8, 4) (5, 4) (5, 4) (4) (4) (4)

Constraints : 4.5 0.397 0.596 0.796 0.354 0.543 0.760 12.15 9.76 4.74

(5, 4) (5, 4) (5, 4) (4) (4) (4)

the difference of Module Deduplication Rate over the

chunk sizes decrease but the difference between the

processing time does not decrease in the same corre-

lation. The efﬁciency becomes bigger as the Duplica-

tion Rate increases.

In our experiments, for the area of r under 0.2,

no combination are found to achieve higher rate and

smaller time ratio. This means in case of lower Dupli-

cation Rate, the efﬁciency by bigger chunk size in the

ﬁrst layer is eliminated due to less penalty of single

layer method.

5.4 Improvement of System

Deduplication Rate (SDR)

Figure 11 shows a series of L1 of Maximum Rate

Combination under varying Duplication Rate r and

TimeConstraint. Figure 12 shows the same chart of a

series of L2. r is set to 0.4, 0.6, 0.8. TimeConstraint

is set to 2.0, 2.5, 3.0, 3.5, 4.0, 4.5. X and Y axis

means the TimeConstraint and the chunk size, re-

spectively, which provide the maximum SDR under

the TimeConstraint. The ﬁgure indicates the smaller

TimeConstraint is, the bigger the chunk sizes are.

This is the result that a small chunk size can be pro-

cessed within a small predeﬁned time constraints. In

case of single layer deduplication system, the chunk

size which provides the maximum SDR under the

TimeConstraint is ﬁxed as one value.

Table 2 shows Maximum Time Combination for

each value of r, 0.2, 0.4, 0.6.

The table indicates our dual layered deduplication

system can provide 30 to 40 % improvement for the

SDR and 4 to 12 % improvement for SPT. In the ta-

ble, the notation of ’NA1’ means that no combination

are found to keep the TimeConstraint, and ’NA2’ that

no combination are solved to achieve over the Dedu-

2.0 2.5 3.0 3.5 4.0 4.5

0 5 10 15 20

Time Constraint [ratio]

Optimal first chunksize [KB]

The first Chunksize

= 0.4

= 0.6

= 0.8

Figure 11: L1 of Maximum Rate combination.

2.0 2.5 3.0 3.5 4.0 4.5

0 5 10 15 20

Time Constraint [ratio]

Optimal second chunksize [KB]

The second Chunksize

= 0.4

= 0.6

= 0.8

Figure 12: L2 of Maximum Rate combination.

plication Rate of the single layer method. Figure 13

shows the improvement. The improvement increases

depending on the TimeConstraint and hits the ceiling

which is caused by the boundary of 4KB chunk size.

6 CONCLUSIONS

In this paper, we propose a new approach to improve

TheParameterOptimizationinMultipleLayeredDeduplicationSystem

149

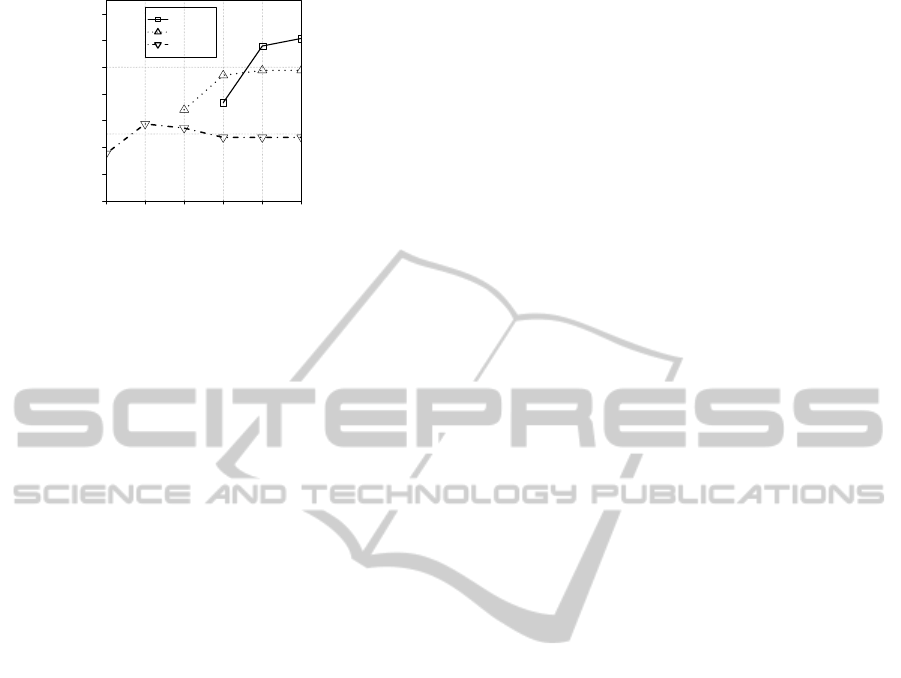
2.0 2.5 3.0 3.5 4.0 4.5

0 2 4 6 8 10 12 14

Time Constraint [ratio]

Improvement of SDR [%]

= 0.4

= 0.6

= 0.8

Figure 13: Improvement of SDR.

the deduplication rate and the performance in backup

operation. Our system consists of a tandem type mul-

tiple layers of deduplication algorithms. The cumu-

lative deduplication rate and processing time ratio are

formularized in the comparison of conventionalsingle

layer deduplication system. Our experiments clarify

the trade-off between the maximum rate and the mini-

mum time, the Pareto optimal solution of chunk sizes,

their dependency with the ﬁle characteristics. The im-

provements are estimated as 17 to 66 % in the dedu-

plication rate and 4 to 12 % in the processing time.

REFERENCES

A. Muthitacharoen, B. Chen, and D. Mazi`eres (2001). A

low-bandwidth network ﬁle system. In Proceeding of

SIGOPS. 18th Symposium on Operating Systems Prin-

ciples., Banff, Canada.

B. Zhu, K. Li, and H. Patterson (2008). Avoiding the

disk bottleneck in the data domain deduplication

ﬁle systeme. In FASTf08: Proceedings of the 6th

USENIX Conference on File and Storage Technolo-

gies, Berkley, CA, USA. USENIX Association.

C. Dubnicki, C.Grayz, et al. (2009). Hydrastor: a scalable

secondary storage. In FAST ’09, 7th USENIX Confer-

ence on File and Storage Technologies.

C. Liu, Y. Lu, C. Shi, G. Lu, D. Lu, and D. Wang

(2008). Admad: Application-driven metadata aware

de-duplication archival storage system. In Fifth IEEE

International Workshop on Storage Network Architec-

ture and Parallel I/Os, 2008., SNAPI’08.

D. Meister and A. Brinkmann (May 2009). Multi-level

comparison of data deduplication in a backup sce-

nario. In Proceedings of SYSTOR 2009, The 2nd An-

nual International Systems and Storage Conference.

ACM.

EMC Corporation (2010). EMC Data Domain Boost Soft-

ware.

G. Wallace, F. Douglis, H. Qian, P. Shilane, S. Smaldone,

M. Chamness, and W. Hsu (2012). Characteristics of

backup workloads in production systems. In Proceed-

ings of the 10th USENIX Conference on File and Stor-

age Technologies.

J. Burrows and D. O. C. W. DC (Apritl 1995). Secure hash

standard.

M. O. Rabin (1981). Fingerprinting by random polynomi-

als. Technical report, Department of Computer Sci-

ence, Harvard University.

N. Park and D J. Lilj (2010). Characterizing datasets for

data deduplication in backup applications. In Work-

load Characterization (IISWC), 2010 IEEE Interna-

tional Symposium.

Quantum Corporation (2009). Data deduplication back-

ground: A technical white paper.

R. Rivest (1992). The MD5 Message Digest Algorithm,

RFC 1321.

U. Manber (1994). Finding similar ﬁles in a large ﬁle sys-

tem. In Proceedings of the USENIX Winter 1994 Tech-

nical Conference.

Y. Tan et al. (2010). Dam: A data ownership-aware multi-

layered de-duplication scheme. In 2010 Fifth IEEE

International Conference on Networking, Architecture

and Storage. IDC-Japan.

Y. Won, J. Ban, J. Min, L. Hur, S. Oh, and J. Lee (Sept.

2008). Efﬁcient index lookup for de-duplication

backup system. In Modeling, Analysis and Simulation

of Computers and Telecommunication Systems, 2008.

MASCOTS 2008. IEEE International Symposium on

(Poster Presentation).

ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems

150