
A New Modified Hough Transform Method for Circle Detection
A. Oualid Djekoune
1
, Khadija Messaoudi
2
and Mahmoud Belhocine
1
1
Robotics and Industrial Automation, Advanced Technologies Development Centrem,
Lotissement 20 Août 1956 Baba Hassen, BP17 Baba Hassen, Algiers, Algeria
2
Systems Architectures and Multimedia, Advanced Technologies Development Centre,
Lotissement 20 Août 1956 Baba Hassen, BP17 Baba Hassen, Algiers, Algeria
Keywords: Hough Transform, Incremental Hough Transform, Circle Hough Transform, Circle Detection.
Abstract: The Hough transform is a powerful tool in image analysis, e.g. circle detection is a fundamental issue in
image processing applications of industrial parts or tools. Because of its drawbacks, various modifications
of the basic circle Hough transform (CHT) method have been suggested. This paper presents a modified
method based on the basic CHT algorithm and using no trigonometric calculations in order to improve the
computational performance of the voting process for a good accuracy and robustness of circle detection in a
binary image. This paper also provides the errors analysis of the proposed method against the basic CHT
method to illustrate that it can replace the basic CHT method for small values of the resolution ε of the angle
θ. It then compete the CORDIC algorithm when it is used in a hardware implementation.
1 INTRODUCTION
Shape recognition is one of the most important tasks
in the image processing and pattern recognition.
Many methods for detecting geometric primitives
have been proposed. The Hough transform (HT) and
its extensions constitute a popular and robust method
for extracting analytic curves. It was first applied to
the recognition of straight lines (Duda, 1972) and
later extended to circles (Davies, 1987), ellipses
(Yip, 1992) and arbitrarily shaped objects (Pao,
1992).
The principal concept of the HT is to define a
mapping between an image space and a parameter
space. Each feature point (or a set of feature points)
in an image is mapped to the parameter space to vote
for the parameters whose associated curves pass
through the data point(s). The votes for each curve
are accumulated, and after all the points in an image
have been considered, local maxima in the
parameter space correspond to the parameters of the
detected curves. The curves detection in the image
space therefore become a peak detection problem in
the parameter space. The advantages of the HT
include robustness to noise, robustness to shape
distortions and to occlusions/missing parts of an
object. Its main disadvantage is the fact that
computational and storage requirements of the
algorithm increase as a power of the dimensionality
of the curve. This means that for straight lines the
computational complexity and storage requirements
are O(n
2
), for circles O(n
3
) and for ellipses O(n
5
)
(Dimitrios, 1999).
In view of this disadvantage, in this paper, we
introduce a new modified CHT method, called
Incremental circle Hough transform (ICHT), that is
aimed at improving the voting process. For each
input point in the image, the new method computes
incrementally the circle point coordinates passing
through the input point using new formulation of the
parametric representation of the circle. By using
approximations on cosine and sine in the parametric
representation of the circle, the new formulation is :
easy to use because the point coordinates of the
circle at the iteration n is computed from the
coordinates point of the circle of the iteration n1
by using simple equations; provides a solution to the
use of trigonometric functions that causes problems
in digital device implementations such as FPGA; can
be seen as a solution to the use of the CORDIC
(Cordinate Rotation Digital Computer) algorithm,
the equations used by our ICHT algorithm are
simpler and very suitable for parallelization in the
calculation of circles point coordinates that passing
through the input point in the image.
In this paper, we show in detail the feasibility
5
Djekoune A., Messaoudi K. and Belhocine M..
A New Modified Hough Transform Method for Circle Detection.
DOI: 10.5220/0004424600050012
In Proceedings of the 5th International Joint Conference on Computational Intelligence (ECTA-2013), pages 5-12
ISBN: 978-989-8565-77-8
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

and the simplicity of the introduced method, and so,
it can replace the basic CHT method not only in
software applications but also in hardware
applications.
The paper is organized as follow: In section 2,
we positioning our work relative to some published
CHT methods existing in the literature. In section 3,
we present in more detail our new ICHT method:
Starting with an overview of the basic CHT method
followed by the ICHT algorithm development, the
errors analysis and the implementation. We compare
the ICHT method with the one often used to
overcome the setback of the basic CHT method for
hardware implementation in the section 4. The
conclusion is given in the section 5.
2 BACKGROUND
Extracting circles from images has received more
attention for several decades because an extracted
circle can be used to yield the location of circular
object in many industrial applications. Many
variations on original CHT method have been
proposed to increase its performance. One type of
method address issues of efficiency to reduce
significantly the amount of computation and storage
required to implement the Hough transform (Lavin,
1986), Another type of method replaces the formal
parameterization of the target object with a look-up
table, the Generalized Hough Transform (GHT),
allowing the Hough approach to be used to detect
arbitrary shapes (Ballard, 1981). A third type of
method uses the probabilistic interpretation of the
Hough approach (Stephens, 1990), (Kälviäinen,
1995). Other type of method uses the randomized
selection of edge points and geometrical properties
of the circle (Bandera, 2006); (Xu, 1990); (Chun,
1995), and the edge orientation information of each
edge pixel to reduce the computing time or the
requirement of the accumulator (Kimme, 1975). And
finally the type of method proposes a variety of
voting scheme used in the Hough transform (Siyu,
2009). An excellent reviews of a number of circle
detection methods based on variations of the Hough
transform can be found in (Yuen, 1990).
Other than the software solution of the CHT
drawbacks, we also find in the literature, the
hardware solution which provides an attractive
solution to computationally intensive applications in
real-time whilst maintaining the flexibility of a
software solution (Tagzout, 2001); (Djekoune,
2004). The Hough Transform has traditionally been
implemented using complex processor architecture.
These are either slow or complicated due to the
transform’s intensive calculations of trigonometric,
multiplication and addition operations (Dixon,
2001). To overcome this major setback, the
CORDIC algorithm is used (Dixon, 2001); (Ferhat-
taleb, 2012). The CORDIC algorithm can be used to
calculate elementary trigonometric functions such as
sine, cosine, tangent, and arctangent as well as ln
and exp.
In this context, we present in this work a new
ICHT method aimed at improving the voting
process. This method fully both exploits the
software and the hardware solution advantages
because it doesn't use any trigonometric calculations,
simple to use, easily fitted into digital device, such
as FPGA, without consuming too device resources,
and very suitable for a parallel implementation.
3 THE PROPOSED ICHT
METHOD
3.1 The Basic CHT Method:
An Overview
A circle with center (a,b) and radius r, in a binary
image, is specified by the parameters (a,b,r) in the
equation:
(1)
with (x,y) the set edge pixels that make up the
circumference of this circle.
The parametric representation of the circle is:
cos
sin
(2)
For each edge pixel, the basic Hough transform
method constructs a circular cone, in the (a,b,r)
parameter space (or Hough space), resulting from
the voting process of the (a,b,r) parameters whose
associated circles pass through the considered pixel
by using a fourfold loop over x, y, a and b (Figure
1). This operation runs slowly because it is mainly
due to the both use a large number of mathematical
operations (1) and trigonometric calculations
(2).This raises the computational cost of the
transform, often to unacceptable levels.
For simplicity, some works in the litterature set
the radius to a constant value (hard coded) or
provide the user with the option of setting a range
(maximum and minimum) prior to running the
application, or use the edge direction information to
limit voting to a section of the cone.
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
6

(a)
(b)
Figure 1: Relationship between a binary image plan and
the Hough space. (a) P
1
, P
2
and P
3
are edge pixels
belonging to a same imaginary circle with r
0
the radius
and (a
0
, b
0
) the coordinates of its center. (b) Each edge
pixel from the binary image generates a circular cone in
the Hough space. The cones in the Hough space intersect
at (a
0
, b
0
,r
0
) corresponding to the parameters of the circle
formed by the edge pixels P
1
, P
2
and P
3
.
3.2 The New ICHT Method
a. Algorithm Development. The main goal of
this work is to try to improve the basic CHT to make
it simple to use, and easily adapted and fitted into
the digital device without consuming too device
resources. Thus combining both advantages of hard
and soft solutions described above.
Our improvement mainly concerns the voting
process, it uses new equations, or formulation, of the
parametric representation of a circle. These
equations compute incrementally the coordinates
point of a circle, such that each coordinates point of
a circle at the iteration n is computed from the
coordinates point of the same circle of the iteration
n1. We proceeded as follows:
For discrete values of the angle, (2) is written as
follows (we have used the same notation as in
(Tagzout, 2001) and (Djekoune, 2004):
cos
sin
2
0
2
0
(3)
with n, ε and
are, respectively, the angle index,
the angle resolution and the number of angle values
in the θ interval.
To make (3) as incremental, it must be written in
the following form:
,
,
(4)
ie, the point coordinates of the circle
,
at
the iteration 1 is only computed from the point
coordinates of the circle
,
of the iteration .
By replacing n by n1 in (3), we will have:
cos
cos
1
coscossinsin
sin
sin
1
sincoscossin
(5)
Making the approximation, in the expression above,
on cosine and sine for the small values of the angle
by assuming cosε=1 and sinε=ε. The equation (5)
becomes:
cossin
sin
sincos
cos
(6)
Note that from (3), we can get:
cos
sin
(7)
By replacing (7) in (6), then rearranging the obtained
expression to get the following general expression of
our new ICHT method:
0
2
(8)
ANewModifiedHoughTransformMethodforCircleDetection
7
We can note that (2) and (8) are almost similar
except that (2) is highly dependent to the
trigonometric functions, which is not the case with
(8). We can therefore conclude that (8) is:
- Purely incremental,
- Doesn't use any trigonometric calculations,
- Simple to use,
- Can be seen as a solution to the use of the
CORDIC algorithm (see section 4),
- Can be easily fitted into digital device such as
FPGA,
- Can be very suitable for parallelization.
b. Error Analysis. In the following, we show the
errors, if exist, caused by the above approximations
when using (8) and (2) to draw circles.
When drawing two circles (Circle
and
Circle
) with the same parameters using (8) and
(2), we note that the points of the two circles overlap
for small values of θ and diverge for larger values
of θ (Figure 2).
There are many criteria which can be considered
to evaluate this divergence, but in our study the most
important point relates to errors analysis. The errors
analysis is measured using: the average error
(E
) and the quadratic error (E
)
between the radii resulting from the generated points
using the two above equations; the difference area
(Diff
) and the Jaccard coefficient (Coef
)
to compare the similarity of the two generated
circles. The Jaccard coefficient measures the ratio of
the intersection area of two sets divided by the area
of their union (Jaccard, 1912).
These errors are computed from different values
of the radius R and the resolution ε of the θ angle.
They are expressed as follows:
1
(9)
1
(10)
with R
n
and R
n
the radii computed from
the coordinates point at the n
th
value of θ using (2)
and (8).
It is interesting to note that our new ICHT
method achieves very small errors for small values
of the resolution ε of the angle θ which remain
within a narrow tolerance despite the high that can
have the radius R. But these errors increase
considerably when the resolution ε increases with
high value of the radius R (Figures 3 to 6).
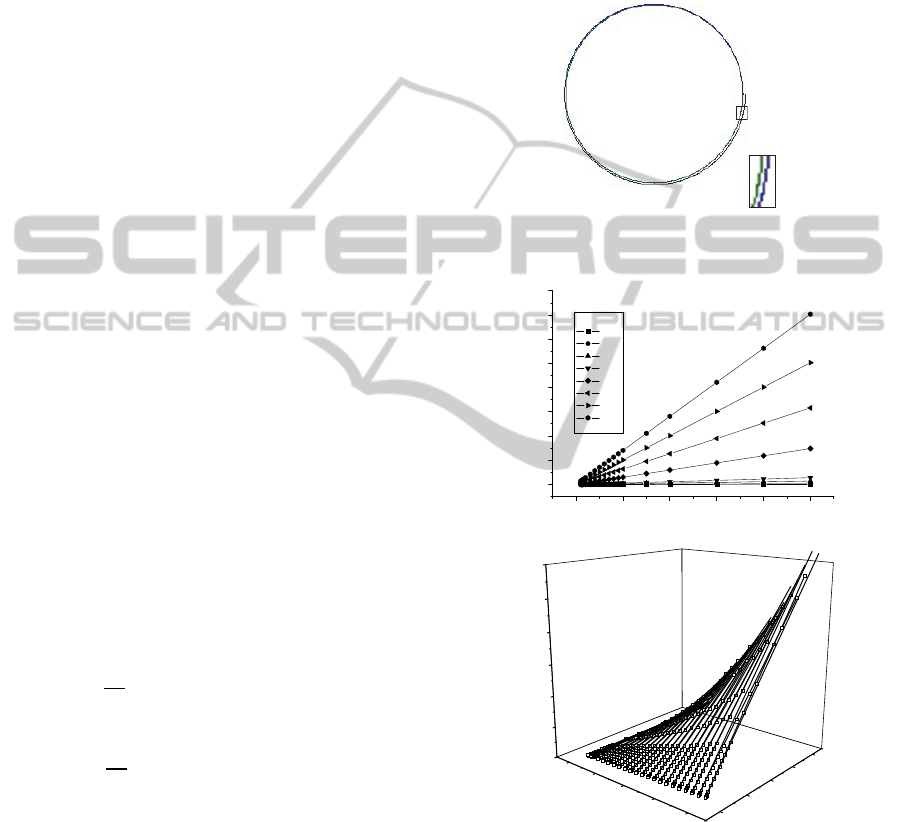
The figures 3 to 6 show that for values of the
resolution ε less than 1°, the errors
,
and
are very small, and
consequently the
value reach the one
value. The one value means that the two circles are
substantially similar. Beyond the value 1° and for
small values of the radius R, the
value
decreases giving rise to significant divergences.
Figure 2: The circles Circle
and Circle
drawn at a
fixed position with radius=100 and ε=0.5°.
(a)
(b)
Figure 3: The average error in (a) 2D and (b) 3D version.
The figures 3 and 4 show that the average error
and the difference area between Circle
and
Circle
circles increases linearly with a slope
depending on the values of the resolution ε of the
angle θ. This gives us an idea of how the computed
points, from expression (8), diverge from those
computed from (2).
0 100 200 300 400 500
0
50
100
150
200
250
300
350
400
0.05
0.1
0.5
1.0
5.0
10.0
15.0
20.0
Average Error
Radius
0
5
10
15
20
0
100
200
300
400
0
50
100
150
200
250
300
A
v
e
r
a
g
e
E
r
r
o
r
R
a
d
i
u
s
E
p
s
i
l
o
n
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
8

(a)
(b)
Figure 4: The quadratic error in (a) 2D and (b) 3D version.
(a)
(b)
Figure 5: The difference area between Circle
and
Circle
circles in (a) 2D and (b) 3D version.
In conclusion, our new ICHT method can replace
the basic CHT method for small values of the
resolution ε of the angle θ with the advantage of
does'nt using any trigonometric calculations, It then
compete the CORDIC algorithm when implemented
into digital device.
(a)
(b)
Figure 6: The Jaccard coefficient in (a) 2D and (b) 3D
version.
Figure 7: The test image.
c. Implementation. The new ICHT method is tested
against the basic CHT method. This will be done to
illustrate the consequences of the used
approximations in the parametric representation of
the circle in the processing time of the voting
process and to see the computational efficiency of
the Hough space of the two methods. The new ICHT
method and the basic CHT method were
implemented in the programming language Matlab
v.7. The implementation was performed using a
0 100 200 300 400 500
-20000
0
20000
40000
60000
80000
100000
120000
140000
160000
180000
200000
Quadratic Error
Radius
0.05
0.1
0.5
1.0
5.0
10.0
15.0
20.0
0
5
10
15
20
0
100
200
300
400
0
20000
40000
60000
80000
100000
120000
Q
u
a
d
r
a
t
i
c
E
r
r
o
r
R
a
d
i
u
s
E
p
s
i
l
o
n
0 100 200 300 400 500
0
20000
40000
60000
80000
100000
120000
140000
160000
0.05
0.1
0.5
1.0
5.0
10.0
15.0
20.0
Diff Area
Radius
0
5
10
15
20
0
100
200
300
400
0
20000
40000
60000
80000
100000
120000
D
i
f
f
A
r
e
a
R
a
d
i
u
s
E
p
s
i
l
o
n
0 100 200 300 400 500
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
0.05
0.1
0.5
1.0
5.0
10.0
15.0
20.0
Jaccard Coe
f
Radius
0
5
10
15
20
0
100
200
300
400
0,0
0,2
0,4
0,6
0,8
1,0
J
a
c
ca
r
d
C
o
e
f
R
a
d
i
u
s
E
p
s
i
l
o
n
ANewModifiedHoughTransformMethodforCircleDetection
9

labtop PC equipped with 2.6 GHz i5 processor and
6GB RAM. A real gray scale image, of size 225x220
pixel is used (Figure 7). The binary edge points
shown in (Figure 8) are obtained by using the
Matlab Canny operator.
The voting process algorithm of the new ICHT
and the basic CHT methods, applied in a real binary
edge image, are performed using
10 and
√
225
220
≅315. The ε resolution
value of the θ angle is initially set by the user.
Figure 8: Binary edge image using Deriche operator.
The table 1 assess the time processing of the two
methods, where the time of the voting process, the
time required to process one binary edge pixel, and
the time ratio are presented. The binary edge image
of the figure 8 is used using different values of the
resolution ε of the θ angle. The processing time per
pixel, in milliseconds, is obtained by dividing the
time of the voting process, expressed in second, by
the number of the binary edge point contained in the
figure 8, in our case this number is equal to 2508.
The time ratio is obtained, in this case, by dividing
the time of the voting process of the basic CHT
method by the time of the voting process of the new
ICHT method. The table 1 not only show that the
new ICHT method is fast more than the basic CHT
method but it is more than two time faster.
Table 1: Processing time of the voting process.
ε(°)
CHT
(s)
ICHT
(s)
Time per
pixel(ms)
CHT/ICHT
Time
ratio
0.05 862.39 412.51 343.85/164.48 2.09
0.1 438 211.60 174.64/84.37 2.07
0.5 96.69 49.55 38.54/19.76 1.95
1.0 50.87 26.24 20.28/10.46 1.94
5.0 10.5 5.15 4.19/2.05 2.04
10.0 5.32 2.51 2.12/1.0 2.12
15.0 3.6 1.62 1.43/0.64 2.22
20.0 2.73 1.20 1.09/0.48 2.27
After evaluating the processing time of the two
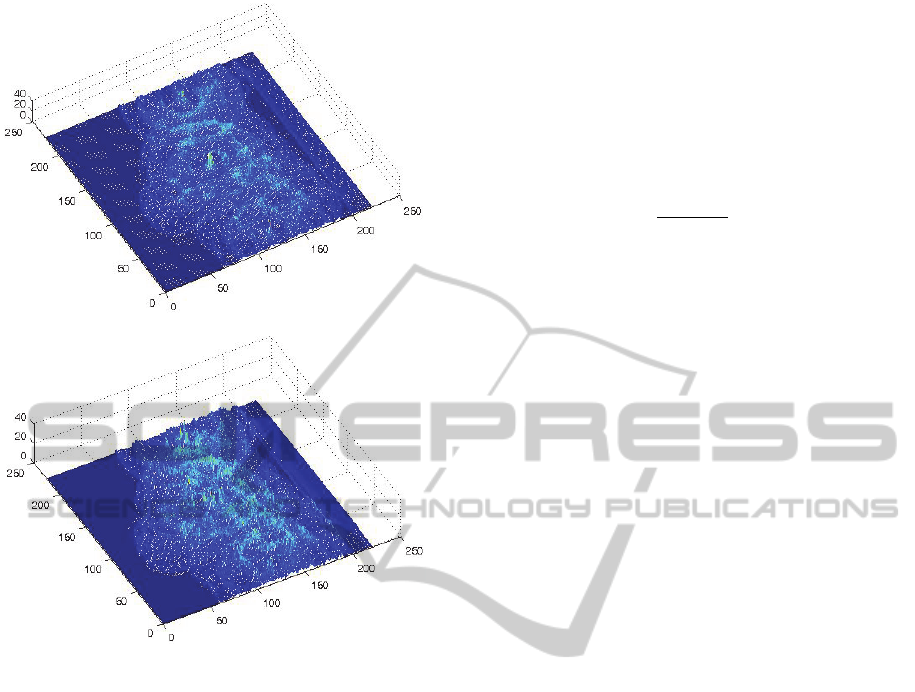
methods, now we try to show the Hough space
obtained from these two methods. The figures 9 and
10 show the plans of the Hough space with a radius
R = 10, and confirm the conclusions done in the
section §3.2. The Hough spaces obtained from these
two methods are the same for values of the
resolution ε less than 1°, and diverge significantly
beyond the value 1°.
(a)
(b)
Figure 9: Hough space plan with radius=20 and ε=0.05°
obtained from both (a) the basic CHT method and (b) our
new ICHT method.
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
10
(a)
(b)
Figure 10: Hough space plan with radius=20 and ε=5°
obtained from both (a) the basic CHT method and (b) our
new ICHT method.
4 THE NEW ICHT METHOD VS
CORDIC ALGORITHM
The CORDIC algorithm, proposed by Volder in
1959 (Volder, 1959), is used to calculate elementary
trigonometric functions such as sine, cosine, tangent,
and arctangent as well as ln and exp. It provides an
iterative method of performing vector rotations by
arbitrary angles using only shifts and adds. The
algorithm is based on the common rotation
equations:
′
cossin
′
cossin
(13)
which rotates a vector in a Cartesian plane by the
angle . These can be rearranged so that:
′
cos∙
tan
′
cos∙
tan
(14)
When restricting the rotation angles so that tanφ
2
, the multiplication by the tangent term is
reduced to simple shift operation. This allows the
vector to be rotated by desired angle in a sequence
of smaller rotations by angle φtan
2
:
∙
∙2
∙
∙2
cos
tan
2
1
12
⁄
1
(15)
The CORDIC algorithm is one of the existing
hardware implementation solutions of the CHT (or
HT) to overcome its intensive calculation of
trigonometric, multiplication and addition
operations. This solution results in a complication of
the final architecture and a significant consumption
of the device resources.
Unlike to the hardware implementation of the
basic CHT where the CORDIC algorithm is used,
our new ICHT method can be hardware
implemented alone which leads better performance
than the implementation of the basic CHT with the
CORDIC algorithm minimizing the used device
resources.
5 CONCLUSIONS
We presented a new modified CHT method with
enhanced formulation for improving the
computational performance and efficiency of the
voting process of the basic CHT. Called Incremental
circle Hough transform (ICHT), the method fully
both exploits the software and the hardware solution
advantages with no trigonometric calculations, it can
be seen as a a solution to the use of the CORDIC
algorithm, and consequently easily fitted into digital
device, such as FPGA, without consuming too
device resources, and very suitable for a parallel
implementation.
We have presented theoretical and errors analysis
of our method, and have shown experimentally that,
for small values of angle, the new method has the
same accuracy as the basic CHT method.
We are currently trying to further improve the
time of the voting process of the proposed ICHT by
changing if possible the expression (8).
ANewModifiedHoughTransformMethodforCircleDetection
11

ACKNOWLEDGEMENTS
The authors would like to thank all those who helped
to achieve this modest work as well as their useful
discussions and comments.
REFERENCES
Ballard, D., 1981. "Generalised Hough transform to detect
arbitrary shapes". In IEEE Trans. Pattern Anal.
Machine Intell.. 13 (2), pp. 111–122.
Bandera, A., Perez-Lorénzo, J.M., Bandera, J.P.,
Sandoval, F., 2006. "Mean shift based clustering of
Hough domain for fast line segment detection", In
Pattern Recognition Lett.. 27 (6), pp. 578–586.
Duda, R., Hart, P., 1972. "Use of the Hough transform to
detect lines and curves in pictures", In Comm. ACM.
15(1), pp.11–15.
Davies, E., 1987. "A modified Hough scheme for general
circle location", In Pattern Recognition Letters. 7,
pp.37–43.
Dimitrios Ioannou, Walter Huda, Andrew F. Laine, 1999.
"Circle recognition through a 2D Hough Transform
and radius histogramming", In Image and Vision
Computing. 17, pp.15–26.
Dixon D.S. Deng, Hossam El Gindy, May 2001. "High-
speed Parameterisable Hough Transform Using
Reconfigurable Hardware", In Proceedings of the Pan-
Sydney area workshop on Visual information
processing. VIP '01. Sydney, Australia, Vol. 11,
pp.51-57.
Djekoune A.O., Achour K., Dec. 2004. “Incremental
Hough Transform: An Improved Algorithm for Digital
Device Implementation”, In Real-Time Imaging. Vol.
10, Issue 6, pp. 351-363.
Ferhat-taleb Alim F., Messaoudi, K., Seddiki, S., and
Kerdjidj, O., 2012. "Modified Circular Hough
Transform using FPGA", In ICM 2012, Algiers.
Ho, Chun, Chen, L., 1995. “A fast ellipse/circle detector
using geometric symmetry”, In Pattern Recognition.
vol.28, no.1, pp: 117-124.
Jaccard, P., 1912. "The distribution of flora in the alpine
zone". In New Phytol. 11 (2), pp.37–50.
Kimme, C., Ballard, D., and Sklansky, J., 1975. “Finding
circles by an array of accumulators”, In Proc. , ACM.
18, pp: 120–122.
Kälviäinen, H., Hirvonen, P., Xu, L., Oja, E., 1995.
"Probabilistic and non-probabilisticHough transforms:
Overview and comparisons", In Image Vision
Comput.. 13 (4), pp. 239–252.
Li, H., Lavin, M.A., LeMaster, R.J., 1986. "Fast Hough
transform: A hierarchical approach", In Computer
Vision Graphics Image Process. 36, pp. 139–161.
Pao, D.C.W., Li, H.F., Jayakumar, R., 1992. "Shapes
recognition using the straight line Hough transform:
theory and generalizaion", In IEEE Transactions on
Pattern Analysis and Machine Intelligence. 14,
pp.1076–1089.
Stephens, R.S., 1990. "A probabilistic approach to the
Hough transform", In Proc. 1990 British Mach. Vis.
Con.. pp. 55–60.
Siyu Guo, Tony Pridmore, Yaguang Kong, Xufang Zhang,
2009. "An improved Hough transform voting scheme
utilizing surround suppression", In Pattern
Recognition Letters. 30, pp. 1241–1252.
Tagzout Samir, Achour Karim, and Djekoune Oualid,
2001. “Hough transform Algorithm for FPGA
implementation”, In Signal Processing, Elsevier, Vol.
81, No. 6, pp. 1295-1301.
Volder. J.E., 1959. "The CORDIC Trigonometric
Computing Technique", In IRE Transactions
on.Electronic Computers, vol. EC-8, N° 3, pp: 330-
334.
Xu, L., Oja, E., Kultanan, P., 1990. “A new curve
detection method: randomized Hough transform
(RHT)”, In Pattern Recognition Letter. vol.11, no.5,
pp: 331-338.
Yip, R., Tam, P., Leung, D., 1992. "Modification of
Hough transform for circles and ellipses detection
using a 2-dimensional array", In Pattern Recognition.
25, pp.1007–1022.
Yuen, H., Princen, J., Illingworth J., Kittler, J., February
1990. "A comparative study of Hough transform
methods for circle finding", In Image and Vision
Computing. Volume 8, Issue 1, pp. 71–77.
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
12
