Deriving the Conceptual Model of a Data Warehouse

from Information Requirements

Natalija Kozmina, Laila Niedrite and Maksims Golubs

Faculty of Computing, University of Latvia, Raina blvd. 19, Riga, Latvia

Keywords: Data Warehouse, Conceptual Model, Requirement Formalization, OLAP Schema Transformation.

Abstract: Business requirements are essential for developing any information system, including a data warehouse.

However, requirements written in natural language may be imprecise. This paper offers a model for

business requirement formalization according to certain peculiarities of elements of multidimensional

models, e.g. the distinction between quantifying and qualifying data. We also propose an algorithm that

generates candidate data warehouse schemas and is based on distinguishing data warehouse schema

elements in formal requirements. Then, resulting schemas are processed by a semi-automated procedure in

order to obtain a data warehouse schema that matches business requirements best of all.

1 INTRODUCTION

Companies should use performance measurement

systems, if they want to succeed in competition with

others. During the performance measurement, its

results should be compared with the target values to

understand, whether goals are achieved or not. For

implementation of a performance measurement

system a data warehouse could be used.

"A data warehouse is a subject-oriented,

integrated, non-volatile, and time-variant collection

of data in support of management decisions"

(Inmon, 2002). Developing a data warehouse that

fits all requirements of potential users is not the

easiest task. There is no common understanding

about the best method for conceptual modeling of

data warehouses and the most expressive modeling

language for that purpose. Conceptual models of

data warehouses can be classified according to their

origination (Rizzi et al., 2006): E/R model based,

UML based, and independent conceptual models,

e.g. Dimensional Fact Model (Golfarelli et al.,

1998). The necessity to develop special conceptual

models for data warehouses is founded on existence

of two types of data that should be modeled –

quantifying and qualifying data, and elements of

multidimensional paradigm, e.g. dimensions,

hierarchies, cubes, whose semantics can’t be

modeled properly with standard modeling

languages. Besides the specialized conceptual

models for data warehouses, developers also need

formal methods to construct these models (Rizzi,

2009). All methods can be classified as supply- or

demand-driven according to the way how the data

warehouse requirements are determined. The

requirements for data warehouses differ from those

applied to other types of systems – here we can

speak about the information requirements (Winter

and Strauch, 2003). In supply-driven methods the

existing models of data sources are investigated to

understand what data is used in an enterprise. In

demand-driven approaches the required data for

analysis needs is established mostly by interviewing

users. However, more new approaches, e.g.

ontology-based (Romero and Abello, 2010), pattern-

based (Jones and Song, 2005), are proposed to gain

the most suitable conceptual model of a data

warehouse for the implementation of the strategy of

an organization and to avoid the limitations of

existing methods. In the supply-driven approach the

constructed conceptual model may not reflect all

analysis needs, because it reflects the operational

needs of data source systems. In the requirement-

driven approach the data warehouse model depends

on interviewed users, their understanding about the

enterprise, and ability to precisely express their

analysis needs.

We propose a method for transforming

information requirements to conceptual model of a

data warehouse. In this case, requirements are

136

Kozmina N., Niedrite L. and Golubs M..

Deriving the Conceptual Model of a Data Warehouse from Information Requirements.

DOI: 10.5220/0004426301360144

In Proceedings of the 15th International Conference on Enterprise Information Systems (ICEIS-2013), pages 136-144

ISBN: 978-989-8565-59-4

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

performance indicators of an organization that are

gathered by interviewing users and formalized in

accordance with the indicators model.

The rest of the paper is organized as follows.

Section 2 describes related work. Section 3

introduces formal model for indicator definition.

Section 4 presents the algorithm that transforms

requirements. Section 5 describes the post-

processing of schemas produced by algorithm.

Section 6 ends the paper with conclusions.

2 RELATED WORK

Demand-driven methods can be divided more

precisely according to the way of identifying

requirements, e.g. user-driven (Westerman, 2001),

(Poe, 1996) process-driven (Kaldeich and Oliveira,

2004), and goal-driven (Giorgini et al., 2005), (List

and Machaczek, 2004) where users are interviewed

and processes, goals, or indicators are modeled and

analyzed to gain precise understanding of analysis

needs of users and the organization. For example,

(Poe, 1996) proposes a catalogue for storage of

users’ interviews to collect end-users’ requirements,

recommends to interview different groups of users

to understand a business completely. In case of the

process-driven approach, a business process is

analyzed, e. g., in (Kaldeich and Oliveira, 2004) the

“AS IS” and “TO BE” process models are

constructed including the analyzed processes, as

well as the corresponding data models. In case of

the goal-driven approach, goals of an enterprise,

goals of analyzed business processes are analyzed

and data that should be analyzed to achieve these

goals is identified. For example, in (Giorgini et al.,

2005) the decisional modeling is performed, facts

are identified and mapped onto entities or relations

of data sources, but hierarchies of each fact are later

constructed by applying supply-driven approach

(Golfarelli et al., 1998).

In information supply-driven approach we can

speak about methods e.g. (Inmon, 2002), (Golfarelli

et al., 1998) that utilize the existing data models of

transaction systems. A data warehouse model is

obtained by transforming models of data sources.

For example, (Golfarelli et al., 1998) analyze many-

to-one associations in the data source models to

construct an attribute tree that is used later to form

dimensions, hierarchies, and other elements of

multidimensional paradigm.

3 THE FORMAL MODEL

FOR INDICATOR DEFINITION

Data warehouses have specific features when they

are used for implementation of performance

measurement systems: new data sources, e.g.

workflow logs, specific data analysis approaches,

e.g. process monitoring based on performance

indicators, and data warehouse model that reflects

the previous two aspects, which may determine the

data items to be included into the data warehouse

model.

Indicators are the focus of data analysis in the

performance measurement process. The definition

of indicators can be expressed on various levels of

formality. We proposed a formal specification of

indicators in our previous work (Niedritis et al.,

2011). At the same time, the data warehousing

models are built to represent the information needs

for data analysis. So, we could perceive indicators

as an information requirement for a data warehouse

system. Therefore, the formalization of indicators

could be based on the nature of elements of

multidimensional models, e.g. the distinction

between quantifying and qualifying data.

The type of an information system to be

developed has some impact on the way of

formulating sentences that express requirements.

Before starting our study, we assumed that

information requirements for data warehouses used

for performance measurement have similar

structure. This assumption was based on our

observations on how the information needs were

described in real life projects. We based the

proposed model also on the structure evaluation of

the sentences that formulate performance indicators

taken from the performance measures database

(Parmenter, 2010).

3.1 Concepts of the Formal Model

of Requirements

The requirement formalization is represented as a

UML class diagram by (Niedritis et al., 2011).

show Refinement Action

month Qualifiyng Data

AVG Aggregation Action

contacts ocurrance Quantifying Data

where

customer type Qualifiyng Data Simple Expression

'key customer' Constant Simp le Expression

Simple Requirement

Condition Type

Operation

Object

Comparison

Simple

Condition

Typified

Condition

Figure 1: Requirement formalization example (Niedritis et

al., 2011).

DerivingtheConceptualModelofaDataWarehousefromInformationRequirements

137

In this paper we use an implementation model of

the requirements formalization for the algorithm

described in Section 4.2, but for better

understanding we give a short description of main

concepts in this section.

Let’s see an indicator example: “Average

number of contacts made with key customers per

month”. Using our proposed requirement model it is

reformulated as follows: “show month, average

(contact occurrence) where customer type is ‘key

customer’ ”. Figure 1 demonstrates the application

of the model. The left column is filled with parts of

the requirement statement and all the rest columns

(left to right) contain names of the model levels.

In the proposed model a requirement can be

classified as Simple or Complex Requirement. A

complex requirement is composed of two or more

simple requirements with an Arithmetical Operator.

A simple requirement consists of a verb (Operation)

that denotes a command, which refers to an Object,

and zero or one Typified Condition. There are two

kinds of data in data warehousing: Quantifying

(measurements) and Qualifying (properties of

measurements). An object is either an instance of

quantifying or qualifying data depending on the

requirement.

A Complex Operation consists of two or more

Actions. There are two possible types of action:

Aggregation (used for calculation and grouping,

“roll-up”) and Refinement (used for information

selection, “drill-down”, as an opposite to an

aggregation). Information refinement is either

showing details, i.e., selecting information about

one or more objects, or slicing, i.e., showing details,

according to a certain constraint (Typified

Condition). Conditions can be simple or complex.

Complex condition joins two or more simple

conditions by Logical Operators (AND, OR, NOT).

Simple condition consists of a Comparison of two

Expressions, for example, “time is greater than

last_access_time – 1 second”. An expression too

may be either a Simple or a Complex Expression. A

complex expression contains two or more simple

expressions with an arithmetical operator between

the simple expressions. A simple expression belongs

either to qualifying data (e.g. “last_access_time”) or

to Constants (e.g. “1 second”).

3.2 The Implementation Model

of Formal Requirements

Formal requirement metadata is implemented using

relational database tables depicted in Figure 2.

Requirements are stored in tables Requirement and

SimpleRequirement. Each business requirement

refers to some theme (Theme), e.g. Finance,

Customer Focus, etc. Simple requirements are

defined by Operation, Object and

TypifiedCondition. An operation is either an

aggregate function (isAggr=1) or a refinement

operation (isAggr=0). An operation can consist of

multiple suboperations, e.g. SUM(AVG(Income)).

To indicate the sequence of them, an attribute

Operation.Index is employed. The value of

Object.Type is either ‘qualifying’ or ‘quantifying’.

A simple condition involves two expressions and

the value of a comparison. The expression type is

defined by Expression.isSimple. A simple

expression consists of either a qualifying data

object, or a constant, and the type of an expression

(Expression.Type) respectively. Otherwise, an

expression is composed of multiple expressions and

an arithmetical (Expression.ArithmeticalOperator)

operator between them. A complex condition

involves conditions and a logical operator.

Requirement

PK ID

isSimple

FK1 Requirement1ID

FK2 Requirement2ID

ArithmeticalOperator

Index

FK3 SimpleReqID

FK4 ThemeID

SimpleRequirement

PK ID

FK1 ObjectID

FK2 TypifiedConditionID

FK3 OperationID

Object

PK ID

Name

Type

isTime

Operation

PK ID

isAggr

Value

Index

SuboperationID

TypifiedCondition

PK ID

Value

FK1 ConditionID

Condition

PK ID

isSimple

FK1 Condition1ID

FK2 Condition2ID

LogicalOperator

Comparison

FK3 Expression1ID

FK4 Expression2ID

Expression

PK ID

isSimple

Type

Constant

FK1 Expression1ID

FK2 Expression2ID

ArithmeticalOperator

FK3 ObjectID

Theme

PK ID

Name

Figure 2: The implementation model of formal

requirements.

4 FROM REQUIREMENTS

TO PRE-SCHEMAS

In this paper we propose a method for transforming

information requirements to the conceptual model of

a data warehouse (see Figure 3). The method uses

requirements from formal requirements database

and generates a simplified data warehouse schema

(pre-schema or candidate schema) by an algorithm

that analyses the structure of requirements. The next

stage of the method is semi-automated candidate

schemas are processed and restructured to remove

ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems

138

duplicates and build dimension hierarchies. Finally,

the improved schemas can be used as data

warehouse schema metadata.

Formal requirements

implementation

model

Pre-schema

Pre-schema Generation

Algorithm

Semi-automated execution

Data warehouse

model

Copy restructured

pre-schema

Pre-schema restructuring component

Figure 3: Pre-schema generation and restructuring.

4.1 A Pre-Schema and its Components

When exploring formal requirements, measures

(C_Measure) that characterize business processes

are determined and so do attributes (C_Attribute)

that describe measures. PreSchema is a candidate

schema of a data warehouse that includes measures

and attributes derived from requirements. In Figure

4 an implementation model for storing candidate

schemas and its elements is depicted.

PreSchema

PK ID

FK1 ThemeID

Index

isAccepted

C_Measure

PK ID

FK1 PreSchemaID

Name

DataType

isAccepted

Theme

PK ID

Name

C_Attribute

PK ID

Name

FK1 PreSchemaID

isTime

isAccepted

C_Aggregation

PK ID

FK1 MeasureID

Value

isAccepted

Index

C_Level

FK1 AttributeID

Name

C_Hierarchy

PK ID

Name

C_LevelHierarchy

FK1 HierarchyID

FK2 LevelID

Index

C_AcceptableAggregation

PK ID

FK1 AttributeID

FK2 AggregationID

isAccepted

Figure 4: A candidate schema (PreSchema) and its

components.

PreSchema.Index represents a link to a simple

requirement in requirement model. If in a formal

requirement a measure has an aggregate function

applied to it, then it is stored in C_Aggregation.

Tables C_Level, C_Hierarchy and

C_LevelHierarchy are employed to define attribute

hierarchies. C_LevelHierarchy.Index is some level’s

sequence number in a hierarchy. The meaning of an

attribute isAccepted in PreSchema, C_Measure,

C_Attribute, C_Aggregation, and

C_AcceptableAggregation is described in Section 5.

4.2 PGA: The Pre-Schema Generation

Algorithm

We propose a pre-schema generation algorithm

(PGA) for distinguishing data warehouse pre-

schema elements in formal requirements stored in an

implementation model (see Figure 2).

In Procedure 1 (MakePreSchema) requirements

are reviewed in a context of the business

requirement theme (lines 1-3). All simple

requirements of a certain theme are processed (lines

4-22). Complex requirements are not reviewed,

because objects, operations, and conditions are

defined in simple requirements only.

If the type of an object is Quantifying, then it is a

measure – C_Measure (lines 11-13). To find

aggregate functions (C_Aggregation) associated

with the measure and to set its order, operations are

checked by Function 1 (ProcessOperations; line 14,

and 23-40). If the type of an object is Qualifying,

then it is processed as an attribute – C_Attribute

(lines 15-18). Finally, simple conditions are handled

by Procedure 2 (ProcessSimpleConditions; line 22,

and 41-54). If an expression in a simple condition

has the type Qualifying, then the appropriate object

is an attribute (lines 46-51). Expressions with the

type Constant are ignored.

5 THE PROCESSING

OF A PRE-SCHEMA

Before discussing the process model of handling

pre-schemas generated by PGA, the following

assumptions should be considered:

 Two measures in a set of pre-schemas have the

same name, iff their semantic meaning is the same.

For instance, if two measures are named “total

number”, however, semantically one of them

corresponds to “total number of students” and the

other one – to “total number of teachers”, then

these two measures should be renamed

respectively.

 Two attributes in a set of pre-schemas have the

same name, iff their semantic meaning is the same.

The explanation is equivalent to the above-

mentioned, but is related to attributes.

 Names of the measures in pre-schemas coincide

with those in the data source.

First of all, an administrator picks up a certain

theme to which a set of pre-schemas gained from

requirements refers. Then, a pre-schema with the

maximum number of attributes is selected. Let us

call such pre-schema P

. If there are multiple P

like pre-schemas with different sets of attributes,

their processing goes independently and is just the

same as the one of P

pre-schema. In Figure 5 we

DerivingtheConceptualModelofaDataWarehousefromInformationRequirements

139

PGA Procedure 1: MakePreSchema, Input: CurrentTheme:Theme

1: IF NOT EXIST Theme WHERE Theme.Name = CurrentTheme.Name

2: THEN (CREATE Theme; Theme.Name:=CurrentTheme.Name;)

3: ELSE FIND Theme WHERE Theme.Name = CurrentTheme.Name;

4: FOR EACH Requirement WHERE Requirement.isSimple = 1

5: AND Requirement.ThemeID = CurrentTheme.ID DO:

6: CREATE PreSchema; PreSchema.Index:=Requirement.Index;

7: PreSchema.ThemeID:=Theme.ID;

8: FIND SimpleRequirement

9: WHERE SimpleRequirement.ID = Requirement.SimpleReqID;

10: FIND Object WHERE Object.ID = SimpleRequirement.ObjectID;

11: IF Object.type = 'Quantifying' THEN (

12: CREATE C_Measure; C_Measure.PreSchema:=PreSchema.ID;

13: C_Measure.Name:=Object.Name;

14: ProcessOperations(SimpleRequirement.OperationID, C_Measure.ID);)

15: ELSE (

16: CREATE C_Attribute; C_Attribute.PreSchemaID:=PreSchema.ID;

17: C_Attribute.Name:=Object.Name;

18: C_Attribute.isTime:=Object.isTime;)

19: FIND TypifiedCondition WHERE

20: TypifiedCondition.ID = SimpleRequirement.TypifiedConditionID;

21: FIND Condition WHERE Condition.ID = TypifiedCondition.ConditionID;

22: RUN ProcessSimpleConditions(Condition.ID, PreSchema); END.

PGA Function 1: ProcessOperations, Input: CurrID:number, CurrMeasureID:number

23: FIND Operation WHERE Operation.ID = CurrID;

24: IF Operation.SuboperationID != NULL

25: THEN (OperationIndex:=ProcessOperations(Operation.SuboperationID, CurrMeasure);

26: IF Operation isAggr = 1 THEN (CREATE C_Aggregation;

27: FIND C_Measure WHERE Measure.ID = CurrMeasure;

28: C_Aggregation.MeasureID:=C_Measure.ID;

29: C_Aggregation.Value:=Operation.Value;

30: C_Aggregation.Index:=(OperationIndex + 1);

31: RETURN OperationIndex + 1.)

32: ELSE

33: RETURN OperationIndex.)

34: ELSE (

35: IF Operation isAggr = 1 THEN (CREATE C_Aggregation;

36: FIND C_Measure WHERE Measure.ID = CurrMeasure;

37: C_Aggregation.MeasureID:=C_Measure.ID;

38: C_Aggregation.Value:=Operation.Value;

39: C_Aggregation.Index:=1;

40: RETURN 1.))

PGA Procedure 2: ProcessSimpleConditions, Input: CurrentConditionID:number, CurrentPreSchema:PreSchema

41: FIND Condition WHERE Condition.ID = CurrentConditionID;

42: IF Condition.isSimple = 1 THEN (

43: FOR EACH Expression

44: WHERE Expression.ID = Condition.Expression1ID

45: OR Expression.ID = Condition.Expression2ID DO:

46: IF Expression.Type = 'Qualifying' THEN (

47: FIND Object WHERE Object.ID = Expression.ObjectID;

48: CREATE C_Attribute;

49: C_Attribute.PreSchemaID:=CurrentPreSchema.ID;

50: C_Attribute.Name:=Object.Name;

51: C_Attribute.isTime:=Object.isTime;) END.

52: ELSE (

53: ProcessSimpleConditions(CurrentCondition.Condition1ID, CurrentPreSchema);

54: ProcessSimpleConditions(CurrentCondition.Condition2ID, CurrentPreSchema);) END.

ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems

140

ignored the case of multiple pre-schemas with the

same maximum number of attributes on purpose for

better understanding.

A pre-schema may contain a set of measures

(M1, M2 …, Mn). Further manipulations with the

pre-schema depend on the number of measures that

it contains. Having more than one measure, certain

rules take place:

1. If there is at least one pre-schema with a set of

measures that in any way intersects with a

measure or a set of measure of another pre-

schema (e.g. (M1, M2) ∩ (M2, M3, M4) = M2;

(M1, M2) ∩ M1 = M1, etc.), then all pre-schemas

with intersecting measures should be

decomposed, because the meaning and

granularity of fact measures are determined by

the finest level attributes.

2. If the set of all pre-schemas contains different

sets of measures (e.g. (M1, M2); (M3, M4, M5);

M6; M7; etc.) that do not have overlapping

elements, then there is no need to decompose the

pre-schemas.

3. If a set of measures is the same for all pre-

schemas assigned to a certain theme, then none of

the pre-schemas should be decomposed.

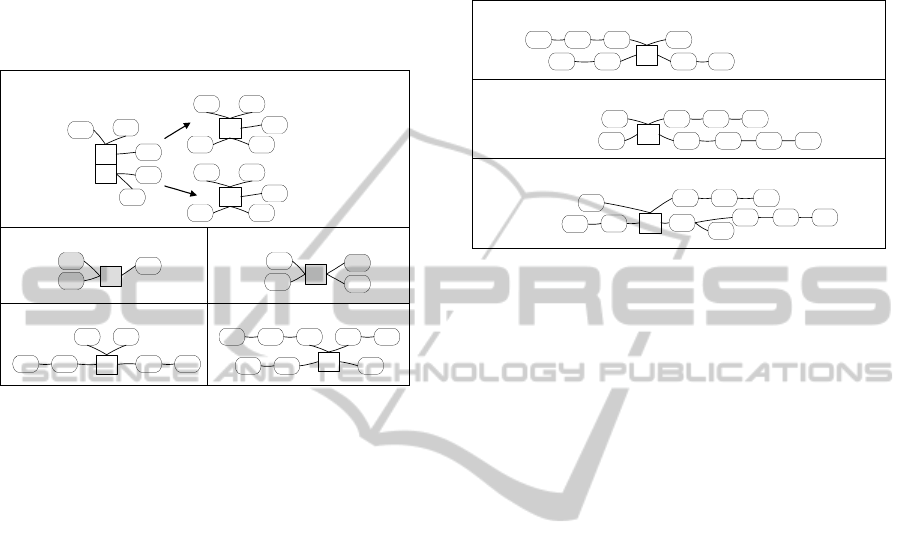
In case of (1), a pre-schema P

is being

decomposed into pre-schemas each of which

contains only one measure, and a set of attributes is

equal to that of P

. An example of decomposing a

pre-schema with two measures is depicted in Figure

6a. Let’s call each of the newly acquired pre-

schemas in Figure 6a P'

and P''

Pre-schemas that contain the same measure as

(or at least one of the decomposed pre-

schemas) are of interest. Let’s call a set of filtered

pre-schemas P. Examples of such pre-schemas are

illustrated in Figure 6 (b – pre-schema P', and c –

pre-schema P'') containing two different measures:

M1 as in P'

, M2 as in P''

PP'

and PP''

are new pre-schemas that consist

of measures and attributes from P'

and P''

respectively, and attributes that exist in each of pre-

schemas of set P but are missing in the pre-schema

(in Figure 6b – attribute A6) and P''

(in Figure

6c – attributes A7, A8, and A9). However, before

the attributes are actually added to either PP'

PP''

, they should be arranged in hierarchies, so that

measures would be described by the finest level

attributes only. In Figure 6d PP'

is an example of

arranging distinct attributes from P'

and P', whereas

in Figure 6e PP''

is the example of arranging those

from P''

and P''.

To order attributes of pre-schemas in hierarchies,

we follow some data-driven algorithm (e.g.

(Golfarelli et al., 1998)). First, an arbitrary attribute

(let’s denote it as A) from a set of distinct attributes

of, say, P'

and P' is selected. Then, in the data

source a certain entity attribute (let’s denote it as

) that corresponds to the measure of a pre-

schema P'

is determined.

Next, we move from M

to all attributes that

have a many-to-one relationship with M

. We

traverse in such way the attributes in data source

until an attribute that corresponds to A is found

). When found, A is classified either as a finest

hierarchy level (if M

is connected to A

directly) or

a coarser hierarchy level (if M

is connected to A

through two or more M:1 associations) of a certain

hierarchy of the pre-schema PP'

Figure 5: The process model of handling pre-schemas generated by PGA.

DerivingtheConceptualModelofaDataWarehousefromInformationRequirements

141

All attributes that can be reached from A

M:1 association and do exist in pre-schema PP'

are

ordered in hierarchy the same way as they have

been traversed in the data source – from finest to

coarsest level. Finally, the property isAccepted of all

processed attributes and measures in the pre-schema

PP'

that have a matching entity attribute in the data

source are updated to 1.

(a) P

A1 A2

A4A5

A1 A2

A4A5

P''

(b) P'

(d) PP'

(e) PP''

A8 A7A9

Figure 6 a: A pre-schema with maximum attribute count

) is being decomposed into two pre-schemas (P'

and

P''

); b, c: two pre-schemas (P' and P''); d, e: PP'

and

PP''

: pre-schemas P'

and

P''

supplemented with

attributes from P' and P'' respectively, ordered in

hierarchies.

If an attribute or a measure exists only in

requirements (i.e., in pre-schemas), then the

property isAccepted of the attribute or measure is

updated to 0. Also, it may happen that A

cannot be

reached from M

by M:1 associations. Then A has

the property isAccepted updated to 0 too. Such

attributes or measures will be reviewed by

administrator later on. Also, an administrator should

review all aggregate functions that are applied to

additive, semi-additive or non-additive measures to

either accept an aggregation if its application to a

certain measure is allowed, or decline if its

application to the measure is inappropriate. The

property isAccepted of the C_Aggregation and

C_AcceptableAggregation is modified in obedience

to the measure type. By that we indicate that certain

elements of the modified P

(or P'

) pre-schema

are ready for further analysis.

If there are any pre-schemas with measures that

differ from those in already processed pre-schemas,

then the algorithm is being iteratively executed from

the step where a pre-schema with the maximum

attribute count is found.

The next step of the process is aimed at making

a union of two or more pre-schemas on condition

that all finest hierarchy level attributes coincide. If

this condition isn’t satisfied, then this step should be

skipped.

(a)

A1 A2

A4 A12A5

(b)

A5 A4 A11

A10

A8 A9

(c)

A11

A10

A8 A9

A12

Figure 7 a, b: An example of hierarchies in two different

pre-schemas with the same finest hierarchy level

attributes and same measures; c: an example of the union

of two pre-schemas.

Consider an example in Figure 7: there are two pre-

schemas with the same finest hierarchy level

attributes and same measures, however, coarser

hierarchy level attributes might differ. Hierarchies

in Figure 7a are: H1a: A5A7; H2a: A1A8A9;

H3a: A2; H4a: A4A12. Hierarchies in in Figure

7b are: H1b: A5; H2b: A2; H3b: A1A8A9;

H4b: A4A6A10A11. It is possible to unite

two (or more) pre-schemas, taking into an account

several rules:

 If two hierarchies are equivalent (H2a ≡ H3b, H3a

≡ H2b), then one of the equivalent hierarchies will

be added with no changes to the united pre-

schema.

 If finest hierarchy level attributes are similar, but

coarser hierarchy level attributes differ, then all

alternative hierarchies will be included in the

united pre-schema (both H4a and H4b).

 If finest hierarchy level attributes are similar, but

in some hierarchies coarser level attributes are

absent, then the hierarchy with the largest number

of levels will be added to the united pre-schema

(only H1a).

As a result, there is a pre-schema with the

following hierarchies: A5A7; A1A8A9; A2;

A4A12; A4A6A10A11 (see Figure 7c).

Data source attributes may be divided into two

groups: the ones that are equivalent to the attributes

in pre-schemas gained from requirements, and the

ones that aren’t. Let’s call the latter descriptive

attributes as they might provide additional

information on the attributes in pre-schemas. An

ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems

142

administrator may add descriptive attributes to pre-

schemas, if it is necessary.

The last step but one is an interview with the

client during which all generated pre-schemas are

being shown. The client should make a decision and

choose one pre-schema that would meet the

requirements for a new schema best of all.

Finally, to indicate that one of the pre-schemas

is selected, an administrator updates the isAccepted

property of a pre-schema to 1, and the pre-schema is

being copied to the data warehouse metadata

repository that mostly complies with CWM

(Solodovnikova, 2008).

6 CONCLUSIONS

In this paper we set forth an approach of building a

candidate schema (pre-schema) of a data warehouse

that complies with the business requirements stated

by the client. We consider requirements as

performance indicators of an organization that are

gathered during the interview and formalized in

accordance with the indicators model described in

detail in (Niedritis et al., 2011).

The contribution of this paper is the pre-schema

generation algorithm (PGA) that employs

indicators, and the description of the semi-

automated pre-schema post-processing. We believe

that pre-schemas acquired this way will be more apt

then schemas gained by applying other demand-

driven methods. During the post-processing, pre-

schema hierarchies are defined by a data-driven

algorithm. However, there certainly are some

presumptions that should be fulfilled first to enable

the usage of PGA; for instance, (i) requirements

have to be formalized in a specific way, (ii)

measures or attributes with the same name but

different semantic meaning should be renamed to be

distinguishable from one another.

Our future work would include the

implementation of the PGA, its testing on a large set

of indicators of an existing data warehouse schemas

followed by its evaluation. Also, quality attributes

for evaluations of accepted pre-schemas should be

introduced. Afterwards, the pre-schemas defined by

PGA would be processed and the resulting pre-

schema(s) would be compared with the existing data

warehouse schemas.

ACKNOWLEDGEMENTS

This work has been supported by ESF project

No.2009/0216/1DP/1.1.1.2.0/09/APIA/VIAA/044.

REFERENCES

Giorgini P., Rizzi S., Garzetti M. 2005. Goal-oriented

requirement analysis for data warehouse design. In:

Proc. of 8th ACM Int. workshop on Data

Warehousing and OLAP (DOLAP'05), ACM Press,

New York, pp 47-56

Golfarelli M., Maio D., Rizzi S. 1998. Conceptual design

of data warehouses from E/R schemes. In: Proc. of

31st Annual Hawaii Int. Conf. on System Sciences

(HICSS'98), Kona, Hawaii, IEEE, USA, 7:334-343

Inmon W.H. 2002. Building the data warehouse. 3rd edn.,

Wiley Computer Publishing

Jones M. E., Song I. 2005. Dimensional modeling:

identifying, classifying and applying patterns. In:

Proc. of 8th ACM Int. workshop on Data

Warehousing and OLAP (DOLAP'05), ACM Press,

New York, pp 29-38

Kaldeich C., Oliveira J. 2004. Data warehouse

methodology: a process driven approach. LNCS 3084.

Springer, Heidelberg, pp 536-549

List B., Machaczek K. 2004. Towards a corporate

Performance Measurement System. In: Proc. of ACM

symposium on Applied Computing (SAC'04), ACM

Press, New York, pp 1344-1350

Niedritis, A., Niedrite, L., Kozmina, N. 2011.

Performance Measurement Framework with Formal

Indicator Definitions. In: Grabis, J., Kirikova, M.

(eds.) BIR 2011. Springer, Heidelberg, LNBIP, 90:44-

Parmenter D. 2010. Key Performance Indicators:

developing, implementing, and using winning KPIs.

2nd edn., Jon Wiley & Sons, Inc.

Poe V. 1996. Building a data warehouse for decision

support. Prentice Hall

Rizzi S. 2009. Conceptual Modeling Solutions for the

Data Warehouse. In: Erickson, J. (ed.) Database

Technologies: Concepts, Methodologies, Tools, and

Applications, IGI Global, pp 86-104

Rizzi S., Abelló A., Lechtenbörger J., Trujillo J. 2006.

Research in data warehouse modeling and design:

dead or alive? In: Proc. of 9th ACM Int. workshop on

Data Warehousing and OLAP (DOLAP'06), ACM

Press, New York, pp 3-10

Romero O., Abello A. 2010. A framework for

multidimensional design of data warehouses from

ontologies. Data and Knowledge Engineering

69:1138-1157

Solodovnikova, D. 2008. Metadata to support data

warehouse evolution. In: Proc. of 17th Int. Conf. on

Information Systems Development (ISD'08), Paphos,

Cyprus, 2008, pp 627-635

DerivingtheConceptualModelofaDataWarehousefromInformationRequirements

143

Westerman P. 2001. Data warehousing using the Wal-

Mart model. Morgan Kaufmann

Winter R., Strauch B. 2003. A method for demand-driven

information requirements analysis in data

warehousing projects. In: Proc. of 36th Annual

Hawaii Int. Conf. on System Sciences (HICSS'03),

Waikoloa, Hawaii, IEEE, USA, pp 1359-1365

ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems

144