Multistep Fuzzy Classifier Design with Self-tuning

Coevolutionary Algorithm

Roman Sergienko

1,2

and Eugene Semenkin

Institute of Commincation Engineering, Ulm University, Ulm, Germany

Department of System Analysis and Operation Research, Siberian State Aerospace University, Krasnoyarsk, Russia

Keywords: Fuzzy Classifier, Michigan Method, Pittsburgh Method, Coevolutionary Algorithm, Self-tuning, Strategy

Adaptation, Multistep Procedure.

Abstract: A method of Michigan and Pittsburgh approaches combining for fuzzy classifier design with evolutionary

algorithms is presented. Michigan-style stage provides fast search of fuzzy rules with the best grade of

certainty values for different classes and smoothing of randomness at initial population forming. Pittsburgh

method provides rules subset search with the best performance and predefined number of the rules and

doesn’t require a lot of computational power. Besides self-tuning cooperative-competitive coevolutionary

algorithm for strategy adaptation is used on Michigan and Pittsburgh stages of fuzzy classifier design. This

algorithm solves the problem of genetic algorithm parameters setting automatically. The next result is

multistep fuzzy classifier design based on multiple repetition of previous fuzzy classifier design. After each

iteration standard deviation of classification performance decreases and classification performance

increases. Results of numerical experiments for machine learning problems from UCI repository are

presented. Fuzzy classifier design methods comparison with alternative classification methods by

performance value demonstrates advantages of the proposed algorithms.

1 INTRODUCTION

Classification can be an important data analysis

problem for control system construction. Fuzzy

classifier (Ishibuchi, 1999) is the classification

algorithm based on fuzzy rules extraction from

numerical data. Superiority of this method upon

other classification algorithms (e.g. neural networks)

is provided by fuzzy rules which are linguistic

expressions and they are available for people

understanding. Thus fuzzy classifier is one of the

data mining methods for knowledge discovery. Each

fuzzy rule consists of fuzzy terms for attributes, a

name of the most appropriate class, and grade

certainty that is calculated with a learning sample

(Ishibuchi, 1999).

Fuzzy classifier design can be considered as

optimization problem. In this case we need to find

the best fuzzy classifier. Fuzzy classifier design

consists of two problems. First one is rule base

generating and second one is membership functions

tuning. It should be noted the first problem is more

complicated because dimension of this problem can

be high and a lot of variables are discrete. So we

observe only fuzzy rule base generating in this

paper.

Because fuzzy rule base generating is

complicated computational problem the popular

method of this problem solving is the genetic-based

machine learning (Herrera, 2008). There are two

basic ways of genetic algorithm applying for fuzzy

rule base generating: Michigan-style method and

Pittsburgh-style method. In Michigan approach

(Holland, 1978) the chromosomes are individual

rules and a rule set is represented by the entire

population. In Pittsburgh method (Smith, 1980) the

chromosomes are rule sets at whole. The problem in

Michigan approach is the conflict between

individual rule fitness and performance of fuzzy rule

set. Pittsburgh-style systems require a lot of

computational burden. So Michigan and Pittsburgh

method combining is the promising approach. In

(Ishibuchi, 2000) hybridization Pittsburgh method

with Michigan-style algorithm using Michigan

method as mutation operator in Pittsburgh-style

algorithm is presented.

A new method of Michigan and Pittsburgh

approaches combining for fuzzy classifier rule base

113

Sergienko R. and Semenkin E..

Multistep Fuzzy Classiﬁer Design with Self-tuning Coevolutionary Algorithm.

DOI: 10.5220/0004426501130120

In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2013), pages 113-120

ISBN: 978-989-8565-70-9

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

design with evolutionary algorithms is presented in

this paper. Fuzzy classifier rule base design consists

of two main stages. At the first stage Michigan

method is used for fuzzy rules search with high

grade of certainty. At the second stage the Pittsburgh

method is applied for subset of the rules searching

with the best classification performance and

predefined number of rules. Constraint for number

of rules is used at this stage of fuzzy classifier

design. As fuzzy classifier is data mining tool it is

more preferable to have minimal number of rules.

Preparatory procedures are attribute fuzzification

and initial population of fuzzy rules forming using a-

priori information from a learning sample.

Another problem with genetic algorithm

applying is the algorithm parameters setting. This

problem is especially essential for optimization

problems with high computational complexity such

as fuzzy rule base generating. There are some

methods for GA parameter setting problem solving.

We suggest special procedure named self-tuning

cooperative-competitive coevolutionary algorithm

for this problem solving (Sergienko, 2010). This

method combines ideas of cooperation and

competition among subpopulations in the

coevolutionary algorithm. We tested this algorithm

for some computationally simple problems for

foundation of its efficiency and then used it for

fuzzy rule base forming. Cooperative-competitive

coevolutionary algorithm for unconstrained

optimization is applied at the Michigan-style stage

and cooperative-competitive coevolutionary

algorithm for constrained optimization is used at the

Pittsburgh-style stage.

The next idea is the multistep fuzzy classifier

design. After multiple fuzzy classifiers forming we

have a set of fuzzy classifiers for each classification

problem. The natural step is a collective forming

fuzzy rule base using a set of classifiers generated

with our approach. It is possible to increase

classification efficiency and decrease diversity of

classification efficiency using this method. For

collective design of fuzzy classifier cooperate-

competitive coevolutionary algorithm can be applied

again. Thus we can repeat this procedure more

times. So we have formulated a multistep procedure

of fuzzy classifier design.

This multistep procedure for fuzzy classifier rule

base design was applied for some machine learning

problems from UCI repository. Statistical

investigations were performed. Results of numerical

experiments are demonstrated. Classification

performance values were compared with results of

alternative classifiers.

Investigation of Michigan and Pittsburgh method

combination for fuzzy classifier rule base design is

introduced in Section 2. The numerical results of

fuzzy classifier design and multistep procedure

suggestion are described in Section 3. The results of

numerical experiments for multistep fuzzy classifier

design are presented in Section 4. Conclusions are

listed in Section 5.

2 A METHOD OF FUZZY

CLASSIFIER DESIGN

The Michigan and Pittsburgh methods combining

for fuzzy classifier design implicates sequential

using of the first and the second approaches. At the

first stage the Michigan method is used for fuzzy

rules search with high grade of certainty. At the

second stage the Pittsburgh method is applied for

subset of the rules searching with the best

classification efficiency with constraint for

maximum number of rules.

A prior to main evolutionary stages of our

method there are two important preparatory steps of

fuzzy classifier design: attribute fuzzification (fuzzy

number semantics setting) and initial population of

fuzzy rules forming for Michigan approach with a

priori information from a learning sample. So let’s

consider the preparatory steps and the main stages of

fuzzy classifier design in more details.

2.1 Attribute Fuzzification

In this work for each attribute of a machine learning

problem five triangular fuzzy numbers and a term

“ignoring” (it means that an attribute isn’t used in

the corresponding fuzzy rule) are determined: 1 –

“very small”, 2 – “small”, 3 – “average”, 4 –

“large”, 5 – “very large”, 6 – “ignoring”. If an

attribute has both negative and positive values it is

better to use words “negative”, “null” and “positive”

instead “small”, “average” and “large” accordingly.

A triangular fuzzy number is characterized by

three parameters: left boundary a, centre b, and right

boundary c. The maximum B and minimum A values

of an attribute are determined from a learning

sample. For uniform filling of attribute variability

interval [A; B] by fuzzy numbers the parameters are

defined by the following equations:

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

114

.4..1 ),1()(

,5..1 ),1()(

,5..2 ),1()(





iiABAc

iiABAb

iiABAa

2.2 Initial Population of Fuzzy Rules

Forming

This step is very important because random

generating of fuzzy rules is unacceptable.

Classification problems can have a lot of attributes.

So, if we use 5 fuzzy terms and term “ignoring” for

each attribute and number of attributes is equal d,

total number of rules is equal 6

-1. In this case

probability of random fuzzy rule generating that

would have at least one corresponding element from

a learning sample is very low. So using a priori

information from a learning sample is necessary for

initial population of fuzzy rules forming. There are

some approaches for this problem solving: (Martín-

Muñoz, 2010, Palacios, 2010, and Nojima, 2010).

Our procedure is considered in the following steps:

1) Let n be a number of rules at Michigan-style

stage of fuzzy classifier design, k be a number of the

classes, d be a number of attributes.

2) Put m=n/k.

3) Sort a learning sample by number of the class

and determine boundaries for each class in the sorted

array (positions of the first and the last elements for

each class).

4) For i:=1 to k do:

4.1) For j:=1 to m do:

4.1.1) Perform random selection of the element

for the class i from a sorted learning sample.

4.1.2) For t:=1 to d do:

4.1.2.1) Determine the nearest centre of a fuzzy

number for attribute t.

4.1.2.2) Put the corresponding fuzzy number as

element of the generated fuzzy rule.

4.1.2.3) Exchange the fuzzy number to a term

“ignoring” with probability equals to 1/6 (we have 6

terms for each attribute).

5) Fill population for Michigan-style stage by

generated fuzzy rules.

This procedure provides generating equal

number of informative fuzzy rules for each class.

2.3 Michigan-style Stage

The main idea of this stage is to improve initial

fuzzy rules with genetic algorithm.

The chromosomes are the fuzzy rules.

Chromosome length is equal to the number of

attributes, each gene is a sign for the corresponding

fuzzy term (1..6). We needn’t to use a gene for

output because the appropriate class for the rule is

determined automatically. Fitness function is grade

certainty of the fuzzy rule that is calculated by a

learning sample (Ishibuchi, 1999). Genetic algorithm

for unconstrained optimization is applied. New

population forming method is modified. After

genetic generation performing parents and child are

combined to the united array. Different fuzzy rules

with the best values of fitness function for each class

are selected to the next generation. This new

population forming method provides diversity of

rules for each class and diversity of classes in

population. For each generation classification

performance is calculated for population at whole.

Population with the best value of classification

performance is used for the next stage of fuzzy

classifier design.

Steps of Michigan-style stage:

1) Let n is population size (number of initial

fuzzy rules), N is generation number, k is number of

classes.

2) Put m=n/k.

3) Calculate classification performance F

initial population for a learning sample (correctly

classified part of a test sample).

4) Remember initial population P

5) For i:=1 to N

5.1) Perform all necessary genetic operators with

population (selection, recombination, and mutation).

5.2) Combine parents and offspring to the united

array.

5.3) Sort the array by number of the class and

determine boundaries for each class in the sorted

array.

5.4) For j:=1 to k do:

5.4.1) Sort a part of the array for class j by grade

certainty.

5.4.2) Find m different rules for class j with the

best value of grade certainty and copy them to the

next population P

5.5) Calculate classification performance F

population P

for a learning sample.

5.6) If F

> F

then F

:=F

and P

:=P

6) Return P

2.4 Pittsburgh-style Stage

The main idea of Pittsburgh style-stage is to find

subset of computed on Michigan-style stage fuzzy

rule set with the best classification efficiency and

MultistepFuzzyClassifierDesignwithSelf-tuningCoevolutionaryAlgorithm

115

constraint satisfaction for maximum number of

rules. Genetic algorithm for constrained

optimization is used for this stage.

The chromosomes are the fuzzy rule sets.

Chromosome length is equal to the population size

for Michigan-style stage. Chromosome genes are

binary. Value “1” means using of the corresponding

rule in the set, value “0” means ignoring of the

corresponding rule. Fitness function is classification

performance for a learning sample. Constraint for

maximum number of rules is used. This value is

specified by a researcher. It depends on

classification problem dimension (number of

attributes and number of classes). The constraint is

used because it is better to have small number of

rules in the final rule base. New generation forming

method is standard (offspring replace parents with

the exception of the best parent). Special methods of

constraint satisfaction for genetic algorithms are

used (e.g. dynamic penalty function, adaptive

penalty function).

Steps of Pittsburgh-style stage:

1) Let N is number of generations, M is

population size, n is chromosome length (n is equal

to population size for Michigan-style stage), G is

constraint for maximum number of used fuzzy rules.

2) Generate M random binary strings with length

equals n and with maximum number of “1” at each

string is not more than G.

3) For i:=1 to N do all necessary genetic

operators and new generation forming.

4) Return the best solution.

2.5 Self-tuning

Cooperative-competitive

Coevolutionary Algorithm

One of the most complicated problems for

application of genetic algorithm is the algorithm

parameters setting. Conventional genetic algorithm

has at least three methods of selection (proportional,

tournament, and rank), three methods of

recombination (one-point, two-point, and uniform).

Mutation probability requires tuning too. For

constrained optimization problems it is necessary to

choose a constraint satisfaction method. Amount of

various combinations can be estimated at tens.

Exhaustive search of combinations requires a lot of

time and computational power. Especially it’s hard

for complicated problems as fuzzy classifier design.

One run of genetic algorithm for fuzzy classifier

design can be in progress for some hours.

Parameters combination selection by chance is also

bad idea as algorithm efficiency on the same

problem can differ very much for different

parameters setting.

We develop an approach (Sergienko, 2010) that

uses both competition and cooperation of individual

genetic algorithms with different parameters setting.

Resource redistribution provides domination of the

subpopulation with the best for problem-in-hand

search strategy. Cooperation of individual

conventional genetic algorithms is provided by

migration of the best solutions to all of the

individual genetic algorithms. So coevolutionary

algorithm efficiency can increase because of positive

effect of subpopulations interacting. This

cooperative-competitive coevolutionary genetic

algorithm needs no tuning of special parameters.

We showed reasonability of cooperate-

competitive coevolutionary algorithm application for

some computationally simple problems and then we

made a decision to use this approach for more

complicated problems such as fuzzy rule base

generating. It is very difficult to perform complex

investigation of self-tuning cooperate-competitive

coevolutionary algorithm for computationally

complex problems because required computational

power or computational time would be huge.

Self-tuning cooperative-competitive

coevolutionary genetic algorithm for unconstrained

optimization is applied at Michigan-style stage of

fuzzy classifier design and coevolutionary genetic

algorithm for constrained optimization is used at

Pittsburgh-style stage. We use three methods of

selection (proportional, tournament, and rank), three

methods of recombination (one-point, two-point, and

uniform), adaptive mutation, and three methods of

constraint satisfaction (“death” penalty, dynamic and

adaptive penalty functions). Totally there are 9

subpopulations with different parameters setting for

Michigan-style stage and 27 subpopulations for

Pittsburgh-style stage. So self-tuning cooperative-

competitive coevolutionary genetic algorithm

provides the solution of GA parameters setting

problem. Another effect is possibility of parallel

computing for fuzzy classifier design.

3 NUMERICAL RESULTS FOR

FUZZY CLASSIFIER DESIGN

AND MULTISTEP

PROCEDURE SUGGESTION

The developed method of fuzzy classifier design has

been applied for a number of classification machine

learning problems from UCI repository:

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

116

- Credit (Australia-1) (14 attributes, 2 classes);

- Liver Disorder (6 attributes, 2 classes);

- Iris (4 attributes, 3 classes);

- Yeast (8 attributes, 10 classes);

- Glass Identification (9 attributes, 7 classes);

- Landsat Images (4 attributes, 6 classes).

Statistical investigations were performed for all

problems. We tested our approach for 20 times for

each classification problem. We calculated mean and

standard deviation for classification performance

values. Statistical significance of our conclusions

was valid with Wilcoxon criteria.

For each problem average and maximum (only

for Pittsburgh-style stage) classification performance

values for each stage and initial number of rules are

presented in Tables 1. The column 1 contains

average performance values after initial rules

forming, the column 2 contains average performance

values after Michigan-style stage, the column 3

contains average performance values after

Pittsburgh-style stage, and the column 4 contains

maximum performance values after Pittsburgh-style

stage. There is feasible number of rules in the

brackets. There are standard deviation values of

classification performance for each method stage in

Table 2 (the column 1, 2, and 3 accordingly). The

column 4 in the Table 2 contains parameter of rules

repeatability p = (20x – y) / 19x, when x is constraint

for the maximum number of rules in the base and y

is number of the unique rules at all 20 generated

bases for each classification problem. Interval for p

is [0;1]. It’s better to increase this parameter.

Table 1: Classification performance values for fuzzy

classifier design.

Problem 1 2 3 4

Credit

(Australia)

0,854 0,870

0,827(10)

0,861(20)

0,873(30)

0,870(10)

0,890(20)

0,891(30)

Liver

Disorder

0,595 0,653

0,666(10)

0,682(15)

0,692(20)

0,687(10)

0,710(15)

0,725(20)

Iris

0,945 0,979

0,908(3)

0,951(4)

0,971(5)

0,975(6)

0,947(3)

0,973(4)

0,987(5)

0,987(6)

Yeast

0,417 0,495

0,573(20)

0,586(30)

0,593(60)

0,598(20)

0,606(30)

0,626(60)

Glass

Identification

0,640 0,687

0,737(20)

0,781(30)

0,757(20)

0,827(30)

Landsat

Images

0,793 0,812

0,838(10)

0,847(15)

0,849(20)

0,849(10)

0,857(15)

0,857(20)

Table 2: Standard deviation values for fuzzy classifier

design.

Problem 1 2 3 4

Credit

(Australia)

0,0093 0,0065

0,0248(10)

0,0123(20)

0,0103(30)

0,00(10)

0,00(20)

0,00(30)

Liver

Disorder

0,0208 0,0110

0,0150(10)

0,0167(15)

0,0173(20)

0,17(10)

0,10(15)

0,09(20)

Iris

0,0152 0,0039

0,0564(3)

0,0262(4)

0,0130(5)

0,0107(6)

0,67(3)

0,56(4)

0,51(5)

0,56(6)

Yeast

0,0186 0,0169

0,0180(20)

0,0171(30)

0,0221(60)

0,00(20)

0,00(30)

0,07(60)

Glass

Identification

0,0226 0,0202

0,0139(20)

0,0183(30)

0,02(20)

0,04(30)

Landsat

Images

0,0123 0,0081

0,0078(10)

0,0042(15)

0,0055(25)

0,36(10)

0,44(15)

0,42(25)

Large number of rules isn’t used at initial

population of fuzzy rules forming stage. For

reasoning of this statement we can show that number

of all possible fuzzy rules varies from 216 (3

attributes) to 4,7·10

(24 attributes) and maximum

number of initial rules equals 200. But all fuzzy rule

bases are operable after initial population forming.

Classification performance values after

Michigan-style stage increase by 0,01-0,08. Besides

diversity of classification performance value

decreases a lot (see the Table 2). So we can conclude

that Michigan-style stage is necessary for light

increment of fuzzy rule set efficiency and smoothing

of randomness at initial population forming.

Population size for Pittsburgh-style stage is equal

to the following: 100 individuals * 27

subpopulations = 2700. Generation number equals

100 because convergence rate for cooperative-

competitive coevolutionary algorithm is higher than

for conventional GA (Sergienko, 2010). In the

Table 1 we can see that classification performance

values after Pittsburgh-style stage performing can be

better than performance values after Michigan-style

stage although number of rules is reduced. It means

that a large rule set is not always better by

performance. “Bad” rules have damaged the effect.

So interpretability of fuzzy rule set is improved and

classification efficiency can be improved too after

Pittsburgh-style stage performing. It’s a positive

feature of Pittsburgh-style stage. Negative one is that

deviation of classification performance value can

increase. Low repeatability of rules is another

problem (see the Table 2, the column 4).

MultistepFuzzyClassifierDesignwithSelf-tuningCoevolutionaryAlgorithm

117

A natural step for fuzzy rules repeatability

increasing and classification performance deviation

decreasing is a collective design fuzzy rule base

using a set of classifiers generated with our

approach. In this case Pittsburgh-style stage of fuzzy

classifier forming is performed again. A set of fuzzy

rule bases is analogy of fuzzy rule base generated

after Michigan-style stage. We also use constraint

for feasible number of rules. For collective forming

of fuzzy classifier cooperate-competitive

coevolutionary algorithm can be applied again. For

example, we have got 20 fuzzy rule sets and then we

can repeat Pittsburgh-style procedure using unique

rules from previous sets as initial rules for

Pittsburgh-style stage. Thus we can repeat this

procedure some more times. So we formulate

multistep procedure of fuzzy classifier design. We

can use threshold value of classification

performance increasing, standard deviation

decreasing, or number of unique rules decreasing as

a stopping criterion for our multistep procedure. The

action sequence for multistep fuzzy classifier

forming is the following:

1) Select start fuzzy rules with a special

procedure (see paragraph 2.2) and repeat this

procedure n times.

2) Perform one-step fuzzy classifier design (see

paragraphs 2.3, 2,4, and 2.5) and repeat this

procedure n times.

3) Form from n fuzzy classifiers initial

population for the next iteration (unite fuzzy rule

bases and delete repetitive fuzzy rules).

4) If stopping criterion is true end else go to

position 2.

Using multistep procedure fuzzy rule

repeatability must increase and classification

efficiency diversity must decrease. Besides it is

possible to increase classification performance. We

have implemented this method and approved our

forecasts.

4 MULTISTRP FUZZY

CLASSIFIER DESIGN

INVESTIGATIONS

Some statistical investigations were performed for

all problems. For each problem maximum and

average classification performance values, standard

deviation of classification performance, and

parameter of rules repeatability are presented in the

Tables 3-8. There is a feasible number of rules in the

brackets. Stopping criterion is average classification

performance increasing less than 0,005 or standard

deviation equals to 0. For some cases we have

performed one or two steps additionally for equal

step number providing for the same problem.

Table 3: Results of multistep fuzzy classifier design for

Credit (Australia-1).

Iteration

Maximum

perform.

Average

perform.

Standard

deviation

Rules

repeat.

0,870(10)

0,890(20)

0,891(30)

0,827(10)

0,861(20)

0,873(30)

0,0248(10)

0,0123(20)

0,0104(30)

0,00(10)

0,00(20)

0,00(30)

0,891(10)

0,919(20)

0,926(30)

0,888(10)

0,918(20)

0,924(30)

0,0017(10)

0,0027(20)

0,0017(30)

0,83(10)

0,83(20)

0,74(30)

0,891(10)

0,919(20)

0,928(30)

0,891(10)

0,919(20)

0,926(30)

0,0000(10)

0,0000(20)

0,0013(30)

0,92(10)

0,89(20)

0,83(30)

Table 4: Results of multistep fuzzy classifier design for

Liver Disorder.

Iterati

Maximum

perform.

Average

perform.

Standard

deviation

Rules

repeat.

0,687(10)

0,710(15)

0,725(20)

0,666(10)

0,682(15)

0,692(20)

0,0173(10)

0,0167(15)

0,0150(20)

0,17(10)

0,10(15)

0,09(20)

0,713(10)

0,739(15)

0,757(20)

0,705(10)

0,731(15)

0,748(20)

0,0045(10)

0,0061(15)

0,0055(20)

0,50(10)

0,61(15)

0,67(20)

0,716(10)

0,739(15)

0,757(20)

0,714(10)

0,735(15)

0,754(20)

0,0023(10)

0,0041(20)

0,0023(20)

0,89(10)

0,77(15)

0,82(20)

0,716(10)

0,742(15)

0,757(20)

0,716(10)

0,738(15)

0,755(20)

0,0000(10)

0,0028(15)

0,0025(20)

0,97(10)

0,88(15)

0,86(20)

Table 5: Results of multistep fuzzy classifier design for

Yeast.

Iterati

Maximum

perform.

Average

perform.

Standard

deviation

Rules

repeat.

0,598(20)

0,606(30)

0,626(60)

0,573(20)

0,586(30)

0,593(60)

0,0180(20)

0,0171(30)

0,0221(60)

0,00(20)

0,00(30)

0,07(60)

0,609(20)

0,641(30)

0,674(60)

0,605(20)

0,633(30)

0,668(60)

0,0024(20)

0,0043(30)

0,0043(60)

0,57(20)

0,59(30)

0,62(60)

0,617(20)

0,651(30)

0,676(60)

0,614(20)

0,647(30)

0,672(60)

0,0025(20)

0,0034(30)

0,0024(60)

0,81(20)

0,77(30)

0,73(60)

0,621(20)

0,651(30)

0,678(60)

0,618(20)

0,649(30)

0,675(60)

0,0020(20)

0,0012(30)

0,0022(60)

0,86(20)

0,83(30)

0,81(60)

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

118

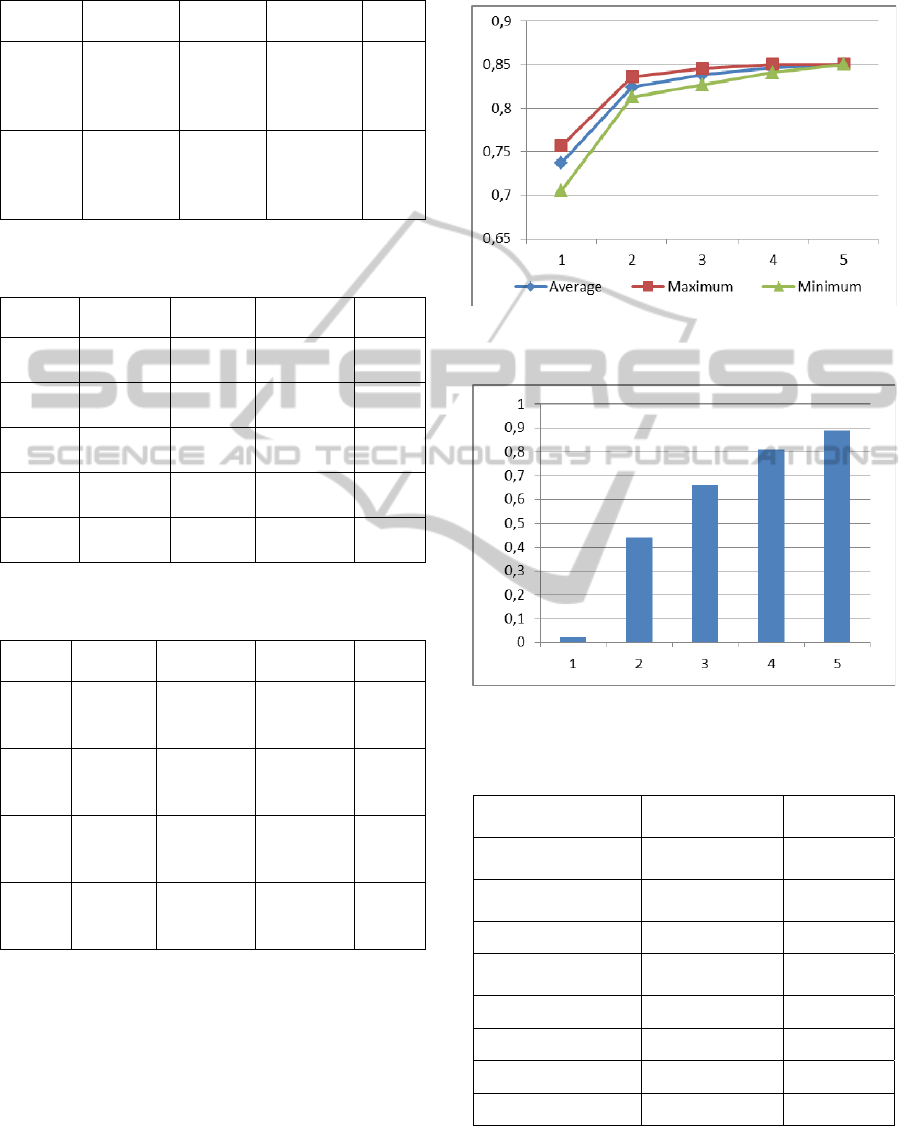
Table 6: Results of multistep fuzzy classifier design for

Iris.

Iteration

Maximum

perform.

Average

perform.

Standard

deviation

Rules

repeat.

0,947(3)

0,973(4)

0,987(5)

0,987(6)

0,908(3)

0,951(4)

0,971(5)

0,975(6)

0,0564(3)

0,0262(4)

0,0130(5)

0,0107(6)

0,67(3)

0,56(4)

0,51(5)

0,56(6)

0,980(3)

0,980(4)

0,987(5)

0,993(6)

0,980(3)

0,980(4)

0,987(5)

0,993(6)

0,0000(3)

0,0000(4)

0,0000(5)

0,0000(6)

0,93(3)

0,69(4)

0,82(5)

0,78(6)

Table 7: Results of multistep fuzzy classifier design for

Glass Identification.

Iteration

Maximum

perform.

Average

perform.

Standard

deviation

Rules

repeat.

0,757(20)

0,827(30)

0,737(20)

0,781(30)

0,0139(20)

0,0183(30)

0,02(20)

0,04(30)

0,836(20)

0,874(30)

0,824(20)

0,861(30)

0,0074(20)

0,0135(30)

0,44(20)

0,44(30)

0,846(20)

0,888(30)

0,838(20)

0,880(30)

0,0063(20)

0,0047(30)

0,66(20)

0,71(30)

0,850(20)

0,888(30)

0,846(20)

0,886(30)

0,0041(20)

0,0025(30)

0,81(20)

0,79(30)

0,850(20)

0,888(30)

0,850(20)

0,886(30)

0,0000(20)

0,0025(30)

0,89(20)

0,87(30)

Table 8: Results of multistep fuzzy classifier design for

Landsat Images.

Iteration

Maximum

perform.

Average

perform.

Standard

deviation

Rules

repeat.

0,849(10)

0,857(15)

0,857(25)

0,838(10)

0,847(15)

0,849(25)

0,0078(10)

0,0042(15)

0,0055(25)

0,36(10)

0,44(15)

0,42(25)

0,851(10)

0,861(15)

0,864(25)

0,850(10)

0,859(15)

0,863(25)

0,0011(10)

0,0014(15)

0,0009(25)

0,69(10)

0,64(15)

0,67(25)

0,853(10)

0,862(15)

0,866(25)

0,852(10)

0,860(15)

0,865(25)

0,0004(10)

0,0015(15)

0,0010(25)

0,86(10)

0,77(15)

0,79(25)

0,853(10)

0,862(15)

0,866(25)

0,852(10)

0,862(15)

0,866(25)

0,0001(10)

0,0004(15)

0,0003(25)

0,94(10)

0,87(15)

0,86(25)

We can see that standard deviation of

classification performance decreases and parameter

of rules repeatability increases for each step of fuzzy

classifier design. Also classification performance

increases for all problems using multistep fuzzy

classifier design.

For illustrating of multistep fuzzy classifier

design features we demonstrate dynamics of

classification performance, deviation, and parameter

of rules repeatability changing at the figures 1-2 for

Glass Identification problem with constraint for

rules number equals to 20.

Figure 1: Classification performance changing for Glass

Identification problem.

Figure 2: Parameter of rules repeatability changing for

Glass Identification problem.

Table 9: Comparison of the classifiers.

Algorithm

Credit

(Australia-1)

Liver

Disorder

One-step fuzzy

classifier design

0,891 0,725

Multistep fuzzy

classifier design

0,928 0,757

Bayesian approach 0,847 0,629

Multilayer

perception

0,833 0,693

Boosting 0,760 0,656

Bagging 0,847 0,630

RSM 0,852 0,632

CCEL 0,866 0,644

For the first two problems comparison with

alternative classification methods has been

MultistepFuzzyClassifierDesignwithSelf-tuningCoevolutionaryAlgorithm

119

performed. These algorithms are Bayesian approach,

multilayer perceptron, boosting (Schapire, 2001),

bagging (Breiman, 1998), random subspace method

(RSM) (Ho, 1998), and cooperative coevolution

ensemble learning (CCEL) (Zhuravlev, 1998 and

Voroncov, 2005). The results were obtained from

(Voroncov, 2005). The comparison by the best

performance value is presented in the Table 9.

5 CONCLUSIONS

The first result is that new method of Michigan and

Pittsburgh approaches combing for fuzzy classifier

rule base design has investigated on some

classification problem from UCI repository. This

method has high operation speed and efficiency as

advantages of both approaches are used. Self-tuning

cooperative-competitive coevolutionary genetic

algorithm for strategy adaptation is used at both

evolutionary stages of fuzzy classifier design. It

allows refusing the genetic algorithm parameters

setting without negative effect for algorithm

efficiency.

The second main result of our work is multistep

fuzzy classifier design investigations. Having

generated some fuzzy classifiers we are able to

construct more effective classifier from previous

classifiers using cooperative-competitive

coevolutionary algorithm again. Using this method

semantically similar fuzzy classifiers are generated.

The approach of multistep fuzzy classifier forming

has the following features:

1) This method improves classification

performance without increasing number of rules.

2) This method reduces diversity of performance

values for multiple algorithm runs, i.e. the method

has higher statistical stability.

3) The method increases repeatability of fuzzy

rules for multiple algorithm runs.

4) Corresponding to features 1-3 trends slow

down for increasing of step number.

5) The method is more effective for more

complicated classification problems (more attributes

and classes).

Fuzzy classifier design methods comparison with

alternative classification methods by performance

value demonstrates that both fuzzy classifier

forming methods have either the same efficiency as

present-day classification algorithms or even they

are more efficient.

REFERENCES

Ishibuchi, H., Nakashima, T., and Murata, T. 1999.

Performance evaluation of fuzzy classifier systems for

multidimensional pattern classification problems.

IEEE Trans. on Systems, Man, and Cybernetics, vol.

29, pp. 601-618.

Herrera, F. 2008. Genetic fuzzy systems: taxonomy,

current research trends and prospects. Evol. Intel., vol.

1, no. 1, pp. 27–46.

Holland, J. H. and Reitman, J. S. 1978. Cognitive systems

based on adaptive algorithms. In D. A. Waterman and

F. Hayes-Roth, editors, Pattern-Directed Inference

Systems. Academic Press, San Diego, CA.

Smith, S. F. 1980. A Learning System Based On Genetic

Adaptive Algorithms. PhD thesis, Department of

Computer Science, University of Pittsburgh,

Pennsylvania.

Ishibuchi, H., Nakashima T., and Kuroda, T. 2000. A

hybrid fuzzy GBML algorithm for designing compact

fuzzy rule-based classification systems. Proc. of 9th

IEEE International Conference on Fuzzy Systems,

(2000), pp. 706-711.

Sergienko, R. B. and Semenkin, E. S. 2010. Competitive

cooperation for strategy adaptation in coevolutionary

genetic algorithm for constrained optimization. Proc.

of 2010 IEEE Congress on Evolutionary Computation,

pp. 1626-1631.

Martín-Muñoz, P. and Moreno-Velo. F. J. 2010. FuzzyCN2:

an algorithm for extracting fuzzy classification rule lists.

Proc. of 2010 IEEE International Conference on Fuzzy

Systems, pp. 1783-1789.

Palacios, A. M., S´anchez L., and ´es Couso. I. 2010.

Preprocessing vague imbalanced datasets and its use in

genetic fuzzy classifiers. Proc. of 2010 IEEE

International Conference on Fuzzy Systems, pp. 2595-

2602.

Nojima, Y., Kaisho, Y., and Ishibuchi, H. 2010. Accuracy

improvement of genetic fuzzy rule selection with

candidate rule addition and membership tuning. Proc.

of 2010 IEEE International Conference on Fuzzy

Systems, pp. 527 – 534.

Schapire, R. 2001. The boosting approach to machine

learning: an overview. MSRI Workshop on Nonlinear

Estimation and Classification, Berkeley, CA.

Breiman, L. Arcing classifiers. 1998. The Annals of

Statistics, vol. 26, pp. 801-849 (Mar. 1998).

Ho, T. K. 1998. The random subspace method for

constructing decision forests. IEEE Trans. on Pattern

Analysis and Machine Intelligence, vol. 20, pp.832-

844 (Aug. 1998).

Zhuravlev, J. I. 1998. An algebraic approach to recognition

or classifications problems. In Pattern Recognition and

Image Analysis, vol. 8, no. 1, pp. 59–100.

Voroncov, V.V. and Kanevsky, D, Y. 2005. Cooperative

coevolution algorithm ensemble learning. Tavricheskiy

Vestnik Informatiki I Matematiki (Tavria's Gerald of

Informatics and Mathematics), pp. 51-66, (Feb. 2005).

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

120