Cognitive Parameter Adaption in Regular Control Structures

Using Process Knowledge for Parameter Adaption

Martin Schmid

, Simon Berger

and Gunther Reinhart

Project Group RMV of Fraunhofer IWU, Beim Glaspalast 5, Augsburg, Germany

Institute for Machine Tools and Industrial Management, Technical University Munich, Munich, Germany

Keywords: Modern Control Systems, Adaption, Neural Network, Machine Learning.

Abstract: The colour control system of an offset printing machine is one example, where modern information

processing technologies allow an improved process control and higher resource efficiency. It is not possible

to measure the printing quality during production start. So no regular closed loop control can be used. For

better system behaviour a simulation model is integrated to calculate the printing quality at any time. To get

an optimal process performance, a high simulation quality must be ensured, which includes a compensation

of process simulation inaccuracies as well as variable influences. Therefore a cognitive system is installed,

which measures the most important influences like the used paper and many other process parameters. After

each production the right model parameters will be calculated by identification algorithms. So a data set

with influences and parameters is available. For the next production run the best-fitting parameters for the

simulation model can be calculated by a Neural Network. Additionally wear and deposits, which change the

machine’s performance, can be compensated. The simulation accuracy and the process control quality rises,

which enables a faster run-up. Savings of paper, ink, energy and time allow an economic application of this

control concept.

1 INTRODUCTION

1.1 Linear Control Theories vs.

Methods of Machine Learning

Controllers are often applied in technical devices

and industrial machines. The controller type depends

on the task. In many processes it is sufficient to use

standard PI- or two-level controller. Therefore a

closed control loop is essentiell, what means that the

process output has to be measured permanently and

fed back into the control system.

There exist several concepts to parameterise the

controller to ensure stability and dynamic system

behaviour. Furthermore powerful computer systems,

powerful libraries and high sophisticated software

tools are available to setup a complete controller in

an easy and fast way.

Although conventional controllers can be used

for many applications there are also disadvantages.

To use standard control theories, the developer

needs to know the transfer function of the machine

as well as the process outputs at any time.

Furthermore the system behaviour has to be nearly

time invariant and approximated as linear.

When one of these conditions is not given, more

sophisticated methods have to be taken into account

(Hafner, 2009); (Ramesh, 2002). If there is no

formal system description, machine learning

methods can be used. The most popular type is the

Neural Network (Huang, 1994); (Moon 2008);

(Rangwala, 1989).

A self-learning system has two states in general.

At first it has to be trained with data representing the

desired behaviour, the so called training set. In the

training sequenzce internal parameters or structures

will be changed, till the Neural Network (or all other

types of supervised learning methods) gives similar

values like the training set (Guanyuz, 2012). When

this step is finished, the system can be used to

calculate outputs to familiar or to new inputs. The

quality of the system strongly depends on the

training set. Additionally the optimal net topology

and a successful training period cannot be predicted

at all. If a self-learning component is used in a

control system, the quality of the complete control

system can vary (Rajagopalan, 1996). A

131

Schmid M., Berger S. and Reinhart G..

Cognitive Parameter Adaption in Regular Control Structures - Using Process Knowledge for Parameter Adaption.

DOI: 10.5220/0004427701310138

In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2013), pages 131-138

ISBN: 978-989-8565-70-9

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

consequence is that the whole system can work

inaccurately or becomes instable. Furthermore it is

difficult to evaluate the quality of the system

(Suzuki, 2011). Moreover there exists only low

knowledge about learning systems in the industry,

because practical applications are implemented only

seldomly in this way.

1.2 Control Structures in Modern

Printing Machines

With powerful web presses paper and foils are

printed in big lots in a short period of time. There

are several control circuits included for printing,

cutting and regulating the speed and position of the

paper web. For the printing quality the so called

optical density is one of the most important control

parameters, which expresses the amount of colour

on the paper and the optical impress of the printed

sheet.

An offset printing machine has four printing

units for each colour black, cyan, magenta and

yellow. Each printing unit is subdivided in up to 40

zones side by side, because the images require

varying amount of ink for each zones. Each zone has

its own ink valve, which can be set individually to

asure the correct amount of ink according to the

printing image. The setting of these valves is called

“zone opening” and can be set through the control

system. The second setting is the speed of the ink

fountain roller, which is equal for all zones. A higher

optical density can be reached by a higher zone

opening or higher roller speed. Both need to be set

correctly to achieve a high printing quality for the

product.

The measurement device for the optical density

needs a specimen field on each sheet. At the

beginning of the printing process the optical density

of this field is too low to be detected by the sensor.

In this time no optical density can be measured and

thus the control circuit is not closed. It is state of the

art to use predefined values at the beginning till the

density is high enough to be detected by the sensor

and close the control circuit. From this point of time

the controllers for the printing quality and the sheet

cutting start working. It has to be considered, that

there are additionally big dead times according to

the machine size, which make the control process

less stable and slower.

The consumables and environmental conditions

like the ambient temperature or humidity also have a

big impact on the printing process.

To prevent an instable behaviour at any time, the

controller is adjusted conservatively. Between start-

up of the machine and reaching the desired optical

density all sheets need to be discarded, because their

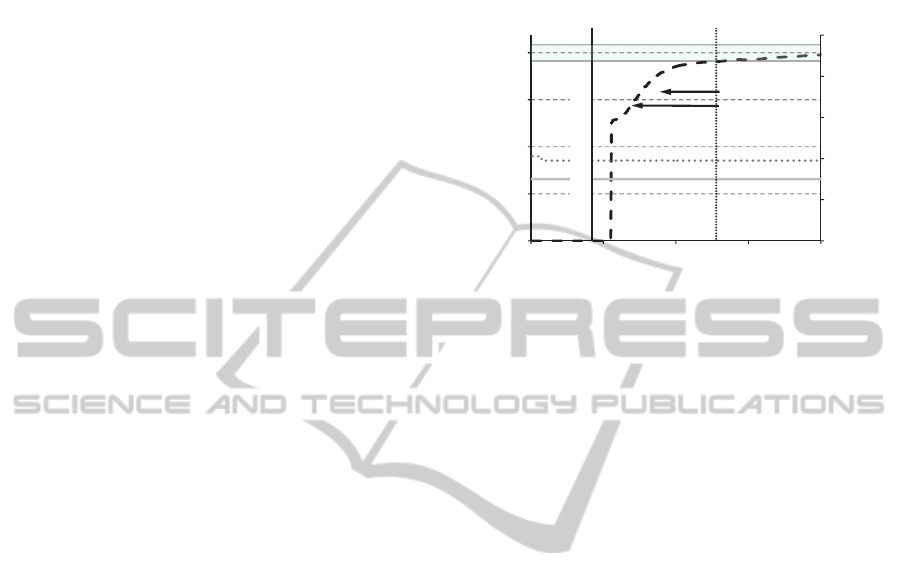
quality level is too low. Figure 1 show the start-up-

period of one zone.

Figure 1: Not acceptable printing quality at the beginning.

The production starts at t = 190 s. At the first 230

seconds no measurements of the optical density are

possible. At t= 500 seconds the optical density is in

the tolerance, so that the product can be sold.

Additionally the zone opening and the ink roller

speed is shown, which stay at a static value at the

beginning.

2 OBJECTIVES

For increasing the resource efficiency and reducing

the production costs, an improved control system is

needed to speed up the starting process for a higher

printing quality in less time. Furthermore, diverse

influences need to be taken into account to heighten

the stability of the control system.

3 APPROACH

3.1 General Concept

To build up a stabil and faster control system it is

essential to get a closed loop, what means, that

output values are available within acceptable time.

In figure 2 all elements of a cognitive model based

control system are shown, which enables these

needs.

A simulation model calculates the output of the

real process in that time, when no measurements can

be taken in the machine. The measured process

output, the optical density, is just needed for

tracking the model to the real printing machine (Rae,

100

0,0

0,4

0,8

1,2

1,6

0 200 400 600 800

Zone Opening/ Ink Roller Speed

Product Quality (optical density)

Time

Slow rising printing Quality at Production start

Zone Opening

Optical Density

- simulat ed

-measured

Ink Roller Speed

Start of Production at t = 190 s

Tol er an ce

Good Quality

aft er 506 s

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

132

1996). Both, the model and the controller are

conventionally designed as regular linear systems.

Because there are many parameters influencing the

system behaviour, the simulation model needs to be

adjusted to behave like the real machine. For this, a

self-learning adaption mechanism is used to estimate

the real machine parameters on basis of former

productions. The simulation model parameters will

be changed, also like the controller parameters.

Figure 2: Model based control with parameter adaption.

For this, the main influences as well as the

machine settings and the machine outputs are

recorded and compressed to key figures. If a

production is finished, model parameters can be

calculated also, which would have enabled a high

simulation quality in this past production run.

Therefore parameter identification algorithms are

used. These parameters and the influences build up

one dataset for this machine and will be stored in a

data base.

The datasets can be calculated only after a

production. To know the best fitting parameters

before the production it is necessary to determine

them at production start.

For this a statistical adaption to the machine

conditions is implemented. To consider varying

influences machine-learning algorithms are used,

which finds out the optimal simulation model

parameters according to the consumables or the

production conditions.

The model accuracy is higher than an initial

parametrisized model. So the machine reaches its

desired quality level sooner and improves the

resource efficiency.

3.1.1 Real Printing Machine

The printing machine includes four printing units for

each colour. Each unit consists of rollers, which are

mechanically linked via friction to the previous and

next roller, excluding the ink fountain rolle The

number of rollers is necessary to transport and

homogenise the ink film. The ink, stored in the ink

supply, will be transported to the next roller over a

gap. The size of the gap determines a minimum zone

opening to transfer ink onto the next rollers. The

separation between coloured and not coloured areas

occurs on the plate roller, whose surface has

different properties based on the image (Wang,

1984). On the non-coloured areas additional water is

used in the offset printing process. Therefore a water

supply is integrated in the printing unit.

r, which is driven separately. This is shown in figure

Figure 3: Schematic of a printing unit.

3.1.2 Simulation Model

Each touching point between two rollers is called

nip. The mathematical description for the ink flow

between two nips is a first order differential equation

(Kipphan, 2002). For one zone there exist up to 50

nips and a printing unit has up to 50 zones. So the

simulation model for a single printing unit consists

up to 2500 linked differential equations.

To reduce the computational complexity a single

differential equation has been derived for one zone,

describing the behaviour according equation 1.











1









(1)

The input of the system is the zone opening

multiplied with the ink fountain roller speed, the

output is the optical density.

The behaviour of the system is described by the

system gain



, the time constant 



and the dead

time 



, which regards the delay caused by the ink

transport. The dead time can be calculated via

kinetic and geometric studies. The time constant can

be approximated analytically. The gain consists of

measureable and not measureable components and

describes the static ratio between the machine

settings and the optical density. The gain is affected

by different influencing variables, the consumables

and the machine state and can not be calculated

analytic.

CognitiveParameterAdaptioninRegularControlStructures-UsingProcessKnowledgeforParameterAdaption

133

3.1.3 Influences and Their Clustering

There are four different sources, which may

influence the machine behaviour. The consumables

paper, ink and water can vary. Even consumables,

which should have theoretically the same properties,

can behave differently because of deviations in their

production process or while storage. The machine

ages also, e. g. the rubber of the rollers gets harder

than new ones.

The area coverage is an example of the

influences of the production properties. It is the ratio

between the coloured to the whole area of a sheet in

percent for one zone. If the area coverage is high,

the zone behaves agilely. Otherwise, when the area

coverage is small, the zone behaves inertly. So the

parameters of the printing job have a prevailing

influence. The last types are environmental

parameters. The humidity in the printing room for

example changes the absorbtion rate of the water on

the rollers, which results in a changing optical

impress and density.

3.1.4 Adaptive Controller

When the model will be adapted to the current

machine state, the controller also should be adapted.

A common way is using the model’s parameter

according empirical methods like

Chien/Hrones/Reswick or Ziegler/Nichols. For the

printing process, the method of

Chien/Hrones/Reswick was chosen because of its

robustness and simple implementation (Aström et

al., 2004).

The controller is set only once before the printing

machine starts. If the controller would be tuned

permanently this could cause instability. The

changes of the machine characteristics during run up

are small enough to be neglected.

Like mentioned before each zone has two inputs,

namely the zone valve opening and the speed of the

ink fountain roller. Both values affect the optical

density independently from each other. It is

important to recognise that the zone valve opening

only influences one zone, but the ink fountain roller

speed impacts all zones. Hence a conventional state

space controller can not be applied. To get a linear

control system, both values must be combined to a

virtual machine setting, which can be controlled by a

standard PI-controller. The virtual figure is the

product of the ink fountain roller speed and the zone

opening, corrected by the zone offset. The black line

in figure 4 shows the linear controller output, which

can be achived through a high ink fountain roller

speed and a low zone opening or vise versa.

Figure 4: Variable ratio between ink fountain roller speed

and zone opening.

At the production start (t

start

) a higher ink roller

speed improves the process dynamic. For a stable

process control a higher zone opening has

advantages (t

stationary

). During the ramp up the ratio

between zone opening and ink roller speed changes

for high process dynamics as well as stable

production.

3.2 Higher Simulation Quality

by Analytic Data Mining

In this section it is described how the values of the

minimum zone valve opening can be calculated from

the data of the former lots. The valves of each zone

needs to be opened by an offset, otherwise no colour

is transferred into the printing unit because of a gap

between the ink fountain roller and the following

roller (see figure 5). The offset directly affects the

output of the model. When the offset is high then the

model calculates that only little ink can flow into the

printing unit and the optical density becomes low

and vice versa.

Figure 5: Physical explanation of the offset.

The distance is initial set to 0.08 mm; in reality a

range of 0.03 till 0.10 mm could be measured.

Reasons can be aging or pollution of the mechanical

parts. The gap is implemented to control the ink

roller speed independent from the other rollers

without any friction. Lower zone openings do not

100

0 20406080100

Ink Roller Speed

Zone Opening

ariable Ratio of the Process Input

Possible process inputs

for one production

Offset

st a r t

st a t i o n a ry

Offset

Distance:

0,03 – 0,1 mm

Pa p er

Ink transport

Ink supply

Zone

Opening

Gap

Ink

Fountain

Roller

Gap

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

134

affect the printing process. This offset makes the

simulation model non-linear and needs to be

considered adequate. Otherwise the model quality

would be too low for the simulation (Eberhard,

2006). This can be done manually, which is very

time consuming. Furthermore the production has to

be stopped for at least three hours to clean and

measure the zone openings. So a method has been

developed to identify the offset by analysing existing

machine data from the prior production runs.

When the optical density has settled then the

zone opening is nearly constant. A higher zone

opening takes more ink on the paper. The amount of

ink can be described via the parameter area

coverage. The higher the area coverage is the more

ink is needed and the higher the zone opening is.

There exists a nearly linear link between the area

coverage and the amount of ink on the paper, shown

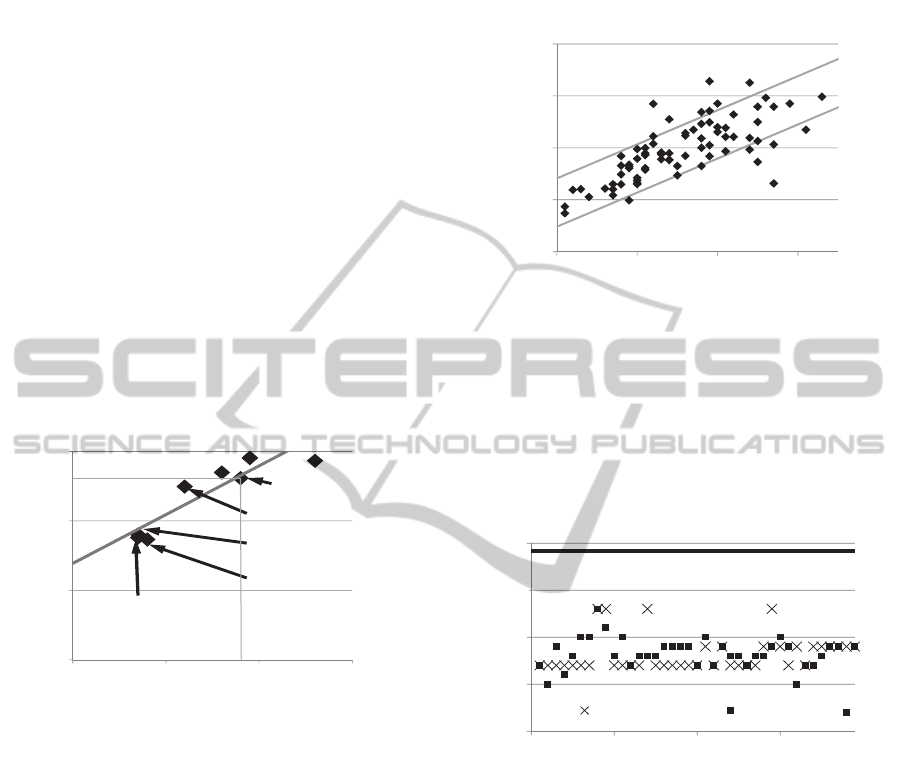
in figure 6. For each production ID there is a pair of

area coverage and stationary zone opening.

Figure 6: Zone opening compared with area coverage.

For example the production with the ID 1989 has

an area coverage of 18 % and a zone opening of

52 %.

Figure 7 illustrates this relation for many

productions of a real printing machine. Each dot

represents one production run of a specified zone.

Using numerical methods a best-fit-line can be

generated. When the area coverage is 0% then no

ink is needed. This set point is equal to the offset,

where no colour is transfered into the printing unit

and on the paper.

In practical operation there are also many

operating points, which do not match exactly the

line. To improve the analyses, a 2-step-filter-

method is used. Therefore a first analysis determines

the most probable operating points. A range of

tolerance is definied on this. Only points in this

range are used for the calculation of the best fit line.

According to figure 8 an offset of 18 percent can be

estimated.

Figure 7: Analytical determination of the zone offset.

This method allows determining the actual offset

value, considering dirt and mechanical imperfections

without direct measurements. Figure 8 shows the

comparison between the calculated and the

measured values. The offsets of all 39 zones of the

printing unit cyan are drawn.

Figure 8: Calculated offsets compared with measurements.

The nominal value for the zone offset is 24 %.

The calculated offsets are in a range between 7 and

18 %, the measurements are between 12 and 18 %

and so the accuracy is much better than using the

nominal values. Despites the huge variability of the

real offsets, it is possible to build up an accurate

simulation model without separate measurements.

It has already been shown, that this method

improves the model quality and so increases the

performance of the simulation model.

It needs to be considered that the information

about the offset is just valid as long as no

maintenance is performed or changes in the

mechanics appear. Otherwise the data about the lots

becomes obsolete and new data must get collected to

get right offset values to consider the machine state.

0 102030

Stationary Zone Opening

Area Coverage

Raw data for analyti

Data M ining

production id: 1823

production id: 1920

production id: ...

production id: 1982

Production id:

1989

0 102030

Static zone Opening

Area Coverage

Overview of an 80 % Filter for all

Operation Points in one Zone

0 102030

Offset

Zone Number

Comparasion Calculated Values

with Measured Values

Measurement Calculation

Nominal value: 24 %

CognitiveParameterAdaptioninRegularControlStructures-UsingProcessKnowledgeforParameterAdaption

135

3.3 Parameter Identification by

Machine Learning Methods

Besides the machine state the consumables and the

process conditions affect the process behaviour. The

simplified simulation model uses a differential

equation to calculate the time behaviour to calculate

the optical density.

3.3.1 Physical Background

The transfer function of the simulation model can be

characterized according equation 1. The model

parameter K

can vary corresponding to the physical

variable ink efficiency. This variable is used to

calculate the optical density at specific machine

settings. It is possible to calculate the ink efficiency

on the basis of the measurements afterwards each

production, but not before. An analytic

determination is also not possible, because there are

too many crossactions between process, paper and

ink and moreover the physical and chemical

processes have not yet been identified. This means

finite element analyses are not possible.

Because of this reasons, a multilayer perceptron

(MLP) is used to estimate the ink efficiency on the

basis of the influence parameters (Hintz, 2003). An

MLP is a kind of Neural Network, which consists of

one input and one output layer and several hidden

layers. Each hidden layer is built of neurons (Bayer

et al., 2011); (Beuschel, 2000).

3.3.2 Usage of an MLP to Calculate the Ink

Efficiency

The MLP reproduces the relationship between the

influence parameters and the optimal model

parameters. For this, at first a training period must

be completed successfully (Zell, 1994); (Faridi,

2011). A supervised learning algorithm, that enables

a fast adaption of the network parameters, requires a

training data set, which includes the input

parameters and the corresponding outputs, namely

the parameter ink efficiency. This parameter is

necessary to calculate the model parameter K

equation 1. The training set is calculated according

former production runs. All measurements will be

analysed and compressed to key figures for the input

variables. The input parameters are the influence

variables like the proberties of the consumables

paper, ink and water, the process conditions like the

temperature and humidity and other physical

characteristics. The corresponding output is the

effective ink efficieny, which can be calculated via

parameter identification algorithms. This is only

possible with completed production runs. The

training period is finished when the net output is

near the desired output. This means, that the net

behaviour is similar to the training sets and thereby

to the machine characteristics.

To use the trained MLP it is necessary to use the

influence parameter of the next production run as net

input. At the start of the production all influence

parameters have to be measured. With these inputs

the MLP can estimate the most probable ink

efficiency for the next production. This enables the

computation of the model parameter K

for an

optimal simulation accuracy of the simulation

model. This enables a parameter adaption of the

model and the controller before the start and without

a closed loop control. It is called cognitive parameter

adaption, because only influence variables are used

and combined in a new way.

3.3.3 Topology of the Neural Network

For this application an MLP net was selected

because it is particularly suitable for handling many

inputs. The input and the output data are linearly

normalized due to their physical range of values.

The output neuron has a linear activation function so

that the ink efficiency can be any value between 0.5

and 2.5. All other neurons obtain a sigmoid

activation function. The number of inputs and output

neurons are held constant. The actual structure of the

Neural Network is not predefined.

3.3.4 Topology Optimisation of the Neural

Network

To find the optimal network structure, several

networks with different structures are trained with

the same training data. The networks vary in the

number of hidden layers and in the total number of

neurons. At the end of the training phase the

performance of each network will be evaluated

automatically using a reference data set. The

network with the least error is assumed to have the

best structure and the best ability to generalise, so

this will be used for further calculation of the ink

efficiency.

3.3.5 Workflow

Before the production starts, the simulation model

sends a request to the Neural Network to deliver the

ink efficiency. The network gathers all input values,

calculates the ink efficiency and sends it to the

simulation model. This step takes up to 20 seconds.

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

136

The training and the optimisation of the network

take up to 30 hours. This is not time critical because

the network gets trained only once a month on a

separate computer. If a new production starts while

training, the old network will be used to calculate

the ink efficiency. This means that the training and

the usage is completely separated.

4 RESULTS

4.1 Improvement of the Machine

Behaviour using a Model based

Controller

Until now no dead times are considered in the

controller design. The same can be stated for many

other important influences. So the controller is

designed slowly to avoid unstable behaviour. This

results in a slow system dynamic according to

figure 1. The desired optical density of 1.6 is

reached at t = 500 seconds and so the machine

produces insufficient quality for more than 300

seconds.

Figure 9 shows the rising of the optical density

using the model based adapted controller. These

values can be compared with figure 1, the controller

and system behaviour is simulated offline.

Figure 9: System dynamic with a model based controller.

At t= 190 seconds the ink roller speed is set to

100 % and the zone opening get up to 70 % for some

seconds and get down after that, so a dynamic ramp

up is possible. Also the variable ratio between zone

opening and roller speed is shown. It can be seen

easily that the machine, which starts at the same

time, just needs 30 seconds to reach good quality.

This means that in this case the efficiency was

increased by the factor of 10 in the simulation. It can

be seen that the density does not overshoot.

4.2 Quality of the Model Adaption

4.2.1 Determining the Zone Offset

The information, which is currently used for the

model, can also be helpful for other purposes. It

could already be proven that the offset in the zone

valve opening has a drift from one side to another

without any visible reasons. This information was

used to demonstrate that an overhaul needs to be

done, which includes cleaning and a mechanical

setup of the zone offsets.

4.2.1 Neural Identification of the Model

Parameter

The Neural Network determines variables, which

cannot be calculated before production start. It needs

to be considered that a Neural Network needs as

many training data sets as possible to cover all

possible variations of the input parameters. The

training sets have to be evenly spread over all

parameters. Furthermore it is also necessary to

substitute old data by new one. This is especially

caused by the aging of the mechanical parts and due

to deposits. Additionally several filters are applied

for the training data, which increases the accuracy of

the data and enables a well-designed network.

5 OUTLOOK AND NEXT STEPS

Most experiments are done on a test printing

machine. Currently it is being integrated into a real

production system. Therefore the model and the

controller have been extended. Furthermore the

Neural Network needs to be optimized so that its

training takes less time. Input parameter with small

effects skipped.

Furthermore the effect of the Neural Network on

the simulation quality has to be determined.

Therefore the real control behaviour with and

without the parameter adaption must be compared.

6 CONCLUSIONS

It is state of the art to apply conventional control

theory for production machines. More powerful

tools like self-learning systems are rejected because

of their non-deterministic behaviour.

To improve the resource efficiency of a printing

machine the capacity of these systems are needed. A

combination of the mathematical deterministic of

100

0,0

0,4

0,8

1,2

1,6

0 200 400 600 800

Zone Opening/ Ink Roller Speed

Product quality (optical density)

Time

Optimized system Behaviour

with an Adapted Controller

Zone Opening

Optical Densit y

-origin

- controlled

Ink Roller Speed

CognitiveParameterAdaptioninRegularControlStructures-UsingProcessKnowledgeforParameterAdaption

137

analytic controllers with an advanced self-learning

system was developed for a printing machine.

For this machine a transfer function model was

designed which describes the principal behaviour.

To identify the model parameter before the

production start, diverse devices and information

about the consumables and the environmental

conditions are used. All influences, whose

correlation can be described analytically, are also

calculated in that way. Influences with unknown

mode of action are regarded with a Neural Network.

Therefore the most important impacts are measured,

conditioned and fed to the network. So it is possible

to predict the machine’s behaviour under varying

operation conditions with unknown effects. The

simulation model and the controller are turned

according the adapted parameter to guarantee a

stable and dynamic production. This enables higher

product quality and efficiency.

ACKNOWLEDGEMENTS

The authors want to express their gratitude to the

state government of Bavaria for its financial support

of the project “CogSYS – Resource Efficiency by

Cognitive Control Systems”.

REFERENCES

Aström, K. J., Hägglund, T., 2004. Revisiting the Ziegler–

Nichols step response method for PID control.

Bayer, J., Osendorfer, C., Smagt, P., 2011: Learning

Sequence Neighbourhood Metrics. Technical

University Munich.

Beuschel, M., 2000. Neuronale Netze zur Diagnose und

Tilgung von Drehmomentschwingungen am

Verbrennungsmotor, Technical University Munich.

Eberhard, M., 2006. Optimisation of Filtration by

Application of Data Mining Methods, Dissertation,

Technical University Munich.

Faridi, A.; Golian, A., 2011: Use of neural network

models to estimate early egg production in broiler

breeder hens through dietary nutrient intake. In:

Poultry Science.

Govindhasamy, J. J.; McLoone, S. F.; Irwin, George W.;

French, J.; Doyle, R. P., 2005: Neural modelling,

control and optimisation of an industrial grinding

process. In: Control Engineering Practice 13.

Guanyuz, Zhou (2012): Online incremental feature

Learning with denoising autoencoders. International

Conference on Artificial Intelligence and Statistic,

2012.

Hafner, R. 2009: Dateneffiziente selbstlernende neuronale

Regler. University Osnabrück.

Hintz, Christian, 2003: Identifikation nichtlinearer

mechatronischer Systeme mit strukturierten

rekurrenten Netzen. Dissertation. Technical University

München.

Huang, S.H; Hong-Chao Z., 1994: Artificial neural

networks in manufacturing: concepts, applications,

and perspectives. IEEE Trans. Comp., Packag.,

Manufact. Technologies.

Kipphan, H., 2002. Handbuch der Printmedien, Springer

Verlag, Berlin.

Moon, P.; et al. , 2008. Ink-jet printing process modeling

using neural networks. International Electronics

Manufacturing Technology Conference.

Rangwala, S. Dornfeld, D. A., 1989. Learning and

optimization of machining operations using computing

abilities of neural networks, IEEE Transactions on

Systems, Man, and Cybernetics.

Ramesh. R., Mannan M.A., Poo A.N., 2002. Support

vector machines model for Classification of Thermal

Error in Machine Tools, in: The International Journal

of Advanced Manufacturing Technology.

Rajagopalan, Ramesh; Rajagopalan, Purnima, 1996.

Applications of Neural Network in Manufacturing.

International Conference on System Sciences.

Suzuki, K, 2011. Artificial Neural Networks - Industrial

and Control Engineering Applications.

Wang, D., 1984. An investigation of the applicacability of

Walker and Fetsko ink transfer equation, Rochester,

New York.

Rae, T.A; et al, 1996. The application of neural Networks

to induction machine control. Proceedings of IEEE.

Zell, A., 1994. Simulation neuronaler Netze, Oldenburg

Verlag, München.

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

138