
Agent based Simulations of Epidemics on a Large Scale
Toward the Right Choice of Parameters
∗
Robert Els
¨
asser
1
, Adrian Ogierman
2
and Michael Meier
2
1
Department of Computer Sciences, University of Salzburg, A-5020 Salzburg, Austria
2
Institute for Computer Science, University of Paderborn, 33102 Paderborn, Germany
Keywords:
Epidemic Algorithms, Power Law Distribution, Disease Spreading, Public Health.
Abstract:
In a world where epidemic outbreaks may take many lives, forecasting and analysis tools are of high impor-
tance - for an urban area such as New York City, a continent like Africa, as well as for the world itself. Such
tools provide valuable insight on different levels and help to establish and improve embankment mechanisms.
In this paper, we present an agent-based algorithmic framework to simulate the spread of epidemic diseases.
Based on the population structure of Germany, we investigate the impact of the number of agents, representing
the population, on the quality of the simulation. Real world data provided by the Robert Koch Institute (Ar-
beitsgemeinschaft Influenza, 2011; Robert Koch Institute, 2012) is used to evaluate our results. In a second
step we empirically analyze the effects of certain non-pharmaceutical countermeasures as applied in the USA
against the Influenza Pandemic in 1918-1919 (Markel et al., 2007). Our simulation and evaluation tool par-
tially relies on the probabilistic movement model presented in (Els
¨
asser and Ogierman, 2012). Based on our
empirical tests, we conclude that the amount of agents in use can have a huge impact on the accuracy of the
achieved simulation results. This reveals several challenges, which have to be taken into account in the design
of forecasting and analysis tools for the spread of epidemics. On the other hand, we show that by utilizing the
right parameters in our algorithmic framework - some of them being obtained from real world observations
(Eubank et al., 2004) - one can efficiently approximate the course of a disease in real world.
1 INTRODUCTION
In order to improve our chances to control an epi-
demic outbreak, we need proper models which de-
scribe the spread of a disease. Institutes, govern-
ments, and scientists all over the world work inten-
sively on forecasting systems to be well prepared if
an unknown disease appears.
In recent years a huge amount of theoretical and
experimental study has been conducted on this topic.
While theoretical analysis provides important and
sometimes even counter intuitive insights into the
behavior of an epidemic (e.g. (Borgs et al., 2010;
Els
¨
asser and Ogierman, 2012)), in an experimental
study one can take many different settings and pa-
rameters (Lee et al., 2008; Lee et al., 2010) into ac-
count. These usually cannot be considered simul-
taneously in a mathematical framework. A specific
topology, for example, may have its own attributes
∗
Partially supported by the Austrian Science Fund
(FWF) under contract P25214 and by DFG project SCHE
1592/2-1.
that are completely different in other topological set-
tings. Small islands connected only by ferries obvi-
ously offer other spreading opportunities than a huge
metropolitan city. Furthermore, the characteristics of
the spread of an epidemic also depend on the behav-
ior of the infected individuals. That is, different peo-
ple spread the disease (in its early stage) in different
ways, which may or may not lead to an outbreak.
The goal of this paper is to present and empiri-
cally analyze a new dynamic model for the spread of
epidemics. One of our objectives is to find the right
parameters, which lead to realistic settings. There-
fore, we investigate a general simulation environment,
in which the different parameters can easily be ad-
justed to real world observations. A second objec-
tive is to evaluate similarities between countermea-
sure approaches in our model and the real world. We
use empirical data for the comparison. Our tool is
agent-based, i.e., the individuals (or groups of such)
are modeled by agents interacting with each other.
The environment approximates the geography of Ger-
many, in which agents may travel between cities.
263
Elsässer R., Ogierman A. and Meier M..
Agent based Simulations of Epidemics on a Large Scale - Toward the Right Choice of Parameters.
DOI: 10.5220/0004429402630274
In Proceedings of the 3rd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2013),
pages 263-274
ISBN: 978-989-8565-69-3
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

Within a city the agents interact according to the prob-
abilistic model presented in (Els
¨
asser and Ogierman,
2012) in a distributed manner. For a detailed descrip-
tion of the algorithmic framework see Section 2.
1.1 Related Work
There is a huge amount of work focusing on the anal-
ysis of epidemic diseases. In this subsection we pro-
vide an overview of the results which are closely re-
lated to the topic of this paper. In our description, we
often rely on the style and wording of (Els
¨
asser and
Ogierman, 2012).
The structure of this subsection is as follows. At
the beginning we present a simple model, which is of-
ten used to simulate an epidemic. Then, we describe
some movement models, on which several studies
w.r.t. the spread of epidemics are based. We conclude
the section by providing an overview of certain em-
pirical results in the field of disease spreading as well
as of the main approaches one can identify.
There is plenty of work considering epidemio-
logical processes in different scenarios and on var-
ious networks. The simplest model of mathemati-
cal disease spreading is the so called SIR model (see
e.g. (Hethcote, 2000; Newman, 2003)). The popula-
tion is divided into three categories: susceptible (S),
i.e., all individuals which do not have the disease yet
but can become infected, infective (I), i.e., the individ-
uals which have the disease and can infect others, and
recovered (R), i.e., all individuals which recovered
and have permanent immunity (or have been removed
from the system). Most papers model the spread of
epidemics using a differential equation based on the
assumption that any susceptible individual has uni-
form probability β to become infected from any in-
fective individual. Furthermore, any infected player
recovers at some stochastically constant rate γ.
This traditional (fully mixed) model can easily be
generalized to a network. It has been observed that the
corresponding process can be modeled by bond per-
colation on the underlying graph (Grassberger, 1983;
Newman, 2002). Interestingly, for certain graphs
with a power law degree distribution, there is no
constant threshold for the epidemic outbreak as long
as the power law exponent is less than 3 (Newman,
2003) (which is the case in most real world networks,
e.g. (Faloutsos et al., 1999; Adamic and Huberman,
2000; Amaral et al., 2000; Ripeanu et al., 2002)).
If the network is embedded into a low dimensional
space, or has high transitivity, then there might exist
a non-zero threshold for certain types of correlations
between vertices (Newman, 2002). However, none of
the papers above considered the dynamic movement
of individuals, which seems to be the main source of
the spread of diseases in urban areas (Eubank et al.,
2004).
In (Eubank et al., 2004) the physical contact pat-
terns are modeled by a dynamic bipartite graph, which
results from movement of individuals between spe-
cific locations. The graph is partitioned into two parts.
The first part contains the people who carry out their
daily activities moving between different locations.
The other part represents the various locations in a
certain city. There is an edge between two nodes, if
the corresponding individual visits a certain location
at a given time. Obviously, the graph changes dynam-
ically at every time step.
In (Eubank et al., 2004; Chowell et al., 2003) the
authors analyzed the corresponding network for Port-
land, Oregon. According to their study, the degrees
of the nodes describing different locations follow a
power law distribution with exponent around 2.8
2
.
For many epidemics, transmission occurs between in-
dividuals being simultaneously at the same place, and
then people’s movement is mainly responsible for the
spread of the disease.
The authors of (Els
¨
asser and Ogierman, 2012)
considered a dynamic epidemic process in a certain
(idealistic) urban environment incorporating the idea
of attractiveness based distributed locations. The epi-
demic is spread among n agents, which move from
one location to another. In each step, an agent is as-
signed to a location with probability proportional to
its attractiveness. The attractiveness’ of the locations
follow a power law distribution (Eubank et al., 2004).
If two agents meet at some location, then a possible
infection may be transmitted from an infected agent
to an uninfected one. The authors obtained two re-
sults. First, if the exponent of the power law distribu-
tion is between 2 and 3, then at least a small (but still
polynomial) number of agents remains uninfected and
the epidemic is stopped after a logarithmic number of
rounds - even if each agent may spread the disease
for f (n) time steps (where f (n) = o(log n)). Sec-
ondly, if the power law exponent is increased to some
large constant, which is argued to be an implication
of certain countermeasures against the spreading pro-
cess, then the epidemic will only affect a polyloga-
rithmic number of agents and the disease is stopped
after (loglogn)
O(1)
steps. In this case each agent is
allowed to spread the disease for a number of time
steps, which is bounded by some large constant. The
results explain possible courses of a disease and point
out why cost-efficient countermeasures may reduce
2
In (Eubank et al., 2004) the degree represents the num-
ber of individuals visiting these places over a time period of
24 hours.
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
264

the number of total infections from a high percentage
of the population to a negligible fraction.
In addition to the theoretical papers described
above, plenty of simulation work has also been
done. Two of the most popular directions are the
so called agent-based and structured meta-population-
based approach, respectively (cf. (Ajelli et al., 2010;
Jaffry and Treur, 2008)). Both models have their ad-
vantages and weaknesses. The main idea of the meta-
population approach is to model whole regions, e.g.
georeferenced census areas around airport hubs (Bal-
can et al., 2009), and connect them by a mobility net-
work. Then, within these regions the spread of epi-
demics is analyzed by using the well known mean
field theory.
The agent-based approach models individuals
with agents in order to simulate their behavior. In this
context, the agents may be defined very precisely, in-
cluding e.g. race, gender, educational level, etc. (Lee
et al., 2008; Lee et al., 2010), and thus provide a huge
amount of detailed data conditioned on the agents set-
ting. Furthermore, these kinds of models are also able
to integrate different locations like schools, theaters,
and so on. Thus, an agent may or may not be infected
depending on his own choices and the ones made by
agents in his vicinity. The main issue of the agent-
based approach is the huge amount of computational
capacity needed to simulate huge cities, continents or
even the world itself (Ajelli et al., 2010). This lim-
itation can be attenuated by reducing the number of
agents, which then entails a decreasing accuracy of
the simulation. In the meta-population approach the
simulation costs are lower, sacrificing accuracy and
some kind of noncollectable data.
To combine the advantages of both systems, hy-
brid environments were implemented (e.g. (Boba-
shev et al., 2007)). The main idea of such systems
is to use an agent-based approach at the beginning
of the simulation up to some point where a suit-
able amount of agents is infected. Then, the sys-
tem switches to a meta-population-based approach.
Certainly, such a system combines the high accuracy
of the agent-based simulations at the beginning of
the procedure with the faster simulation speed of the
meta-population-based approach at stages in which
both systems may provide similar predictions. Here,
the situation to switch between both approaches (in
both directions) is defined by a threshold T describ-
ing a specific amount of infected agents. In (Boba-
shev et al., 2007), the authors compared average epi-
demic trajectories produced by both approaches and
determined which threshold value (if any) results in
equivalent average trajectories. For certain epidemics,
especially unknown ones, this adjustment may be dif-
ficult or even not feasible at all.
These kind of simulations are also used to investi-
gate the impact of (non-)pharmaceutical countermea-
sures on the behavior of an epidemic. Germann et
al. (Germann et al., 2006) investigated the spread of
a pandemic strain of the influenza virus through the
U.S. population. They used publicly available 2000
U.S. Census data to identify seven so-called mixing
groups, in which each individual may interact with
any other member. Each class of mixing group is
characterized by its own set of age-dependent prob-
abilities for person-to-person transmission of the dis-
ease. They considered different combinations of so-
cially targeted antiviral prophylaxis, dynamic mass
vaccination, closure of schools and social distancing
as countermeasures in use, and simulated them with
different basic reproductive numbers R
0
. It turned
out that specific combinations of the countermeasures
have a different influence on the spreading process.
For example, with R
0
= 1.6 social distancing and
travel restrictions did not really seem to help, while
vaccination limited the number of new symptomatic
cases per 10,000 persons from ∼ 100 to ∼ 1. With
R
0
= 2.1, such a significant impact could only be
achieved with the combination of vaccination, school
closure, social distancing and travel restrictions.
1.2 Our Results
The results of this paper are two-fold. First, we show
that by increasing the number of agents we are able
to significantly improve the accuracy of our results in
the scenarios we have tested. This is due to different
phenomena, which are only visible if the amount of
agents in use is large enough. For example, if the
number of agents exceeds a certain value, then the
epidemic manages to keep a specific (low) amount
of infected individuals over a long time period. Fur-
thermore, the number of agents has to be above some
threshold to allow the epidemic to enter some specific
areas/cities in the environment we used. Obviously, a
certain amount of agents is also needed to avoid sig-
nificant fluctuations in our results. However, we could
not determine the right threshold for the specific in-
stances, which certainly depends on the properties of
the simulated environment and the population size.
The second main result of this paper is that by
setting the parameters properly, one can approximate
the effect of some non-pharmaceutical countermea-
sures, which are usually adopted if an epidemic out-
break occurs. This observation is supported by the
empirical study of (Markel et al., 2007). Interest-
ingly, the right choices of parameters in our experi-
ments seem to be in line with previous observations in
AgentbasedSimulationsofEpidemicsonaLargeScale-TowardtheRightChoiceofParameters
265

real world (e.g. the right power law exponent seems to
be in the range 2.6-2.9, cf. (Eubank et al., 2004)). To
analyze the effect of the countermeasures mentioned
above, we integrate the corresponding mechanisms
on a smaller scale, and then verify their impact on a
larger scale too.
2 THEORETICAL MODELS AND
ALGORITHMIC FRAMEWORK
Our model is based on the distributed algorithmic
framework introduced in (Els
¨
asser and Ogierman,
2012). In that paper a (rough) asymptotic analysis
of the spread of a disease in a large urban environ-
ment was considered, while in our paper we include
its spread on a larger scale with several hundred cities,
and provide a more precise (empirical) analysis on a
smaller as well as on a larger scale. Hereby, the cities
are chosen from a list in descending order of their
population size. Since we do not consider cities in-
habiting less than one agent on expectation, the num-
ber of agents is the limiting factor here. It is intu-
itively clear that large (and thus attractive) cities play
a major role in a fast spread of an epidemic since a
higher population density entails a potentially higher
infection probability. Excluding such hotspots would
of course slow down the infection spread. The prob-
lem is, this could only be achieved by quarantine the
whole city itself. One cannot assume inhabitants liv-
ing and working there would or could leave every-
thing behind. Therefore we consider such strategies
only on a smaller scale.
In our model, the agents may not only move be-
tween locations within a city but between cities as
well. Furthermore, due to simplicity the agents are
not categorized (i.e., they do not provide further prop-
erties like gender etc.). Note, we are not interested in
the evaluation of such details. In the following, we
briefly introduce the model.
Environment and Movement. Our model incorpo-
rates both intra- and inter-city movement. We model
the inter-city movement using a complete graph G =
(V,E). In this graph, each c ∈ V corresponds to a city
of Germany. However, depending on the size, not ev-
ery city is contained in V . The population is repre-
sented by n =
∑
c∈V
n
c
agents, with n
c
being the number
of agents assigned to c proportional to its real world
population. Furthermore, each city contains a num-
ber of so called cells described below. Agents may
move independently from one cell to another or even
travel to another city in each step. Each city c ∈ V is
assigned an attractiveness d
c
proportional to its pop-
ulation size (w.r.t. the whole population). Note, after-
wards d
c
does not change anymore. Let A
i,s,t
be the
event that agent i travels from city s to t. Let further
p be the probability that an agent decides to travel
at all, and let dist(s,t) be the Euclidean distance be-
tween cities s and t. Then, the probability that event
A
i,s,t
occurs is given by
Pr(A
i,s,t
) = p ·
d
t
· dist
−1
(s,t)
∑
(s, j)∈E
d
j
· dist
−1
(s, j)
.
Thus, the probability for an agent entering a specific
city is governed by the distance to said city, its popu-
lation size as well as the current position of the con-
sidered agent.
Since our model incorporates intra-city movement
as well, each c ∈ V is a clique of cells on its own.
These cliques are defined by G
c
= (V
c
,E
c
) with κn
c
being the size of V
c
(recall that n
c
is the number of
agents assigned to city c). Note, κ does not affect the
amount of agents but the amount of cells only. The
nodes v ∈ V
c
are the cells described above. Here,
κ > 0 is a constant, which will be specified in the
upcoming experiments. The cells represent locations
within a city an agent can visit. Each cell may contain
agents (individuals), depending on the cells so called
attractiveness. The attractiveness d of a cell v is cho-
sen randomly with probability proportional to 1/d
α
,
where α > 2 is a constant depending on the simu-
lation run. In each step, if an agent decides not to
visit another city, then it moves to a randomly chosen
cell according to the distribution of the attractiveness’
among the cells. This also holds for the first cell an
agent is accommodated in after entering a city.
Epidemic. We use three different states to model
the distributed spreading process. These states par-
tition the set of agents into three groups; I ( j) con-
tains the infected agents in step j, U( j) contains the
uninfected (susceptible) agents in step j, and R ( j)
contains the resistant agents in step j. Whenever
it is clear from the context, we simply write I , U,
and R , respectively. If at some step j an uninfected
agent i visits a cell (within a city) which also contains
agents of I ( j), then i becomes infected with proba-
bility 1 − (1 − γ)
I
0
( j)
, with I
0
( j) being the number of
infected individuals in the same cell. We refer to the
concrete value of γ in the upcoming simulations.
Countermeasures. In our model, the countermea-
sures are governed by the parameters α and κ. That
is, high values of these two parameters imply a high
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
266

level of countermeasures and vice-versa. With coun-
termeasures applied, individuals avoid places with a
large number of persons more often, waive needless
tours, and are more careful when meeting other peo-
ple. While α is mostly responsible for a decreas-
ing number of visitors within a cell, and thus for the
avoidance of crowded areas for example, κ governs
the total space available for all individuals. That is,
if κ increases, then more cells are available for the
total number of individuals, and meetings within the
same cell are less frequent. Thus, κ basically mod-
els how careful people interact with each other when
they meet. As pointed out in (Markel et al., 2007),
a single countermeasure alone is most likely not suf-
ficient to stop an epidemic. Therefore, we assume a
combination of countermeasures to be in place, which
then would be able to sufficiently influence the pa-
rameters α and κ. Although the models described
above already provide everything needed to simulate
the use of countermeasures, one aspect is still miss-
ing. When do we activate/deactivate the countermea-
sures and what order of magnitude should they have?
We use two different types of countermeasure-models
for this purpose: a (multi-tier) level based approach
considering the amount of infected agents in the cur-
rent step, and a ratio based approach considering the
amount of newly infected agents in the current step
compared to the one in the step before. In the follow-
ing, we use α
0
and κ
0
as initial values for α and κ,
respectively.
In the level based model, we have one or more
levels, and within each level a certain pair of param-
eters α and κ is used. Let LM
m
stand for the level
based model with m levels L = {l
1
,...,l
m
} ∪ l
0
. Fur-
ther, let T = {l
d
0
,l
u
0
,l
d
1
,l
u
1
,..., l
d
m
,l
u
m
} be the set defining
the transition points for all levels, i.e., l
d
i
defines the
transition point from level i to i − 1 whereas l
u
i
de-
fines the transition point from level i to i + 1. Note,
l
u
i
= l
d
i+1
does not necessarily hold. Additionally,
α
0
,α
1
,...,α
m
and κ
0
,κ
1
,...,κ
m
define the parameters
α and κ, which are applied in the corresponding levels
l
0
,. .. ,l
m
. For example, model LM
2
uses 2 levels. Let
us assume that l
d
0
= 0, l
u
0
= l
d
1
= 10, l
u
1
= l
d
2
= 20, l
u
2
=
∞. That is, if at most 10 percent of the population
of a city is infected in step i, α
0
and κ
0
are applied
to simulate the spread of the disease. If the num-
ber of infected individuals is larger than 10 percent,
then α
1
and κ
1
are used. Should the amount of infec-
tions go even above 20 percent, both parameters are
raised to α
2
and κ
2
, respectively. Similarly, both pa-
rameters are lowered to the previous values whenever
the amount of infections falls below the correspond-
ing transition values.
In contrast, the ratio based model RM uses a non
static approach. Let the set of newly infected nodes of
a city c in step i be denoted by I
∗
c
(i). Furthermore, let
α
i
and κ
i
denote the corresponding parameters used
in step i. If
|I
∗
c
(i)|
|I
∗
c
(i−1)|
≥ a, for some constant a, then
we set α
i+1
= α
i
+ z
1
and κ
i+1
= κ
i
+ z
2
, where z
1
,z
2
are some small constants which will be specified later.
Consequently, if
|I
∗
c
(i)|
|I
∗
c
(i−1)|
≤ 1/a, then we set α
i+1
=
max{α
0
,α
i
− z
1
} and κ
i+1
= max{κ
0
,κ
i
− z
2
}. The
values applied in the various models are specified in
Section 3.5.
3 EXPERIMENTAL ANALYSIS
As already stated in Section 1, the environment ap-
proximates the geography of Germany with up to 10
million agents. Note, the obtained results are almost
identical for the same simulations utilizing 100 mil-
lion agents. Depending on the number of agents, our
simulations use several hundred cities as visitable ar-
eas spread all over the country. Each city is assumed
to be reachable from any other city. However, an
agent may travel at most 1000 km within a single time
step. Each time step represents a whole day in the real
world. Consequently, an agent moving from one city
to another has to wait until its destination is reached
before it can interact with other agents at its destina-
tion.
3.1 Setup and Implementation
The experiments, including the ones with 100 mil-
lion agents, were mostly performed on a computa-
tion node of the Doppler cluster at the University of
Salzburg. This node integrates a quad-socket AMD
Opteron 6274 CPU (16 physical cores at 2.1 GHz
each) with 512 GB RAM (32 x 16GB DIMMs). An
Intel Xeon E5430 CPU (2,66 GHz, 4 physical cores)
has been used as a secondary evaluation unit for ex-
periments which were not so critical in terms of time.
Our simulator is implemented in Java and uses
an agent-based core architecture, where each agent,
depending on the number of overall agents in use,
represents several inhabitants during the simulation.
Furthermore, our system is completely event driven.
Overall we are able to perform large scale experi-
ments with more than 100 million agents in a reason-
able time frame. Since such huge amounts of agents
generate a significant impact in terms of performance,
several parallelization approaches are implemented.
For example, several worker threads are used, which
are chosen accordingly to the number of available
physical cores.Furthermore, to decrease the compu-
AgentbasedSimulationsofEpidemicsonaLargeScale-TowardtheRightChoiceofParameters
267

tational time for inter-city travels, we also take ad-
vantage of a parallelization approach concerning the
agents themselves.
3.2 Simulations
In the upcoming sections we present and evaluate our
results. Due to space limitations, only a selection of
the results is presented here. In the following we fo-
cus on
1. the impact of the number of agents on the char-
acteristics of the simulated epidemic compared to
real world data, and
2. the impact of non-pharmaceutical countermea-
sures on the behavior of the epidemic (e.g. social
distancing, school closures, and isolation (Markel
et al., 2007)).
Furthermore, we also analyze our parameter set-
tings. Although this is only a short part, our settings
seem to coincide with the real world observations of
(Eubank et al., 2004), and thus provide an additional
valuable insight. Note that the figures presented in
this section show values based on the real world pop-
ulation size and not on the number of agents. Thus,
a direct comparability is given without the need to
scale.
3.3 Relevance of the Chosen Parameters
Based on real world observations (e.g. (Eubank et al.,
2004)), we chose α = 2.8 and κ = 1 as a starting point
for a series of simulations concerning α and κ, re-
spectively. Each plot represents values averaged over
50 different simulation runs for each parameter con-
stellation utilizing 10 million agents. The parameter
notation is given in Table 1.
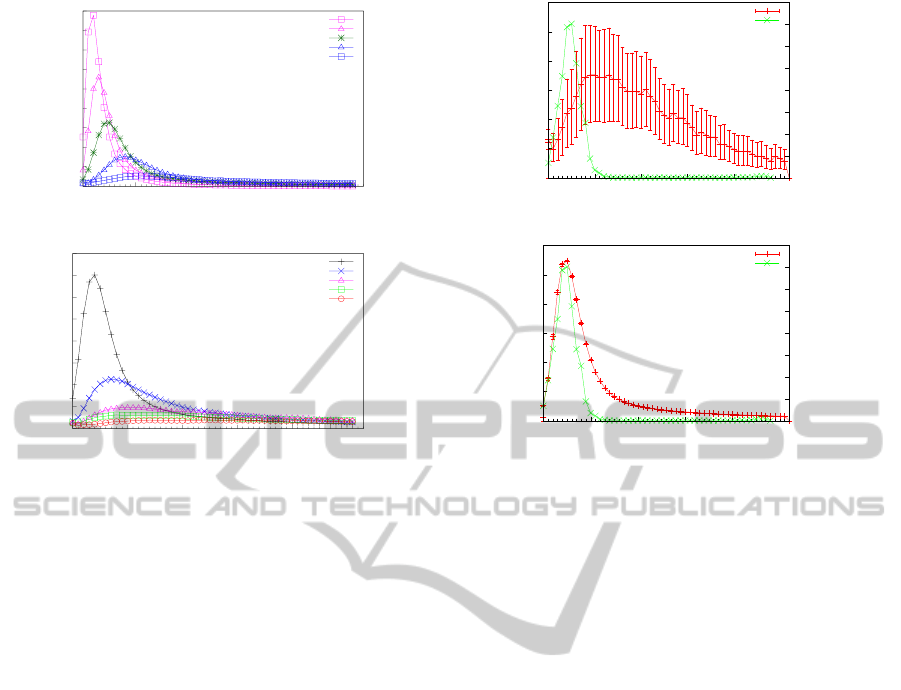
In Figure 1(a) and 1(b) we analyze the impact of
α and κ on the behavior of the epidemic, and compare
the results to the characteristics of a typical Influenza
case reported by the RKI
3
. To increase the readabil-
ity, we omit to add the RKI-plot as the 6th one. In-
stead we refer the reader to Fig. 2. Note, although
the plots for α = 2.4 and α = 2.6 may seem more
similar to the RKI-curve at first sight, the differences
to the RKI-plot (cf. Table 2 for an example of simi-
larity measures) are significant when scaled properly.
Besides, of all five α-values α = 2.8, which has also
been obtained in (Eubank et al., 2004) in a different
context, represents the best tradeoff between curve
similarity and amount of infections. All remaining
parameters were set to identical values as in Case 1
(cf. Section 3.4). For κ a similar phenomenon can be
observed. With increasing κ (including fractional val-
ues), the characteristics of the curve (i.e., the amount
Table 1: The parameter notation used in the evaluation.
γ With this probability an agent v ∈ U is being
infected independently by each w ∈ I occu-
pying the same cell at the same time.
D
↑
I
The amount of steps an agent v ∈ I is infec-
tious, thus being able to infect others.
City
init
Initial amount of cities the infection is being
placed in.
Agent
init
Amount of initially infected agents which
are placed in City
init
different cities.
α The power law exponent used to compute
the attractiveness of the cells within each
city.
κ A multiplicative factor to increase/decrease
the amount of cells proportional to the ini-
tially assigned amount of agents. With κ = 1
the amount of agents is identical to the num-
ber of cells within each city.
of infected individuals at the peak vs. total number of
infections and total duration of the outbreak) become
less and less accurate. Even if we increase the value
to 2, the obtained curve does not follow the charac-
teristics of the real world observations reported by the
RKI
3
anymore.
In terms of the probability of infection γ we sim-
ply chose a reasonable value low enough to model an
Influenza epidemic, but high enough to provoke an
outbreak. This seemed reasonable due to the (at least
to our knowledge) lack of concrete values deduced
from real world observations.
3.4 Case 1 - Number of Agents
Before we present the results for this case, we first in-
troduce the relevant sources for comparison. For Sub-
case a), we compare our results to real world data pro-
vided by the RKI (Robert Koch Institute, 2012) Surv-
Stat system for the year 2007. The parameter values
were taken from reference data provided by the RKI
(Arbeitsgemeinschaft Influenza, 2011) where possi-
ble, or set to reasonable ones otherwise. In Subcase
b) then, a disease for a fictional epidemic is presented.
3.4.1 RKI: Basis of Comparison
In this case, we compare our results to the real world
data provided by the RKI
3
. For this purpose we use
two different data sources: the official report of the
3
The Robert Koch Institute (RKI) is the central fed-
eral institution in Germany responsible for disease con-
trol and prevention and is therefore the central fed-
eral reference institution for both, applied and response-
orientated research. (Source: http://www.rki.de/EN/Home/
homepage node.html)
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
268
0
2e+06
4e+06
6e+06
8e+06
1e+07
1.2e+07
1.4e+07
1.6e+07
1.8e+07
0 10 20 30 40 50
Newly Infected Inhabitants
Week
alpha 2.4
alpha 2.6
alpha 2.8
alpha 3.0
alpha 3.2
(a) 2.4 ≤ α ≤ 3.2
0
1e+06
2e+06
3e+06
4e+06
5e+06
6e+06
7e+06
8e+06
0 10 20 30 40 50
Newly Infected Inhabitants
Week
kappa 1.0
kappa 2.0
kappa 3.0
kappa 4.0
kappa 5.0
(b) 1 ≤ κ ≤ 5
Figure 1: A composition of some simulation runs concern-
ing varying α (1(a)) and κ (1(b)) only. All other parameters
are identical to Case 1 (cf. Section 3.4). Each result rep-
resents the average of 50 different simulation runs with 10
million agents for the topology of Germany.
Influenza epidemiology of Germany for 2010/2011
(Arbeitsgemeinschaft Influenza, 2011) and an online
database containing obligatory reports called SurvS-
tat (Robert Koch Institute, 2012).
Relevance. The data for the SurvStat database and
the report of 2010/2011 itself were obtained from
more than 1% of all primary care doctors spread all
over Germany. Note that not every infected person
consults a doctor, which implies that the data of the
SurvStat system contains only the serious courses
of the disease. Nonetheless, these sources provide
a valuable tool to obtain insight into the spread
and persistence of the Influenza virus in Germany.
Further, due to the data’s significance, it is possible
to estimate the number of infections within certain
areas as well. Since the spread of infections in the
real world is influenced by factors like seasonal
fluctuations or the virus’ aggressiveness, the number
of total infections may significantly differ from
year to year, cf. (Robert Koch Institute, 2012) for
different years. However, the course of the curve
usually does not change. Consequently, we do
not focus on absolute values in our simulations,
but on the characteristics of our results. These
characteristics remain, up to some scaling factor,
identical over the whole data set provided by the RKI.
0
100000
200000
300000
400000
500000
600000
0 10 20 30 40 50
0
500
1000
1500
2000
2500
3000
3500
4000
Newly Infected Inhabitants(Simulation)
Newly Infected Inhabitants(RKI Data)
Week
Simulation
SurvStat 2007
(a) 10.000 Agents
0
1e+06
2e+06
3e+06
4e+06
5e+06
6e+06
0 10 20 30 40 50
0
500
1000
1500
2000
2500
3000
3500
4000
Newly Infected Inhabitants(Simulation)
Newly Infected Inhabitants(RKI Data)
Week
Simulation
SurvStat 2007
(b) 10.000.000 Agents
Figure 2: Simulation results for Case 1a) (red) in compar-
ison to real world data (green) provided by the RKI for a
varying amount of agents. Each result represents the av-
erage of 50 different simulation runs. The reliability of the
averaged value is indicated by the corresponding confidence
interval.
3.4.2 Subcase a)
The Parameters in this case are as follows. We set
γ = 7%, D
↑
I
to 5 days, the amount of initially infected
cities City
init
to 1 (namely Berlin), and the amount of
initially infected agents Agent
init
to 0.0015% of the
overall agents used for these simulations. Further-
more, α = 2.8 and κ = 1.
Each obtained plot represents the average of 50
different simulation runs. Figure 2 shows the results
for the first subcase. Here, the green curve represents
the real world data provided by the RKI for the year
2007 while the red curve represents our simulation re-
sults. Note that both curves vary significantly in terms
of absolute numbers. However, this is not our focus
here. Due to the level of abstraction in our model and
since the RKI data only contains reported cases (see
above), the absolute numbers do not coincide. Addi-
tionally, as stated above, the data provided by the RKI
also differs significantly (in terms of absolute num-
bers but not the disease characteristics) from year to
year (cf. (Robert Koch Institute, 2012)). Therefore,
we focus on the course of the disease and the result-
ing characteristics of the plotted curves.
It is easy to see that the more agents are used, be-
ginning from Figure 2(a) up to Figure 2(b), the more
the curve characteristics converge. Moreover, the ac-
AgentbasedSimulationsofEpidemicsonaLargeScale-TowardtheRightChoiceofParameters
269

curacy of each simulation run increases as well (cf.
the confidence intervals in Figure 2). With at least
500.000 agents in use, both curves become similar.
Note that we shifted the outbreak position of the RKI
data to the origin to create a comparable situation.
Since the moment of an outbreak varies in reality as
well (cf. (Robert Koch Institute, 2012)) and the be-
ginning of the disease is not important for us, this re-
location does not have any influence on the data or the
evaluation itself.
To obtain a more formal evaluation, we define
three measures, which are used to compare our results
to the data provided by the RKI. These are: the time
to peak (TTP), the epidemic duration (ED), and the
area of the curve (AC). The time to peak describes the
week with the maximum amount of newly infected
agents of the corresponding curve. The area of the
curve is simply the summation of the area between the
origin and the endpoint EP (defined by the epidemic
duration). Finally, the endpoint of the epidemic dura-
tion is the week in which only a minor amount of new
infections occur, and no significant new infections are
observed anymore. Minor infections are defined to
start at a step i and last till the last step j of the sim-
ulation while for all steps i ≤ i
0
≤ j it holds that the
amount of newly infected agents does not exceed 9%
of the maximum value.
In Table 2 we consider the relative values of these
measurements compared to the RKI data. That is,
the numbers given in this table represent the ratio be-
tween the value obtained in our simulations and the
value provided by the RKI. For example, a value of
4.00 for TTP in the case of 10.000 agents implies that
the time to peak in our case divided by the time to
peak in the real world data is 4.
Using the individual deviation measurements, we
define a global deviation value by the formula
1
3
·
TTP +
1
3
· AC +
1
3
· ED. For simplicity we consider
each individual measurement uniformly weighted.
The results, which confirm our previous observations,
are given in Table 2 and Figure 3.
All obtained results and previous statements
imply a fragile balance between the accuracy, the
parameter setting, and the amount of agents in use.
3.4.3 Subcase b)
In Contrast to Subcase a), the Epidemic here is a Fic-
tional One. We set γ = 1.5%, D
↑
I
to 5 days, the amount
of initially infected cities City
init
to 1 (namely Berlin),
and the amount of initially infected agents Agent
init
to
0.0015% of the overall agents used for these simula-
tions. Furthermore, α = 2.8 and κ = 1.
Table 2: Quantitative comparison and deviation measure-
ments of the achieved results in Case 1a) with respect to the
data provided by the RKI. The results refer to the following
properties: time to peak (TTP), the epidemic dration (ED),
and the area of the curve (AC). Here, the AC is starting at
the origin and ending at the endpoint EP defined by the ED.
All values are given as a relative deviation concerning the
data provided by the RKI. The deviation value itself is com-
puted utilizing
1
3
· TTP +
1
3
· AC +
1
3
· ED.
Deviation
Agents TTP
ED /
EP
(week)
AC
Deviation
Value
10 K 2,33 3,53/53 5,58 3,81
25 K 2,00 3,53/53 4,71 3,41
50 K 1,83 3,47/52 3,70 3,00
100 K 1,33 2,87/43 3,10 2,43
250 K 1,17 2,27/34 2,59 2,01
500 K 1,17 1,87/28 2,29 1,77
1 M 1,17 1,67/25 2,16 1,66
2.5 M 1,00 1,53/23 2,00 1,51
5 M 1,00 1,47/22 1,92 1,46
10 M 1,00 1,40/21 1,88 1,43
0
1
2
3
4
5
6
10K 25K 50K 100K 250K 500K 1M 2.5M 5M 10M
Deviation measure
Simulation runs to the corresponding agent numbers
TTP
ED
AC
Deviation value
Figure 3: A visual representation of the data of Table 2.
In this subcase, we chose γ relatively low com-
pared to the subcase above to emphasize the distor-
tion. We show a significantly varying course of dis-
ease, which even exceeds the distortion of Subcase a).
Using these parameters we were able to identify mul-
tiple curve characteristics, partially shown in Figure
4. The differences are significant. First, we observed
the extinction of the disease almost instantly after the
outbreak, followed by a completely unpredictable be-
havior including an increasing as well as a decreasing
influence of the disease, up to a self-stabilizing infec-
tion spreading (cf. Fig. 4(a) and 4(b)). Since no other
parameter was altered, only the different number of
agents could have such a strong influence on the re-
sults.
Combined, both subcases indicate a significant in-
fluence of the amount of agents in use on the spread-
ing process itself. One main goal in such simula-
tions is to gain some speedup with a lower number
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
270
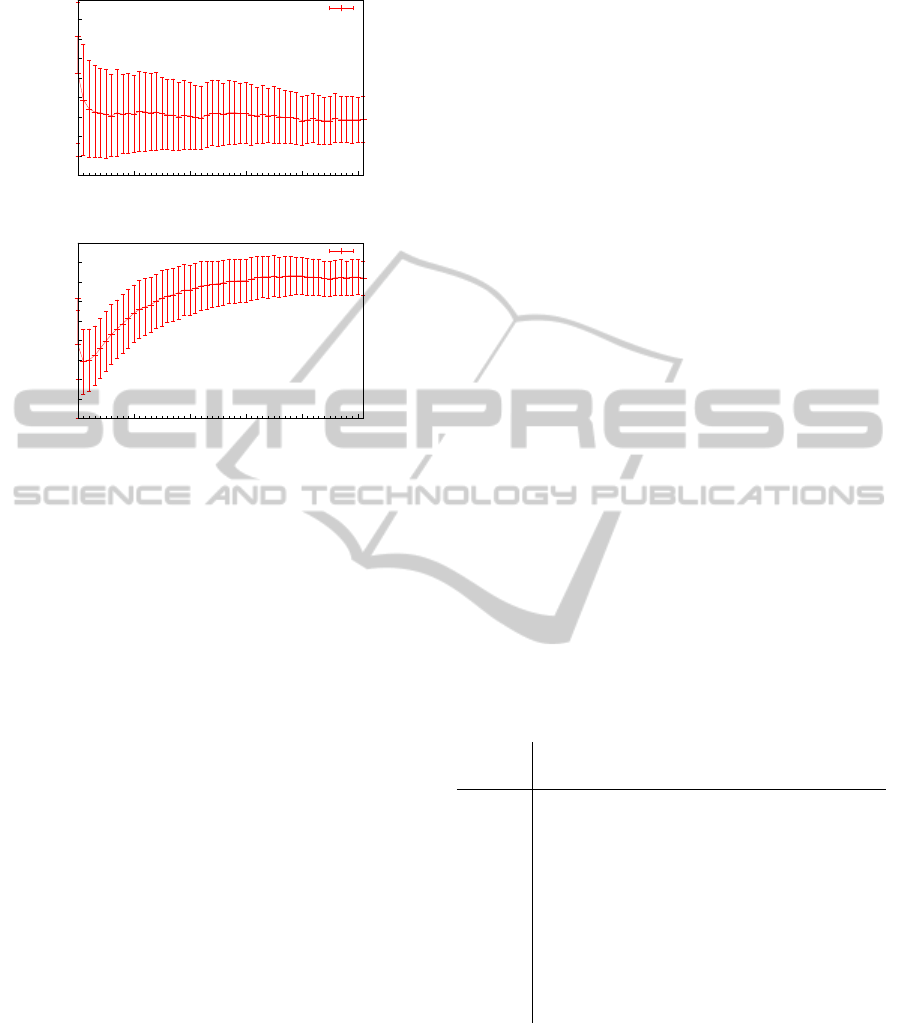
-20000
0
20000
40000
60000
80000
100000
120000
140000
160000
0 10 20 30 40 50
Newly Infected Inhabitants(Simulation)
Week
Simulation
(a) 100.000 Agents
0
20000
40000
60000
80000
100000
120000
140000
160000
180000
0 10 20 30 40 50
Newly Infected Inhabitants(Simulation)
Week
Simulation
(b) 10.000.000 Agents
Figure 4: Simulation results for Case 1b) (red) for a varying
amount of agents. Each result represents the average of 50
different simulation runs. The reliability of the averaged
value is indicated by the corresponding confidence interval.
of agents while keeping the collectible data (for ex-
ample the number of infections) almost identical in
terms of accuracy. Now, this seems to be a very fragile
premise which cannot necessarily be achieved. Note,
we did not explicitly tune the settings for the dif-
ferent amount of agents since such possibilities may
not be present or applicable for medical forecasting
and disease estimation systems. Especially for un-
known or largely unexamined diseases this may be
very problematic. However, due to the dependency of
the amount of cells in a city and the amount of agents
in use, this is done, to some extent, implicitly by our
model.
3.5 Case 2 - Non-pharmaceutical
Countermeasures
Now we extend our analysis to incorporate non-
pharmaceutical countermeasures such as school clo-
sures and social distancing. Here, we stick to a fic-
tional epidemic simply because it simplifies the pre-
sentation, i.e., due to the increase of γ to 12%, a faster
spread is achieved and the impact of the used counter-
measures is amplified. Similar to Case 1, we set D
↑
I
to
5 days, the amount of initially infected cities City
init
to
1 (namely Berlin), and the amount of initially infected
agents Agent
init
to 0.00075% of the overall agents (to
compensate the higher γ at the beginning). All rele-
vant parameters concerning the countermeasure mod-
els can be found in Table 4 and 5.
We assume that such countermeasures basically
affect the parameters α and κ, since the individu-
als will most likely avoid places with a large num-
ber of persons, waive needless tours, and be more
careful when meeting other people. Although one
of these modifications alone is most likely not suf-
ficient (Markel et al., 2007), we can simply assume a
combination of these strategies to be in place, which
then would be able to sufficiently influence α and κ.
For obvious reasons, we cannot compare our simula-
tion results to current real world data, which consider
different epidemics with varying (or no) countermea-
sures in use. Therefore, we use the work of Markel et
al. (Markel et al., 2007) for this purpose. Especially
Figure 5 is of particular interest. There, the direct cor-
relation between establishing countermeasures and a
decreasing amount of new infections (and vice versa)
is well highlighted. We observed an identical effect in
our simulations (cf. Figures 6, 7, 8 and Table 3). Note
that different combinations of countermeasures used
in (Markel et al., 2007) entail different kinds of im-
pacts on the death rates. In contrast, we do not focus
on specific combinations but on sufficient ones to ac-
tually achieve an immediate impact on the epidemic.
Table 3: Percentage of the overall infected inhabitants (Case
2). Column NOCM represents the percentage of overall in-
fections without any countermeasures in use, whereas the
other columns state the gain compared to the case without
countermeasures for the corresponding level based and ratio
based model, respectively.
Agents
Infected Agents (in percent)
NOCM LM
1
LM
2
LM
3
RM
10k 55,45 40,36 24,38 25, 26 31,93
25k 58.57 16, 72 1,56 15, 18 33,43
50k 76,20 13, 49 21,50 28,40 42, 51
100k 75,08 11, 75 −0.29 16, 50 27,88
250k 81,37 11, 13 18,95 16,38 40, 30
500k 85,77 18, 05 16,15 20,04 39, 26
1M 86,12 1.84 14,53 12,16 37, 41
2,5 M 88,22 12,47 14,66 13,42 35,47
5M 87,39 11, 33 8,50 8,90 29,81
10M 88,06 8, 0 9,30 9, 15 32,08
As already described in Section 2, two different
countermeasure approaches are of main interest for
us: the level based (LM
1
, LM
2
and LM
3
), and the ratio
based (RM), respectively. Both use different mecha-
nisms and parameters to achieve the embankment of
the epidemic. Recall that all transition points in the
level based model are chosen w.r.t. the ratio between
the amount of currently infected individuals and the
population size of the city.
AgentbasedSimulationsofEpidemicsonaLargeScale-TowardtheRightChoiceofParameters
271
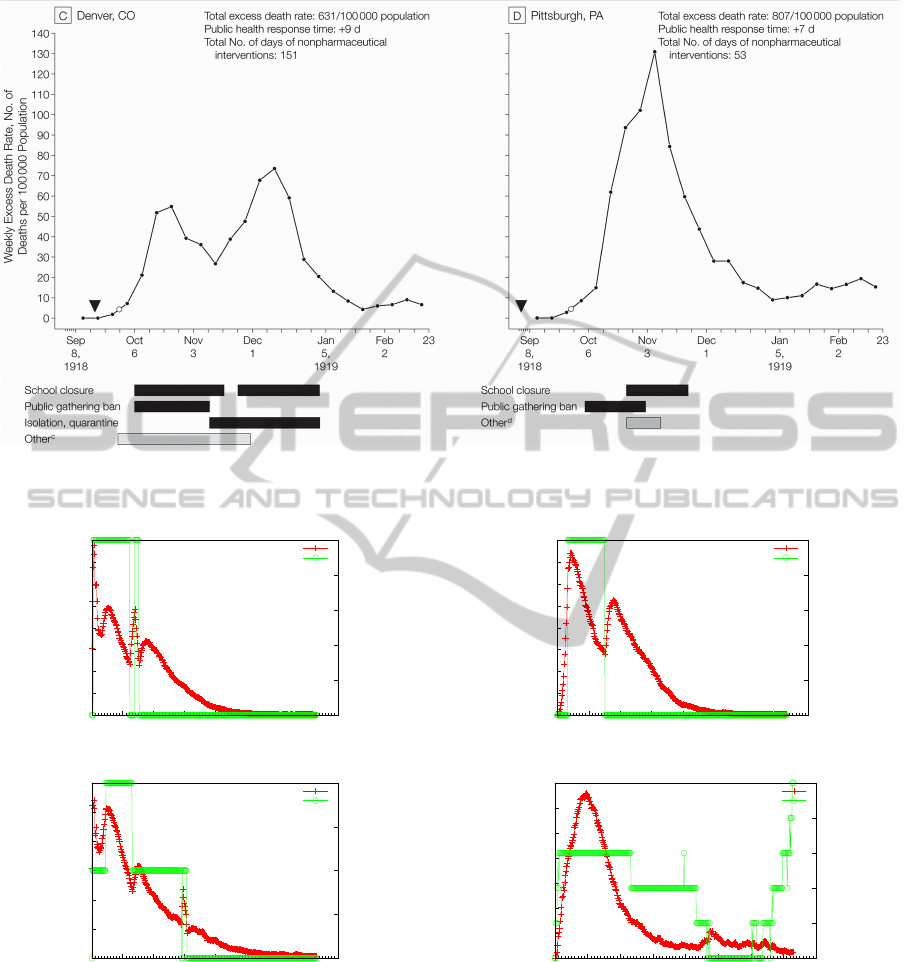
Figure 5: Weekly excess death rates from September 8, 1918, through February 22, 1919 (Markel et al., 2007, Figure 3).
0
20000
40000
60000
80000
100000
120000
140000
160000
0 50 100 150 200 250 300 350 400
0
0.2
0.4
0.6
0.8
1
Infected Inhabitants
Activated Countermeasure Level l
j
Day
Simulation
Level
(a) Model LM
2
, 10 million agents
0
20000
40000
60000
80000
100000
120000
0 50 100 150 200 250 300 350 400
0
0.5
1
1.5
2
Infected Inhabitants
Activated Countermeasure Level l
j
Day
Simulation
Level
(b) Model LM
3
, 10 million agents
Figure 6: Example results for BER for Case 2. The number
of agents refers to the total amount in the simulation.
Similar to Case 1, the results with at most 10 mil-
lion agents in use are presented for each model. Al-
though the level based approach is completely dif-
ferent compared to the ratio based approach, the
achieved results are similar. However, the overall in-
crease of α and κ by the ratio based approach may
be noticeably higher, especially if a large number of
0
10000
20000
30000
40000
50000
60000
70000
80000
0 50 100 150 200 250 300 350 400
0
0.2
0.4
0.6
0.8
1
Infected Inhabitants
Activated Countermeasure Level l
j
Day
Simulation
Level
(a) Model LM
2
, 10 million agents
0
5000
10000
15000
20000
25000
30000
35000
0 50 100 150 200 250 300 350 400
0
1
2
3
4
5
Infected Inhabitants
Activated Countermeasure Level l
j
Day
Simulation
Level
(b) Model RM, 10 million agents
Figure 7: Example results for HAM for Case 2. The number
of agents refers to the total amount in the simulation.
agents is used (cf. for example Figure 8(b)). That is,
while all LM-models use α ≤ 3.3, the RM-model goes
above 4. This implies that the LM-models are more
cost efficient, since both α and κ are kept lower and
therefore less effort is needed to achieve and maintain
said values.
Additionally, to be able to compare our results to
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
272

Table 4: Parameters for the level based countermeasure models relevant for
Case 2.
Level
LM
1
LM
2
LM
3
l
u
i
l
d
i
α
i
κ
i
l
u
i
l
d
i
α
i
κ
i
l
u
i
l
d
i
α
i
κ
i
0 6% 0% 2.8 1.0 4% 0% 2.8 1.0 2% 0% 2.8 1.0
1 ∞ 4% 3.3 1.2 6% 2% 3.1 1.1 4% 1% 3.0 1.0
2 - - - - ∞ 4% 3.3 1.2 6% 2% 3.1 1.1
3 - - - - - - - - ∞ 4% 3.3 1.2
Table 5: Parameters for the ratio based coun-
termeasure model relevant for Case 2.
RM Model
a z
1
z
2
α
0
κ
0
2 0.2 0.1 2.8 1.0
0
5000
10000
15000
20000
25000
0 50 100 150 200 250 300 350 400
0
0.5
1
1.5
2
2.5
3
Infected Inhabitants
Activated Countermeasure Level l
j
Day
Simulation
Level
(a) Model LM
3
, 10 million agents
0
1000
2000
3000
4000
5000
6000
0 50 100 150 200 250 300 350 400
0
1
2
3
4
5
6
Infected Inhabitants
Activated Countermeasure Level l
j
Day
Simulation
Level
(b) Model RM, 1 million agents
Figure 8: Example results for PB for Case 2. The number
of agents refers to the total amount in the simulation.
the findings in (Markel et al., 2007), we examine the
following three cities in more detail: BER (population
size: ≈ 3.5 million), HAM (population size : ≈ 1.8
million) and PB (population size: ≈ 146.000). Fig-
ures 6, 7 and 8 represent a composition of some inter-
esting results for each city and model in use. Note
that the green curve in these figures represents the
countermeasure level for the LM models at the cor-
responding time, and indicates the number of times
z
1
,z
2
have increased α, κ in the RM model. Recall,
in the RM-model level j implies α
i
= α
0
+
j
∑
k=1
z
1
and
κ
i
= κ
0
+
j
∑
k=1
z
2
for a step i.
Our results confirm the impact, influenced by
the effectiveness of the countermeasures, of different
countermeasures observed in the real world (Markel
et al., 2007). Compared to Figure 5, our simula-
tions show a similar behavior (i.e., more than one
peak during the epidemic). It is easy to see that the
countermeasures presented in (Markel et al., 2007)
directly influence the course of the epidemic. The
same property can be observed in our results (cf. Fig-
ure 6(b), 7(a) or 8(a)). One can see that depending
on the countermeasure level (indicated by the acti-
vated/used level), the number of infections increases
or decreases. Note that although our figures show the
number of infected individuals and not the death rate
as shown in Figure 5, a comparison is still possible
since this deviation can be normalized using a scaling
factor.
Furthermore, we observe that small adjustments
of the two parameters α and κ entail a significant im-
pact on the number of overall infections (cf. Table 3).
Among others, it was shown that if the power law ex-
ponent (and κ as well) is assumed to be some large
constant, then even a very aggressive epidemic with
γ = 100% will affect no more than a polylogarithmic
number of the population. Our findings now back up
these observations.
In conclusion, in this case we showed the im-
pact of different countermeasures on the behavior of
a population w.r.t. our model. Although some com-
plexity of the real world is lacking, the similarities
to real world observations are still present. Starting
with settings for the environment, and therefore im-
plicitly the individuals’ behavior, based on real world
observations (cf. Section 3.3) relatively low level
countermeasures were sufficient to embank or at least
significantly suppress an outbreak. Essentially the
same properties were already observed in reality (cf.
(Markel et al., 2007)). This underlines the impor-
tance of behavioral and environmental models based
on power law distributions.
4 CONCLUSIONS
Agent based simulators offer various possibilities to
perform very detailed experiments. However, the pa-
rameters used in these experiments highly influence
the results one might obtain. As we have seen, even
the number of agents has a significant impact on the
quality of the results. This includes the reliability of
different simulation runs with an identical parameter
setting. By using the right parameter settings and a
AgentbasedSimulationsofEpidemicsonaLargeScale-TowardtheRightChoiceofParameters
273

proper number of agents, it is possible to approximate
the course of a disease as observed in the real world.
Furthermore, our experiments indicate that the algo-
rithmic framework presented in this paper is able to
describe, to some extent, the impact of certain non-
pharmaceutical countermeasures on the behavior of
an epidemic.
REFERENCES
Adamic, L. A. and Huberman, B. A. (2000). Power-
law distribution of the world wide web. Science,
287(5461):2115.
Ajelli, M., Goncalves, B., Balcan, D., Colizza, V., Hu, H.,
Ramasco, J., Merler, S., and Vespignani, A. (2010).
Comparing large-scale computational approaches to
epidemic modeling: Agent-based versus structured
metapopulation models. BMC Infectious Diseases,
10(190).
Amaral, L. A., Scala, A., Barthelemy, M., and Stanley,
H. E. (2000). Classes of small-world networks. PNAS,
97(21):11149–11152.
Arbeitsgemeinschaft Influenza (2011). Bericht zur Epi-
demiologie der Influenza in Deutschland Saison
2010/11.
Balcan, D., Hu, H., Goncalves, B., Bajardi, P., Poletto, C.,
Ramasco, J. J., Paolotti, D., Perra, N., Tizzoni, M.,
den Broeck, W. V., Colizza, V., and Vespignani, A.
(2009). Seasonal transmission potential and activity
peaks of the new influenza A(H1N1): a Monte Carlo
likelihood analysis based on human mobility. BMC
Medicine, 7:45.
Bobashev, G. V., Goedecke, D. M., Yu, F., and Epstein,
J. M. (2007). A hybrid epidemic model: combining
the advantages of agent-based and equation-based ap-
proaches. In Proc. WSC ’07, pages 1532–1537.
Borgs, C., Chayes, J., Ganesh, A., and Saberi, A. (2010).
How to distribute antidote to control epidemics. Ran-
dom Struct. Algorithms, 37:204–222.
Chowell, G., Hyman, J. M., Eubank, S., and Castillo-
Chavez, C. (2003). Scaling laws for the movement
of people between locations in a large city. Physical
Review E, 68(6):661021–661027.
Els
¨
asser, R. and Ogierman, A. (2012). The impact of the
power law exponent on the behavior of a dynamic epi-
demic type process. In Proc. SPAA’12.
Eubank, S., Guclu, H., Kumar, V., Marathe, M., Srinivasan,
A., Toroczkai, Z., and Wang, N. (2004). Modelling
disease outbreaks in realistic urban social networks.
Nature, 429(6988):180–184.
Faloutsos, M., Faloutsos, P., and Faloutsos, C. (1999). On
power-law relationships of the internet topology. In
SIGCOMM ’99, pages 251–262.
Germann, T. C., Kadau, K., Longini, I. M., and Macken,
C. A. (2006). Mitigation strategies for pandemic in-
fluenza in the United States. PNAS, 103(15).
Grassberger, P. (1983). On the critical behavior of the
general epidemic process and dynamical percolation.
Mathematical Biosciences, 63(2):157 – 172.
Hethcote, H. W. (2000). The mathematics of infectious dis-
eases. SIAM Review, 42(4):599–653.
Jaffry, S. W. and Treur, J. (2008). Agent-Based and
Population-Based Simulation: A Comparative Case
Study for Epidemics. In Louca, L. S., Chrysan-
thou, Y., Oplatkova, Z., and Al-Begain, K., editors,
ECMS’08, pages 123–130.
Lee, B. Y., Bedford, V. L., Roberts, M. S., and Carley, K. M.
(2008). Virtual epidemic in a virtual city: simulat-
ing the spread of influenza in a us metropolitan area.
Translational Research, 151(6):275 – 287.
Lee, B. Y., Brown, S. T., Cooley, P. C., Zimmerman, R. K.,
Wheaton, W. D., Zimmer, S. M., Grefenstette, J. J.,
Assi, T.-M., Furphy, T. J., Wagener, D. K., and Burke,
D. S. (2010). A computer simulation of employee vac-
cination to mitigate an influenza epidemic. American
Journal of Preventive Medicine, 38(3):247 – 257.
Markel, H., Lipman, H. B., Navarro, J. A., Sloan, A.,
Michalsen, J. R., Stern, A. M., and Cetron, M. S.
(2007). Nonpharmaceutical Interventions Imple-
mented by US Cities During the 1918-1919 Influenza
Pandemic. JAMA, 298(6):644–654.
Newman, M. E. J. (2002). Spread of epidemic disease on
networks. Phys. Rev. E, 66(1):016128.
Newman, M. E. J. (2003). The structure and function of
complex networks. SIAM Review, 45(2):167–256.
Ripeanu, M., Foster, I., and Iamnitchi, A. (2002). Mapping
the gnutella network: Properties of large-scale peer-
to-peer systems and implications for system. IEEE
Internet Computing Journal, 6(1):50–57.
Robert Koch Institute (2012). SurvStat@RKI. A web-based
solution to query surveillance data in Germany.
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
274
