
A Generic and Flexible Framework for Selecting Correspondences
in Matching and Alignment Problems
Fabien Duchateau
Universit
´
e Lyon 1, LIRIS, UMR5205, Lyon, France
Keywords:
Data Integration, Schema Matching, Ontology Alignment, Entity Resolution, Entity Matching, Selection of
Correspondences.
Abstract:
The Web 2.0 and the inexpensive cost of storage have pushed towards an exponential growth in the volume
of collected and produced data. However, the integration of distributed and heterogeneous data sources has
become the bottleneck for many applications, and it therefore still largely relies on manual tasks. One of this
task, named matching or alignment, is the discovery of correspondences, i.e., semantically-equivalent elements
in different data sources. Most approaches which attempt to solve this challenge face the issue of deciding
whether a pair of elements is a correspondence or not, given the similarity value(s) computed for this pair. In
this paper, we propose a generic and flexible framework for selecting the correspondences by relying on the
discriminative similarity values for a pair. Running experiments on a public dataset has demonstrated the im-
provment in terms of quality and the robustness for adding new similarity measures without user intervention
for tuning.
1 INTRODUCTION
Organizations, companies, science labs and Internet
users produce a large amount of data everyday. Fu-
sioning catalogs of products, generating new knowl-
edge from scientific databases, helping decision-
makers during catastrophic scenarios or creating new
mashups are only a few examples of application that
involve the integration of distributed and heteroge-
neous data sources. Unfortunately, the data integra-
tion task is still largely performed manually, in a
labor-intensive and error-prone process. One of the
basic task when integrating data sources deals with
the discovery of semantically-equivalent elements,
and the link drawn between such elements is a corre-
spondence. Given the nature of the data sources, this
task is referred to as schema matching (Bellahsene
et al., 2011; Bernstein et al., 2011), ontology align-
ment (Euzenat and Shvaiko, 2007; Avesani et al.,
2005) or entity resolution (Fellegi and Sunter, 1969;
Winkler, 2006). An example of schema matching task
which occurs during the creation of a mediation sys-
tem for flight booking is the discovery of correspon-
dences between the Web forms (of the flight compa-
nies) and the mediated schema. A similar problem
involving ontology alignment may be found in query
answering on the Linked Open Data: one needs to un-
derstand the relationships between the concepts and
properties of the ontologies of the knowledge bases to
return complete and minimal query results. In entity
resolution, the merging of two databases about prod-
ucts sold by different companies imply the detection
of identical products.
To tackle these challenges, matching tools apply
a diversity of similarity measures between two ele-
ments to exploit the different information stored in the
data sources. For most of the tools, the values com-
puted by these similarity measures are finally com-
bined into a global similarity score (Doan et al., 2003;
Aumueller et al., 2005; Christen, 2008; Bozovic and
Vassalos, 2008). This score can be used to rank and
present to the user the top-K candidate correspon-
dences for a given element. A tool can also automat-
ically select the correspondences by comparing this
global score with a threshold. In all cases, this task,
that we further name selection of correspondences,
is therefore crucial in the matching process. Yet, we
advocate that this global score is sufficient neither for
a manual nor for an automatic selection of the corre-
spondences. Indeed, it can reflect the strong impact
of similarity measures of the same type if the com-
bination function is not correctly tuned. Besides, the
score aggregates all computed similarity values, al-
though most of them may not be significant. Thus,
129
Duchateau F..
A Generic and Flexible Framework for Selecting Correspondences in Matching and Alignment Problems.
DOI: 10.5220/0004430401290137
In Proceedings of the 2nd International Conference on Data Technologies and Applications (DATA-2013), pages 129-137
ISBN: 978-989-8565-67-9
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

applying a threshold on the global score to select cor-
respondences may not be the best solution because
a correct correspondence rarely achieves high values
for all similarity measures. Finally, a similarity mea-
sure returns similarity scores but we usually do not
know its inability for discovering a correspondence.
Many measures are applied in a similar fashion, or on
the same elements. Understanding the ignorance of a
measure is crucial. In addition, the values computed
by the measures may not all be useful. For instance,
most terminological measures return a high similarity
value between mouse and mouse, but these elements
may not be related (one if a reference to the animal
and the other to a computer device). In such case, a
contextual similarity measure may disambiguate the
two words, and the value computed by this contex-
tual measure is discriminative for the pair of elements.
Thus, it is important to measure the ignorance of a
similarity measure. For those reasons, the selection
and the tuning of the similarity measures for select-
ing the correspondences are one of the ten challenges
identified by Shvaiko and Euzenat (Shvaiko and Eu-
zenat, 2008).
In this paper, we propose a framework which
aims at selecting the correspondences indepen-
dently of the similarity measures. It takes into ac-
count both the ignorance and the differences between
the similarity measures and the discriminative simi-
larity values of a candidate correspondence. In addi-
tion, our approach is flexible when one needs to add
or remove a similarity measure. As a consequence,
no tuning is required from the user to combine the
similarity measures. The main contributions of this
paper can be summarized as follows: (i) a flexible
model for representing similarity measures and com-
puting their dissimilarity and ignorance, (ii) a robust
framework for selecting the correspondences regard-
less of the similarity measures and (iii) the valida-
tion of this approach by using a benchmark with real-
world datasets. The rest of this paper is organized as
follows: Section 2 presents the related work in data
integration, and more specifically how matching ap-
proaches select the correspondences. Next, we pro-
vide in Section 3 the formal definitions for our prob-
lem. In Section 4, we describe our framework for se-
lecting correspondences. An experimental validation
is presented in Section 5. Finally, we conclude and
outline future work in Section 6.
2 RELATED WORK
As the matching process covers different but related
domains, these recent books provide the related work
in entity resolution (Talburt, 2011), schema match-
ing (Bellahsene et al., 2011) and ontology align-
ment (Euzenat and Shvaiko, 2007). Schema match-
ing and ontology mainly deal with metadata (e.g., la-
bels, properties, constraints) while entity matching is
at the instance level. Yet, both use similarity mea-
sures to obtain similarity values between metadata or
instances, although the types and nature of the simi-
larity measures may differ. The combination of sim-
ilarity measures and the decision maker for select-
ing a pair as a correspondence is a common issue in
the matching domains.
To combine the results of different similarity mea-
sures, the simplest solution is to use a function (e.g.,
weighted average). For instance, most of the systems
which participate in the Ontology Alignment Eval-
uation Initiative (Euzenat et al., 2011) compute ini-
tial similarity values with terminological, structural or
instance-based measures, and they may refine the re-
sults by applying reasoning. The combination of the
measures may be performed with more complex func-
tion, such as artificial neural networks (Gracia et al.,
2011). This trend is confirmed in the entity matching
task, where most tools combine the measures with a
numeric or rule-based function (K
¨
opcke and Rahm,
2010). Some approaches dynamically select the mea-
sures to be applied : RiMOM (Li et al., 2009) is a
multiple strategy dynamic ontology matching system
and it selects the best strategy (composed of one or
several similarity measures) to apply according to the
features of the ontologies to be matched. The schema
matcher YAM also dynamically combines similarity
measures according to machine learning techniques
(Duchateau et al., 2009), with the benefit of automat-
ically tuning the thresholds for each measure.
Most matching approaches are based on a thresh-
old to select correspondences. In schema match-
ing, Glue (Doan et al., 2003), COMA++ (Aumueller
et al., 2005), Quickmig (Drumm et al., 2007) or
ASID (Bozovic and Vassalos, 2008) automatically
select their correspondences given a threshold. The
threshold value can be manually tuned, for instance
with a Graphical User Interface as in Agreement
Maker (Cruz et al., 2007). In a similar fashion, the
entity matching approach FEBRL enables users to
choose between a threshold or an automatic selec-
tion based on a nearest neighbor classifier (Chris-
ten, 2008). In (Panse et al., 2013), the authors use
a probabilistic model to minimize the impact of cor-
respondences which have been incorrectly selected.
The ontology alignment system S-Match++ does not
return a global similarity value for a candidate pair
of elements, but the type of relationship between the
elements (e.g., subsomption) (Avesani et al., 2005).
DATA2013-2ndInternationalConferenceonDataManagementTechnologiesandApplications
130

Thus, the decision to select a pair as a correspondence
mainly depends on the result of a SAT solver.
To summarize, our framework aims at tackling is-
sues from the previously described systems. First,
the similarity measures combined by a tool cannot
have the same impact, because some of them are very
similar for computing a score. On the contrary, the
specificity of other measures should be reflected dur-
ing the combination. Thus, our framework includes a
model to classify these measures, and our matching
approach is then independent from these measures,
thus providing more genericity. To avoid the tun-
ing task required by most matching tools, especially
when adding or removing a similarity measure, our
framework should be flexible: the combination of the
similarity measures does not depend on the type of
measure. A last remark deals with the similarity val-
ues: many values are not interesting enough to be ex-
ploited, and candidate correspondences do not obtain
useful scores for all measures. Thus, our framework
is selective because only the most interesting values
should be used to compute a global similarity value
for a candidate correspondence.
3 PRELIMINARIES
In this section, we formally define the problem and
we present our running example.
3.1 Formalizing the Problem
The matching process deals with data sources, which
can be schemas, ontologies, models and/or a set of
instances. Let us consider a set of data sources D.
A data source d ∈ D is composed of a set of ele-
ments E
d
, each of them associated with an identi-
fier and attributes. Optionally, these elements may be
linked by relationships. The size of a data source, or
its number of elements, is noted |E
d
|. The matching
problem consists of discovering correspondences, i.e.,
links between the semantically-equivalent elements
from different data sources. Let us note S the set of
similarity measures used by a tool to discover these
identical elements. To assess a degree of similarity
between two elements e ∈ E
d
and e
0
∈ E
d
0
, a sim-
ilarity measure sim ∈ S computes a similarity value
sim(e,e
0
) between these elements as follows:
sim(e,e
0
) → [0,1]
As explained in (Euzenat and Shvaiko, 2007), we as-
sume that all similarity measures return values which
can be normalized in the range [0,1]. Thus, this def-
inition includes the similarity measures which return
a value in ℜ or those which compute a semantic re-
lationship (e.g., equivalence or hyponymy). Similarly
to most matching approaches, we focus on one to one
matching, i.e., a correspondence only involves two el-
ements from different data sources.
Since a similarity measure mainly exploits a few
properties of the data sources (e.g., an element at-
tribute, the relationship between elements, etc.), the
matching process often applies different similarity
measures, thus producing a similarity matrix. All
similarity values are then combined into a global
similarity score. The combination function may be
complex and require tuning. The set of final corre-
spondences between d and d
0
is noted M (d,d
0
) and
it contains simple correspondences represented as a
tuple (e, e
0
). These final correspondences are se-
lected among all possible candidate correspondences
(mainly the Cartesian product of E
d
and E
d
0
) ac-
cording to their global similarity score (or confidence
score). This selection is performed manually (e.g.,
by proposing a ranking of the correspondences with
the highest global scores) or automatically (e.g., the
matching process selects the correspondences with a
global score above a given threshold). Note that the
mapping function is not in the scope of this paper.
3.2 Running Example
Based on the previous definitions, we describe a run-
ning example. For sake of clarity, it has been con-
strained to two data sources d,d
0
∈ D. Each of
them contains three elements: E
d
= {a,b, c} and
E
d
0
= {a
0
,b
0
,d
0
}. All possible pairs of elements are
candidate correspondences, for which their similar-
ity has to be verified. The set of correct correspon-
dences (i.e., provided by an expert) contains two cor-
respondences (a, a
0
) and (b,b
0
). To match these two
data sources, we use a set of four similarity mea-
sures S = {sim
1
,sim
2
,sim
3
,sim
4
}. Table 1 presents
the similarity matrices of each measure, i.e., the simi-
larity values computed for each pair of elements. For
instance, the pair of elements (a,a
0
) obtains a simi-
larity value equal to 0.8 with the measure sim
1
. Next,
we illustrate our framework with this example.
4 A GENERIC FRAMEWORK TO
SELECT CORRESPONDENCES
In this section, we describe our framework to select
and combine the most relevant similarity values for
a given pair of elements regardless of the number of
similarity measures. The basic intuition is that the
AGenericandFlexibleFrameworkforSelectingCorrespondencesinMatchingandAlignmentProblems
131

Table 1: Similarity Matrices for Similarity Measures sim
1
, sim
2
, sim
3
, and sim
4
.
sim
1
a b c
a’ 0.8 0 0
b’ 0 0.3 0
d’ 0.8 0 0.7
sim
2
a b c
a’ 0.1 0.1 0.1
b’ 0.2 0.1 0.2
d’ 0.8 0.2 0.6
sim
3
a b c
a’ 0.6 0.2 0.1
b’ 0.3 0.9 0.4
d’ 0.3 0.2 0.2
sim
4
a b c
a’ 0 0 0.5
b’ 0 0.5 0
d’ 0 0 0
confidence score of a pair (i.e., the global similar-
ity value) has to reflect the presence of discrimina-
tive similarity values for that pair and the diversity
of the types of similarity measures which computed
these similarity values. In other words, a confidence
score should be higher for a candidate correspondence
which obtains discriminative similarity values with
a terminological, a semantic and a constraint-based
measures rather than for a candidate correspondence
which obtains the same values with three terminolog-
ical measures. In the rest of this section, we describe
a model to classify similarity measures and compute
their dissimilarity (Section 4.1). Then, we explain
the meaning of a discriminative similarity value for
a candidate correspondence (Section 4.2). The clas-
sification model and the discrimination definition can
finally be used to compute a confidence score and se-
lect the correspondences (Section 4.3).
4.1 A Model for Comparing Similarity
Measures
Matching approaches combine different types of simi-
larity measures in order to exploit all properties of the
data sources and to increase the chances of discov-
ering correct correspondences (Euzenat and Shvaiko,
2007). However, one needs to correctly tune the
matching tool when possible to avoid that a set of
similar measures (e.g., terminological) has too much
impact in the global similarity score. Indeed, the
types and differences between similarity measures are
rarely taken into account. In addition, their ignorance,
or inability to detect a similarity, is not considered.
For instance, two elements labeled mouse would be
matched with a high score by a terminological mea-
sure, although one of them may refer to as a com-
puter device while the other may stand for an animal.
This is due to the fact that the terminological measure
only uses the string labels to detect a similarity, and
no other information such as external resource, con-
straints, element context, etc. Consequently, the ig-
norance of a similarity measure should reflect its lim-
itations in terms of information that it uses to detect
a similarity. Similarity measures have been largely
studied in the literature (Euzenat and Shvaiko, 2007;
Cohen et al., 2003). And a classification of these mea-
sures has been proposed (Euzenat et al., 2004) and
later refined (Shvaiko and Euzenat, 2005). In a similar
fashion, we provide a non-exhaustive list of features
of similarity measures:
• the type or category (e.g., terminological, linguis-
tic, structural)
• the type of input (e.g., character strings, records)
• the type of output (e.g., number, semantic rela-
tionship)
• the use of external resources (e.g., a dictionary, an
ontology)
To compare the similarity measures, we propose
to represent them as binary vectors according to their
features. A feature is in our context a property that
the similarity measure fulfills or not. Each similarity
measure sim
i
∈ S is represented by a binary vector
v
i
∈ V . The size of a vector is |v
i
|, i.e., the number
of features. We can see the set of binary vectors as
a matrix, where f
ih
represents the binary value of the
h
th
feature for the i
th
vector.
In our running example, the four similarity mea-
sures are represented by vectors with 8 features, as
shown in Figure 1. For instance, the third similar-
ity measure is not terminological but it exploits the
structure and the constraints of the data source with a
dictionary as external resource. It is applied against
the elements and the relationships of the data sources.
Figure 1: Binary Vectors for each Similarity Measure.
We finally obtain a classification of the similar-
ity measures. This classification not only highlights
the features of the measures but also indicates the ig-
norance of a measure (with respect to the features).
For instance, a terminological measure such as sim
1
would not detect a similarity between synonyms in
most cases. It is possible to refine the classification
by adding more features. The goal is to compute the
DATA2013-2ndInternationalConferenceonDataManagementTechnologiesandApplications
132

differences of each similarity measure with regards to
the other ones. For each binary vector v
i
∈ V , we
compute its difference score noted ∆
sim
i
with regards
to the other vectors by applying Formula 1. The main
intuition is that a vector is different from another one
if its features are different. Thus, we analyse each fea-
ture of a vector and we calculate the rate of dissimilar
values in the other vectors for the same feature. Given
a number n of similarity measures and a number g of
features, a difference score ∆
sim
i
is computed as:
∆
sim
i
=
∑
g
h=1
(
∑
n
j6=i, j=1
f
jh
⊕ f
ih
n−1
)
g
(1)
The function f
jh
⊕ f
ih
is the boolean operation exclu-
sive or, which excludes the possibility of same val-
ues for both features. In other words, it returns 1 if
the boolean features are different, 0 else. If all bi-
nary vectors are identical, the difference score equals
0, but this indicates that the vector representation of
the measures is not detailed enough.
We then normalize this difference score in the
range [0,1] to obtain the dissimilarity of a measure
with regards to others. This normalization is shown
in Formula 2:
dissim
sim
i
=
∆
sim
i
∑
n
a=1
∆
sim
a
(2)
The dissimilarity score measures the percentage of
features which are different from other measures. We
note that the following statement holds with the nor-
malization:
∑
sim
i
∈S
dissim
sim
i
= 1.
Table 2 provides the difference and dissimilarity
scores for each measure in our example. For in-
stance, the difference score of the similarity measure
sim
1
equals
2
3
+
1
3
+
1
3
+
1
3
+
1
3
+0+
1
3
+
1
3
8
= 0.33. Its dissim-
ilarity score is equal to
0.33
(0.33+0.33+0.67+0.375)
= 0.19.
This means that the similarity measure sim
1
has 19%
of different features compared to other measures, or
sim
1
has an ignorance degree equal to 81%.
Table 2: Difference and Dissimilarity Scores of each Mea-
sure.
sim
1
sim
2
sim
3
sim
4
∆ 0.33 0.33 0.67 0.375
dissim 0.19 0.19 0.40 0.22
4.2 Discriminative Measures
In real-case scenarios, a correct correspondence
would certainly not obtain a high similarity value for
all measures. Therefore, combining the similarity val-
ues of all measures to compute a global score may
not seem suitable. Besides, if a measure returns high
similarity values for most candidate correspondences
(e.g., a measure based on data types), then these high
values may not be useful to disambiguate a conflict
between two pairs of elements. Thus, we propose
to discover which similarity measures are discrimi-
native for a candidate correspondence, i.e., the mea-
sures which computed a significant value for that cor-
respondence w.r.t. others.
To fulfill this goal, we are interested in evaluating
the range inside which a value is considered as dis-
criminative. We use the mean and the standard de-
viation to obtain this range of values. Jain et al. have
demonstrated that these formulas are efficient when
we do not need to estimate their values (Jain et al.,
2005). Besides, the standard deviation is sensitive to
extreme values, i.e., the ones that discriminate. Let
us consider a similarity measure sim
i
∈ S which has
computed a value for all possible correspondences,
i.e., |E
d
| × |E
d
0
|. We can compute the average µ and
the standard deviation σ of this measure sim
i
as fol-
lows:
∀e ∈ E
d
,∀e
0
∈ E
d
0
, µ =
∑
sim
i
(e,e
0
)
|E
d
| × |E
d
0
|
σ =
s
∑
(sim
i
(e,e
0
) − µ)
2
|E
d
| × |E
d
0
|
As the standard deviation represents the dispersion of
a value distribution, the range of values close to the
average is given by:
rnd
sim
i
= [µ − σ, µ + σ]
Note that the lower limit of that range equals to 0 if
µ−σ < 0, and the upper limit is equal to 1 if µ+σ > 1.
The similarity values in the range rnd
sim
i
do not dis-
criminate a candidate correspondence. Therefore, a
discriminative similarity value for a candidate cor-
respondence (e,e
0
) should not belong to the range
rnd
sim
i
. We note γ(e,e
0
) the set of measures that
discriminate a candidate correspondence, i.e., the
measures that satisfy this condition: ∀sim
i
,sim
i
∈
γ(e,e
0
) ⇐⇒ sim
i
(e,e
0
) /∈ rnd
sim
i
.
In our example, we can compute the average of the
measure sim
1
. The nine values have an average and
a standard deviation equal to 0.28 and 0.35 respec-
tively. Consequently, the range of non-discriminative
values is [0,0.63]. For instance, the pair (a,a
0
) is dis-
criminated by the measure sim
1
since the value com-
puted for this candidate correspondence (0.8) is not
in that range. Note that all underlined values in the
similarity matrices of Table 1 indicate that the corre-
sponding measure is discriminative for the candidate
correspondence. Thus, γ(a, a
0
) = {sim
1
,sim
3
}.
By selecting a subset of the similarity measures,
we express the fact that the discriminative similarity
AGenericandFlexibleFrameworkforSelectingCorrespondencesinMatchingandAlignmentProblems
133

values have more impact than others during the cor-
respondences selection. However, a candidate corre-
spondence may not have any discriminative values in
the first round, and thus it is not considered for com-
puting its confidence score. To identify the discrimi-
native measures for such candidate correspondences,
we iterate the process by noting γ
k
(e,e
0
) the k
th
itera-
tion of this process. At the end of each step, the previ-
ous similarity values are discarded, and we compute a
new average and standard deviation, thus generating
a set of new discriminative measures (or an empty
set). This set is then merged into Γ
t
(e,e
0
) as shown
with this formula:
Γ
t
(e,e
0
) =
t
[
k=1
γ
k
(e,e
0
)
The question is how to determine a value for the num-
ber of iterations t. We can use the same techniques
than the matching tools such as a threshold value (i.e.,
there is no more iteration if the average of similarity
values reaches a threshold value) or the first k itera-
tions. We can also iterate until all elements of a data
source have been discriminated by at least one mea-
sure, and/or when an iteration has no more discrimi-
native values to propose.
Let us compute the set of discriminative measures
for the second iteration in our running example. We
first discard the discriminative similarity values from
the matrices that were previously identified (i.e., the
underlined values). What happens for the similarity
measure sim
1
? The new average and standard de-
viation computed for the remaining 6 values equals
0.04 and 0.24 respectively. The similarity value 0.3
for (b,b
0
) is a discriminative value at this iteration.
Consequently, sim
1
is added in the set of discrim-
inative measures for the candidate correspondence
(b,b
0
) and Γ
2
(b,b
0
) = {sim
1
,sim
3
,sim
4
}.
4.3 Computing a Confidence Score
The next step deals with the computation of a con-
fidence score for a given candidate correspondence.
This score is based on the discriminative similarity
measures and their associated value. Indeed, the in-
tuition is that we should be confident in a correspon-
dence which obtains high similarity values computed
by distinct and low-ignorance measures. Given a pair
m = (e,e
0
) and its discriminative similarity values
< sim
1
(e,e
0
),.. ., sim
n
(e,e
0
) > with sim
1
,.. ., sim
n
∈
Γ
t
(e,e
0
), the confidence score con f
t
(e,e
0
) for the t
th
iteration is calculated as follows:
con f
t
(e,e
0
)
=
n
∑
i=1
dissim
sim
i
×
∑
n
i=1
sim
i
(e,e
0
)
n
In this formula, we average the discriminative simi-
larity values and we multiply the result by the sum of
all dissimilarities of the measures. As both are in the
range [0,1], the confidence score also has values in the
range [0, 1]. Note that our formula is also a weighted
average like in other approaches, however it does not
require any tuning due to the independence and the
model for the similarity measures.
Back to our example, we can compute the confi-
dence scores of all candidate correspondences which
have discriminative values at the first iteration. That
is, the pairs (a, a’), (a, d’), (b, b’), (c, a’), and (c,
d’). Let us detail the probability for the first pair to be
correct:
con f (a,a
0
) = (0.19 + 0.40) ×
0.8 + 0.6
2
= 0.41
The confidence score for the other candidate corre-
spondences are: conf(a, d’) = 0.30, conf(b, b’) =
0.43, conf(c, a’) = 0.19, and conf(c, d’) = 0.25. We
notice that although the similarity values for the pairs
(a, a’) and (a, d’) are close, we have more confi-
dence in the former pair since it obtains discrimina-
tive similarity values with more dissimilar similarity
measures. The candidate correspondence (c, a’) is
penalized by sim
3
since this measure mainly computes
high similarity values, except for this candidate pair.
4.4 Discussion
We finally discuss several points of our approach:
• When the confidence scores of two correspon-
dences involving the same element are very
close, they can be part of a complex correspon-
dence. This needs to be checked by using refined
techniques to discover these complex correspon-
dences (Bilke and Naumann, 2005; Dhamankar
et al., 2004; Saleem and Bellahsene, 2009).
• The boolean features are produced objectively.
Designers or users of a similarity measure knows
whether the measure satisfies a feature or not. A
challenging perspective is the automatic definition
of the binary vector. In the OAEI track bench-
mark
1
, the objective is to detect the ability of a
matching tool by duplicating a dataset with a mi-
nor change (e.g., changing the language, or delet-
ing the annotations) (Euzenat et al., 2011). By
applying a similarity measure to this OAEI track,
one is able to check if the measure is resistant to
the change, and thus can compute the binary vec-
tor of that similarity measure.
1
Ontology Alignement Evaluation Initiative (January
2013), http://oaei.ontologymatching.org/
DATA2013-2ndInternationalConferenceonDataManagementTechnologiesandApplications
134

• In the current version, we use binary vectors,
which means that a measure owns the feature or
not. We could relax this binary constraint by al-
lowing real values. In that case, the vector shows
the probability that the measure satisfies the fea-
ture, or the degree of ignorance for the feature.
However, such a modification has an impact on
the difference score formula.
• If we do not discriminate the similarity measures
for a given candidate correspondence, the confi-
dence score would be equal to the average of all
similarity values computed for that candidate cor-
respondence.
• It is possible that all similarity measures have the
same similarity score, despite their different fea-
tures. For instance, the four similarity measures
of the running example could have obtained each
a score equal to 0.25. In such case, the dissimi-
larity scores still have a significant impact, since
they are used only for the discriminative values
that have been calculated.
• Our approach can be plugged into most match-
ing approaches, especially those that computes a
global similarity score. Our confidence score may
be used to select correspondences either manu-
ally (the user can select within the list of top-k
correspondences based on their confidence score)
or automatically (all confidence scores above a
threshold are returned). Besides, our confidence
score reflects the types and ignorance of the simi-
larity measures which have computed the discrim-
inative similarity values.
• Finally, our approach does not require any tuning
for combining the similarity measures, because
we select the values computed by similarity mea-
sures if they are sufficiently discriminative.
5 EVALUATION
In this section, we validate our approach in an En-
tity Matching context. We first describe the evalua-
tion protocol (benchmark and another tool), then we
compare our approach with another entity matching
tool in terms of matching quality, and we finally show
the robustness of our approach when adding new sim-
ilarity measures.
5.1 Evaluation Protocol
To demonstrate the benefits of our framework, we
have implemented it and tested against a benchmark
for entity resolution (Kopcke et al., 2010). This
benchmark
2
contains four datasets and has been eval-
uated by their authors with a matching tool (whose
name is unknown due to licensing). We refer to this
matching tool as BenchTool in the rest of the paper.
The four datasets mainly cover two domains: Web
products (Abt-Buy and Amazon-GoogleProducts) and
publications (DBLP-Scholar and DBLP-ACM). The
size of the data sources contained in these datasets
vary from 1081 (Abt) entities to 64283 (Scholar),
with an average around 2000 entities. The set of per-
fect correspondences is provided for each dataset and
their size varies from 1097 (Abt-Buy) to 5347 (DBLP-
Scholar) (Kopcke et al., 2010). The matching quality
is computed with the three well-known metrics (Eu-
zenat and Shvaiko, 2007; Bellahsene et al., 2011).
Precision calculates the proportion of relevant corre-
spondences among the discovered ones. Recall com-
putes the proportion of correct discovered correspon-
dences among all correct ones. Finally, the F-measure
evaluates the harmonic mean between precision and
recall. Since both tools obtain a score for these met-
rics which is close to the F-measure (e.g., precision
equal to 97%, recall to 95% and F-measure at 96%),
we only present the plots for the F-measure.
The configuration of our framework is as follows.
We have 5 similarity measures : three of them are ter-
minological (Jaro Winkler, Monge Elkan, Smith Wa-
terman from the Second String API
3
), another one is
based on the frequency of the words in fields such as
description or title (Duchateau et al., 2009), and the
last one is the Resnik measure applied to the Word-
net dictionary (Resnik, 1999). All these measures
have been classified with the 8 features described in
Section 4.1. The number of iterations is limited to 2
and the conditions for selecting a correspondence is a
combination of threshold and top-1: for each element
from the source, its correspondence is the candidate
correspondence with the best confidence score only
if this score is above a threshold. This threshold is
computed by averaging all similarity values. For the
BenchTool, we assume that the best tuning was per-
formed by the authors when they ran it against the
Entity Matching Benchmark (Kopcke et al., 2010).
5.2 A Quality Comparison with
BenchTool
Our first experiment aims at showing the matching
quality obtained by our approach with regards to the
BenchTool approach. Figure 2 depicts the results of
2
Entity Matching benchmark (January 2013), http://
dbs.uni-leipzig.de/en/research/projects/object matching/
3
API at http://secondstring.sourceforge.net/
AGenericandFlexibleFrameworkforSelectingCorrespondencesinMatchingandAlignmentProblems
135
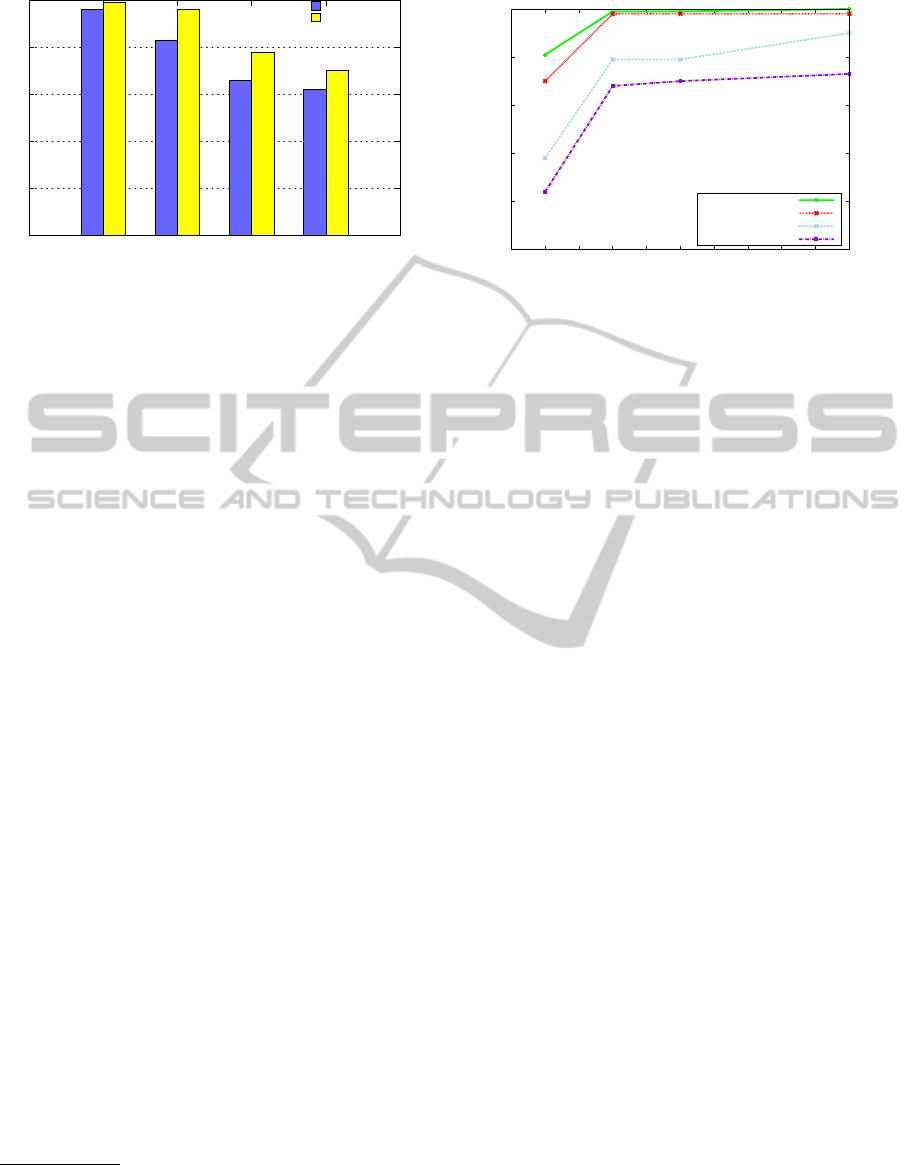
BenchTool
OurApproach
0
20
40
60
80
100
DBLP−ACM DBLP−Scholar Abt−Buy Amazon−GP
F−measure Value
Figure 2: Results of BenchTool and our approach in terms
of F-measure for the 4 datasets.
the two systems for the four datasets. For the publica-
tions datasets, which are easier to match, both tools
obtain an acceptable matching quality and our ap-
proach achieves a F-measure score above 95%. The
products datasets are more difficult to match for two
reasons: first, a description field is confusing because
it contains either full sentences or sets of keywords.
Secondly, two products may slightly differ (e.g, two
hard drives of different size from the same manufac-
turer). For these datasets, BenchTool obtains a F-
measure around 60 − 65%. Our approach performs
better with a F-measure between 70% to 78%. Al-
though our tool was not specifically designed for the
entity matching task, we note that it achieves a bet-
ter F-measure for all datasets. This means that our
generic framework for selecting correspondences in-
dependently from the similarity measures is effective.
5.3 Demonstrating Robustness
and Flexibility
In a second experiment, we demonstrate the robust-
ness and the flexibility of our approach regardless of
the similarity measures. A majority of matching ap-
proaches requires some tuning for combining similar-
ity measures (e.g., setting weights). Thus, when a new
similarity measure is added, it is necessary to recon-
figure the tool. Since our framework considers each
similarity measure individually, there is no need for
tuning
4
and we demonstrate that the matching quality
does not decrease when adding more measures. We
have compared the variation of the F-measure value
when increasing the number of similarity measures.
To perform this experiment, five measures from the
Second String API have been added (e.g., Affine Gap,
4
The similarity measure has to be described according
to the boolean features, which is still simpler than tuning a
combination function. And such description can be shared
and reused in an ontology for instance.
0
20
40
60
80
100
0 1 2 3 4 5 6 7 8 9 10
F-measure
Number of similarity measures
DBLP-ACM
DBLP-Scholar
Abt-Buy
Amazon-GP
Figure 3: Results of our approach for the 4 datasets when
varying the number of similarity measures.
Jaccard), and the measures have been randomly se-
lected. We have run this experiment 10 times for each
dataset to limit the impact of the randomness. Fig-
ure 3 illustrates the average F-measure (of all runs)
for the four datasets with various number of similar-
ity measures. When adding more measures and with-
out any tuning, the trend of the plots is an increase or
stabilization of the F-measure value. For the DBLP-
Scholar dataset, the F-measure value is equal to 70%
with one measure, and then it increases to reach 98%
with 10 measures. For the products datasets, the 5
terminological measures which have been added are
not sufficient to improve strongly the results. Other
types of similarity measures are necessary to increase
the matching quality of these datasets. To conclude,
our framework is robust and flexible to the number of
similarity measures that can be added without tuning.
6 CONCLUSIONS
In this paper, we have proposed a novel framework
for selecting correspondences in a matching or ontol-
ogy problem. Contrary to other approaches, our ap-
proach does not require any tuning to combine those
measures. The experiments against an entity reso-
lution benchmark have demonstrated both the major
improvement of our approach in terms of quality and
its robustness regardless of the number of similarity
measures involved in the matching. As for the per-
spectives, we plan to perform more experiments, both
with other data integration tasks (schema matching,
ontology alignment) and with various configurations
of the parameters (number of iterations, number of
features). Although the definition of features for the
similarity measures can be designed in an ontology
and shared with others users, it would be interesting
DATA2013-2ndInternationalConferenceonDataManagementTechnologiesandApplications
136

to automatically compute the dissimilarity scores, for
instance by analyzing the distribution values of the
measures. Converting the binary vectors into real-
valued vectors would refine the degree of ignorance
of the measures. Such vectors may be computed with
specific datasets, in which a minor change reflects a
feature.
REFERENCES
Aumueller, D., Do, H. H., Massmann, S., and Rahm,
E. (2005). Schema and ontology matching with
COMA++. In ACM SIGMOD, pages 906–908.
Avesani, P., Giunchiglia, F., and Yatskevich, M. (2005). A
large scale taxonomy mapping evaluation. In Interna-
tional Semantic Web Conference, pages 67–81.
Bellahsene, Z., Bonifati, A., and Rahm, E. (2011). Schema
Matching and Mapping. Springer-Verlag, Heidelberg.
Bernstein, P. A., Madhavan, J., and Rahm, E. (2011).
Generic schema matching, ten years later. PVLDB,
4(11):695–701.
Bilke, A. and Naumann, F. (2005). Schema matching using
duplicates. ICDE, 0:69–80.
Bozovic, N. and Vassalos, V. (2008). Two-phase schema
matching in real world relational databases. In ICDE
Workshops, pages 290–296.
Christen, P. (2008). Febrl -: an open source data clean-
ing, deduplication and record linkage system with a
graphical user interface. In SIGKDD International
Conference on Knowledge Discovery and Datamin-
ing, KDD’08, pages 1065–1068. ACM.
Cohen, W., Ravikumar, P., and Fienberg, S. (2003). A com-
parison of string distance metrics for name-matching
tasks. In In Proceedings of the IJCAI-2003.
Cruz, I. F., Sunna, W., Makar, N., and Bathala, S. (2007).
A visual tool for ontology alignment to enable geospa-
tial interoperability. J. Vis. Lang. Comput., 18(3):230–
254.
Dhamankar, R., Lee, Y., Doan, A., Halevy, A., and Domin-
gos, P. (2004). iMAP: Discovering Complex Semantic
Matches between Database Schemas. In ACM SIG-
MOD, pages 383–394.
Doan, A., Madhavan, J., Dhamankar, R., Domingos, P., and
Halevy, A. Y. (2003). Learning to match ontologies
on the semantic web. VLDB J., 12(4):303–319.
Drumm, C., Schmitt, M., Do, H. H., and Rahm, E. (2007).
Quickmig: automatic schema matching for data mi-
gration projects. In CIKM, pages 107–116. ACM.
Duchateau, F., Coletta, R., Bellahsene, Z., and Miller, R. J.
(2009). (Not) Yet Another Matcher. In CIKM, pages
1537–1540.
Euzenat, J. et al. (2004). State of the art on ontology match-
ing. Technical Report KWEB/2004/D2.2.3/v1.2,
Knowledge Web.
Euzenat, J., Ferrara, A., van Hage, W. R., Hollink, L., Meil-
icke, C., Nikolov, A., Ritze, D., Scharffe, F., Shvaiko,
P., Stuckenschmidt, H., Sv
´
ab-Zamazal, O., and dos
Santos, C. T. (2011). Results of the ontology align-
ment evaluation initiative 2011. In OM.
Euzenat, J. and Shvaiko, P. (2007). Ontology matching.
Springer-Verlag, Heidelberg (DE).
Fellegi, I. P. and Sunter, A. B. (1969). A theory for record
linkage. Journal of the American Statistical Associa-
tion, 64:1183–1210.
Gracia, J., Bernad, J., and Mena, E. (2011). Ontology
matching with cider: evaluation report for oaei 2011.
In OM.
Jain, A., Nandakumar, K., and Ross, A. (2005). Score nor-
malization in multimodal biometric systems. Pattern
Recognition, 38(12):2270–2285.
K
¨
opcke, H. and Rahm, E. (2010). Frameworks for entity
matching: A comparison. Data Knowl. Eng., 69:197–
210.
Kopcke, H., Thor, A., and Rahm, E. (2010). Learning-based
approaches for matching web data entities. IEEE In-
ternet Computing, 14(4):23–31.
Li, J., Tang, J., Li, Y., and Luo, Q. (2009). Rimom: A dy-
namic multistrategy ontology alignment framework.
IEEE Trans. on Knowl. and Data Eng., 21(8):1218–
1232.
Panse, F., Ritter, N., and van Keulen, M. (2013). Indeter-
ministic handling of uncertain decisions in deduplica-
tion. Journal of Data and Information Quality.
Resnik, P. (1999). Semantic similarity in a taxonomy:
An information-based measure and its application to
problems of ambiguity in natural language. Journal
of Artificial Intelligence Research, 11:95–130.
Saleem, K. and Bellahsene, Z. (2009). Complex schema
match discovery and validation through collaboration.
In OTM Conferences (1), pages 406–413.
Shvaiko, P. and Euzenat, J. (2005). A survey of schema-
based matching approaches. Journal of Data Seman-
tics IV, pages 146–171.
Shvaiko, P. and Euzenat, J. (2008). Ten challenges for ontol-
ogy matching. In OTM Conferences (2), pages 1164–
1182.
Talburt, J. R. (2011). Entity Resolution and Information
Quality. Elsevier.
Winkler, W. E. (2006). Overview of record linkage and cur-
rent research directions. Technical report, Bureau of
the Census.
AGenericandFlexibleFrameworkforSelectingCorrespondencesinMatchingandAlignmentProblems
137
