A New Relational Spatial OLAP Approach for Multi-resolution

and Spatio-multidimensional Analysis of Incomplete Field Data

Mehdi Zaamoune

, Sandro Bimonte

, François Pinet

and Philippe Beaune

IRSTEA, TSCF, 24 Av. des Landais, Aubière, France

Agaetis, 10 allée Evariste Galois, 63 000 Clermont-Ferrand, France

Keywords: Spatial OLAP, Incomplete Continuous Field, Multi-resolution Geographic Data.

Abstract: Integrating continuous spatial data into SOLAP systems is a new research challenge. Moreover,

representation of field data at different scales or resolutions is often mandatory for an effective analysis.

Thus, in this paper, we propose a logical model to integrate spatial dimensions representing incomplete field

data at different resolutions in a classical SOLAP architecture.

1 INTRODUCTION

Spatial Data Warehouse (SDW) and Spatial OLAP

(SOLAP) systems play an important role in helping

decision-makers obtain the maximum benefits of

these large amounts of geographic data (Bédard et

al., 2001). These technologies extend Data

Warehouse (DW) and OLAP systems to integrate

spatial data with warehoused classical data to

achieve the on-line analysis of large georeferenced

data sets. SOLAP systems integrate advanced OLAP

and Geographic Information Systems (GIS) in a

unique framework usually based on the relational

storage (i.e. Oracle, etc.) of spatial data according to

the vector model, and their analysis through SOLAP

operators (Spatial Roll-Up, Spatial Slice, etc.)

implemented by the SOLAP server (e.g.

Map4Decision, etc.) and visualized by means of

tabular, graphical and cartographic displays (Gomez

et al., 2012). SDW are modeled according to the

spatio-multidimensional model that extends the

traditional multidimensional model to define spatial

dimensions (i.e. analysis axes with spatial attributes)

and spatial measures (i.e. analysis subjects) that

integrate geographic information using the vector

model (Bédard et al., 2007). SOLAP technology can

be applied in different domains (e.g. archeology,

public health, etc.).

Geographic information can be represented by

two models, depending on the nature of data:

discrete (vector) and continuous field (Mennis et al.,

2005). Continuous fields (also called continuous

spatial data) represent physical phenomena that

continuously change in space (Paolino et al., 2010),

for example the temperature, population, etc. Two

representations of field data have been proposed:

incomplete and complete (Paolino et al., 2010).

Incomplete representations store a sample of points

and need additional functions to calculate the field in

non-sampled areas (e.g. grid of points, TIN, etc.)

(e.g. Figure 2). Complete representations associate

estimated values to regions and assume that these

values are valid for each point in the regions (e.g.

raster). For those representations some ad-hoc

analysis operators have been defined that allow a

point by point analysis (i.e. map algebra (Mennis et

al., 2005)). Representation of geographic data at

different scales or resolutions (e.g. Figure 2-b) is

mandatory for an effective analysis of spatial

complex phenomena since it represents a

geovisualization method (Camossi et al., 2009).

Consequently, these resolutions or scales represent

decision-makers analysis needs that should be

explicitly represented in any data and query model.

Indeed, in the context of Geographic Information

Systems and Spatial Databases Management

Systems (SDBSM), several works addresses this

issue by proposing conceptual, logical and physical

data models and analysis techniques (Parent et al.,

2006).

Motivated by the important analysis capabilities

offered by the continuous field representation of

geographic data when integrated in SOLAP systems

(visualization, querying, etc.) recently some works

investigated the extension of the spatio-

145

Zaamoune M., Bimonte S., Pinet F. and Beaune P..

A New Relational Spatial OLAP Approach for Multi-resolution and Spatio-multidimensional Analysis of Incomplete Field Data.

DOI: 10.5220/0004434501450152

In Proceedings of the 15th International Conference on Enterprise Information Systems (ICEIS-2013), pages 145-152

ISBN: 978-989-8565-59-4

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

multidimensional model and SOLAP operators with

complete and incomplete field data (cf. Section 6).

In the same way, handling multi-resolutions of

spatial data into spatial multidimensional models has

been proposed in few works (Yvan et al., 2002)

(Gascueña and Guadalupe 2009) that propose

conceptual models to represent SDW with several

representations (scales, resolutions, etc.) of spatial

dimensions and measures.

However, to best of our knowledge existing

works concerning field data and multi-resolutions

lack of a complete implementation in a full-featured

SOLAP architecture, or in other terms they do not

propose a coupled relational and SOLAP server

model for a generic SOLAP architecture allowing (i)

the map algebra operators, (ii) the multi-resolution,

and (iii) a continuous view of the field.

In order to handle the spatio-multidimensional

analysis of incomplete regular grid field data at

different resolutions, we propose in this paper: (i) a

specific logical model, extending the well-know

relational star schema; (ii) and some new MDX-

based defined functions. We validate our proposal

using a real case study concerning the odor

monitoring, and we provide some experiments

showing the feasibility also in terms of storage and

computation performances.

2 MODELING AND ANALYSIS

REQUIREMENTS

In order to show our proposal, we present a case

study based on data issued from the monitoring of

urban odor. For each 15 minutes and type of odor

(e.g. NO2) a regular grid map (field) is produced by

means of some sample points and a simulation

model (ADMS5) . The simulation model estimates

odors for a whole urban area and produces 100*100

thematic grids. Examples of points grid are provided

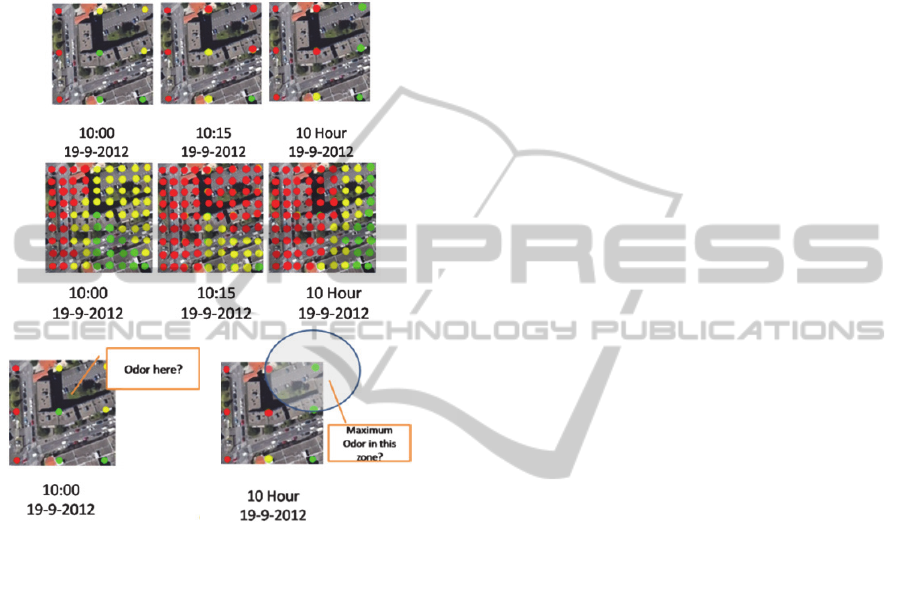
in figure 2-a (odor values are represented by color:

green, yellow, red) for 10:00 19-2-2012 and 10:15

19-2-2012. Let us now suppose that the user wants

to aggregate data along a temporal dimension (year,

month, day, hour, minute) using the average to

obtain an aggregated odor map. This is an OLAP

operation of RollUp on the temporal dimension that

corresponds to a local map algebra operation (Figure

2-a

).Moreover, since space is represented in a

continuous way, decision-makers should be able to

ask for the result of any OLAP query in any point of

the spatial dimension (for example, s/he should be

interested in the odor value at 10:00 in the area

behind the building) (Figure 2-c). It is also possible

to apply a spatial slice operator on the spatial

dimension (i.e. using a spatial predicate to select a

subset of warehoused data) (Figure 2-d). In order to

answer to these last two queries spatial interpolation

methods are necessary, since in incomplete field

only the values provided by the simulation model

are stored. Spatial interpolation is the process of

prediction of almost exact values of attributes at

unsampled locations from measurements made at

control points within the same area (O'Sullivan and

Unwin, 2002). In our case the interpolation function

used is the bilinear interpolation, which is a local

deterministic method. It uses the 2 * 2 grid sample

points closest to the unknown point and calculates a

distance weighted average which determines in what

proportion the value of a neighbour impact on the

value of the point to be estimated (Figure 1).

Finally, as stated in the previous section, since

visualization of spatial data at different resolutions is

mandatory for the exploration/analysis process,

decision-makers should be able querying spatial

warehoused data at different resolutions. It is very

important to note that for each spatial phenomenon a

set of useful known resolutions exist, so they could

be predefined according to data and users needs.

Moreover, in order to calculate values at finer

resolutions spatial interpolation functions as

previously described can be used.

To summarize, spatio-multidimensional analysis

of field data implies: supporting (i) OLAP classical

operators as Map Algebra, (ii) continuous view of

spatial data, (iii) spatial slice operators using field

data, and (iv) visualizing and querying data at

different predefined resolutions.

3 SPATIO-MULTIDIMENSIONAL

MODEL FOR INCOMPLETE

FIELD DATA

In this section we describe our spatio-

multidimensional model for handling incomplete

fields at different resolutions. Our model extends the

classical spatio-multidimensional models to generate

the continuity of the phenomena over the studied

area, and represents pre-defined levels of resolution.

In particular, a “Cube” is composed of “Facts”

and “Dimensions”. A “Dimension” is composed of

“Hierarchies”, which are composed of “Levels”. A

“Level” can be spatial or conventional. This means

that it can contain “Spatial attributes” (e.g. points,

etc.), or contain only alphanumerical attributes

ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems

146

respectively. “Facts” is composed of “Spatial

Measures” or “Conventional Measures”. Moreover,

our extension defines a “Field level” as a special

type of spatial level where each member has a

geometric attribute (e.g. point), a “neighbourhood

relationship” association, and a resolution level to

which it belongs.

(a)

(b)

Figure 2: a) Local map algebra aggregation over

incomplete field. b) Multiresolution representation over

incomplete field c) Querying an unsampled point d)

Querying an unsampled zone.

Indeed, as described in the previous section a

spatial interpolation function uses a set of points,

which depend on the function (e.g. bilinear function

uses a 2*2 grid), to estimate the unknown value.

Thus, in our approach values are represented by

measures, the “Neighbourhood relation” links each

detailed "Field level" to its neighbours in the less

detailed level. As soon as the value of a high

resolution "Field level" is required its neighbours are

found through the “Neighbourhood relation”.

However, this type of relationship can be

implemented in different ways, depending on the

intended purpose as shown in the next section. In

our case, we want to estimate the value of any point

(x, y) of a Field level, so neighbours are found on

the fly by the relation "Neighbourhood relation". In

the case of a change in the level of resolution, the

members of a high resolution (e.g. 200*200), are

predefined and therefore, their respective

neighbours, which belongs to the resolution

100*100, can be pre-stored as attributes.

As described in the model, a hierarchy can

contain several field levels representing the

phenomena at different resolutions. This means that

changing resolutions implies navigating into the

hierarchy and calculating values by means of the

interpolation function or an ad-hoc aggregation

function when we move from less detailed resolution

to more detailed one, or vice versa.

The odor SDW of our case study using our

spatio-multidimensional model is shown in Figure 3.

This instance describes the dimensions and facts

that constitute our cube.

In addition to the dimensions (Source, Tracer and

Time), the "Facts" class has a classical measure

“odorMeasure” and a derived measure

“EstimatedOdorMeasure”. The derived measure is

calculated according to two functions:

a) Interpolatepoint”(continuity).

b) "InterpolateBilinear" (multiresolution).

In our case, the interpolation function used is the

"bilinear interpolation". The relationship whose

cardinalities are "2, 4" represents the

“Neighbourhood relation”. A member of the

"Incomplete Field Level" can have 2 or 4

neighbours, depending on its position in the grid 2*2

that surrounds it. The “Neighbourhood relation” can

be used to retrieve neighbours of a location (x,y) to

estimate the value in that position (continuity), or to

retrieve a high resolution member’s neighbours in

the lower level of resolution to estimate its value

(multiresolution on the fly).

4 RELATIONAL AND OLAP

MODELS

In this section we present the implementation of our

spatio-multidimensional model in a typical relational

SOLAP architecture based on SQL (the Relational

DBMS standard language) and MDX, which is the

de-facto standard of OLAP Servers. This provides a

generality character to our approach, being possible

to be implemented in any architecture of this kind.

Let us suppose to have one “Field level”

representing points at the resolution 100*100, and

then the logical model of our case study is

represented as in fig. 4. It is a classical star schema.

This model is composed of a fact table containing

measures with foreign keys to dimension tables.

Each dimension table is denormalized, and has

attributes representing levels.

ANewRelationalSpatialOLAPApproachforMulti-resolutionandSpatio-multidimensionalAnalysisofIncompleteField

Data

147

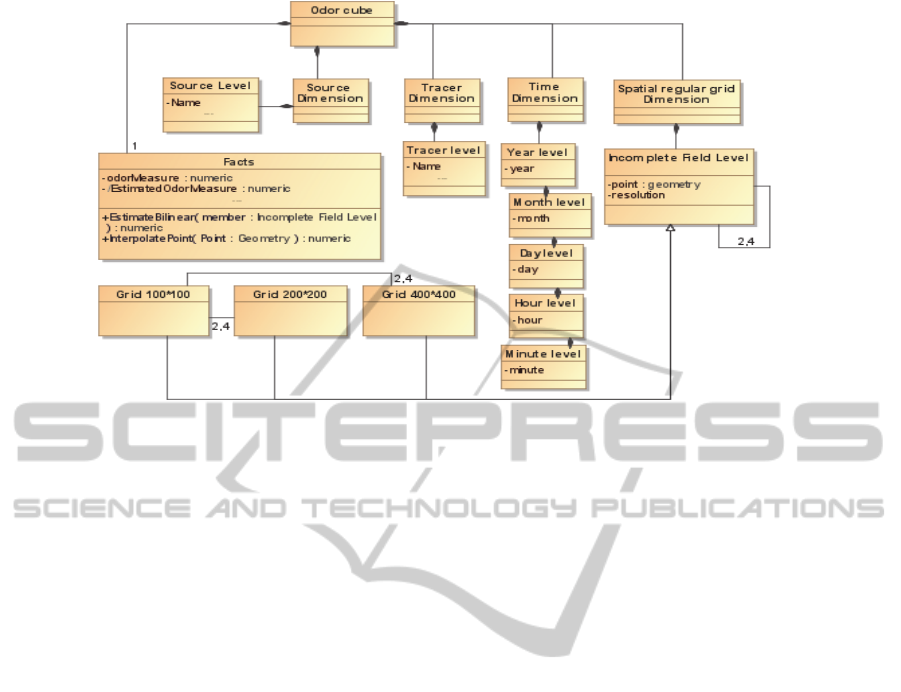
Figure 3: Odor SDW multi-dimensional model.

Let us also suppose to have a classical OLAP

model based on that logical schema, where the

spatial level is called

[Field].[res100]. As we

can see, the dimensions that constitute the model

are: the temporal dimension, which consists of five

levels of granularity (Year, month, day, hour and

minute); the Source dimension that expresses the

source of the pollutant (e.g. cars); the Tracer

dimension is the type of pollutant (eg NO2), which

is also defined by its identifier and name; and the

“Field dimension” that represent a regular grid of

points and consists of one level representing the

regular grid at the 100*100 resolution, which is

composed of an identifier and a geometry

representing a point. The measure «Concentration of

odor» represents the values for all members

representing the field at a 100*100 resolution. This

representation of incomplete field data in the

multidimensional model allows making queries as

Map Algebra operators (point by point aggregation)

such as the following:

Query 1: Select average odor for each field member

during 2012.

SELECT [Field].[res100]. Members ON

ROWS, {[time].[2012]} ON COLUMNS

FROM [odorCube] WHERE

[Measures].[value]

4.1 Incomplete Field

In order to implement field levels we have defined a

GeoMDX user-defined function that represents a

spatial interpolation as:

NumericType InterpolatePoint(Geometry)

This function takes as input a geometry (point) and

returns a numerical value, which is a derived

measure in the OLAP model, representing an

estimated value calculated using the neighbourhood

values of the point given in input. Thus, let us

suppose that we want to retrieve a value of the field

in a location whose geometric property is set to the

geometric coordinates POINT(-72.1235 42.3521).

Then in order to answer to that need using the

Bilinear interpolation function, decision-makers

have to simply use a GeoMDX function in the

following way:

InterpolatePoint(POINT(-

72.1235 42.3521)).

Thus, the function will look for the neighbours of

the point given as a parameter, in the field level

([Field].[res100]), on the basis of the distance, and

then find neighbours’ respective values in the fact

table, evaluate the value of the point to estimate

using these values, and then return an estimated

derived measure. Here is an example query that uses

the "InterpolatePoint" function:

Query 2: Select a field member’s value at

coordinates (721148 3140020) for the year 2012.

With member [Measures].[value] as'

InterpolatePoint(ST_GeomFromText("

POINT (721148 3140020)"))'

SELECT [Measures].[value]ON ROWS,

[time].[2012] ON COLUMNS

FROM [odorCube]

Note that generally MDX allows defining user-

defined functions in several programming languages

(i.e. Java, .NET, etc.) depending of the OLAP Server

used. In this work we have used a Java-based

implementation in GeoMondrian (see Sec. 5). In the

ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems

148

interpolation is done using an existing interpolation

Java API “javax.media.jai api” (JAI).

Figure 4: Classical star schema integrating regular grid of

points.

In this way we achieve the continuous view of

field data using incomplete fields as stated in

Section 2.

4.2 Multiresolution

Theoretically, we can measure a value of a field at

every position inside a geographic space. However,

not all resolutions are necessarily relevant. Indeed,

according to the type of analysis performed by the

user, a more or less detailed resolution can be

requested. The multiresolution is an approach that

consists in defining resolution levels likely to

improve the rendering of the requests made by the

user. To model an incomplete field at several

resolutions in a multi-dimensional model, we

propose two Approaches based on the “Classical

Star Schema”: The “field aggregation star-schema”

approach and the “field interpolation star schema”

approach.

4.2.1 Field Aggregation Star-schema

Approach

Based on the star schema model previously

described, we propose a logical schema where the

spatial dimension presents different field levels at

different resolutions (fig. 5-a). This model extends

the spatial dimension of figure 4

with 2 other levels

each representing a different level of resolution

(

[Field].[res200] and [Field].[res400]).

Each level of the field dimension is composed of an

identifier and a geometry representing a point.

The

fact table is associated, classically, to the most

detailed level of the field dimension.

In this way, decision-maker can explore

warehoused field data at different resolutions during

the same analysis MDX-based session. Only need to

change the level of resolution in the query to change

the level of details of the result. Using this approach,

we use in an MDX query, the appropriate level of

resolution of the field dimension as in the following

where the Query 1 becomes:

Query 3: Select average odor for each field member

at the 400*400 resolution during 2012.

SELECT [Field].[res400]. Members ON

ROWS, {[time].[2012]} ON COLUMNSFROM

[odorCube]

WHERE [Measures].[value]

4.2.2 Field Interpolation Star-schema

Approach

As stated in Section 2, in order to provide field data

at finer resolutions, spatial interpolation methods can

be used. Then, here we propose a variation of the

previously proposed schema for handling multiple

field resolution levels, by associating the fact table

to the field at less detailed resolution as shown on

figure 5-b. In our approach moving from fact table

values to finer spatial members’ values implies

applying spatial interpolation functions. Note that

this approach is possible only when dealing with

spatial data, because according to the Tobler law

geographical position of data can be used for

estimating missing values.

We have implemented a GeoMDX function in

the same way of the function defined in Section 4.1:

Numeric-type InterpolateBilinear (Field

Member)

However, this function, named "InterpolateBilinear"

is prepared to receive as input a field level member

instead of geometry and return an interpolated value

of this member. We can also see that in this case, the

neighbors of each member of a higher resolution

than the original one are also stored in the “Field”

(Neighbours2, Neighbours3), since members of each

resolution are pre-defined in advance, but their

values are not since they depend on other

dimensions.

Calling this function as follows:

InterpolateBilinear

([Field].[res400].CurrentMember) in the

formula of a derived measure, allows to find the

values of all the members of the level “res400”

(incomplete field at a 400*400 resolution) using

their neighbors “Neighbors3” . Thus, the query 3 can

be performed as follows:

SELECT

{[Field].[res400].Members} ON ROWS,

{[time].[2012]} ON COLUMNS

FROM [odorCube]

Where [Measures].[EstimatedValue]

ANewRelationalSpatialOLAPApproachforMulti-resolutionandSpatio-multidimensionalAnalysisofIncompleteField

Data

149

(a) (b)

Figure 5: (a) Field Aggregation Star Schema (FASS), (b) Field Interpolation Star Schema (FISS).

While in the multidimensional SOLAP schema,

the "InterpolateBilinear" function is called in the

“EstimatedValue” calculated measure formula as:

formula="InterpolateBilinear([Field].

[res400].CurrentMember)"

As we can see in the previous query, the call of the

calculated measure enables to find the values at a

given scale transparently to the decision maker as a

classical aggregation (SQL). This approach is

motivated by performance issues as described in the

next section.

5 EXPERIMENTATIONS

In this section we detail the performances of the two

approaches proposed in Section 4.2 (FASS and

FISS) in terms of storage and time computation.

The computer used for the following tests has the

following configuration: processor Intel® core ™ i3

2,20 GHz, RAM 4 Go, Operating system Windows 7

professional, System OS 64 bits.

In particular, spatial data is stored in PostGIS

Spatial DBMS. PostGIS is an open source software

that adds support for geographic objects to

the PostgreSQL object-relational database. PostGIS

follows the Simple Features for SQL specification

from the Open Geospatial Consortium (OGC); we

use GeoMondrian as a SOLAP server; and JPivot as

a client. GeoMondrian is an Open Source Spatial

Online Analytical Processing Server.

In order to test our proposal we define different

cases where the spatial dimension presents: one field

level at the 100*100 resolution; two levels at the

resolutions 100*100 and 200*200; and finally three

levels at the resolutions 100*100, 200*200 and

400*400. We also vary the size of the temporal

dimension in order to understand impact of the

spatial and non spatial dimension on performances.

Figure 6-a shows the size of the fact table

measured in function of the number of spatial and

temporal members (spatial finest resolution /

temporal finest granularity) using the two

approaches. We can easily see two important

differences: i) the field aggregation approach is

expensive in terms of storage than the field

interpolation one since the latter stores only facts

values at a less detailed spatial granularity, ii) in the

field interpolation approach the size of the fact table

only varies depending on the size of the non spatial

dimensions. Thus, even increasing the size of the

spatial dimension, the fact table does not change

since it contains only measures related to the first

level of resolution.

In order to evaluate computation performance we

execute the queries previously cited, where we

combine roll-up operation on non spatial

dimensions, and spatial slice operators over different

field resolutions.

Figure 6-b represents the execution time of the

query 3, which consists in generating values of the

members at different resolutions taking into account

different sizes of the time dimension. This figure

shows a certain degree of approximation in

execution time between the two approaches to a

certain level. Beyond this level, we note that the gap

widens considerably. Thus, minimizing storage and

relations has allowed the field interpolation

approach we propose to have better execution time

than the field aggregation approach at all resolution

levels (100*100, 200*200 and 400*400). Figure 9

shows that the execution time in the “field

approach” increases depending on the number of

spatial and temporal members, whereas in the “field

interpolation approach”, it increases mainly

ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems

150

(a) (b)

Figure 6: a) Fact table size with the field aggregation and the field interpolation approaches b) Execution time for Query 3

for the Field aggregation Star Schema and the Field Interpolation Star Schema approaches.

of temporal members. Indeed the size of the spatial

dimension does not influence much on performance, since

there is no relationship between the fact table and the

members who belong to high resolutions.

6 RELATED WORK

In order to integrate fields data in a SOLAP model,

(Ahmed and Miquel, 2005) propose a

multidimensional model for handling continuous

discrete fields, storing a sample of points as spatial

members, to create a discrete cube which is

interpolated in the client-side to simulate a

continuity. (McHugh, 2008) defines new types of

dimensions handling fields as a regular grid of

squares (raster): “hybrid dimension”, “mixed hybrid

dimension”, “mixed matrix dimension” and

“geometric matrix dimension”. She also defines the

“matrix cube” where facts are cells of the matrix

grid. The “field aggregation approach” presented in

section 4.2.1 is based on this work. However, the

“field interpolation approach” we propose, although

it gives the same result, it is more efficient in terms

of storage and execution time. (Gomez et al., 2012)

presents a discrete data model for representing

continuous fields and an algebra that makes use of

OLAP operators (e.g. Dice, Slice, Roll-up, Drill-

down …). However, the discrete model the authors

propose does not support the continuous aspect of

the field, which consists to retrieve a value for each

point with coordinates x and y in the map. In

(Gomez et al., 2010), the authors propose a

multidimensional model handling fields. They

define two types of fields, “field” and “tempfield”

(spatial field and temporal field), and semantics for

the operators associated to these data types. They

include the notion of field dimensions and field

measures. They define the “field dimension” as a

dimension containing at least one level that is a field

(temperature, precipitation…), the “field measure”

as a measure represented by a field and the “field

hierarchy” as a set of related field levels, which

allows a field to be seen at different levels of

granularity. They also propose a physical model for

data warehouses with continuous fields. However,

no implementation has been proposed and the

hierarchical relationship between field levels has not

been brought to light. (Bimonte and Myoung, 2011)

provide a multidimensional model that integrates

field data independently from their implementation,

as measures and dimensions. They also present a

formal representation of the spatio-multidimensional

model schema where they define the concepts of

field dimensions, field measures, and field views. To

our knowledge, no implementation including the

continuous appearance of incomplete field or the

multiresolution over incomplete fields has been

proposed.

Representation of multidimensional data under

different resolution levels or scales may be

considered as multirepresentation. (Bernier et al.,

2005) proposes an approach to provide on-Demand

multi-scale maps. Although this approach models

maps features at different scales by using spatial

hierarchies, but it does not contain measures. (Yvan

et al., 2002) defines a UML-based conceptual model

that integrates multiple geometric and semantic

representations properties of spatial levels. However,

this work does not present a complete

multidimensional model with facts and hierarchies.

Moreover, (Bédard et al., 2002) suggests

(without providing details) using a different spatial

data warehouse for each representation. Therefore,

changing the representation corresponds to move to

ANewRelationalSpatialOLAPApproachforMulti-resolutionandSpatio-multidimensionalAnalysisofIncompleteField

Data

151

another spatial data warehouse. (Gascueña and

Guadalupe 2009) propose a conceptual model with a

multi-representation of spatial members. They also

propose a physical schema, but any implementation

into a classical ROLAP architecture is presented.

Finally, (McGuire et al., 2008)define a snowflake

schema for an environmental application where

three dimensions represent the same spatial

members at different resolutions.

7 CONCLUSIONS AND FUTURE

WORK

In this paper we present a multidimensional model

for incomplete fields at several resolutions and its

implementation in a SOLAP architecture based on

standards (e.g. SQL and MDX). We are working on

using spatial data mining to speed-up map algebra

operations and implement a SOLAP visualization

client. We also work in integrating other

interpolation functions to generalize the proposed

approach.

ACKNOWLEDGEMENTS

The authors wish to thank the FEDER and the region

for funding this project and project partners who

provide us the data.

REFERENCES

Ahmed, T. O. and M. Miquel (2005). "Multidimensional

Structures Dedicated to Continuous Spatiotemporal

Phenomena." 01/2005; In proceeding of: Database:

Enterprise, Skills and Innovation, 22nd British

National Conference on Databases, BNCOD 22,

Sunderland, UK, July 5-7, 2005, Proceedings.

Bédard, Y., T. Merrett, et al. (2001). "Fundamentals of

Spatial Data Warehousing for Geographic Knowledge

Discovery." Data Mining and Knowledge Discovery

Bédard, Y., S. Rivest, et al. (2007). "Spatial On-Line

Analytical Processing (SOLAP): Concepts,

Architectures and Solutions from a Geomatics

Engineering Perspective." Data Warehouses and

OLAP: Concepts, Architectures and Solutions. IGI

Global, 2007. 298-319. Web. 23 Jan. 2013.

doi:10.4018/987-1-59904-364-7.ch013.

Bernier, E., Y. Bédard, et al. (2005). "UMapIT: An On-

Demand Web Mapping Tool Based On A Multiple

Representation Database." 8th ICA WORKSHOP on

Generalisation and Multiple Representation, A

Coruña, July 7-8th.

Bimonte, S. and K. Myoung (2011). "Towards a Model for

the Multidimensional Analysis of Field Data."

Advances in Databases and Information Systems

,Lecture Notes in Computer Science Volume 6295,

2011, pp 58-72.

Camossi, E., E. Bertino, et al. (2009). " Adaptive

Management of Multigranular Spatio-Temporal Object

Attributes." SSTD 2009: 320-337.

Gascueña, C. M. and R. Guadalupe (2009). "A

Multidimensional Methodology With Support For

Spatio-Temporal Multigranularity In The Conceptual

And Logical Phases." IGI Global.

Gomez, L., A. Vaisman, et al. (2010). "Physical Design

and Implementation of Spatial Data Warehouses

Supporting Continuous Fields." DaWaK'10

Proceedings of the 12th international conference on

Data warehousing and knowledge discovery, Pages

25-39.

Gomez, L. I., S. A. Gomez, et al. (2012). "A Generic Data

Model and Query Language for Spatiotemporal OLAP

Cube Analysis." EDBT '12 Proceedings of the 15th

International Conference on Extending Database

Technology, Pages 300-311 ACM New York, NY,

McGuire, M., A. Gangopadhyay, et al. (2008). "A user-

centered design for a spatial data warehouse for data

exploration in environmental research." Ecological

Informatics, Volume 3, Issues 4–5, Pages 273–285.

McHugh, R. (2008). "Intégration de la structure

matricielle dans les cubes spatiaux."

Mennis, J., R. Viger, et al. (2005). "Cubic Map Algebra

functions for spatio-temporal analysis." Cartography

and Geographic Information Systems.

Paolino, L., M. Sebillo, et al. (2010). "Integrating Discrete

and Continuous Data in an OpenGeospatial-Compliant

Specification." Transactions in GIS Volume 14, Issue

6, pages 731–753, December 2010.

Parent, C., S. spaccapietra, et al. (2006). "Conceptual

Modelling for Traditional and Spatio-temporal

Applications." 2006 XVIII, 465 p. 115 Illus.

Hardcover.

Yvan, B., M. J. Proulx, et al. (2002). "Modeling

multirepresentations into spatial data warehouses : A

UML-Based approach." Symposium on Geospatial

Theory, Processing and Applications, Ottawa.

O'Sullivan, D. and D. J. Unwin (2002). Geographic

Information Analysis - John Wiley & Sons, 15 nov.

2002 - 448 pages.

ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems

152