
A Library to Support the Development of Applications that Process Huge
Matrices in External Memory
Jaqueline A. Silveira, Salles V. G. Magalh
˜
aes, Marcus V. A. Andrade and Vinicius S. Conceic¸
˜
ao
Departamento de Inform
´
atica, Universidade Federal de Vic¸osa (UFV), Vic¸osa, Brazil
Keywords:
External Memory Processing, GIS, External Algorithms.
Abstract:
This paper presents a new library, named TiledMatrix, to support the development of applications that process
large matrices stored in external memory. The library is based on some strategies similar to cache memory
management and its basic purpose is to allow that an application, originally designed for internal memory
processing, can be easily adapted for external memory. It provides an interface for external memory access
that is similar to the traditional method to access a matrix. The TiledMatrix was implemented and tested in
some applications that require intensive matrix processing such as: computing the transposed matrix and the
computation of viewshed and flow accumulation on terrains represented by elevation matrix. These applica-
tions were implemented in two versions: one using TiledMatrix and another one using the Segment library that
is included in GRASS, an open source GIS. They were executed on many datasets with different sizes and,
according the tests, all applications ran faster using TiledMatrix than Segment. In average, they were 7 times
faster with TiledMatrix and, in some cases, more than 18 times faster. Notice that processing large matrices
(in external memory) can take hours and, thus, this improvement is very significant.
1 INTRODUCTION
Matrix processing is a central requirement for many
applications as image analysis, computer graphics ap-
plications, terrain modelling, etc. In many cases, the
matrix is huge and it can not be stored/processed in
internal memory requiring external processing. For
example, in terrain modeling, the recent technologi-
cal advances in data collection such as Light Detec-
tion and Ranging (LIDAR) and Interferometric Syn-
thetic Aperture Radar (IFSAR) have produced a huge
volume of data and most computers cannot store or
process this huge volume of data internally. Since
the time required to access and transfer data to and
from external memory is generally much larger than
internal processing time (Arge et al., 2001), external
memory algorithms must try to minimize the number
of I/O operations. That is, these algorithms should be
designed based on a computational model where the
cost is the number of data transfer operations instead
of CPU time. One of these models was proposed by
Aggarwal and Vitter (Aggarwal and Vitter, 1988).
In this context, some external memory libraries
such as LEDA-SM (Crauser and Mehlhorn, 1999),
Segment (GRASS, 2011) and STXXL (Dementiev
et al., 2005) have been developed to reduce and
optimize the access operations in external memory.
The STXXL and LEDA-SM libraries provide external
memory data structures such as vectors, queues, trees,
and basic funtions for searching and sorting. The Seg-
ment library, on the other hand, provides a data struc-
ture to store large matrices in external memory.
This work presents a new efficient library, named
TiledMatrix, to support the development of applica-
tions that process large matrices stored in external
memory. This library is based on the use of some spe-
cial data structures to manage hard disk accesses and,
thus, to reduce the number of I/O operations. The ba-
sic idea is to subdivide the matrix into blocks whose
size allows that some blocks can be stored in inter-
nal memory and these blocks are managed as a cache
memory. The proposed library was implemented and
tested in some applications as computing the matrix
transposition and the viewshed and flow accumulation
on huge terrains represented by digital elevation ma-
trix. As the tests showed, the applications can run
much faster using TiledMatrix than using the Segment
library. In average, the performance was 7 times bet-
ter and, in some cases, more than 18 times faster. It
is worth to notice that, processing large matrices (in
external memory) can take hours and, thus, this im-
provement is very significant.
153
A. Silveira J., V. G. Magalhães S., V. A. Andrade M. and S. Conceição V..
A Library to Support the Development of Applications that Process Huge Matrices in External Memory.
DOI: 10.5220/0004435001530160
In Proceedings of the 15th International Conference on Enterprise Information Systems (ICEIS-2013), pages 153-160
ISBN: 978-989-8565-59-4
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

2 RELATED WORK
In situations where an application needs to process
a huge volume of data that does not fit in internal
memory, the data transference between the internal
and external memories often becomes a bottleneck.
Thus, the algorithms for external memory should be
designed and analyzed considering a computational
model where the algorithm complexity is evaluated
based on I/O operations. A model commonly used
was proposed by Aggarwal and Vitter (Aggarwal and
Vitter, 1988) and it defines an I/O as the transfer-
ence of one disk block of size B between the exter-
nal and internal memories. The performance is eval-
uated considering the number of such I/Os and the
algorithm complexity is related to the number of I/Os
performed by fundamental operations such as scan-
ning or sorting N contiguous elements stored in exter-
nal memory where scan (N) = θ (N/B) and sort (N) =
θ (
N
B
log
M/B
N
B
) and M is the internal memory size.
Some libraries such as LEDA-SM (Crauser and
Mehlhorn, 1999), STXXL (Dementiev et al., 2005)
and Segment (GRASS, 2011) have been created to
support the implementation of external memory algo-
rithms.
LEDA-SM library was designed as an extension of
LEDA (Mehlhorn and N
¨
aher, 1995) library for han-
dling huge data sets. It provides implementations of
some I/O efficient algorithms as sorting and graph al-
gorithms and data structures such as external memory
stack, queue, heap and B
+
-tree.
STXXL is an open source library for handling large
data sets and it provides algorithms for data scanning,
sorting, merging, etc and several external memory
containers.
Segment is a library included in GRASS (an open
source GIS) (GRASS, 2011) which was developed for
handling large matrices in external memory. Basi-
cally, it subdivides the original matrix into small sub-
matrices (called segments) which are stored in exter-
nal memory and some of these segments are kept in
internal memory and managed as a cache memory.
It is important to notice that all libraries listed
above, except Segment, do not allow operations with
matrices in external memory. And, as described be-
low, although TiledMatrix has a similar purpose as
Segment, the former includes some additional features
that makes it more efficient than the latter (see exper-
imental results in section 4).
3 TiledMatrix LIBRARY
TiledMatrix was designed to support the development
of applications that require the manipulation of huge
matrices in external memory. And, as is known,
any application requiring external memory process-
ing should be designed focusing the I/O operations
reduction and, in general, this reduction is achieved
either by reordering the data considering the access
sequence (Arge et al., 2001; Fishman et al., 2009;
Haverkort et al., 2007) or by adapting the algorithm
to use a more efficient access pattern (Haverkort and
Janssen, 2012; Meyer and Zeh, 2012). In this con-
text, the TiledMatrix library was developed to allow
easy adaptation of algorithms originally designed for
internal memory to process huge matrices stored in
external memory. The idea is to make the matrix ac-
cesses transparent to the application, that is, matrix
acesses will be managed by TiledMatrix.
More specifically, a huge matrix is subdivided in
small rectangular blocks (tiles) whose size allows that
some blocks can be stored in internal memory in a
data structure named MemBlocks. Thus, when a given
matrix cell needs to be accessed, the block containing
that cell is loaded in MemBlocks and then, any further
access to cells in that block can be done efficiently.
Since it is not possible to store all blocks in inter-
nal memory, the MemBlocks structure is managed as
a cache memory adopting a replacement policy. The
library provides the following policies: LRU - Least
Recently Used (Guo and Solihin, 2006), FIFO - first
in first out (Grund and Reineke, 2009) and random
selection (Chandra et al., 2005).
The library was developed as general as possible
and it gives many options to the application developer.
It is possible to define the block size (that is, the num-
ber of rows and columns), the MemBlocks size and
also, it is possible to select the replacement policy.
The LRU policy was implemented using a timestamp
assigned to each block in memory. Thus, when a cell
in a block B is accessed, the B timestamp is updated to
be greater than the others and, therefore, when a block
needs to be evicted, the block with smallest timestamp
is chosen. In the FIFO policy it was used an array
to store the order in which the blocks were loaded.
Also, to reduce the writing operations, for each block
in memory is used a dirty flag to indicate if the block
needs to be written back to the disk when it is evicted.
Additionally, in order to reduce the number of I/O
operations during the block transference to/from the
disk, the library uses the LZ4 algorithm (Lz4, 2012)
for fast data compression. The idea is to compress
the block before writing it in the disk and decom-
press when it is loaded into the memory. As the tests
showed, this strategy makes the library more efficient
and, in many cases, the applications run two times
faster when compression is used. Figure 1 presents
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
154

Figure 1: Example of data structures used in TiledMatrix.
the data structures used by TiledMatrix library: in
this example, the external memory matrix was di-
vided in 16 square blocks and the MemBlocks array
is able to store 5 blocks; the replacement policy used
was the LRU. The matrix Position stores the posi-
tion where the corresponding matrix block is stored in
the MemBlocks array (the value −1 indicates that the
corresponding block is not loaded into the memory).
Then, if a cell in block (0,1) is accessed, the Position
matrix indicates the block is stored in the slot 2 of
MemBlocks and thus, that block does not need to be
(re)loaded into memory. On the other hand, suppos-
ing the MemBlocks is already full, if a cell in the block
(1,2) is accessed, that block needs to be loaded and,
in this case, a block stored in MemBlocks is evicted to
open room for the “new” block. According the Times-
tamp array, the block (2,3) has the smallest times-
tamp. Thus, it will be evicted; but, since its dirty
flag is set true, it is compressed, written to disk and
the corresponding cell in Position matrix is set to −1.
Next, the block (1,2) is loaded, decompressed, stored
in the slot 3 of MemBlocks and the Position matrix is
updated to indicate the block position in MemBlocks.
3.1 TiledMatrix versus Segment
It is important to mention that, although the Segment
library, included in GRASS (GRASS, 2011), is based
on similar concepts as TiledMatrix, in the implemen-
tation of TiledMatrix it was used some different strate-
gies that makes it more efficient than Segment.
Firstly, Segment does not use data compression to
reduce disk I/O. Also, Segment allows only the use
of LRU replacement policy but, in the two libraries,
this policy was implemented based on different meth-
ods for blocks marking. In Segment, the blocks are
marked with a timestamp which is updated as follows:
when a new block is accessed, its timestamp is set to
zero and all other blocks timestamp are incremented
by one; thus, if a block needs to be evicted, the block
with higher timestamp is selected. As one can see,
if there are n blocks in the memory, each step of the
block marking takes O(n) time. On the other hand,
in TiledMatrix, when a block is accessed, only that
block timestamp is increased; thus, the block having
the smallest timestamp is evicted. In this case, the
block marking requires a constant time.
Another important difference between TiledMa-
trix and Segment is the process to determine if a
block is already loaded in internal memory and, if
yes, where it is stored. In TiledMatrix, when a cell
in a block needs to be accessed, it is fast to determine
if the block is loaded in internal memory (and where it
is stored) since it just needs to access the correspond-
ing block position in the Position matrix. Thus, this
operation can be executed in constant time. But, in
Segment, it is necessary to sweep the array that stores
the blocks in internal memory to check (and access)
the block; To try to reduce this overhead, the library
keeps the position of the last block loaded. Again, in
the worst case, this operation requires linear time.
Therefore, in TiledMatrix, an access to a block
loaded in memory, in all cases, takes O(1) CPU time
while in Segment it can take O(n) CPU time. Notice
that this performance improvement in the block ac-
cess operation makes the TiledMatrix more efficient
than the Segment because the block access is a basic
operation which is executed many times.
4 EXPERIMENTAL TESTS
In order to evaluate the TiledMatrix performance,
some experimental tests were carried out to compare
TiledMatrix against the Segment library. The tests
were based on three applications that require inten-
sive matrix processing: computing the transposed ma-
trix and the computation of viewshed and flow accu-
mulation on terrains represented by elevation matrix.
For each application it was selected one algorithm
that was adapted for external memory processing, that
is, to process the matrix stored in disks. Thus, for
each algorithm was generated two versions: one us-
ing TiledMatrix to manage the access to matrix stored
in external memory and another one using Segment.
The algorithms used in the tests are described be-
low. They were implemented in C++, compiled us-
ing gcc 4.5.2 and the tests were executed in a Core i5
computer, 4GB of RAM memory, 1TB Sata Hard Disk
running Ubuntu Linux 12.10 64bits operating system.
In all applications the external memory libraries were
configured to use, at most, 3GB of RAM. The results
of these tests are presented in section 4.4.
4.1 Matrix Transposition
The algorithm for matrix transposition is based on the
trivial method where the input matrix is read sequen-
tially (row by row) from the disk and each cell (i,j)
is stored in the position (j,i) in a temporary matrix M
ALibrarytoSupporttheDevelopmentofApplicationsthatProcessHugeMatricesinExternalMemory
155

handled by the library TiledMatrix or Segment. Then,
the transposed matrix M is written to the disk.
4.2 Viewshed
Given a terrain T represented by an elevation ma-
trix, let O be a point in the space (the observer) from
where other terrain points (the targets) will be visu-
alized. Both observer and target can be at a given
height above the terrain. Usually, it is assumed that
the observer has a range of vision ρ, the radius of in-
terest, which means that the observer can see points
at a given distance ρ. Thus, a target T is visible from
O if and only if the distance of T from O is, at most,
ρ and the straight line from O to T is always strictly
above the terrain, that is, there is no point in this line
whose height is smaller or equal than the elevation of
the corresponding terrain point. See Figure 2.
Figure 2: Target’s visibility: T
2
is visible, but T
1
and T
3
are
not .
The viewshed of O corresponds to all terrain
points that can be seen by O; formally,
viewshed(O) =
{
p ∈ T | a target on p is visible from O
}
where the radius of interest ρ is left implicit. Since the
terrain is represented by raster DEMs, the viewshed
can be represented by a square (2ρ + 1) × (2ρ + 1)
matrix of bits where 1 indicates that the correspond-
ing point is visible and 0 is not. By definition, the
observer is in the center of this matrix.
Then, the visibility of a target on a cell c
t
can be
determined by checking the slope of the line connect-
ing the observer and the target and the cells’ elevation
on the rasterized segment. More precisely, suppose
the segment is composed by the cells c
0
,c
1
,··· ,c
t
where c
0
and c
t
are respectively the cells correspond-
ing to the observer and target projections. Let α
i
be
the slope of the line connecting the observer to the cell
c
i
, that is, α
i
=
ζ(c
i
)−(ζ(c
0
)+h
o
)
dist(c
0
,c
i
)
where ζ(c
0
) and ζ(c
i
)
are, respectively, the elevation of the cells c
0
and c
i
and dist(c
0
,c
i
) is the “distance” (the number of cells)
between these two cells. Thus, the target on c
t
is visi-
ble if and only if the slope
ζ(c
t
)+h
t
−(ζ(c
0
)+h
o
)
dist(c
0
,c
p
)
is greater
than α
i
for all 0 < i < t. If yes, the corresponding cell
in the viewshed matrix is set to 1; otherwise, to 0.
Notice that the viewshed computation demands an
intensive matrix processing and, for terrains whose
matrix does not fit in internal memory, it is neces-
sary a very large number of external memory accesses
since the matrix is accessed non-sequentially.
There are many methods for viewshed computa-
tion (Franklin and Ray, 1994; Haverkort et al., 2007)
and, in particular, (Franklin and Ray, 1994) proposed
a linear time method where the visibility is computed
along a ray (segment) connecting the observer O to
the center of a cell in the boundary of a square of side
2R + 1 centered at O. Thus, this ray is counterclock-
wise rotated around the observer following the cells
in that boundary (see Figure 3).
Figure 3: Sweeping the terrain.
This algorithm can be easily adapted for external
memory processing using either the library TiledMa-
trix or Segment. The basic idea is, when a matrix cell
needs to be accessed, this access is managed by one
of these libraries as previously described.
4.3 Flow Accumulation
Another important group of applications requiring
intensive matrix processing is the drainage network
computation on terrains. Informally, the drainage net-
work of a terrain delineates the path that water flows
through the terrain (the flow direction) and the amount
of water that flows into each terrain cell (the flow ac-
cumulation). In other words, the flow direction con-
sists in assigning directions to terrain cells such that
these directions predict the path taken by an overland
flow running in the terrain (Tarboton, 1997). The flow
direction in a cell c can be defined as the direction of
the lowest neighbor cell whose elevation is lower than
the elevation of c. Additionally, the flow accumula-
tion of a cell c is the number of other cells whose flow
achieves c (informally, the flow accumulation means
the amount of flow running through each cell) sup-
posing that each cell receives a rain drop. Figure 4
shows an example of a flow direction matrix and the
flow accumulation matrix computed from it.
It is important to notice that the flow direction
computation needs to include some steps to treat de-
pressions and flat areas on the terrains and, in general,
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
156

Figure 4: Drainage network computation: (a) flow direc-
tion; (b) flow accumulation.
these steps are not very simple and use some com-
plex data structures. Thus, the adaptation of flow di-
rection algorithms for external processing is not very
easy since it is necessary to make some modifications
in the algorithm implementation. Therefore, in the
tests, we decided to use only a flow accumulation al-
gorithm because it could be easily adapted for extenal
processing using TiledMatrix or Segment.
In this case, given the flow direction matrix com-
puted by using the algorithm RWFlood (Magalh
˜
aes
et al., 2012), which is based on graph topological sort-
ing where the idea is to process the flow direction as
a graph where each matrix cell is a vertex and there
is a directed edge connecting a cell c
1
to a cell c
2
if
and only if c
1
flows to c
2
. Initially, all vertices in the
graph have 1 unit of flow. Then, in each step, a cell c
with in-degree 0 is set as visited and its flow is added
to next(c) flow where next(c) is the cell following c
in the graph. After processing c, the edge connect-
ing c to next(c) is removed (i.e., next(c)’s in-degree is
decremented) and if the in-degree of next(c) becomes
0, next(c) is also similarly processed. More precisely,
for the tests, we adapted the algorithm presented by
Haverkort and Janssen (Haverkort and Janssen, 2012)
to use TiledMatrix and Segment.
4.4 Performance Evaluation
As stated before, the TiledMatrix was evaluated com-
paring the execution time of the three applications us-
ing two libraries: TiledMatrix and Segment. Also,
to evaluate the impact of block compression for the
TiledMatrix performance, we used two versions of
this library: one including compression and another
one does not. In all cases, the libraries TiledMatrix
and Segment were configured to use LRU as the re-
placement policy and the block size was set as fol-
lowing: for matrix transposition and viewshed, it was
used square blocks with 1000 x 1000 cells and in flow
accumulation, blocks 250 x 250 cells.
The matrices used in the tests were obtained from
SRTM website and they represent 30 meters resolu-
tion terrains corresponding to regions from the United
States of America. For the matrix transposition, we
used different matrix sizes from a same region and,
since the processing time for computing the viewshed
and the flow accumulation depends on terrain topog-
raphy, in these two cases, we used different terrain
sizes from two different regions: one corresponding
to a very hilly terrain and the other, to a smoother
one. More precisely, in the flow accumulation, the in-
put are the flow direction matrices computed by using
the algorithm RWFlood (Magalh
˜
aes et al., 2012) us-
ing these terrain datasets. And, in the viewshed com-
putation it was used a radius of interest covering the
whole terrain and the observer was positioned 50 me-
ters above the terrain.
Notice that, although an input matrix can fit in in-
ternal memory, maybe the processing algorithm can
not be executed internally because it needs to use
some additional data structures. Thus, considering
that the terrain matrices are represented using 2 bytes
per cell, a terrain dataset with N cells requires 2N
bytes. In the tests, the matrix transposition algorithm
uses only one matrix (with 2N bytes) to store the input
data. On the other hand, the viewshed algorithm uses
two matrices: the (input) terrain matrix with 2N bytes
and the (output) viewshed matrix with N bytes (one
byte per cell), thus requiring 3N bytes in total. And,
finally, the flow accumulation algorithm uses 3 ma-
trices: the input flow direction matrix (N bytes), the
indegree matrix (N bytes) and the accumulated flow
matrix (4N bytes) requiring 6N bytes in total.
The tests results are presented in the Tables 1 and
2 and also, in the graphs in the Figures 6 and 5. Ac-
cording the results, all applications ran faster using
TiledMatrix than Segment and, in general, they were
7 times faster with TiledMatrix. But, in some cases,
the TiledMatrix can make the application more than
18 times faster (for example, flow accumulation on
3.4 GB terrains). This performance increase can be
explained by two reasons: the data transference is re-
duced because of block compression and the use of
more efficient strategies for block management.
Another interesting observation is the speedup
achieved when the compression was used in Tiled-
Matrix. In all cases, the application performance us-
ing TiledMatrix was better when compression was en-
abled than when it was not. In average, the compres-
sion usage improved the application performance in
50% and, in some situations, this performance im-
provement was almost 200%.
4.5 Computing the Block Size
The performance of an external memory algorithm
is affected by some elements as: the internal mem-
ory size, the block size and shape (number of cells in
rows and columns). Ideally, the best case for an exter-
ALibrarytoSupporttheDevelopmentofApplicationsthatProcessHugeMatricesinExternalMemory
157
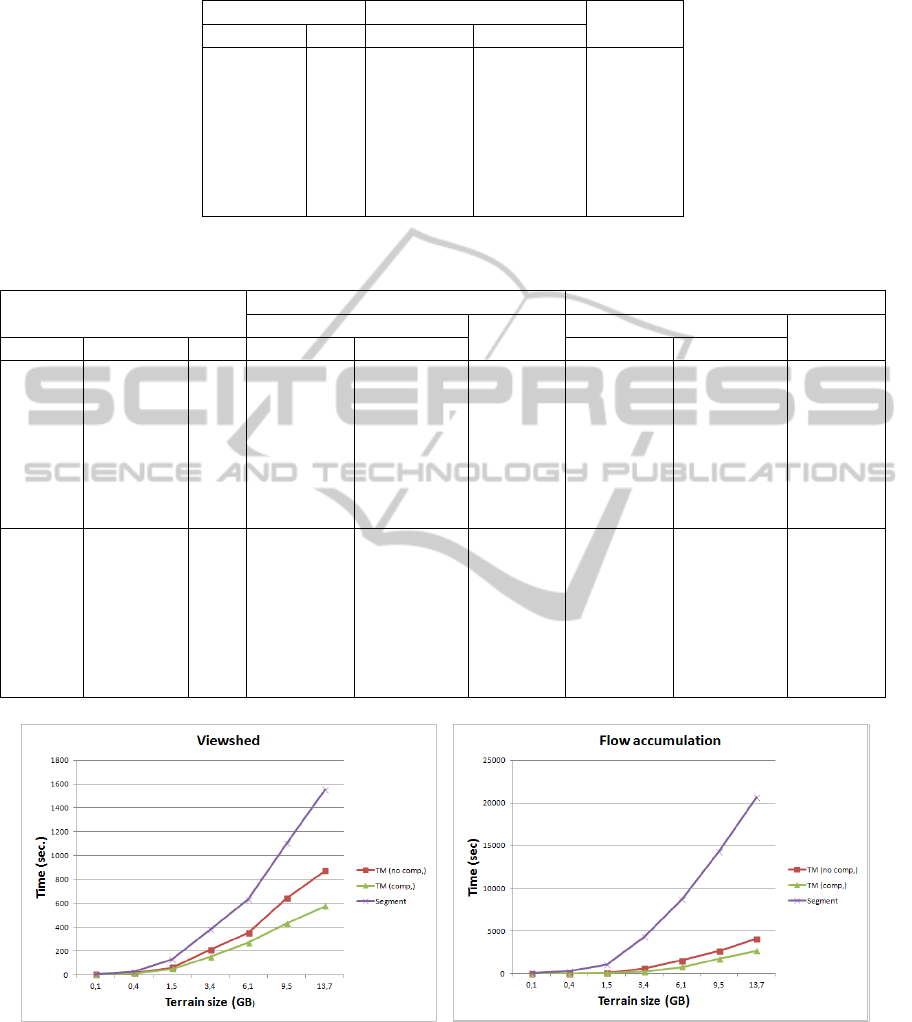
Table 1: Time (in seconds) to transpose a matrix using TiledMatrix (with and without compression) and Segment libraries.
Matrix Size TiledMatrix
row × col GB w/o comp. with comp. Segment
5000
2
0.1 1.34 1.08 2.97
10000
2
0.4 5.47 4.09 11.59
20000
2
1.5 25.49 18.49 62.97
30000
2
3.4 92.18 79.28 251.51
40000
2
6.1 234.32 178.67 486.35
50000
2
9.5 365.38 249.72 800.42
60000
2
13.7 507.63 335.39 1246.18
Table 2: Time (in seconds) to compute viewshed a terrain using TiledMatrix (with and without compression) and Segment
libraries.
Viewshed flow accumulation
Terrain TiledMatrix TiledMatrix
Dataset row × col GB w/o comp. with comp. Segment w/o comp. with comp. Segment
5000
2
0.1 3.69 3.15 6.33 7.10 3.86 65.25
10000
2
0.4 14.24 12.35 26.96 26.79 15.29 277.75
20000
2
1.5 58.50 49.49 115.66 119.7 65.26 1038.15
1 30000
2
3.4 182.76 147.16 344.24 612.11 242.78 4336.54
40000
2
6.1 365.82 278.45 648.47 1685.65 938.57 8542.93
50000
2
9.5 591.41 426.39 1036.57 2927.60 1927.28 14640.51
60000
2
13.7 906.19 609.76 1568.51 4736.27 3243.15 22977.13
5000
2
0.1 3.90 3.19 7.03 6.82 3.89 65.03
10000
2
0.4 15.08 12.65 28.76 26.10 15.07 276.51
20000
2
1.5 61.21 51.46 132.81 113.60 64.98 1032.23
2 30000
2
3.4 211.85 151.56 378.65 642.27 237.24 4305.04
40000
2
6.1 352.41 270.04 631.750 1557.33 798.03 8703.05
50000
2
9.5 643.91 434.58 1106.22 2624.07 1713.16 14299.41
60000
2
13.7 872.69 575.72 1552.40 4056.73 2663.41 20625.91
(a) (b)
Figure 5: Running time charts for (a) viewshed and (b) flow accumulation computation considering different terrain sizes
from Dataset 2.
nal memory algorithm would be to have any block al-
ready loaded in internal memory when one of its cells
is accessed and a block should be evicted only when
it is no longer needed. But, usually, it is not very easy
to achieve this case when the algorithm has to process
data sets that are too large to fit into internal memory.
Also, when the library needs to store (load) a
block to (from) the disk, it is necessary to perform a
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
158

Figure 6: Running time chart for the matrix transposition
considering different terrain sizes (in number of cells).
seek operation to reach the block position in the disk
and, then, transfer it to (from) the disk. The seek op-
eration cost can be amortized using larger block size,
that is, the larger the block size, the smaller the signif-
icance of seek operation cost for the data transference.
On the other hand, larger blocks size usually increases
the cache miss penalty since the time needed to store
(load) a large block to (from) the disk is greater.
Thus, in order to achieve a good efficiency when
using TiledMatrix, the block size needs to be defined
to try to reduce the number of times a same block
is evicted and reloaded while achieving a high disk
transfer rate. And, it is important to notice that this
definition depends on the application because it needs
to be done, mainly, based on the access pattern used
by the application. To illustrate how the block size
can be defined based on the application analysis, let
us describe the block size definition for the three ap-
plication used in the tests.
In the matrix transposition algorithm, the matrix
is sequentially accessed row by row, thus the block
size should be defined such that it should be possible
to store, in internal memory, as many blocks as nec-
essary to cover a whole row. Therefore, since in the
tests the memory size available is 3GB, we defined a
block with 1000 × 1000 cells.
In the viewshed computation, the block size was
defined based on the Franklin and Ray algorithm ac-
cess pattern. More precisely, as it was showed in
(Ferreira et al., 2012), if the internal memory can store
2
ρ
ω
+ 2
blocks where ρ is the radius of interest and
the block size is ω × ω cells then when a block is
evicted by LRU policy, it will no longer be needed.
Thus, as the memory size is 3GB, we defined blocks
with 1000×1000 cells to allow that the required num-
ber of blocks can be stored in internal memory.
Finally, in the flow accumulation problem, the
block size definition is a little more complex since
Figure 7: Computing the flow accumulation in a 18 × 18
matrix (divided in blocks with 3 × 3 cells). The chain of
cells detached with a dotted line is processed when cell c is
visited by the row-major access.
there is not a specific access pattern because the topo-
logical sorting is based on the flow direction which
can be very different for each terrain. Notice that the
algorithm used for the topological sorting accesses the
matrix in two ways: mainly, the matrix is accessed
using a row-major order and, occasionally, the access
sequence follows a chain of cells whose input degree
is 1. Figure 7 illustrates these accesses: initially, the
matrix is processed in row-major order (and all blocks
intercepting the first row are loaded in the memory)
and when the cell c is processed, since its in-degree is
0, the access sequence needs to follow its flow direc-
tion because its neighbor in-degree also becomes 0.
This process is repeated for all cells indicated using
a dark gray which requires that 8 blocks are accessed
(loaded). After processing this chain, the row-major
access sequence is restored in cell d.
Notice that when a chain of cells with in-degree
0 is followed, the access sequence could need several
blocks loading and this process could force a block
eviction that will be accessed again soon. For exam-
ple, in the Figure 7, the block containing cell d was
loaded during the processing of the first row and it
will be accessed again after processing the referred
chain. Thus, if the processing forces the d’s block to
be evicted, this block will be reloaded to process d.
Therefore, in the flow accumulation, we used a
small block in order to increase the amount of blocks
that can be stored internally. According empirical ex-
periments, a good block size for the this problem is
250 × 250 cells, since bigger sizes led to many block
swaps operations and smaller sizes led to very low
disk transfer rate.
5 CONCLUSIONS AND FUTURE
WORKS
We presented a new library, named TiledMatrix, to
ALibrarytoSupporttheDevelopmentofApplicationsthatProcessHugeMatricesinExternalMemory
159

support the development of applications that process
large matrices stored in external memory. This library
uses some special data structures and cache memory
management algorithms to reduce the number of I/Os.
The basic purpose is to allow that an application orig-
inally designed for internal memory processing can
be easily adapted for external memory. The library
provides an interface for external memory access that
is similar to the traditional internal matrices access.
An interesting strategy included in this library was the
use of data compression to reduce the transference be-
tween the internal and external memories.
The TiledMatrix was implemented and tested in
some applications that require intensive matrix pro-
cessing such as: computing the transposed matrix and
the computation of viewshed and flow accumulation
on terrains represented by elevation matrix. These ap-
plication were implemented in two versions: one us-
ing TiledMatrix and another one using the Segment li-
brary. They were executed on many datasets with dif-
ferent sizes and, according these tests, all applications
ran faster using TiledMatrix than Segment. In aver-
age, they were 7 times faster with TiledMatrix and, in
some cases, more than 18 times faster. Also, the tests
showed that the compression usage improved the ap-
plication performance in 50% and, in some situations,
this performance improvement was almost 200%.
The TiledMatrix source code is available in
www.dpi.ufv.br/˜marcus/TiledMatrix
As a future work, we intend to evaluate the Tiled-
Matrix in some other applications and to develop
strategies to define the block size according to the al-
gorithm memory access pattern and the memory size.
ACKNOWLEDGEMENTS
This research was supported by CNPq, CAPES,
FAPEMIG and Gapso.
REFERENCES
Aggarwal, A. and Vitter, J. S. (1988). The input/output
complexity of sorting and related problems. Commun.
ACM, 31(9):1116–1127.
Arge, L., Toma, L., and Vitter, J. S. (2001). I/o-efficient
algorithms for problems on grid-based terrains. J. Exp.
Algorithmics, 6.
Chandra, D., Guo, F., Kim, S., and Solihin, Y. (2005). Pre-
dicting inter-thread cache contention on a chip multi-
processor architecture. In Proceedings of the HPCA
’05, pages 340–351, Washington, DC, USA. IEEE
Computer Society.
Crauser, A. and Mehlhorn, K. (1999). Leda-sm : Extending
leda to secondary memory. In Vitter, J. S. and Zaro-
liagis, C. D., editors, Algorithm engineering (WAE-
99) : 3rd International Workshop, WAE’99, volume
1668 of Lecture Notes in Computer Science, pages
228–242, London, UK. Springer.
Dementiev, R., Kettner, L., and Sanders, P. (2005).
Stxxl : Standard template library for xxl data sets.
http://stxxl.sourceforge.net/. Acessed July 15, 2012.
Ferreira, C. R., Magalh
˜
aes, S. V. G., Andrade, M. V. A.,
Franklin, W. R., and Pompermayer, A. M. (2012).
More efficient terrain viewshed computation on mas-
sive datasets using external memory. In ACM SIGSPA-
TIAL GIS 2012, Redondo Beach, CA.
Fishman, J., Haverkort, H. J., and Toma, L. (2009). Im-
proved visibility computation on massive grid terrains.
In Wolfson, O., Agrawal, D., and Lu, C.-T., editors,
GIS, pages 121–130. ACM.
Franklin, W. R. and Ray, C. (1994). Higher isn
´
t neces-
sarily better – visibility algorithms and experiments.
6th Symposium on Spatial Data Handling, Edinburgh,
Scotland.
GRASS, D. T. (2011). Geographic resources anal-
ysis support system (GRASS GIS) software.
http://grass.osgeo.org. Accessed July 15, 2012.
Grund, D. and Reineke, J. (2009). Abstract interpretation
of FIFO replacement. In Palsberg, J. and Su, Z., ed-
itors, Static Analysis, 16th International Symposium,
SAS 2009, volume 5673 of LNCS, pages 120–136.
Springer.
Guo, F. and Solihin, Y. (2006). An analytical model for
cache replacement policy performance. pages 228–
239. SIGMETRICS Perform.Eval. Rev.
Haverkort, H., ], L., and Zhuang, Y. (2007). Computing vis-
ibility on terrains in external memory. In Proceedings
of the Ninth ALENEX/ANALCO.
Haverkort, H. and Janssen, J. (2012). Simple i/o-efficient
flow accumulation on grid terrains. CoRR - Compting
Research Repository, abs/1211.1857.
Lz4 (2012). Extremely fast compression algorithm.
http://code.google.com/p/lz4/. Accessed June 1, 2012.
Magalh
˜
aes, S. V. G., Andrade, M. V. A., Franklin, W. R.,
and Pena, G. C. (2012). A new method for comput-
ing the drainage network based on raising the level
of an ocean surrounding the terrain. 15th AGILE In-
ternational Conference on Geographical Information
Science, pages 391–407.
Mehlhorn, K. and N
¨
aher, S. (1995). Leda: a platform for
combinatorial and geometric computing. Commun.
ACM, 38(1):96–102.
Meyer, U. and Zeh, N. (2012). I/o-efficient shortest
path algorithms for undirected graphs with random or
bounded edge lengths. ACM Transactions on Algo-
rithms, 8(3):22.
Tarboton, D. (1997). A new method for the determination
of flow directions and contributing areas in grid digital
elevation models. Water Resources Research, 33:309–
319.
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
160
