Online Dynamic Smooth Path Planning for an Articulated Vehicle

Thaker Nayl, George Nikolakopoulos and Thomas Gustafsson

Control Engineering Group Department of Computer Science, Electrical and Space Engineering,

Lule˚a University of Technology, Lule˚a, Sweden

Keywords:

Articulated Vehicle, Path Planning, Obstacle Avoidance.

Abstract:

This article proposes a novel online dynamic smooth path planning scheme based on a bug like modiﬁed

path planning algorithm for an articulated vehicle under limited and sensory reconstructed surrounding static

environment. In the general case, collision avoidance techniques can be performed by altering the articu-

lated steering angle to drive the front and rear parts of the articulated vehicle away from the obstacles. In

the presented approach factors such as the real dynamics of the articulated vehicle, the initial and the goal

conﬁguration (displacement and orientation), minimum and total travel distance between the current and the

goal points, and the geometry of the operational space are taken under consideration to calculate the update on

the future way points for the articulated vehicle. In the sequel the produced path planning is being online and

iteratively smoothen by the utilization of Bezier lines before producing the necessary rate of change for the

vehicle’s articulated angle. The efﬁciency of the proposed scheme is being evaluated by multiple simulation

studies.

1 INTRODUCTION

Recently, there have been signiﬁcant advances in

designing automated articulated vehicles mainly for

their utilization in the mining industry, where the aim

has been the overall increase of the production, while

making the working conditions for the human opera-

tors safer (Scheding et al., 1999). In most of the cases,

these vehicles are remotely operated, while there is

a continuous trend for increasing the autonomy lev-

els, especially in the area of path planning and obsta-

cle avoidance as the vehicles need: a) to perceive the

changing environment, based on the onboard sensory

systems and b) autonomously plan their route towards

the ﬁnal objective (Roberts et al., 2000).

For the classical task of path planning, with an

obstacle detection and avoidance capability, the sim-

plest technique to solve the problem is the altering of

the vehicle’s orientation, while predicting a non colli-

sion path, based on the vehicle’s kinematic model, the

sensing range and the safety range. In this approach a

ﬁnite optimal sequence of control inputs, according to

the initial vehicle position and the desired goal point

is being generated, which is able to take under consid-

eration positioning and measuring uncertainties, such

that the collision with any obstacle at a given future

time never occurs.

From another point of view, path planning can be

divided in two main categories according to the as-

sumptions of: a) global approaches where it is being

assumed that the map is a priori available, and b) a

partially known and reconstructed surrounding envi-

ronment based on reactive approaches, which utilizes

sensors like infrared, ultrasonic and local cameras.

Characteristic examples of the ﬁrst case are the Road–

Map algorithm (Nilsson, 1969), the Cell Decomposi-

tion (Chazelle, 1987), the Voronoi diagrams (Guechi

et al., 2008), the Occupancy Grinds (Usher, 2006)

and the new Potential Fields techniques (Ge and Cui,

2000), while in most of the cases, a ﬁnal step of

smoothing the produced path curvatures, by the uti-

lization of Bezier curves is being utilized (

Skrjanc and

Klanˇcar, 2010).

For the second case of a partially known and on-

line reconstructed environment, the Bug family al-

gorithms are well known mobile vehicle navigation

methods for local path planning based on a minimum

set of sensors and with a decreased complexityfor on-

line implementation (Ng and Br¨aunl, 2007). One of

the most commonly utilized path planning algorithm

in this category is the Bug1 and Bug2 (Lumelsky and

Stepanov, 1986). Bug1 algorithm exhibits two behav-

iors; motion to goal with boundary following and a

corresponding hit point and leave point, while Bug2

algorithm presents similar behaviors like the Bug1 al-

gorithm, except from the fact that it tries to follow

177

Nayl T., Nikolakopoulos G. and Gustafsson T..

Online Dynamic Smooth Path Planning for an Articulated Vehicle.

DOI: 10.5220/0004438301770183

In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2013), pages 177-183

ISBN: 978-989-8565-71-6

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

the ﬁxed line from a start point to the goal, during

obstacle avoidance. Other Bug algorithms that also

incorporate range sensors are TangentBug (Kamon

et al., 1998), DistBug (Kamon and Rivlin, 1997) and

VisBug (Lumelsky and Skewis, 1990). Tangent Bug

algorithm is an improvement of the Bug2 algorithm

since it is able to determine the shorter path to the

goal using a range sensor with a 360

inﬁnite orien-

tation resolution. DistBug has a guaranteed conver-

gence and will ﬁnd a path if one exists, while it re-

quires the perception of its own position, the goal po-

sition and the range sensory data (Buniyamin et al.,

2011). The VisBug algorithm, needs global informa-

tion to update the value of the minimum distance to

the goal point, during the boundary following and for

determining the completion of a loop during the con-

vergence to the goal. In all the presented path plan-

ning algorithms, the vehicle is being modeled as a

point within the world space, without any constraint

in the movements, while the actual kinematics of the

vehicle, which is important especially in the case of

non–holonomic vehicles are being neglected.

The novelty of this article stems from the proposal

of a new bug like path planning algorithm based on

the dynamic model of an articulated vehicle, which is

able to consider: a) the physical constraints of the ve-

hicle, b) proper obstacle detection and avoidance, and

c) smooth path generation based on an online Bezier

lines processing of the produced way points. In the

presented approach the solution to the path planning

problem is generated online, based on partial and on-

line sensory information of the vehicle’s surrounding

environment, while the path is being calculated by

solving the inverse kinematic problem of the articu-

lated vehicle or by calculating the optimal articulation

angle. Moreover, as in the case of all the exploration

and ﬁnal goal seeking algorithms, it is assumed that

the vehicle is constantly aware of the ﬁnal goal co-

ordinates. During the convergence to this goal and

based on the limited range sensing of the surrounding

environment, the vehicle is able to detect and avoid

obstacles, while continue converging to the optimum

goal. This approach is providing an online and sub

optimal solution, when compared with the global path

planning techniques, and it can be directly applied to

the case of articulated vehicles. As it has been applied

in the previous path planning algorithms for the case

of a priori known space conﬁguration, in the proposed

scheme, the Bezier curves are being also utilized for

ﬁltering the produced way points and thus guarantee

for an online smooth path planning due to the Bezier’s

line property of continuous higher-order derivatives.

The rest of the article is organized as it follows.

In Section 2 the model of the articulated vehicle and

the corresponding state space equations will be pre-

sented. In Section 3 the proposed novel scheme for

smooth path planning and obstacle avoidance based

on the articulated vehicle’s dynamics will be intro-

duced, while in Section 4 multiple simulation results

will be depicted that prove the efﬁcacy of the path

planning scheme in different test cases. Finally, the

concluding remarks are provided in Section 5.

2 ARTICULATED VEHICLE

MODEL

An articulated vehicle is constructed by two parts,

a front and a rear, linked with a rigid free joint,

while each body has a single axle and the wheels are

all non–steerable, with the steering action to be per-

formed on the joint, by changing the corresponding

articulated angle γ between the front and the rear of

the vehicle (Nayl et al., 2011) as it being also pre-

sented in Figure 1.

P2=(X2,Y2)

Ө1

Ө2

P1=(

Figure 1: Articulated vehicle’s geometry.

The main assumptions to derive the kinematic

model of the articulated vehicle are: a) the steering

angle γ remains constant under small displacement,

b) dynamical effects due to low speed, like tire char-

acteristic, friction, load and breaking force are being

neglected, c) it’s assumed that the vehicle moves on a

plane without slipping effects, during low-level con-

trol, the vehicle’s velocities are bounded within the

maximum allowed velocities, which prevents the ve-

hicle from slipping, and c) each axle is composed of

two wheels and when replaced by a unique wheel, can

get:

= V

cos θ

(1)

= V

sin θ

(2)

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

178

The steering angle γ is being deﬁned as the difference

between the orientation angles of the front θ

and the

rear parts θ

of the vehicle.

The velocity V

at the front andV

at the rear parts

have the same changing with respect to the velocity at

the rigid free joint of the vehicle, and it can be deﬁned

by the relative velocity vector equations as it follows:

= V

cos γ+

sinγ (3)

sinγ =

cos γ (4)

where

and l

, l

are the angular velocities and

the lengths of the front and rear parts of the vehicle

respectively. By combining these equations it yields:

sinγ+ l

cosγ+ l

(5)

while the angles γ and θ

can be measured with a

great accuracy. For the case that there is a steering

limitation for driving the rear part, according to the

coordinates of the point P

= (X

), the geometrical

relationship between P

and P

is provided by:

= X

− l

cosθ

− l

cosθ

(6)

= Y

− l

sinθ

− l

sinθ

(7)

The realistic dynamic motion behavior of the articu-

lated vehicle with initial parameters [X

], is

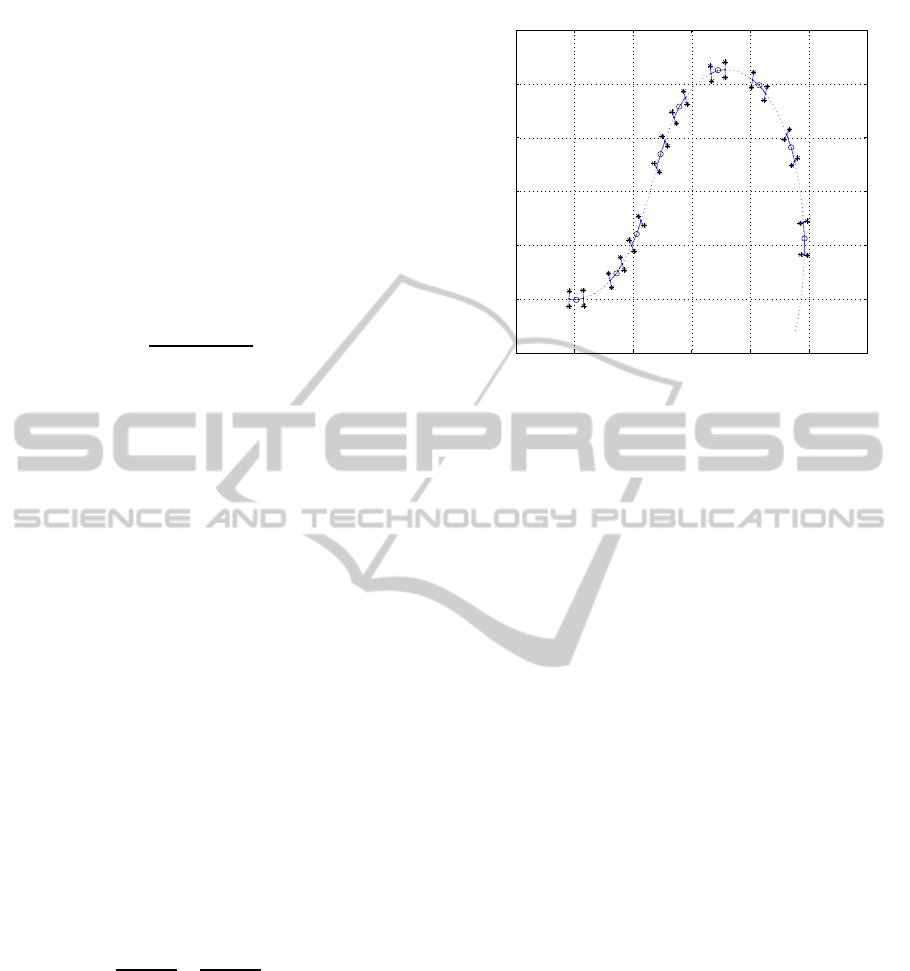
depicted in Figure 2, where the vehicle is requested to

reach the goal destination with a speciﬁc orientation.

As it can be observed, when the dynamics of the vehi-

cle are being incorporated the motion and the overall

behavior of the vehicle signiﬁcantly deviates from the

case where the vehicle is being considered of having

the dynamics of an unconstraint point and this is one

of the major contributions of this article.

The state parameters of the articulated vehicle are;

X = [X Y θ γ]

and the manipulated variables are u =

γ]

, while the kinematic model of the articulated

vehicle, in a state space formulation can be written as

it follows:



















cosθ 0

sinθ 0

sinγ

cosγ+l

0 1











(8)

where

is the rate of change for the articulated an-

gle.

3 ON LINE SMOOTH PATH

PLANNING FOR AN

ARTICULATED VEHICLE

The introduced path planning algorithm can be ap-

plied for the objective of moving a vehicle from a

−5 0 5 10 15 20 25

−2

X (m)

Y (m)

Start point

Reference path

Figure 2: Realistic dynamic motion behavior of the articu-

lated vehicle starting at [0 0 0 − 10

] with V = 1m/s and

γ = 0

for the ﬁrst 5sec of movement, while

γ = 3.5

for

the next 6 sec to reach the goal point at [20 2]. The vehicle

dimensions are l

= l

= 0.6m and W = 0.58m.

starting point to the goal point, while detecting and

avoiding identiﬁed obstacles based on the real vehi-

cles dynamic equations of motion. As a common

property of the Bug like algorithms, the proposed

scheme initially faces the vehicle towards the goal

point, which it is being assumed to be a priori known.

In the proposed path planning module it is also be-

ing assumed that the vehicle is able to online sense

the surrounding environment based on the available

sensory systems. The proposed scheme is able to

replan the produced path, by generating new way

points, after the identiﬁcation of an obstacle and pro-

duce proper path deformations that need to be done

for avoiding it. In all these cases the produced set

of new way points are utilized as control points for

a Bezier curve algorithm for online smoothing of the

suggested path. The overall proposed concept of the

novel path planning algorithm is being presented in

the following Figure 3.

As it can be observed from this diagram the algo-

rithm starts by deﬁning the current position and orien-

tation of the vehicle, denoted by [X

, Y

, θ

] and the

ﬁnal goal position denoted by [X

, Y

, θ

]. Based on

the onboard sensory system, the vehicle identiﬁes the

surrounding environment and obstacles and generates

the way points for reaching the goal destination. In

the sequel the way points are been smoothen by the

utilization of Bezier ﬁltering, while as a last step and

based on the vehicles dynamics, an open loop control

signal (articulated angle) is being generated to guide

the vehicle. In the presented approach it is also as-

sumed that the system is fully observable and good

and timely available measurements can be provided

OnlineDynamicSmoothPathPlanningforanArticulatedVehicle

179

Path

Planning

Obstacle

Avoidance

Algorithm

Smooth

Path

and Control

commands

Articulated

Vehicle

Range

Sensor

Initialization

Vehicle and

Target

Information

[dobs, Ɵobs]

Noise

[Xr Yr Ɵr]

[Xt Yt]

Current States [ΔX, ΔY, ΔƟ]

Figure 3: Block diagram of the proposed path planning al-

gorithm based on the nonlinear articulated kinematic model.

for the displacement and orientation of the vehicle.

The assumed sensory system is able to detect the

obstacles and the surrounding environment, measure

the distance of the articulated robot from the obsta-

cle d

obs

∈ ℜ, while a sensing radius θ

obs

∈ ℜ is being

considered, reﬂecting real life sensing limitations. In

the presented approach all the obstacles and the sur-

rounding environment are being considered as point

clouds in a 2-dimensional space, while the overlap-

ping obstacles are being clustered and represented by

a single and uniﬁed obstacle.

Modefied path

Goal point

dobs

Өg

Өk

Өobs

min

Figure 4: Notations and overall concept of the proposed

path planning algorithm.

The overall ﬂowchart diagram for path planning

and obstacle avoidance for the case of an articulated

vehicle is being depicted in Figure 5, while is can be

summarized as it follows:

[Step 1: Initialization] Deﬁne initial [X

] and

Start

Is the goal

reached?

End

Environment model,

range sensor

produce

obs, Ɵobs)

Start motion by:

k+1, Yk+1,Ɵk+1]=

k, Yk,Ɵk]+

T*[ΔX, ΔY, ΔƟ]

Compute a new Ɵt,

β = Ɵ

g - Ɵk

[Xr, Yr,Ɵr]=[Xk, Yk,Ɵk]

change steering control

angle ɣ in smooth

movement using Bezier

curve

Any obstacle

around? d

obs ≤

safe range

Yes

Compute

k+1, Yk+1,Ɵk+1]=

k, Yk,Ɵk]+

T*[ΔX, ΔY, ΔƟ]

Small right or left

turn

Initiate robot and

goal parameters

r, Yr,Ɵr, ɣ] and

g, Yg]

Any obstacle

in front? Ɵ

obs ≤

safe angle

Yes

Judge right or left turn

according to Ɵ

obs and

duplicate β

Define robot’s

dynamics and

constraints

Set

Velocity=0

Figure 5: Main ﬂowchart of path planning motion.

goal [X

], deﬁne the articulated vehicle’s speciﬁc

parameters V, d

min

, θ

min

, d

obs

, θ

obs

, the path update

rate deﬁned as T and the vehicle’s mechanical and

physical constraints that needs to be taken under con-

sideration. Set [X

] = [X

], with k ∈ Z

the sample index.

[Step 2: Path Update] Utilize Equations (1), (2), (6),

(7) and (8) to update the coordinates of the next way

point as:

k+1

] = [X

] + T ∗ [∆X ∆Y ∆θ]

calculate:

= arctan

k+1

−Y

k+1

− X

β = θ

− θ

to produce γ with θ

the angle between the line that

connects the center of gravity of the vehicle’s front

part to the goal point and the X axis, while β is the

difference angle among the vehicle’s orientation an-

gle, with the X axis and θ

. During the application

of this step, constraints can be imposed on the artic-

ulated vehicle just by bounding the allowable articu-

lation within γ

≤

γ ≤ γ

−

, with

and

−

representing

the maximum and the minimum bounds on the artic-

ulated angle.

[Step 3: Obstacle Avoidance] The obstacle avoid-

ance strategy becomes active when the safety condi-

tions d

min

and θ

min

are satisﬁed. This can be evaluated

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

180

by calculating the update of the distance from the ob-

stacle and the obstacle’s angle by:

Dis

obs

k+1

− X

obs

)

+ (Y

k+1

−Y

obs

)

obs

= arctan

k+1

−Y

obs

k+1

− X

obs

obs,g

= θ

obs

− θ

while in the case that the following conditions are

true:

(Dis

obs

< d

min

) AND (θ

obs,g

< θ

min

)

(Dis

obs

< d

min

) AND (θ

obs,g

< −θ

min

)

the changing in the steering angle is being duplicated

and Step 3 is repeated again till the condition in (9) is

false and the algorithm continues from Step 2 or the

bounds on the articulated angle cannot meet and the

algorithm jumps to Step 4.

[Step 4: Reaching Final Goal] If [X

k+1

] =

] ± Dis

tolr

, set velocity = 0 and the path plan-

ning algorithm has been terminated. Otherwise, the

algorithm jumps to Step 2 and the whole process is

being repeated in order to avoid collisions with the

obstacles until vehicle reaches the goal tolerance dis-

tance.

During the execution of the proposed path plan-

ning algorithm, and especially Step 2, the proposed

path planning algorithm always smoothes the pro-

duced way points by the utilization of Bezier curve

ﬁltering. The mathematical formulation of the applied

Bezier smothering is denoted as:

B(t) =

∑

i=0

(

) (1− t)

n−i

, t ∈ [0,1] (9)

The number n of the considered control points for the

Bezier curve generation plays a signiﬁcant role in the

ﬁnal shape of the produced smooth path as it can be

observed from Figure 6, where multiple Bezier lines

are being displayed with respect to different num-

ber of control points. A n degree Bezier line always

passes through the ﬁrst and last control points and it

can be provedthat it alwayslies within the convexhull

of the control points, while being tangent to the lines

connecting the way points (Chaudhry et al., 2010).

4 SIMULATION RESULTS

For simulating the efﬁcacy of the proposed path plan-

ner, the following articulated vehicle’s characteristics

have been considered: l

= l

= 0.6m, W = 0.58m,

while the vehicle’s speed is constant and equal to

0 1 2 3 4 5 6 7 8 9 10 11

X (m)

Y (m)

Figure 6: Bezier curves based on different number of con-

trol points resulting in different paths, (Black line-solid path

produced from the generated way points, red line-dots for 6

points, green line-dash dot for 4 points and the blue line-

dash for 3 points).

1msec. Moreover, the constraints imposed on the ar-

ticulated angle γ have been deﬁned as ±0.523 rad

and random measurement Gaussian noise with a ﬁxed

variance was added to all measurements of the range

sensor to simulate the real life measurement distor-

tion.

The effectiveness of the proposed algorithm will

be evaluated in arenas of different types and dimen-

sions. More analytically, the algorithm is simulated

on three types of environments with different obsta-

cle conﬁgurations, where the vehicle and obstacle ge-

ometry is described in a 2D workspace. The obtained

outputs of the path planning solutions from the indi-

cated starting points to the goal points is being de-

picted in Figures 7, 8 and 9, displaying cases with the

same sensing radius d

obs

= 3m and various d

min

As it can be observed in all the examined cases

the vehicle is able to avoid all the obstacles, includ-

ing the bounding surrounding (e.g. walls), which can

also be considered as obstacles without loss of gener-

ality. In the presented simulations, the articulated ve-

hicle is achieving to reach the reference ﬁnal goal, in-

dependently of the initial vehicle’s orientation, while

in all the simulations the safety radius has been also

displayed with the red circle notation. The basic as-

sumption in all these simulations is that the articu-

lated vehicle, in every time instant, is aware of the

coordinates of the ﬁnal goal and thus the path is being

tuned in every step based on the identiﬁed obstacles,

while the vehicle explores the surrounding environ-

ment towards the ﬁnal goal. In an obstacle free envi-

ronment, the optimal solution to this problem would

have been a straight line connecting the initial with

the goal point, a case that can be easily identiﬁed in

the presented simulation in Figure 7. The online iden-

OnlineDynamicSmoothPathPlanningforanArticulatedVehicle

181

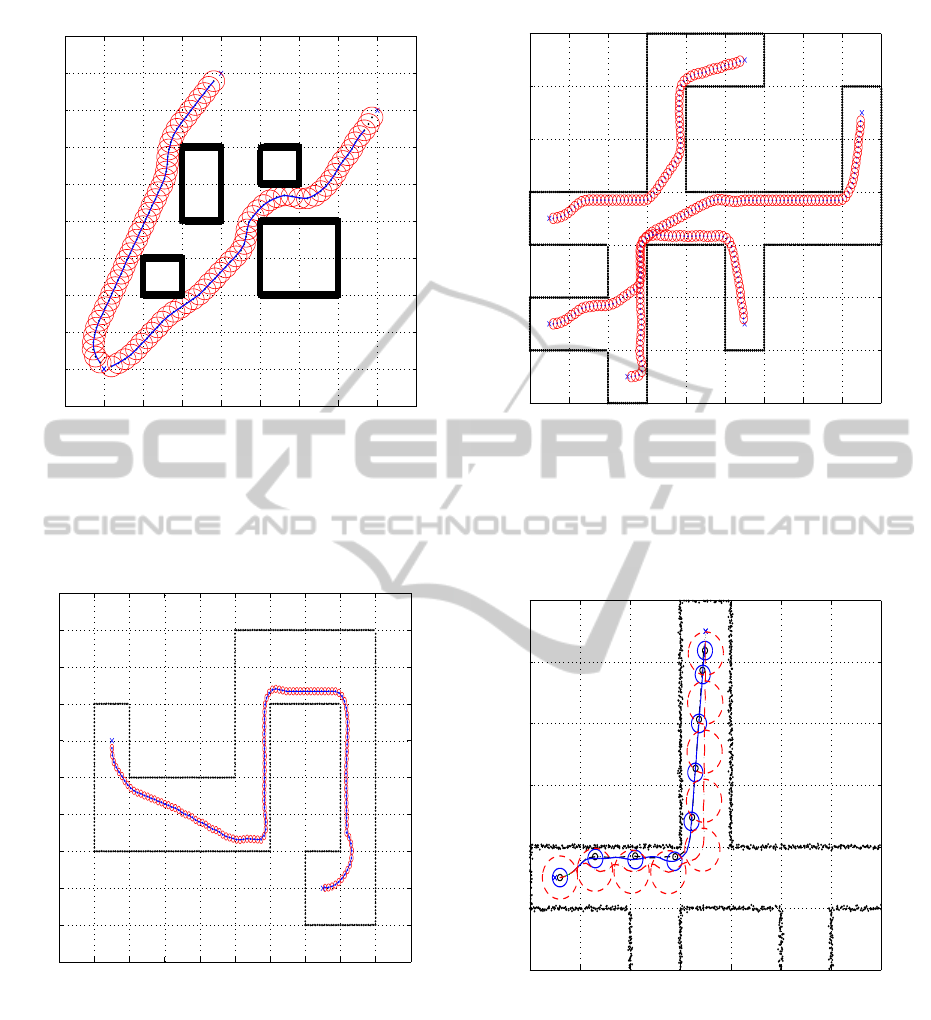
−5 0 5 10 15 20 25 30 35 40

−5

X (m)

Y (m)

Goal point 1

Goal point 2

Figure 7: Different shape obstacles placed in the workspace.

During these simulations the vehicle starts from different

initial angles at [0, 0, 120

, 7.5

] and [0, 0, 20

, 7.5

] to

reach the goal points located at [15, 40] and [35, 35] respec-

tively, with safe distance d

min

= 3m, d

obs

= 3m.

−10 0 10 20 30 40 50 60 70 80 90

−5

X (m)

Y (m)

Start point

Goal point

Figure 8: Path planning in an arena having boundaries on

both sides of the road a fact that restricts the articulated ve-

hicle motions. During this simulation scenario the vehicle

is starting from the initial posture [5, 25, − 90

, 7.5

] and

the goal is located at [65, 5] and d

min

= 0.5m, d

obs

= 3m.

tiﬁcation of obstacles produces distortions from fol-

lowing the straight line, connecting the robot with the

ﬁnal goal point, while the sensing and safety radius

are having a major effect on the path calculation. As

it can observed in Figure 10, the safety radius plays a

very signiﬁcant role in shape of the path. In this Fig-

10 20 30 40 50 60 70 80 90 100

X (m)

Y (m)

Start point 3

Goal point 3

Start point 2

Start point 1

Goal point 1

Goal point 2

Figure 9: Path planning in an arena having more compli-

cated boundaries on both sides of the road, with noise mea-

surement. The scenario is starting from different initial pos-

tures [15, 45], [15, 25] and [35, 15] with initial [θ, γ] =

[10

, 7.5

] and the goals are located at [65, 75], [95, 65]

and [65, 25] respectively with d

min

= 1.0m, d

obs

= 3m.

10 20 30 40 50 60 70 80

X (m)

Y (m)

Start point

Goal

point

Figure 10: During these simulations the vehicle is starting

from the initial posture [15, 45, 0, 5

] and the goal point

is located at [45, 85], while during movement different safe

distances d

min

have been utilized as 0.5, 1.5 and 3.5m, with

the same d

obs

= 3m.

ure, different paths with different safe distances d

min

and with the same sensing radius d

obs

are being pre-

sented. In the case that the vehicle is moving in a

bounded space, the selection of a relatively big safety

radius introduces oscillations in the translation of the

robot due to sequential safety violations that produce

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

182

corresponding change in the direction of the vehicle

for avoiding the obstacle. In case that small safety ra-

dius are being selected, this effect is being vanished

and smooth and shorter, non oscillatory, paths can be

produced.

Finally it should be stated that the arenas in Fig-

ures 8 and 9 are typical realistic examples of areas

where articulated vehicles operate, as the mine tun-

nels and the civil roads are. In the presented simu-

lations the consideration of the articulated vehicle’s

dynamic motion is obvious especially in the time in-

stances where the vehicle is turning towards the goal

and while performing at the same time obstacle avoid-

ance. This effect is of paramount importance for the

case of articulated vehicles as classical point dynamic

approaches in path planning will obviously results in

non-realistically achievable paths that would directly

lead to collisions.

5 CONCLUSIONS

In this article a novel online dynamic smooth path

planning scheme based on a bug like modiﬁed path

planning algorithm for an articulated vehicle under

limited and sensory reconstructed surrounding static

environment has been proposed. In the presented ap-

proach factors such as the real dynamics of the ar-

ticulated vehicle, the initial and the goal conﬁgura-

tion, the minimum and total travel distance between

the current and the goal points, the geometry of the

operational space, and the path smothering approach

based on Bezier lines have been taken under consider-

ation to produce a proper path for an articulated vehi-

cle, which can be followed by correspondingly alter-

ing the vehicle’s articulated angle. The efﬁciency of

the proposed scheme has been evaluated by multiple

simulation studies.

REFERENCES

Buniyamin, N., Wan Ngah, W., Sariff, N., and Mohamad,

Z. (2011). A simple local path planning algorithm

for autonomous mobile robots. International journal

of systems applications, Engineering & development,

5(2):151–159.

Chaudhry, T., Gulrez, T., Zia, A., and Zaheer, S. (2010).

B´ezier curve based dynamic obstacle avoidance and

trajectory learning for autonomous mobile robots. In

Intelligent Systems Design and Applications (ISDA),

2010 10th International Conference on, pages 1059–

1065. IEEE.

Chazelle, B. (1987). Approximation and decomposition of

shapes. Advances in Robotics, 1:145–185.

Ge, S. and Cui, Y. (2000). New potential functions for mo-

bile robot path planning. Robotics and Automation,

IEEE Transactions on, 16(5):615–620.

Guechi, E., Lauber, J., and Dambrine, M. (2008). On-line

moving-obstacle avoidance using piecewise bezier

curves with unknown obstacle trajectory. In Control

and Automation, 2008 16th Mediterranean Confer-

ence on, pages 505–510. IEEE.

Kamon, I., Rimon, E., and Rivlin, E. (1998). Tangentbug:

A range-sensor-based navigation algorithm. The In-

ternational Journal of Robotics Research, 17(9):934–

953.

Kamon, I. and Rivlin, E. (1997). Sensory-based motion

planning with global proofs. Robotics and Automa-

tion, IEEE Transactions on, 13(6):814–822.

Lumelsky, V. and Skewis, T. (1990). Incorporating

range sensing in the robot navigation function. Sys-

tems, Man and Cybernetics, IEEE Transactions on,

20(5):1058–1069.

Lumelsky, V. and Stepanov, A. (1986). Dynamic path plan-

ning for a mobile automaton with limited information

on the environment. Automatic Control, IEEE Trans-

actions on, 31(11):1058–1063.

Nayl, T., Nikolakopoulos, G., and Guastafsson, T. (2011).

Kinematic modeling and simulation studies of a lhd

vehicle under slip angles. In Computational Intelli-

gence and Bioinformatics/755: Modelling, Identiﬁca-

tion, and Simulation. ACTA Press.

Ng, J. and Br¨aunl, T. (2007). Performance comparison of

bug navigation algorithms. Journal of Intelligent &

Robotic Systems, 50(1):73–84.

Nilsson, N. (1969). A mobile automaton: An application

of artiﬁcial intelligence techniques. Technical report,

DTIC Document.

Roberts, J., Duff, E., Corke, P., Sikka, P., Winstanley, G.,

and Cunningham, J. (2000). Autonomous control of

underground mining vehicles using reactive naviga-

tion. In Robotics and Automation, 2000. Proceed-

ings. ICRA’00. IEEE International Conference on,

volume 4, pages 3790–3795. IEEE.

Scheding, S., Dissanayake, G., Nebot, E., and Durrant-

Whyte, H. (1999). An experiment in autonomous nav-

igation of an underground mining vehicle. Robotics

and Automation, IEEE Transactions on, 15(1):85–95.

Skrjanc, I. and Klanˇcar, G. (2010). Optimal cooperative

collision avoidance between multiple robots based on

bernstein–b´ezier curves. Robotics and Autonomous

systems, 58(1):1–9.

Usher, K. (2006). Obstacle avoidance for a non-holonomic

vehicle using occupancy grids. In 2006 Australasian

Conference on Robotics and Automation.

OnlineDynamicSmoothPathPlanningforanArticulatedVehicle

183