Overview of Bounded Support Distributions and Methods for Bayesian
Treatment of Industrial Data
Kamil Dedecius
1
and Pavel Ettler
2
1
Institute of Information Theory and Automation, Academy of Sciences of the Czech Republic,
Pod Vod´arenskou vˇeˇz´ı 4, 182 08 Prague, Czech Republic
2
COMPUREG Plzeˇn, s.r.o., N´adraˇzn´ı 18, 306 34 Plzeˇn, Czech Republic
Keywords:
Statistical Analysis, Bayesian Analysis, Truncated Distributions, Beta Distribution.
Abstract:
Statistical analysis and modelling of various phenomena are well established in nowadays industrial practice.
However, the traditional approaches neglecting the true properties of the phenomena still dominate. Among
others, this includes also the cases when a variable with bounded range is analyzed using probabilistic dis-
tributions with unbounded domain. Since many of those variables nearly fulfill the basic conditions imposed
by the chosen distribution, the properties of used statistical models are violated rather rarely. Still, there are
numerous cases, when inference with distributions with unbounded domain may lead to absurd conclusions.
This paper addresses this issue from the Bayesian viewpoint. It briefly discusses suitable distributions and
inferential methods overcoming the emerging computational issues.
1 INTRODUCTION
Modern industrial control systems rely on statisti-
cal modelling of various phenomena in the produc-
tion process, for instance the relevant physical vari-
ables, reliability and health of the controlled systems.
For this sake, usually traditional approaches provid-
ing easy and fast computations are exploited. As an
example consider the least-squares based regression
or state-space modelling with Kalman filters. Such
methods are often explicitly or implicitly based on
evaluation of statistical distributions with unbounded
support, e.g. the normal distribution. Recognizing
the limitations, a number of new methods concerning
modelling with bounded support distributions have
appeared in the last decade. Their need is obvious:
• Signals occurring in industrial systems are
bounded in principle. Limitations start from phys-
ical limits of measured signals and margins given
by performance of system’s actuators, through
given ranges of measurement units and, e.g. their
A/D converters to limitations given by interpreta-
tions of variables within digital computers.
• In many cases, modelling with distributions with
unbounded supports can lead to hardly inter-
pretable or even principally impossible values like
negative pressure in a hydraulic system, negative
rolling force in the rolling mill, negative fuel con-
sumption in engines, reversed direction of current
flow in electrical devices, reliability in percents
out of interval [0, 100] etc.
This paper focuses on bounded support distribu-
tions like the uniform distribution, triangular distri-
butions, beta distribution and its various modifica-
tions and truncated normal distribution. We adopt the
Bayesian framework,allowing consistent treatment of
uncertainty connected with models and estimated val-
ues. Since the use of this type of distributions usually
calls for approximations (in the Bayesian framework
particularly), the expectation-maximization, varia-
tional Bayesian inference and Markov chain Monte
Carlo methods are discussed as well. The paper ends
with an illustrative example of Bayesian beta regres-
sion of real rolling mill control data.
2 BAYESIAN INFERENCE
The Bayesian inference denotes a group of statistical
methods for estimation of unknown parameters us-
ing the Bayes’ rule, incorporating newevidence (data)
into the prior knowledge in order to obtain posterior
knowledge, better reflecting the data-generating real-
ity (system).
380
Dedecius K. and Ettler P..
Overview of Bounded Support Distributions and Methods for Bayesian Treatment of Industrial Data.
DOI: 10.5220/0004439003800387
In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2013), pages 380-387
ISBN: 978-989-8565-70-9
Copyright
c
 2013 SCITEPRESS (Science and Technology Publications, Lda.)

The prior information about the parameter θ,
which can be single or multivariate, discrete or contin-
uous, is represented by a probability distribution with
a probability density function (pdf) f(θ). More pre-
cisely, it should be written f(θ|α), where α is a set
of parameters of the prior distribution, called hyper-
parameters, to avoid confusion with model param-
eters. The prior distribution is updated by new ob-
served data x, obeying the model (sampling distribu-
tion, likelihood) f(x|θ) via the Bayes’ rule
f(θ|x) =
f(x|θ) f(θ)
f(x)
(1)
∝ f (x|θ) f(θ). (2)
While (1) is a full version of the Bayes’ rule, in which
f(x) =
Z
f(x|θ) f(θ)dθ
is the marginal pdf of x, independent of θ and there-
fore a constant with respect to θ. Its role is to normal-
ize the posterior distribution to get a proper distribu-
tion with a unit area under the pdf. Notation (2) is a
commonly used shorthand for unnormalized pdf.
If the prior distribution of θ is chosen from a class
of distributions conjugate to the model, then the pos-
terior distribution is of the same type. This particu-
larly appealing fact, providing analytical form of the
posterior pdf and allowing dynamic modelling with
parameter pdf repeatedly updated and used as prior
for the next time step, is connected with the exponen-
tial class of distributions.
The Bayesian prediction is provided by the poste-
rior predictive distribution. For a new data point ˜x, the
predictive distribution given previous data x reads
f(˜x|x) =
Z
f( ˜x|θ) f(θ|x)dθ.
This equation expresses the distribution of a new
point averaged over the distribution of θ.
Besides the inclusion of prior information and
prediction, the Bayesian framework provides many
other techniques, most of them consistently built on
principles of probability theory. A few examples
are systematic model selection and model averaging,
hypotheses testing, hierarchical modelling, recursive
modelling, distributed parameter estimation etc. Fur-
thermore, being embedded in the dynamic decision
making, the Bayesian approach allows to dynamically
and adaptively reflect the evolution of reality during
modelling.
3 DISTRIBUTIONS WITH
BOUNDED SUPPORT
In this section we overview selected continuous uni-
variate distributions with bounded support. Their
more extensive treatise or dealing with multivariate
distributions would exceed the limited extent of the
paper. For this reason, we adopt a simplification: only
the pdf and the first raw and second central moments
are given for each discussed distribution. Also note
that the distributions with bounded support may arise
either in model or in the prior.
3.1 Uniform Distribution
The uniform distribution of a random variable X ∼
U(a,b) on a compact set [a,b] has the pdf
f(x|a, b) = (b− a)
−1
for x ∈ (a,b)
and moments
E[X] =
b− a
2
varX =
(b− a)
2
12
.
As a maximum entropy distribution under known sup-
port it is suitable merely for cases when no additional
knowledge about a random variable is present. In
the Bayesian modelling it represents a popular nonin-
formative (vague) prior distribution, however, its use
is usually connected with the need of sampling from
posterior distribution. An example of uniform pdf on
[-0.5, 0.5] is depicted in Fig. 1
−0.6 −0.2 0.2 0.4 0.6
0.6 1.0 1.4
x
f(x)
Figure 1: Uniform pdf U(−0.5,0.5).
3.2 Triangular Distribution
The triangular distribution on [a,b] with mode ˆx of a
random variable X ∼ Tri(a,b, ˆx) has the pdf
f(x|a, b, ˆx) =











0 for x < a,
2(x−a)
(b−a)( ˆx−a)
for a ≤ x ≤ ˆx,
2(b−x)
(b−a)(b− ˆx)
for ˆx < x ≤ b,
0 for x > b.
(3)
OverviewofBoundedSupportDistributionsandMethodsforBayesianTreatmentofIndustrialData
381

The interesting moments are
E[X] =
a+ b+ ˆx
3
varX =
a
2
+ b
2
+ ˆx
2
− a(b+ ˆx) − bˆx
18
.
The triangular distributions are suitable for cases
when the number of data samples is very limited, pre-
venting reconstruction of possibly more elaborated
distribution form. They also arise under certain con-
ditions like the sum of two equivalent uniformly dis-
tributed independent random variables, or as a prior
distribution of standard deviation under uniformly
distributed variance. An example of pdfs with vari-
ous modes is depicted in Fig. 2.
−0.6 −0.4 −0.2 0.0 0.2 0.4 0.6
0.0 0.5 1.0 1.5 2.0
x
f(x)
0
−0.3
0.4
Mode
0
−0.3
0.4
Figure 2: Triangular pdf with a = −0.5, b = 0.5 and various
modes.
3.3 Beta Distribution
The “basic” beta distribution is a very popular for
its flexibility in modelling random variables with
bounded range (0,1). Variables with other ranges can
be easily transformed by translation and scaling. Its
two parameters α,β > 0 drive the shape of the distri-
bution, allowing for convexand concave shapes, sym-
metry, left and right skewness and high or low kurto-
sis and even a flat form of the uniform distribution
U(0,1), see Fig. 3.
The standard pdf of a beta-distributed random
variable X ∼ B(α,β) has the form
f(x|α,β) =
1
B(α,β)
x
α−1
(1− x)
β−1
,
where
B(α,β) =
Γ(α)Γ(β)
Γ(α+ β)
is the beta function, Γ(·) denotes the gamma function.
Under this form, the moments are
E[X] =
α
α+ β
varX =
αβ
(α+ β)
2
(α+ β + 1)
.
This beta distribution is conjugate to the binomial
model Bi(n, p) with parameters n ∈ N and p ∈ [0,1],
as the prior for p.
Under several conditions, the parameterization
used above may not be suitable. This occurs, e.g.,
if the random variable X is modelled as a dependent
variable given independent regressors. (Ferrari and
Cribari-Neto, 2004) propose parametrization with the
mean µ = α/(α+β) and precision φ = α+β, yielding
a beta distribution B(µφ,(1− µ)φ) with pdf
f(x|µ, φ) =
Γ(φ)
Γ(µφ)Γ(1− µ)φ)
x
µφ−1
(1− x)
(1−µ)φ−1
(4)
with moments
E[X] = µ
varX =
µ(1− µ)
1+ φ
.
This form is exploited in beta regression, e.g. (Ferrari
and Cribari-Neto, 2004) and (Branscum et al., 2007).
0.0 0.2 0.4 0.6 0.8 1.0
0 1 2 3 4
x
f(x)
Shape par.
2, 10
10, 10
1, 1
1, 10
Figure 3: Beta pdf with various shaping parameters α,β.
There exists also a whole class of beta distribu-
tions called generalized beta distributions, yielding
tens of more or less common distributions including
χ
2
, lognormal, gamma etc. as special cases. The ex-
tent of this class is far beyond the scope of this paper.
3.4 Beta-rectangular Distribution
As noted in (Hahn, 2008) the definition of the beta
distribution in terms of mean and precision (4) nei-
ther considers tail-area events nor greater flexibility
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
382

in variance specification. Therefore, (Hahn, 2008)
proposed a mixture of beta distribution and a uniform
distribution, giving it the name beta rectangular dis-
tribution. A random variable X ∼ BR(µ,φ,θ) has then
pdf
f(x|µ, φ,θ) = θ + (1− θ) f
B
(x|µ,θ),
where µ and φ are the mean and precision of a beta
component f
B
(·) and θ ∈ [0,1] is a mixing parame-
ter (weight). Due to the distributions’ support, the
constant density of the uniform distribution is equiv-
alent directly to θ. The moments of this mixture are
straightforwardly
E[X] =
θ
2
+ (1− θ)µ
varX =
µ(1− µ)
1+ φ
(1− θ) [1+ θ(1+ φ)]+
θ
12
(4− 2θ).
It is worth to notice that the uniform component
is equivalently a beta distribution B(1/2,2) and the
mixture can be viewed as a beta mixture with one
component fixed. The beta-uniform mixture was re-
cently proposed to improve robustness of beta regres-
sion to outliers, (Bayes et al., 2012). Some examples
of the beta-rectangular distribution are in Fig. 4.
0.0 0.4 0.8
0.0 0.5 1.0 1.5 2.0 2.5
x
f(x)
0.0 0.4 0.8
0.0 0.5 1.0 1.5 2.0 2.5
x
0.0 0.4 0.8
0.0 0.5 1.0 1.5 2.0 2.5
x
0.0 0.4 0.8
0 1 2 3 4
x
f(x)
0.0 0.4 0.8
0 1 2 3 4
x
0.0 0.4 0.8
0 1 2 3 4
x
Figure 4: Various forms of beta-rectangular pdf. Left: beta
component with parameters µ = 0.5, φ = 10 and θ = 0 (red),
θ = 0.5 (blue), θ = 1 (green). The special cases in red and
green correspond to pure beta and uniform distributions, re-
spectively. Right: parameters [θ, µ, φ]: [0.25, 0.3, 30] (red),
[0.5, 0.6, 30] (blue) and [0.75, 0.9, 30] (green).
3.5 Inflated Beta Distributions
Another approach to the issue of tail-area events are
the so-called inflated beta distributions. Similarly to
the beta-rectangular distribution (beta-uniform mix-
ture), the inflated beta distributions are themselves
mixtures. The pdf of a zero-inflated (or one-inflated)
beta distribution can be written in the form
f
c
(x|θ,µ,φ) = θ1
c
(x) + (1− θ) f
B
(x|µ,φ), (5)
where c = 0 or c = 1 for zero-inflated and one-inflated
distribution, respectively; f
B
(x|µ,φ) is a beta pdf (4)
and 1
c
(x) is an indicator function equal to one if
x = c and zero otherwise. The interest in bounded-
support distributions implies that the zero-and-one-
inflated beta distribution should be expressed simi-
larly to (5) with two weights for the cases c = 0 and
c = 1, with the complement to 1 reserved for the beta
component, similarly to (Rigby and Stasinopoulos,
2005).
Another expression of zero-and-one-inflated beta
was proposed in (Ospina and Ferrari, 2010) as a mix-
ture of beta and Bernoulli distributions with pdf
f
{0,1}
(x|θ, p,µ, φ) = θf
Ber
(x; p) + (1 − θ) f
B
(x;µ,φ),
(6)
where f
Ber
(·) is a Bernoulli component with param-
eter p ∈ [0,1] and f
B
(·) is again a beta component
1
.
An example is depicted in Fig. 5. The first and second
moments are then
E[X] = θp+ (1− θ)µ
varX = θp(1 − p) + (1− θ)
µ(1− µ)
1+ φ
+ θ(1− θ)(p− µ)
2
.
The inflated beta distributions have been used in the
0.0 0.2 0.4 0.6 0.8 1.0
0.0 0.2 0.4 0.6
x
f(x)
Figure 5: Zero-and-one-inflated beta pdf with parameters
θ = 0.6, p = 0.3, µ = 0.4 and φ = 5.
non-Bayesian generalized linear models (GLM), e.g.
(Rigby and Stasinopoulos, 2005).
3.6 Truncated Normal Distribution
From the class of truncated distributions we choose
the normal one. The truncated normal distribution
follows from restricting the normal distribution with a
1
The discrete Bernoulli component in (6) is also under-
stood as a pdf, that is, a Radon-Nikod´ym derivative of of the
distribution with respect to a dominating counting measure.
OverviewofBoundedSupportDistributionsandMethodsforBayesianTreatmentofIndustrialData
383

mean µ and variance σ
2
to a bounded interval, either
from one or both sides, by truncation, i.e., by cutting
the tails out of interest and subsequent renormaliza-
tion. A random variable obeying the (two-sided) trun-
cated normal distribution, X ∼ tN (µ,σ
2
,a, b) has the
pdf
f(x|µ, σ
2
,a, b) =
σ
−1
φ

x−µ
σ

Φ

b−µ
σ

− Φ

a−µ
σ

,
where φ(·) denotes the pdf of the standard normal dis-
tribution N (0,1) and Φ(·) used for renormalization is
its distribution function. The moments are
E[X] = µ+
φ

a−µ
σ

− φ

b−µ
σ

Φ

b−µ
σ

− Φ

a−µ
σ

σ
varX = σ
2


1+
a−µ
σ
φ

a−µ
σ

−
b−µ
σ
φ

b−µ
σ

Φ

b−µ
σ

− Φ

a−µ
σ



−σ
2


φ

a−µ
σ

− φ

b−µ
σ

Φ

b−µ
σ

− Φ

a−µ
σ



2
Four examples of truncated normal distribution on in-
terval [-0.5, 0.5] are depicted in Fig. 6.
−0.6 −0.4 −0.2 0.0 0.2 0.4 0.6
0.5 1.0 1.5
x
f(x)
std = 0.25
std = 0.5
std = 0.75
std = 1.0
Figure 6: Truncated normal pdf with a = −0.5,b = 0.5,
mean µ = 0 and various standard deviations.
The truncated normal distribution is popular in
parameter estimation, however, it was almost disre-
garded in the industrial practice. Another distribution
with a great potential is the truncated Student’s t dis-
tribution, whose heavier tails provide more robust sta-
tistical computations. The main issues of truncated
distributions is that analytical computations are rarely
possible and a sort of rather demanding Monte Carlo
method (like Gibbs sampling) is usually unavoidable.
4 COMPUTATIONAL ISSUES
In many cases, the Bayesian inference of the poste-
rior distribution of parameters θ given data is analyt-
ically intractable. The difficulty lies in the normaliz-
ing constant of the posterior distribution, which of-
ten contains special functions (c.f. the beta distri-
bution, normalized by a beta function). Among the
most popular ways around the problems are stochastic
simulations, particularly Markov Chain Monte Carlo
(MCMC) and the expectation-maximization (EM) al-
gorithm. In addition to them, we discuss also the vari-
ational Bayesian inference (Jordan, 1999) that has be-
come a popular analytical approach often providing
similar accuracy as the Gibbs sampler, but at a much
greater speed.
4.1 Expectation Maximization
The Expectation-Maximization (EM) algorithm for
two-stage iterative finding of maximum likelihood
or maximum a posteriori (MAP) estimates of latent
variables of probabilistic models was proposed by
(Dempster et al., 1977). Similarly to the notation
introduced earlier, we consider a model of observed
variables X governed by a set of parameters θ. Sup-
pose, that direct optimization of the likelihood f(X|θ)
is difficult and, under existence of discrete or con-
tinuous hidden variable Z, optimization of f(X, Z|θ)
is much easier. Recall, that the marginalization rule
yields
f(X|θ) =
Z
f(X, Z|θ)dZ,
providing a way to the desired likelihood. It is
straightforward to show that the existence of a dis-
tribution q(Z) allows to write
log f(X|θ) = L(q,θ) + D(q|| f), (7)
where
D(q|| f) = −
Z
q(Z) log
f(Z|X, θ)
q(Z)
dZ (8)
is the Kullback-Leibler divergence of q and f (Kull-
back and Leibler, 1951). It is a premetric, i.e. a non-
negative functional satisfying D(q|| f ) = 0 if q = f
almost everywhere. The term
L(q,θ) =
Z
q(Z) log
f(X, Z|θ)
q(Z)
dZ (9)
is a lower bound of (7), which reaches maximum if
q(Z) = f(Z|X, θ).
Starting from a crude estimate θ
∗
, the two steps of the
EM algorithm are
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
384

1. Expectation (E-step) – the lower bound L(q,θ
∗
)
is maximized with respect to q(Z) with the cur-
rent value θ
∗
being fixed. The aim is to get q(Z)
as close to f(Z|X, θ
∗
) as possible, that is to min-
imize the Kullback-Leibler divergence in (7). By
substitution q(Z) = f(Z|X,θ
∗
) into (9),
L(q,θ) = E
Z|X,θ
∗
[log f(X,Z|θ)]
− E
Z|X,θ
∗
[log f(Z|X, θ
∗
)]
= Q (θ,θ
∗
) + const., (10)
where the constant independent of θ is the entropy
of q.
2. Maximization (M-step) – the pdf q(Z) is fixed and
L(q,θ) is maximized with respect to θ in order to
obtain a new value θ
′
. This increases the lower
bound and consequently the log likelihood in (7).
Since the distribution q(Z) is fixed, the Kullback-
Leibler divergence to f(Z|X,θ
′
) is positive. Using
(10),
θ
′
= arg max
θ
Q (θ,θ
∗
).
Then θ
∗
← θ
′
and the algorithm is repeated until con-
vergence.
The EM algorithm and its variants like GEM (gen-
eralized EM) or ECM (expectation conditional maxi-
mization) are particularly popular in estimation of fi-
nite mixtures. Here, the latent variable Z denotes the
component from which the available data originate.
4.2 Variational Bayes
The variational Bayesian (VB) inference, rooted in
the field of calculus of variations, serves for analytic
approximation of the posterior pdf of parameters and
potentially other latent variables (Jaakkola and Jor-
dan, 2000). Let us denote Z = (Z
1
,.. . ,Z
n
) as the
set comprising both parameters and latent variables.
The goal is to find analytically tractable approxima-
tion q(Z) of f(Z|X). Similarly to EM decomposition
(7), we may write
log f(X) = L(q) + D(q|| f), (11)
where the analogues of (8) and (9) are
D(q|| f) = −
Z
q(Z) log
f(Z|X)
q(Z)
dZ
L(q) =
Z
q(Z) log
f(Z|X)
q(Z)
dZ.
Unlike in the EM algorithm, the elements of Z are
factorized into M independent factors Z
i
,i = 1,..., M,
such that
q(Z) =
M
∏
i=1
q
i
(Z
i
).
This, put back into (11) yields
L(q) =
Z
∏
i
q
i
(Z
i
)
"
log f(X, Z)−
∑
i
logq
i
(Z
i
)
#
dZ
=
Z
q
j
(Z
j
)E
i6= j
[log f(X,Z)]dZ
− E
j
[logq
j
(Z
j
)] + const.
where
E
i6= j
[log f(X, Z)] =
Z
log f(X, Z)
∏
i6= j
q
i
(Z
i
)dZ
i
.
This directly yields the VB-optimal factors
logq
∗
j
(Z
j
) = E
i6= j
[log f(X, Z)]+ const.
The additive constant changes to multiplicative in ex-
ponentiation, providing the solution
q
∗
j
(Z
j
) ∝ exp{E
i6= j
[log f(X, Z)]}.
The resulting algorithm is very similar to the
expectation-maximization, but unlike it, VB com-
putes the posterior distributions of all parameters. The
expectations are taken with respect to variables not in
the current factor, which, in turn, are recomputed in
the same way. The algorithm is guaranteed to con-
verge and, under convexity of the lower bound, to the
global maximum (Boyd and Vandenberghe, 2004).
It is necessary to stress that the variational
Bayesian method provides analytic approximations
of the posterior distribution of parameters and latent
variables. The sacrifice is their factorized treatment
(11), neglecting the dependency properties carried by
the true joint posterior pdfs. An alternative expecta-
tion propagation algorithm (Minka, 2001) overcomes
this issue by exploiting reversed order of pdfs in the
Kullback-Leibler divergence in (11). The price is ele-
vated level of computational difficulties.
A recent example of the VB algorithm used in
conjunction with bounded variables is presented in
(Ma and Leijon, 2011). It provides a method for VB
estimation of beta mixture models. An interesting
part of the paper is approximate analytic solution of
otherwise analytically intractable integrals emerging
from special (gamma or beta) functions in the beta
distribution. This reveals the pervasive computational
problems connected even with the very standard dis-
tributions with bounded support.
4.3 Simulation from Posterior
The industrial practice often deals with complicated
models, for which the inference is neither analyti-
cally nor approximately (in the EM and VB sense)
tractable. This issue is yet emphasized when distri-
butions with bounded support are used. The form
OverviewofBoundedSupportDistributionsandMethodsforBayesianTreatmentofIndustrialData
385

of resulting analytically unreachable posteriors need
to be evaluated by simulations, exploiting a (usually
big) set of draws to represent the distributions. In
high-dimensional problems, the Markov chain Monte
Carlo (MCMC) methods dominate this field. The idea
of Markov chain simulation is to simulate a random
walk in the space of unknown (multivariate) param-
eter θ. The random walk converges to a stationary
distribution close to the target posterior f (θ|x) (Gel-
man et al., 2003). Two popular MCMC methods,
the Metropolis-Hastings (Metropolis et al., 1953) and
Gibbs algorithms (Geman and Geman, 1984), have
become standards in Bayesian modelling.
Metropolis-Hastings Algorithm: first draws a
starting point θ accomplishing f (θ|x) > 0 from some
suitable distribution. Then, it recursively exploits
a Markov transition kernel (proposal distribution)
q(θ
′
|θ) in the following way:
1. Sample a candidate point θ
′
from q(θ
′
|θ).
2. Calculate
r = min

1,
f(θ
′
|x)q(θ|θ
′
)
f(θ|x)q(θ
′
|θ)

. (12)
3. Move to θ
′
with probability r, else stay at θ.
The choice of the Markov transition kernel is gen-
erally uneasy: the main requirements, besides easy
sampling and computing of r, is a reasonable distance
travelled in the parameter space with each transition
and high acceptance rate. For example, a normal
kernel with high variance leads to a low acceptance
rate as the proposed samples often lay in regions with
small pdf value. On the other hand, a very low vari-
ance produces high acceptance rate in regions with
high pdf, but it takes a lot of iterations until the pro-
posed samples explore more distant regions (which is
called slow mixing).
Gibbs Sampling: is a special case of the
Metropolis-Hastings algorithm. It divides θ into
m parts θ = (θ
1
,.. . ,θ
m
). Each iteration cycles
through these components, drawing each subset con-
ditional on the value of all the others (Gelman et al.,
2003). First, an ordering of components is chosen at
random and each θ
′
i
is sampled from the conditional
distribution f(θ
′
i
|θ
′
1
,.. . ,θ
′
i−1
,θ
′
i+1
,.. . ,θ
m
). The
Markov transition kernel can be shown to have a spe-
cial form allowing jumps only of those components
of θ
′
that match the previous θ. Under this condition,
the value of r in equation (12) is always 1, thus every
jump is accepted. This suppresses slow mixing of the
chain.
In both the Metropolis-Hastings and Gibbs algo-
rithms, the initial values can be chosen either ran-
domly or using initial points from some crude approx-
imation (e.g. via EM). This is also the reason for dis-
carding a subset of the first iterations (usually several
thousands) called burn-in, that is likely far from the
target distribution. The drawback of both algorithms
is the correlation of samples, significantly influenc-
ing the mixing and other properties of simulations.
Also fine tuning of MCMC methods is a tedious time-
consuming task, requiring careful prior and post-hoc
analyses to ensure that the simulated values of θ are
close to the target distribution of θ|y.
5 EXAMPLE OF APPLICATION
As an illustrative example, we estimate the Bayesian
beta regression model (e.g. (Ferrari and Cribari-Neto,
2004) and (Branscum et al., 2007)) on a 20 data points
from a rolling mill, depicted in Fig. 7. The horizon-
tal axis represents discrete time, the vertical axis de-
scribes the control in 0.01%. We fitted the model (4)
using a logit link function as follows
y
i
|µ
i
,φ ∼ B(µ
i
φ,(1− µ
i
)φ)
logit(µ
i
) = β
0
+ β
1
x
i
, i = 1,.. ., 20.
corresponding with the reparameterized beta distribu-
tion (4). The coefficients (β
0
,β
1
) together with preci-
sion φ were estimated as independent,
f(β
0
,β
1
,φ) = f(β
0
,β
1
) f(φ)
with β
0
and β
1
being normal and φ gamma distributed.
The model was estimated in GNU R interfacing
with OpenBUGS through the BRugs package. The
chain length was 50 000 samples with initial 4000
samples serving for burn-in.
5 10 15 20
0.005 0.015 0.025
time
0.01%
Figure 7: Time × control in 0.01%. Points are true mea-
surements, red line is interpolation obtained by beta regres-
sion.
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
386

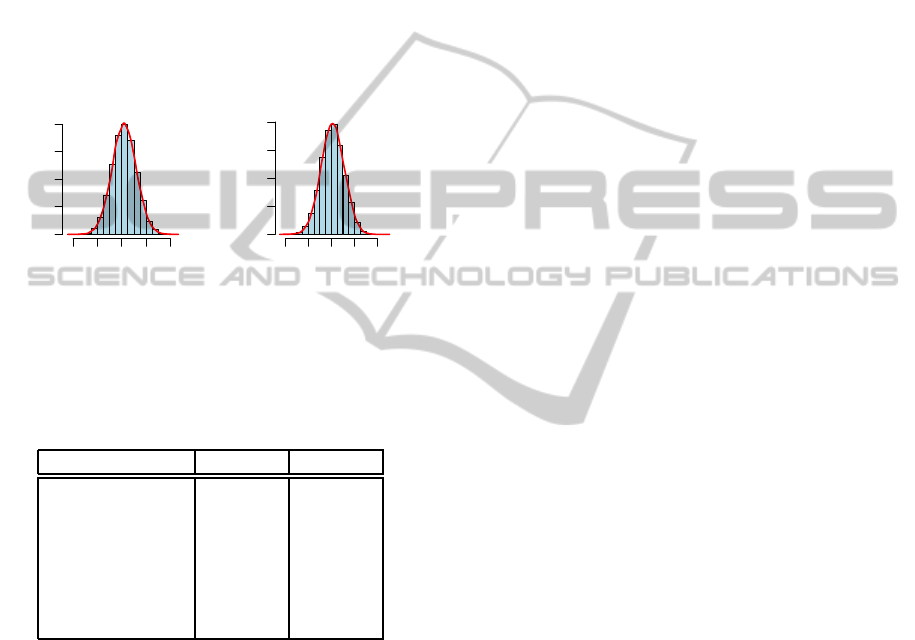
Results of estimation of regression coefficients are
given in Table 1. The mean values of posterior dis-
tributions are
ˆ
β
0
= −5.799 and
ˆ
β
1
= 0.11, with the
corresponding 95% credibility intervals (defined as
highest density intervals) being [−7.762,−3.827] and
[−1.853,2.075] for β
0
and β
1
, respectively. One of
the rules of thumb recommends that the simulation
should be run until the Monte Carlo error for each
parameter of interest falls below 5% of the sample
standard deviation. Table 1 shows that the simulation
reached less than 0.6% for both coefficients.
The posterior distributions of β
0
and β
1
are de-
picted in Fig. 8 as histograms of Monte Carlo samples
together with kernel density estimates (in red).
−10 −6 −2
0.0 0.2 0.4
−4 0 4
0.0 0.2 0.4
Figure 8: Bayesian beta regression – posterior distributions
of β
0
(left) and β
1
(right). Histograms depict relative fre-
quency of MCMC samples, red lines are respective kernel
density estimates.
Table 1: Results of MCMC estimation of beta regression
model.
˜
x
x
x
2.5
,
˜
x
x
x
50
and
˜
x
x
x
97.5
denote 2.5%, 50% and 97.5%
quantiles of posterior distributions.
β
0
β
1
mean -5.799 0.110
st. dev. 1.001 1.005
MC error 5.486e-3 5.177e-3
˜
x
x
x
50
-5.802 0.113
˜
x
x
x
2.5
-7.762 -1.853
˜
x
x
x
97.5
-3.827 2.075
MC error/stdev 0.548% 0.515%
For comparison, the betareg package was used
for beta regression in frequentist statistical framework
(Ferrari and Cribari-Neto, 2004). The model had the
same structure, the link function was identically the
logit. Coefficients estimates were
ˆ
β
0
= −5.866 and
ˆ
β
1
= 0.115, respectively, model precision was 2578.
ACKNOWLEDGEMENTS
The research project is supported by the grant M
ˇ
SMT
7D12004 (E!7262 ProDisMon).
REFERENCES
Bayes, C. L., Baz´an, J. L., and Garc´ıa, C. (2012). A new ro-
bust regression model for proportions. Bayesian Anal-
ysis, 7(4):841–866.
Boyd, S. and Vandenberghe, L. (2004). Convex Optimiza-
tion. Cambridge University Press.
Branscum, A. J., Johnson, W. O., and Thurmond, M. C.
(2007). Bayesian beta regression: Applications to
household expenditure data and genetic distance be-
tween foot-and-mouth disease viruses. Australian &
New Zealand Journal of Statistics, 49(3):287–301.
Dempster, A. P., Laird, N. M., and Rubin, D. B. (1977).
Maximum likelihood from incomplete data via the
EM algorithm. Journal of the Royal Statistical So-
ciety. Series B (Methodological), 39(1):1–38.
Ferrari, S. and Cribari-Neto, F. (2004). Beta regression for
modelling rates and proportions. Journal of Applied
Statistics, 31(7):799–815.
Gelman, A., Carlin, J. B., Stern, H. S., and Rubin, D. B.
(2003). Bayesian Data Analysis, Second Edition
(Chapman & Hall/CRC Texts in Statistical Science).
Chapman and Hall/CRC, 2 edition.
Geman, S. and Geman, D. (1984). Stochastic relaxation,
Gibbs distributions, and the Bayesian restoration of
images. IEEE Trans. Pattern Anal. Mach. Intell.,
6:721–741.
Hahn, E. (2008). Mixture densities for project management
activity times: A robust approach to PERT. European
Journal of Operational Research, 188(2):450–459.
Jaakkola, T. and Jordan, M. (2000). Bayesian parameter es-
timation via variational methods. Statistics and Com-
puting, 10(1):25–37.
Jordan, M. I. (1999). An introduction to variational meth-
ods for graphical models. In Machine Learning, pages
183–233.
Kullback, S. and Leibler, R. A. (1951). On information
and sufficiency. The Annals of Mathematical Statis-
tics, 22(1):79–86.
Ma, Z. and Leijon, A. (2011). Bayesian estimation of
beta mixture models with variational inference. Pat-
tern Analysis and Machine Intelligence, IEEE Trans-
actions on, 33(11):2160–2173.
Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N.,
Teller, A. H., and Teller, E. (1953). Equation of state
calculations by fast computing machines. The Journal
of Chemical Physics, 21(6):1087–1092.
Minka, T. P. (2001). Expectation propagation for approx-
imate Bayesian inference. In UAI ’01: Proceedings
of the 17th Conference in Uncertainty in Artificial In-
telligence, pages 362–369, San Francisco, CA, USA.
Morgan Kaufmann Publishers Inc.
Ospina, R. and Ferrari, S. (2010). Inflated beta distributions.
Statistical Papers, 51:111–126. 10.1007/s00362-008-
0125-4.
Rigby, R. A. and Stasinopoulos, D. M. (2005). Generalized
additive models for location, scale and shape. Jour-
nal of the Royal Statistical Society: Series C (Applied
Statistics), 54(3):507–554.
OverviewofBoundedSupportDistributionsandMethodsforBayesianTreatmentofIndustrialData
387