
Path Following Control of Rhombic Like Vehicles
Performance Assessment with Dynamic Vehicle Model
Nuno Silva
1
, Alberto Vale
1
and Luca Baglivo
2
1
Instituto de Plasmas e Fus˜ao Nuclear, Instituto Superior T´ecnico, Universidade T´ecnica de Lisboa,
Av. Rovisco Pais 1, 1049-001 Lisboa, Portugal
2
Laboratory of Robotics and Systems in Engineering and Science, Instituto Superior T´ecnico,
Universidade T´ecnica de Lisboa, Av. Rovisco Pais 1, 1049-001 Lisboa, Portugal
Keywords:
Rhombic Like Vehicles, Path Following, Dynamic Vehicle Modelling.
Abstract:
This paper addresses the path following problem of a wheeled mobile robot with rhombic like kinematics
(drivable and steerable wheels both at front and rear) operating in cluttered environments. Four path following
controllers are developed to steer the kinematic model of a rhombic like vehicle (RLV) along a desired path:
three are based on feedback laws derived at a kinematic level with geometrical inspiration; the fourth is a
nonlinear controller built upon a kinematic model of a RLV using Lyapunov functions. All the developed
controllers are capable of performing under two situations: when both wheels follow the same path, or when
each wheel follows a different path. The dynamic modelling of a RLV is lastly introduced. Simulated results
present a comparative performance assessment of the controllers while dealing, or not, with vehicle dynamics.
The main conclusions of these controllers are summarized, leading to a possible application in the actual
vehicles that will operate in the remote handling missions of the International Thermonuclear Experimental
Reactor (ITER).
1 INTRODUCTION
Rhombic like vehicles (RLVs) as described in
(Ribeiro and Lima, 1997) and depicted in Fig. 1,
distinguish themselves from the typical unicycle and
car like vehicles, by allowing to control the linear
speed, v
i
, and orientation, θ
i
, of each wheel i ∈
{Rear,Front}. In fact, vehicles with rhombic like
kinematics are a set of nonholonomic vehicles char-
acterized for enabling a decoupling of the vehicle’s
orientation from the vehicle’s velocity vector, creat-
ing a controllable sideslip angle, β (Fig. 1). In a
RLV both wheels can follow the same path, referred
as Line Guidance (LG), or each wheel can follow a
different path, referred as Free Roaming (FR) (Vale
et al., 2012). A RLV is particularly suitable for op-
erations in cluttered scenarios where a high degree of
vehicle mobility is essential. This issue is detailed in
(Ribeiro and Lima, 1997) and strengthened in (Vale
et al., 2012), where the applicability of a RLV in the
cluttered environments of ITER (International Ther-
monuclear Experimental Reactor) was studied. Sev-
eral RLVs will operate in Tokamak Building (TB) and
Hot Cell Building (HCB) of ITER, where Fig. 2 il-
lustrates one of the levels of TB. Remote Handling
C
x
y
y
C
x
C
θ
F
θ
R
θ
m
F
M
R
M
F
β
M
R
{I}
!
β
"
#
$
"
%
$
"
#
&
"
%
&
!
'
(
))
())
*
*
C
{M}
Figure 1: Rhombic like vehicle (RLV) kinematic (left) and
dynamic (right) variables and parameters.
(RH) systems will play an important role in ITER
and one of such systems is the Cask and Plug Re-
mote Handling System (CPRHS) depicted in Fig. 2:
a RLV responsible for RH operations of transporta-
tion of activated components and equipment inside
the TB. The CPRHS can reach dimensions of 8.50m
x 2.62m x 3.70m (length, width, height), a mass of
100T when fully loaded and has to operate within a
narrow safety margin of 10 to 30 cm. It has to be
noticed that the kinematic capabilities of RLVs can
further be extended to load transport in a wide set of
scenarios, such as storage warehouses, industrial sites
and cargo harbours. In (Vale et al., 2012), a motion
planning of the CPRHS in ITER is detailed. The tra-
48
Silva N., Vale A. and Baglivo L..
Path Following Control of Rhombic Like Vehicles - Performance Assessment with Dynamic Vehicle Model.
DOI: 10.5220/0004439500480057
In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2013), pages 48-57
ISBN: 978-989-8565-71-6
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

X
Y
X
Y
Cask
Pallet
CPRHS
CTS
C
a
s
k
Palle
t
CTS
CTS
Figure 2: The CRPHS composition (left) and its typical op-
erating scenario in a 3D and 2D view (middle and right,
respectively).
jectories (path and speed profile) outputted from the
aforementioned work are considered to be the opti-
mal motion solution in the scenarios of ITER. It is the
purpose of the current paper to study different path
following solutions for a RLV with the characteris-
tics of the CPRHS, along previously optimized tra-
jectories. Moreover, this paper focuses on path fol-
lowing and not on trajectory tracking, since the ob-
jective is to steer a RLV along the optimized trajecto-
ries, while the vehicle’s speed tracks the desired speed
profile embedded in the trajectory. In contrast, tra-
jectory tracking requires the vehicle to track a time-
parameterized reference (Luca and Oriolo, 1998).
To solve the path following problem for unicycles,
in (Micaelli and Samson, 1993; Lapierre et al., 2006)
are employed nonlinear control techniques, either in
the form of Lyapunovbased methods or throughfeed-
back linearization. Noticeable performance results
and proof of stability in relation to a feasible path are
detailed. Concerning car like vehicles, (Luca and Ori-
olo, 1998) details a path following controller based
on feedback linearization methods, which exploit the
chained form representation of the kinematic model
of a car like vehicle. Despite achieving good per-
formances, in order to guarantee stability, some con-
straints must be made on the initial pose (position and
orientation) of the vehicle and in the path itself. For
All-Wheel-Steering vehicles, class to which RLVs be-
long to, (Hiraoka et al., 2009) exploresthe application
of sliding mode controllersto the path following prob-
lem, improving robustness to uncertainties at a cost of
compromising steering smoothness.
The only references to path following for RLVs
are made in (Micaelli and Samson, 1993; Morin and
Samson, 2011) at a kinematic level only. In (Mi-
caelli and Samson, 1993) nonlinear control methods
are used to derive feedback control laws that enable
one wheel of the RLV to converge to a reference path,
whereas the other wheel determines the vehicle’s ori-
entation while following the path. In (Morin and
Samson, 2011) the application of transverse functions
to the control of RLVs is studied, placing a comple-
mentary constraint when the steering angles of both
wheels are equal to ±π/2, which is contoured using
practical stabilization (Morin and Samson, 2011) via
specific maneuvering embedded in the control design.
In this paper, and motivated by the abovemen-
tioned considerations, the authors propose four path
following controllers for RLVs, which can be divided
in two groups: three are categorized as geometrical
controllers and are based on feedback laws derived at
a kinematic level with geometrical inspiration; while
the fourth is a nonlinear controller, built upon a kine-
matic model of the vehicle using Lyapunovfunctions.
The geometrical controllers represent a good compro-
mise between complexity vs. performance and enable
a first line of awareness to the control problem. In re-
lation to the nonlinear controller, two nonlinear feed-
back control laws are derived, acting independently
on the vehicle’s orientation and sideslip angle, and
thereby extracting the full capabilities of a RLV. In
striking contrast with the work done in (Micaelli and
Samson, 1993), the nonlinear controller proposed in
this paper allows for a RLV to follow a path formed
by poses in a simple manner. Moreover, in relation
to (Morin and Samson, 2011) the RLV kinematic con-
straint θ
R
,θ
F
6= ±π/2 is lifted by considering as con-
trol inputs v
R
,v
F
,θ
R
and θ
F
, as opposed to (Morinand
Samson, 2011) where only
˙
θ
R
,
˙
θ
F
and the longitudi-
nal speed of the vehicle are used.
While operating in the scenarios of ITER, a RLV
like the CPRHS is estimated to have a considerable
speed for a vehicle with a mass up to 100T. Such
kinetic energy in a vehicle with the dimensions and
weight of the CPRHS, while operating under a 10 to
30 cm safety margin, represents a major challenge.
Hence, a dynamic model of an RLV is detailed to en-
able a more realistic CPRHS simulation. The impact
of simulated vehicle dynamics, mainly in the from of
wheel slippage, in the developed four path following
controllers, is compared against the strictly kinematic
situation, where no slippage occurs.
The paper is organized as follows: Section 2 de-
tails the kinematic model of a RLV and formulates the
path following control problem; Section 3 presents
the four path following controllers; Section 4 presents
the dynamic model of a RLV; Section 5 lays out the
results; and Section 6 outlines the conclusions and di-
rections for future work.
2 PROBLEM FORMULATION
This section comprises a mathematical formulation of
the kinematic model of a RLV, essential for the de-
PathFollowingControlofRhombicLikeVehicles-PerformanceAssessmentwithDynamicVehicleModel
49

sign of the path following controllers of Section 3,
followed by a precise problem statement.
2.1 Vehicle Kinematic Modelling
The formulation of a kinematic model for a RLV es-
tablishes the mathematical equations which relate the
temporal variations of the vehicle pose, with the linear
velocities on the wheels (i.e. steering plus the wheel
linear speed). It consists on a pure geometrical study
that is carried out without considering vehicle dy-
namic propertiessuch as mass, inertia, slip or friction.
On this line, and referring to Fig. 1, consider the
state vector q = [x
c
y
c
θ
m
] as a representation of the
vehicle pose in the frame {I}, with (x
c
,y
c
) the coor-
dinates of the center of the vehicle and θ
m
the orien-
tation of the vehicle. Also, consider v
t
as the vehi-
cle’s total speed and β the controllable sideslip angle,
both defined in {I} (Fig. 1). A kinematic model for
a RLV in {I}, that allows the simulation of the vehi-
cle motion directly through the desired total speed v
t
of the vehicle, instead of imposing an individual lin-
ear speed for each wheel, was introduced in (Wang,
2001) as follows:
˙x
c
˙y
c
˙
θ
m
=
cos(θ
m
+ β)
sin(θ
m
+ β)
cosβ[tanθ
F
−tanθ
R
]
M
v
t
. (1)
This modelling entails that the wheels of the ve-
hicle roll without slipping, a constraint inherent to
the nonholonomy of RLVs, and also considers a rigid
body constraint, common to this type of vehicles, as
follows:
v
F
cosθ
F
= v
R
cosθ
R
. (2)
The possibility of directly control β, allows the ve-
hicle to move either with both wheels following the
same path (LG), or with each wheel following a dif-
ferent path (FR) (Vale et al., 2012).
2.2 Error Coordinates
A path following controller should reduce to zero i)
the distance from the vehicle to the path and ii) the
angle between the current orientation of the vehicle
and the desired orientation at the path. This motivates
the development of a kinematic model for a RLV in
a Serret-Frenet {F} frame that moves along the path,
as depicted in Fig. 3. This type of approach can be
found in (Micaelli and Samson, 1993) for wheeled
mobile robots, where {F} is attached to the path point
closest to the vehicle. This implies that the initial
position error of the vehicle in relation to the path,
would have to be smaller than the smallest radius of
c
p
Path described
by the center
of the vehicle
x
y
o
P
C
θ
m
β
θ
d
{I}
{F}
θ
c
Desired
Pose
r
!
"
!
Figure 3: RLV variables and {F} frame definitions.
curvature present in the path. The current work fol-
lows the approach taken in (Lapierre et al., 2006)
for wheeled mobile robots and in (Lapierre and Jou-
vencel, 2008) for underwater vehicles, which starting
from the grounds established in (Micaelli and Sam-
son, 1993), lifts the initial condition constraint en-
tirely, by attaching {F} to a virtual moving target
along the path. This introduces an extra degree of
freedom at the controller design stage.
Consider Fig. 3, where P is an arbitrary path point
to be followed and C is the CoG of the vehicle. As-
sociated with P, consider the corresponding Serret-
Frenet frame{F}, with the signed curvilinear abscissa
of P along the path denoted as s. One can either ex-
press C as q = (X,Y,0) in a selected inertial reference
frame {I} or as (s
1
,y
1
,0) in {F}. Stated equivalently,
C can be given in (X,Y) or (s
1
,y
1
) coordinates. Fur-
thermore, define θ
c
as the angle of the tangent to the
path at P,
˙
θ
c
= c
c
(s)˙s with c
c
(s) the path curvature as
a function of s, and θ
d
as the desired orientation of the
vehicle at the path. Referring to the aforementioned
literature and using (1), one can obtain ( ˙s
1
, ˙y
1
) as
˙s
1
= − ˙s(1− c
c
(s)y
1
) + v
t
cosθ
˙y
1
= −c
c
(s)˙ss
1
+ v
t
sinθ
˙
θ = ω
m
+
˙
β− c
c
(s)˙s
, (3)
where θ = θ
m
+ β− θ
c
and ω
m
=
˙
θ
m
.
This kinematic model of a RLV in {F}, with s
1
not
necessarily equal to zero, plays an important role in
the development of the nonlinear controller presented
in Section 3.4.
2.3 Path Following
With the background given in the current section, and
with reference to Fig. 3, the path following problem
under study can be formulated as:
Consider the kinematic model for RLVs given by
(1) and (3). Given a LG or FR path to be fol-
lowed parametrized in terms of its length and a de-
sired speed profile v
t
d
(t) > v
t
min
> 0 for the vehicle
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
50

total speed v
t
, derive the feedback control laws for
the linear speeds v
F
,v
R
and orientations θ
F
,θ
R
of the
wheels, or alternatively β and ω
m
, so that s
1
, y
1
and
θ tend to zero.
In the current paper, the desired speed profile
mentioned above is embedded in the trajectory pro-
vided by the motion planning described in (Vale et al.,
2012). Moreover, the formulation of the control laws
for β and ω
m
requires a transformation [ω
m
,β,v
t
] →
[v
F
,v
R
,θ
F
,θ
R
], detailed in Section 3, since, ulti-
mately, one must determine the linear speeds and ori-
entations of the wheels that drive the vehicle to the
path.
3 PATH FOLLOWING CONTROL
DESIGN
In what follows are unveiled the four path following
controllers developed for RLVs, which represents the
major novelty of this paper.
3.1 Alonzo Kelly Modified Controller
Two feedback control laws are here introduced by
the authors that solve the problem enunciated in Sec-
tion 2.3. The Alonzo Kelly Modified(AKM) path fol-
lowing controller draws its inspiration on the Inverse
Kinematic Model (IKM) for RLVs proposed by A.
Kelly in (Kelly, 2010). The formulation of the AKM
controller herein presented is capable of both LG and
FR, requiring only as input from the motion planning
stage the path poses to be followed.
Referring to Fig. 1, the IKM described in (Kelly,
2010) and presented here in (4), enables the trans-
formation [ω
m
,β,v
t
] → [v
F
,v
R
,θ
F
,θ
R
]. To obtain
the values of v
F
,v
R
,θ
F
,θ
R
, while respecting the
rigid body constraint (2) and, therefore, guarantee-
ing that the wheels roll without slipping, one can
use the trigonometric relations θ
i
= arctan
v
i
y
v
i
x
, for
Path described
by the center
of the vehicle
Desired Pose
on the path
β
θ
d
β
d
θ
m
C
P
x
y
o
{I}
Figure 4: Alonzo Kelly Modified controller representation
and variables definition.
the wheels’ orientation, and v
i
=
q
v
2
i
x
+ v
2
i
y
, for the
wheels’ speed, with i ∈ {R,F}.
v
Fx
v
Fy
v
Rx
v
Ry
=
cosβ 0
sinβ M
F
cosβ 0
sinβ −M
R
"
v
t
ω
m
#
(4)
Hence, this IKM enables the formulation of a path
following controller that only requires as input the de-
sired pose of the vehicle at the path, [P
x
,P
y
,θ
d
], and
upon the control of β and ω
m
, outputs the values of
v
F
,v
R
,θ
F
,θ
R
that enable the vehicle to converge and
follow the desired path (Fig. 4). Moreover, the kine-
matic singularity θ
R
,θ
F
6= ±π/2 present in (Morin
and Samson, 2011) is lifted entirely with the addi-
tional v
F
,v
R
control inputs introduced here. As men-
tioned previously, v
t
is assumed to follow the desired
speed profile embedded in the trajectory as described
in (Vale et al., 2012).
A control law for β is used to direct the vehicle’s
velocity towards the desired path point, as depicted in
Fig. 4. Referring to the IKM (4) and excluding, for
the moment, the effect of ω
m
in the velocity of each
wheel, the β control law orientates the wheels in a
manner that they point towards the desired path point.
Such an objective can be embodied in the geometric
law that follows:
β = arctan
P
y
−C
y
P
x
−C
x
− θ
m
. (5)
where (P
x
,P
y
) are the coordinates of the center of the
path pose being followed and (C
x
,C
y
) the coordinates
of the center of the vehicle (Fig. 4). By replacing (5)
in (4), the wheels’ velocity and, therefore, the vehi-
cle’s velocity is, at all times, directed towards the de-
sired path pose.
A control law for ω
m
is responsible for orientating
the vehicle with the desired orientation at the path. A
function that embodies this objective, can be formu-
lated as follows:
ω
m
=
(θ
d
− θ
m
)k
ω
m
t
n
, (6)
with t
n
the simulation step and k
ω
m
a positive gain that
tunes the vehicle’s response rate to orientation varia-
tions.
Another degree of freedom inherent to the AKM
controller is the choice of the path point to follow. In
the formulation of (5) and (6) is chosen the closest
path point P, this being the orthogonal projection of
the C on the path (Fig. 4). Though, by introducing
an offset on the path point to be followed, referred in
the literature as lookahead distance, the performance
PathFollowingControlofRhombicLikeVehicles-PerformanceAssessmentwithDynamicVehicleModel
51

of the controller can be significantly improved. In
fact, due to the impossibility of the vehicle’s wheels
to instantaneously change orientation or speed, the in-
troduction of a lookahead distance might guarantee
that when the vehicle actually reaches the path point
”looked at”, the pose becomes the desired one. More-
over, the lookahead distance can be fixed or speed
dependant, depending on whether there is a varying
speed profile, as it happens in the present case.
In brief, as tunable parameters the AKM con-
troller has the choice of the lookahead point P and
the gain k
ω
m
.
3.2 Arc Path Following Controller
A geometric control method has been developed by
the authors, named Arc Path Following (APF) con-
troller, capable of both LG and FR. The key idea of
APF is to exploit the high degree of mobility of RLVs
by computing a simple but effective feedback con-
trol law based on geometric and kinematic reasoning.
Since the vehicle is free to define its Instantaneous
Center of Rotation (ICR) in R
2
, it is in any case possi-
ble (unless specific physical constraints exist) to com-
pute the generalized circular path that steers the vehi-
cle from the current pose to the desired one. Thereby
this strategy solves the problem enunciated in Sec-
tion 2.3. The concept is captured in Fig. 5. A sim-
ilar approach using circular path manifolds in a more
general framework has been found in (Kim and Mi-
nor, 2007), whereas the use of clothoids is proposed
in (De Cecco et al., 2007).
The general solution to the desired ICR (ICR
d
) ex-
pressed in the mobile reference frame {M}, arises as
(ICR
d
)
M
=
1
2
T
x
+
T
y
tan
(
θ
e
/
2
)
1
2
T
y
+
T
x
tan
(
θ
e
/
2
)
, (7)
where θ
e
= θ
m
−θ
d
and T = [T
x
,T
y
] is the vector P−C
expressed in {M} (see Fig. 5).
The desired radius of curvature for the front (Rd
F
)
and rear (Rd
R
) wheels, expressed in {M}, are
(Rd
F
)
M
=
Rd
F
x
Rd
F
y
T
= (F)
M
− (ICR
d
)
M
, (8)
(Rd
R
)
M
=
Rd
R
x
Rd
R
y
T
= (R)
M
− (ICR
d
)
M
, (9)
with (F)
M
= [
M
2
0
] and (R)
M
= [
−
M
2
0
].
Thus the feedback control laws, one for each
wheel, can be written, using (7)-(9), as
θ
F
= arctan
Rd
F
y
Rd
F
x
−
π
2
sign
Rd
F
y
, (10)
θ
R
= arctan
Rd
R
y
Rd
R
x
−
π
2
sign
Rd
R
y
. (11)
Desired Instantaneous Center of Rotation (
)
x
y
o
{I}
Path described
by the center
of the vehicle
Desired Pose on
the Path
!
"
#
$
#
%
&
#
'
!
(
"
(
)
*
{M}
#
(
!
(
+
!
(
,
Figure 5: Arc Path Following controller representation and
variables definition.
Expanding (10) and (11), the feedback control
laws become:
θ
F
= arctan
−T
y
tan(θ
e
/2) − T
x
(M − T
x
)tan(θ
e
/2) + T
y
+
+
π
2
sign
T
y
+
T
x
tan(θ
e
/2)
, (12)
θ
R
= arctan
−T
y
tan(θ
e
/2) − T
x
−(M + T
x
)tan(θ
e
/2) + T
y
+
+
π
2
sign
T
y
+
T
x
tan(θ
e
/2)
. (13)
Equations (12) and (13) present singularities
which can be easily solved. They come from three
singular cases:
1. both numerator and denomitator in the arctan
functions are zero;
2. θ
e
= 0 in the sign function, that is when the cur-
rent vehicle attitude is equal to the desired one.
3. T
x
= T
y
= 0 in the sign function, that is when the
current reference point is equal to the desired one.
Case 1) occurs when either the current position of
the forward or the rear wheel are coincident with the
desired ones. To solve this case it is sufficient to set,
respectively, ICR
d
= (F)
M
or ICR
d
= (R)
M
.
Case 2) is solved by substituting (12)-(13) by their
limit as θ
e
→ 0:
θ
F
= θ
R
= arctan
Ty
Tx
. (14)
Case 3) occurs when the referencepoint ofthe cur-
rent and desired vehicle pose are coincident (C = P).
This is solved by setting ICR
d
= (C)
M
.
It has to be noticed that all the singularities de-
scribed above do not consist in discontinuities of the
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
52

control laws. They are degeneracy cases of the solu-
tions expressed by (7) and (12)-(13) due to special ge-
ometric configurations in the problem definition. By
the above considerations, the control law is smooth
for every possible vehicle pose.
Similarly to the AKM controller, the APF con-
troller formulation enables the introduction of a
lookahead distance, i.e. it is not mandatory that P is
the orthogonal projection of C on the path (Fig. 5).
This represents an extra degree of freedom in the con-
troller that can be exploited to achieve smoother and
better path following performances.
In brief, the APF controller has the choice of the
lookahead point P as its only tunable parameter.
3.3 Stanley Modified Controller
The Stanley Method Modified (SMM) path following
controller, is an extension to RLVs of the path fol-
lowing controller used by Stanford University’s au-
tonomous car entry in the DARPA Grand Challenge,
named Stanley (Thrun et al., 2006). This controller
is capable of both LG and FR, though, it requires
as inputs the path to be followed by both wheels, in
contrast with the other controllers here presented that
only require the path poses.
Considering the path following controller de-
scribed in (Thrun et al., 2006), the SMM employs two
nonlinear feedback functions of the cross-track errors
e
F
and e
R
, respectively, which are a measure of the
distance from the center of each wheel to the nearest
point on the respective wheel path, as shown in Fig. 6.
The SMM approach results in two control laws, one
for each wheel, responsible for converging e
F
and e
R
to zero and for which exponential convergence can be
shown (Thrun et al., 2006).
The feedback control laws for θ
F
and θ
R
can be
written, with reference to Fig. 6, as
θ
F
= θ
e
F
+ arctan
ke
F
v
F
, (15)
θ
R
= θ
e
R
+ arctan
ke
R
v
R
, (16)
where: θ
F
,θ
R
are the required outputs; v
F
,v
R
are the
desired front and rear wheel speeds, respectively, em-
bedded in the trajectory as described in (Vale et al.,
2012); k is a gain parameter, chosen equally for both
wheels to maintain vehicle symmetry; e
F
,e
R
repre-
sent the cross-track errorsfor the frontand rear wheel,
respectively; and θ
e
F
,θ
e
R
describe the orientation of
the nearest path segment, measured relative to the ve-
hicle’s own orientation (see Fig. 6). The first term
of (15) and (16) simply keeps the wheel parallel to the
respective wheel path. When the cross-track error is
Path described by the
center of the vehicle
x
y
o
{I}
!
"
Path described by
the rear wheel
Path described by
the front wheel
Figure 6: Stanley Method Modified controller representa-
tion and variables definition.
non-zero, the second term adjust the steering of each
wheel in (nonlinear) proportion to the cross-track er-
ror: the larger this error, the stronger the steering re-
sponse towards the respective wheel path.
Against to what was mentioned for the AKM con-
troller, the formulation above for the SMM controller
precludes the introduction of a lookahead distance.
The referencepath point to be followed by each wheel
must inevitably be the orthogonal projections of the
contact points of the wheels in the respective wheel
path.
In brief, the SMM controller has the gain k as its
only tunable parameter.
3.4 Nonlinear Based Controller
Two nonlinear feedbackcontrol laws have beendevel-
oped by the authors to steer the kinematic model (3),
along a desired path and at constant speed (˙v
t
= 0).
The Nonlinear Control Based (NCB) path follow-
ing controller, has its grounds on the work done in
(Micaelli and Samson, 1993; Lapierre et al., 2006)
on path following control for kinematic models of
wheeled mobile robots and in (Lapierre and Jouven-
cel, 2008) on the same topic but for autonomous un-
derwater vehicles. In contrast to the work described in
(Micaelli and Samson, 1993), the usage of the virtual
target principle enables the formulation of the path
following problem in a non-singular manner, thus
guaranteeing global convergence to the path. More-
over, the NCB controller sets apart from the kine-
matic controller developed in (Lapierre and Jouven-
cel, 2008) by deliberately controlling the rate of evo-
lution of the vehicle’s sideslip angle,
˙
β, separately
from the vehicle’s angular speed, ω
m
. This enables
the vehicle to convergeand follow a desired LG or FR
path, exploiting the full maneuverability of a RLV.
Referring to Fig 3, the objective of deriving a con-
trol law for
˙
β can be embodied in the Lyapunov func-
tion candidate (see (Lapierre et al., 2006))
PathFollowingControlofRhombicLikeVehicles-PerformanceAssessmentwithDynamicVehicleModel
53

V
1
=
1
2
s
2
1
+ y
2
1
+
1
2γ
θ− δ
β
(y
1
,v
t
)
2
, (17)
under the assumptions (A.1) y
1
v
t
sinδ
β
(y
1
,v
t
) ≤
0,∀y
1
∀v
t
, (A.2) δ
β
(0,v
t
) = 0 and (A.3) lim
t→∞
v
t
(t) 6=
0. Also, let the desired approach angle function δ
β
be
defined by
δ
β
= −θ
β
tanh
k
δ
β
y
1
v
t
, (18)
where 0 < θ
β
< π/2 and k
δ
β
is an arbitrary positive
gain. Notice how equation (18) satisfies the first and
second assumptions.
In (17) the first term captures the distance between
the vehicle and the path, which must be reduced to 0.
In turn, this term also precludes the introduction of a
lookahead distance in the NCB controller. The sec-
ond term shapes the approach angle of β to the path
as a function of the ’lateral’ distance y
1
and speed
v
t
, by forcing it to follow a desired orientation pro-
file embedded in (18). The parameter γ accounts only
for normalization purposes. The first assumption pro-
vides an adequate reference sign definition to drive
the vehicle to the path, i.e. turn the vehicle left when
on the right side of the path, and turn right in the other
situation. A.2 imposes the condition that β must be
such that the vehicle’s velocity is tangent to the path
when y
1
= 0, regardless of the vehicle orientation. Fi-
nally, the last assumption states that the vehicle does
not tend to a state of rest, case when the controllability
cannot be guaranteed.
Consider the following kinematic control laws for
s, the virtual moving target, and β as:
˙s = v
t
cosθ+ k
s
s
1
, (19)
˙
β =
˙
δ
β
+ c
c
(s)˙s−
˙
θ
m
− γy
1
v
t
sinθ− sinδ
β
θ− δ
β
− k
β
(θ− δ
β
),
(20)
with k
β
and k
s
positive gains. This yields
˙
V
1
= −k
s
s
2
1
+ y
1
v
t
sinδ
β
− k
β
θ− δ
β
2
γ
≤ 0, (21)
where the presence of the term y
1
v
t
sinδ
β
in the pre-
vious equation justifies A.1. Moreover, (21) depicts
the importance of the virtual target control law (19)
on guaranteeing global convergence to the path.
Therefore, the kinematic control laws (19)-(20)
drive s
1
,y
1
and θ asymptotically to zero, i.e. the ve-
hicle converges asymptotically to the path. The proof
builds similarly to the ones found in (Micaelli and
Samson, 1993; Lapierre et al., 2006) and (Lapierre
and Jouvencel, 2008).
The second objective of deriving a control law for
ω
m
can be embodied in the Lyapunov function candi-
date
V
2
=
1
2γ
(θ
m
− θ
d
− δ
ω
m
(y
1
,v
t
))
2
, (22)
under the assumption (A.4) δ
ω
m
(0,v
t
) = 0 and with
δ
ω
m
defined in a similar manner as in (18).
The Lyapunov function (22) captures the orienta-
tion error between the current orientation of the vehi-
cle and the desired orientation at the path, which must
be reduced to zero. A.4 guarantees that the vehicle’s
orientation must be equal to the desired orientation at
the path when y
1
= 0.
By makingthe kinematiccontrol law forω
m
=
˙
θ
m
,
required for Lyapunov stability, as
ω
m
=
˙
δ
ω
m
+
˙
θ
d
− k
ω
m
(θ
m
− θ
d
− δ
ω
m
), (23)
with k
ω
m
a positive gain,
˙
V
2
becomes
˙
V
2
= −k
ω
m
(θ
m
− θ
d
− δ
ω
m
)
2
γ
≤ 0. (24)
Hence, control law (23) drives θ
m
− θ
d
asymptot-
ically to zero, i.e. the vehicle’s orientation converges
asymptotically to the desired orientation at the path.
Similarly, the proof is alike to the ones found in (Mi-
caelli and Samson, 1993; Lapierre et al., 2006) and
(Lapierre and Jouvencel, 2008).
To determine the values of v
F
,v
R
,θ
F
and θ
R
, the
IKM (4) is used. The required value of ω
m
is obtained
directly from the control law (23), while β is obtained
by integrating the output of the control law (20). Sim-
ilarly to the AKM controller, v
t
is provided by the tra-
jectory.
In brief, the NCB controller has the following tun-
able parameters: the normalization parameter γ, the
gains k
δ
β
, k
δ
ω
m
, k
β
, k
s
and k
ω
m
, and the approach an-
gles θ
β
and θ
ω
m
.
4 DYNAMIC MODELLING
The RLV kinematic models (1) and (3), are able
to capture the essentials of the motion of RLVs.
However, the non-slipping assumptions in which the
derivation of the kinematic model was based, will
hardly be satisfied in reality if the vehicle’s kinetic
energy is significant. Hence, the dynamic formulation
that follows aims to provide a more accurate simula-
tion scenario for the test of the controllers developed
in Section 3. In the present case, the RLV is regarded
as a rigid vehicle with a strictly planar motion. Hence,
it has three degrees of freedom: x and y translation,
and a rotation about the z-axis. The Newton-Euler
equations of motion for a rigid vehicle in the vehicle
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
54

frame {M}, attached to the vehicle at its mass center
C, are (Jazar, 2008):
F
x
= m˙u− mω
m
v
F
y
= m˙v+ mω
m
u
M
z
=
¨
θ
m
I
zz
. (25)
The symbols m and I
zz
represent, respectively, the
mass and moment of inertia, around the z axis, of the
vehicle. In the frame {M}, u and v denote the longi-
tudinal and transverse speeds of the vehicle, respec-
tively.
To determine the forces F
x
, F
y
and moment M
z
,
must be noticed that the vehicle motion is a conse-
quence of forces acting at the vehicle’s wheels. In
fact, the forces acting on the vehicle can be cate-
gorized as: transverse forces, F
s
i
, and longitudinal
forces, F
l
i
, acting on the wheels, with i ∈ {R, F} . This
formulation entails, with reference to Fig. 1:
m˙u− mω
m
v =F
l
F
cosθ
F
− F
s
F
sinθ
F
+ F
l
R
cosθ
R
− F
s
R
sinθ
R
, (26)
m˙v+ mω
m
u =F
l
F
sinθ
F
+ F
s
F
cosθ
F
+ F
l
R
sinθ
R
+ F
s
R
cosθ
R
, (27)
¨
θ
m
I
zz
=F
l
F
sinθ
F
M
F
+ F
s
F
cosθ
F
M
F
− F
l
R
sinθ
R
M
R
− F
s
R
cosθ
R
M
R
. (28)
To calculate F
s
i
and F
l
i
, is followed the approach
taken in (Fonte, 2011), where a simplified linear tire
model is used, as follows:
F
s
i
= C
s
α
i
, α
i
=
θ
i
− arctan
v±
˙
θ
m
M
i
u
, (29)
F
l
i
= C
l
σ
i
, σ
i
=
v
i
− v
ef f
i
cosα
i
max
|v
i
|,
v
ef f
i
cosα
i
. (30)
The following definitions apply (Fonte, 2011): C
l
=
f(F
z
i
) andC
s
= f(F
z
i
) are the longitudinal and corner-
ing stiffness, respectively, which depend on the nor-
mal force applied at the wheel, F
z
i
, and considered
equal for both wheels (F
z
F
= F
z
R
); α
i
is the wheel
slip angle; σ
i
is the wheel longitudinal slip ratio;
v
ef f
i
is the effective rolling speed of wheel i given by
v
ef f
i
=
q
u
2
+
v±
˙
θ
m
M
i
2
; v
i
is the inputted wheel
speed (at the actuator level); and ± is positive for
i = F and negative for i = R.
The combined slip effects, which occur when both
F
s
i
,F
l
i
6= 0, is taken into account by clipping (29) and
(30) as stated in (Jazar, 2008):
F
2
s
i
+ F
2
l
i
= (µF
z
i
)
2
, (31)
where µ is the friction coefficient between the tire and
the contact surface.
Furthermore,a discrete first ordermodel in the lin-
ear speed of the wheels and a discrete second order
model in the orientation of the wheels, is used to sim-
ulate the typical behavior of wheel actuators.
5 RESULTS
This section illustrates the simulated performance of
the four path following controllers described in Sec-
tion 3. The simulationswere performedusing the Tra-
jectory Evaluator and Simulator (TES) software de-
veloped under the scope of previous grants of Remote
Handling with the domestic agency Fusion for Energy
(F4E), as described in (Vale et al., 2012). The vehi-
cle simulated was a RLV with the characteristics of
the CPRHS, while following a trajectory to port 14 in
level B1 of TB of ITER (Fig. 7). The trajectory used
in the simulations is a discrete FR path, at constant
speed, formed by a set of consecutive poses, as de-
picted in Fig. 7. This trajectory was calculated using
the motion planning realized in (Vale et al., 2012).
The performance of the four controllers is as-
sessed by measuring the cross-track error of the cen-
ter of the vehicle, e
C
, along the path, as depicted in
Figs. 8 and 9. To determine the influence of vehicle
dynamics in the performance of the controllers, two
series of tests were realized: on the first, the vehicle
total speed, v
t
, is set constant to 0.15 m/s and the mass
is 50T (Fig. 8); on the second test, v
t
is set to 0.4 m/s
and the mass is 100T (Fig. 9). On both series of tests,
each of the controllers is tested individuallyunder two
situations, these being using the kinematic model (1),
Complete Path
Lift Exit (Zoom)
Port 14 Entrance (Zoom)
Figure 7: Path used in the simulation: FR path from lift to
port 14 in level B1 of TB of ITER.
PathFollowingControlofRhombicLikeVehicles-PerformanceAssessmentwithDynamicVehicleModel
55
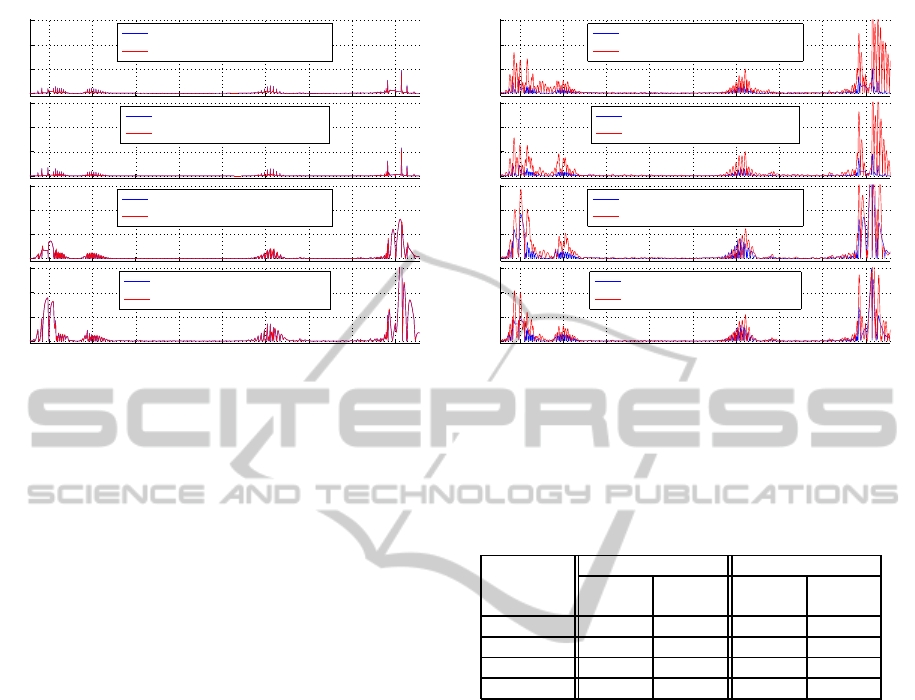
0
0.02
0.04
0.06
e
C
[m]
AKM (Kinematic Simulation)
AKM (Dynamics Simulation)
0
0.02
0.04
0.06
APF (Kinematic Simulation)
APF (Dynamics Simulation)
0
0.02
0.04
0.06
SMM (Kinematic Simulation)
SMM (Dynamics Simulation)
10 20 30 40 50 60 70 80 90
0
0.02
0.04
0.06
Distance along the path [m]
NCB (Kinematic Simulation)
NCB (Dynamics Simulation)
Figure 8: Cross-track error, e
C
, comparison for each of the
four controllers, while simulating, or not, vehicle dynamics,
in a trajectory to port 14 in level B1 of TB of ITER. The
vehicle speed is 0.15 m/s and the mass is 50T.
or using the dynamic model (25), for simulating the
motion of a RLV. Though, it is important to mention
that actuators dynamics is always present across the
tests and the controllers gains are kept the same.
As it can be seen in Figs. 8 and 9, the controllers
performancedeterioratesas v
t
increases and while ne-
gotiating turns (zoomed areas in Fig. 7). More im-
portantly, Fig. 8 demonstrates how wheel slippage at
0.15 m/s for a 50T RLV is negligible, since the perfor-
mance of the controllers is the same regardless of the
utilization of a kinematic or dynamic model for ve-
hicle simulation. In contrast, Fig. 9 depicts how the
performance of the controllers worsens at 0.4 m/s for
a 100T RLV if a dynamic vehicle model, instead of a
kinematic one, is used for simulation. This result en-
hances the importance of including vehicle dynamic
considerations in the design of the controllers.
Overall, the AKM and APF controllers attain sim-
ilar performances and surpass the NCB and SMM
controllers. This demonstrates how the inclusion of a
lookahead distance contours the non consideration of
vehicle and actuators dynamics in the path following
controllers formulation. To achieve the results shown
for the AKM and APF controllers, a 0.09 m looka-
head distance was used. This allowed a superior per-
formance while using a kinematic model for vehicle
simulation. Though, it is also the reason of the strong
oscillations while using a dynamic model for simula-
tion (Fig. 9). In fact, a high lookahead distance (e.g.
1 m) increases e
C
, but enables the controller to better
stabilize the vehicle under high wheel slippage. Table
1 summarizes the controllers performance at port 14
entrance (Fig. 7), this being the most critical part of
0
0.02
0.04
0.06
e
C
[m]
AKM (Kinematic Simulation)
AKM (Dynamics Simulation)
0
0.02
0.04
0.06
APF (Kinematic Simulation)
APF (Dynamics Simulation)
0
0.02
0.04
0.06
SMM (Kinematic Simulation)
SMM (Dynamics Simulation)
10 20 30 40 50 60 70 80 90
0
0.02
0.04
0.06
Distance along the path [m]
NCB (Kinematic Simulation)
NCB (Dynamics Simulation)
Figure 9: Cross-track error, e
C
, comparison for each of the
four controllers, while simulating, or not, vehicle dynamics,
in a trajectory to port 14 in level B1 of TB of ITER. The
vehicle speed is 0.4 m/s and the mass is 100T.
Table 1: RMSE of e
C
for each of the controllers at port 14
entrance, while using a kinematic, or a dynamic, model for
vehicle simulation. Units are in [mm].
Controllers
Kinematic Model Dynamic Model
0.15 m/s 0.40 m/s
0.15 m/s 0.40 m/s
50T 100T
AKM 1.8 4.3 1.7 25.2
APF 2.1 3.6 1.9 22.5
SMM 12.1 23.2 12.2 36.1
NCB 25.7 16.1 25.8 26.4
the path.
In relation to the NCB controller, a comparison
between Figs. 8 and 9 reveals that, while using a kine-
matic model for simulation, the NCB performance is
better at 0.4 m/s than at 0.15 m/s. Although it seems
contradictory, this is justified by (18), which depicts
how, for the same gains, a stronger path deviation cor-
rection is achieved if the vehicle total speed, v
t
, is
higher. This issue can be mitigated at a kinematic
level by increasing the NCB gains. Though, while
dealing with vehicle dynamics, high gains would in-
crease vehicle instability and decrease path following
performance.
It should be noticed that all the four path following
controllers perform well within the 30 cm safety mar-
gin established for the scenario, even while dealing
with the dynamics of a 100T vehicle at 0.4 m/s. The
maximum e
C
registered was 11.95 cm for the SMM
controller at 0.4 m/s with dynamics.
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
56

6 CONCLUSIONS
Four path following controllers for RLVs were de-
veloped and implemented. Alongside, the dynamic
modelling of a RLV was realized. The tests aimed to
assess the controllers performance while using either
the kinematic or the dynamic vehicle model for sim-
ulation. All the controllers perform within the strict
safety margin constraints established for the cluttered
scenarios of ITER and attain good results, even in
the presence of some wheel slippage. The study of
four distinct controllers enables the conclusion that
both the AKM and APF controllers slightly stand out
from the other two, due to the inclusion of a looka-
head distance which contours the vehicle and actua-
tors dynamicsissue. The SMM controller still enables
a good performance, while being very simple, and is a
good choice if the path of the wheels is available. The
NCB controller also achieves a good performance and
possesses the biggest room for improvement, by en-
abling the inclusion of vehicle and actuators dynamics
through backstepping techniques.
The results were obtained only in simulation and
a future route would pass by performing experimen-
tal tests at a small scale, to begin with, and, ultimately,
at a larger scale. The results show that when the ve-
hicle’s mass and speed is significant, the controllers
performance deteriorates. Hence, an improved ver-
sion of the controllers is being developed, that takes
into account dynamic considerationsat the controllers
design stage.
ACKNOWLEDGEMENTS
The work was supported by FCT in the frame of the
Contract of Associate Laboratories of Instituto de Plas-
mas e Fus˜ao Nuclear – Laborat´orio Associado/IST (Pest-
OE/SADG/LA0010/2011).
REFERENCES
De Cecco, M., Bertolazzi, E., Miori, G., Oboe, R., and
Baglivo, L. (2007). PC-sliding for vehicles path plan-
ning and control - Design and evaluation of robustness
to parameters change and measurement uncertainty.
In Proceedings of the 4th International Conference
on Informatics in Control, Automation and Robotics
(ICINCO), pages 11–18, Angers.
Fonte, D. (2011). Motion Planning for a Rhombic-Like Ve-
hicle Operating in ITER Scenarios. PhD thesis, Insti-
tuto Superior T´ecnico.
Hiraoka, T., Nishihara, O., and Kumamoto, H. (2009). Au-
tomatic path-tracking controller of a four-wheel steer-
ing vehicle. Vehicle System Dynamics, 47(10):1205–
1227.
Jazar, R. N. (2008). Vehicle Dynamics: Theory and Appli-
cation. Springer.
Kelly, A. (2010). A Vector Algebra Formulation of Kine-
matics of Wheeled Mobile Robots. Technical report,
Robotics Institute.
Kim, Y. and Minor, M. a. (2007). Path Manifold-based
Kinematic Control of Wheeled Mobile Robots Con-
sidering Physical Constraints. The International Jour-
nal of Robotics Research, 26(9):955–975.
Lapierre, L. and Jouvencel, B. (2008). Robust nonlinear
path-following control of an AUV. IEEE Journal of
Oceanic Engineering, 33(2):89–102.
Lapierre, L., Soetanto, D., and Pascoal, A. (2006). Non-
Singular Path-Following Control of a Unicycle in the
Presence of Parametric Modeling Uncertainties. In-
ternational Journal of Robust and Nonlinear Control,
16(10):485–503.
Luca, A. D. and Oriolo, G. (1998). Feedback control of a
nonholonomic car-like robot. In Laumond, J.-P., ed-
itor, Robot motion planning and control, chapter 4th.
Springer.
Micaelli, A. and Samson, C. (1993). Trajectory tracking for
unicycle-type and two-steering-wheels mobile robots.
Technical report, INRIA.
Morin, P. and Samson, C. (2011). Control of two-steering-
wheels vehicles with the Transverse Function ap-
proach. In Proceedings of the 50th IEEE Confer-
ence on Decision and Control and European Con-
trol Conference (CDC-ECC), number 3, pages 7349–
7355, Orlando.
Ribeiro, M. and Lima, P. (1997). Conceptual study on flex-
ible guidance and navigation for ITER remote han-
dling transport casks. In Proceedings of the 17TH
IEEE/NPSS Symposium on Fusion Engineering, vol-
ume 2, pages 969–972, San Diego.
Thrun, S., Montemerlo, M., and Dahlkamp, H. (2006).
Stanley: The robot that won the DARPA Grand Chal-
lenge. Journal of Field Robotics, 23(9):661–692.
Vale, A., Valente, F., Ribeiro, I., Ferreira, J., and Ventura, R.
(2012). Motion planning and localization approaches
for mobile robot navigation in ITER. In Proceedings
of Rob´otica 2012, pages 75–80, Guimar˜aes.
Wang, D. (2001). Trajectory Planning for a Four-Wheel-
Steering Vehicle. In Proceedings of the IEEE Interna-
tional Conference On Robotics And Automation, vol-
ume I-IV, pages 3320–3325, Seoul.
PathFollowingControlofRhombicLikeVehicles-PerformanceAssessmentwithDynamicVehicleModel
57
