
A Decision-Guided Energy Framework for Optimal Power, Heating,
and Cooling Capacity Investment
Chun-Kit Ngan
1
, Alexander Brodsky
1
, Nathan Egge
1
and Erik Backus
2
1
Department of Computer Science, George Mason University, 4400 University Drive, Fairfax, VA 22030, U.S.A.
2
Facilities Management Department, George Mason University, 4400 University Drive, Fairfax, VA 22030, U.S.A.
Keywords: Decision Guidance, Energy Investment, Optimization Model.
Abstract: We propose a Decision-Guided Energy Investment (DGEI) Framework to optimize power, heating, and
cooling capacity. The DGEI framework is designed to support energy managers to (1) use the analytical and
graphical methodology to determine the best investment option that satisfies the designed evaluation
parameters, such as return on investment (ROI) and greenhouse gas (GHG) emissions; (2) develop a DGEI
optimization model to solve energy investment problems that the operating expenses are minimal in each
considered investment option; (3) implement the DGEI optimization model using the IBM Optimization
Programming Language (OPL) with historical and projected energy demand data, i.e., electricity, heating,
and cooling, to solve energy investment optimization problems; and (4) conduct an experimental case study
for a university campus microgrid and utilize the DGEI optimization model and its OPL implementations,
as well as the analytical and graphical methodology to make an investment decision and to measure trade-
offs among cost savings, investment costs, maintenance expenditures, replacement charges, operating
expenses, GHG emissions, and ROI for all the considered options.
1 INTRODUCTION
Sustainable enterprise development has been
considered a significant and competitive strategy of
corporate growth in manufacturing and service
organizations. A significant part of sustainable
development involves new technologies for local
electricity, heating, and cooling generation. Making
optimal decisions on planning and investment of
these technologies to support commercial and
industrial facilities is an involved problem because
of complex operational dependencies of these
technologies. This is exactly the focus of this paper.
Currently, the existing approaches to support the
optimization of energy plants can be divided into
two categories: (1) optimal operation of an energy
system and (2) a better plant-process design
(Broccard et al., 2010). The former category is
related to the optimized scheduling of an electric
power plant. Some researchers, such as Bojic and
Stojanovic (Bojić and Stojanović, 1998), proposed
an optimization procedure based on a MILP solver
(SAS Institute, 2012) to provide an operation
diagram which allows users to find an optimum
composition of energy consumption that minimizes
the operating expenses of an energy system
(Brodsky and Wang, 2008); (Brodsky et al., 2009);
(Brodsky et al., 2011). The latter approach includes
the analysis of simulations carried out to determine
the most suitable matching between a plant and its
loads that could increase the plant power output.
Some researchers, e.g., Savola et al., (Savola and
Keppo, 1997) did extensive research to propose an
off-design simulation and mathematical modelling
of the operation at part loads and a Mixed-Integer
Non-Linear Programming (MINLP) optimization
model for increasing power production (Savola and
Fogelholm, 2007); (Tuula Savola et al., 2007).
However, neither of the above approaches
considers optimizing the complex interactions
between the existing components and the newly
added energy equipment that would result in a
higher operating cost, such as the charges on
electricity and gas consumptions, as well as
significant environmental impacts, i.e., greenhouse
gas (GHG) emissions, e.g., carbon dioxide (CO
2
)
and mono-nitrogen oxide (NO
x
). Without
considering such interactions for every time interval
over an investment time horizon, it would be
impossible to make optimal recommendations on
357
Ngan C., Brodsky A., Egge N. and Backus E..
A Decision-Guided Energy Framework for Optimal Power, Heating, and Cooling Capacity Investment.
DOI: 10.5220/0004447503570369
In Proceedings of the 15th International Conference on Enterprise Information Systems (ICEIS-2013), pages 357-369
ISBN: 978-989-8565-59-4
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

energy planning and investment.
Thus this paper focuses on addressing the above
shortcomings. More specifically, the contributions of
this paper are as follows. First, we propose a
Decision-Guided Energy Investment (DGEI)
Framework shown in Figure 1. Given electricity,
heating, and cooling generation processes, utility
contracts, historical and projected demand, facility
expansions, and Quality of Service (QoS)
requirements, the DGEI framework is designed to
recommend optimal settings of decision control
variables. These decision control variables include
the amount of electricity, heating, and cooling that is
generated by the supply of water and gas, which is
inputted to each deployed component in every time
interval. The goal of the DGEI framework is to learn
optimal values of those decision control variables in
order to minimize the total operating cost within the
required quality of service and within the bound for
GHG emissions, as well as to take into account all
components’ interactions. Second, to support the
DGEI framework, we develop a DGEI optimization
model, i.e., a MILP formulation construct, to solve
the adjusted cost minimization problem.
Furthermore, we implement the DGEI optimization
model by using the IBM Optimization Programming
Language (OPL) (Hentenryck, 1999); (The IBM
Corporation, 2012). Third, we propose an analytical
and graphical methodology to determine the best
available investment option based upon the
evaluation parameters shown in Figure 1. The
parameters include investment costs, maintenance
expenditures, replacement charges, operating
expenses, cost savings, return on investment (ROI),
and GHG emissions. Finally, we use the
methodology and the DGEI framework to conduct
an experimental case study on the microgrid at the
Fairfax campus of George Mason University
(GMU). This study has been conducted and used by
the GMU Facilities Management Department (FMD)
to make actual investment decisions.
Figure 1: Decision-Guided Energy Investment (DGEI)
Framework.
The rest of the paper is organized as follows.
Using the GMU Fairfax campus microgrid as an
example, we describe its energy investment problem
in Section 2. We explain our DGEI framework and
optimization model in Section 3 and demonstrate the
OPL implementation in Section 4. In Section 5, we
present the analytical and graphical methodology to
determine an optimal investment option. In Section
6, we conduct the experimental analysis on the
GMU energy investment case and illustrate the
relationships among the investment costs, ROI, and
GHG emissions of the various options in tabular and
graphical formats. We also explain and draw the
conclusion for the investment options from the
graphs and tables in detail on the GMU energy
investment problem. In Section 7, we conclude and
briefly outline the future work.
2 PROBLEM DESCRIPTION
OF REAL CASE STUDY
Consider the real case study at GMU, in which the
GMU Facilities Management Department (FMD) is
planning to extend and or expand the existing energy
equipment in order to meet the current and future
demand of electricity, heating, and cooling across
the expanding Fairfax campus in Virginia. Presently,
the GMU existing energy facilities at the Fairfax
campus operate a centralized heating and cooling
plant (CHCP) system and utilize the electricity
purchased from the Dominion Virginia Power
Company (DVPC) to satisfy all the energy demand.
Over the past 10 years, the campus has experienced
a significant growth on a square-foot basis in terms
of land use. Since the campus continues its
expansion at a rapid rate, the existing CHCP system
and the electricity consumption have reached a
saturated point where the current capacity and
facilities will not be able to satisfy the future energy
demand, i.e., electricity, heating, and cooling. For
these reasons, a study has been conducted to
determine the best available investment option, e.g.,
a new cogeneration (CoGen) plant, with regards to a
possible methodology to meet the current and future
electricity, heating, and cooling demand, while also
addressing the optimal operations of the newly
added facility with the existing energy equipment.
The diagram in Figure 2 depicts the GMU energy
generation process which supplies heating, cooling,
and electricity to the entire Fairfax campus. The
GMU energy facilities have a CHCP system to
supply the hot and cold water (see the red and blue
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
358
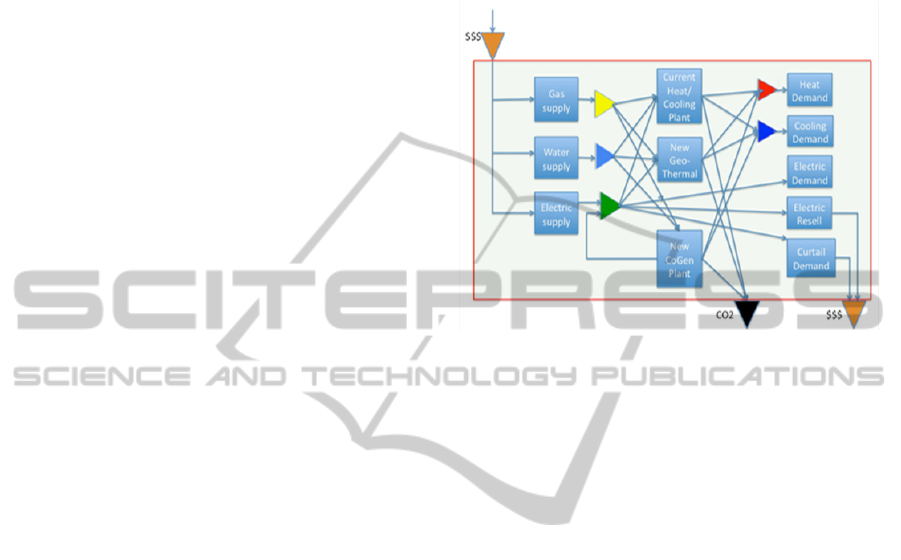
resources) which are distributed across the facilities
to the campus buildings to meet the heating and
cooling demand (see the upper two sub-processes on
the right), i.e., heating and air-conditioning to the
buildings. To supply the heating and cooling to the
campus buildings, the CHCP system needs the
inputs, i.e., natural gas (see the yellow resource on
the left), water (see the light blue resource on the
left), and electric power (see the green resource on
the left). These resources come from the gas supply,
i.e., Washington Gas Light Company (WGLC), the
water supply, i.e., Fairfax County Water Authority
(FCWA), and the electricity supply, i.e., Dominion
Virginia Power Company (DVPC), correspondingly.
In addition, the facilities also need to satisfy the
electricity demand across the entire campus, where
the electricity demand is beyond the demand from
the CHCP consumption. Any excessive electric
power supply can also be resold to the DVPC (see
the electricity resell on the right). Furthermore, the
facilities also commit a curtailment demand (see the
curtailment demand on the right) to the energy
curtailment program through EnergyConnect (EC),
Inc. Both the electricity resell and the curtailment
commitment can bring certain revenues and savings
to offset the overall operational costs on a monthly
basis and the capital expenditures in the long run.
The facilities also generate greenhouse gas (GHG)
emissions, such as carbon dioxide (CO
2
) (see the
black resource at the bottom right).
Given the expansion of the GMU Fairfax
campus, in addition to the increasing electricity
demand, the heating and cooling demand is also
expected to increase. The CHCP system will not
have enough capacity to meet the future need. The
GMU plan is to employ a procurement strategy, i.e.,
the deployment of the best available investment
option, which will satisfy projected demand and
minimize investment costs, maintenance
expenditures, replacement charges, operating
expenses, and GHG emissions, as well as maximize
cost savings and return on investment (ROI) at the
same time. The FMD managers are now considering
some viable options. One of the considerable options
is to integrate a new cogeneration (CoGen) plant
(see the lower sub-process in the middle), i.e., the
Combined Heating and Power (CHP) Plant (Biezma
and San Cristobal, 2006); (Broccard, et al., 2010),
into the existing facilities shown in Figure 2. The
new CoGen plant has turbines to generate electricity
to complement the electricity demand, uses the
generated heat as a by-product to complement the
heating demand, and collaborates with the ammonia
process technology (American Electric Power Inc.,
2012) to supply the cooling demand. Now, the
challenging question is how to analytically
determine the best investment option that satisfies all
the energy demand, i.e., electricity, heating, and
cooling, at the lowest operating costs.
Figure 2: Prospective Heating, Cooling, and Electric
Power Facilities at the GMU Fairfax campus.
3 DECISION-GUIDED ENERGY
INVESTMENT (DGEI)
FRAMEWORK
AND OPTIMIZATION MODEL
To answer the above question, we propose the DGEI
framework depicted in Figure 1. This framework is
composed of six energy-investment libraries, i.e.,
Energy Generation Process (EGP), Energy
Contractual Utility (ECU), Energy Historical
Demand (EHD), Energy Future Demand (EFD),
Energy Facility Expansion (EFE), Quality of Service
(QoS) requirements, and a DGEI optimizer. The
EGP is an extensible library that enables domain
experts to construct an energy generation process to
supply electricity, heating, and cooling. The ECU is
a library that contains energy contractual terms for
calculating bill utilities, e.g., an electricity bill, a
water bill, and a gas bill. The EHD and EFD are the
libraries that store historical and projected energy
demand respectively. The EFE library archives the
facility expansion of an organization in terms of
square-footage increase. The QoS library stores the
QoS requirements that the energy facilities of an
organization need to meet, e.g., the maximal power
interruptions allowed per monthly pay period in an
organization. The DGEI optimizer supports energy
managers to utilize all the libraries, i.e., EGP, ECU,
EHD, EFD, EFE, and QoS, as inputs to the decision
ADecision-GuidedEnergyFrameworkforOptimalPower,Heating,andCoolingCapacityInvestment
359

optimization process, which minimizes operating
expenses and maximize cost savings. This decision
optimization process not only optimizes the
interactions between the existing and the
considerable energy facility options but also
minimizes the environmental impacts on the
surroundings, i.e., minimizing the GHG emissions.
In addition to the GHG emissions, energy managers
also utilize (1) return on investment (ROI), i.e., the
gain return efficiency among different investments,
(2) the investment costs, i.e., an amount spent to
acquire a long-term asset, and (3) equipment
expenses, i.e., maintenance expenditures plus
replacement charges, to evaluate all the available
investments and then to determine the best option.
To solve an energy investment optimization
problem in terms of minimizing the operating cost
and the GHG emissions is to formulate a DGEI
optimization model. This model optimally learns
decision control variables, which require several
input data sets, i.e., the historical and projected
electricity, heating, and cooling demand over a time
horizon, the electric and gas contractual utility, the
operational parameters and capacity constraints of
the existing and the new electric power plants, as
well as the energy aggregation of the supply and
demand, e.g., electricity, gas, heating, and cooling,
to minimize the entire operating expenses. Using the
GMU energy investment optimization problem over
the 10-year time horizon as an example, we explain
the above terminologies used in this case study in
the following subsections.
3.1 Electricity, Heating, and Cooling
Demand over a Time Horizon
The electricity, heating, and cooling demand over a
time horizon is the input, including the usage of the
historical and projected quantities, which are
provided from the GMU Facilities Management
Department, to the DGEI optimization model that
requires the domain users to define all (i.e., past plus
future), past, and future power intervals over the 10-
year time horizon.
AllPowerIntervals is a set of all powerIntervals,
where each powerInterval is a tuple which includes
several attributes, i.e., pInterval, payPeriod, year,
month, day, hour, and weekDay. We use negative
and zero integers to represent the past time horizon
and positive integers to denote the future time
horizon. For example, pInterval is an hourly time
interval of the energy demand, where -8759 ≤
pInterval ≤ 78840. payPeriod is a monthly pay
period of the energy demand, where -11 ≤
payPeriod ≤ 108. Other attributes’ intervals
include 2011 ≤ year ≤ 2020, 1 ≤ month ≤ 12, 1 ≤
day ≤ 31, 0 ≤ hour ≤ 23, and 0 ≤ weekDay ≤ 6.
PastPowerIntervals is a set of past powerIntervals
of tuples, where -8759 ≤ pInterval ≤ 0, -11 ≤
payPeriod ≤ 0, year = 2011, 1 ≤ month ≤ 12, 1 ≤
day ≤ 31, 0 ≤ hour ≤ 23, and 0 ≤ weekDay ≤ 6.
FuturePowerIntervals is a set of future
powerIntervals of tuples, where 1 ≤ pInterval ≤
78840, 1 ≤ payPeriod ≤ 108, 2012 ≤ year ≤ 2020, 1
≤ month ≤ 12, 1 ≤ day ≤
31, 0 ≤ hour ≤ 23, and 0 ≤
weekDay ≤ 6.
After declaring the power intervals, the quantities
of electricity, heating, and cooling demand can be
stored in their arrays over their power intervals.
These three quantities of demand are provided by
the GMU Facilities Management Department.
demandKw[AllPowerIntervals] ≥ 0 is an array of
electricity demand over the AllPowerIntervals.
This array stores both the historical and the
projected demand over the PastPowerIntervals and
the FuturePowerIntervals respectively.
demandHeat[FuturePowerIntervals] ≥ 0 is an array
of projected heating demand over the
FuturePowerIntervals.
demandCool[FuturePowerIntervals] ≥ 0 is an array
of projected cooling demand over the
FuturePowerIntervals.
3.2 Electric and Gas Contractual
Utility
To determine the total operating cost, we need to
compute the consumption expenses of electricity and
gas supply according to their utility contracts.
The consumption expenses of electricity include
both the peak demand charge and the total power
consumption charge that are explained in detail as
follows.
3.2.1 Peak Demand Charge
For the electricity supply,
utilityKw[AllPowerIntervals] ≥ 0 is an array of
electricity supplied from the DVPC over the
AllPowerIntervals.
historicUtilityKw[i] is an array of past electricity
demand from the GMU, i.e.,
historicUtilityKw[i] = demandKw[i],
which satisfies the constraint, i.e., utilityKw[i]
== historicUtilityKw[i], where i ∈
PastPowerIntervals. This constraint is to assure that
the electricity consumed by the GMU in the past
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
360

year, i.e., 2011, is equivalent to the supply from the
DVPC.
payPeriodSupplyDemand[p] is the peak demand
usage per future pay period (p). This peak demand
usage meets the below contractual constraints (C1
and C2) and is determined based upon the highest of
either (C1) or (C2):
C1: The highest average kilowatt measured in
any hourly time interval of the current billing month
during the on-peak hours of either between 10 a.m.
and 10 p.m. from Monday to Friday for the billing
months of June through September or between 7
a.m. and 10 p.m. from Monday to Friday for all
other billing months.
C2: 90% of the highest kilowatt of demand at the
same location as determined under (C1) above
during the billing months of June through September
of the preceding eleven billing months.
The logic constraints of both C1 and C2 can be
expressed as follows:
if (i.payPeriod == p ∧ i.weekDay ≥ 1
∧ i.weekDay ≤ 5 ∧ ((i.month ≥ 6 ∧
i.month ≤ 9 ∧ i.hour ≥ 10 ∧ i.hour ≤
22) ∨ (i.month ≤ 5 ∧ i.month ≥ 10 ∧
i.hour ≥ 7 ∧ i.hour ≤ 22)))
payPeriodSupplyDemand[p] ≥
utilitykW[i]
else if (i.month ≥ 6 ∧ i.month ≤ 9 ∧
i.payPeriod ≥ p – 11 ∧ i.payPeriod ≤ p
∧ i.weekPay ≥ 1∧ i.weekDay ≤ 5 ∧ i.hour
≥ 10 ∧ i.hour ≤ 22)
payPeriodSupplyDemand[p] ≥ 0.9 *
utilitykW[i];
, where i ∈
AllPowerIntervals, p ∈ FuturePayPeriods, and 1 ≤
FuturePayPeriods ≤ 108. Using these logic
constraints, we can determine the optimal peak
demand usage per future pay period, which
consumes more than the expected electricity supply
per powerInterval from the DVPC.
generationDemandCharge[p], i.e.,
generationDemandCharge[p] = 8.124 *
payPeriodSupplyDemand[p];, is the Electricity
Supply (ES) service charge, i.e., the peak demand
charge, where p ∈ FuturePayPeriods, and 8.124 is
the dollar charge per kW.
3.2.2 Total Power Consumption Charge
payPeriodKwh[p] is the total power consumption
per future pay period, i.e.,
payPeriodKwh[p] =
∑utilitykW[i];, where i ∈ AllPowerIntervals, p
∈ FuturePayPeriods, and i.payPeriod = p.
payPeriodKwhCharge[p] is the total kWh charge
per future pay period, i.e., payPeriodKwhCharge[p]
≥ 0, which satisfies the below contractual
constraints:
if (payPeriodKwh[p] ≤ 24000)
payPeriodKwhCharge[p] = 0.01174 *
payPeriodKwh[p]
else if (payPeriodKwh[p] ≤ 210000)
payPeriodKwhCharge[p] = 0.01174 *
24000 + 0.00606 *
(payPeriodKwh[p] – 24000)
else
payPeriodKwhCharge[p] = 0.01174 *
24000 + 0.00606 * 186000 +
0.00244 * (payPeriodKwh[p] –
210000);
, where p ∈ FuturePayPeriods,
0.01174 is the dollar charge of the first 24000 kWh
consumed, 0.00606 is the dollar charge of the next
186000 kWh consumed, and 0.00244 is the dollar
charge of the additional kWh consumed. Note that if
payPeriodSupplyDemand[p] is 1000 kW or more,
210 kWh for each peak demand usage over 1000 kW
is added to the total power consumption to calculate
payPeriodKwhCharge[p].
3.2.3 Total Electricity Cost
The total electricity cost per future pay period is the
sum of payPeriodKwhCharge[p] and
generationDemandCharge[p], i.e.,
electricCostPerFuturePayPeriod =
(payPeriodKwhCharge[p] +
generationDemandCharge[p]);
, where p ∈
FuturePayPeriods.
Table 1: Descriptions for the Constant Values in the DGEI
Optimization Model of the GMU Energy Investment
Problem.
Constant Description
0.9
Percentage of the highest kW of demand
during the billing months of June through
September of the preceding 11 billing
months
8.124
Amount ($) of Electricity Supply (ES)
demand charged per kW
24000 First ES kWh
0.01174
Amount ($) of the first 24000 ES kWh
charged per kWh
186000 Next ES kWh
0.00606
Amount ($) of the next 186000 ES kWh
charged per kWh
210000
Sum of the first ES kWh and the next ES
kWh
0.00244
Amount ($) of the additional ES kWh
charged per kWh
210
kWh for each ES kW of demand over 1000
kW
The total electricity cost of all the
ADecision-GuidedEnergyFrameworkforOptimalPower,Heating,andCoolingCapacityInvestment
361

FuturePayPeriods is the aggregations of all the total
electricity costs per future pay period, i.e.,
electricCost = ∑(payPeriodKwhCharge[p]
+ generationDemandCharge[p]);, where p ∈
FuturePayPeriods.
Table 1 summarizes the descriptions of all the
constant values from the electric utility contract used
in the DGEI optimization model for the GMU
energy investment problem.
3.2.4 Total Gas Consumption Charge
Regarding the gas supply,
utilityGas[FuturePowerIntervals] ≥ 0 is an array of
gas supplied from the WGLC over the
FuturePowerIntervals. The total gas cost of all the
FuturePowerIntervals is the aggregations of all the
total gas utility per future power interval, i.e.,
gasCost = (∑(utilityGas[i]/btuPerDth))
* gasPricePerDth;, where i ∈
FuturePowerIntervals, btuPerDth = 1000000 BTU,
which is the amount of energy per decatherm, and
gasPricePerDth = $6.5, which is the gas charge per
decatherm.
3.2.5 Total Operating Cost
The total operating cost is the sum of the total
electricity cost of all the future pay periods and the
total gas cost of all the future power intervals, i.e.,
totalCost = electricCost + gasCost;.
3.3 Operational Parameters
and Capacity Constraints
of the CHCP and the Cogen Plant
In addition to the supply and demand of gas and
electricity, the operational parameters and the
capacity constraints of the CHCP and the CoGen
plant are also considered.
3.3.1 The CHCP Plant
For the CHCP plant,
gasIntoCHCP[FuturePowerIntervals] ≥ 0 is an array
of natural gas input to the CHCP over the
FuturePowerIntervals to generate the heat supply.
kwIntoCHCP[FuturePowerIntervals] ≥ 0 is an array
of power input to the CHCP over the
FuturePowerIntervals to generate the cool supply.
heatOutCHCP[FuturePowerIntervals] ≥ 0 is an array
of heat output from the CHCP over the
FuturePowerIntervals to satisfy the partial heating
demand. coolOutCHCP[FuturePowerIntervals] ≥ 0
is an array of cool output from the CHCP over the
FuturePowerIntervals to satisfy the partial cooling
demand. The CHCP constraints include:
heatOutCHCP[i] * gasPerHeatUnit ≤
gasIntoCHCP[i];, i.e., the amount of gas
consumed to generate the heat cannot be more than
that of the gas input;
coolOutCHCP[i] * kwhPerCoolUnit ≤
kwIntoCHCP[i];, i.e., the amount of electric
power consumed to generate the cool cannot be
more than that of the power input;
heatOutCHCP[i] ≤ chcpMaxHeatPerHr;, i.e.,
the amount of heat generated cannot be more than
the maximal heat output of the CHCP; and
coolOutCHCP[i] ≤ chcpMaxCoolPerHr;, i.e.,
the amount of cool generated cannot be more than
the maximal cool output of the CHCP, where i ∈
FuturePowerIntervals, gasPerHeatUnit = (1 / 0.78),
and kwhPerCoolUnit = (1 / 0.94).
3.3.2 The CoGen Plant
For the CoGen plant,
gasIntoCogen[FuturePowerIntervals] ≥ 0 is an array
of gas input to the CoGen plant over the
FuturePowerIntervals to generate the power supply.
kwOutCogen[FuturePowerIntervals] ≥ 0 is an array
of power output from the CoGen plant over the
FuturePowerIntervals to satisfy the partial electricity
demand. heatOutCogen[FuturePowerIntervals] ≥ 0 is
an array of heat output from the CoGen plant over
the FuturePowerIntervals to satisfy the partial
heating demand.
coolOutCogen[FuturePowerIntervals] ≥ 0 is an array
of cool output from the CoGen plant over the
FuturePowerIntervals to satisfy the partial cooling
demand. The constraints of the CoGen plant include:
kwOutCogen[i] * cogenGasPerKwh ≤
gasIntoCogen[i];, i.e., the amount of gas
consumed to generate the power cannot be more
than that of the gas input;
kwOutCogen[i] ≤ cogenMaxKw;, i.e., the
amount of power generated cannot be more than
the maximal electricity output of the CoGen plant;
heatOutCogen[i] ≤ cogenHeatPerKwh *
kwOutCogen[i];
, i.e., the amount of heat
generated cannot be more than the maximal heat
supply that is restricted by the power output of the
CoGen plant;
heatOutCogen[i] ≤ cogenMaxHeatPerHr *
(kwOutCogen[i]/cogenMaxKw);, i.e., the
amount of heat generated cannot be more than the
maximal heat output of the CoGen plant;
coolOutCogen[i] ≤ (cogenMaxHeatPerHr *
(kwOutCogen[i]/cogenMaxKw) -
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
362

heatOutCogen[i]) *
cogenHeatToCoolRatio;, i.e., the amount of
cool generated cannot be more than the maximal
cool supply that is restricted by the power and heat
output of the CoGen plant; and
coolOutCogen[i] ≤ cogenMaxCoolPerHr;,
i.e., the amount of cool generated cannot be more
than the maximal cool output of the CoGen plant,
where i ∈ FuturePowerIntervals, cogenMaxKw =
7200 kW is the maximal power output,
cogenHeatPerKwh = 10300 kWh is the amount of
heat generated per kWh, cogenHeatToCoolRatio =
cogenMaxCoolPerHr/cogenMaxHeatPerHr is the
ratio of converting heat to cool supply,
cogenMaxHeatPerHr = 40000000 BTU is the
maximal heat supply of the CoGen plant per hour,
cogenMaxCoolPerHr = 2400 Tons is the maximal
cool supply of the CoGen plant per hour,
cogenGasPerKwh =
gasBTUPerGallon/kWhPerGallon/cogenGasToKwh
Efficiency is the amount of natural gas consumed
per kWh, for gasBTUPerGallon = 114000 BTU is
the amount of energy generated per gallon of gas,
kwhPerGallon = 33.41 is the amount of kWh
generated per gallon of gas, and
cogenGasToKwhEfficiency = 0.33 is the efficiency
of the CoGen plant to generate power from natural
gas.
3.4 Energy Aggregations of Supply
and Demand
The aggregations of energy supply and demand
within the entire energy system include:
kwIntoCHCP[i] + demandKw[i] ≤
utilityKw[i] + kwOutCogen[i];, i.e., the
amount of power input to the CHCP and the power
demand from the GMU cannot exceed the amount
of power supply provided from the DVPC and the
power output generated from the CoGen plant,
where i ∈ FuturePowerIntervals.
demandReduction[i] ≤ (utilityKw[i] +
kwOutCogen[i]) - (kwIntoCHCP[i] +
demandKw[i]);
, i.e., the power supply reduction
cannot exceed the difference between the total
power supply (utilityKw[i] + kwOutCogen[i]) and
the total power demand (kwIntoCHCP[i] +
demandKw[i]), where
demandReduction[FuturePowerIntervals] ≥ 0 is an
array of extra power supply that can be cut from
the power inputs over the FuturePowerIntervals,
and i ∈ FuturePowerIntervals.
∑demandReduction[i] ≤
maxKwReductionPerPayPeriod;
, i.e., the total
power reductions over the future power intervals
cannot exceed the allowable maximal power
interruptions per future pay period, where i ∈
FuturePowerIntervals, p ∈ FuturePayPeriods, and
i.payPeriod = p.
utilityGas[i] ≥ gasIntoCogen[i] +
gasIntoCHCP[i];, i.e., the gas input to the
CoGen plant and to the CHCP cannot exceed the
gas supply provided from the WGLC, where i ∈
FuturePowerIntervals.
heatOutCogen[i] + heatOutCHCP[i] ≥
demandHeat[i];, i.e., the heat demand from
GMU cannot exceed the heat supply generated
from the CoGen plant and the CHCP, where i ∈
FuturePowerIntervals.
coolOutCogen[i] + coolOutCHCP[i] ≥
demandCool[i];, i.e., the cool demand from
GMU cannot exceed the cool supply generated
from the CoGen plant and the CHCP, where i ∈
FuturePowerIntervals.
3.5 DGEI Optimization Model
After declaring all the input data sets and the above
constraints, which the input data sets need to satisfy,
the DGEI optimization model for the GMU energy
investment problem can be formulated as follows in
Figure 3.
Figure 3: The DGEI Optimization Model for the GMU
Energy Investment Problem.
ADecision-GuidedEnergyFrameworkforOptimalPower,Heating,andCoolingCapacityInvestment
363
4 OPL IMPLEMENTATION
FOR DGEI OPTIMIZATION
MODEL
The DGEI optimization model has been
implemented by using the OPL language. Using the
GMU historical data of power usage in the past year,
i.e., 2011, and its projected electricity, cooling, and
heating demand over a future time horizon from
2012 to 2020, we use the OPL language to
implement and demonstrate the DGEI optimization
model to solve the GMU energy investment problem
and minimize the operating cost.
The intuition of using the OPL language is that
its optimization formulation looks like the DGEI
optimization model. When comparing the DGEI
optimization model in Figure. 3 with the OPL
formulation from Figure 4.1 to Figure 4.9, we realize
that both models are very similar to each other. Only
some notations and syntaxes are different that is
shown in Table 2. For example, instead of using the
summation sign (∑) in the DGEI optimization
model, the OPL language uses the keyword, “sum”,
to perform the aggregation. Rather than using the if-
then statement in the mathematics, the OPL uses the
specific construct with the implication operatior
(=>).
Table 2: Differences between DGEI Optimization model
and OPL formulation model.
DGEI Optimization Model OPL Formulation Model
Notation: Summation Sign
∑
Example:
∑(demandKw[i] – kW[i]) ≤
2 * annualBound
Syntax: sum
Example:
sum(i in PowerIntervals :
i.pInterval >= 1)
(demandKw[i] - kW[i]) <=
annualBound * 2
Notation: If-then Statement
Example:
if (payPeriodKwh[p] ≤
24000)
payPeriodKwhCharge[p] =
0.01174 * payPeriodKwh[p]
Syntax: =>
Example:
(payPeriodKwh[p] <=
24000) =>
(payPeriodKwhCharge[p]
== 0.01174 *
payPeriodKwh[p])
Notation: Where clause
Example:
peakDemandBound[p] ≤
payPeriodSupplyDemand[p
], where p ∈ PayPeriods
Syntax: forall
Example:
forall (p in PayPeriods)
peakDemandBound[p] <=
payPeriodSupplyDemand[
p]
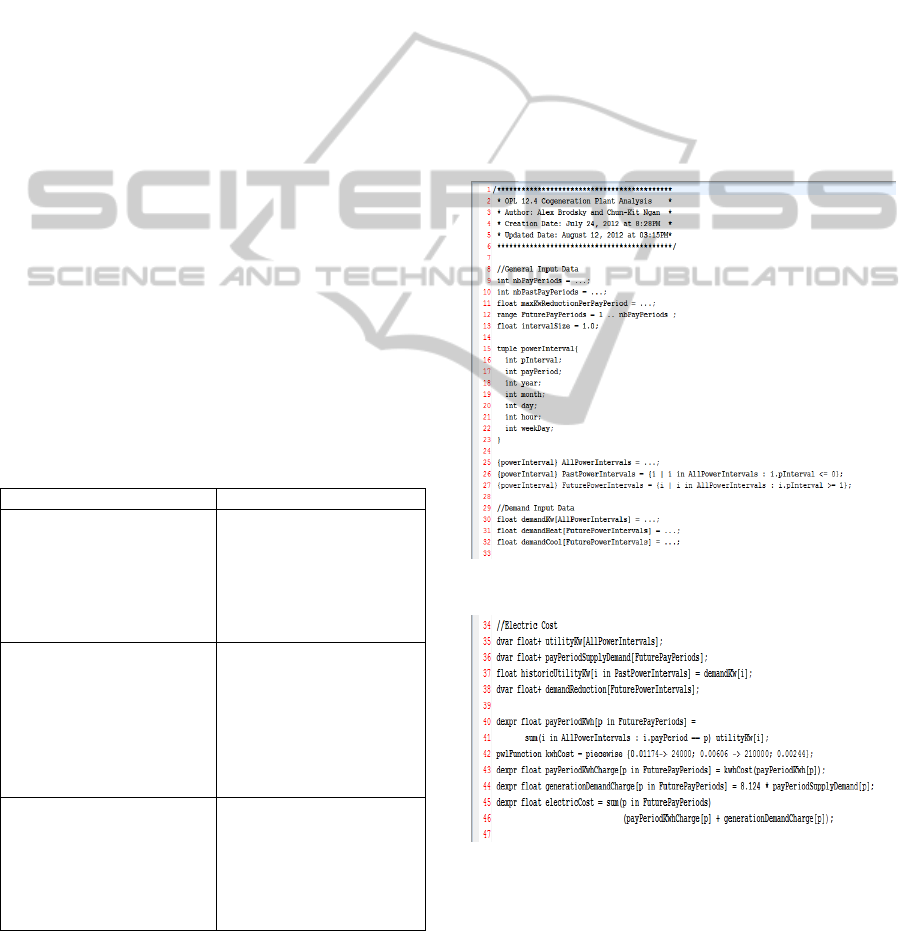
More specifically, the OPL implementation
construct is described as follows. In Figure 4.1, from
the line number 9 to 12, the value 12, i.e., the total
12 months of 2011, is assigned to the variable
nbPastPayPeriods, the value 108, i.e., the total 108
months from 2012 to 2020, is assigned to the
variable nbPayPeriods, and the value 0 is assigned to
the maximal power interruptions, i.e.,
maxKwReductionPerPeriod. The FuturePayPeriods
is ranged from 1 to 108. From the line number 15 to
23, we declare a tuple of a power interval that has
the attributes, including pInterval, payPeriod, year,
month, day, hour, and weekDay. The line number 25
to 27 declares and initializes AllPowerIntervals that
include both PastPowerIntervals and
FuturePowerIntervals. The line number 30 to 32
declares and initializes the
demandKw[AllPowerIntervals], the
demandHeat[FuturePowerIntervals], and the
demandCool[FuturePowerIntervals] arrays.
Figure 4.1: General and Demand Input Data.
Figure 4.2: Total Electricity Cost.
Figure 4.2 declares the decision control variables,
i.e., utilityKw[AllPowerIntervals],
payPeriodSupplyDemand[FuturePayPeriods], and
payPeriodKwh[FuturePayPeriods], to compute
payPeriodKwhCharge[FuturePayPeriods] and
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
364

generationDemandCharge[FuturePayPeriods] that
are summed together to determine the total
electricity cost over all the future pay periods while
satisfying the electric contractual constraints.
Figure 4.3 declares the constants, i.e.,
gasPricePerDth and btuPerDth, and
utilityGas[FuturePowerIntervals] to calculate the
total gas cost over all the future power intervals.
Figure 4.3: Total Gas Cost.
Figure 4.4 declares the objective function to
minimize the total operating cost, i.e., the total
electricity cost plus the total gas cost.
Figure 4.4: Total Operating Cost.
Figure 4.5 declares the constants, i.e.,
gasPerHeatUnit, kwhPerCoolUnit,
chcpMaxHeatPerHr, and chcpMaxCoolPerHr, and
the arrays, i.e.,
gasIntoCHCP[FuturePowerIntervals],
kwIntoCHCP[FuturePowerIntervals],
heatOutCHCP[FuturePowerIntervals], and
coolOutCHCP[FuturePowerIntervals], used in the
CHCP capacity constraints.
Figure 4.5: Operational Parameters and Data Structures of
the CHCP Plant.
Figure 4.6 declares the constants from the line
number 71 to 79, and the arrays, i.e.,
gasIntoCogen[FuturePowerIntervals],
heatOutCogen[FuturePowerIntervals],
coolOutCHCP[FuturePowerIntervals], and
kwOutCHCP[FuturePowerIntervals], which are used
in the capacity constraints of the CoGen plant.
Figure 4.6: Operational Parameters and Data Structures of
the CoGen Plant.
Figure 4.7 defines all the capacity constraints for the
CHCP and the CoGen plant.
Figure 4.7: Capacity Constraints of the CHCP and the
CoGen Plant.
Figure 4.8 defines the contractual constraints for the
electricity bill.
Figure 4.8: Contractual Electricity Utility Constraints.
ADecision-GuidedEnergyFrameworkforOptimalPower,Heating,andCoolingCapacityInvestment
365

Figure 4.9 defines the constraints for the energy
aggregations of electric power, gas, heat, and cool.
Figure 4.9: Energy Aggregations of Supply and Demand.
5 ANALYTICAL
METHODOLOGY ON
EVALUATION AMONG
ENERGY INVESTMENT
OPTIONS
For domain experts being able to formulate and
implement the above DGEI optimization model to
determine the best investment option, we propose an
analytical methodology that guides the domain
experts to achieve this goal. The methodology
includes six steps.
STEP 1: Collect historical energy demand, such
as electricity, heating, and cooling, from each
building unit, and forecast those demands in terms of
growth on a square-foot basis over the future time
horizon.
STEP 2: Identify all the possible energy
investment options, such as the expansion of current
facilities and the procurement of cogeneration
plants.
STEP 3: Formulate, implement, and execute the
DGEI optimization model that integrates historical
and projected energy demand, electric and gas
contractual utility, operational parameters and
capacity constraints of energy equipment, as well as
energy aggregations of supply and demand in each
considered option under the assumption of optimal
interactions among available resources.
STEP 4: Compute the annualized evaluation
parameters for each option based upon the results
from the optimization process in STEP 3.
The parameters include the investment cost (I
i
),
equipment cost (E
i
), i.e., maintenance expenditure
(M
i
) plus replacement charge (R
i
), operating expense
(C
i
), i.e., the charges on electricity and gas
consumptions, cost saving (S
i
), i.e., C
0
– C
i
, where i
≥ 0 denotes an investment option and C
0
is the
operating cost of a base investment option that the
other available options compare with, and return on
investment (ROI
i
), i.e., S
i
/ (I
i
– I
0
), as well as the
GHG emissions (MTCDE
i
), i.e., G
i
* 0.053
MTCDE/Million-Btu + P
i
* 0.513 MTCDE/Million-
Wh, shown in Table 3, against the various
investment options, where 0.053 and 0.513 are the
factors, which are calculated from the historical data.
Note that the base investment option is the option
that the current capacity of the existing facilities is
expanded without procuring any new energy
equipment.
Using the ROI and GHG emissions, domain
users and experts can plot the analytical graphs to
illustrate the relationships among the ROI, GHG
emissions, and investment expenses, which enable
the domain experts to determine the best investment
option among all of the options being considered.
Table 3: Evaluation Parameters of ROI and GHG
Emissions for Determining the Best Investment Option.
Parameter Symbol
Investment Cost I
i
Maintenance Expenditure M
i
Replacement Charge R
i
Equipment Cost E
i
Operating Expense C
i
Cost Saving S
i
Return on Investment ROI
i
Average Annual Gas Consumption MBTU G
i
Average Annual Electric Power
Consumption MWh
P
i
GHG Emission MTCDE
i
STEP 5: Remove any option that is dominated by
the other options in terms of the evaluation
parameters.
STEP 6: Construct a trade-off graph to evaluate
the options that are not dominated among others and
then make a final decision.
Note that although STEP 1, 2, 4, 5, and 6 are
typical processes of evaluations, STEP 3 is not
typical at all as the problem that we solve is a non-
trivial optimization problem.
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
366
6 ANALYTICAL
METHODOLOGY
ON EXPERIMENTAL CASE
STUDY
After the process from STEP 1 to STEP 3 in the
experimental case study at GMU, the four
investment options, including ① the expansion of
the existing CHCP only, ② the addition of a CoGen
plant to the existing CHCP, ③ the half capacity of
the Option ① with the half planned capacity of the
CoGen plant, and ④ the full capacity of the Option
① with the full planned capacity of the CoGen
plant, have been chosen to be evaluated to meet the
electricity, heating, and cooling demand of the
Fairfax campus over the next 9 years from 2012 to
2020.
In STEP 4, using the evaluation parameters, i.e.,
ROI and GHG emissions, discussed in Section 5 and
the OPL to solve the GMU energy investment
problem in Section 4, we obtained Table 4 and
Figure 5 that can be used to determine the best
investment option.
Table 4: Evaluation Parameters of ROI and GHG
Emissions for Determining the GMU Energy Investment
Options.
Investment
Option
Investment Cost
($M)
Annual
Maintenance
Cost ($)
1 Expanded
CHCP
$34.293
$343,200
1 CoGen Plant
+ 1 Current
CHCP
$65.328 $655,600
½ CoGen Plant
+ ½ Expanded
CHCP
$46.995 $499,400
1 CoGen Plant
+ 1 Expanded
CHCP
$99.621 $998,800
Investment
Option
Annualized
Replacement
Cost ($M)
Annualized
Equipment Cost
($M)
1 Expanded
CHCP
$3.429 $3.772
1 CoGen Plant
+ 1 Current
CHCP
$3.850 $4.506
½ CoGen Plant
+ ½ Expanded
CHCP
$4.699 $5.199
1 CoGen Plant
+ 1 Expanded
CHCP
$7.279 $8.278
Table 4: Evaluation Parameters of ROI and GHG
Emissions for Determining the GMU Energy Investment
Options. (Cont.)
Investment
Option
Annualized
Average
Operational
Cost ($M)
Annualized
Saving over the
Expanded
CHCP ($M)
1 Expanded
CHCP
$6.244 $0.000
1 CoGen Plant
+ 1 Current
CHCP
$5.494 $0.016
½ CoGen Plant
+ ½ Expanded
CHCP
$5.557 -$0.740
1 CoGen Plant
+ 1 Expanded
CHCP
$5.492 -$3.754
Investment
Option
ROI (%)
Average Annual
Gas
Consumption
(MBTU)
1 Expanded
CHCP
0.000% 510,500.00
1 CoGen Plant
+ 1 Current
CHCP
0.052% 523,622.22
½ CoGen Plant
+ ½ Expanded
CHCP
-5.827% 520,888.89
1 CoGen Plant
+ 1 Expanded
CHCP
-5.747% 523,600.00
Investment
Option
Average Annual
Electric Power
Consumption
(MWh)
GHG Emission
(MTCDE)
1 Expanded
CHCP
141,433.33 99611.799
1 CoGen Plant
+ 1 Current
CHCP
141,333.33 100255.977
½ CoGen Plant
+ ½ Expanded
CHCP
141,344.44 100116.811
1 CoGen Plant
+ 1 Expanded
CHCP
141,333.33 100254.799
In STEP 5, the Option ③ and ④ are the dominated
cases that can be removed from our consideration
list because of the negative ROI.
In STEP 6, according to the Table 4 and Figure
5, we can conclude that the Option ① should be
chosen because of the three observations. First, the
GHG emissions and the equipment cost of the
Option ① are the lowest. Second, even though the
ADecision-GuidedEnergyFrameworkforOptimalPower,Heating,andCoolingCapacityInvestment
367

ROI of the Option ②, i.e., 0.052%, is marginally
better than that of the Option ①, the GHG
emissions of the Option ② is the highest among all
the options being considered. Third, it is not
economical at all for GMU to invest $31 million
dollars, i.e., the Option ② investment cost minus
the Option ① investment cost, more to earn only
0.052% ROI in the next 9-year timeframe. Thus, the
Option 1 is the best long-term option for GMU.
Figure 5: ROI (%) and GHG Emissions (MTCDE) vs.
Investment Cost ($M) across the Four Investment Options.
7 CONCLUSIONS AND FUTURE
WORK
In this paper, we propose a Decision-Guided Energy
Investment (DGEI) Framework to optimize power,
heating, and cooling capacity. The DGEI framework
is designed to support energy managers to (1) use
the analytical and graphical methodology to
determine the best investment option that satisfies
the designed evaluation parameters, such as ROI and
GHG emissions; (2) develop a DGEI optimization
model to solve energy investment problems that the
operating expenses are minimal in each considered
investment option; (3) implement the DGEI
optimization model using the IBM OPL language
with historical and projected energy demand data,
i.e., electricity, heating, and cooling, to solve energy
investment optimization problems; and (4) conduct
an experimental case study on the Fairfax campus
microgrid at George Mason University (GMU) and
utilize the DGEI optimization model and its OPL
implementations, as well as the graphical and
analytical methodology to make the investment
decision and trade-offs among the cost savings,
investment costs, maintenance expenditures,
replacement charges, operating expenses, GHG
emissions, and return on investment (ROI) for all the
considered options.
Technically, the core challenge is the
development of the DGEI optimization model that is
very accurate in terms of the contractual terms and
engineering constraints, and yet efficient and
scalable, which is done by the careful modelling of
mainly continuous decision variables and using
constructs that avoid introduction of combinatorics,
e.g., explicit or implicit binary variables, into the
model. However, the DGEI optimization problem
that we formulate is implemented by using the OPL
language. This OPL construct is then sent to the
IBM CPLEX solver which is the branch-and-bound-
based algorithm with the exponential time
complexity, i.e., 2
, where k is the number of
decision control variables, and N is the size of the
learning data set. Thus the furture research focus
will develop a new algorithm that will be able to
solve the energy investment problems at a lower
time complexity.
Concerning the real case study at George Mason
University and its CHCP system, it is clear that
GMU must develop and research other available
options beyond those discussed in the analysis of
this paper in order to meet the future needs of the
Fairfax campus demand. Thus, the DGEI framework
further developed will aid the GMU energy decision
makers to determine the optimal solutions that will
satisfy the GMU short- and long-term power,
heating, and cooling demand. Note that our
framework is applicable to solve any energy
investment problem in different domains of industry.
Therefore, the future work includes the advanced
development of the DGEI libraries and optimization
models that enable domain users and experts to
integrate more clean and efficient energy equipment,
such as geothermal electric power facilities, into the
existing plants optimally in order to support the
continuous development of enterprises and
organizations.
REFERENCES
Alrazgan, A., Nagarajan, A., Brodsky, A., and Egge, N.,
(2011). Learning Occupancy Prediction Models with
Decision-Guidance Query Language. Proceedings of
the 44
th
Hawaii International Conference on System
Sciences. Koloa, Kauai, Hawaii, U.S.A.
American Electric Power Inc., (2012). CCS Front End
Engineering & Design Report American Electric
Power Mountaineer CCS II Project Phase 1.
Columbus, Ohio, U. S. A.
http://cdn.globalccsinstitute.com/sites/default/files/pub
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
368

lications/32481/ccs-feed-report-gccsi-final.pdf on
January 30, 2012.
Biezma, M. and San Cristobal, J., (2006). Investment
Criteria for the Selection of Cogeneration Plants – a
State of the Art Review. Journal of Applied Thermal
Engineering, Vol. 26 Issues 05 - 06, p. 583–588.
Broccard, M., Girdinio, P., Moccia, P., Molfino, P., Nervi,
M., and Pini Prato, A., (2010). Quasi Static Optimized
Management of a Multinode CHP Plant. Journal of
Energy Conversion and Management, Vol. 51, Issue
11, p. 2367–2373.
Brodsky, A. and Wang. X. S., (2008). Decision-Guidance
Management Systems (DGMS): Seamless Integration
of Data Acquisition, Learning, Prediction, and
Optimization. Proceedings of the 41
st
Hawaii
International Conference on System Sciences.
Waikoloa, Big Island, Hawaii, U. S. A.
Brodsky, A., Bhot, M. M., Chandrashekar, M., Egge, N.E.,
and Wang, X.S., (2009). A Decisions Query Language
(DQL): High-Level Abstraction for Mathematical
Programming over Databases. Proceedings of the 35
th
SIGMOD International Conference on Management
of Data. Providence, RI, U. S. A.
Brodsky, A., Cherukullapurath, M., Awad, M., and Egge,
N., (2011). A Decision-Guided Advisor to Maximize
ROI in Local Generation and Utility Contracts.
Proceedings of the 2
nd
European Conference and
Exhibition on Innovative Smart Grid Technologies.
Manchester, U.K.
Brodsky, A., Egge, N., and Wang, X. S., (2011). Reusing
Relational Queries for Intuitive Decision
Optimization. Proceedings of the 44
th
Hawaii
International Conference on System Sciences. Koloa,
Kauai, Hawaii, U.S.A.
Brodsky, A., Henshaw, S. M., and Whittle, J., (2008).
CARD: A Decision-Guidance Framework and
Application for Recommending Composite
Alternatives. Proceedings of the 2
nd
ACM
International Conference on Recommender Systems.
Lausanne, Switzerland.
Hentenryck, P. V. (1999). The OPL Optimization
Programming Language. The MIT Press.
M. Bojić, M. and Stojanović, B., (1998). Journal of
Energy Conversion and Management, Vol 39 Issue 07,
p. 637–642.
SAS Institute, Inc., (2012). SAS/OR(R) 9.22 User's Guide:
Mathematical Programming. http://support.sas.com/
documentation/cdl/en/ormpug/63352/HTML/default/v
iewer.htm#ormpug_milpsolver_sect001.htm on April
29, 2012.
Savola, T. and Keppo, I., (1997). Off-design Simulation
and Mathematical Modeling of Small-scale CHP
plants at part loads. Journal of Applied Thermal
Engineering, Vol 25 Issues 08 - 09, p. 1219–1232.
The IBM Corporation. (2012). Optimization Programming
Language (OPL). http://pic.dhe.ibm.com/infocenter/
cosinfoc/v12r4/index.jsp?topic=%2Filog.odms.ide.hel
p%2FOPL_Studio%2Fmaps%2Fgroupings_Eclipse_a
nd_Xplatform%2Fps_opl_Language_1.html.
Tuula Savola, T. and Fogelholm, C., (2007). MINLP
Optimization Model for Increased Power Production
in Small-scale CHP Plants. Journal of Applied
Thermal Engineering, Vol 27 Issue 01, p. 89–99.
Tuula Savola, T, Tveit, T., and Fogelholm, C., (2007). A
MINLP Model Including the Pressure Levels and
Multiperiods for CHP Process Optimization. Journal
of Applied Thermal Engineering, Vol 27 Issues 11–12,
p. 1857–1867.
APPENDIX: ABBREVIATION
Abbreviation Full Name
CHCP
Centralized Heating and Cooling
Plant
CO
2
Carbon Dioxide
CoGen Cogeneration
DGEI
Decision-Guided Energy
Investment
DVPC
Dominion Virginia Power
Company
EC EnergyConnect
ECU Energy Contractual Utility
EFD Energy Future Demand
EFE Energy Facility Expansion
EGP Energy Generation Process
EHD Energy Historical Demand
ES Electricity Supply
FCWA Fairfax County Water Authority
FMD
Facilities Management
Department
GHG Greenhouse Gas
GMU George Mason University
MILP
Mixed Integer Linear
Programming
MINLP
Mixed Integer Non-Linear
Programming
NO
x
Mono-Nitrogen Oxide
OPL
Optimization Programming
Language
QoS Quality of Service
ROI Return On Investment
WGLC Washington Gas Light Company
ADecision-GuidedEnergyFrameworkforOptimalPower,Heating,andCoolingCapacityInvestment
369
