Adaptive Filtering for Stochastic Volatility by using Exact Sampling

ShinIchi Aihara

, Arunabha Bagchi

and Saikat Saha

Department of Mechanical Systems, Tokyo University of Science Suwa, 5000-1 Toyohira, Chino, Nagano, Japan

Department of Applied Mathematics, Twente University, P.O.Box 217,7500AE, Ensched, The Netherlands

Department of Electrical Engineering, Lik¨oping University, SE-58183 Lik¨oping Sweden

Keywords:

Particle Filter, Stochastic Volatility, Parameter Identiﬁcation, Adaptive Filter.

Abstract:

We study the sequential identiﬁcation problem for Bates stochastic volatility model, which is widely used as

the model of a stock in ﬁnance. By using the exact simulation method, a particle ﬁlter for estimating stochastic

volatility is constructed. The systems parameters are sequentially estimated with the aid of parallel ﬁltering

algorithm. To improve the estimation performance for unknown parameters, the new resampling procedure is

proposed. Simulation studies for checking the feasibility of the developed scheme are demonstrated.

1 INTRODUCTION

In the early 1960s, the linear ﬁltering theory is formu-

lated by Kalman and Bucy (Kalman and Bucy, 1961)

and nonlinear ﬁltering has already been well devel-

oped by many researchers, see Bensoussan (Bensous-

san, 1992) and the bibliography therein. The realiza-

tion problem for the nonlinear ﬁlter is still not easy.

The recent development of particle ﬁltering theory

(Doucet et al., 2000) enable us to realize the nonlin-

ear ﬁltering in an easy way with the aid of the digital

computer.

In this paper we consider the Bates model which

is used in the ﬁance problem. In this model, we ob-

serve the tick value of stock price and need to esti-

mate the movement of the volatility process for trad-

ing the stock and/or options. It is not possible to apply

the nonlinear ﬁltering theory to this volatility estima-

tion problem, because this is out of the usual ﬁlter-

ing problem in the continuous stochastic systems (Ai-

hara and Bagchi, 2006). To circumvent this difﬁculty,

the particle ﬁlter theory is usually applied in (Aihara

et al., 2008; Capp´e et al., 2005; Javaheri, 2005). The

Bates model is given by

= µ

dt +

√

+ S

−λm

dt, (1)

= κ(θ−v

)dt + ξ

√

(2)

where B

and Z

are standard Brownian motion pro-

cesses with correlation ρ and Z

denotes the pure-

jump process. Noting that the process S

denotes

the stock value, the observation data y

= logS

is given by

= (µ

−λm

−

)dt +

√

+ dq

, (3)

where q

is a compound Poisson process with in-

tensity λ and Gaussian distribution of jump size,i.e.,

N(µ

,σ

), and the mean relative jump size is given

by m

= E(exp(U

) −1) = exp(µ

+ σ

/2) −1 and

where the λm

term in (1) compensates for the in-

stantaneous change in expected stock introduced by

the pure-jump process Z

. The particular properties

of this model are

1. The observation mechanism (3) contains the sig-

nal dependent noise.

2. The observation noise has a correlation with the

systems noise.

From the ﬁrst property, the estimation of stochastic

volatility becomes out of ﬁltering problem. To cir-

cumvent this difﬁculty, all systems are discretized and

the particle ﬁlter is applied in (Aihara et al., 2008;

Johannes and Polson, 2006). However the usual dis-

cretization method transformed the original continu-

ous non-Gaussian system into the conditional Gaus-

sian. Recently, Brodie and Kaya (Broadie and Kaya,

2006; Smith, 2008; van Haastrecht and Pelsser, 2010)

proposed the exact simulation method from the fact

that the original system has a non-central chi-square

distribution and we use this technique to the particle

ﬁltering (Aihara et al., 2012). Introducing the new

Brownian motion

1−ρ

−ρB

), (4)

326

Aihara S., Bagchi A. and Saha S..

Adaptive Filtering for Stochastic Volatility by using Exact Sampling.

DOI: 10.5220/0004454703260335

In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2013), pages 326-335

ISBN: 978-989-8565-70-9

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

from the second property, (2) becomes

= κ(θ−v

)dt + ξ

√

1−ρ

+ξρ(dy

−(µ

−λm

−

)dt −dq

). (5)

Although in (Aihara et al., 2012) the exact particle ﬁl-

tering procedure has been applied to the systems (5)

and (3), the priority property of the exact simulation

method can not be guaranteed and the ﬁnal parameter

estimation results are not satisfactory. In this paper,

we introduce the rejection and acceptance method for

enjoying the exact simulation method and construct

the parallel ﬁltering algorithm with an new resam-

pling procedure for parameter identiﬁcation.

In Sec. 2, we review the exact particle ﬁltering

with the new use of rejection and resampling proce-

dure. For the real application to the ﬁnance problem,

the market price of risk terms are included in the orig-

inal dynamics in Sec. 3. Simulation studies for ﬁl-

tering and smoothing are presented in Sec. 5. The

new parallel ﬁlter algorithm is developed for estimat-

ing the systems unknown parameters sequentially in

Sec. 4. Finally some simulation studies for parameter

estimation are presented in Sec. 6.

2 EXACT PARTICLE FILTERING

2.1 Exact Sampling

In order to perform the particle ﬁlter, the original

system is usually approximated to the discrete-time

one by using the Euler method. This approximation

easily causes bias from the original continuous sys-

tem. For example, the discrete-time volatility pro-

cess v

often becomes negative value. To avoid this

bias, we propose the exact sampling method which is

developed by Broadie and Kaya (Broadie and Kaya,

2006),Smith (Smith, 2008) and (van Haastrecht and

Pelsser, 2010) for simulating the Heston process. In

this paper, from (5) we can obtain the optimal impor-

tance function p(v

). Hence we generate

samples from this optimal importance function. Now

we shall present the exact sampling procedure. For

simplicity we consider the time intervalt

< t

and set

the following assumption: At most one jump occurs

in this time interval and we observe y

and y

2.1.1 Exact Sampling from p(v

)

From (1), the volatility process v

is represented by

= ˜v

κ(

θ−v

)ds

√

1−ρ

, (6)

where

˜v

= v

+ ρξ{y

−y

−(µ

−λm

)(t

−t

) −∆q

}

κ = κ−

ρξ

θ =

κθ

∆q

= jump sample from q

for t

< t < t

Now assuming that ˜v

≥0, we ﬁnd that the transition

law of v

given by v

and y

is expressed as the

non-central chi-square random variable χ

(λ

) with d

degrees of freedom and non-centrality parameter λ

(1−ρ

)(1−e

−

κ(t

−t

)

(λ

), (7)

where

d =

(1−ρ

)

and

κe

−

κ(t

−t

)

(1−ρ

)(1−e

−

κ(t

−t

)

˜v

Hence by using MATLAB code ”ncx2rnd.m”, we can

get a sample v

For the case that ˜v

< 0, this event may occur

when v

is very small in generating particles by using

the data y

−y

. In the real world, we have already

get the value y

−y

. Hence v

should satisfy

+ ρξ{y

−y

−(µ

−λm

)(t

−t

) −∆q

}

θ(t

−t

) ≥ 0. (8)

2.1.2 ˜v

< 0 Case

We use the rejection and resampling procedure. At the

time t

, we already get many particles say v

(i)

. Hence

we check the above inequality (8) for each v

(i)

. If the

particles which do not satisfy (8) are found, we ignore

these and perform a resampling procedure.

2.2 Construction of Probability Density

Function

If we use the Euler scheme for discretization, the

generated sample becomes the conditionally Gaus-

sian. However for the exact sampling scheme , the

AdaptiveFilteringforStochasticVolatilitybyusingExactSampling

327

processes generated are governed by the non-central

chi-square distribution. Although the explicit func-

tion form of this distribution is not possible, we can

numerically evaluate the pdf by using the MATLAB

code, ”ncx2pdf.m”.

• p(v

) form

Noting that the jump occurs at most one time dur-

ing the time interval [t

], i.e, the probability

that the jump occurs is λe

−λ(t

−t

)

and no jump

becomes 1 −λe

−λ(t

−t

)

, and the jump size U

Gaussian with mean µ

and variance σ

, we have

p(v

)

= (1−e

−λ(t

−t

)

λ(t

−t

))

× p(v

,∆q

= 0)

+ e

−λ(t

−t

)

λ(t

−t

)

∞

−∞

p(v

)

2πσ

exp(−

−µ

)

2σ

)dU

= (1−e

−λ(t

−t

)

λ(t

−t

))

×pdf of

(

(1−ρ

)(1−e

−

κ(t

−t

)

(

)

+ e

−λ(t

−t

)

λ(t

−t

)

∞

−∞

pdf of

(

(1−ρ

)(1−e

−

κ(t

−t

)

×χ

(

−

κe

−

κ(t

−t

)

ξ(1−ρ

)(1−e

−

κ(t

−t

)

2πσ

exp(−

−µ

)

2σ

)dU

(9)

where

κe

−

κ(t

−t

)

(1−ρ

)(1−e

−

κ(t

−t

)

×{v

+ ρξ{y

−y

−(µ

−λm

)(t

−t

)}}

In (9), the ﬁrst term implies that we have no jump

and the second term is caused from the jump size

∈N(µ

,σ

• p(v

) form

It follows from (2) that

p(v

) = pdf of

(1−e

−κ(t

−t

)

4κ

(λ

where

d =

4θκ

and

4κe

−κ(t

−t

)

(1−e

−κ(t

−t

)

• p(y

ds) form

In this case, from

= (µ

−λm

−

)dt +

(dv

−κ(θ−v

)dt)

1−ρ

√

+ dq

we easily get

p(y

ds) =

1−e

−λ(t

−t

)

λ(t

−t

)

2π(1−ρ

)

×exp[−

2(1−ρ

)

−[y

+ (µ

−λm

−

κρθ

)(t

−t

)

−(

−

κρ

)

ds+

−v

)]}

]

−λ(t

−t

)

λ(t

−t

)

2π((1−ρ

)

ds+ σ

)

×exp[−

2((1−ρ

)

ds+ σ

)

−[y

+ (µ

−λm

−

κρθ

)(t

−t

)

−(

−

κρ

)

ds+ µ

−v

)]}

]

(10)

2.3 Exact Particle Filter Algorithm

Now we can perform the exact particle ﬁlter. The

weight w

(i)

is given by the following recursive form:

for i = 1,··· , N and k = 1,··· ,m

(i)

= w

(i)

k−1

p(y

k−1

(i)

ds)p(v

(i)

k−1

)

p(v

(i)

k−1

)

. (11)

Of course we need to perform the resampling

scheme in the above ﬁltering algorithm.

It is also possible to construct the smoothing algo-

rithm by using forward ﬁltering-backward sampling

scheme by Doucet et. al. (Doucet et al., 2000)

Algorithm(Sample realization).

• Run the particle ﬁlter to obtain

(i)

,ω

(i)

)

1≤k≤m,1≤i≤N

• By using the systematic resampling method, we

generate new index J

from {ω

(i)

}

1≤i≤N

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

328

• Set ˜v

(i)

as v

• For k = m−1 to 1;

Resample to get J

from

{ω

(i)

p( ˜v

(i)

)}

1≤i≤N

Set ˜v

(i)

as v

• ˜v

(i)

= [ ˜v

(i)

, ˜v

(i)

,··· , ˜v

(i)

] is the realized particles for

smoothing with 1/N probability.

3 MARKET PRICE OF RISK

For estimation we also need the dynamics of the state

and v

under the actual probability measure P . We

specify the market price of risk for B

and Z





= d





−



√

0 λ

√



dt.

We ignore the jump-timing risk premium and the

jump-size risk is assumed to be included in µ

. Now

the dynamics of y

and v

under P is given by

= (µ

−λm

+ (λ

−

)dt +

√

+ dq

= (κθ−(κ−λ

ξ)v

)dt + ξ

√

1−ρ

+ ξρ(dy

−(µ

−λm

−(

−λ

)dt −dq

Hence it is possible to apply our particle ﬁler algo-

rithm to this world measure dynamics. The corre-

sponding dynamics is transformed to

= ˜v

κ(

θ−v

)ds+

√

1−ρ

where

˜v

= v

+ ρξ{y

−y

−(µ

−λm

)(t

−t

) −∆q

}

κ = κ−

ρξ

+ ξ(ρλ

−λ

)

θ =

κθ

p(v

) becomes

p(v

) = pdf of

(1−e

−(κ−ξλ

)(t

−t

)

4(κ−ξλ

)

(λ

where

d =

4θκ

and

4(κ−ξλ

−(κ−ξλ

)(t

−t

)

(1−e

−(κ−ξλ

)(t

−t

)

Noting that

= (µ

−λm

+ (λ

−

)dt

(dv

−κθdt + (κ −λ

ξ)v

)dt)

1−ρ

√

+ dq

we also have

p(y

ds) =

1−e

−λ(t

−t

)

λ(t

−t

)

2π(1−ρ

)

×exp[−

2(1−ρ

)

−[y

+ (µ

−λm

−

κρθ

)(t

−t

)

−(

−

κρ

+ ρλ

−λ

)

ds+

−v

)]}

]

−λ(t

−t

)

λ(t

−t

)

2π((1−ρ

)

ds+ σ

)

×exp[−

2((1−ρ

)

ds+ σ

)

−[y

+ (µ

−λm

−

κρθ

)(t

−t

)

−(

−

κρ

+ ρλ

−λ

)

ds+ µ

−v

)]}

]

4 SIMULATION STUDIES FOR

FILTERING AND SMOOTHING

In this section, we simulate the proposed ﬁltering and

smoothing equations with known systems parameters

for Heston model without any market price of risk

terms for simplicity.

The systems parameters are listed in Table-1 and

in this case the point ”zero” is acceptable.

Table 1: Model parameters.

κ θ µ

ρ ξ

True 0.8638 1.0000 0.0100 -0.1050 2.5017

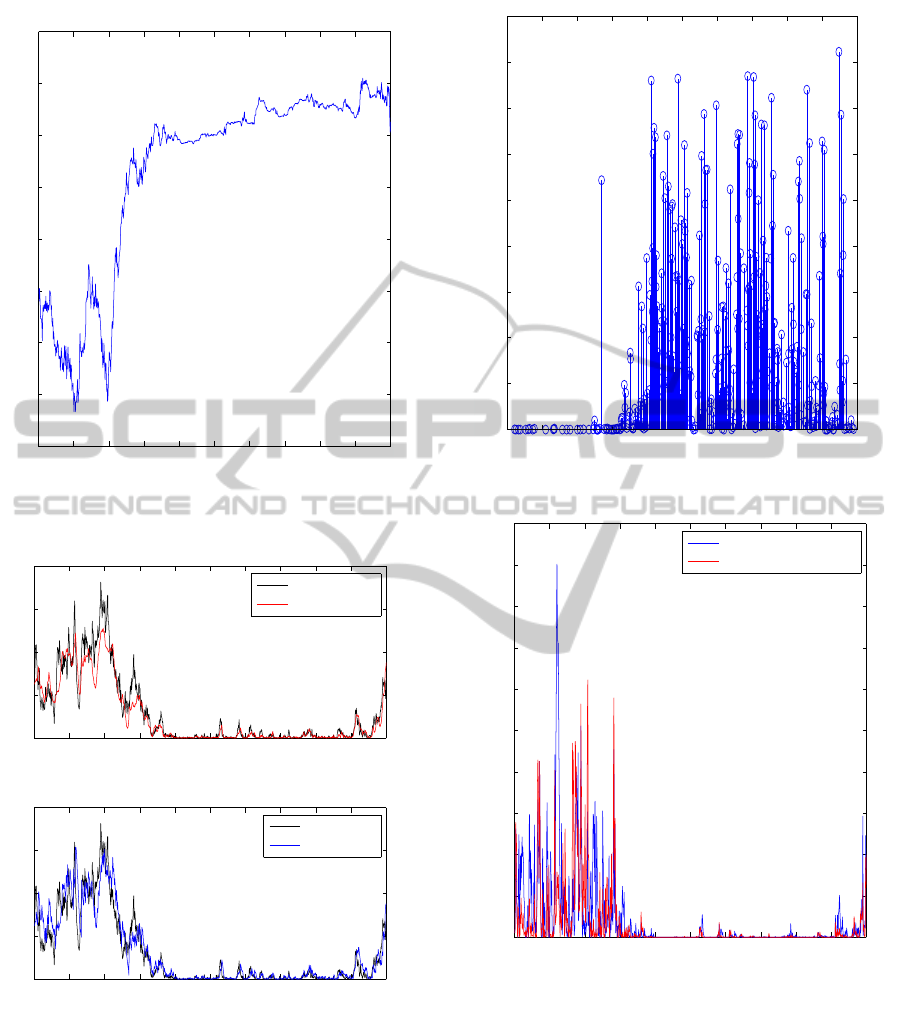
We present the log price in Fig.1. As shown in

Fig.2, the volatility process hits ”zero” at many times

because the degree of freedoms is less than 2. The

rejection and resampling rate is shown in Fig.3.

AdaptiveFilteringforStochasticVolatilitybyusingExactSampling

329

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

−0.3

−0.2

−0.1

0.1

0.2

0.3

0.4

0.5

Log price

Time (year)

Log Price

Figure 1: Observation data y

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

0.2

0.4

0.6

0.8

True value and estimated value of volatility

Time (year)

Volatility

True value

Smoothed estimate

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

0.2

0.4

0.6

0.8

True value and estimated value of volatility

Time (year)

Volatility

True value

Filtered estimate

Figure 2: True and estimated v

5 PARALLEL FILTERING

ALGORITHM

In a market, traders buy or sell stocks from their feel-

ing of the volatility movement of the traded stock.

Form this fact, we need to estimate the volatility itself

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Time (year)

Rejection and resampling rate

Figure 3: Rejection and resampling rate.

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

0.01

0.02

0.03

0.04

0.05

0.06

0.07

0.08

0.09

0.1

Time (year)

Exact square error

Filter case:sum =4.0674

Smoothing case : sum=3.0109

Figure 4: Mean square errors.

rather than the parameters in the model. The estimate

of the volatility should be online. Hence, in this sec-

tion, we construct the recursiveonline estimate for the

volatility. Of course to obtain the estimate of volatil-

ity, we also get the estimate of systems parameters at

the same time. Here the unknown parameters are de-

noted by

α = [κ,θ,ν

,ρ,ξ,λ,ν

,σ

,λ

Now we set candidates of unknown parameter α such

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

330

that

( j)

∈ uniformly random vectors in Θ, j = 1,··· ,M

If we know an a-priori information for Θ, we may

set the pdf p

(α). For each α

( j)

, we solve the par-

ticle ﬁlter ˆv

(α

( j)

) from Section 2.3. Hence from

(B.D.O.Anderson and J.B.Moore, 1979), we get the

posteriori density given by

p(α

( j)

)

{Σ

i=1

(i)

k−1

(α

( j)

)LF

k,i

}p(α

( j)

k−1

)

j=1

{Σ

i=1

(i)

k−1

(α

( j)

)LF

k,i

}p(α

( j)

k−1

)

where

k,i

= p(y

k−1

(i)

(α

( j)

)ds).

The estimates of volatility and parameters are given

ˆv

= Σ

j=1

ˆv

(α

( j)

)p(α

( j)

) (12)

= Σ

j=1

( j)

p(α

( j)

). (13)

5.1 New Resampling Procedure

The sample of parameter {α

( j)

}

j=1

is drawn only

from the initial information (in this paper we set the

uniform distribution). Hence for a long time period

the estimates of parameters are sometimes stacked

with some biases. This may cause from the fact that

there are so many unknown parameters while we get

a scaler observation data. In order to improve this

property, a resampling for the candidates for param-

eters α

( j)

is usually performed in MCMC algorithm

in (Johannes and Polson, 2006). In the parallel ﬁlter-

ing algorithm, we already get the posterior probability

p(α

( j)

) and from this distribution, we propose to

get new samples for α

( j)

by using the following pro-

cedure:

1. We set the resampling time t

(

∑

j=1

(α

( j)

))

−1

≤

we generate new sample α

( j)

from the step 2) to

6).

2. Calclulate

= Σ

j=1

( j)

p(α

( j)

)

α(i)

= Σ

j=1

(α

( j)

(i))

p(α

( j)

(i)|y

) −(

( j)

(i))

for i = 1,2,··· ,10.

3. We denote the parameter range at the resampling

time point t = t

lb(i,t

) ≤ α(i) ≤ ub(i,t

) for i = 1,2,··· ,10,

where lb(i,t) = lb(i) and ub(i,t) = ub(i) for t <

the ﬁrst resampling time.

4. From the calculated

and

, we reset the pa-

rameter range from t

p−1

lb(i,t

) = max(lb(i,t

p−1

(i) −3

α(i)

)

and

ub(i,t

) = min(ub(i,t

p−1

+ 3

α(i)

5. Construct the candidates of parameter k;

(i) = lb(i,t

) +

ub(t

) −ub(t

)

−1

(i−1).

for k = 1,2,··· ,M

6. Construct the posterior distribution for each pa-

rameter α(i) by using the Gaussian approxima-

tion:

P(α(i)|y

) ∼ N (α(i);

,ε

1/2

α(i)

where ε

is a user deﬁned parameter to increase

diversity.

7. Allocate n

copies of the particle α

(i) from

= the number of

(k−1) + ˜u

∈ (F

(α

k−1

(i)),F

(α

(i))]

for ˜u= uniform random number, where F

is an

approximated Gaussian distribution (step 6)):

(α

(i))

(i)

−∞

√

2πε

α(i)

exp[−

2(ε

(i))

(α(i) −

)

]dα(i)

(lb(i,t

))

8. Construct new candidate; for j = 1,2, ··· , M

( j)

= [α

(1),α

(2),··· ,α

(10)].

9. Reset p(α

( j)

) = 1/M

6 SIMULATION STUDIES

We set the following parameters in Table 2.

The lower and upper bounds for parameters are set as

Here we set dt = 0.001, T = 1,M = 100,M

= 60 and

= 20dt,ε

= 1.1, ε

= 1.1,ε

= 1.15,ε

= 1.01,ε

1.01, ε

= 1.15,ε

= 1.15, and

= 1.15. In Fig.5, we show the true volatility state

AdaptiveFilteringforStochasticVolatilitybyusingExactSampling

331

Table 2: Model parameters.

κ θ µ

True 0.8638 1.1000 0.6000 -0.1500

ξ λ µ

True 2.1017 5.4000 -0.3000 0.2500

True 0.1882 0.1723

Table 3: Lower and upper bounds of model parameters.

κ θ µ

Upper 1.6412 2.0900 1.140 -0.001

Lower 0.0086 0.0011 0.006 -0.300

ξ λ µ

Upper 3.9932 10.260 -0.0030 0.4570

Lower 0.0210 0.0540 -0.5700 0.0025

Upper 0.35758 0.62174

Lower 0.0018 0.0032

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

0.1

0.2

0.3

0.4

Time (year)

Volatility v

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

−0.6

−0.4

−0.2

0.2

Time (year)

Compoud Poisson process

Figure 5: The true volatility state and compound Poisson

process.

and compound Poisson process. The observed log

price is also shown in Fig.6. The estimated volatil-

ity is shown in Fig.7 with the square error in Fig.8.

We also present the resampling rates of the parti-

cle ﬁlter of this algorithm in Fig. 9.

The estimates of unknown parameters are demon-

strated from Figs 10 to 19 with the corresponding his-

togram for 0 ≤t ≤ 1.

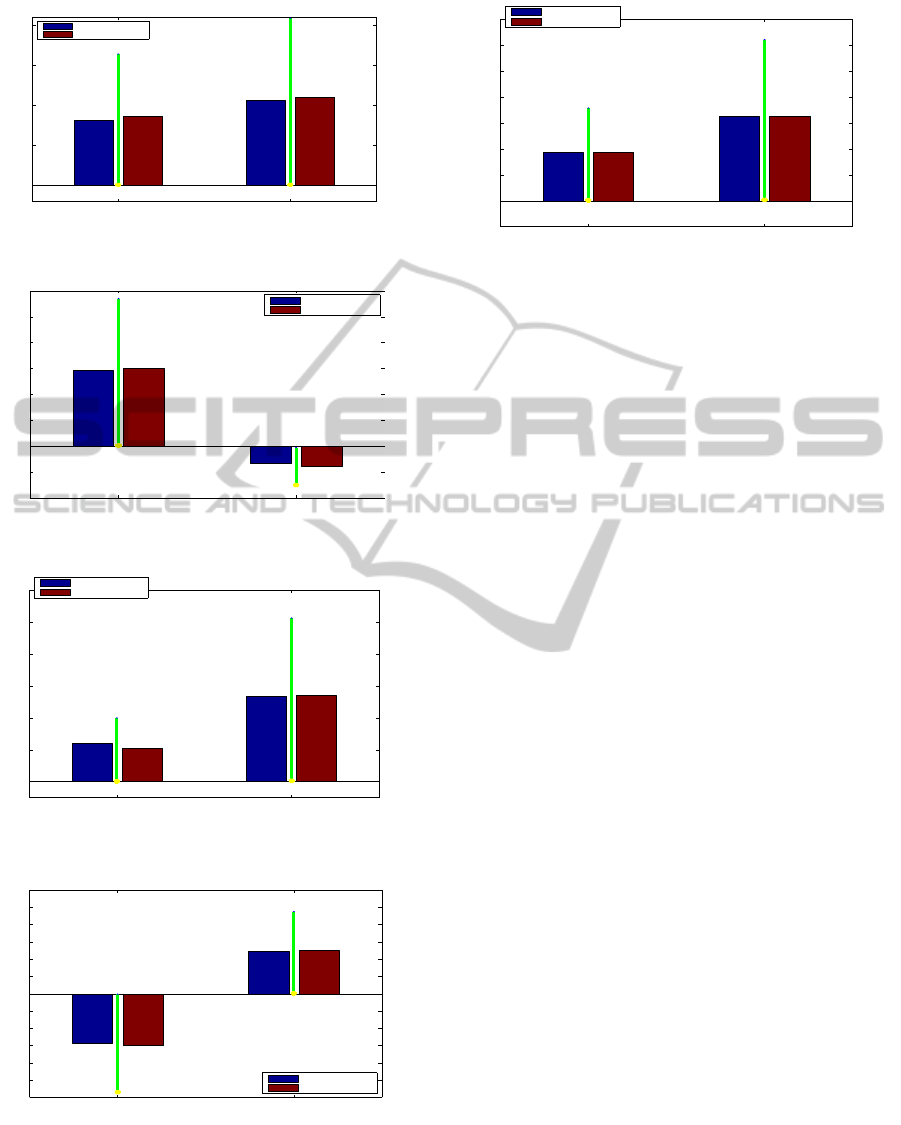
The true and estimated parameters at t = 1 are

shown in Figs. 20-24 where the green line indicated

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

−0.9

−0.8

−0.7

−0.6

−0.5

−0.4

−0.3

−0.2

−0.1

0.1

Time (year)

Log price

Figure 6: Observed log price.

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

True value and estimated value of volatility

Time (year)

Volatility

True value

Filtered state1.1

Figure 7: True and estimated volatility.

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

0.005

0.01

0.015

0.02

0.025

0.03

0.035

0.04

Time (year)

Exact square error

Square error:sum =2.3106

Figure 8: Square error of estimated volatility.

the upper and lower bounds for each parameters at

t = 0.

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

332

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

Time (year)

Rejection and resampling rate

Figure 9: Square error of estimated volatility

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

Time (year)

True and estimated parameters

Estimated value

Lower bound

Upper bound

True value

0 0.5 1 1.5

100

150

200

250

300

350

400

Parameter

Mean =0.935

Cov. =1.8e−02

Figure 10: Estimated κ and histogram for 0 ≤t ≤ 1

7 CONCLUSIONS

By using the non-central chi-square random genera-

tion method, we developed the particle ﬁlter for esti-

mating the stochastic volatility process. The sequen-

tial estimation for the systems unknown parameters

are performed with the aid of the new resampling pro-

cedure. In this procedure, we need to choose the re-

sampling time t

and the user deﬁned parameter ε

obtain the good numerical results. This turning prob-

lem is still an open problem.

0 0.2 0.4 0.6 0.8 1

0.5

1.5

2.5

Time (year)

True and estimated parameters

Estimated value

Lower bound

Upper bound

True value

0 0.5 1 1.5 2 2.5

100

150

200

250

300

350

400

450

500

Parameter

Mean =1.22

Cov. =2.7e−02

Figure 11: Estimated θ and histogram for 0 ≤ t ≤ 1

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

1.2

1.4

Time (year)

True and estimated parameters

Estimated value

Lower bound

Upper bound

True value

0 0.2 0.4 0.6 0.8 1 1.2

100

150

200

250

300

350

400

450

500

Parameter

Mean =0.651

Cov. =6.1e−03

Figure 12: Estimated µ and histogram for 0 ≤ t ≤ 1.

0 0.2 0.4 0.6 0.8 1

−0.35

−0.3

−0.25

−0.2

−0.15

−0.1

−0.05

Time (year)

True and estimated parameters

Estimated value

Lower bound

Upper bound

True value

−0.25 −0.2 −0.15 −0.1 −0.05 0

100

200

300

400

500

600

Parameter

Mean =−0.118

Cov. =3.5e−04

Figure 13: Estimated ρ and histogram for 0 ≤t ≤ 1.

AdaptiveFilteringforStochasticVolatilitybyusingExactSampling

333

0 0.2 0.4 0.6 0.8 1

0.5

1.5

2.5

3.5

Time (year)

True and estimated parameters

Estimated value

Lower bound

Upper bound

True value

0 1 2 3 4

100

150

200

250

300

350

400

450

Parameter

Mean =2.61

Cov. =6.2e−02

Figure 14: Estimated ξ and histogram for 0 ≤t ≤ 1.

0 0.2 0.4 0.6 0.8 1

Time (year)

True and estimated parameters

Estimated value

Lower bound

Upper bound

True value

0 2 4 6 8 10

100

200

300

400

500

600

Parameter

Mean =5.88

Cov. =4.7e−01

Figure 15: Estimated λ and histogram for 0 ≤t ≤ 1

0 0.2 0.4 0.6 0.8 1

−0.7

−0.6

−0.5

−0.4

−0.3

−0.2

−0.1

Time (year)

True and estimated parameters

Estimated value

Lower bound

Upper bound

True value

−0.5 −0.4 −0.3 −0.2 −0.1 0

100

150

200

250

300

350

400

Parameter

Mean =−0.251

Cov. =1.6e−03

Figure 16: Estimated µ

and histogram for 0 ≤t ≤ 1

0 0.2 0.4 0.6 0.8 1

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0.45

0.5

Time (year)

True and estimated parameters

Estimated value

Lower bound

Upper bound

True value

0 0.1 0.2 0.3 0.4 0.5

100

200

300

400

500

600

Parameter

Mean =0.274

Cov. =1.0e−03

Figure 17: Estimated σ

and histogram for 0 ≤t ≤ 1

0 0.2 0.4 0.6 0.8 1

Time (year)

True and estimated parameters

Estimated value

Lower bound

Upper bound

True value

0 2 4 6 8 10

100

200

300

400

500

600

Parameter

Mean =5.88

Cov. =4.7e−01

Figure 18: Estimated λ

and histogram for 0 ≤t ≤ 1

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

Time (year)

True and estimated parameters

Estimated value

Lower bound

Upper bound

True value

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

100

150

200

250

300

350

400

450

500

Parameter

Mean =0.359

Cov. =1.7e−03

Figure 19: Estimated λ

and histogram for 0 ≤t ≤ 1

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

334

1 2

0.5

1.5

at T=1

κ θ

Estimated value

True value

Figure 20: Estimated κ and θ at t = 1.

1 2

−0.4

−0.2

0.2

0.4

0.6

0.8

1.2

at T=1

Estimated value

True value

Figure 21: Estimated µ

and ρ at t = 1.

1 2

at T=1

ξ λ

Estimated value

True value

Figure 22: Estimated ξ and λ at t = 1.

1 2

−0.5

−0.4

−0.3

−0.2

−0.1

0.1

0.2

0.3

0.4

0.5

at T=1

Estimated value

True value

Figure 23: Estimated ξ and λ at t = 1.

1 2

−0.1

0.1

0.2

0.3

0.4

0.5

0.6

at T=1

Estimated value

True value

Figure 24: Estimated λ

and λ

at t = 1.

REFERENCES

Aihara, S. and Bagchi, A. (2006). Filtering and identiﬁ-

cation of heston’s stochastic volatility and its market

risk. J. Economical Dynamics and Control, 30:2363–

2388.

Aihara, S., Bagchi, A., and S.Saha (2008). Estimating

volatility and model parameters of stochastic volatil-

ity models with jumps using particle ﬁlter. Proc. of

17th IFAC World Congress.

Aihara, S., Bagchi, A., and S.Saha (2012). Identiﬁcation of

bates stochastic volatility model by using non-central

chi-square random generation method. Proc. of IEEE

ICASSP 2012.

B.D.O.Anderson and J.B.Moore (1979). Optimal Filtering.

Prentice-Hall, Inc., Englewood Cliffs, New Jersey.

Bensoussan, A. (1992). Stochastic Control of Partially Ob-

servable Systems. Cambridge University Press, Cam-

bridge.

Broadie, M. and Kaya, O. (2006). Exact simulation of

stochastic volatility and other afﬁne jump diffusion

processes. Operations Research, 54(2):217–231.

Capp´e, O., E.Moulines, and Ryd´en, T. (2005). Inference in

Hidden Markov Models. Springer Science+Business

Media, Inc., New York.

Doucet, A., Godsil, S., and Andrieu, C. (2000). On se-

quential monte carlo sampling methods for bayesian

ﬁltering. Statistics and Computing, 10:197–208.

Javaheri, A. (2005). Inside Volatility Arbitrage. John Wiley

& Sons, Inc, Hoboken.

Johannes, M. and Polson, N. (2006). MCMC method for

ﬁnancial econometrics. In Y.Ait-Sahalia and Hansen,

L., editors, Handbook of Financial Econometrics. El-

sevier.

Kalman, R. and Bucy, R. (1961). New results in linear ﬁl-

tering and prediction theory. Trans. ASME - Journ.

Basic Engineering, 83 (Series D):95–108.

Smith, R. (2008). An almost exact simulation method for

the heston model. Journal of Computational Finance,

11(1):115–125.

van Haastrecht, A. and Pelsser, A. (2010). Efﬁcient, al-

most exact simulation of the heston stochastic volatil-

ity model. IJTAF, 13:1–43.

AdaptiveFilteringforStochasticVolatilitybyusingExactSampling

335