
Kalman Filter-based Estimators for Dual Adaptive Neural Control
A Comparative Analysis of Execution Time and Performance Issues
Simon G. Fabri and Marvin K. Bugeja
Department of Systems and Control Engineering, University of Malta, Msida, Malta
Keywords:
Dual Adaptive Control, Kalman Filter, Neural Networks, Intelligent Control.
Abstract:
The real time implementation of neural network-based dual adaptive control for nonlinear systems can become
significantly demanding because of the amount of network parameters requiring estimation. This paper ex-
plores the effect of three different estimation algorithms for dual adaptive control of a class of multiple-input,
multiple-output nonlinear systems in terms of tracking performance and execution time. It is shown that the
Unscented and Square-root Unscented Kalman filter estimators lead to a significant improvement in tracking
performance when compared with the Extended Kalman filter, but with an appreciable increase in execution
time. Such issues need to be given due consideration when implementing controllers for on-line operation.
1 INTRODUCTION
The use of dual adaptive techniques for neural net-
work closed-loop control of nonlinear systems has
been investigated from different perspectives in the
recent past (Bugeja and Fabri, 2007; Bugeja et al.,
2009;
ˇ
Simandl et al., 2005). Inspired by the pioneer-
ing work of Fel’dbaum (Fel’dbaum, 1965), these dual
adaptive methods handle joint estimation and control
of nonlinear systems that are subject to functional un-
certainty by characterizing them within a stochastic
framework.
Neural networks are used to learn the unknown
nonlinear functions in real-time, whereas the dual
controller generates system inputs that exhibit two
desirable properties: (a) caution; whereby the un-
certainty of the neural network estimates is taken
into consideration by the controller so as to maintain
good tracking capabilities, and (b) probing; whereby a
component of the input is used to excite the system so
that the neural network training algorithm reduces the
functional uncertainty rapidly and efficiently (Fabri
and Kadirkamanathan, 2001; Filatov and Unbehauen,
2004).
The dual adaptive control paradigm is rooted in
the methodology of stochastic estimation and con-
trol. Stochastic algorithms are employed for estima-
tion of the neural network parameters which often ap-
pear in nonlinear form. Such estimators effectively
“train” the neural networks to capture the system’s
nonlinear functions recursively in real-time, based on
measurements of its inputs and outputs. Nonlinear
stochastic estimators which have been proposed in the
dual adaptive control literature include the Extended
Kalman filter (Fabri and Kadirkamanathan, 1998), the
Unscented Kalman filter (Bugeja and Fabri, 2009)
and the Gaussian Sum filter (
ˇ
Simandl et al., 2005).
The aim of this paper is to investigate and com-
pare the computational demand of a select set of non-
linear estimation algorithms when applied within the
context of neural network, dual adaptive control of a
class of uncertain, nonlinear, multiple-input/multiple-
output dynamic systems. Computational demand
analysis is a crucial consideration for the implemen-
tation of control algorithms which operate on com-
puter hardware in real-time (
˚
Astr
¨
om and Wittenmark,
2011). The discrete-time nature of such digital con-
trol systems entails that the control law, including the
estimation algorithm, executes, calculates and gener-
ates a fresh control signal with minimal delay at ev-
ery sampling instant. As a consequence, the estima-
tion and control algorithms must execute well within
the sampling period at which the discrete-time control
law is operating.
The analysis reported in this work would be of
help for designers to judge the feasibility of imple-
menting a particular estimation algorithm for real-
time, dual adaptive neuro-control. Three nonlinear
estimation techniques are considered and analysed in
this paper - the Extended, Unscented and Square-root
Unscented Kalman Filter algorithms - all three being
variations of the well-known Kalman filter method-
169
Fabri S. and Bugeja M..
Kalman Filter-based Estimators for Dual Adaptive Neural Control - A Comparative Analysis of Execution Time and Performance Issues.
DOI: 10.5220/0004455601690176
In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2013), pages 169-176
ISBN: 978-989-8565-70-9
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

ology for the nonlinear case. These algorithms are
evaluated by testing their effect on the execution time
and on the capability of the dual adaptive controller to
meet the control system’s performance requirements
when embedded within the closed loop control sys-
tem.
The rest of the paper is organized as follows: Sec-
tion 2 presents the background of the dual adaptive
control problem for nonlinear systems and describes
the control and estimation algorithms. This is fol-
lowed by Section 3 where the performance and com-
putational demands of the different estimation algo-
rithms are tested and the results are analysed. Con-
clusions are provided in Section 4.
2 ESTIMATION AND CONTROL
In this work we consider multiple-input, multiple-
output (MIMO) systems with nonlinear dynamics of
the following form:
y
y
y
k
= f
f
f (x
x
x
k−1
) + G
G
G(x
x
x
k−1
)u
u
u
k−1
+ ε
ε
ε
k
(1)
where y
y
y
k
∈ R
s
is a vector of s outputs,
u
u
u
k
∈ R
s
is an s-input control vector, x
x
x
k−1
:=
h
y
y
y
T
k−n
...y
y
y
T
k−1
u
u
u
T
k−1−p
...u
u
u
T
k−2
i
T
∈ R
s(n+p)
is
the system state vector (N.B. 0 ≤ p ≤ n and the
u
u
u terms vanish from the state vector if p = 0),
vector field f
f
f (x
x
x
k−1
) : R
s(n+p)
7→ R
s
and matrix
G
G
G(x
x
x
k−1
) : R
s(n+p)
7→ R
s×s
contain the unknown non-
linear functionals governing the system dynamics,
and ε
ε
ε
k
∈ R
s
represents an additive output white
noise signal assumed to be zero-mean Gaussian of
covariance R
R
R
ε
ε
ε
.
The control objective is for the output vector y
y
y
k
to track a reference input vector y
y
y
d
d
d
k
∈ R
s
despite the
uncertainty in the nonlinear functionals comprising f
f
f
and G
G
G.
2.1 Neural Network Estimation Model
Two multilayer perceptron (MLP) neural networks
are used to estimate and approximate the nonlinear
system functionals within an arbitrarily large compact
set χ
χ
χ in which the state vector is known to be con-
tained. The estimates from the neural networks will
be utilized within a dual adaptive control law.
Neural network
ˆ
f
f
f =
ˆ
f
1
···
ˆ
f
s
T
is used to approx-
imate the functionals in f
f
f := [ f
1
··· f
s
]
T
, where
ˆ
f
i
ap-
proximates f
i
. Neural network
ˆ
g
g
g = [ ˆg
1
··· ˆg
s
2
]
T
is used
to approximate the functionals in G
G
G, where ˆg
(i−1)s+ j
approximates G
i, j
according to the notation:
G
G
G :=
G
1,1
··· G
1,s
.
.
.
.
.
.
G
s,1
··· G
s,s
,
ˆ
G
G
G =
ˆg
1
··· ˆg
s
.
.
.
.
.
.
ˆg
s
2
−s+1
··· ˆg
s
2
.
Each of the two networks contains one hidden layer of
sigmoidal neurons whose outputs are represented by
vectors φ
φ
φ
f
f
f
,φ
φ
φ
g
g
g
for the
ˆ
f
f
f ,
ˆ
g
g
g networks respectively such
that:
ˆ
f
i
= φ
φ
φ
T
f
f
f
ˆ
w
w
w
f
f
f
i
; i = 1···s
ˆg
i
= φ
φ
φ
T
g
g
g
ˆ
w
w
w
g
g
g
i
; i = 1···s
2
(2)
where
ˆ
w
w
w
f
f
f
i
,
ˆ
w
w
w
g
g
g
i
denote the synaptic weight vectors of
networks
ˆ
f
f
f and
ˆ
g
g
g respectively. The individual MLP
sigmoidal activation functions are given by
φ
f
i
=
1 + exp(−
ˆ
s
s
s
f
f
f
i
ˇ
x
x
x)
−1
; i = 1···L
f
,
ˇ
x
x
x =
x
x
x
T
1
T
φ
g
i
=
1 + exp(−
ˆ
s
s
s
g
g
g
i
ˇ
x
x
x)
−1
; i = 1···L
g
,
ˇ
x
x
x =
x
x
x
T
1
T
with L
f
,L
g
denoting the number of neurons in
the hidden layer of the
ˆ
f
f
f ,
,
,
ˆ
g
g
g networks respectively,
and
ˆ
s
s
s
f
f
f
i
,
ˆ
s
s
s
g
g
g
i
denoting the corresponding hidden layer
weight vectors that shape the sigmoid of the i
th
acti-
vation function.
Let us group together all the unknown network
weights into one vector
ˆ
z
z
z =
h
ˆ
p
p
p
T
f
f
f
ˆ
p
p
p
T
g
g
g
i
T
, where
ˆ
p
p
p
f
f
f
=
h
···
ˆ
w
w
w
T
f
f
f
i
···
ˆ
s
s
s
T
f
f
f
i
···
i
T
and
ˆ
p
p
p
g
g
g
=
h
···
ˆ
w
w
w
T
g
g
g
i
···
ˆ
s
s
s
T
g
g
g
i
···
i
T
are
the weights associated with the
ˆ
f
f
f and
ˆ
g
g
g networks re-
spectively and which require on-line estimation. Ac-
cording to the Neural Network Universal Approxima-
tion Theorem (Haykin, 1999), there exists a set of
optimal (constant) weights such that an appropriately
sized neural network can approximate any smooth
nonlinear function within a compact subset of its in-
put space, up to any desired degree of accuracy. For
our case, let us denote this optimal set of weights as
z
z
z
∗
=
h
p
p
p
f
f
f
∗
T
p
p
p
g
g
g
∗
T
i
T
, these being the unknown optimal
values of
ˆ
z
z
z,
ˆ
p
p
p
f
f
f
and
ˆ
p
p
p
g
g
g
respectively. Let us assume that
the accuracy achieved with this set of optimal weights
is such that the network approximation error can be
considered negligible. In this case, system equation
(1) can be equivalently re-written in terms of the fol-
lowing optimal neural network estimation model:
z
z
z
∗
k+1
= z
z
z
∗
k
+ ρ
ρ
ρ
k
y
y
y
k
=
ˆ
f
f
f (x
x
x
k−1
, p
p
p
∗
f
f
f
k
) +
ˆ
G
G
G(x
x
x
k−1
, p
p
p
∗
g
g
g
k
)u
u
u
k−1
+ ε
ε
ε
k
= h
h
h(x
x
x
k−1
,u
u
u
k−1
,z
z
z
∗
k
) + ε
ε
ε
k
(3)
where
h
h
h(x
x
x
k−1
,u
u
u
k−1
,z
z
z
∗
k
) :=
ˆ
f
f
f (x
x
x
k−1
, p
p
p
∗
f
f
f
k
) +
ˆ
G
G
G(x
x
x
k−1
, p
p
p
∗
g
g
g
k
)u
u
u
k−1
and ρ
ρ
ρ
k
is a Gaussian process noise with known covari-
ance Q
Q
Q
ρ
ρ
ρ
, generally set to have very small magnitude.
The latter noise signal was not present in the origi-
nal system equation but is included in the estimation
model because it aids the weight estimation process.
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
170

2.2 Parameter Estimation
The optimal neural network parameters vector z
z
z
∗
ap-
pearing in model (3) is unknown and needs to be es-
timated recursively in real-time while the control ac-
tions are being executed. In this work, z
z
z
∗
is treated as
a random variable having an initial condition that is
assumed to be Gaussian distributed with known mean
ˆ
z
z
z
0
and covariance P
P
P
0
. These parameters appear non-
linearly in function h
h
h(x
x
x
k−1
,u
u
u
k−1
,z
z
z
∗
k
) of the model’s
output equation (3). As a consequence, even with
Gaussian additive noise, the distribution of the param-
eters will no longer remain Gaussian because of the
nonlinear effects of the system dynamics. Thus non-
linear stochastic estimation methods need to be ap-
plied. Three such approaches are considered here:
• the Extended Kalman filter (EKF),
• the Unscented Kalman filter (UKF),
• the Square-root Unscented Kalman filter
(SRUKF).
There exist other nonlinear estimation algorithms
such as Particle filters and Gaussian Sum filters but
these fall outside the scope of the analysis reported in
this work.
2.2.1 The EKF Estimator
Use of the EKF algorithm as a nonlinear estimator for
the parameters of neural networks is well documented
(Haykin, 2001). The EKF is based on a rather crude,
first-order linearization of the system dynamics, upon
which a Kalman filter is applied. It effectively ignores
the non-Gaussian distribution of the random variables
and propagates the density functions by means of the
standard Kalman filter equations which would only be
correct in a linear scenario, where Gaussianity is pre-
served. This assumption often leads to a well-known
disadvantage of the EKF: divergence of the parameter
estimates when propagated through time.
Let us denote the estimate to vector z
z
z
∗
calculated
at time step k as
ˆ
z
z
z
k
. The EKF algorithm, operating in
predictive mode, recursively generates estimates for
the parameters of the neural network controller being
considered in this work, as follows:
Algorithm 1 - EKF:
Initialize with
ˆ
z
z
z
0
and P
P
P
0
. Then at every time step k...
1. Calculate ∇
∇
∇
h
h
h
k−1
, the Jacobian of h
h
h
x
x
x
k−1
,u
u
u
k−1
,z
z
z
∗
k
with respect to z
z
z
∗
k
evaluated at
ˆ
z
z
z
k
:
∇
∇
∇
h
h
h
k−1
=
∇
∇
∇
f
f
f
k−1
∇
∇
∇
g
g
g
k−1
=
"
∂
ˆ
f
f
f
k−1
∂p
p
p
∗
f
f
f
k
ˆ
p
p
p
f
f
f
k
∂
ˆ
G
G
G
k−1
u
u
u
k−1
∂p
p
p
∗
g
g
g
k
ˆ
p
p
p
g
g
g
k
#
2. Approximate the covariance of the output mea-
surement’s distribution:
P
P
P
yy
k
= ∇
∇
∇
h
h
h
k−1
P
P
P
k
∇
∇
∇
T
h
h
h
k−1
+ R
R
R
ε
ε
ε
3. Calculate the Kalman gain:
K
K
K
k
= P
P
P
k
∇
∇
∇
T
h
h
h
k−1
P
P
P
yy
−1
k
4. Use the current output measurement to generate
the innovations:
i
i
i
k
= y
y
y
k
−h
h
h(x
x
x
k−1
,u
u
u
k−1
,
ˆ
z
z
z
k
)
5. Predict the parameter estimate:
ˆ
z
z
z
k+1
=
ˆ
z
z
z
k
+ K
K
K
k
i
i
i
k
6. Predict the covariance of the estimate:
P
P
P
k+1
= P
P
P
k
−K
K
K
k
∇
∇
∇
h
h
h
k−1
P
P
P
k
+ Q
Q
Q
ρ
ρ
ρ
.
Step 1 of this algorithm highlights a second crucial
disadvantage of the EKF algorithm, namely that it en-
tails a prior, off-line derivation of the Jacobian ma-
trix for calculation in step 1. This derivation can be-
come rather complex in the context of our neural net-
work control schemes that typically demand hundreds
of network parameters (Bugeja, 2011). Space limita-
tions preclude us from showing the derivation and fi-
nal form of this Jacobian matrix. Suffice to say that it
will be of size s ×(L
f
(s + L
a
) + L
g
(s
2
+ L
a
)), where
L
a
= s(n + p) + 1 denotes the length of vector
ˇ
x
x
x.
2.2.2 The UKF Estimator
The UKF is based on the Unscented Tranformation
which propagates the mean and covariance of the
random variables through appropriate nonlinear
transformations (Julier and Uhlmann, 2004). A
set of so-called sigma points are chosen from the
statistics of the nonlinear transformation so as to
propagate second-order properties of the probability
distribution. As a consequence, the UKF is a more
accurate estimator than the EKF (Wan and van der
Merwe, 2001). In addition, unlike the EKF, it does
not require any derivations or calculation of complex
Jacobian matrices. When applied within the context
of the neural network controller discussed in this
paper, the algorithm takes the following form:
Algorithm 2 - UKF:
Initialize with
ˆ
z
z
z
0
and P
P
P
0
. Then at every time step k...
1. Form a matrix
¯
Z
Z
Z
k
whose columns are the 2N + 1
sigma vectors
¯
z
z
z
i
k
generated as follows:
¯
z
z
z
1
k
=
ˆ
z
z
z
k
¯
z
z
z
i
k
=
ˆ
z
z
z
k
+ γσ
σ
σ
i
k
i = 2,...,N + 1
¯
z
z
z
i
k
=
ˆ
z
z
z
k
−γσ
σ
σ
i
k
i = N + 2,...,2N + 1
KalmanFilter-basedEstimatorsforDualAdaptiveNeuralControl-AComparativeAnalysisofExecutionTimeand
PerformanceIssues
171

where σ
σ
σ
i
k
is the i
th
column of Σ
Σ
Σ
k
, the latter de-
noting the lower-triangular Cholesky factoriza-
tion of P
P
P
k
such that Σ
Σ
Σ
k
Σ
Σ
Σ
T
k
= P
P
P
k
. In practice,
this is obtained by calling a Cholesky factoriza-
tion function in software, denoted in this paper as
chol
{
P
P
P
k
}
.
N denotes the length of
ˆ
z
z
z
k
(in this case N =
L
f
(s + L
a
)+L
g
s
2
+ L
a
) and γ =
√
N + λ where
λ = α
2
(N + κ) −N, α being a constant that de-
termines the spread of the points in the sigma
vectors around
ˆ
z
z
z
k
, typically set within the range
1 ≥ α ≥ 10
−4
. κ is a constant scaling parameter
normally set to 3 −N.
2. Propagate the sigma vectors through the neural
network estimation model’s output equation:
¯
y
y
y
i
k
=
¯
f
f
f
i
k−1
+
¯
G
G
G
i
k−1
u
u
u
k−1
where
¯
f
f
f
i
k−1
=
ˆ
f
f
f
x
x
x
k−1
,
¯
z
z
z
q
q
q
i
k
;
¯
G
G
G
i
k−1
=
ˆ
G
G
G
x
x
x
k−1
,
¯
z
z
z
r
r
r
i
k
;
i = 1,...,2N + 1; vectors
¯
z
z
z
q
q
q
i
k
,
¯
z
z
z
r
r
r
i
k
are the columns
of matrices
¯
Z
Z
Z
q
q
q
k
,
¯
Z
Z
Z
r
r
r
k
which in turn are submatrices
of size
L
f
(s + L
a
)×2N + 1
and
L
g
s
2
+ L
a
×
2N + 1
respectively, taken from the matrix of
sigma vectors
¯
Z
Z
Z
k
after repartitioning it as follows:
¯
Z
Z
Z
k
=
¯
Z
Z
Z
q
q
q
k
¯
Z
Z
Z
r
r
r
k
.
3. Approximate the mean and covariance of the dis-
tribution of the output measurement using the
propagated sigma vectors, calculated by the fol-
lowing weighted summations:
ˆ
y
y
y
k
=
2N+1
∑
i=1
W
m
(i)
¯
y
y
y
i
k
P
P
P
yy
k
=
2N+1
∑
i=1
W
c
(i)
¯
y
y
y
i
k
−
ˆ
y
y
y
k
¯
y
y
y
i
k
−
ˆ
y
y
y
k
T
+ R
R
R
ε
ε
ε
P
P
P
zy
k
=
2N+1
∑
i=1
W
c
(i)
¯
z
z
z
i
k
−
ˆ
z
z
z
k
¯
y
y
y
i
k
−
ˆ
y
y
y
k
T
where the so-called unscented transform weights
are given by
W
m
(1)
=
λ
N + λ
, W
c
(1)
=
λ
N + λ
+ 1 −α
2
+ β
W
m
(i)
= W
c
(i)
=
1
2(N + λ)
, i = 2,...,2N + 1.
β is a constant parameter that depends upon prior
knowledge of the estimate’s distribution where,
for the Gaussian prior case, β = 2 is optimal.
4. The Kalman gain is calculated as:
K
K
K
k
= P
P
P
zy
k
P
P
P
yy
−1
k
5. The innovations are calculated as:
i
i
i
k
= y
y
y
k
−
ˆ
y
y
y
k
6. Predict the parameter estimate:
ˆ
z
z
z
k+1
=
ˆ
z
z
z
k
+ K
K
K
k
i
i
i
k
7. Predict the covariance of the estimate:
P
P
P
k+1
= P
P
P
k
−K
K
K
k
P
P
P
yy
k
K
K
K
T
k
+ Q
Q
Q
ρ
ρ
ρ
In its credit, and in contrast with the EKF, the UKF
algorithm does not make use of the Jacobian ma-
trix. Additionally, several studies have been pub-
lished which illustrate the improved performance of
the UKF over the EKF for estimation of variables in
nonlinear systems (Julier and Uhlmann, 2004; Wan
and van der Merwe, 2001).
2.2.3 The SRUKF Estimator
The numerical properties of the UKF algorithm can
be further improved by a square-root implementation,
leading to the SRUKF algorithm (Wan and van der
Merwe, 2001). This guarantees that the covariance
matrices remain positive semi-definite.
Additionally, whereas the UKF needs to perform
a Cholesky factorization of the covariance matrix
at every time step in order to compute its square
root Σ
Σ
Σ
k
(refer to Step 1 in the UKF algorithm), the
SRUKF propagates Σ
Σ
Σ
k
directly, avoiding the recursive
Cholesky factorization operations. In the parameter
estimation scenario, this leads to a computational
complexity which has the same order as that of
the EKF in terms of floating point instructions per
iteration (Wan and van der Merwe, 2001). However
this does not necessarily translate to an equal or a
similar execution time, especially when the amount
of parameters is high, leading to a large number of
sigma points (LaViola, 2003). When applied to the
neural network controller developed in this paper, the
SRUKF algorithm takes the following form:
Algorithm 3 - SRUKF:
Initialize with
ˆ
z
z
z
0
and Σ
Σ
Σ
0
= chol
{
P
P
P
0
}
. Then at every
time step k...
1. Form matrix
¯
Z
Z
Z
k
of 2N + 1 sigma vectors as fol-
lows:
¯
z
z
z
1
k
=
ˆ
z
z
z
k
¯
z
z
z
i
k
=
ˆ
z
z
z
k
+ γσ
σ
σ
i
k
i = 2,...,N + 1
¯
z
z
z
i
k
=
ˆ
z
z
z
k
−γσ
σ
σ
i
k
i = N + 2,...,2N + 1
where σ
σ
σ
i
k
is the i
th
column of Σ
Σ
Σ
k
. The constants
N, γ, λ and α are defined in an identical manner
as for the UKF.
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
172

2. Propagate the sigma vectors through the neural
network output equation:
¯
y
y
y
i
k
=
¯
f
f
f
i
k−1
+
¯
G
G
G
i
k−1
u
u
u
k−1
where
¯
f
f
f
i
k−1
,
¯
G
G
G
i
k−1
,
¯
z
z
z
q
q
q
i
k
,
¯
z
z
z
r
r
r
i
k
are defined in the
same way as for the UKF.
3. Approximate the mean and the Cholesky factor of
the covariance of the output measurement’s dis-
tribution through the following weighted summa-
tions of the propagated sigma vectors:
ˆ
y
y
y
k
=
2N+1
∑
i=1
W
m
(i)
¯
y
y
y
i
k
Σ
Σ
Σ
y
k
= qr
nh
q
W
c
(2:2N+1)
¯
y
y
y
2:2N+1
k
−
ˆ
y
y
y
k
p
R
R
R
ε
ε
ε
io
Σ
Σ
Σ
y
k
= cholupdate
Σ
Σ
Σ
y
k
,
¯
y
y
y
1
k
−
ˆ
y
y
y
k
, W
c
(1)
P
P
P
zy
k
=
2N+1
∑
i=1
W
c
(i)
¯
z
z
z
i
k
−
ˆ
z
z
z
k
¯
y
y
y
i
k
−
ˆ
y
y
y
k
T
where the unscented transform weights
W
m
(i)
, W
c
(i)
and parameter β are defined as
in the UKF algorithm.
4. The Kalman gain is calculated as:
K
K
K
k
= (P
P
P
zy
k
)/Σ
Σ
Σ
y
T
k
)/Σ
Σ
Σ
y
k
5. The innovations are calculated as:
i
i
i
k
= y
y
y
k
−
ˆ
y
y
y
k
6. Predict the parameter estimate:
ˆ
z
z
z
k+1
=
ˆ
z
z
z
k
+ K
K
K
k
i
i
i
k
7. Predict the Cholesky factor of the covariance of
the estimate as either:
Option 1:
Σ
Σ
Σ
k+1
= λ
−0.5
RLS
cholupdate
Σ
Σ
Σ
k
, K
K
K
k
Σ
Σ
Σ
y
k
,−1
where λ
RLS
is a constant forgetting factor param-
eter set to a value just less than 1 e.g. 0.9995,
or Option 2:
Σ
Σ
Σ
k+1
= cholupdate
Σ
Σ
Σ
k
, K
K
K
k
Σ
Σ
Σ
y
k
,−1
+ D
D
D
ρ
ρ
ρ
k
where
D
D
D
ρ
ρ
ρ
k
= −Diag
{
Σ
Σ
Σ
k
}
+
q
Diag
2
{
Σ
Σ
Σ
k
}
+ Diag
Q
Q
Q
ρ
ρ
ρ
with function Diag
{
·
}
denoting the formation of
a diagonal matrix whose diagonal elements are a
copy of the diagonal terms in the matrix of the
function’s argument.
The qr{·}, ·/· and cholupdate{·} symbols used in
steps 3, 4 and 7 of the above algorithm denote func-
tions that execute QR factorization, efficient least
squares and Cholesky factor updating operations re-
spectively. More details on this can be found in (Wan
and van der Merwe, 2001).
2.3 The Control Law
The ideal solution to the dual control problem in-
volves the minimization of a cost function whose so-
lution is practically impossible to implement in most
situations (Fabri and Kadirkamanathan, 2001). Some
adaptive control schemes thus optimize a much more
basic cost function which leads to control laws, such
as Heuristic Certainty Equivalence (HCE) and Cau-
tious control, that lack the desirable effects of dual
control. These lead to an inferior performance typi-
cally exhibiting large overshoots in HCE, or long re-
sponse times in Cautious control. A better alterna-
tive, as used in this work, is to adopt a suboptimal
cost function but which to a certain extent still retains
dual-like properties in its control actions.
This work is based on the suboptimal dual cost
function originally proposed in (Milito et al., 1982)
for linear stochastic systems, but generalized to the
case of nonlinear MIMO systems as follows:
J
inn
= E
n
y
y
y
k+1
−y
y
y
d
d
d
k+1
T
Q
Q
Q
1
1
1
y
y
y
k+1
−y
y
y
d
d
d
k+1
+
u
u
u
T
k
Q
Q
Q
2
2
2
u
u
u
k
+
i
i
i
T
k+1
Q
Q
Q
3
3
3
i
i
i
k+1
I
k
o
,
where E{·}denotes mathematical expectation over all
random variables, I
k
is the information state at time-
step k defined as I
k
:=
{
y
y
y
k
...y
y
y
0
u
u
u
k−1
...u
u
u
0
}
, and i
i
i
is the innovations vector from the estimator. Design
parameters Q
Q
Q
1
1
1
and Q
Q
Q
2
2
2
are (s ×s) positive definite di-
agonal matrices with real positive elements. Q
Q
Q
3
3
3
is
an (s ×s) diagonal matrix satisfying −Q
Q
Q
1
1
1
≤ Q
Q
Q
3
3
3
≤ 0
0
0
element-wise. Matrix Q
Q
Q
1
1
1
imposes a penalty on track-
ing errors and matrix Q
Q
Q
2
2
2
induces a penalty on large
control inputs. Q
Q
Q
3
3
3
affects the innovations vector. Its
setting determines whether the control law will act in
HCE mode, Cautious mode or alternatively induce the
desired dual adaptive control characteristics.
The optimization of cost function J
inn
subject to
the dynamics of the system as represented by the op-
timal neural network model (3), leads to a dual control
law of the following form:
u
u
u
k
=
G
G
G
0
0
0T
k
Q
Q
Q
1
1
1
G
G
G
0
0
0
k
+ Q
Q
Q
2
2
2
+ N
N
N
k
−1
×
G
G
G
0
0
0T
k
Q
Q
Q
1
1
1
y
d
k+1
− f
f
f
0
0
0
k
−κ
κ
κ
k
(4)
where f
f
f
0
0
0
k
, G
G
G
0
0
0
k
, N
N
N
k
and κ
κ
κ
k
are terms which depend
on the variables of the selected estimator. A detailed
derivation and full description of this control law falls
outside the scope of this paper. Further details on
the control aspect of the work may be obtained from
(Bugeja, 2011). N
N
N
k
and κ
κ
κ
k
depend on the covariance
estimates from the estimator and embody informa-
tion regarding the uncertainty of the estimates at every
time instant k. When matrix Q
Q
Q
3
3
3
is set equal to −Q
Q
Q
1
1
1
,
KalmanFilter-basedEstimatorsforDualAdaptiveNeuralControl-AComparativeAnalysisofExecutionTimeand
PerformanceIssues
173

the terms N
N
N
k
and κ
κ
κ
k
will become null and vanish from
control law (4). The controller will thus ignore the
uncertainty of the estimates, leading to an HCE con-
troller which tends to generate aggressive inputs that
may be beneficial for probing the system but at the
expense of excessive overshoot and a low degree of
stability. At the other extreme, with Q
Q
Q
3
3
3
= 0
0
0, the con-
trol law gives maximum attention to the uncertainty
terms, which leads to Cautious control. Whereas this
does not give rise to excessive overshoot and a low de-
gree of stability, it is typically too weak to make the
system react promptly and generate probing signals
which enhance the estimation process. Both these ex-
tremes are inferior to Dual control in terms of per-
formance. When Q
Q
Q
3
3
3
is set in between these two ex-
tremes, the controller will exhibit dual-like character-
istics obtained by reasonably balancing out the ag-
gressive probing of HCE and the sluggish actions of
Cautious control.
3 TESTING AND RESULTS
The structure of the complete control algorithm can
be subdivided in terms of the following tasks:
TASK A - Measurement of the system outputs y
y
y
k
.
TASK B - Model Estimation (EKF, UKF, SRUKF):
I. Calculation of Jacobian matrix (for EKF) or
sigma vectors matrix (for UKF, SRUKF), fol-
lowed by the output measurement covariance or
its Cholesky factor (for SRUKF).
II. Calculation of Kalman gain, innovations, pa-
rameter prediction, and parameter covariance
prediction.
TASK C - Dual Control Law Calculations:
I. Calculation of f
f
f
0
0
0
k
, G
G
G
0
0
0
k
, N
N
N
k
, κ
κ
κ
k
.
II. Calculation of u
u
u
k
.
TASK D - Input of u
u
u
k
to the system.
In the EKF estimator, TASK B(I) is covered in steps
1, 2 and TASK B(II) is implemented in steps 3, 4, 5, 6
of Algorithm 1. In the UKF and SRUKF estimators,
TASK B(I) is implemented in steps 1, 2, 3 and TASK
B(II) is covered in steps 4, 5, 6, 7 of Algorithms 2 and
3.
Whereas TASK B(I) for the EKF involves an ex-
tensive prior off-line effort to derive equations for the
Jacobian matrix ∇
∇
∇
h
h
h
k−1
that can be rather complex in a
neural networks scenario, calculation of the numerical
value of ∇
∇
∇
h
h
h
k−1
and P
P
P
yy
k
during run-time in steps 1 and
2 is rather straightforward. By contrast, the Jacobian-
free UKF and SRUKF estimators require no prior off-
line effort at all for TASK B(I), but instead shift the
effort within steps 1 to 3 during run-time through rel-
atively more intense calculations for Cholesky or QR
factorizations and weighted summations across sigma
vectors. This computational effort is not trivial in a
neural networks scenario where the amount of param-
eters, and consequently also the number of sigma vec-
tors, is large.
A number of simulation trials were performed in
order to validate the effects of the three estimators on
the control system. The objective of these trials is
twofold, namely to quantify across the three estima-
tors: (a) the ability of the control algorithm to track
the reference input vector y
y
y
d
d
d
k
, (b) the time taken for
execution of the complete control algorithm, with spe-
cific focus on the impact of TASKS B and C.
Simulation trials were performed on MATLAB
using a 2-input, 2-output dynamic MIMO system hav-
ing the form of Equation (1) with n = 2, p = 1 and
nonlinear functions:
f
f
f =
0.7x
1
x
3
1+x
2
2
+x
2
3
+ 0.25x
5
+ 0.5x
6
0.5x
4
sinx
2
1+x
2
1
+x
2
4
+ 0.5x
6
+ 0.3x
5
,
G
G
G =
"
cos
2
x
3
0.1
1+3x
2
1
+x
2
4
x
2
1
0.1x
6
−5.5
#
.
The measurement noise covariance R
R
R
ε
ε
ε
= 5 ×10
−4
I
I
I
(I
I
I denotes the identity matrix) and that of the model
process noise Q
Q
Q
ρ
= 1 ×10
−5
I
I
I. The two neural net-
works in the estimation model are structured with
L
f
= L
g
= 7 hidden layer neurons. This leads to a
total of N = 140 neural network parameters requir-
ing estimation. The initial condition of the parame-
ter vector
ˆ
z
z
z
0
is generated at random from the interval
[−0.1,0.1] and its covariance P
P
P
0
= 0.8I
I
I. The UKF
and SRUKF parameter α is set to 0.9. 2N + 1 = 281
sigma vectors, each composed of N = 140 elements,
are required by these two algorithms. The control law
was tested under three different settings of Q
Q
Q
3
3
3
corre-
sponding to HCE, Cautious and Dual control modes
(Q
Q
Q
3
3
3
= −0.3I
I
I in the latter case).
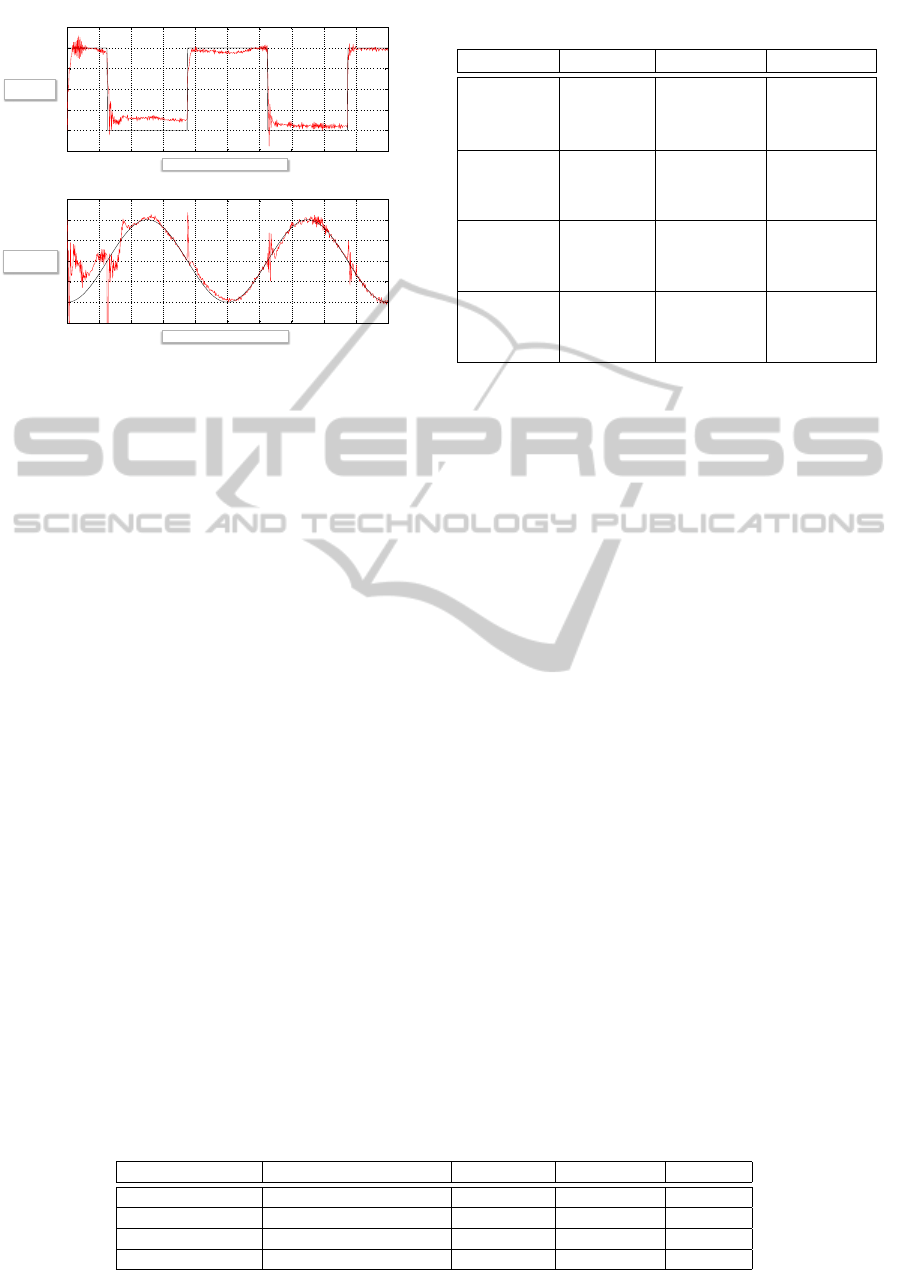
Figure 1 shows a sample of results for dual control
with a UKF estimator over a 10s interval. The ref-
erence input signals are shown in black and the two
system outputs in colour. Notice how the proposed
adaptive control system results in good tracking of the
reference inputs following an initial period of “learn-
ing” due to the controller’s lack of knowledge of the
nonlinear system functions in f
f
f and G
G
G. The single
trial results of Figure 1 are however not sufficient to
characterize the general performance of the control
system due to variations introduced by the random
effects of the noise and the initial parameter vector.
A Monte Carlo characterization was therefore per-
formed by repeating the experiment over 150 trials,
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
174
0 1 2 3 4 5 6 7 8 9 10
-1.5
-1
-0.5
0
0.5
1
1.5
time in seconds
y1
0 1 2 3 4 5 6 7 8 9 10
-1.5
-1
-0.5
0
0.5
1
1.5
time in seconds
y2
Time in seconds
Time in seconds
output
y1
output
y2
Figure 1: Tracking results with Dual control using UKF.
each time generating fresh realizations of the noise
signals and the initial neural network parameters. Q
Q
Q
2
2
2
was set to 0.1I
I
I in all three cases. In each individ-
ual trial, all three control modes (HCE, Cautious and
Dual) and all three estimators (EKF, UKF, SRUKF)
were subjected to the same realization of random sig-
nals so as to ensure a fair comparison. The SRUKF
estimator is tested for both Cholesky factor predic-
tion options in step 7 of the algorithm. The tracking
performance at the end of each trial was quantified in
terms of an error metric C =
∑
k
end
k=0
||y
y
y
d
d
d
k
−y
y
y
k
||
2
which
captures the squared tracking error over the whole
simulation interval which was set to 5s in these trials.
Lower values of C indicate a better tracking perfor-
mance. The Monte Carlo analysis results are summa-
rized in Table 1, showing the mean value of C and
its variance across all trials for each possible com-
bination of control mode and estimator. The results
clearly show the superior performance of Dual con-
trol over the Cautious and HCE modes in all estima-
tors, with C exhibiting the smallest mean and variance
in each case. Moreover, comparing across estimators,
the inferior control performance arising from the in-
accuracies of the EKF estimator is clearly evident in
all control modes. On the other hand, the UKF and
the two SRUKF options exhibit an error metric hav-
ing means and variances of the same order, reflecting
similar tracking performance.
The simulation experiments were also used to
time the main steps of the estimation and control al-
Table 1: Results of Monte Carlo analysis.
Estimator Mode Mean of C Var of C
HCE 15384.0 1.90×10
10
EKF Cautious 4562.0 3.03 ×10
9
Dual 43.4 4.32 ×10
3
HCE 99.8 6.29 ×10
4
UKF Cautious 42.7 464.8
Dual 35.6 318.5
HCE 90.8 2.18 ×10
4
SRUKF
Cautious 44.0 485.2
option 1
Dual 36.2 336.9
HCE 101.0 7.90 ×10
4
SRUKF
Cautious 43.9 611.4
option 2
Dual 35.6 319.8
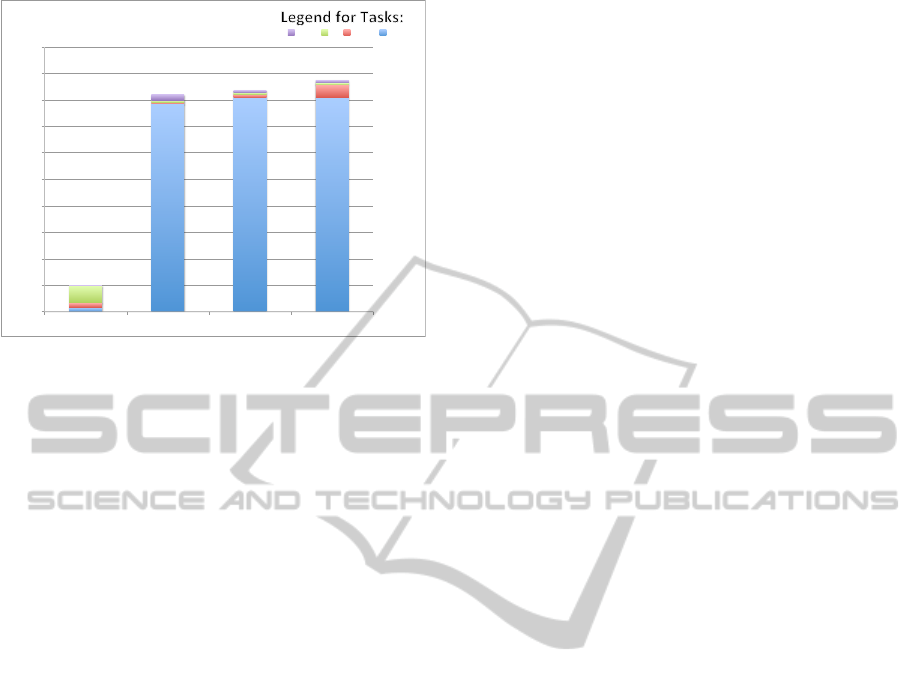
gorithm across all estimator types. The results, shown
in Table 2, show the mean execution time in mil-
liseconds (ms) calculated over 250 iterations for the
following operations: one complete iteration, Task
B(I), Task B(II) and Task C. Figure 2 is a graphi-
cal depiction of the same results, but expressed as
a factor of the EKF iteration time so as to interpret
the measurements independently of any absolute time
values which would vary according to the hardware
on which the algorithms are executed. Such normal-
ized timings for the separate tasks are shown in dif-
ferent colours as indicated in the legend on Figure
2. The results demonstrate that the execution time
of the UKF/SRUKF increases by a factor of approxi-
mately 8 to 9 with respect to the EKF. This is mainly
due to TASK B(I) in the UKF/SRUKF algorithm, par-
ticularly step 2 of the algorithms which propagates
the 281 sigma vectors through the neural network.
This step takes around 7.5 times the total EKF iter-
ation time, notwithstanding that the UKF/SRUKF al-
gorithms were carefully coded without slow for/next
loops in order to maintain efficient timing. The
SRUKF’s total execution time is of the same order as
that of the UKF, albeit slightly longer, especially with
Option 2. In fact, TASK B(I) in the SRUKF takes
a longer duration than the UKF because of the QR
factorization and Cholesky factor update operations
in step 3 which takes approximately thrice the time
of the corresponding step in the UKF. Although this
is somewhat compensated by the shorter duration of
step 1 in the SRUKF, due to the absence of Cholesky
factorization, this reduction is minimal when com-
Table 2: Execution time in ms (MATLAB running on a 3GHz Pentium 4 CPU with 2GB RAM).
One complete iteration TASK B(I) TASK B(II) TASK C
EKF 10.9 1.8 1.9 7.0
UKF 89.7 85.7 0.6 0.8
SRUKF option 1 91.3 88.3 1.3 0.7
SRUKF option 2 95.5 88.3 5.3 0.7
KalmanFilter-basedEstimatorsforDualAdaptiveNeuralControl-AComparativeAnalysisofExecutionTimeand
PerformanceIssues
175
!"
#"
$"
%"
&"
'"
("
)"
*"
+"
#!"
,-." /-." 01/-."23425#" 01/-."23425"$"
Factor'of'EKF'itera-on'-me'
Execu-on2-me'graph''
expressed'as'a'factor'of'EKF'itera-on'-me'
678" 9" :;<<=" :;<="
Figure 2: Execution time as a factor of the EKF case.
pared with the increased duration of step 3. TASK
B(II) in the two SRUKF cases is also significantly
longer than that of the UKF, particularly with option
2. The dominant component here is the Cholesky fac-
tor update operation in step 7 and, for the case of op-
tion 2, the additional operations required for calcu-
lation of D
D
D
ρ
ρ
ρ
k
. The execution time of the EKF algo-
rithm is dominated by TASK C, which is around 9
times longer than the corresponding task in the other
estimators. However this duration is still much less
pronounced than the contribution of TASK B(I) in the
UKF/SRUKF cases.
4 CONCLUSIONS
The results of the previous section clearly illustrate
the general tracking superiority of Dual control over
Cautious and HCE control. In addition, use of the
UKF or SRUKF estimators leads to even better track-
ing results than the EKF - C is reduced by circa 18%
on average in the Dual control case. The SRUKF of-
fers no significant advantages in terms of tracking per-
formance with respect to the UKF, neither with option
1 nor option 2.
However, this improvement in tracking perfor-
mance comes at the cost of significantly increased
execution time. The UKF and SRUKF with option
1 respectively take 8.2 and 8.4 times longer than the
EKF-based controller, while the SRUKF with option
2 takes around 8.8 times longer.
One therefore concludes that Dual control with a
UKF-based estimator should be used for best track-
ing performance, provided that the hardware is able to
execute the estimation and control algorithm within a
small percentage of the sampling interval. If this con-
dition is not satisfied, the faster EKF-based Dual con-
troller could be implemented instead but with a com-
promise; namely an inferior tracking performance.
REFERENCES
˚
Astr
¨
om, K. J. and Wittenmark, B. (2011). Computer-
Controlled Systems: theory and design. Dover Pub-
lications, U.S.A, 3rd edition.
Bugeja, M. K. (2011). Computational Intelligence Meth-
ods for Dynamic Control of Mobile Robots. PhD the-
sis, University of Malta, Dept. of Systems and Control
Engineering, Msida, Malta.
Bugeja, M. K. and Fabri, S. G. (2007). Dual adaptive
control for trajectory tracking of mobile robots. In
Proceedings of the IEEE International Conference on
Robotics and Automation (ICRA 07), pages 2215–
2220, Rome, Italy.
Bugeja, M. K. and Fabri, S. G. (2009). A novel dual adap-
tive neuro-controller based on the unscented trans-
form for mobile robots. In Proceedings of the Inter-
national Conference on Neural Computation (ICNC
2009), pages 355–362, Funchal Madeira, Portugal.
Bugeja, M. K., Fabri, S. G., and Camilleri, L. (2009). Dual
adaptive control of mobile robots using neural net-
works. IEEE Transactions on Systems, Man and Cy-
bernetics - Part B, 39(1):129–141.
Fabri, S. and Kadirkamanathan, V. (1998). Dual adaptive
control of nonlinear stochastic systems using neural
networks. Automatica, 34(2):245–253.
Fabri, S. G. and Kadirkamanathan, V. (2001). Functional
Adaptive Control: An intelligent systems approach.
Springer-Verlag, London.
Fel’dbaum, A. A. (1965). Optimal Control Systems. Aca-
demic Press, New York.
Filatov, N. and Unbehauen, H. (2004). Adaptive Dual Con-
trol: Theory and applications. Springer, Berlin.
Haykin, S. (1999). Neural Networks: A comprehensive
foundation. Prentice-Hall, Upper Saddle River, NJ,
2nd edition.
Haykin, S., editor (2001). Kalman Filtering and Neural
Networks. John Wiley and Sons.
Julier, S. J. and Uhlmann, J. K. (2004). Unscented filtering
and nonlinear estimation. Proceedings of the IEEE,
92(3):401–422.
LaViola, J. (2003). A comparison of Unscented and Ex-
tended Kalman filtering for estimating quaternion mo-
tion. In Proceedings of the 2003 American Control
Conference, pages 2435–2440.
Milito, R., Padilla, C. S., Padilla, R. A., and Cadorin,
D. (1982). An innovations approach to dual con-
trol. IEEE Transactions on Automatic Control, AC-
27(1):133–137.
ˇ
Simandl, M., Kr
´
al, L., and Hering, P. (2005). Neural net-
work based bicriterial dual control of nonlinear sys-
tems. In Preprints of the 16th IFAC World Congress,
volume 16, Prague, Czech Republic.
Wan, E. A. and van der Merwe, R. (2001). The Unscented
Kalman Filter. In Haykin, S., editor, Kalman Filtering
and Neural Networks, Adaptive and Learning Systems
for Signal Processing, Communications and Control,
chapter 7, pages 221–280. John Wiley and Sons.
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
176
