Set-membership Method for Discrete Optimal Control
R´emy Guyonneau, S´ebastien Lagrange, Laurent Hardouin, Mehdi Lhommeau
Laboratoire d’Ing´enierie des Syst`emes Automatis´es (LISA), Universit´e d’Angers,
62 Avenue Notre Dame du Lac, Angers, France
Keywords:
Non-linear Systems, Interval Analysis, Guaranteed Numerical Integration, Optimal Control.
Abstract: The objective of this paper is twofold. First we propose a new approach for computing C
t
0
,t
f
the subset
of initial states of a system from which there exists at least one trajectory reaching a target T in a finite
time t
f
from a time t
0
. This is done considering a discrete time t
k
and a control vector continuous over
a time [t
k−1
,t
k
]. Then, using the previously mentioned work and given a cost function, the objective is to
estimate an enclosure of the discrete optimal control vector from an initial state of C
t
0
,t
f
to the target. Whereas
classical methods do not provide any guaranty on the set of state vectors that belong to the C
t
0
,t
f
, interval
analysis and guaranteed numerical integration allow us to avoid any indetermination. We present an algorithm
able to provide guaranteed characterizations of the inner C
−
t
0
,t
f
and an the outer C
+
t
0
,t
f
of C
t
0
,t
f
, such that
C
−
t
0
,t
f
⊆ C
t
0
,t
f
⊆ C
+
t
0
,t
f
. In addition to that, the presented algorithm is extended in order enclose the discrete
optimal control vector of the system, form an initial state to the target, by a set of discrete trajectories.
1 INTRODUCTION
We consider a control system, defined by the differ-
ential equation
˙
x(t) = f(x(t),u(t)) (1)
where x(t) ∈ R
n
be the state vector of the system,
u(t) ∈ U be the control vector. This system is studied
over a bounded time t
k
∈[t
0
,t
f
], considering a discrete
time
t
k
= t
0
+ k×δ
t
,t
k
≤t
f
,k ∈{1,···, m}, (2)
It will be assumed that δ
t
is small enough so that the
control vector u(t) can be assumed to be continuous
over [t
k
,t
k+1
]. Associated to the differential equation
(1) we define the flow map
ϕ(t
0
,t
k
;x
0
,u(t)) = x(t), (3)
where x(t) denotes the solution to (1) with the
initial condition x(t
0
) = x
0
and the control function
u(t) ∈ U, where U = {u : [t
0
,t
k−1
] → U|u is con-
tinuous over [t
k
,t
k+1
]} denotes the set of admissible
controls. Note that in the later the notation u
k
will
refer to u(t) : [t
k
,t
k+1
] → U, with u(t) continuous
over [t
k
,t
k+1
]. Given X
0
a set of possible initial values
x
0
, the reachable set of the system (1) at the time t
k
is
ϕ(t
0
,t
k
;X
0
,U) = { ϕ(t
0
,t
k
;x
0
,u(t))|
ϕ(t
0
,t
0
;x
0
,u(t)) = x
0
and ϕ : [t
0
,t
k
] ×X
0
×U →R
n
is a solution of (1) for some
u(t) ∈ U}.
(4)
The trajectory from t
k
to t
k
is defined by
φ([t
k
,t
k
];X,U) = {
˜
X ⊆R
n
|∃t
k
∈[t
k
,t
k
],
˜
X = ϕ(t
k
,t
k
;X,U)}.
(5)
Let K ⊂ R
n
be a state constraint such that x(t) ∈ K,
and T be a compact set in K (the target). C
t
0
,t
f
corre-
sponds to the subset of initial states of K from which
there exists at least one solution of (1) reaching the
target T in finite time t
f
from a time t
0
:
C
t
0
,t
f
= {x
0
∈ K|∃u(t) ∈U,ϕ(t
0
,t
f
;x
0
,u(t)) ∈T}
(6)
Given that the input vector is continuous over
[t
k
,t
k+1
], the first objective of this paper is to compute
an inner and outer approximations, C
−
t
0
,t
f
and C
+
t
0
,t
f
, of
C
t
0
,t
f
(Lhommeau et al., 2011; Delanoue et al., 2009).
Such problems of dynamics control under constraints
refer to viability theory (Aubin, 2006) (see (Aubin,
1990) for a survey). The proposed method to char-
acterize C
t
0
,t
f
, which has similarities with dynamic
programming (Kirk, 2004), has the advantage that it
is guaranteed whereas numerical methods give only
an approximation. An interval analysis based method
193
Guyonneau R., Lagrange S., Hardouin L. and Lhommeau M..
Set-membership Method for Discrete Optimal Control.
DOI: 10.5220/0004458001930200
In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2013), pages 193-200
ISBN: 978-989-8565-70-9
Copyright
c
 2013 SCITEPRESS (Science and Technology Publications, Lda.)

is used to compute the approximations, such that
C
−
t
0
,t
f
⊆ C
t
0
,t
f
⊆ C
+
t
0
,t
f
, by using guaranteed numeri-
cal integration (VNODE-LP
1
). Note that an obvious
approximations would be C
−
t
0
,t
f
=
/
0 and C
+
t
0
,t
f
= K.
The proposed method aims at computing a better en-
closure of C
t
0
,t
f
.
In a second part, we got interested to the optimal
control problem. Given a cost function J and an ini-
tial state x
0
∈ C
t
0
,t
f
, we propose a numerical method
to evaluate an enclosure of the discrete optimal con-
trol u(t) ∈ U such that ϕ(t
0
,t
f
;x
0
,u(t)) ∈ T and u(t)
continuous over [t
k
,t
k+1
].
The paper is organised as follow. First some in-
terval analysis tools are presented in Section 2 as they
are used to compute the inner and outer approxima-
tions. Section 3 presents the proposed algorithm to
compute C
t
0
,t
f
and is followed by experimental re-
sults in Section 4. Finally Section 5 discusses about
the optimal control problem and Section 6 concludes
this paper.
2 INTERVAL ANALYSIS
Interval analysis for ordinary differential equations
was introduced by Moore (Moore, 1966) (See (Nedi-
alkov et al., 1999) for a description and bibliography
on this topic). These methods provide numerically re-
liable enclosures of the exact solution of differential
equations.
Interval analysis usually considers only closed inter-
vals. The set of these intervals is denoted IR. An in-
terval is usually denoted using brackets. An element
of an interval [x] is denoted by x. An interval vector
(box) [x] of R
n
is a Cartesian product of n intervals. If
[x] = [x
1
,x
1
] ×···×[x
n
,x
n
] is a box, then its width is
w([x]) = w([x
1
]) ×···×w([x
n
]), (7)
where w([x
i
]) = x
i
−x
i
. The set of all boxes of R
n
is
denoted by IR
n
.
The Bisect() function divides an interval [x] into two
intervals [x
1
] and [x
2
] such as [x
1
] ∪[x
2
] = [x], [x
1
] ∩
[x
2
] =
/
0 and w([x
1
]) = w([x
2
]).
The main concept of interval analysis is the extension
of real functions to intervals, which is defined as fol-
lows. Let f : R
n
→ R
m
be a continuous real function,
and [f] : IR
n
→ IR
m
be an inclusion function. Then
[f] is an inclusion function of f if and only if for every
[x] ∈ IR
n
,{f(x)|x ∈ [x]} ⊆ [f]([x]).
Hence, an interval inclusion allows computing en-
closures of the image of boxes by real functions. It
1
A C++ package for computing bounds on solutions in Initial
Value Problems for Ordinary Differential Equations, by N. Nedi-
alkov.
now remains to show how to compute such inclu-
sions. The first step is to compute formally the in-
terval extension of elementary functions. For exam-
ple, we define [x
,x] + [y,y] := [x + y,x + y]. Similar
simple expressions are obtained for other functions
like −,×,÷,x
n
,
√
x,exp,··· This process gives rise
to the so-called interval arithmetic (see (Jaulin et al.,
2001)).
Then, an interval inclusion for real functions com-
pound of these elementary operations is simply ob-
tained by changing the real operations to their inter-
val counterparts. This interval inclusion is called the
natural extension.
Interval arithmetic can be used to compute guaranteed
integration. In the later, the Nedialkov method is used
to compute:
- [x]
∗
such that [x]
∗
⊃ ϕ(t
k
,t
k+1
;[x],[u
k
]),
- K
∗
such that K
∗
⊃ φ([t
k
,t
k+1
];[x],[u
k
]).
Note that the Nedialkov method is one chosen solu-
tion over several methods, one could chose a different
approach.
Given a bounded set E of complex shape, one usu-
ally defines an axis-aligned box or paving, i.e. an
union of non-overlapping boxes, E
+
which contains
the set E : this is known as the outer approximation of
it. Likewise, one also defines an inner approximation
E
−
which is contained in the set E. Hence we have
the following property
E
−
⊆ E ⊆E
+
(8)
3 CHARACTERIZATION OF C
T
0
,T
F
This section presents an algorithm able to provide an
inner and an outer approximation of C
t
0
,t
f
assuming
that the input u(t
k
) is continuous over [t
k
,t
k+1
], and
boundedso it is possible to determinatea box[u
k
] such
that u(t) ∈ [u
k
] over [t
k
,t
k+1
]. That is, the obtained
results will be dependant of the time’s step δ
t
.
For each time t
k
the algorithm computes a gridding of
K (a slice), noted S(t
k
). The resolution of the gridding
is δ
K
= (δ
x
1
,··· ,δ
x
i
,··· ,δ
x
n
) where δ
x
i
corresponds
to the resolution of the i
th
dimension of K (Figure 1).
A cell s
i
of S(t
k
) can be
- unreachable if no state x in this cell allows the
system to reach the target at time t
f
, for all possi-
ble input vectors. The set of all the unreachable
cells of S(t
k
) is noted S
u
(t
k
)
S
u
(t
k
) = { s
i
∈S(t
k
)|∀u(t) ∈ U,
φ([t
k
,t
f
];s
i
,u(t)) ∩T =
/
0}
(9)
- reachable if for all the states x of this cell it exists
an input vector that allows the system to reach the
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
194

target at time t
f
with a trajectory entirely included
in the state space domain K. The set of all the
reachable cells of S(t
k
) is noted S
r
(t
k
).
S
r
(t
k
) = {s
i
∈ S(t
k
)|∃u(t) ∈ U,
ϕ(t
k
,t
f
;s
i
,u(t)) ⊆ T and
φ([t
k
,t
f
];s
i
,u(t)) ⊆ K}
(10)
- indeterminate if it is neither reachable or unreach-
able. The set of all the indeterminate cells of S(t
k
)
is noted S
i
(t
k
).
S
i
(t
k
) = S(t
k
) \(S
r
(t
k
) ∪S
u
(t
k
)) (11)
It can be noticed that
C
−
t
0
,t
f
= S
r
(t
0
),
C
+
t
0
,t
f
= S
r
(t
0
) ∪S
i
(t
0
).
(12)
The time’s step δ
t
of the input vector (step time dur-
ing which one the input vector is continuous and
bounded) and the resolutions δ
x
i
,i = 1, ··· ,n, are de-
fined by the desired precision of the C
+
t
0
,t
f
and C
−
t
0
,t
f
characterizations. Note that C
−
t
0
,t
f
can be empty if the
precision is too rough.
Figure 1: An example of slice set and slice S(t
k
), with
K = ([x
1
,x
1
],[x
2
,x
2
]) a two dimensional state space do-
main. The following color scheme is held for all the figures
of this paper: blue (dark grey) →unreachable, red (medium
grey) → reachable, yellow (light grey) → indeterminate.
3.1 The C
t
0
,t
f
Algorithm
We propose an iterative algorithm (Algorithm 1) that
computes for each slice S(t
k
), three subsets S
r
(t
k
),
S
u
(t
k
) and S
i
(t
k
) such as
S(t
k
) = S
r
(t
k
) ∪S
u
(t
k
) ∪S
i
(t
k
)
S
r
(t
k
) = {s
i
⊆ S(t
k
)|s
i
is reachable}
S
u
(t
k
) = {s
i
⊆ S(t
k
)|s
i
is unreachable}
S
i
(t
k
) = {s
i
⊆ S(t
k
)|s
i
is indeterminate}
(13)
Those subsets are computed from t
f
to t
0
using
guarantee numerical integration. After the initializa-
tion of the subsets at time t
f
the other subsets at time
t
k
are built using the reachability information of the
cells s
i
⊆ S(t
k+1
). Note that the ADD algorithm is
presented in Section 3.2.
Lines 1 to 3 of the Algorithm 1 initialise the three
subsets of the slice S(t
f
). For this particular slice, the
reachable cells are the ones included in the target, the
Algorithm 1: COMPUTATION OF C
t
0
,t
f
.
Data: K,T, t
0
, t
f
, U
1 S
r
(t
f
) = {s
i
∈ S(t
f
)|s
i
⊆ T};
2 S
u
(t
f
) = {s
i
∈ S(t
f
)|s
i
∩T =
/
0};
3 S
i
(t
f
) = S(t
f
) \(S
r
(t
f
) ∪S
u
(t
f
));
4 for t
k
←t
f−1
to t
0
do
5 L =
/
0 ;
6 forall the [u
k
] ∈ U do
7 L.add(K) ;
8 while L is not empty do
9 [x] = L .pop out();
10 [x]
∗
= ϕ(t
k
,t
k+1
;[x],[u
k
]);
11 if [x]
∗
∩K =
/
0 then
12 ∀s
i
⊆[x],ADD(S
u
(t
k
),s
i
);
13 else if [x]
∗
⊆ S
r
(t
k+1
) then
14 if φ([t
k
,t
k+1
];[x],[u
k
]) ⊆ K then
15 ∀s
i
⊆ [x],ADD(S
r
(t
k
),s
i
);
16 else
17 ∀s
i
⊆ [x],ADD(S
i
(t
k
),s
i
);
18 else if [x]
∗
⊆ S
u
(t
k+1
) then
19 ∀s
i
⊆[x],ADD(S
u
(t
k
),s
i
));
20 else if [x] can be bisected then
21 ([x
1
],[x
2
]) = BISECT([x]);
22 L.add([x
1
]),L.add([x
2
]);
23 else
24 ∀s
i
⊆[x],ADD(S
i
(t
k
),s
i
));
Result: {S(t
k
)},t
k
= t
0
,··· ,t
f
.
unreachable cells are the ones that do not intersect
the target and the indeterminate cells are all the oth-
ers ones (the cells intersecting the target without been
included). Then lines 4 to 24, the others slice subsets
are built. Line 6 it can be notices that all the possible
control vectors are considered to determine the reach-
ability of the cells. Line 8 to 24 a Set Inversion Via
Interval Analysis approach (Jaulin and Walter, 1993)
is used to determinate the reachability of the current
slice cells. It can be noticed that the computation of ϕ
line 10 is done using guaranteed numerical integration
(VNODE-LP). Line 14, a cell can be reachable only
if the trajectory is included in the state space K. Usu-
ally the computation of the inclusion flow is based on
the Banach fixed-point theorem and the application of
the Picard-Lindelof operator (see (Berz and Makino,
1998; Nedialkov et al., 1999) for details). Line 21,
the box is bisected among the grid. It means that, line
20, the box [x] can not be bisected if it contains only
one cell. In other words, the algorithm stops when all
the indeterminate boxes have a grid cell size.
Set-membershipMethodforDiscreteOptimalControl
195

The result of the algorithm has to be interpreted as
C
+
t
0
,t
f
= S
r
(t
0
) ∪S
i
(t
0
)
C
−
t
0
,t
f
= S
r
(t
0
)
(14)
The Figure 2 represents three cases of the Algo-
rithm 1:
- [x
1
]
∗
⊂S
u
(t
k+1
), then {s
i
⊆S(t
k
)|s
i
⊆[x
1
]} can be
added to S
u
(t
k
) (Line 19 of the algorithm),
- [x
2
]
∗
⊂S
r
(t
k+1
), then {s
i
⊆S(t
k
)|s
i
⊆[x
2
]} can be
added to S
r
(t
k
) [x
2
]
∗
(Line 15 of the algorithm),
- [x
3
]
∗
is neither included in S
u
(t
k+1
) or S
r
(t
k+1
),
and the box [x
3
] is too small to be bisected, thus
{s
i
∈ S(t
k
)|s
i
⊆ [x
3
]} can be added to S
i
(t
k
) (Line
24 of the algorithm).
Figure 2: The reachability of the cells s
i
⊆ S(t
k+1
) are
used to build the subsets of the slice S(t
k
). Denote
that [x
i
]
∗
= ϕ(t
k
,t
k+1
;[x
i
],[u
k
]),i = 1,2,3, with [x
1
]
∗
⊂
S
u
(t
k+1
), [x
2
]
∗
⊂ S
r
(t
k+1
) and [x
3
]
∗
is neither included in
S
u
(t
k+1
) or S
r
(t
k+1
).
3.2 The ADD algorithm
The slide’s cell reachability is updated regards to all
the possible control vectors [u
k
] ∈ U. For a given cell,
the reachability information can be different consid-
ering two different control vectors. That is why it
is needed to consider priorities for the update of the
reachability information of a cell and thus the com-
puting of the three subsets S
r
(t
k
),S
u
(t
k
) and S
i
(t
k
).
That is the purpose of the ADD function. For ex-
ample if a control vector [u
1,k
] leads to a reachability
information for a cell s
i
⊆S(t
k
) whereas a control vec-
tor [u
2,k
] leads to a indeterminate information for the
same cell, this cell s
i
belongs to S
r
(t
k
) (is reachable)
because it has been proved that it exists a control vec-
tor, [u
2,k
], that leads the cell to S
r
(t
k+1
). Figure 3
presents the several reachability information priori-
ties.
Figure 3: The reachability information priorities. A cell
noted unreachable can be updated to reachable or indeter-
minate, a cell noted indeterminate can only be updated to
reachable and a cell noted reachable can not be updated at
all.
4 EXPERIMENTATION
In order to validate the proposed method the algo-
rithm has been implemented in C++ using VNODE-
LP library. Be considered the following two-
dimensional system
(
˙x
1
= x
2
+ v×cos(θ),
˙x
2
= sin(x
1
) + v×sin(θ),
(15)
the following input vector













U = [u
1,k
] ∪[u
2,k
] ∪[u
3,k
]
[u
i,k
] = ([v
i
],θ
i
),
[u
1,k
] = ([−0.25, 0.25],π/2),
[u
2,k
] = ([3.75, 4.25],π/2),
[u
3,k
] = ([9.75, 10.25],π/2),
(16)
the following parameters









δ
t
= 0.5,
t
0
= 0, t
f
= 10,
δ
x
1
= 0.5, δ
x
2
= 0.5,
K = ([−30, 30],[−30, 30]),
(17)
and the following target
T = ([−15.1,−9.9], [1.9,7.1]). (18)
The Figure 4 shows four slices. The PC we use has
two processors (Intel(R) Core(TM)2 CPU 6420 @
2.13 Ghz), and it takes 1457s (24min 17s) to compute
all the slices S(t
k
). The details of the computation
time are presented in the Table 1.
The slice S(0) provides the C
+
t
0
,t
f
= S
r
(0) ∪S
i
(0) and
C
−
t
0
,t
f
= S
r
(0) characterizations of C
t
0
,t
f
. Note that it
is possible to increase the precision of the approxima-
tion of C
t
0
,t
f
by reducing the values of δ
x
1
and δ
x
2
.
5 DISCRETE OPTIMAL
CONTROL ENCLOSURE
The previous algorithm computes two guaranteed ap-
proximations C
−
t
0
,t
f
and C
+
t
0
,t
f
of C
t
0
,t
f
. It is possi-
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
196

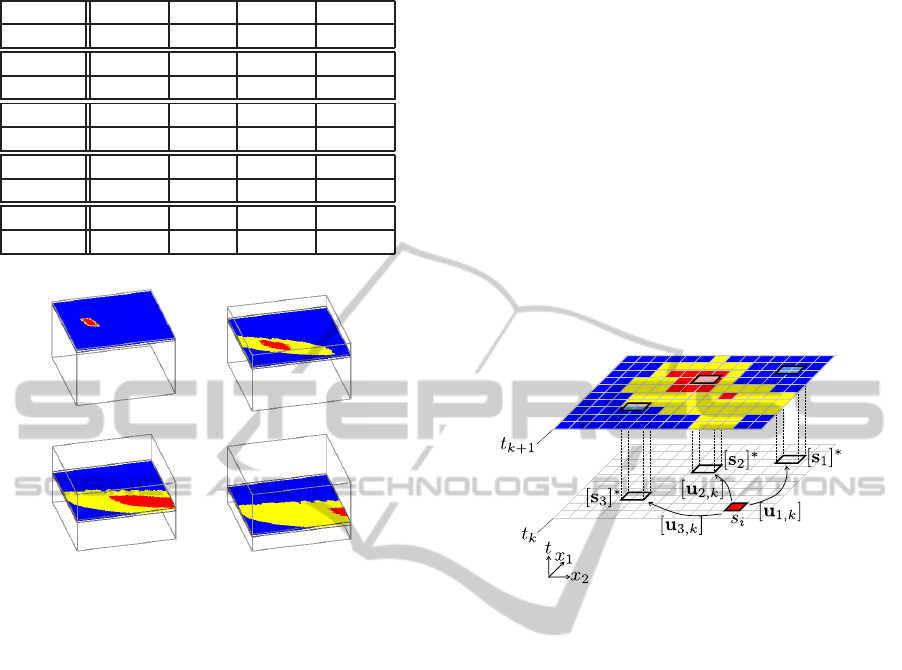
Table 1: Slices computation time.
slice S(9.5) S(9) S(8.5) S(8)
time (s) 2.56 5.55 11.95 22.6
slice S(7.5) S(7) S(6.5) S(6)
time (s) 40.66 61.78 71.86 75.6
slice S(5.5) S(5) S(4.5) S(4)
time (s) 76.41 79.6 82.88 87.89
slice S(3.5) S(3) S(2.5) S(2)
time (s) 93.96 98.59 102.79 105.87
slice S(1.5) S(1) S(0.5) S(0)
time (s) 106.78 108.5 109.23 111.73
Figure 4: Four slices: (from left top to right bottom) S(9.5),
S(7.5), S(5) and S(2.5).
ble to extend this algorithm to be able to deal with
optimal control. Considering a given cost function
J(x(t),u(t)), the idea of the algorithm is to enclose
the cost of the trajectories that allow to reach a cell
s
i
⊆S(t
k+1
) from a cell s
j
⊆S(t
k
). Note that the input
is still assumed to be continuous and bounded over
[t
k−1
,t
k
].
To simplify we assume that the cost function to
minimize is
J =
Z
u(t)
2
dt. (19)
It can obviously be extended to other cost functions.
Note that is J is dependant of the state x, the cost of
an input vector between two time steps can still be
computed using interval arithmetic and the evaluation
of the trajectory φ([t
k
,t
k+1
],x
k
,u
k
).
Instead of characterizing the cells with the reachabil-
ity of the target this section provides a method to add
the input control that could be used to reach the target.
The modifications of the previous algorithm are pre-
sented in Subsection 5.1, Subsection 5.2 details how
to build a graph using the added control vectors, and
Subsection 5.3 explains how to use the graph to en-
close the optimal control input. Note that the found
enclosure corresponds to the enclosure of the optimal
trajectory assuming that the input vector is bounded
between each time steps.
5.1 The Algorithm Modifications
The idea is to use the C
t
0
,t
f
computation to enclose
the optimal trajectory from an initial state [x
0
] ∈C
t
0
,t
f
to the target T. To this end it is needed to slightly
modify the presented algorithm. The purpose of this
new algorithm is to define for all the cells s
i
⊆S(t
k
) a
set of input vectors U(s
i
) that leads the cell to S
r
(t
k+1
)
or S
i
(t
k+1
) (Figure 5):
U(s
i
) = {[u
k
] ∈ U|ϕ(t
k
,t
k+1
;s
i
,[u
k
]) 6⊆ S
u
(t
k+1
)},
(20)
with s
i
∈ S(t
k
), t
k
< t
f
.
Each time a cell s
i
⊆ S(t
k
) may be added to S
i
(t
k
) or
S
r
(t
k
) (lines 15,17 and 24 of the Algorithm 1) the cur-
rent input vector [u
k
] has to be added to U(s
i
).
Figure 5: Example of added control vectors for a cell s
i
⊆
S(t
k
): U(s
i
) = {[u
2,k
],[u
3,k
]}, [u
1,k
] is not relevant since it
leads to S
u
(t
k+1
). Note that [s
j
]
∗
= ϕ(t
k
,t
k+1
;s
i
,[u
j,k
]), j =
1,2,3.
Considering the cost function it is possible to asso-
ciate a cost J([u
k
]) to each control vector [u
k
] ∈U(s
i
),
s
i
⊆ S(t
k
). In the following a control vector [u
k
] will
be abusively associated to its cost J([u
k
]).
5.2 A Graph Building
Given an initial state [x
0
] ∈ C
t
0
,t
f
, the idea is to build
a graph starting with a node n
0
(t
0
) and ending with a
node n
T
(t
f
) (Figure 7), such as
n
0
(t
0
) = {s
i
⊆ S(t
0
)|s
i
∩[x
0
] 6=
/
0}
n
T
(t
f
) = {s
i
⊆ S(t
f
)|s
i
∩T 6=
/
0}
(21)
N defines the set of nodes of the graph. A node
n
i
(t
k
) ∈ N is defined by a set of cells s
i
⊆ S(t
k
). Two
nodes n
i
(t
k
) and n
j
(t
k+1
) are linked if
∃[u(t
k
)] ∈ U|∀s
i
∈ n
i
(t
k
),ϕ(t
k
,t
k+1
;s
i
,[u
k
]) ⊆ n
j
(t
k+1
)
(22)
with J([u
k
]) the weight of the edge that links the two
nodes n
i
(t
k
) and n
j
(t
k+1
).
It is possible to define a set of control vector U(n
i
(t
k
))
for a node n
i
(t
k
) ∈ N corresponding to all the control
vectors U(s
i
) of all the cells s
i
⊆ n
i
(t
k
):
U(n
i
(t
k
)) = {U(s
i
),∀s
i
∈ n
i
(t
k
)}. (23)
Set-membershipMethodforDiscreteOptimalControl
197

Note that for efficiency reason it is recommended
to avoid control vector redundancy in U(n
i
(t
k
)),
∀n
i
(t
k
) ∈ N (otherwise identical nodes will appear
several times in the graph).
The graph is built from n
0
(t
0
) to n
T
(t
f
) using the cor-
responding edge sets. Algorithm 2 details the nodes
building and the Figure 6 presents an example of
graph building.
Algorithm 2: NODES.
Data: S, n
0
(t
0
), n
T
(t
f
)
1 L = n
0
(t
0
),N =
/
0 ;
2 while L is not empty do
3 n
i
(t
k
) = L .pop out();
4 N.add(n
i
(t
k
));
5 if t
k
< t
f
then
6 for all [u
k
] ∈ U(n
i
(t
k
)) do
7 n
i
(t
k+1
) = {s
i
⊆ S(t
k+1
)|
ϕ(t
k
,t
k+1
;n
i
(t
k
),[u
k
]) ∩s
i
6=
/
0};
8 L.add(n
i
(t
k+1
));
9 N.add(n
T
(t
f
));
Result: N.
Figure 6: Example of graph building. Starting from a node
n
0
(t
0
) = {s
i
⊆ S(t
0
)|s
i
∩ [x
0
] 6=
/
0}, two nodes are com-
puted: n
1
(t
1
) = {s
i
⊆S(t
1
)|s
i
∩[x
1
] 6=
/
0} and n
2
(t
1
) = {s
i
⊆
S(t
1
)|s
i
∩[x
2
] 6=
/
0}, with [x
1
] = ϕ(t
0
,t
1
;n
0
(t
0
),[u
1,0
]) and
[x
2
] = ϕ(t
0
,t
1
;n
0
(t
0
),[u
2,0
]). The same principle is repeated
for the other nodes. It can be noticed that
- the top figure corresponds to the superimposition of the
three slices S(t
0
), S(t
1
), and S(t
2
),
- some cells can belong to different nodes, as the dark grey
cell is attached to the node n
22
(t
2
) and n
21
(t
2
).
The computed graph corresponds to all the possible
trajectories of the system that may lead to the target
at t
f
from an initial state [x
0
] at t
0
. A priori it en-
closes the optimal trajectory. This graph has a partic-
ularity: as the nodes of the graph are cell sets, it can
be associated a reachability information for each node
n
i
(t
k
) ∈ N
- a node n
i
(t
k
) is reachable if all the cells s
i
∈n
i
(t
k
)
are reachable,
- a node n
i
(t
k
) is indeterminate if at least one cell
s
i
∈ n
i
(t
k
) is not reachable.
This can be extended to the paths of the graph
- a path is reachable if all the nodes of the path are
reachable,
- a path is indeterminate if at least one node of the
path is indeterminate. It can be noticed that an
indeterminate path may correspond to a trajectory
that does not exist considering the system. They
have to be considered carefully.
5.3 Exploitation of the Graph
Using this graph, it is possible, with a shortest path
algorithm, to compute two informations:
- an enclosure of the optimal control vector to reach
the target T from an initial state [x
0
] ∈ C
t
0
,t
f
,
- an evaluation of the cost of this control vector.
The chosen shortest path algorithm is a general-
ization of the Dijkstra algorithm (Dijkstra, 1971).
The classical Dijkstra algorithm is presented Algo-
rithm 3. The input of this algorithm is a graph G,
composed by a set of nodes N linked to each oth-
ers with weighted edges. J(n
i
) corresponds to the
weight of the node n
i
and J(n
i
,n
j
) corresponds to
the weight of the edge linking the nodes n
i
and n
j
(in our case it corresponds to the cost of the control
vector from n
i
to n
j
). The Dijkstra algorithm can
easily be extended for edges with interval weights
as the min() function can be extended to intervals
(min([x
1
,x
1
],[x
2
,x
2
]) = [min(x
1
,x
2
),min(x
1
,x
2
)] e.g.
min([3,9],[5,7]) = [3,7]). Note that with interval
weights it may not be possible to choose between two
paths, in this case, both paths are solutions.
As some paths may not correspond to possible tra-
jectories of the studied system (indeterminate paths),
a reachable sub-graph has to be considered. Be a
graph G, it is possible to build a sub-graph G
r
defined
by all the reachable paths of G. In this case G corre-
sponds to all the trajectories that may lead the system
to the target and G
r
corresponds to all the guaranteed
trajectories that lead the system the target from the
initial state.
Processing an interval Dijkstra algorithm over G
r
it is possible to find a set P
∗
r
of shortest guaranteed
paths for this sub-graph.
P
∗
r
= {shortest paths P ∈ G
r
} (24)
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
198

Algorithm 3: Dijkstra Algorithm.
Data: G
1 initialize the nodes as unmarked;
2 ∀n
i
∈N, J(n
i
) = +∞;
3 L(n
0
) = 0;
4 while it exists an unmarked node do
5 n
L
= the unmarked node with the lowest J;
6 note n
L
as marked;
7 for all unmarked nodes n
U
linked to n
L
do
8 J(n
U
) = min(J(n
U
),J(n
L
) + J(n
L
,n
U
));
Result: weighted node set N.
As mentioned before, when it is not possible to deter-
minate if a path is shorter than an other one the two
paths have to be kept as solution. For example if a
path P
1
has a cost J(P
1
) = [20,25] and a path P
2
has a
cost J(P
2
) = [22,30], it is not possible to determinate
which path is shorter (J(P
1
) 6≮ J(P
2
) since 25 > 22,
and J(P
2
) 6≮ J(P
1
) since 22 > 20). In this case the
two paths P
1
and P
2
have to be kept as they may both
be the shortest path.
The paths so obtained are guaranteed to exist, but may
not be the shortest paths considering the graph G. The
idea is to consider P
∗
r
as an upper bound of the shortest
path of G.
Knowing P
∗
r
and processing an other interval Dijkstra
algorithm over G it is possible to finally find the path
set P
∗
that encloses the shortest path of G:
P
∗
= {paths P ∈G that may be better than P
∗
r
}∪P
∗
r
(25)
Note that a path may be better than an other, if it is
not possible to determinate which path is shorter.
Figure 7: A graph example. Each node corresponds to a set
of cells. The edges have interval weights corresponding to
the costs J([u
k
]) of the control vectors [u
k
] ∈ U. Note that
n
0
,n
1
,n
2
,n
12
,n
21
,n
121
,n
211
are reachable nodes whereas
n
11
,n
111
,n
212
are indeterminate nodes.
Example of the Figure 7
Considering the graph G of the Figure 7, the following
reachable sub-graph can be computed:
- N
r
= {n
0
,n
1
,n
2
,n
12
,n
21
,n
121
,n
211
,n
T
} corre-
sponding to the reachable nodes and edges,
with N
r
the node set of G
r
.
For the reader information here are the computation
of all the path costs:
- J(P(n
0
,n
1
,n
11
,n
111
,n
T
)) = [6,10]
- J(P(n
0
,n
1
,n
12
,n
121
,n
T
)) = [11,15]
- J(P(n
0
,n
2
,n
21
,n
211
,n
T
)) = [5,9]
- J(P(n
0
,n
2
,n
21
,n
212
,n
T
)) = [14,18]
Using the interval Dijkstra algorithm it is possi-
ble to evaluate the optimal paths of the graph
G
r
, P
∗
r
= {P(n
0
,n
2
,n
21
,n
211
,n
f
)}. By process-
ing an other interval Dijkstra algorithm over G
and keeping only the paths that may be better
that P
∗
r
we obtain P
∗
= {P(n
0
,n
1
,n
11
,n
111
,n
T
)} ∪
P
∗
r
. It can be concluded that the optimal path
of the system for this example is included in
P
∗
= {P(n
0
,n
1
,n
11
,n
111
,n
f
),P(n
0
,n
2
,n
21
,n
211
,n
T
)}
and has a cost J(P
∗
) = [5,9].
6 CONCLUSIONS
In this paper, we have introduced two interval-based
algorithms. The first one allows, given a step time,
to compute an evaluation of the subset C
t
0
,t
f
of initial
states from which there exists at least one trajectory of
the system reaching the target T in finite time t
f
from
a time t
0
, assuming that the input vector is continuous
and bounded over a time [t
k−1
,t
k
]. The result of this
work is an outer and inner characterisation of C
t
0
,t
f
.
Then adapting this work we have defined an other al-
gorithm to deal with discrete optimal control charac-
terization. This second algorithm computes a graph
corresponding to all the possible discrete trajectories
that might lead the system from an initial state to the
target. Using a generalized Dijkstra algorithm, it is
possible to use this graph in order to enclose the dis-
crete optimal control vector and evaluate is cost. As
future work we are planing to modify the algorithm in
order to be independent of the time step.
REFERENCES
Aubin, J.-P. (1990). A survey of viability theory. SIAM
Journal on Control and Optimization, 28(4):749–788.
Aubin, J.-P. (2006). Viability Theory. Systems and Control.
Springer Verlag.
Berz, M. and Makino, K. (1998). Verified integration of
odes and flows using differential algebraic methods
on high-order taylor models. Reliable Computing,
4:361–369.
Set-membershipMethodforDiscreteOptimalControl
199

Delanoue, N., Jaulin, L., Hardouin, L., and Lhommeau, M.
(2009). Guaranteed characterization of capture basins
of nonlinear state-space systems. In Filipe, J., Cetto,
J., and Ferrier, J.-L., editors, Informatics in Control,
Automation and Robotics, volume 24 of Lecture Notes
in Electrical Engineering, pages 265–272. Springer
Berlin Heidelberg.
Dijkstra, E. (1971). EWD316: A Short Introduction to the
Art of Programming. Holland.
Jaulin, L., Kieffer, M., Didrit, O., and Walter, E. (2001).
Applied Interval Analysis. Springer.
Jaulin, L. and Walter, E. (1993). Set inversion via interval
analysis for nonlinear bounded-error estimation. Au-
tomatica.
Kirk, D. (2004). Optimal Control Theory: An Introduction.
Dover books on engineering. Dover Publications, In-
corporated.
Lhommeau, M., Jaulin, L., and Harouin, L. (2011). Cap-
ture basin approximation using interval analysis. In-
ternational Journal of Adaptative Control and Signal
Processing.
Moore, R. E. (1966). Interval analysis. Prentice-Hall series
in automatic computation. Prentice-Hall.
Nedialkov, N. S., Jackson, K. R., and Corliss, G. F. (1999).
Validated solutions of initial value problems for ordi-
nary differential equations. Applied Mathematics and
Computation, 105(1):21 – 68.
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
200