
Tensor Systems
Multilinear Modeling and Applications
G. Pangalos
1
, A. Eichler
1
and G. Lichtenberg
2
1
Institute of Control Systems, Hamburg University of Technology, Eißendorfer Straße 40, Hamburg, Germany
2
Faculty of Life Sciences, Hamburg University of Applied Sciences, Lohbr
¨
ugger Kirchstraße 65, Hamburg, Germany
Keywords:
Multilinear Systems, Hybrid Systems, Tensor Decomposition, Heating Systems, Multi-Agent Systems.
Abstract:
Tensor systems are a framework for modeling of multilinear hybrid systems with discrete and continuous
valued signals. Two examples from building services engineering and multi-agent systems show applications
of this framework. A tensor model of a heating system is derived and approximated by tensor decomposition
methods first. Second, a tensor model of a multi-agent system with a structure already given in a decomposed
form is reduced further by the same decomposition methods. The validity of these low rank approximations is
shown for both examples.
1 INTRODUCTION
Multilinear models are a subclass of nonlinear mod-
els which is interesting for engineering applications
because several systems behave multilinear, as shown
by the examples. In most applications the processes
are driven by some automation device with fixed sam-
pling time. Thus, only discrete time models are inves-
tigated here.
The class of multilinear models obviously in-
cludes linear continuous valued models but moreover,
all discrete valued models are inherently multilinear,
see (Lichtenberg, 2010). As multilinearity is mathe-
matically closely related to tensor calculus, there are
tensor representations of multilinear systems. Of spe-
cial interest are discrete time hybrid systems consist-
ing of a multilinear continuous valued subsystem and
an arbitrary discrete valued subsystem connected by
a quantizer and an injector. These can be represented
by so-called Hybrid Tensor Systems defined in (Licht-
enberg, 2011). This modeling approach was first ap-
plied to the identification problem of discrete valued
models from continuous data, (Lichtenberg and Eich-
ler, 2011).
Over the last years simulation of building and
heating systems has attracted a lot of interest, see
e.g. (Nouidui et al., 2012) or (Wetter, 2006). In these
approaches nonlinear models are derived and simu-
lated, mostly for performance evaluation. Heating
systems are application examples for hybrid tensor
systems because of their physical structure, see (Pan-
galos and Lichtenberg, 2012). This paper shows in
detail how to derive a multilinear one zone model of
a large scale building using RC-models of the walls.
Another field of applications are distributed net-
work systems like Multi-Agent Systems (MAS),
which have received considerable attention over the
past ten years, because of its broad variety of applica-
tions, see (Ren and Beard, 2007; Ren and Cao, 2011).
To perform tasks like Decision-Making or Policy For-
mulation, hybrid MASs are required, (Srinivasan and
Choy, 2010). These can be represented by the same
class of hybrid tensor systems.
Numerical tensor calculus with special interest
on decomposition methods is an active reseach field
in applied mathematics, see e.g. (Hackbusch, 2012).
Tensor models can be approximated by standard ten-
sor decomposition techniques - similar to model re-
duction techniques for linear systems. Most of the
latter techniques like PCA use singular value decom-
postion (SVD) of matrices as workhorse for the re-
duction process. For tensor systems, so-called higher-
order SVD decomposition algorithms are appropriate
reduction methods, see (Kolda and Bader, 2009).
The paper is organized as follows. After this intro-
duction the class of hybrid tensor systems is described
in section 2. The model of a complex heating system
is developed, validated, represented by a hybrid ten-
sor system, and finally decomposed in section 3. In
section 4 multilinear modeling and transformation to
a tensor system is shown for a hybrid MAS. Final con-
clusions are drawn in section 5.
275
Pangalos G., Eichler A. and Lichtenberg G..
Tensor Systems - Multilinear Modeling and Applications.
DOI: 10.5220/0004475602750285
In Proceedings of the 3rd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2013),
pages 275-285
ISBN: 978-989-8565-69-3
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

2 TENSOR SYSTEMS
Tensor representations of multilinear systems are in-
troduced in (Lichtenberg, 2011) and reviewed in this
section. All linear systems can be represented by this
class, which on the other hand is a subset of the class
of polynomial systems.
First, a matrix format to describe multilinear sys-
tems is introduced. Next, it is shown how to represent
these systems as tensor models. Finally, the notation
is extended to hybrid systems which include continu-
ous and discrete states and inputs.
2.1 Multilinear Matrix Models
With the help of the symbol ⊗ denoting the standard
Kronecker product, the monomial vector introduced
in the following Definition contains all possible mul-
tilinear terms.
Definition 2.1. The monomial vector is defined as
m(x, u)=
1
u
m
⊗ ··· ⊗
1
u
1
⊗
1
x
n
⊗ ··· ⊗
1
x
1
(1)
where x ∈ R
n
is the state vector and u ∈ R
m
is the
input vector.
With the monomial vector, a multilinear state
space model can be written in matrix form
Φ(x) = F m(x, u) , (2)
y = G m(x, u) , (3)
where Φ(x) denotes the next state vector, y ∈ R
l
the output vector, F ∈ R
n×2
(n+m)
the transition matrix
and G ∈ R
l×2
(n+m)
the output matrix.
Example 2.1. Consider the state transition function
of a multilinear second order model with one input
and next state vector
f
11
+ f
12
x
1
+ f
15
u+ f
16
ux
1
f
22
x
1
+ f
23
x
2
+ f
24
x
1
x
2
+ f
26
ux
1
+ f
27
ux
2
+ f
28
ux
1
x
2
.
The state space model (2) is given as
Φ(x
1
)
Φ(x
2
)
=
f
11
f
12
0 0 f
15
f
16
0 0
0 f
22
f
23
f
24
0 f
26
f
27
f
28
1
x
1
x
2
x
1
x
2
u
ux
1
ux
2
ux
1
x
2
.
(4)
In the following, the output equation (3) will not
be considered – for a description of multilinear input-
output models see (Lichtenberg, 2011).
For multilinear models (2), linear state and input
variable transformations
˜x
i
=
x
i
− b
i
a
i
∀i = 1, . . . , n (5)
˜u
i
=
u
i
− b
n+i
a
n+i
∀i = 1, . . . , m (6)
are computable in closed form. The transformed state
transition matrix is given by
e
F = diag
i=1,...,n
1
a
i
FT −
b 0
n×2
(n+m)
−1
(7)
where diag denotes the diagonal matrix with ele-
ments a
i
,
T =
1 0
b
n+m
a
n+m
⊗ ··· ⊗
1 0
b
1
a
1
is a transformation matrix, b is a column vector con-
taining the b
i
’s and 0
n×2
(n+m)
−1
denotes a zero ma-
trix with dimension (n × 2
(n+m)
− 1). Linear transfor-
mations allow a numerical preconditioning of models
which is used in section 3.4.
2.2 Multilinear Tensor Models
To rewrite (2) in a compact tensor notation, follow-
ing standard definitions from e.g. (Kolda and Bader,
2009) or (Cichocki et al., 2009) are introduced.
Definition 2.2. A Tensor
X ∈ R
I
1
×I
2
×···×I
n
of order n is an n-way array where elements x
i
1
i
2
···i
n
are indexed by i
j
∈ {1, 2, . . . I
j
} for j = 1, . . . , n.
Example 2.2. The elements of a tensor X ∈ R
2×3×2
can be illustrated and arranged in 3 dimensions as
X
=
x
211
x
221
x
231
x
111
x
121
x
131
x
212
x
222
x
232
x
112
x
122
x
132
.
Definition 2.3. A Kruskal tensor
K = [X
1
, X
2
, . . . , X
n
] · λ ∈ R
r
1
×r
2
×···×r
n
is a tensor of dimension (r
1
, . . . , r
n
), with elements
given by the sums of the outer products of the col-
umn vectors of so-called factor matrices X
i
∈ R
r
i
×r
,
weighted by the elements of the so-called weighting
or parameter vector λ. An element of the multidimen-
sional tensor K is given by
K
jk...p
=
r
∑
i=1
λ
i
(X
1
)
ji
(X
2
)
ki
. . . (X
n
)
pi
If no weighting vector is given, it is assumed to be
a vector of ones, i.e. λ = (1 1 . . . 1)
T
.
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
276

Definition 2.4. The contracted product of two ten-
sors Y ∈ R
I
1
×...×I
n
and X ∈ R
I
1
×...×I
n
×I
n+1
×...×I
n+m
is
h
X
|
Y
i
(k
1
, . . . , k
m
) =
I
1
∑
i
1
···
I
n
∑
i
n
x
i
1
,...,i
n
,k
1
,...,k
m
y
i
1
,...,i
n
,
(8)
is a tensor of dimension I
n+1
× . . . × I
n+m
.
Example 2.3. Consider a tensor X ∈ R
2×2×3
and a tensor Y ∈ R
2×2
. To calculate the con-
tracted product Z =
h
X
|
Y
i
∈ R
3
, the matching
dimensions have to be multiplied elementwise, as
highlighted in red in the following illustrations.
=
z
1
z
2
z
3
x
211
x
221
x
111
x
121
x
212
x
222
x
112
x
122
x
213
x
223
x
113
x
123
y
21
y
22
y
11
y
12
=
z
1
z
2
z
3
x
211
x
221
x
111
x
121
x
212
x
222
x
112
x
122
x
213
x
223
x
113
x
123
y
21
y
22
y
11
y
12
=
z
1
z
2
z
3
x
211
x
221
x
111
x
121
x
212
x
222
x
112
x
122
x
213
x
223
x
113
x
123
y
21
y
22
y
11
y
12
A simple notation for tensor spaces is introduced:
R
×
(n+m)
2
:= R
n+m
z}|{
2×...×2
.
The state transition function (2) of a multilin-
ear state space model can then be rewritten with the
monomial Kruskal tensor
M(x, u) =
1
u
m
, . . . ,
1
u
1
,
1
x
n
, . . . ,
1
x
1
.
in terms of a contracted tensor product as
Φ(x) =
h
F
|
M(x, u)
i
, (9)
where the transition tensor F ∈ R
×
(n+m)
2×n
contains all
parameters of the model while the structure is given
by the monomial tensor M(x, u) ∈ R
×
(n+m)
2
.
2.3 Decomposed Tensor Models
As contracted products could be efficiently computed
in Kruskal form, and monomial tensors are easily
given in this form by their internal structure, it is
worth looking for decompositions
F = [F
u
m
, . . . , F
u
1
, F
x
n
, . . . , F
x
1
, F
Φ
] · λ
f
(10)
of the state transition tensor having r
x
factors. This
will be illustrated by the Example 2.1. Setting the
matrix factors of (10) accordingly leads to
F
x
1
=
1 0 1 0 0 1 0 0 1 0
0 1 0 1 1 0 1 1 0 1
,
F
x
2
=
1 1 1 1 1 0 0 1 0 0
0 0 0 0 0 1 1 0 1 1
,
F
u
=
1 1 0 0 1 1 1 0 0 0
0 0 1 1 0 0 0 1 1 1
,
F
Φ
=
1 1 1 1 0 0 0 0 0 0
0 0 0 0 1 1 1 1 1 1
.
Together with the continuous valued parameter vector
λ
f
=
f
11
f
12
f
15
f
16
f
22
f
23
f
24
f
26
f
27
f
28
T
they form the state transition tensor
F = [F
u
, F
x
2
, F
x
1
, F
Φ
] · λ
f
.
The contracted product can now be calculated by sim-
ple matrix operations (Lichtenberg, 2011)
h
F
|
M(x, u)
i
= (11)
F
T
Φ
λ
f
~
F
T
u
1
u
~
F
T
x
2
1
x
2
~
F
T
x
1
1
x
1
,
where ~ denotes the (element-wise) Hadamard prod-
uct. It can be checked that calculating the contracted
product (9) leads to the transition equation (4).
At a first glance, for Example 2.1 this tensor nota-
tion does not seem to be more compact than the ma-
trix notation. It is easy to verify that the system matrix
has n ·2
(m+n)
= 16 elements, whereas the tensor repre-
sentation takes r
x
(1 + 3n + 2m) = 90 elements as the
dimension of the n + m factor matrices is 2 × r
x
, F
Φ
has dimension n ×r
x
and the parameter vector has an-
other r
x
entries.
But looking at the model of the heating system
that will be introduced in section 3 with n = 12 states,
no inputs m = 0 and r
x
= 46 factors, this would lead
to 12 · 2
12
= 49152 elements in matrix representation
whereas only 46(1 + 3 · 12) = 1702 Kruskal tensor el-
ements need to be stored.
For construction of the factor matrices and the pa-
rameter vector set the columns of the factor matrices
to
0
1
, if the summand contains the corresponding
state and to
1
0
otherwise. The product of states is
weighted by a constant given in the parameter vector.
The factor matrix F
Φ
indicates to which next state el-
ement the summand is added.
TensorSystems-MultilinearModelingandApplications
277

This can is shown exemplarily by the first sum-
mand of the Example. All first rows of the factor ma-
trices are
1
0
, i.e. the first summand of the first next
state does not depend on any current state or input but
is equal to the first entry f
11
of the parameter vector.
With standard tensor decomposition algorithms
like CP-ALS low rank approximations of the state
transition tensor could be found, see (Kolda and
Bader, 2009).
2.4 Boolean Tensor Models
In the following, Boolean variables will be indicated
by underlining. Heading for tensor models of hybrid
systems, the binary state x ∈ B
N
and input u ∈ B
M
are
defined. The state transition function of a Boolean
tensor state space model
Φ(x) =
h
F
|
L(x, u)
i
, (12)
with a transition tensor F ∈ B
×
(N+M)
2×N
describes a
binary dynamical system by a contracted product with
a Boolean literal tensor L(x, u) ∈ B
×
(N+M)
2
defined as
L(x, u) =
¯u
n
u
n
, · · · ,
¯u
1
u
1
,
¯x
n
x
n
, · · · ,
¯x
1
x
1
,
(13)
where the bar symbol is used to denote the negation
of a variable.
If the values of the state and input variables are
from a continuous domain but the transition tensor is
still Boolean, the resulting next state is in general a
continuous variable.
With the help of the symbol
h
·
|
·
i
+
defining a
contracted real tensor product which converts any
Boolean FALSE to a real zero and a Boolean TRUE to a
real one, the state transition of an algebraic Boolean
tensor state space model
Φ(x) =
h
F
|
L(x, u)
i
+
, (14)
can be defined, where
L(x, u) =
1 − u
n
u
n
, · · · ,
1 − u
1
u
1
,
1 − x
n
x
n
, · · · ,
1 − x
1
x
1
. (15)
It has the property that - if all initial states and inputs
are Boolean - the state and output trajectories only
take values 0 and 1 and thus, show a behavior which
includes the behavior of the binary system.
Transformation of (14) to monomial form is pos-
sible and given by
Φ(x) =
h
F
|
M(x, u)
i
+
, (16)
with the transition tensor F ∈ Z
×
(n+m)
×n
having inte-
ger elements which are easy computable from F .
2.5 Hybrid Tensor Models
Figure 1 shows a block diagram of the class of hybrid
systems investigated further. The outputs are omitted,
it is assumed that the states can be measured.
Multilinear System
h
F
|
M
i
Quantizer
β
Binary System
h
F
|
L
i
Injector
α
v
w
w
v
u
u
Figure 1: Block diagram of a multilinear hybrid system.
Without loss of generality, it is assumed that all
discrete signals are encoded Boolean. The contin-
uous valued subsystem and the discrete valued sub-
system are connected via a quantizer and an injector
given in the next Definitions, see (Lichtenberg, 2011),
where H is a hybrid space. The hybrid state and input
vectors
x
e
=
x
x
∈ R
n
× B
N
(17)
u
e
=
u
u
∈ R
m
× B
M
(18)
are given by appending the Boolean signal vectors to
the continuous signal vectors.
Definition 2.5. The standard injector is the func-
tion α : H
I
1
×···×I
N
→ R
I
1
×···×I
N
, which is given for all
elements with index vector i ∈ N
N
by
(α(x
e
))
i
=
1 ∈ R if x
i
= TRUE ,
0 ∈ R if x
i
= FALSE ,
x
i
if x
i
∈ R .
(19)
Definition 2.6. The standard quantizer is the func-
tion β : R
I
1
×···×I
N
→ B
I
1
×···×I
N
, which is given for all
elements with index vector i ∈ N
N
by
(β(x
e
))
i
= σ(x
i
−
1
2
) , (20)
where the Heaviside function is given as
σ(x) =
1 if x ≥ 0 ,
0 otherwise .
(21)
These definitions make the need of explicite equa-
tions for w, w, v and v obsolete, as they can be cal-
culated with the help of the standard injector and
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
278
the standard quantizer which are also used for the
next Definition - an extension of the contracted ten-
sor product taking into account Boolean as well as
continuous values.
Definition 2.7 (Hybrid Contracted Tensor Product).
The notation
h
·
|
·
i
for the hybrid contracted tensor
product implies that all values are mapped to the cor-
rect domains given by the domain of the tensor on the
left side of the contracted product
h
F
|
M
i
=
h
F
|
α(M(β(x)))
i
(22)
with standard quantizer and injector.
If the tensor on the left side has hybrid domains,
quantization and injection are applied to compute the
results corresponding to the domain on the left hand
side.
By using this Definition, the state transition func-
tion of a hybrid tensor system can be written in a very
compact way as
Φ(x
e
) =
F
e
M
e
(x
e
, u
e
)
. (23)
This will be illustrated by Examples in the following
sections.
3 HEATING SYSTEMS EXAMPLE
The heating system mentioned in the introduction will
now be modeled as a hybrid tensor system. This is
possible because of the inherit multilinear nature of
heating systems.
The heating system consists of a boiler with
burner, a consumer, where a building temperature can
be measured and a pump, which is controlled (see
Figure 2)
Boiler
Burner
Consumer
Pump
Figure 2: Heating system.
Signals being real or Boolean will be clear from
the context, therefore no underlines or ”undertildes”
will be used in this section.
For each of the elements of the heating system,
first the thermal balances are stated and then trans-
formed. After a validation of the model the factor
matrices and parameter vector are given such that the
system can be represented as a tensor system.
3.1 Differential Equations
The continuous valued states of the system are the
supply temperature T
s
, the return temperature T
r
and
the buildings temperature T
b
. Day oscillation and year
oscillation of the ambient temperature are modeled
by four continuous valued states T
a1
. . . T
a4
, two for
each oscillation. Two Boolean states X
l
and X
u
deter-
mine whether or not the buildings temperature is in
the interval where the thermostatic valves are linear,
in the lower or in the upper saturation. Two further
Boolean states H
l
and H
u
determine a supply temper-
ature above an upper limit or below a lower limit and
a Boolean state U that states if the boiler is running or
not. The state vector is given by x ∈ R
7
× B
5
x = [T
s
T
r
T
b
T
a1
T
a2
T
a3
T
a4
X
l
X
u
H
l
H
u
U]
T
.
(24)
Controlled Pump
The flow rate
˙
V is a consequence of the room tempera-
ture T
b
and the reference temperature for the room T
br
.
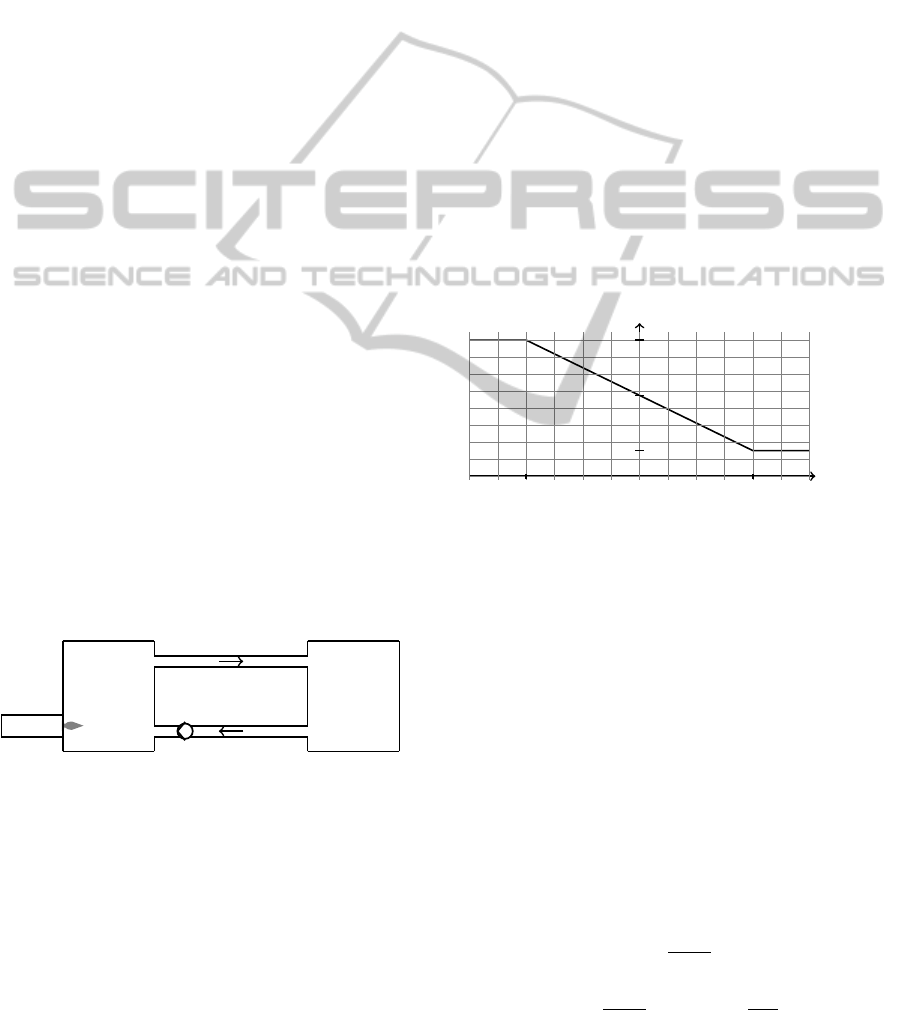
The relationship is shown in Figure 3.
T
b
− T
br
˙
V
−∆T
b
∆T
b
˙
V
m
˙
V
a
˙
V
a
Figure 3: Flow rate over control error of the room tempera-
ture.
In this Figure
˙
V
m
is the mean flow rate for T
b
= T
br
and
˙
V
a
is the amplitude from the mean flow rate at ref-
erence room temperature to its extrema. The extrema
in the flow rate are reached at a room temperature that
is at least ∆T
b
different from the reference room tem-
perature.
To state the flow rate
˙
V in terms of the discrete
states and the room temperature, the discrete states
X
l
=
1 if T
b
> T
br
− ∆T
b
0 else
(25)
X
u
=
1 if T
b
> T
br
+ ∆T
b
0 else
(26)
are introduced. Thus the flow rate
˙
V is given as
˙
V =
˙
V
m
+
˙
V
a
+
T
br
˙
V
a
∆T
b
−
˙
V
a
X
l
. . .
−
T
br
˙
V
a
∆T
b
+
˙
V
a
X
u
−
˙
V
a
∆T
b
T
b
X
l
. . .
TensorSystems-MultilinearModelingandApplications
279

+
˙
V
a
∆T
b
T
b
X
u
. (27)
Boiler
The thermal balance of the boiler is given as
˙
T
s
V
b
ρc = T
r
˙
V ρc − T
s
˙
V ρc + P
max
U . (28)
Using the Euler forward method with sampling time t
s
to discretize this differential equation and rearranging
leads to
T
s
(k + 1) = T
s
(k) −
t
s
V
b
T
s
(k)
˙
V (k). . . (29)
+
t
s
V
b
T
r
(k)
˙
V (k) +
t
s
V
b
ρc
P
max
U(k) .
Dropping the time index, denoting the next state by
the operator Φ and substituting (27) for the flow rate
gives
Φ(T
s
) = T
s
1 −
t
s
(
˙
V
a
+
˙
V
m
)
V
b
+ T
r
t
s
(
˙
V
a
+
˙
V
m
)
V
b
. . .
+T
s
X
l
˙
V
a
t
s
(∆T
b
−T
br
)
∆T
b
V
b
− T
r
X
l
˙
V
a
t
s
(∆T
b
−T
br
)
∆T
b
V
b
. . .
+T
b
T
s
X
l
˙
V
a
t
s
∆T
b
V
b
− T
b
T
r
X
l
˙
V
a
t
s
∆T
b
V
b
. . . (30)
+T
s
X
u
˙
V
a
t
s
(∆T
b
+T
br
)
∆T
b
V
b
− T
r
X
u
˙
V
a
t
s
(∆T
b
+T
br
)
∆T
b
V
b
. . .
−T
b
T
s
X
u
˙
V
a
t
s
∆T
b
V
b
+ T
b
T
r
X
u
˙
V
a
t
s
∆T
b
V
b
+ P
max
U
t
s
V
b
cρ
.
Ambient Temperature
The ambient temperature is modeled as an oscillator
with two frequencies. One for the temperature oscil-
lation over the day and one for the oscillation of the
year. The sinusoidal curves estimate the ambient tem-
perature roughly.
The continuous time state space model can be
given by
˙
T
a1
˙
T
a2
˙
T
a3
˙
T
a4
=
0 1 0 0
−ω
2
d
0 0 0
0 0 0 1
0 0 −ω
2
y
0
T
a1
T
a2
T
a3
T
a4
T
a
=
1 0 1 0
T
a1
T
a2
T
a3
T
a4
+ T
a,m
. (31)
Note that a multilinear state space model allows a
constant term, here T
a,m
. Using the Euler forward
method, the state equation in discrete time with sam-
pling time t
s
is given by
Φ
T
a1
T
a2
T
a3
T
a4
=
1 t
s
0 0
−ω
2
d
1 0 0
0 0 1 t
s
0 0 −ω
2
y
1
T
a1
T
a2
T
a3
T
a4
.
(32)
The output equation of system (31) does not change.
Building
The temperature of the building T
b
is introduced as the
average temperature of all rooms. The temperature
can be given as
k
b
˙
T
b
= k
r,b
(T
r
− T
b
) − k
b,a
(T
b
− T
a
) , (33)
where k
b
is the capacity of the building, k
r,b
the heat
transfer coefficient from the radiators to the building
and k
b,a
the heat transfer coefficient from the building
to the outside. Again using the Euler forward method
for temporal discretization and substituting the output
equation of (31) gives
Φ(T
b
) = T
b
1 −
t
s
(k
r,b
+k
b,a
)
k
b
+ T
r
t
s
k
r,b
k
b
. . .
+T
a1
t
s
k
b,a
k
b
+ T
a3
t
s
k
b,a
k
b
+
t
s
k
b,a
T
a,m
k
b
. (34)
The parameters k
b
, k
r,b
, k
b,a
are estimated with real
measurement data of the building. The validation of
the model is described in the next section, where the
numerical values of the constants are given in Table 3.
Consumer
The thermal balance of the consumer is given by
˙
T
r
(t)V
c
ρc = T
s
(t)
˙
V (t)ρc − T
r
(t)
˙
V (t)ρc −
˙
Q
d
(t) .
(35)
The heat demand
˙
Q
d
can be calculated in terms of
the return temperature and the building temperature
as
˙
Q
d
(t) = (T
r
(t) − T
b
(t))k
r,b
. (36)
Inserting (36) and (27) into (35) and discretizing
the result gives
Φ(T
s
) = T
s
t
s
(
˙
V
a
+
˙
V
m
)
V
c
. . . (37)
+ T
r
1 −
t
s
(k
r,b
+ c
˙
V
a
ρ + c
˙
V
m
ρ)
V
c
cρ
. . .
+ T
b
k
r,b
t
s
V
c
cρ
− T
s
X
l
˙
V
a
t
s
(∆T
b
− T
br
)
∆T
b
V
c
. . .
+ T
r
X
l
˙
V
a
t
s
(∆T
b
− T
br
)
∆T
b
V
c
− T
b
T
s
X
l
˙
V
a
t
s
∆T
b
V
c
. . .
+ T
b
T
r
X
l
˙
V
a
t
s
∆T
b
V
c
− T
s
X
u
˙
V
a
t
s
(∆T
b
+ T
br
)
∆T
b
V
c
. . .
+ T
r
X
u
˙
V
a
t
s
(∆T
b
+ T
br
)
∆T
b
V
c
+ T
b
T
s
X
u
˙
V
a
t
s
∆T
b
V
c
. . .
− T
b
T
r
X
u
˙
V
a
t
s
∆T
b
V
c
,
where the time dependencies are dropped.
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
280

Bang Bang Controller
The discrete states H
l
and H
u
are used to determine
whether or not the supply temperature T
s
is below
a lower limit, here: 75
◦
C or above an upper limit,
here: 95
◦
C. The signal U steering the boiler is then
computed by
Φ(U ) =
U if 75
◦
C < T
s
< 95
◦
C
1 if T
s
≤ 75
◦
C
0 if T
s
≥ 95
◦
C
. (38)
3.2 Validation of the Consumer
In this section the validation of the consumer is
shown. For this purpose the discrete bang bang con-
troller is replaced by a PI-controller as in the real
building. The ambient temperature is modeled sep-
arately. For the validation, the ambient temperature
is taken from measurement data. Not all states are
displayed but just the supply temperature T
s
, the re-
turn temperature T
r
and the flow rate
˙
V . Note that
the flow rate is not a state of the system but depends
on the buildings temperature T
b
and the two Boolean
states X
l
and X
u
. The system has two main time scales
caused by the oscillating ambient temperature over
the day and over the year.
The temperatures over a whole year, starting Jan-
uary 1
st
are given in Figure 4. The mismatch in the
return temperature in the summer is probably caused
by a later detected bypass of the boiler.
0 100 200 300
30
40
50
60
70
80
Time [days]
Temperature [°C]
Measurement:
Simulation:
T
s
T
s
T
r
T
r
Figure 4: Supply and return temperatures over a year.
The flow rate over the year is given in Figure 5.
This shows a quite good fit of the signals in a year
scale. Now the second scale should be investigated.
Therefore in Figure 6 the temperatures are given and
in Figure 7 the flow rate is given for two days. As
one can see also the day scale has a good fit. Still
remaining for validation is the use of an oscillator for
the ambient temperature. Figure 8 shows the ambient
temperature from measurements and the results from
the oscillator over a year in the upper plot and the
0 100 200 300
0
5
x 10
−3
Time [days]
Flow rate [m
3
/s]
Measurement: Simulation:
Figure 5: Flow rates over a year.
55
60
65
Temperature
103 103.5 104 104.5 105
35
40
Time [days]
[°C]
Measurement:
Simulation:
T
s
T
s
T
r
T
r
Figure 6: Supply and return temperatures over two days.
103 103.5 104 104.5 105
3
4
x 10
−3
Time [days]
Flow rate [m
3
/s]
Measurement: Simulation:
Figure 7: Flow rates over two days.
0 100 200 300
0
10
20
30
Time [days]
103 103.5 104 104.5 105
5
10
15
20
Time [days]
Ambient temperature [°C]
Measurement Simulation
Figure 8: Measurement and simulation of the ambient tem-
perature.
ambient temperatures over two days in the lower plot.
The parameters for the signal generator are given in
Table 1
For completeness Table 2 states the used material
constants and Table 3 states all estimated parameters.
TensorSystems-MultilinearModelingandApplications
281

Table 1: Parameters of the ambient temperature signal gen-
erator.
Frequency Symbol Value
Day oscillation ω
d
−
2π
86400
2
rad
s
Year oscillation ω
y
−
2π
31536000
2
,
rad
s
Table 2: Material constants of water.
Density of water ρ 1000
Kg
m
3
Specific heat
c
4182
W s
Kg K
capacity of water
Table 3: Parameters of the building model.
Parameter Symbol Value
Volume boiler V
b
1.05m
3
Volume consumer V v 5m
3
Mean flow rate
˙
V
m
4.75 · 10
−3
m
3
s
Flow rate amplitude
˙
V
a
3.25 · 10
−3
m
3
s
Building reference
T
br
21
◦
C
temperature
Linear temperature
∆T
b
4
◦
Camplitude of
the thermostat
Thermal capacity
k
b
10
10
W s
K
of the building
Total heat transfer
k
r,b
2.5 · 10
4
W
K
coefficient
(radiator building)
Total heat transfer
k
b,a
4.7338 · 10
4
W
K
coefficient
(building ambiance)
Mean ambient
T
a,m
12.5
◦
C
temperature
Maximal power
P
max
1.1MW
of the boiler
The initial state vector used is
x(0) =
253 323 294 0 −
5π
86400
. . .
−
5π
86400
− 12.5 0 1 0 0 0 1
T
. (39)
Note that the simulation was performed with SI-units,
such that the temperatures are in Kelvin. For bet-
ter legibility the temperatures in Table 3 were given
in
◦
C.
3.3 System Tensor
With the difference equations from the section 3.1 it
is now straight forward to construct the system ten-
sor. Here just the first entries of the system tensors
factor matrices, that correspond to the next state of
the supply temperature T
s
are given. The entries are
constructed as shown in Example 2.1 The Factor ma-
trices, in order of the states (24) are:
F
T
s
=
0 1 0 1 0 . . .
1 0 1 0 1 . . .
, F
T
r
=
1 0 1 0 1 . . .
0 1 0 1 0 . . .
F
T
b
=
1 1 1 1 0 . . .
0 0 0 0 1 . . .
, F
T
a1
=
1 1 1 1 1 . . .
0 0 0 0 0 . . .
F
T
a2
=
1 1 1 1 1 . . .
0 0 0 0 0 . . .
, F
T
a3
=
1 1 1 1 1 . . .
0 0 0 0 0 . . .
F
T
a4
=
1 1 1 1 1 . . .
0 0 0 0 0 . . .
, F
X
l
=
1 1 0 0 0 . . .
0 0 1 1 1 . . .
F
X
u
=
1 1 1 1 1 . . .
0 0 0 0 0 . . .
, F
H
l
=
1 1 1 1 1 . . .
0 0 0 0 0 . . .
F
H
u
=
1 1 1 1 1 . . .
0 0 0 0 0 . . .
, F
U
=
1 1 1 1 1 . . .
0 0 0 0 0 . . .
F
Φ
=
1 1 1 1 1 . . .
0 0 0 0 0 . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
(40)
The matrix F
Φ
has dimension 12 × 46 to assign
the 46 summands of the system to the corresponding
next state. Note, that the factor matrices are not com-
plete but just given for the first five summands of the
first next state. Since all entries that were looked at
correspond to the first next state, the first five entries
of the first row of F
Φ
are 1. The corresponding part
of the parameter vector is given by
λ
f
=
1 −
t
s
(
˙
V
a
+
˙
V
m
)
V
b
t
s
(
˙
V
a
+
˙
V
m
)
V
b
˙
V
a
t
s
(∆T
b
−T
br
)
∆T
b
V
b
−
˙
V
a
t
s
(∆T
b
−T
br
)
∆T
b
V
b
˙
V
a
t
s
∆T
b
V
b
.
.
.
. (41)
3.4 Tensor Decomposition
In this section a reduction of the tensor rank is per-
formed using tensor decomposition techniques. With
the factor matrices (40) and the parameter vector (41)
defined in section 3 a state transition tensor
F =
F
T
s
, F
T
r
, F
T
b
, F
T
a1
, F
T
a2
, F
T
a3
, F
T
a4
, . . . (42)
F
X
l
, F
X
u
, F
H
l
, F
H
u
, F
U
, F
Φ
· λ
f
(43)
is constructed. The Tensor Toolbox (Bader and
Kolda, 2012) and the command cp
als is used to re-
duce the rank of the tensor F, which was constructed
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
282

to have a tensor rank of 46. Using the Toolbox, the
rank of the system tensor is reduced to 23, which has
a fit of over 99%. The first five entries of the first two
factor matrices are
F
1
=
−0.999 0.999 1.000 1.000 1.000 . . .
0.045 −0.054 0.009 0.007 0.000 . . .
,
F
2
=
0.988 0.984 0.999 1.000 1.000 . . .
−0.152 −0.179 0.040 0.031 0.000 . . .
.(44)
The corresponding entries in the parameter vector are
λ =
10.443 6.967 4.322 2.598 2.587 . . .
T
.
(45)
The results of the simulation with the original and the
decomposed state transition tensor are given in Fig-
ure 9. One can see, that the main system dynamics
are captured with the decomposed system. The sup-
ply temperature drops to 75
◦
C if 95
◦
C is reached and
rises again. Also the offset and the dynamics of the re-
turn temperature show similar behavior for both state
transition functions.
0 5 10 15 20
50
100
Temperature [°C]
Original system
0 5 10 15 20
50
100
Time [hours]
Temperature [°C]
Decomposed system
T
s
T
b
T
r
Figure 9: Original and decomposed system.
The value of the states has a big impact on the
results. For this reason a state transformation (see
section 2) was performed such that all states of
the transformed system are in the interval [0 0.5].
Since we have a 12
th
order system a very small
factor in front of the multiplication of all states
(which was not used, i.e. 0 in the original sys-
tem) can give a next state many orders of magni-
tude away from the original next state. This ef-
fect can be reduced significantly by normalizing the
states to the interval [0 0.5]. To illustrate this is-
sue assume, that T
s
= T
r
= T
b
= 300. To calculate the
next state of T
s
the multiplication of all three temper-
atures is not used, i.e. Φ(T
s
) = . . . + 0 · T
s
T
r
T
b
+ . . ..
Assume a CP decompostion is performed and the
factor is now 0.001. This still gives a very good
fit for the tensor. The next state of T
s
however
is 300
3
· 0.001 = 27 · 10
3
different to that of the orig-
inal system. In contrast to that consider a trans-
formed system. Now the states are transformed.
They are assumed to be in the interval [280 300]
and therefore transformed with
˜
x =
x−280
40
leading
to T
s
= T
r
= T
b
= 0.5. Again calculating the error of
the next state gives 0.5
3
· 0.001 = 125 · 10
−6
trans-
forming this error back to the original coordinates
gives an error of 5 · 10
−3
.
4 MULTI-AGENT SYSTEMS
EXAMPLE
A MAS consists of a group of agents (e.g. vehicles
with their computing entities) that exchange informa-
tion and share knowledge to solve a common task like
in (Balaji and Srinivasan, 2010). The demand of au-
tonomous MAS’s with the ability to perform tasks as
Decision-Making or Policy Formulation leads to hy-
brid MAS’s. There are various different applications
of hybrid MAS’s and many different ways to describe
them, e. g. (Srinivasan and Choy, 2010). How a hy-
brid MAS is modeled as tensor system is shown in the
following.
Graphs are a natural way to describe the com-
munication topology between agents of an MAS,
see (Mesbahi and Egerstedt, 2010). A directed
Graph G(V , E) consists of a set of N ver-
tices, representing the single agents, and a set of
edges E ⊆ V × V , describing the communication
topology. If agent i receives information from
agent k, there is an edge (k, i) ∈ E. The mainly
used matrix representation of graphs for MAS is the
Laplacian L. The normalized Laplacian is defined
as (Ren and Beard, 2007)
L
ik
:=
1 if i = k and |N
i
| 6= 0
−
1
|N
i
|
if k ∈ N
i
0 otherwise.
(46)
Here N
i
is the set of neighbors of agent i, that is de-
fined as N
i
= {k|(k, i) ∈ E}, and |N
i
| is its cardinality.
Consider a MAS of N equal agents, where each
agent i = 1 . . . N is described by the switched system
Φ(x
i
) = ax
i
+ u
i
if Φ
−1
(x
i
) ≥ 0.5
Φ(x
i
) = bx
i
+ u
i
if Φ
−1
(x
i
) < 0.5 , (47)
with x
i
, u
i
∈ R being continuous signals
and Φ
−1
(x
i
) = x
i
(k − 1) denoting the previous state.
By introducing the discrete signal z
i
= β(Φ
−1
(x
i
)),
TensorSystems-MultilinearModelingandApplications
283

being the quantized state variable, system (47) can be
written as the multilinear system
Φ(x
i
) = (a − b)z
i
x
i
+ bx
i
+ u
i
. (48)
This can be described as a tensor system for one
agent i by
Φ(x
i
)=
F
i
M
e
(x, z, u)
=
F
i
u
, F
i
z
, F
i
x
M
e
(x, z, u)
(49)
with F
i
u
=
1 0
0 1
, F
i
z
=
b 1
a − b 0
, F
i
x
=
0 1
1 0
.
The control input is determined by the communi-
cation topology as u = −Lx like simple consensus
algorithms propose (Mesbahi and Egerstedt, 2010)
with x = (x
1
. . . x
N
)
T
, u and z defined respectively.
The discrete system is easily described by
Φ(z) = β(x). (50)
The continuous part can be described as a continuous
tensor system of the form Φ(x) =
F
M
e
(x, z)
+
. It
is obvious that the continuous system only contains
multilinear terms of the form x
i
z
i
introduced by the
system equations of the single agents in (48), whereas
the control input is linear in x. Thus the standard
monomial tensor of dimension R
×
2N
2
is very sparse.
A special formation monomial tensor is introduced
here as M
e
F
(x, z) ∈ H
2×2×N
M
e
F
(x, z) =
1 . . . 1
z
1
z
N
,
1 . . . 1
x
1
x
N
, I
N
.
(51)
This is a tensor of rank N in contrast to the standard
monomial tensor of rank 1.
With (51) a state transition function of a hybrid
tensor system for the overall system, with state vec-
tor x
e
= (x, z)
T
is defined as
Φ(x
e
) =
F
e
F
M
e
F
(x, z)
(52)
with F
e
F
=
F
F
z
, F
F
x
, F
F
I
, F
F
Φ
∈ R
2×2×N×2N
. The state
transition tensor F
F
has the factor matrices with 2N
factors
F
F
Φ
=
I
N
I
N
0
0 0 I
N
,
F
F
I
=
I
N
−L I
N
,
F
F
x
=
1
T
3N
0
1
,
F
F
z
=
1
T
N
b
a − b
1
T
2N
1
0
. (53)
The factor matrix F
F
Φ
specifies the state, x
e
= (x, z
)
T
.
First the continuous state vector x is considered. Due
to the identity matrices in F
F
Φ
and F
F
I
, the first N
columns of the factor matrices describes the internal
dynamics of the agents. This can be easily seen by
comparing the first N columns of F
F
x
and F
F
z
with F
i
x
and F
i
z
in (49). The Laplacian in F
F
I
describes the
communication between the different agents. The
fact, that the communication is linear in the states x
i
,
explains the second N vectors in F
F
x
and F
F
z
since
0
1
,
1
0
,
1
z
i
,
1
x
i
= x
i
.
The discrete signal z is simply calculated
by Φ(z) = β(x), which explains the choice of
the last N columns in F
F
x
and F
F
z
.
Next, a hybrid tensor system with N = 100 agents
is modeled. The considered connected graph is di-
rected and contains 473 random edges. The internal
dynamics of the single agents is described by (48)
with a = 0.5 and b = 1. The number of factors of
the exact system tensor is 300 = 3N. CP decompo-
sitions of the system tensor from rank 1 to 299 have
been calculated with cp als.
0 100 200 300
0
5
10
Tensor norm error
Rank
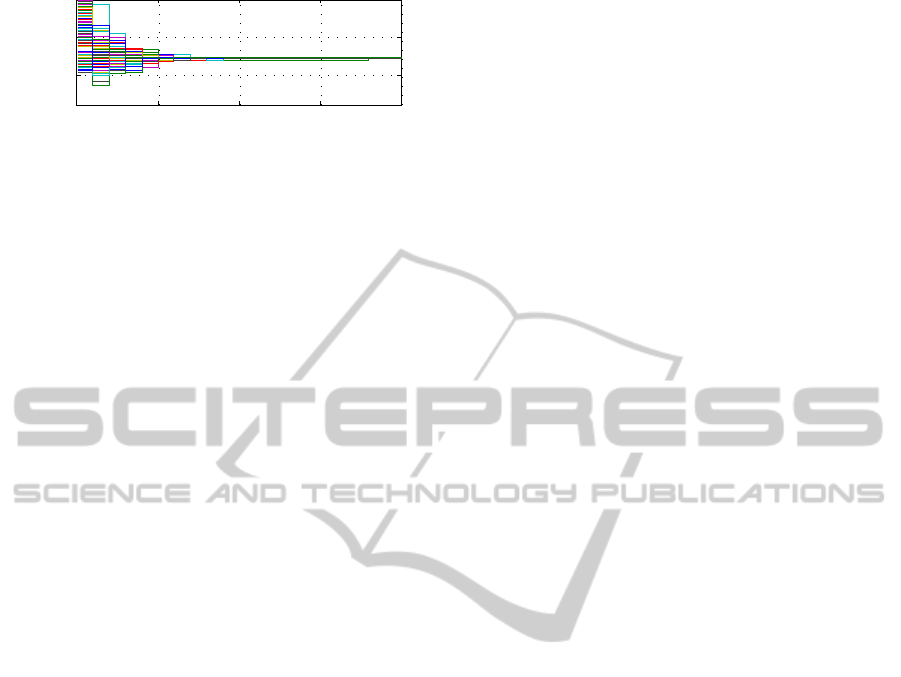
Figure 10: Frobenius norm of error.
0 0.05 0.1 0.15 0.2
0
0.5
1
Continuous state
signals
Discrete time steps
Figure 11: Continuous valued state trajectories for rank 200
approximation.
The Frobenius error between the exact and ap-
proximated hybrid tensor model is shown for tensor
approximations of different rank in Figure 10. A ten-
sor of rank 200 = 2N describes the system dynam-
ics almost exactly. The Frobenius error for graphs
of every tested different size shows qualitatively the
same shape. Thus it can be supposed that the sys-
tem is in fact not a tensor system of rank 3N but
of 2N. In Figure 11, continuous state trajectories of
the rank 200 approximation are shown. The maximal
mean squared error between the original and approx-
imated trajectories for a rank 200 approximation is
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
284
0 0.05 0.1 0.15 0.2
0
0.5
1
Continuous state
signals
Discrete time steps
Figure 12: Continuous valued state trajectories for rank 150
approximation.
with < 10
−17
negligible and thus approximation and
original system match exactly. For comparison the
rank 150 approximation is shown on Figure 12. Here
the same consensus value of approximately 0.2 is
reached with the same convergence shape. However,
the states does not exactly converge to the real consen-
sus value but reach an envelope around it, which gets
small for higher order approximations. For approxi-
mations with smaller order instability of the conver-
gence process may occur.
5 CONCLUSIONS
Hybrid tensor systems are an adequate framework for
modeling discrete time multilinear systems with con-
tinuous and discrete valued states and inputs. A hy-
brid tensor model of a complex heating system is de-
rived as a real-world example. All parameters are
stored in a state transition tensor which in a second
step is reduced to a low rank Kruskal tensor using
standard decomposition techniques. As simulations
show, this decomposed tensor is still capable to cap-
ture the main dynamics of the heating system.
As a second application example from a quite dif-
ferent application domain, a hybrid tensor model of a
Multi-Agent System (MAS) is built. Structural con-
traints are imposed in an easy way, a reduced rank
state transition tensor of the system is again computed
by tensor decomposition algorithms and simulations
are carried out based on the decomposed model. The
reduced rank model converges to the same final values
as the original one. Moreover, the original N-agents
system can be modeled exactly by a hybrid tensor sys-
tem with a small rank of 2N.
Further research will be done to investigate the
stability behaviour of hybrid tensor systems. Another
focus will be the derivation of tensor representations
for nonlinear normal forms - as well for general non-
linear as for multilinear systems. Tensor decompo-
sition techniques will play an important role in these
fields and extensions of the continuous algorithms to
hybrid spaces would be essential tools for analysis
and design of multilinear hybrid systems.
ACKNOWLEDGEMENTS
This work was partly supported by the project ModQS
of the Federal Ministry of Economics and Technol-
ogy, Germany.
REFERENCES
Bader, B. and Kolda, T. (2012). MATLAB Tensor Toolbox
Version 2.5. Available online.
Balaji, P. and Srinivasan, D. (2010). An Introduction
to Multi-Agent Systems, volume 310 of Studies in
Computational Intelligence, chapter 1, pages 1–27.
Springer.
Cichocki, A., Zdunek, R., Phan, A., and Amari, S. (2009).
Nonnegative Matrix and Tensor Factorizations. Wi-
ley, Chichester.
Hackbusch, W. (2012). Tensor Spaces and Numerical Ten-
sor Calculus, volume 42 of Springer Series in Com-
putational Mathematics. Springer-Verlag Berlin Hei-
delberg.
Kolda, T. and Bader, B. (2009). Tensor Decompositions and
Applications. SIAM Review, 51(3):455–500.
Lichtenberg, G. (2010). Tensor Representation of Boolean
Functions and Zhegalkin Polynomials. In Interna-
tional Workshop on Tensor Decompositions.
Lichtenberg, G. (2011). Hybrid Tensor Systems. Habilita-
tion, Hamburg University of Technology.
Lichtenberg, G. and Eichler, A. (2011). Multilinear Al-
gebraic Boolean Modelling with Tensor Decomposi-
tions Techniques. In 18th IFAC World Congress, page
TuC01.2.
Mesbahi, M. and Egerstedt, M. (2010). Graph Theoretic
Methods for Multiagent Networks. Princeton Univer-
sity Press.
Nouidui, T.S., Zuo, K.P.W., and Wetter, M. (2012). Valida-
tion and Application of the Room Model of the Mod-
elica Buildings Library. 9th International Modelica
Conference, pages 727–736.
Pangalos, G. and Lichtenberg, G. (2012). Approach to
Boolean Controller Design by Algebraic Relaxation
for Heating Systems. In 4th IFAC Conference on Anal-
ysis and Design of Hybrid Systems.
Ren, W. and Beard, R. (2007). Distributed Consensus in
Multi-Vehicle Cooperative Control - Theory and Ap-
plications. Communications and Control Engineering.
Springer Publishing Company, Incorporated.
Ren, W. and Cao, Y. (2011). Distributed Coordination of
Multi-agent Networks. Springer-Verlag London Lim-
ited.
Srinivasan, D. and Choy, M. (2010). Hybrid Multi-Agent
Systems, volume 310 of Studies in Computational In-
telligence, chapter 2, pages 29–42. Springer.
Wetter, M. (2006). Multizone Building Model for Thermal
Building Simulation in Modelica. 5th International
Modelica Conference, pages 517–526.
TensorSystems-MultilinearModelingandApplications
285
