Spectral Solutions of a Combined Multiﬂuid–population Balance Model

Describing Bubbly Flow

A Numerical Study of weighted Residual Methods

Jannike Solsvik and Hugo A. Jakobsen

Department of Chemical Engineering, Norwegian University of Science and Technology (NTNU), Trondheim, Norway

Keywords:

Population Balance Equation, Multiﬂuid Model, Weighted Residual Methods, Tau, Orthogonal Collocation,

Least-squares.

Abstract:

Fluid particle breakage and coalescence phenomena are important for optimal operation for industrial process

units like the bobble column reactors. The population balance equation (PBE) can be applied to describe the

evolution of populations of countable entities such as the bubbles in the bubble column. In recent literature,

the least-squares methods has been adopted for the approximate solution of population balance (PB) models.

Adopting a weighted residual method such as the least-squares method, the distribution function resolved

instead of obtaining only a few moments of the distribution function. The performance of the least-squares

method for PB problems should be compared to other techniques in the family of weighted residual methods.

The aim of the present study is to evaluate the orthogonal collocation, tau and last-squares methods for the

solution of a combined multiﬂuid-PB model describing bubbly ﬂows.

1 INTRODUCTION

Despite the simple construction of the bubble

columns and their widespread use for chemical re-

actions and separation in the process industries, our

understanding of the complex ﬂows in these vessels

is still very limited. The complexity of the hydro-

dynamics in the bubble columns relates to the evo-

lution of phenomena such as breakage, coalescence,

growth and convective transport of the bubbles. In the

mathematical modeling framework, the PBE (Ramkr-

ishna, 2000; Jakobsen, 2008; Randolph and Larson,

1988; Sporleder et al., 2012) is considered a concept

for describing the evolution of populations of count-

able entities such as the bubbles in the bubble col-

umn. Adopting the PB modeling technique to bubbly

ﬂows, the dispersed gas phase is treated as a popula-

tion of bubbles distributed not only in physical space

but also in an abstract property space. The quantity

of basic interest in PB modeling is the statistical den-

sity function representing the behavior of the popula-

tion of bubbles. The evolution of the statistical den-

sity function must take into account the different pro-

cesses that control the population of the bubbles in

the vessel, such as breakage, coalescence, growth and

convective transport. Thus the PBE provides a sta-

tistical description of the dispersed phase where the

Figure 1: Sketch of a bubble column reactor. The parameter

ξ is a characteristic property of the bubble, for example the

bubble diameter. Because of the different interaction pro-

cesses, the distribution of the bubbles evolves.

102

Jakobsen H. and Solsvik J..

Spectral Solutions of a Combined Multiﬂuid–population Balance ModelDescribing Bubbly Flow - A Numerical Study of weighted Residual Methods.

DOI: 10.5220/0004477401020107

In Proceedings of the 3rd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2013),

pages 102-107

ISBN: 978-989-8565-69-3

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

density function may be denoted by f(r,ξ,t) where r

is the spatial position vector, ξ is the property of inter-

est of the dispersed phase, and t is the time. Moreover,

f(r,ξ,t)dξ represents the average number of particles

per unit volume around the point r (r, r + dr) in the

time t, with the property between ξ and ξ + dξ. The

resulting PBE is characterized mathematically as a

non-linear integro-partial differential equation which

must be solved by a suitable numerical method.

In recent publications, the least-squares method

has been adopted for the solution of PB problems,

e.g. (Dorao and Jakobsen, 2006b; Dorao and Jakob-

sen, 2007b; Dorao and Jakobsen, 2008; Dorao and

Jakobsen, 2009; Dorao and Jakobsen, 2007a; Dorao

and Jakobsen, 2006a; Nayak et al., 2011; Sporleder

et al., 2011; Zhu et al., 2009a; Zhu et al., 2009b; Pa-

truno et al., 2009; Patruno, 2010; Borka and Jakobsen,

2012a). The least-squares method has also been ap-

plied to other chemical reactor problems such as the

pellet equations and ﬁxed packed bed reactors (Rout

et al., 2011; Rout and Jakobsen, 2012; Solsvik and

Jakobsen, 2012; Sporleder et al., 2011). However,

the least-squares technique is a method in the family

of weighted residual. Thus, it is of interest to reveal

the properties of the least-squares method compared

to other methods in the weighted residual framework

like the orthogonal collocation and tau methods.

The aim of the present study is to compare the per-

formance of different solution techniques in the fam-

ily of weighted residual methods. The solution meth-

ods is evaluated for a combined multiﬂuid-PB model

describing bubbly ﬂow. The evaluation should con-

sider residual measures, computational time, imple-

mentation issues, and complexity of the algebraic the-

ory of the methods.

2 THE MODEL

The combined multiﬂuid-PB model considered in the

present study is based upon the work of (Nayak et al.,

2011; Borka and Jakobsen, 2012a; Borka and Jakob-

sen, 2012b; Borka and Jakobsen, 2012c). The steady-

state model holds one dimension in physical space

and one dimension in the property space (bubble di-

ameter). The model equations is outlined in the se-

quel.

The main advantages of the novel model by

(Nayak et al., 2011) is that both the PBE and the

momentum equation of the dispersed gas phase is in

terms of the internal coordinate ξ. Hence, the inner

coordinate space physics can be resolved provided

that a sufﬁcient numerical method is available. In par-

ticular, the least-squares, tau, Galerkin and orthogonal

collocation methods in the weighted residual frame-

work can be applied to solve the model proposed by

(Nayak et al., 2011).

In the following, the multiﬂuid–PB model is out-

lined for bubbly ﬂows in a cold-ﬂow column.

2.1 The dispersed Phase

The two-dimensional (one dimensiona in the physical

space and one dimension in the property space) PBE

is presented by:

∂

∂z



(ξ,z) f

d,m

(ξ,z)



∂

∂ξ



(ξ,z) f

d,m

(ξ,z)



= −b(ξ) f

d,m

(ξ,z)

+V(ξ)

max

h(ξ,ζ)b(ζ)

d,m

(ζ,z)

V(ζ)

dζ

− f

d,m

(ξ,z)

(ξ

max

−ξ

)

1/3

min

c(ξ,ζ)

d,m

(ζ,z)

(z)V(ζ)

dζ

V(ξ)

(ξ

−ξ

min

)

1/3

min

c([ξ

− ζ

]

1/3

,ζ)

[ξ

− ζ

]

2/3

d,m

(ζ,z)

(z)V(ζ)

d,m

([ξ

− ζ

]

1/3

,z)

V(ξ) −V(ζ)

dζ

(1)

in which f

d,m

is the mass density function [kg/m

/m].

The bubbles are transported in physical space accord-

ing to velocity v

and in the property space according

to velocity v

. Moreover, the internal coordinate is

the bubble diameter. The breakage rate and daughter

size redistribution function proposed by (Coulaloglou

and Tavlarides, 1977), and the coalescence model by

(Prince and Blanch, 1990) are adopted. The breakage

frequency yields:

b(z,ξ) =

1/3

2/3

exp



−

σk

2/3

5/3



(2)

where k

and k

are empirical parameters, which de-

pend on the system properties. The daughter size re-

distribution function is given as:

h(ξ,ζ) =2P(ξ,ζ) = 2

2.4





V(ζ)

× exp

−4.5

[2V(ξ) −V(ζ)]

V(ζ)

(3)

The coalescence model by (Prince and Blanch, 1990)

is deﬁned as the product of a collision volume rate

(ξ,ζ) and the coalescence probability λ

(ξ,ζ):

c(ξ,ζ) = h

(ξ,ζ)λ

(ξ,ζ) (4)

SpectralSolutionsofaCombinedMultifluid--populationBalanceModel DescribingBubblyFlow-ANumericalStudyof

weightedResidualMethods

103

The expression for the coalescence probability is

given as:

(ξ,ζ) = exp







−



(ξ,ζ)ρ

16σ



1/2

1/3







(ξ,ζ)



2/3







(5)

where the equivalent radius is deﬁned as:

(ξ,ζ) =





−1

(6)

The collision volume rate is given as:

(ξ,ζ) =

[ξ+ ζ]



β[εξ ]

2/3

+ β[εζ]

2/3



1/2

(7)

The bubble growth velocity is estimated as:

(z,ξ) = −

ξv

3ρ

(z)

∂ρ

(z)

∂z

(8)

The momentum equation of the dispersed phase is

given as:

∂

∂z



d,m

(ξ,z)v

(ξ,z)



−

∂

∂ξ



d,m

(ξ,z)v

(ξ,z)



−

d,m

(ξ,z)

(z)

∂ρ

(z)

∂z

+ f

d,m

(ξ,z)g+ f

drag

(ξ,z)

(9)

The dispersed phase fraction:

(z) =

∞

d,m

(ξ,z)

(z)

dξ (10)

The gas-phasepressure is assumed equal to the liquid-

phase pressure: P = P

= P

. The ideal gas law

gives the relationship between the pressure and the

dispersed phase density:

p(z) −

(z) = 0 (11)

The drag force is deﬁned as:

drag

= −

d,m

(ξ,z)

(z)

(ξ,z) − v

(z)|



(ξ,z) − v

(z)



(12)

where

max



min



Rep

(1+ 0.15Re

0.687



Eo+ 4



(13)

(z,ξ) − v

(z)|ξ

(14)

Eo =

g(ρ

− ρ

)ξ

(15)

2.2 The Continuous Phase

The liquid continuity equation:



(z)ρ

(z)



= 0

(16)

or integrated:

(z)ρ

(z) = α

(z = 0)ρ

(z = 0) (17)

The momentum equation:

(z)ρ

(z)

(z) =

(z)



−

dp(z)

−

(z)



−

∞

drag

(ξ,z)dξ + α

(z)ρ

(18)

The summation of the phase area fraction must be

unity:

+ α

= 1 (19)

The wall friction factor is calculated as:

(z) =



0.79ln



(z)



− 1.64



−2

(20)

3 NUMERICAL METHODS

Basically, spectral methods are based upon using a

representation of the solution function over the entire

computational domain via a truncated series expan-

sion (Finlayson, 1972):

(ξ) ≈ f

(ξ) =

∑

j=0

(ξ) (21)

in which ϕ

(ξ) denotes the basis function and α

de-

notes the basis coefﬁcients. A nodal basis is obtained

if the truncated series expansion (21) is given in terms

of Lagrangian basis polynomials ℓ

(ξ):

f(ξ) ≈ f

(ξ) =

∑

j=0

ℓ

(ξ) (22)

in which the basis coefﬁcients are meaningful in the

sense that they correspond to the solution function

values at the collocation points.

The methods of weighted residual is presented by

the following generalized inner product:

Ω

R (ξ; f

, f

,..., f

(ξ)dΩ = 0

for i = 0, 1, ...,P

(23)

where w

are weighting functions and R is the resid-

ual. The particular choice of the weighting function

deﬁnes the particular solution approximation tech-

nique in the family of weighted residual methods:

SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

104

• the least-squares method

∂

∂f

R (ξ, f

, f

,..., f

) (24)

• the tau method

= ℓ

(ξ) (25)

• the orthogonal collocation method

= δ(ξ − ξ

) (26)

The tau (Lanczos, 1938) and least-squares (Jiang,

1998; Bochev and Gunzburger, 1998; Pontaza, 2003)

methods have not obtained the same popularity as the

orthogonal collocation method (Villadsen and Stew-

ard, 1967; Villadsen, 1970; Villadsen and Michelsen,

1978; Michelsen and Villadsen, 1981) in the chem-

ical reactor engineering society. However, the tau

method is similar to the Galerkin method (Galerkin,

1915). The essential difference between the Galerkin

and the tau methods is the treatment of the boundary

conditions. Theory of the least-squares method from

a chemical engineering point of view is given by (Do-

rao, 2006; Zhu, 2009; Sporleder, 2011). Furthermore,

the algebra and implementation issues using the least-

squares method for the solution of a PB problem is

provided by (Solsvik and Jakobsen, 2013).

4 RESULTS

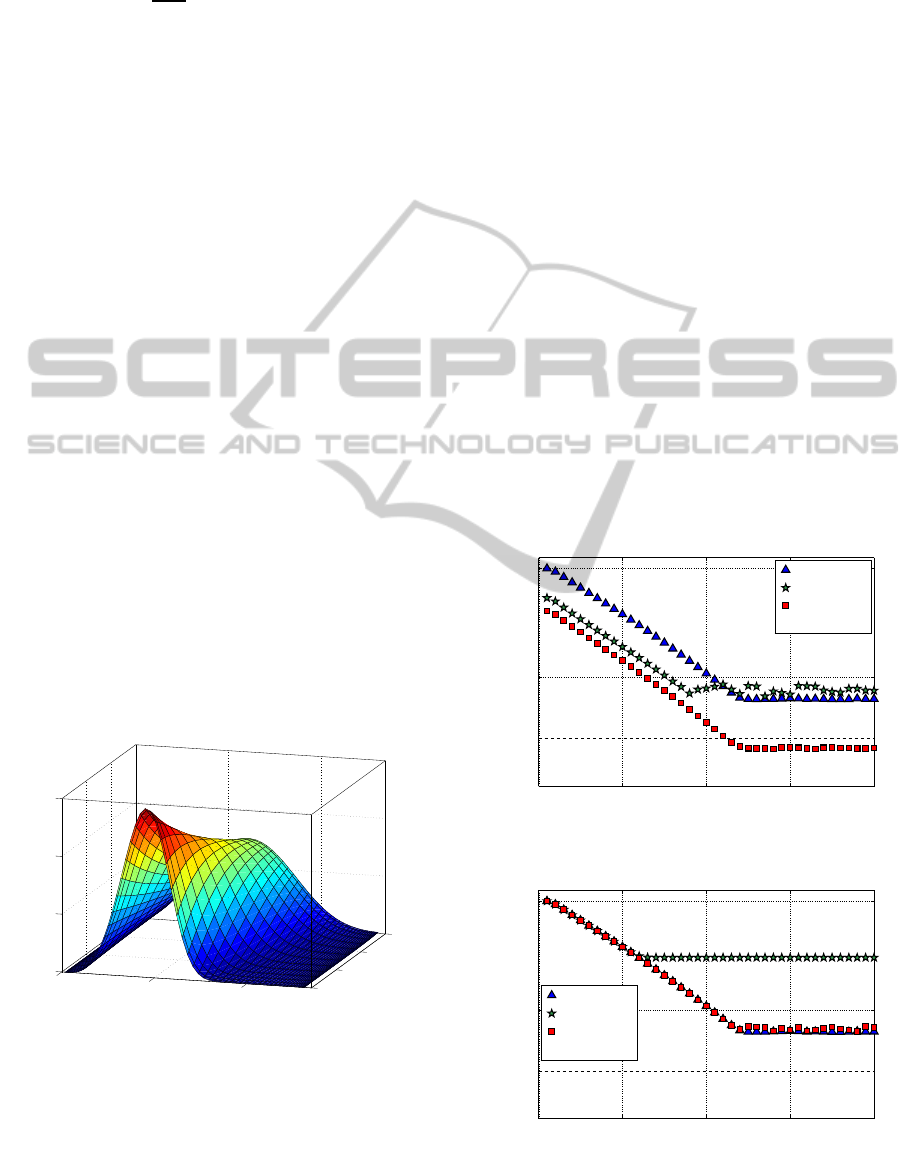
The solution of the PBE (1) is presented in ﬁgure 2.

The PB model has been solved with the orthogonal

collocation, tau and least-squares methods.

0.01

0.02

z [m]

ξ [m]

f [kg/m

Figure 2: Solution of a PB problem. The bubble size distri-

bution along the bubble column height.

Two residual measure deﬁnitions have been em-

ployed to evaluate the accuracy of the solution meth-

ods. The residual measure deﬁnitions are based on

(i) the problem operator form and (ii) the algebraic

system form. The former residual deﬁnition measure

the residual of the governing equation, while the lat-

ter deﬁnition gives the residual of the algebraic equa-

tion system that is actually solved. Noticeable, for the

orthogonal collocation method the problem operator

form and the algebraic system form coincide. Fig-

ure 3 shows the residual versus the number of itera-

tions adopting the residual measure deﬁnition based

on the algebraic system form. Based on this partic-

ular residual measure, the tau method is signiﬁcantly

favorable above the orthogonal collocation and least-

squares methods. The orthogonal collocation and

least-squares methods obtain the same accuracy, but

with differences in the number of iteration to reach

convergence, in which the least-squares method re-

quires less iteration to reach its minimum residual

value. In ﬁgure 4 the residual measure deﬁnition

based on the problem operator form is adopted. For

this particular residual measure deﬁnition, the tau and

orthogonal collocation show the same performance.

On the other hand, the least-squares method obtains a

signiﬁcant larger value of the residual measure. Thus,

the least-squares method does not fulﬁll the govern-

ing equation as well as the orthogonal collocation and

tau methods. The least-squares method requires fur-

ther attention to reveal the signiﬁcantly larger resid-

0 10 20 30 40

−20

−10

Residual

Iterations

Collocation

LSQ

Tau

Machine accuracy

Figure 3: Residual (algebraic system form) as a function of

the number of iterations.

0 10 20 30 40

−20

−10

Residual

Iterations

Collocation

LSQ

Tau

Machine accuracy

Figure 4: Residual (problem operator form) as a function of

the number of iterations.

SpectralSolutionsofaCombinedMultifluid--populationBalanceModel DescribingBubblyFlow-ANumericalStudyof

weightedResidualMethods

105

ual measure on the problem operator form compared

to the orthogonal collocation and tau methods.

The orthogonal collocation method is favorable

considering the simplicity of implementation com-

pared to the tau and leas-squares methods. Moreover,

the orthogonal collocation method uses less computa-

tional costs per iteration than the relatively more com-

putational demanding tau and least-squares methods.

5 CONCLUSIONS

The accuracy of the orthogonal collocation, tau and

least-squares method can be evaluated on different

residual measure deﬁnitions. Dependent on the resid-

ual measure deﬁnition adopted, the relatively perfor-

mance of the numerical methods may change signiﬁ-

cantly. However, the simulation results of the present

PB problem indicate that the orthogonal collocation

and tau method are favorable above the least-squares

method considering accuracy. Nevertheless, the or-

thogonal collocation method uses less computational

costs per iteration than the tau and least-squares meth-

ods. Furthermore, the orthogonal collocation method

holds the simplest algebraic theory, and is thus asso-

ciated with the simplest implementation issues.

REFERENCES

Bochev, P. B. and Gunzburger, M. D. (1998). Finite ele-

ment methods of least-squares type. SIAM REVIEW,

40:789–837.

Borka, Z. and Jakobsen, H. A. (2012a). Evaluation of

breakage and coalescence kernels for vertical bubbly

ﬂows using a combined multiﬂuid–population balance

model solved by least squares method. Procedia En-

gineering, 42:623–633.

Borka, Z. and Jakobsen, H. A. (2012b). Least squares

higher order method for the solution of a com-

bined multiﬂuid–population balance model: Model-

ing and implementation issues. Procedia Engineering,

42:1121–1132.

Borka, Z. and Jakobsen, H. A. (2012c). On the modeling

and simulation of higher order breakage for vertical

bubbly ﬂows using the least squares method: Appli-

cation for bubble column and pipe ﬂows. Procedia

Engineering, 42:1270–1281.

Coulaloglou, C. A. and Tavlarides, L. L. (1977). Descrip-

tion of interaction processes in agitated liquid–liquid

dispersions. Chemical Engineering Science, 32:1289–

1297.

Dorao, C. A. (2006). High order methods for the solution

of the population balance equation with applications

to bubbly ﬂows. PhD thesis, Norwegian University of

Science and Technology (NTNU).

Dorao, C. A. and Jakobsen, H. A. (2006a). Application of

the least-squares method for solving population bal-

ance problems in R

d+1

. Chem Eng Sci, 61:5070–

5081.

Dorao, C. A. and Jakobsen, H. A. (2006b). A least squares

method for the solution of population balance prob-

lems. Computers & Chemical Engineering, 30:535–

547.

Dorao, C. A. and Jakobsen, H. A. (2007a). Least-squares

spectral method for solving advective population bal-

ance problems. J. of Computational and Applied

Mathematics, 201:247–257.

Dorao, C. A. and Jakobsen, H. A. (2007b). Time–space–

property least squares spectral method for population

balance problems. Chemical Engineering Science,

62:1323–1333.

Dorao, C. A. and Jakobsen, H. A. (2008). hp-adaptive

least squares spectral element method for population

balance equations. Applied Numerical Mathematics,

58:563–576.

Dorao, C. A. and Jakobsen, H. A. (2009). Time–property

least-squares spectral method for population balance

equations. J. Math. Chem., 46:770–780.

Finlayson, B. A. (1972). The method of weighted residuals

and variational principles, volume 87 of Mathematics

in Science and Engineering. New York: Academic

Press.

Galerkin, B. G. (1915). Series solution of some problems

in elastic equilibrium of rods and plates. Vestn Inzh

Tech, 19:897–908.

Jakobsen, H. A. (2008). Chemical reactor modeling: Mul-

tiphase reactive ﬂows. Berlin: Springer.

Jiang, B.-N. (1998). The least-squares ﬁnite ele-

ment method: Theory and applications in computa-

tional ﬂuid dynamics and electromagnetics. Berlin:

Springer.

Lanczos, C. (1938). Trigonometric interpolation of empir-

ical and analytical functions. J Math Phys, 17:123–

199.

Michelsen, M. L. and Villadsen, J. (1981). Polynomial so-

lution of differential equations. In Mah, R. S. H. and

Seider, W. D., editors, Foundations of computer-aided

chemical process design,, pages 341–368. New York:

Engineering Foundation.

Nayak, A. K., Borka, Z., Patruno, L. E., Sporleder, F.,

Dorao, C. A., and Jakobsen, H. A. (2011). A com-

bined multiﬂuid-population balance model for verti-

cal gas–liquid bubble-driven ﬂows considering bubble

column operating conditions. Industrial & Engineer-

ing Chemical Research, 50:1786–1798.

Patruno, L. E. (2010). Experimental and numerical inves-

tigations of liquid fragmentation and droplet genera-

tion for gas processing at high pressures. PhD the-

sis, Norwegian University of Science and Technology

(NTNU).

Patruno, L. E., Dorao, C. A., Svendsen, H. F., and Jakob-

sen, H. A. (2009). Analysis of breakage kernels for

population balance modelling. Chemical Engineering

Science, 64:501–508.

Pontaza, J. P. (2003). Least-squares variation principles

and ﬁnite element mehtods: Theory, formulations, and

SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

106

models for solid and ﬂuid mechanics. PhD thesis,

Texas A&M University.

Prince, M. J. and Blanch, H. W. (1990). Bubble coalescence

and break-up in air-sparged bubble columns. AIChE

J, 36(10):1485–1499.

Ramkrishna, D. (2000). Population balance: Theory and

applications to particulate systems in engineering.

San Diego: Academic Press.

Randolph, A. D. and Larson, M. A. (1988). Theory of par-

ticulate processes. Analysis and techniques of contin-

uous crystallization. San Diego: Academic Press, 2

edition.

Rout, K. R. and Jakobsen, H. A. (2012). Reactor perfor-

mance optimization by the use of a novel combined

pellet reﬂecting both catalyst and adsorbent proper-

ties. Fuel Processing Technology, 99:13–34.

Rout, K. R., Solsvik, J., Nayak, A. K., and Jakobsen,

H. A. (2011). A numerical study of multicomponent

mass diffusion and convection in porous pellets for

the sorption-enhanced steam methane reforming and

desorption processes. Chemical Engineering Science,

66:4111–4126.

Solsvik, J. and Jakobsen, H. A. (2012). Effect of jacobi

polynomials on the numerical solution of the pellet

equation using the orthogonal collocation, Galerkin,

tau and least squares methods. Computers & Chemi-

cal Engineering, 39:1–21.

Solsvik, J. and Jakobsen, H. A. (2013). On the solution

of the population balance equation for bubbly ﬂows

using the high-order least-squares method: Imple-

mentation issues. Reviews in Chemical Engineering,

29(2):63–98.

Sporleder, F. (2011). Simulation of chemical reactors using

the least-squares spectral element method. PhD the-

sis, Norwegian University of Science and Technology

(NTNU).

Sporleder, F., Borka, Z., Solsvik, J., and Jakobsen, H. A.

(2012). On the population balance equation. Reviews

in Chemical Engineering, 28:149–169.

Sporleder, F., Dorao, C. A., and Jakobsen, H. A. (2011).

Model based on population balance for the simulation

of bubble columns using methods of the least-squares

type. Chemical Engineering Science, 66:3133–3144.

Villadsen, J. (1970). Selected approximation methods for

chemical engineering problems. København: Dan-

marks Tekniske Højskole.

Villadsen, J. and Michelsen, M. L. (1978). Solution of Dif-

ferential Equation Models by Polynomial Approxima-

tion. Englewood Cliffs, NJ: Prentice-Hall.

Villadsen, J. V. and Steward, W. E. (1967). Solution of

boundary-value problems by orthogonal collocation.

Chemical Engineering Science, 22:1482–1501.

Zhu, Z. (2009). The least-squares spectral element method

solution of the gas–liquid multi-ﬂuid model coupled

with the population balance equation. PhD the-

sis, Norwegian University of Science and Technology

(NTNU).

Zhu, Z., Dorao, C. A., and Jakobsen, H. A. (2009a). On

the coupled solution of a combined population bal-

ance model using the least-squares spectral element

method. Industrial Engineering Chemical Research,

48:7994–8006.

Zhu, Z., Dorao, C. A., and Jakobsen, H. A. (2009b). Solu-

tion of bubble number density with breakage and coa-

lescence in a bubble column by least-squares method.

Progress in Computational Fluid Dynamics, 9:436 –

446.

SpectralSolutionsofaCombinedMultifluid--populationBalanceModel DescribingBubblyFlow-ANumericalStudyof

weightedResidualMethods

107