Singular and Non-singular Path Following Control

of a Wheeled Mobile Robot of (2,0) Type

Joanna Płaskonka

Institute of Computer Engineering, Control and Robotics, Wroclaw University of Technology,

Janiszewskiego 11/17, Wroclaw, Poland

Keywords:

Path Following, Wheeled Mobile Robot, Serret-Frenet Frame, Nonholonomic Constraints, Model-Based

Control.

Abstract:

This paper relates to the problem of a path following task for a wheeled mobile platform of (2,0) type. Two

kinematic control algorithms, Micaelli-Samson algorithm and Soetanto-Lapierre-Pascoal algorithm, which are

based on either the Serret-Frenet frame with an orthogonal projection or the Serret-Frenet frame with a non-

orthogonal projection of a robot on the desired path, were presented. The additional condition that should be

imposed on the function δ, which is a parameter depending on a linear velocity of the robot and on a distance

error, was described. The inﬂuence of the function δ on the convergence of the non-singular algorithm has

been shown using computer simulations.

1 INTRODUCTION

There are three groups of problems related to a motion

control of autonomous vehicles:

• point stabilization,

• trajectory tracking (the robot has to follow a de-

sired curve which is time-parametrized),

• path following (the task of the robot is to fol-

low a curve parametrized by a curvilinear distance

from a ﬁxed point).

Various approaches to designing kinematic control

strategies for wheeled mobile robots can be used –

more general, which could be applied for few types

of mobile platforms, and dedicated to particular types

of wheeled mobile robots. Better results are usually

obtained for the latter ones. The examples of the al-

gorithms dedicated to a certain type of mobile robots

may be found e.g. in (Samson, 1992), (De Luca et al.,

1998), (Morro et al., 2011), (Płaskonka, 2012). One

can also consider a coordinated path following con-

trol for a group of wheeled mobile platforms, see e.g.

(Xiang et al., 2009), (Ronen and Arogeti, 2012).

Different ideas of describing the position of the

robot relative to the path were proposed in the litera-

ture. The one, which is the most commonly applied,

bases on the Serret-Frenet frame that moves along the

desired curve. In this paper two path parametrization

approaches are presented. In the ﬁrst one the Serret-

Frenet frame is attached to the point on the path that

is closest to the robot, see e.g. (Samson, 1992), (Mi-

caelli and Samson, 1993). Unfortunately such an ap-

proach imposes on the vehicle stringent initial con-

ditions constraints. The second approach (Soetanto

et al., 2003) does not have such a drawback as the po-

sition of the virtual target to be tracked by the robot is

deﬁned by a non-orthogonal projection of the vehicle

on the path. That approach inspired many scientists,

not only those who are focused on control algorithms

for mobile platforms, (Indiveri et al., 2007), (Xiang

et al., 2009), (Liu et al., 2012).

This paper addresses the problem of the realiza-

tion of a path following task by a wheeled mobile

robot of (2,0) type. The aim of the paper is to present

two path following algorithms, Micaelli-Samson al-

gorithm (Micaelli and Samson, 1993) and Soetanto-

Lapierre-Pascoal algorithm (Soetanto et al., 2003),

and indicate that one should take into account an ad-

ditional condition related to a function δ, that was

introduced in both of the mentioned kinematic con-

trol algorithms to broaden the control stability do-

main, which – to the best of author’s knowledge –

was not mentioned in the literature so far. In addition,

the inﬂuence of the function δ on the convergence of

Soetanto-Lapierre-Pascoal control algorithm has been

presented. The results of additional simulations pre-

senting the inﬂuence of values of controller’s param-

eters on the realization of the path following tasks

268

Plaskonka J..

Singular and Non-singular Path Following Control of a Wheeled Mobile Robot of (2,0) Type.

DOI: 10.5220/0004479202680275

In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2013), pages 268-275

ISBN: 978-989-8565-71-6

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

and simulations taking into account the velocity con-

straints have been provided as well.

2 MODEL OF A ROBOT

All wheeled mobile robots can be classiﬁed into one

of ﬁve generic types, (Campion et al., 1996). In this

paper the considerations will be restricted to a robot

belonging to the (2,0) type which is a two-wheel

differential-drive robot, also called in the literature

a unicycle. In general such a type of a robot con-

sists of a platform equipped with either one or several

ﬁxed wheels with a common axle. It might also have

a passive caster wheel which serves as a support.

Fig. 1 depicts a unicycle which can be described

by generalized coordinates q = (x, y, θ)

. The point

Figure 1: The unicycle’s parameters.

M (a robot’s guidance point) is located in the mid-

dle of the wheel axle of the vehicle. The variables

x and y denote the position of the point M relative

to the inertial frame, while θ is a robot’s orientation.

Taking into account the assumptions that the robot’s

wheels are non-deformable and the robot is moving

on a plane without slippage of its wheels, the kine-

matic model of the considered wheeled mobile robot

can be described by the equations







˙x = vcos θ,

˙y = vsin θ,

θ = ω,

(1)

where symbols v and ω denote unicycle’s linear and

angular velocities, respectively.

3 DESCRIPTION OF THE ROBOT

RELATIVE TO A DESIRED

PATH

The position of the robot may be described not only

relative to an inertial frame, but also relative to a de-

sired path. For this purpose one may attach to a path

the Serret-Frenet frame which in general consists of

vectors tangent, normal and binormal to a desired

curve. The considered robot is moving on a plane so

in that case the Serret-Frenet frame consists only of

vectors tangent and normal to the path.

The main difference between a trajectory and a

path is that the ﬁrst one is parametrized by the time,

while the latter one is parametrized by a curvilinear

distance s(t) from a ﬁxed point, i.e. from the begin-

ning of the path. In other words, a trajectory is a spe-

cial case of a path when s(t) = t. The path P is char-

acterized by a curvature κ(s), which is the inversion

of the radius of the circle tangent to the path at a point

characterized by the parameter s. The desired orien-

tation of the mobile platform satisﬁes the equation

= ±κ(s) ˙s. (2)

The sign on the right side of the equation (2) de-

pends on the direction of moving along a desired

curve (negative when the Serret-Frenet frame moves

in the clockwise direction, positive otherwise).

3.1 The Serret-Frenet Frame with

an Orthogonal Projection

of a Robot on the Path

In this approach a virtual target to be tracked is de-

ﬁned by the robot’s orthogonal projection on the de-

sired path, see Fig. 2. The point M’ is the orthogonal

Figure 2: The Serret-Frenet frame deﬁnition in a case

of an orthogonal projection of a robot on the path.

projection of the point M on the path P and l is the

SingularandNon-singularPathFollowingControlofaWheeledMobileRobotof(2,0)Type

269

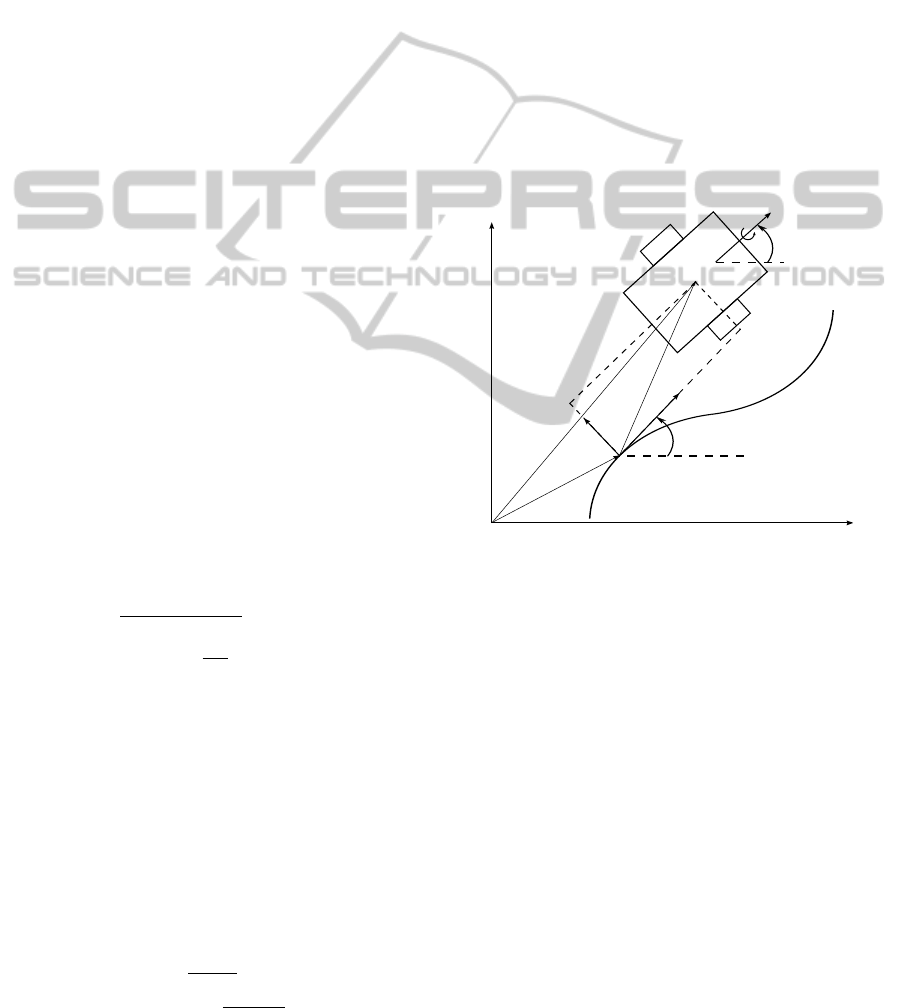
distance error between the actual vehicle and the vir-

tual one. The relationship between the position of the

point M relative to an inertial frame and its position

relative to the Serret-Frenet frame can be described

by the equation







0 1





, (3)

where

= R = Rot(z, θ

) =





cosθ

−sin θ

sinθ

cosθ

0 0 1





(4)

After differentiating and transforming the equation

(3), one has

= R

− R

. (5)

Using the relationships

= (0 l 0)

, (6)

= (x y 0)

(7)

and

= ( ˙s 0 0)

, (8)

as the reference vehicle is moving along a desired path

in the direction of X axis of the Serret-Frenet frame,

the equation (5) can be rewritten as













cosθ

sinθ

−sin θ

cosθ

0 0 1









˙x

˙y





−





0 −

0 0

0 0 0













−





˙s





, (9)

which leads to

l = (−sinθ

cosθ

)



˙x

˙y



, (10)

˙s =

(cosθ

sinθ

)

1 ∓ κ(s)l



˙x

˙y



. (11)

To avoid singularity l = ±

κ(s)

one has to ensure that

during the control process an inequality |l κ(s)| < 1

holds, which means that the parametrization is local.

In addition, one can determine the orientation error

θ = θ − θ

(12)

and its derivative

θ =

θ −

θ ∓ κ(s) ˙s. (13)

Finally the kinematic model of a wheeled mobile

robot of (2,0) type derived with respect to Serret-

Frenet frame can be described by the following sys-

tem of equations











l = vsin

θ,

˙s =

vcos

1∓κ(s)l

θ = ω ∓

κ(s)vcos

1∓κ(s)l

(14)

3.2 The Serret-Frenet Frame with

a Non-orthogonal Projection

of a Robot on the Path

The methodology described in this subsection avoids

the occurrence of the singularities which are present

in control strategies based on the approach presented

in subsection 3.1. This is done by using the Serret-

Frenet frame which is not attached to the point on the

path that is closest to the vehicle, see Fig. 3. As a re-

sult one has to take into account an extra controller

design parameter. In that situation there are three path

following errors – an orientation error

θ and two dis-

tance errors, s

in the direction of the X axis and y

in the direction of Y axis of the Serret-Frenet frame.

Such an approach was proposed in (Soetanto et al.,

2003).

Figure 3: The Serret-Frenet frame deﬁnition in a case

of a non-orthogonal projection of a robot on the path.

The velocity of r

is equal to

= R

− R

(15)

with

= (s

, (16)

= (x y 0)

(17)

and

= ( ˙s 0 0)

. (18)

From (15) one gets





˙s

˙y









cosθ

sinθ

−sin θ

cosθ

0 0 1









˙x

˙y





−





0 −

0 0

0 0 0













−





˙s





(19)

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

270

and thus

˙s



cosθ

sinθ





˙x

˙y



− ˙s(1 − y

κ(s)), (20)

˙y



−sin θ

cosθ





˙x

˙y



− ˙sκ(s)s

. (21)

There is no singularity related to distance errors in

equations (20)-(21). For the unicycle the kinematic

model expressed with respect to the Serret-Frenet

frame with a non-orthogonal projection of a robot

on the path is given by the following equations







˙s

= − ˙s(1 − κ(s)y

) + vcos

θ,

˙y

= −κ(s) ˙ss

+ vsin

θ,

θ = ω ∓κ(s) ˙s.

(22)

4 PATH FOLLOWING

ALGORITHMS

The considered control problem is to design a kine-

matic control law such that the wheeled mobile robot

of (2,0) type follows a desired path and path follow-

ing errors converge to zero. The desired path has to

be admissible, i.e. it can be realized without slippage

of robot’s wheels.

It is assumed that a direction of a movement along

the desired curve is opposite to the clockwise direc-

tion, this means that

θ = κ(s) ˙s. (23)

Hence the equations describing path following er-

rors for a case of an orthogonal projection of a robot

on the path have a form as below

l = vsin

θ,

θ = ω −

κ(s)vcos

1−κ(s)l

(24)

and in a case of a non-orthogonal projection are equal

˙s

= − ˙s(1 − κ(s)y

) + vcos

θ,

˙y

= −κ(s) ˙ss

+ vsin

θ,

θ = ω −κ(s) ˙s.

(25)

4.1 Singular Control Algorithm

Micaelli-Samson kinematic control law (Micaelli and

Samson, 1993) for the system (24) is equal to

ω =

κ(s)vcos

1−κ(s)l

∂δ(l,v)

∂l

vsin

θ +

∂δ(l,v)

∂v

˙v +

− λ

∂ f

∂l

sin

θ−sinδ(l,v)

θ−δ(l,v)

− k|v|(

θ − δ(l, v))

k > 0, λ

> 0,

(26)

where v(t) and ˙v(t) are bounded, v(t) does not tend to

zero when t tends to inﬁnity, the functions

f (l) : (−r, r) → R

and

δ(l, v) : R × R → R

are C

and C

respectively and the following condi-

tions are satisﬁed:

• f (±r) = ±∞,

• f (0) = δ(0, v) = 0,

•

∂ f

∂l

(l) > 0, ∀l,

• v f (l)sin δ(l, v) ≤ 0,∀l, ∀v.

The function δ was introduced to set the desired val-

ues for the orientation error

θ during transients. What

is more, the following inequality should hold

|δ(l, v)| <

, ∀l, ∀v. (27)

The system (24) with a closed-loop of the feedback

signal (26) is asymptotically stable. In addition, if

f (l) tends to inﬁnity when l tends to

max

, it is pos-

sible to keep l(t) in the open interval



−

max



when l(0) belongs to this interval.

Proof. Consider the Lyapunov function



(l) +



θ − δ(l, v)





. (28)

The time-derivative of V

= f

∂ f

∂l

l +

(

θ − δ)(

θ −

δ) =

= f

∂ f

∂l

vsin δ + (

θ − δ)[

(ω+

−

κ(s)vcos

1−κ(s)l

−

∂δ

∂l

vsin

θ −

∂δ

∂v

˙v)+

+ f

∂ f

∂l

sin

θ−sinδ

θ−δ

] =

= f

∂ f

∂l

vsin δ − k|v|(

θ − δ)

(29)

is non-positive. This means that lim

t→∞

(t) = V

1lim

and f (l) and (

θ − δ) are bounded.

is uniformly

continuous because its derivative is bounded as sum

of bounded functions. By Barbalat’s lemma

tends

to zero. Therefore f

∂ f

∂l

vsin δ → 0 and v(

θ − δ) → 0.

Differentiating (

θ − δ) with respect to time gives



θ − δ



= −λ

∂ f

∂l

sin

θ−sinδ

θ−δ

−k λ

|v|(

θ − δ).

(30)

Hence



θ − δ



] = 2v ˙v(

θ − δ) − λ

∂ f

∂l

sin

θ−sinδ

θ−δ

−k λ

|v|v

(

θ − δ)

(31)

SingularandNon-singularPathFollowingControlofaWheeledMobileRobotof(2,0)Type

271

is the sum of two terms which tend to zero and third

term which is uniformly continuous. As v

(

θ − δ)

tends to zero, the extension of Barbalat’s lemma (Mi-

caelli and Samson, 1993) tells us that



θ − δ



]

also tends to zero which implies that the term

∂ f

∂l

sin

θ−sinδ

θ−δ

→ 0. The expression

sin

θ−sinδ

θ−δ

re-

quires a special comment. It can be rewritten in the

following way

sin

θ − sinδ

θ − δ

sin

θ−δ

cos

θ+δ

θ−δ

(32)

which for (

θ − δ) → 0 tends to cos δ or one can also

notice that for (

θ − δ) → 0 the expression

sin

θ−sinδ

θ−δ

equal to the derivative of the sine function. If only

δ does not tend to

mπ

, m ∈ Z, the the whole term

sin

θ−sinδ

θ−δ

does not tend to zero. This fact was not

indicated in (Micaelli and Samson, 1993). It seems

reasonable to assume that δ should be less than

for all l and for all v. Under this assumption f

∂ f

∂l

tends to zero. At the beginning it was assumed that

∂ f

∂l

(l) > 0 which leads to v f → 0. Using the facts that

θ−δ) → 0 and v f → 0, one may conclude that v

tends to zero and V

1lim

= 0. Thus both f and (

θ − δ)

tend to zero. From the properties of the function f , l

also tends to zero and therefore δ → 0. Finally one

conclude that

θ tends to zero which completes the

proof.

4.2 Non-singular Control Algorithm

The control algorithm proposed in (Soetanto et al.,

2003) for the system (25) is equal to

˙s = v cos

θ + k

ω = κ(s) ˙s +

δ(y

, v) − γy

sin

θ−sinδ(y

,v)

θ−δ(y

,v)

− k

(

θ − δ(y

, v)),

, k

> 0, γ = const,

(33)

where the following assumptions have been made

• lim

t→∞

v(t) 6= 0, e.g. v = const,

• δ(0, v) = 0,

• ∀

∀

vsin δ(y

, v) ≤ 0.

What is more, the following inequality should hold

|δ(y

, v)| <

, ∀y

, ∀v, (34)

which was not mentioned in (Soetanto et al., 2003).

The control algorithm guarantees the convergence of

, s

and

θ to zero. That can be shown using the

following Lyapunov function

+ y

) +

2γ

(

θ − δ(y

, v))

(35)

and carrying out the similar reasoning to one which

was presented in the subsection 4.1. The complete

proof of the convergence can be found in (Płaskonka,

2013).

5 SIMULATION RESULTS

The simulations were carried out to illustrate the be-

haviour of the wheeled mobile robot of (2,0) type

with the non-singular Soetanto-Lapierre-Pascoal con-

troller. The initial position of the platform was equal

to (x

, y

, θ

) = (12, 2,

). The desired path was the

circle described by the equations

x(s) = R cos





y(s) = Rsin





where R = 2 m.

5.1 The Inﬂuence of Different Values

of δ Function on the Realization

of the Task

Parameters of the kinematic controller were set to the

values presented below:

• v = 1,

• k

= 1,

• k

= 1000,

• γ = 1,

• θ

= {

, π, 2π},

• δ = −sign(v)θ

tanhy

The results of the simulations were presented in

Fig. 4-11.

Figure 4: The path following for the unicycle, XY plot

(Soetanto-Lapierre-Pascoal algorithm, θ

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

272

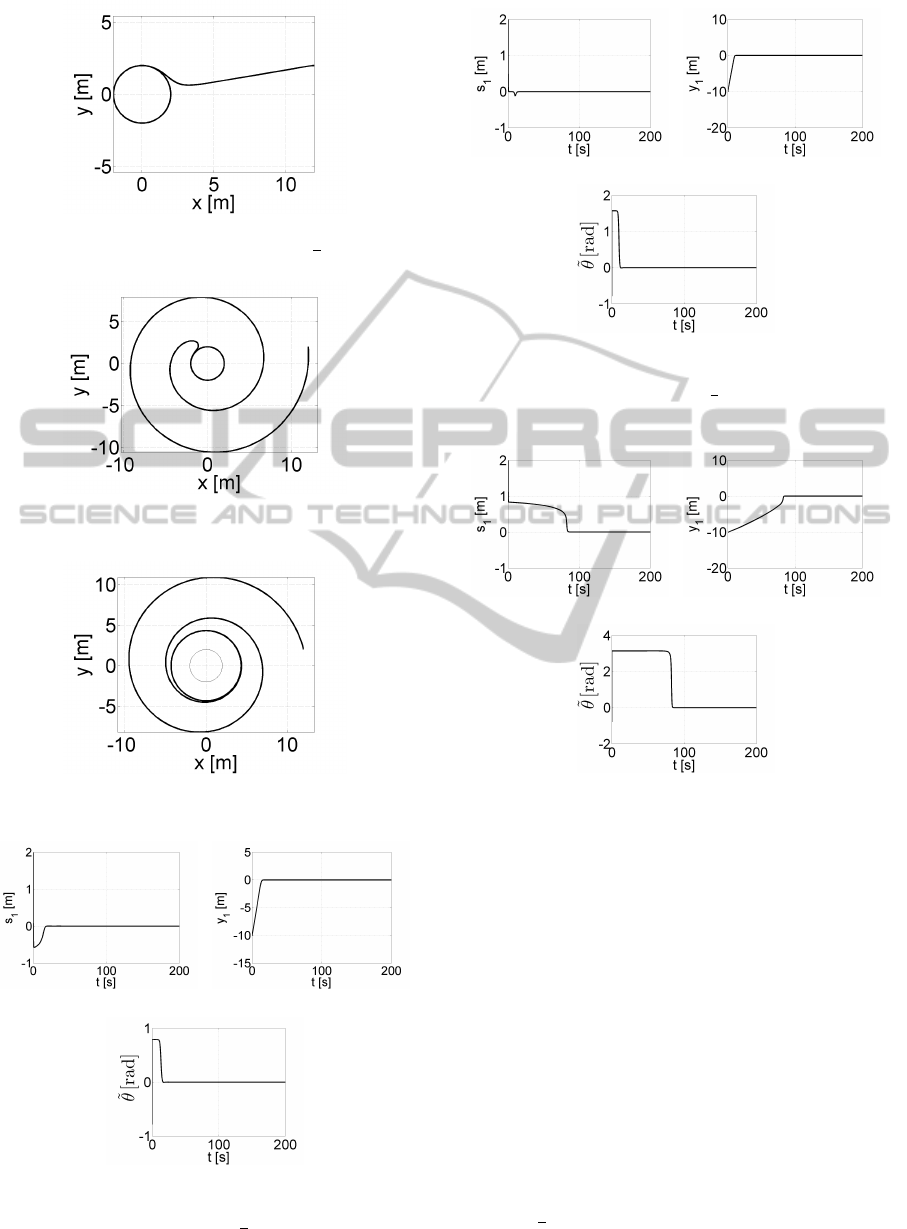
Figure 5: The path following for the unicycle, XY plot

(Soetanto-Lapierre-Pascoal algorithm, θ

Figure 6: The path following for the unicycle, XY plot

(Soetanto-Lapierre-Pascoal algorithm, θ

= π).

Figure 7: The path following for the unicycle, XY plot

(Soetanto-Lapierre-Pascoal algorithm, θ

= 2π).

(a) (b)

(c)

Figure 8: The path following for the unicycle (Soetanto-

Lapierre-Pascoal algorithm, θ

): (a) the distance error

, (b) the distance error y

, (c) the orientation error

θ.

(a) (b)

(c)

Figure 9: The path following for the unicycle (Soetanto-

Lapierre-Pascoal algorithm, θ

): (a) the distance error

, (b) the distance error y

, (c) the orientation error

θ.

(a) (b)

(c)

Figure 10: The path following for the unicycle (Soetanto-

Lapierre-Pascoal algorithm, θ

= π): (a) the distance error

, (b) the distance error y

, (c) the orientation error

θ.

5.2 The Inﬂuence of Different Values

of k

Parameters on the Realization

of the Task

Parameters of the kinematic controller were set to the

values presented below:

• v = 1,

• k

= {0.1, 1, 10, 100, 1000, 10000},

• k

= {0.1, 1, 10, 100, 1000, 10000},

• γ = 1,

• θ

• δ = −sign(v)θ

tanhy

SingularandNon-singularPathFollowingControlofaWheeledMobileRobotof(2,0)Type

273

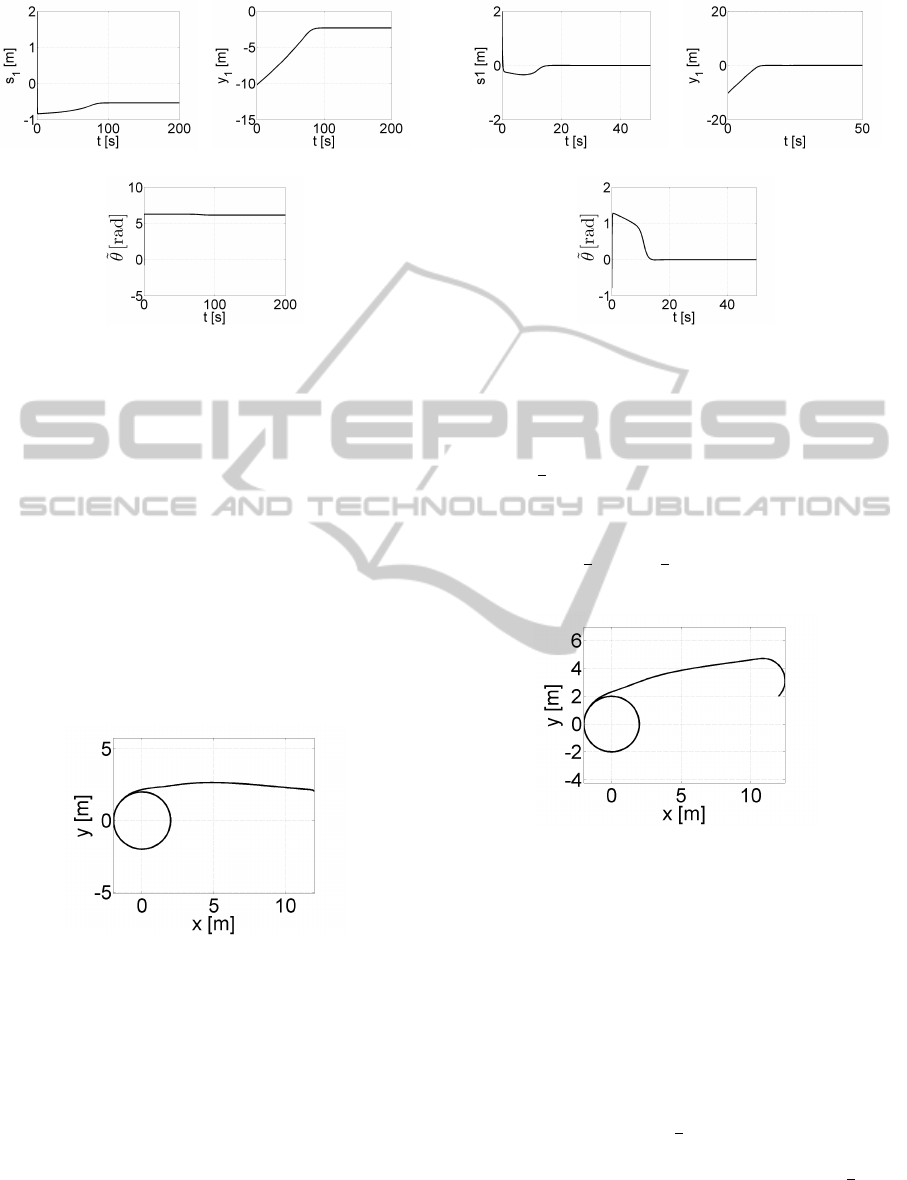
(a) (b)

(c)

Figure 11: The path following for the unicycle (Soetanto-

Lapierre-Pascoal algorithm, θ

= 2π): (a) the distance error

, (b) the distance error y

, (c) the orientation error

θ.

The chosen quality indicator for the presented algo-

rithm is equal to

Q =

∑

k=1

∑

j=1

where I

dt, I

dt and

, u

are control inputs. Table 1 presents values of Q

for selected values of the control parameters k

. The

quality indicator reached the minimum for k

= 1 and

= 10. The results of the simulations for those pa-

rameters were presented in Fig. 12-13.

Figure 12: The path following for the unicycle, XY plot

(Soetanto-Lapierre-Pascoal algorithm, k

= 1, k

= 10).

5.3 The Simulations Taking into

Account Velocity Constraints

Parameters of the kinematic controller were set to the

values presented below:

• v = 1,

• k

= 1,

• k

= 10,

• γ = 1,

(a) (b)

(c)

Figure 13: The path following for the unicycle (Soetanto-

Lapierre-Pascoal algorithm, k

= 1, k

= 10): (a) the dis-

tance error s

, (b) the distance error y

, (c) the orientation

error

θ.

• θ

• δ = −sign(v)θ

tanhy

The velocity constraint imposed on the on the robot

is chosen as −

≤ ω ≤

[rad/s]. The results of the

simulations were presented in Fig. 14-15.

Figure 14: The path following for the unicycle, XY plot

(Soetanto-Lapierre-Pascoal algorithm, simulations taking

into account velocity constraints).

6 CONCLUSIONS

In the paper singular and non-singular kinematic path

following controllers have been presented. It was sug-

gested to take into account an additional condition im-

posed on the function δ which is a parameter of both

algorithms. According to that condition the values of

δ should be smaller than

. The simulations of the

Soetanto-Lapierre-Pascoal algorithm have shown that

it is reasonable to limit values of δ. For θ

the

convergence of the algorithm was unacceptably slow.

Simulation analysis has shown that the presented al-

gorithm works properly for different values of the k

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

274

Table 1: The values of the quality indicator Q obtained in the simulations for selected values of k

parameters.

0.1 1 10 100 1000 10 000

0.1 631.9 513.2 512.4 681.9 1 801.3 12 835.6

1 607.3 514.2 490.1 664.3 1 789.1 12 824.1

10 626.3 518.7 497.5 699.0 1 836.5 12 873.4

100 635.9 526.5 506.1 734.4 2 013.2 13 148.5

1000 710.4 600.8 580.5 815.6 2 339.1 14 886.6

10 000 1 438.4 1 328.3 1 307.9 1 543.8 3 131.6 18 164.1

(a) (b)

(c)

Figure 15: The path following for the unicycle (Soetanto-

Lapierre-Pascoal algorithm, simulations taking into account

velocity constraints): (a) the distance error s

, (b) the dis-

tance error y

, (c) the orientation error

θ.

parameters, however choosing large values of the con-

troller’s parameters is undesirable due to a signiﬁcant

control cost. What is more, the path following task is

realized correctly by the considered wheeled mobile

robot when the Soetanto-Lapierre-Pascoal algorithm

is modiﬁed by adding velocity constraints.

An extension of this work could be testing if the

other kinds of δ function, not necessarily sigmoid-

like, could be applied for the presented algorithms.

REFERENCES

Campion, G., Bastin, G., and d’Andr

ea Novel, B. (1996).

Structural properties and classiﬁcation of kinematic

and dynamic models of wheeled mobile robots. IEEE

Transactions on Robotics and Automation, 12(5):47–

61.

De Luca, A., Oriolo, G., and Samson, C. (1998). Feed-

back control of a nonholonomic car-like robot. In

Laumond, J.-P., editor, Robot Motion Planning and

Control, pages 171–253. Springer-Verlag.

Indiveri, G., Nuchter, A., and Lingemann, K. (2007). High

speed differential drive mobile robot path following

control with bounded wheel speed commands. Pro-

ceedings of the 2007 IEEE International Conference

on Robotics and Automation, pages 2202–2207.

Liu, C., McAree, O., and Chen, W.-H. (2012). Path fol-

lowing for small UAVs in the presence of wind dis-

turbance. Proceedings of the UKACC International

Conference on Control, pages 613–618.

Micaelli, A. and Samson, C. (1993). Trajectory tracking for

unicycle-type and two-steering-wheels mobile robots.

Technical Report No. 2097, INRIA, Sophia-Antipolis,

France.

Morro, A., Sgorbissa, A., and Zaccaria, R. (2011). Path fol-

lowing for unicycle robots with an arbitrary path cur-

vature. IEEE Transactions on Robotics, 27(5):1016–

1023.

Płaskonka, J. (2012). The path following control of a uni-

cycle based on the chained form of a kinematic model

derived with respect to the Serret-Frenet frame. Pro-

ceedings of 17th International Conference on Methods

and Models in Automation & Robotics, MMAR 2012,

27(5):1016–1023.

Płaskonka, J. (2013). Different kinematic path following

controllers for a wheeled mobile robot of (2,0) type.

Sent for publication.

Ronen, R. and Arogeti, S. (2012). Coordinated path follow-

ing control for a group of car-like vehicles. Proceed-

ings of the IEEE 12th International Conference on

Control, Automation, Robotics & Vision, pages 719–

724.

Samson, C. (1992). Path following and time-varying feed-

back stabilization of a wheeled mobile robots. Pro-

ceedings of the IEEE Int. Conf. on Advanced Robotics

and Computer Vision, pages 1.1–1.5.

Soetanto, D., Lapierre, L., and Pascoal, A. (2003). Adap-

tive, non-singular path-following control of dynamic

wheeled robots. Proceedings of the IEEE Conference

on Decision and Control, 2:1765–1770.

Xiang, X., Lapierre, L., Jouvencel, B., and Parodi, O.

(2009). Coordinated path following control of mul-

tiple wheeled mobile robots through decentralized

speed adaptation. Proceedings of the IEEE/RSJ In-

ternational Conference on Intelligent Robots and Sys-

tems, pages 4547–4552.

SingularandNon-singularPathFollowingControlofaWheeledMobileRobotof(2,0)Type

275