Predicting Cases of Ambulatory Care Sensitive Conditions

W. Haque and D. C. Finke

Department of Computer Science, University of Northern British Columbia, Prince George, Canada

Keywords: Predictive Analytics, Ambulatory Care Sensitive Condition, Healthcare, Data Mining.

Abstract: Proper management of ambulatory care sensitive conditions does not only enhance patient care, but also

reduces healthcare costs by minimizing hospitalizations. In order to strategically allocate resources, it is

essential to rely on informed forecasting decisions. Among other factors, the healthcare data is deeply

affected by seasonality, granularity, missing information and the sheer volume. We have used the ten-year

history from a Discharge Abstract Database to build predictive models and perform multi-dimensional

analysis on key metrics such as age, gender, and demographics. The valuable insights suggest that

investments in some areas appear to be working and should continue whereas other areas suggest a need for

reallocation of resources. The results have been confirmed using two distinct time series models. The

forecasted data is integrated with existing data and presented to users through data visualization tools with

capabilities to drill down to reports of finer granularity. It is observed that though some diagnoses appear to

be on an upward trend in prevalence over the next few years, other ACSC-related diagnoses will continue to

occur with either the same or slightly less frequency.

1 INTRODUCTION

Ambulatory care sensitive conditions (ACSC) are

medical conditions such as hypertension, asthma,

diabetes, and COPD which are normally treatable in

an outpatient setting. Identification of

disproportionately high levels of ACSC cases in

specific regions, health service delivery areas

(HSDAs), or public demographics is key to reducing

health care costs and enhancing patient care; most

ACSC cases are preventable (Oster and Bindman,

2003) and do not require hospitalization (Brown et

al., 2001); (Schrieber and Zielinski, 1997). Many

variables affect the distribution of ACSC cases –

such as region, age, socioeconomic conditions and

availability of health services. These variables can

be difficult to identify because of the sheer quantity

of data and the raw format in which it is stored. Data

mining tools can be used to find these data patterns

and to forecast reliably. Examples include the

prediction of the number of cases into several years

in the future, the probability that a person fitting a

demographic set has an ACSC diagnosis, and more.

The external variables (such as new breakthroughs

in disease management or environmental factors

causing more significant disease symptoms) that

influence health care make predicting these metrics

challenging. The data mining algorithms based on

moving averages, linear regressions equations, and

seasonal patterns are designed to reduce the impact

of unknown and undetectable variables. Thus the

algorithms are capable of detecting trends in data

even when it contains a small percentage of outlying

data which could potentially skew the results.

Predictions that show a lack of disease treatment and

management performance (e.g. in a specific

community) will convince health care decision

makers to revisit areas that may have been neglected

but deserve attention.

2 RELATED WORK

It is the nature of ACSC that treatment differs from

normal inpatient care. Additional challenges are

often present such as the frequency of diagnoses

being made, which may be many over a short period

of time (Starfield et al., 1991). Examinations into

demographics and locales that experience higher

rates have been an interesting research in the health

care field. Observations include a higher rate of

ACSC occurrences in younger children and poorer

areas (Parker and Schoendorf, 2000). Research also

shows that non-Caucasian individuals tend to visit

Haque W. and Finke D..

Predicting Cases of Ambulatory Care Sensitive Conditions.

DOI: 10.5220/0004479800720079

In Proceedings of the 2nd International Conference on Data Technologies and Applications (DATA-2013), pages 72-79

ISBN: 978-989-8565-67-9

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

physicians for ACSC-related circumstances at a

lesser rate than Caucasian individuals. The

correlation between income and patient’s race

supports the notion that income is related to

accessibility and frequency of ACSC treatment in

potential patients (Lieu et al., 1993). Furthermore,

remote and aboriginal communities were observed

to have increased risk of complications with diabetes

(Booth et al., 2005). It is likely that other ACSC

diagnoses follow a similar pattern. The difference

between areas with a higher overall income and the

poorer areas may show a lack of health care access

for some people (Roos et al., 2005).

Time is a significant component in variations in

ACSC case data. In Ontario, between the years

1994-1999, acute complications of diabetes

decreased by roughly 6% per year (Booth et al.,

2005). In U.S., research into childhood asthma

showed an overall increase in visitations for the

ACSC disease between the years 1980-1998.

However, the data does show a recent stabilization

of the proportion of youth admitted for asthma

(Akinbami and Schoendorf, 2002).

Researching the causes of and situations for

ACSC cases is critical in improving a key health

care performance metric: Primary Health Care

(PHC). It has been identified by professionals that

improving PHC significantly improves the treatment

of ACSC and prevention of ACSC hospitalizations.

By looking for symptoms related to the onset of

ACSC, this pre-emptive care is most effective

(Caminal et al., 2004).

3 METHODOLOGY

The Discharge Abstract Database (DAD), consisting

of approximately one million rows and over seven

hundred sparsely populated columns, formed the

basis of this study. Upon pivoting, this yielded over

twenty-six million rows that were to be analyzed.

Earlier, we had used Business Intelligence (BI) tools

and techniques to efficiently analyze this database

and presented statistically significant trends and

patterns (Haque and Edwards, 2012). We have now

extended this study using advanced analytics for

developing predictive models. There are several

methods which can be deemed viable for predictive

analytics. Our data mining solution focuses

primarily on time-based mining and requires input

sets with equally distributed time slices. Mining

models for the identified metrics have been created

and trained individually for each dimension (or set

of dimensions) in order to attain maximum level of

accuracy. Microsoft SQL Server Analysis Services

(SSAS) tools are used to achieve our solution

(Microsoft Corp, 2013). Furthermore, separate

models are developed using the software R and its

various multivariate linear regression algorithms

(Gentleman et al., 2012).

Other available algorithms include Microsoft

Clustering, Decision Trees, Neural Networks, and

Linear Regression. The Clustering algorithm was

immediately invalidated because it did not support a

continuous type attribute (ACSC data is continuous

as opposed to discrete). While the other algorithms

could be used for our predictions, they would require

a mapping between the id fields in the date

dimension and integer values. Linear Regression

was the most applicable, because the input series for

our data was primarily based on increase and

decrease in number of cases. However, the

Microsoft Time Series algorithm is a special

implementation of a blend of the Linear Regression

algorithm and ARIMA. It is designed to operate with

date key values and simplifies the process of

forecasting over time ranges. As a result, time series

was our choice of data mining technique. This

technique allows use of a combination of the

proprietary Microsoft ARTXP algorithm and

popular ARIMA algorithm (MSDN, 2012).

As Microsoft Time Series does not supply

control over every variable used by ARTXP or

ARIMA algorithms, a comparison of our SSAS

results with those produced by R is used to enhance

our confidence and support the results of our data

mining solution.

3.1 Data Challenges

The data integrity issues encountered ranged from

formatting that prevents straightforward integration

into an existing cube structure to absence of data that

could have been a useful metric for forecasting. An

example of such data is the ethnicity of an individual

identified with ACSC.

3.1.1 Time Series Stationarity

A requirement of the ARIMA time series data

mining algorithm is stationarity of the input time

slices. “Stationarity has three components. First, the

series has a constant mean, which implies that there

is no tendency for the mean of the series to increase

or decrease over time. Second, the variance of the

series is assumed constant over time. Finally, any

autocorrelation pattern is assumed constant

throughout the series.” (Barao, 2008) In general, the

volatility of the health care data causes a lack of

PredictingCasesofAmbulatoryCareSensitiveConditions

stationarity. The process of differencing is used to

reduce or eliminate non-stationarity from the input

series. In both manual and automatic differencing

(done by time series implementation examining

autoregressive values) (MSDN, 2012), the

application of the differencing process cannot

resolve the externally influenced changes in input

series mean. Thus, increasing the levels of

differencing in ACSC data cannot redeem ARIMA

as useful for all model applications. As a result, we

are limited to the use of ARTXP time series

algorithm for several predictions.

Due to inherent seasonality in our ACSC data,

creating mining models at a finer granularity

becomes a greater challenge because finding a fitting

historic model curve becomes more difficult.

Trimming the input set of irregular data can help to

improve the generation of historic model.

3.1.2 Input Data Limitations

The input set for time series models should have a

large number of slices in order to create a strong

historic model and reduce the overall impact of

irregularities. In general, using between 32-40 time

slices is the minimum for an acceptable ARTXP

model. The existing set of ACSC data gives us 36

fiscal quarter slices. It is also critical that data is

supplied continuously through all periods – a lack of

data for an input slice means we must either

determine it as zero, or take the mean of previous

time slices, adding error. A similar problem exists

when the series is fully populated but the metric

values lack significant variation. This occurs more

frequently as data granularity becomes finer when

incorporating additional attributes.

Ethnicity has been observed to be a strong

influencer of the frequency and severity of ACSC

occurrences. The DAD, however, does not contain

any aggregations on ethnic demographics. As a

result, we cannot explore or forecast change in

ACSC in varying ethnic groups. We instead choose

to explore how changing gender and age

demographics will affect ACSC prevalence.

3.1.3 Conformed Date Dimension

Time series data mining predictions output their data

as a set of SQL rows split by attributes and future

time slices. An inconsistency exists between the way

SQL creates a date dimension and the way the time

series implementation creates future time slices in

fiscal quarters. The forecasting tool produces data

whose date fields progress in ¼ of a calendar year.

However, the Northern Health (NH) conformed date

dimension uses fiscal quarters aligning along

specific months. As a result, a mapping query is

needed to link the predicted data to the NH

conformed date dimension. The mapping query

prevents the quarter-year output from the mining

prediction from becoming offset from the proper

fiscal quarters.

3.1.4 Storing Forecasted Data

Output from mining model predictions in SSAS is

exported to a SQL table. We have two options when

storing: either update the existing prediction results

table or create a new one for the prediction. When a

large number of unique predictions are done, the

number of tables would become large with the latter

choice. This not only adds complexity to the cube

but additional tables require that SSAS data source

view must be updated for every new table; this

makes calculations more complex, involving

multiple separate relations’ fields as opposed to a

single standard field. Updating existing prediction

tables require distinguishing between sets of rows

using a key column. This solution results in longer

lookup times and increased space complexity, but

this is less of an issue in analytical work than it

would be in a transactional scenario. The cube is

only periodically processed; the lookup on the data

in the database only occurs when the DAD is

updated. As a result, we used a single table whose

rows are differentiated by the key.

4 DATA MINING/PREDICTIONS

The use of data mining functionality in SQL Server

requires creation of a mining structure (with models)

and preparation of two sets of data: a training set,

and a template set. The latter is required for

forecasting in the instance where partial future data

needs to be added to an existing model (such as in

the case of ACSC predictions based on future census

population) and consists of relations with arity and

domain equivalent to the model’s training data.

Training sets are needed for each unique collection

of dimensions used to slice the data.

The SSAS data mining tools support two modes

of creation: the model can be created on top of the

cube, or it can be created based on the corresponding

SQL database. The latter option requires special

formatting of the forecast output data. Though our

ultimate intent is to update the cube, having access

to the SQL database content gives us additional

control over the mining results. With results in SQL

DATA2013-2ndInternationalConferenceonDataManagementTechnologiesandApplications

rows, we can easily tie in new data with existing

data as well as split the data by arbitrary conditions.

Therefore, the SQL mode was a preferred choice for

use in our solution.

4.1 Preparation of Training Data

Our training data set consists of numbers of cases

and interventions over a given period of time.

Existing raw data resides in a SQL database from

where we gather appropriate dimensions for the

measures that are being forecast. Preparation of

training data can include any number of dimensions

and conditions. Each row with an ACSC flag in the

diagnosis table represents a unique case. By

aggregating on unique attribute groups, we can

obtain the number of cases belonging to those

groups. As we are working at the SQL level, we

must replicate the calculation for the measure in the

training query. Because each row in the diagnosis

fact table is considered a case, we can select a sum

of the number of rows where one or more of their

dimension parameters match. For example, we could

choose a count of rows where genders match. Thus,

the output set would consist of two columns; one

column specifies the gender, and the other displays

the number of rows/cases corresponding to that

gender. The output is stored in a temporary staging

table.

4.2 Training the Model

SSAS mining structures are used to process data

from the staging tables; the chosen algorithm learns

the patterns in the input data and enables forecasting

based on those patterns. Initially, a univariate

analysis was done. We considered the variations in

either number of ACSC cases or total cases when

divided by various attributes relevant to prescribed

time-based metrics. Eventually, population was

identified as an important predictor for a

multivariate analysis.

In SSAS, the data source view is prepared to

accept newly forecast data for cube processing

without additional configuration. The control

parameters used by the algorithm to learn the trends

in its input series are given in Table 1. The mining

model processes the data based on these values and

exports it as a series of SQL rows. By completing

the query process the raw output data can be

combined with other forecast data as well as DAD

data.

SSAS does not allow control over the algorithm

learning process past these parameters. Instead,

heuristic algorithms assist in determining the values

that compose the prediction algorithm’s equation.

This equation is based on the linear change in input

series as well as some constant variance values. In

case of ARIMA, the additional process of

differencing is used to get the best possible forecast

equation; SSAS deems the equation fitting when

stationarity is maximized. Using the mining model

viewer in SSAS, we examine the short-term results

of the forecast as well as how accurately the

historical model collection matches up with existing

data. Prediction results are exported to the SQL

database once the model is deemed acceptably

accurate.

Table 1: Model parameters.

Parameter

Property

Use

Mthly/Qtrly

value

FORECAST_

METHOD

Controls the algorithm used

by SSAS in forecasting

ARIMA or

ARTXP

HISTORIC_MODEL_

COUNT

Multiplier for historic

models

HISTORIC_

MODEL_GAP

Number of time slices each

historic model spans.

12 / 8

MINIMUM_SERIES_

VALUE

Series values cannot be

predicted below this

threshold (case counts

cannot be negative)

MISSING_ VALUE_

SUBSTITUION

Value used when points in

the middle of the series are

absent.

values (<10)

MEAN:

values (>10)

PERIODICITY_HINT Seasonality of data 12 / 4

4.3 Integrating Forecasted Data

In order to combine raw forecast data with existing

data in the cube, it needs to be assigned the

appropriate foreign keys for various dimensions.

Output strings are parsed for attribute members

found in dimension tables. A lookup is executed for

finding the key value that corresponds with the

attribute members and finally the data is inserted

into a table for completed predictions. An additional

key is used to identify the unique prediction fields;

for example, a different identifier key is used for a

prediction on the gender attribute than for prediction

on both gender and age group. This identifier

enables us to choose the right data from the cube for

visual reports.

Further examination of the accuracy of the

historical models is conducted by averaging

percentage difference for each time slice. In general,

mining models that generate historical prediction

values of less than 30% difference from the actual

values are accepted for use in deliverable reports.

PredictingCasesofAmbulatoryCareSensitiveConditions

ACSC cases

Predictions with few attributes tend to have

differences of less than 5-6%. Data is finally

formatted to be processed by the SSAS cube. New

entries in tables linked to forecasts and forecast-

related dimensions become a part of the cube. Upon

completion, the case count metrics can be split by

the unique prediction identifiers described above.

4.4 Data Visualization

Charts and tables enable users to easily observe

trends in the ACSC metrics; many charts are broken

down by fiscal quarters or fiscal years and show the

change in ACSC over time. Aggregations take place

at levels such as on diagnosis or locale. Data is

aggregated on diagnosis, institution, locale cluster,

HSDA/LHA, and discharge disposition.

4.4.1 Dashboard

The dashboard presents a high-level overview of the

ACSC data. Visualization of data at this level is not

filtered. Common attributes for slicing charts and

tables include diagnosis, age group, and gender. The

users can select up to 5 years into the future. A user

may choose to exclude historical data, forecasted

data, or any combination. Forecast information in

the chosen future period is clearly identified, either

by a description or by an alternate colour. Tooltips

offer additional details on series seen in charts.

Other reports include metrics broken down by

ACSC diagnoses, Discharge Disposition, and ACSC

prevalence by geographic clusters/location.

4.4.2 Other Reports

The drilldown reports provide information about the

core ACSC metrics at a finer granularity. New

information on various charts is displayed in the

same manner as the dashboard, wherever predictions

for the attributes present in those charts produced

results with acceptable accuracy. Users can choose

to filter data by members of the corresponding

attribute, as well as the specified time period. As

explained earlier, forecasting results become

increasingly sparse as more attributes are introduced.

For the sake of space, the dashboard or other

drilldown reports are not included in this paper.

5 ANALYSIS OF RESULTS

In this section, we present some observations from

each of the models developed in SSAS and R,

closeness of results between the two, and significant

trends found from the data forecast by each

corresponding mining model. We have selected the

most representative results from our study.

5.1 Quarterly vs. Monthly Aggregation

The first noticeable result is the quality of forecasts

when using monthly vs. quarterly aggregation of

data. Both SSAS and R models result in higher

quality predictions when using quarterly

aggregation. This is observed by examining R’s

AIC, AICc, and BIC values which determine the

ideal fit from a pool of candidate models. AIC

represents the amount of information suspected to

have been lost by the model. BIC values operate in

the same manner as AIC, but incur a more

significant penalty when additional attributes are

included in the model. This helps to prevent

overfitting to the training data. We use these values

as a confidence measure for R’s models.

The label associated with R models comes in the

form ARIMA(0,0,0)(0,0,1)[12] (Figure 1). It is a

representation of the equation used by ARIMA for

generating the model. The two tuples in parentheses

imply that the model combines two equations. The

first index in a tuple is the number of regressive

terms, the second is the number of deviations in the

series that do not follow a seasonal pattern, and the

last is the lagged forecast error in the equation.

Finally, the label “[12]” implies the model’s

seasonality, which in this case is monthly.

Figure 1: Monthly ACSC count forecasts produced by R.

In Figure 1, values prior to 2010 are data from

DAD. The data beyond 2010 shows predicted metric

values by the ARIMA algorithm and the bands

around this line represent the 85% and 90%

confidence levels. The values of AIC, AICc, and

BIC are 504.96, 505.19, and 513.01, respectively. A

higher value of these metrics implies a lower relative

quality of forecast. Relatively, these values are high

DATA2013-2ndInternationalConferenceonDataManagementTechnologiesandApplications

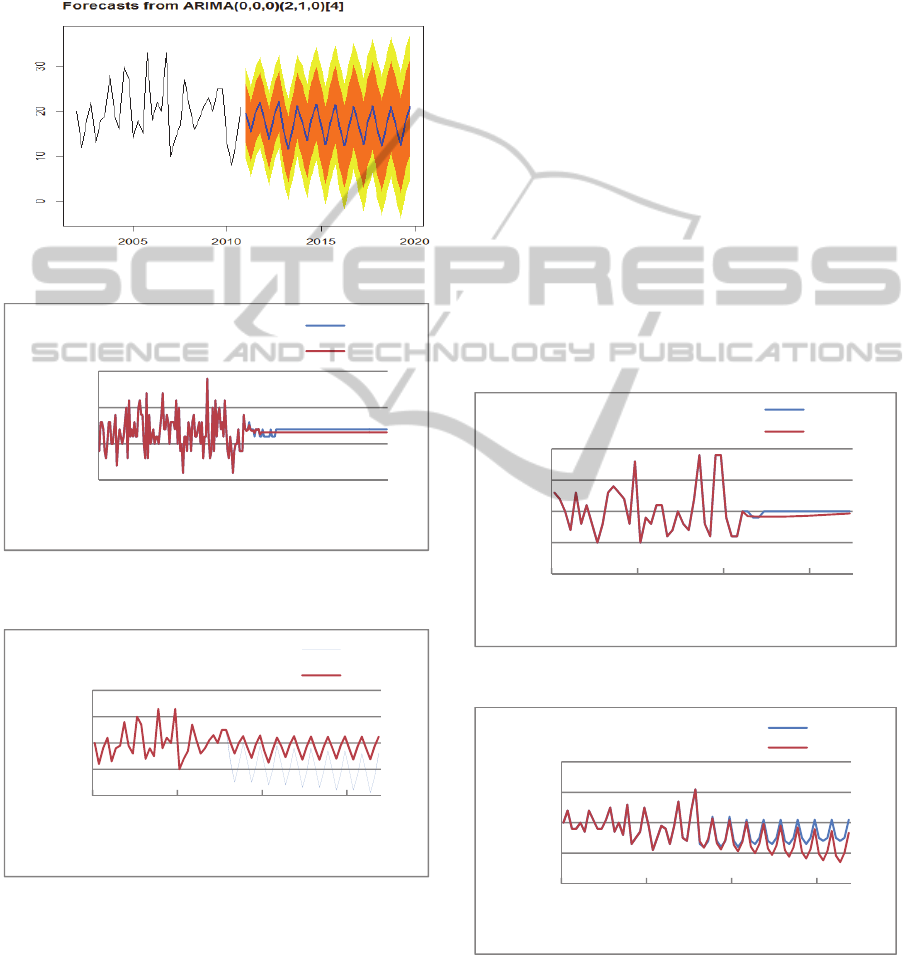
and therefore the level of confidence in this model is

low. An additional observation in this chart is the

absence of any variation in the predicted period.

This commonly occurs when the input series does

not have strong seasonality – as a result, the

algorithm resorts to detecting a mean of the series.

Figure 2: Quarterly ACSC cases forecast produced by R.

Figure 3: Monthly ACSC cases forecast by SSAS and R

models.

Figure 4: ACSC cases forecast by SSAS and R models.

Figure 2 shows the same metrics using quarterly

data due to much more pronounced seasonality. This

results in improved AIC, AICc, and BIC values

(roughly 200 each) and a forecast that retain

seasonal trends; the peak in forecast values is at the

quarter of each fiscal year. The corresponding

results from our SSAS models are shown in Figure 3

and Figure 4; similar trends were observed.

5.2 Reducing the Number of Attributes

An experiment separating the genders produced

significant variation between the predicted values.

For example, it was observed that the male category

in 30-39 age group showed a poor forecast of

seasonality from both the R and SSAS models

(Figure 5). Though both models were unable to

detect and represent the quarterly seasonal pattern,

the values of AIC, AICc, BIC in the R model were

204.96, 205.32, and 208.13, respectively. These

values, relative to our other successful predictions,

show that the model has a good degree of accuracy.

For this age group, the forecast results were

significantly improved when the male and female

input sets were combined and forecasted on (Figure

6). Both SSAS and R models created forecasts with

strong seasonality and both produced nearly

identical output. AIC, AICc, and BIC values of

approximately 195 show a close fit to DAD data in

the R model.

Figure 5: ACSC cases forecast for 30-39 yr males.

Figure 6: ACSC cases forecast for all 30-39 yr old.

Figure 7 shows the breakdown of ACSC actual

and predicted data (4 year into the future) with only

the gender attribute. This scenario resulted with a

2001 2006 2011 2016

ACSCCases

Timebymonth

11‐19yrs

SSAS

2002/03 2007/08 2012/13 2017/18

ACSCCases

FiscalQuarters

11‐19yrs

SSAS

2002/03 2006/07 2010/11 2014/15

ACSCCases

FiscalQuarters

30‐39yrs‐ M

SSAS

2002/03 2007/08 2012/13 2017/18

ACSCCases

FiscalQuarters

30‐39yrs

SSAS

ACSC cases

PredictingCasesofAmbulatoryCareSensitiveConditions

very acceptable confidence level of 89.5%. This also

demonstrates that predicting on the aggregated case

count produces a more accurate forecast.

Figure 7: Quarterly ACSC cases forecast by gender.

5.3 Some observed Trends

Accurate forecasting of ACSC metrics allows

management to make informed decisions on the

choice of future healthcare strategies instead of

making simple extrapolations from past data.

Sample Observation 1. As an example, Figure 8

identify the 70-75 year old as an age group in which

overall ACSC frequency is on the decline.

Following a spike at around 2007, our models

project a consistent decrease in ACSC occurrence.

Because the forecasting models are heavily

influenced by more recent events, the actual

decrease may not end up being as sharp as the

forecast. However, this does promote the idea that

existing activities designed for improving the ACSC

care of seniors have helped and will continue to help

that group.

Sample Observation 2. In recent years, the number

of ACSC cases in the Region 1 (Figure 9) has stayed

higher than the period around year 2004. Data

predicted by our models suggests that while the

ACSC numbers may stabilize at their current levels

for a couple years, the yearly average trend should

begin to return to previous levels after 2-3 years.

However, though the yearly cases on average will

begin to decline, 4

quarter spikes in ACSC will

remain. Region 2 occurrences (Figure 10) will

continue to remain reasonably high after identifying

a recent increase in their prevalence. Earlier time

slices have influenced the model such that the

expected threshold will not be as extreme as the

2008 peak.

Sample Observation 3. The overall number of ACSC

cases in all groups and diagnoses (Figure 11)

appears to remain constant over the forecast period.

In the chart, a diagnosis category with a historical

value approximately twice the forecast value is one

whose ACSC count per year has not changed (the

historical period is twice the forecast period). Within

these counts, COPD and Diabetes appear to be on a

slight increase in prevalence over the next 5 years

and other ACSC-related diagnoses will continue to

occur with either the same or slightly less frequency.

Figure 8: ACSC cases forecast for 70-75 yr females.

Figure 9: Historical and Forecasted Quarterly ACSC cases

in Region 1.

Figure 10: Yearly ACSC prevalence as a percentage of

population in Region 2.

Figure 11: ACSC cases in each diagnosis (2002-2010,

forecast to 2015).

100

200

300

400

2002/03 2007/08 2012/13

ACSCCases

FiscalQuarters

Allcases

2002/03 2006/07 2010/11 2014/15

70‐75yrs‐ F

SSAS

ACSCCases

FiscalQuarters

DATA2013-2ndInternationalConferenceonDataManagementTechnologiesandApplications

6 CONCLUSIONS

Data mining tools have been applied to ACSC data.

The resulting predictions have identified both, areas

and groups that need attention and those that are

headed in a positive direction. Because of the

inconsistent nature of health-related data, these

trends are more reliable when data is aggregated.

Despite this limitation, improvements to the health

care system can be targeted towards high-impact

locations and critical demographic groups identified

by our predictive models. COPD and Diabetes

diagnosis groupings appear to be on the rise and

require additional health care focus. Conversely,

population such as the 70-75 age group may be

receiving adequate treatment thus decreasing the

morbidity of these cases. Visualizations methods

provide a clear and easy to understand interface for

correctly distinguishing factual existing data and

predicted/forecasted data. The reporting tools offer

drill-down capabilities for further insight into any

desired set of existing and forecasted information

over specified time ranges. The models developed

offer a strong confidence level where stable

forecasting of ACSC-related health data is possible.

The SSAS environment was confirmed as an

effective means of creating forecasting models for

the ACSC data by observing similar results with R.

As a result, SSAS was deemed a beneficial tool for

creating a data mining solution for ACSC as it

simplified the task of designing mining structures

and models without the need for statistics expertise.

The reporting is also more intuitive and interactive.

The tight integration with the existing analytics cube

further centralized the task of data mining and

incorporation of new data into the data warehouse.

ACKNOWLEDGEMENTS

This research was funded by Northern Health, BC

under the Innovation & Development Commons

Program. The authors extend their sincere

appreciation for the support and guidance provided

by Michel Aka and Dr. Bill Clifford of Northern

Health in access/interpretation of data, validation of

results and completion of this research.

REFERENCES

Akinbami, L. J. & Schoendorf, K. C., 2002. Trends in

Childhood Asthma: Prevalence, Health Care

Utilization, and Mortality. Pediatrics, 1 August,

110(2), pp. 315-322.

Barao, S. M. M., 2008. Linear and Non-Linear Time

Series Analysis: Forecasting Financial Markets, s.l.:

Instituto Superior de Ciencias do Trabalho e da

Empresa.

Booth, G. L., Hux, J. E., Fang, J. & Chan, B. T., 2005.

Time Trends and Geographic Disparities in Acute

Complications of Diabetes in Ontario, Canada.

Diabetes Care, May, 28(5), pp. 1045-1050.

Brown, A. et al., 2001. Hospitalization for Ambulatory

Care-Sensitive Conditions: A Method for Comparative

Access and Quality Studies Using Routinely Collected

Statistics. Canadian Journal of Public Health, April,

92(2), pp. 155-159.

Caminal, J. et al., 2004. The role of primary care in

preventing ambulatory care sensitive conditions.

Public Health, 14(3), pp. 246-251.

Gentleman, R., Ihaka, R. & et. al., 2012. The R Project for

Statistical Computing. [Online]

Available at: http://www.r-project.org/

[Accessed 12 November 2012].

Haque, W. & Edwards, J., 2012. Ambulatory Care

Sensitive Conditions: A Business Intelligence

Perspective. York, Canada, s.n., pp. 31-39.

Lieu, T. A., Newacheck, P. W. & McManus, M. A., 1993.

Race, ethnicity, and access to ambulatory care among

US adolescents. American Journal of Public Health,

July, 83(7), pp. 960-965.

Microsoft Corp, 2013. Business Intelligence. [Online]

Available at: http://www.microsoft.com/en-us/bi/

MSDN, 2012. Microsoft Time Series Algorithm Technical

Reference. [Online]

Available at: http://msdn.microsoft.com/en-

us/library/bb677216.aspx

[Accessed 7 September 2012].

Oster, A. & Bindman, A., 2003. Emergency Department

Visits for Ambulatory Care Sensitive Conditions:

Insights into Preventable Hospitalizations. Medical

Care, 41(2), pp. 198-207.

Parker, J. D. & Schoendorf, K. C., 2000. Variation in

Hospital Discharges for Ambulatory Care-Sensitive

Conditions Among Children. Pediatrics, 1 October,

106(3), pp. 942-948.

Roos, L., Walld, R., Uhanova, J. & Bond, R., 2005.

Physician Visits, Hospitalizations, and Socioeconomic

Status: Ambulatory Care Sensitive Conditions in a

Canadian Setting. HSR: Health Services Research,

August, 40(4), pp. 1167-1185.

Schrieber, S. & Zielinski, T., 1997. The Meaning of

Ambulatory Care Sensitive Admissions: Urban and

Rural Perspectives. The Journal of Rural Health,

13(4), pp. 276-284.

Starfield, B., Weiner, J., Mumford, L. & Steinwachs, D.,

1991. Ambulatory care groups: a categorization of

diagnoses for research and management. Health

Services Research, 26(1), pp. 53-74.

PredictingCasesofAmbulatoryCareSensitiveConditions