
A Bayesian Approach to Modeling Dynamical Systems in the Social
Sciences
Shyam Ranganathan
1
, Viktoria Spaiser
2
and David J. T. Sumpter
1,2
1
Department of Mathematics, Uppsala University, Uppsala, Sweden
2
Institute for Futures Studies, Stockholm, Sweden
Keywords:
Bayesian Methods, Model Selection, Dynamical Systems, Mathematical Modeling, Social Sciences.
Abstract:
The paper presents a new modeling approach using longitudinal or panel data to study social phenomena
and to make predictions of dynamic changes. While the most common way in social sciences to study the
relations between variables is using regression, our modeling approach describes the changes in variables as
a function of all included variables, using differential equations with polynomial terms that capture linear
and/or nonlinear effects. The mathematical models represented by these differential equations are derived
directly from data. The models can then be run forward to forecast future changes. A two-step model-fitting
approach is applied to identify the best-fit models and included visualisation methods based on phase portraits
help to illustrate modeling results. We show this approach on an example relating democracy to economic
growth.
1 INTRODUCTION
Since the 1960s when James S. Coleman published
his book an mathematical sociology (Coleman, 1964),
sociologists and other social scientists have been
working on mathematical modeling of social phe-
nomena. However, it is only recently with the avail-
ability of increasing computational power and sophis-
ticated modeling tools that the field of mathematical
social sciences is beginning to flourish. Mathemati-
cal modeling can be used both to study macro-level
phenomena (Saperstein, 2000; Ashimov et al., 2011;
Weber, 2012) as well as interactions at the micro-level
(Coleman, 1964; de Marchi, 2005).
A widely adopted way of mathematically model-
ing relations between two or more variables is the re-
gression equation, with the dependent variable y and
the independent variable or predictor x (in case of a
multivariate regression x1, x2, ... represent the differ-
ent independent variables), intercept β
0
, slope β
1
(in
case of a multivariate regression β
1
, β
2
, ... represent
the different slopes related to the different predictors)
and error term ε with i....n observations.
y
i
= β
0
+ β
1
x
i
+ ε
i
(1)
y
i
= β
0
+ β
1
x1
i
+ β
2
x2
i
+ ... + ε
i
(2)
Data is used to estimate these equations and the
strength of the relations. This approach can be ex-
tended to quite complex and sophisticated statistical
models (Wooldridge, 2010). Such approaches are
necessary to get a better understanding of social pro-
cesses, but they have two limitations in the way they
relate to the reality of social processes.
The starting point to empirical modeling is usu-
ally a social science theory, which tells the researchers
what variables are to be considered and how they are
expected to relate to each other in terms of cause-
effect relationships (Treiman, 2009; Ostrom, 1990;
Lewis-Beck, 1995). The purpose of the empirical
modeling is then primarily theory testing and revising
theories. While these are important parts of doing so-
cial science research, theoretical models usually need
to be continuously tuned to account for data patterns.
Secondly, empirical modeling in social sciences
does not always sufficiently take into account the fact
that social systems are complex and dynamic. The
most common way to study the interaction between
variables is to compute linear or logistic regressions
(Ostrom, 1990; Menard, 2001; Andersen, 2007). But,
irrespective of the specific models used, the interpre-
tation of results is most often static.
We suggest a novel approach to empirically based
mathematical modeling in social science. Our data-
driven Bayesian modeling approach uses the data it-
self to inform model selection from a pool of feasible
models. While traditionally a regression of one vari-
125
Ranganathan S., Spaiser V. and J. T. Sumpter D..
A Bayesian Approach to Modeling Dynamical Systems in the Social Sciences.
DOI: 10.5220/0004480901250131
In Proceedings of the 3rd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2013),
pages 125-131
ISBN: 978-989-8565-69-3
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

able on another is performed, we model the changes
in one variable as a function of all included vari-
ables (explained in Methods section below). Differ-
ential equations represent the mathematical models
of a variable’s change in time. We define a set of
polynomial terms that express various possibilities of
how variables may interact, allowing non-linear ef-
fects and build a model using Ordinary Least Squares
(OLS) regression with these polynomial terms. The
differential equation and therefore the mathematical
model consists then of one or more of those polyno-
mial terms that best describe the change in the vari-
able as a function of itself and/or included predictors.
A two step model fitting, using the maximum like-
lihood approach and the Bayes factor, is then used to
look at how closely any candidate model fits the avail-
able data.
Compared to the theory-testing approach, ours
is an exploratory modeling approach. Such an ex-
ploratory approaches in social sciences may help to
find new and unexpected patterns and explanations
(Gelman, 2004; Stebbins, 2001; Tukey, 1977). This
explorative approach is not completely a-theoretical,
since theories still suggest which variables we investi-
gate. But instead of defining how the variables should
interact and then testing this pre-defined relation in
the data, we allow the data to inform us about the
mathematical linear or non-linear relationships be-
tween the variables.
Our methodologycan be applied to any social sys-
tem which has reasonable amounts of longitudinal or
panel data, that is data with repeated measurement
over time. On the macro-level the method can be used
to study cross-national development dynamics, for in-
stance, the relationship between a country’s gross do-
mestic product, child mortality and education levels.
If regional or city district data is available it is pos-
sible to use the method to study for instance neigh-
bourhood segregation processes. On a meso-level the
researched entities could be organisations, companies
or schools, to study, for instance, dynamic female
employment patterns of companies. Finally, the ap-
proach is applicable to micro-level data like register-
based data or panel-data to study social phenomena
on the individual level.
We present first a discussion of the statistical
method used in our approach in the next section and
then give a simple example, applying the method to
study the interaction of GDP per capita and democ-
racy for a set of 189 countries from 1980 to 2006.
Along with the paper, we present an R package
(Bayesian Dynamical System Model, bdsm, to be
found on CRAN http://cran.r-project.org) that imple-
ments this novel mathematical modeling approach
and that will allow researchers to apply our method
to their specific research field. Future predictions and
policy suggestions, which are important components
for the study of social phenomena, can also be gen-
erated using this method and therefore using our R
package.
2 METHODS
Suppose that we are studying a social system with
N indicator variables x
i
, i = 1, ..., N. Let us assume
that we have longitudinal or panel data for the N vari-
ables for M entities (such as individuals, countries,
organisations etc.) over a length of time T. Let us
denote the data as x
j
i
(t) and the changes in the vari-
ables over a time period as dx
j
i
(t) = x
j
i
(t + 1) − x
j
i
(t),
where j = 1, ..., M and t = 1, ..., T. We use this data to
construct what is called a phase portrait of the system.
2.1 Phase Portrait
In dynamical systems theory, a phase portrait refers
to a plot of the evolution of two variables with re-
spect to each other (Strogatz, 2000). For example, in
a system with only two variables x
1
and x
2
(and for
only 1 individual, say), the phase portrait would refer
to a plot of x
2
(t) against corresponding x
1
(t). This
plot shows the co-evolution of the two variables, and
the phase portrait itself can be represented mathemati-
cally using Ordinary Differential Equations (ODE) as
dx
1
dt
= f
1
(x
1
, x
2
),
dx
2
dt
= f
2
(x
1
, x
2
) for some appropriate
functions f
1
and f
2
. Note that when we have discrete
data, we need to use difference equations instead of
differential equations. Here we assume that the dis-
crete data are the result of sampling from continuous
functionsand hence the ODEs represent the same pro-
cess from which the corresponding discrete data can
be obtained by suitable sampling.
Since the differential equations hold for any value
of x
1
and x
2
, we could look at all the possible trajec-
tories of the two variables starting at any point. Thus
we can think of the available panel data with many
individuals as corresponding to the different trajec-
tories obtained in the same system but with different
initial conditions. Thus in our modeling approach, we
look at the data phase portrait, where we look at the
changes in the indicator variables dx
i
(t) as a function
of the values of all the variables {x
i
(t)} (or the current
’state’ of the system).
We abstract individual entities as different initial
conditionsin the system trajectory. In other words, we
assume that any individualentity on reaching a certain
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
126

‘state’ (represented by a unique set {x
i
(t)} ) will ex-
perience the same effect, albeit with some additional
noise. This approach may of course be problematic
in studies that emphasise the differences between dif-
ferent entities and hence their different development
trajectories (for example, the economic model in the
communist Soviet Union was fundamentally differ-
ent from that in the United States during a large part
of the twentieth century). However the current ap-
proach provides a ’mean-field’ approximation to the
basic underlying process in all cases.
2.2 Model Selection
In general, if we take f
i
to be polynomial of suffi-
ciently high degree (including products of variables),
so that we can model any general non-linearity in the
system. For most applications we assume that the
functions are polynomial in the indicator variables
with each term being of degree −1, 0, 1 in the vari-
ables or a product of such terms. We also allow for
terms that are quadratic in the variables. This keeps
the number of models to evaluate sufficiently small
for computational purposes. The terms comprising
products of variables capture non-linearities in the
system, which can occur due to interactions. These
higher order terms can typically result in multi-stable
states, which are characterisitic of realistic social sys-
tems. Moreover, because we include both degree -1
and degree 2 terms the resulting models are cubic. In
this current study, we assume that any further non-
linearities due to degree 3 or higher order terms are
relatively negligible, but this has to be tested on a
case-by-case basis depending on the particular system
being modeled. Our R-package provides the option to
include order 3 polynomial terms.
In our standard implementation of a two variable
model, we look at functions containing one or more
of the following terms:
f
1
(x
1
, x
2
) = a
0
+
a
1
x
1
+
a
2
x
2
+ a
3
x
1
+ a
4
x
2
+
a
5
x
1
x
2
+
a
6
x
2
x
1
+
a
7
x
1
x
2
+ a
8
x
1
x
2
+ a
9
x
2
1
+ a
10
x
2
2
+
a
11
x
2
1
+
a
12
x
2
2
There are 13 models with one term and, in general,
13
m
, models with m terms that describe the relations
between the two variables included in the model.
In the first stage of our fitting process, we aim to
rapidly narrow our search by finding the maximum-
likelihood model for each possible number of terms,
m. We fit the yearly samples of the yearly changes
in the indicator variables using multiple linear re-
gression over all 8, 192 possible functions f
1
(x
1
, x
2
)
consisting of the polynomial terms shown above. For
each possible number of terms we find the model
with the greatest likelihood (equivalently the model
that minimises the sum of squared errors with the
observed data). We repeat the same process to obtain
the best possible f
2
(x
1
, x
2
) and use the log-likelihood
value to rank the different models.
In general, the log-likelihood of the best fit for dx
i
models with m terms is
L
i
(m) = logP(dx
i
|x
1
, ...x
N
, m, φ
∗
i,m
) (3)
where φ
∗
i,m
is the set of unique parameter values ob-
tained from the best fit regression out of all of the
13
m
models with m terms. Assuming that the actual
observations are due to the underlying model with ad-
ditional Gaussian noise, L
i
(m) is the logarithm of the
error sum of squares (ESS) scaled by the variance
(Bishop, 2006). The log-likelihood value is also di-
rectly related to the coefficient of determination or the
R
2
value as R
2
= 1−
ESS
N
obs
∗Data variance
.
2.3 Bayes Factor
An important question about the robustness of par-
ticular models is why we choose a particular num-
ber of terms. For polynomial function fitting L
i
(m) ≥
L
i
(m − 1), that is the maximum likelihood is mono-
tonically increasing with additional terms, since each
term allows an extra degree of freedom on curve fit-
ting. For a finite data set this extra degree of free-
dom can fit artifactual patterns due to noise. As a re-
sult, reliance on L
i
(m) alone can lead to overfitting
the data by selecting too many terms and thus accept-
ing a model that accurately fits the existing data but
that generalises poorly to unseen data and has little
predictive power.
To address this problem and evaluate the fit of
these models we adopt a Bayesian approach. We cal-
culate the Bayesian marginal-likelihood or evidence
B(m) for the set of models which have the largest log-
likelihood within their respective number of terms.
Note that ‘Bayes factor,’ which refers to a ratio of
model likelihoods is used in Bayesian literature to
compare pairs of models (Robert, 1994). We use
the same term in this paper to refer to the Bayesian
marginal likelihood as defined above, with the un-
derstanding that this quantity would have the same
function as the Bayes factor when comparing between
more than two models.
The Bayes factor compensates for the increase in
the dimensions of the model search space by integrat-
ing over all parameter values, i.e.,
B
i
(m) =
Z
φ
i,m
P(dx
i
|x
1
, ..., x
N
, m, φ
∗
i,m
)π(φ
i,m
)dφ
i,m
(4)
ABayesianApproachtoModelingDynamicalSystemsintheSocialSciences
127

The Bayes factor is thus the likelihood averaged over
the parameter space with a prior distribution defined
by π(φ
i,m
). We choose a non-informative prior distri-
bution (Ley and Steel, 2009). For example, π(φ
i,m
)
can be chosen to be uniform over the range of pa-
rameter values. This range of values is chosen to in-
clude all feasible values but to be small enough for
the integral to be computed using Monte Carlo meth-
ods. B
i
(m) is computationally expensive to calculate,
even for models with a small number of terms. There-
fore we first identify the best fit model for each num-
ber of terms using maximum-likelihood,since models
of equal complexity can be more fairly evaluated in
terms of their maximum likelihood. We then compare
those selected in terms of the Bayes factor to fairly
compare models of varying complexity.
2.4 Correlated Errors
Calculating the best fit regressions for dx
i
indepen-
dently, as we do above, is equivalent to assuming that
the errors in the differential equations are uncorre-
lated. In fact, there is a possibility that the errors are
correlated due to any systematic reason causing the
errors, for example the same omitted variable. In so-
cial systems this may be more likely the norm than the
exception. In this case we have to include an error co-
variance matrix in our approach and use a generalised
least squares approach to finding the regression coef-
ficients. If the error covariance matrix is almost diag-
onal with off-diagonal elements negligible compared
to the diagonal elements, this reduces to the ordinary
least squares approach used here.
To test if the errors are in fact significantly corre-
lated, we use the “seemingly unrelated regressions”
approach (Amemiya, 1985). For example, in the two
variable case, the two regressions for dx
1
and dx
2
are
first performed under the assumption that the errors
are in fact uncorrelated. We then estimate an error co-
variance matrix from the model suggested by this first
step and the data, and use it to estimate the param-
eters based on a generalised least squares approach.
This process may be iterated until the true param-
eters are obtained. If the covariance matrix is “al-
most” diagonal, indicating that error terms are uncor-
related, the parameters estimated by the “seemingly
unrelated regressions” approach will not differ signif-
icantly from the parameters obtained assuming uncor-
related errors. If not, we haveto account for the differ-
ence in our calculation of Log-likelihood values and
Bayes factor using an algorithm that uses the error co-
variance matrix in its calculations.
2.5 Model Complexity
When generating data-driven models, it is important
to have a handle on model complexity. Specifically, in
systems with many variables, model complexity is de-
cided both by the number of terms used in the model
and by the number of explanatory variables used in
each differential equation. For example, in three vari-
able models we would like to determine whether or
not we require all of these variables to model the rates
of change of each variable. To do this, we calculate
Bayes factor for models including all three indicators
and compare them to those including just pairs of in-
dicators. For three indicators there are now
33
m
mod-
els with m terms and we generally restrict our analysis
to those with up to m = 5 terms. By plotting B
i
(m) for
three variable models as a function of m and compar-
ing this to B
i
(m) for two variable models we can as-
sess the utility of adding a third explanatory variable
to the model.
Similarly, our algorithm weights all possible mod-
els equally and evaluates their log-likelihood and
Bayes factor values. But for systems with many vari-
ables, there are just too many models available even
with the polynomial restriction. This makes the task
computationally impossible. To resolve this problem,
we can resort to a pruning algorithm which looks at
models with increasing number of terms. In each
stage, only the top M models survive, and in the next
stage only the ’descendants’ of these models - models
which are the same as the M survivors from the previ-
ous stage except for an additional term - are evaluated.
This keeps the number of feasible models evaluated in
each step of the algorithm reasonable while a suitable
value of M, say 10, 000 will make sure that most fea-
sible models are always tested.
3 APPLICATION
To give an example of an application of our ap-
proach, let us investigate a frequently studied macro-
level phenomenon. Political scientists have been dis-
cussing the correlation between a country’s GDP and
the level of democracy for 50 years while drawing a
wide variety of conclusions (Lipset, 1959; Diamond
and Marks, 1992; Barro, 1999; Boix and Stokes,
2003; Krieckhaus, 2003). The correlation between
GDP per capita and democracy is usually represented
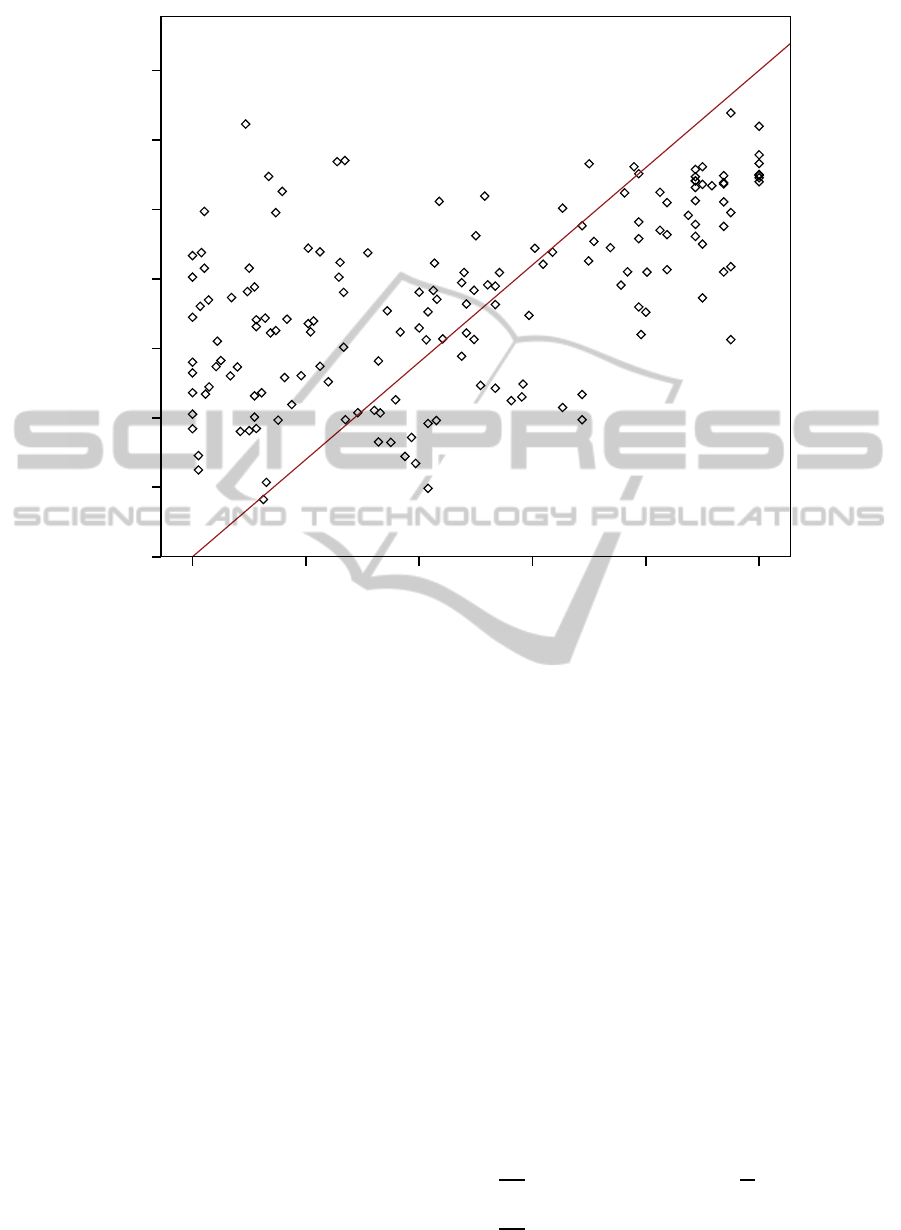
in scatter plots like in Figure 1.
Having longitudinal data allows to estimate
various sophisticated panel regression models
(Wooldridge, 2010). The most common ones are
fixed effect (Allison, 2005) and random effect
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
128
Democracy
1.00.80.60.40.20.00
log GDP per capita
12.00
11.00
10.00
9.00
8.00
7.00
6.00
5.00
2006
Quatar
United Arab
Emirates
Kuwait
Bahrain
Saudi
Arabia
Oman
Lybia
Zimbabwe
Myanmar
Morocco
Mexico
Liechtenstein
Norway
Mali
Liberia
Sierra Leone
Namibia
Nicaragua
Sao Tome
Congo
Kiribati
USA
Greece
South Korea
Bulgaria
Botswana
Kazachstan
Israel
Slovakia
Costa Rica
Poland
Vanautu
Kenya
Figure 1: The figure shows a correlation scatter plot for GDP per capita and democracy in the year 2006 for 189 countries. The
democracy index is based on Freedom House civil and political rights scores weighted for the actual human rights situation
(based on Cingranelli/Richards Human Rights data project) in the respective countries (Welzel, 2013). Most of the outliers at
the bottom right are oil-rich Middle East countries with high GDP but low democracy levels.
models (Laird and Ware, 1982). In these regression
analyses lagged or difference variables are used
as dependent variables to predict the value or the
difference of the independent variable at some later
point in time (Wooldridge, 2010). Autoregressive
(ibid.), two-stage least-square (Garson, 2013) and
simultaneous equation models (Wooldridge, 2010)
are further elaborated model specifications. There are
also non-linear versions panel regression models, like
logit regression models (ibid.).
In the analysis of GDP per capita and democracy
Barro (1996, 1999) used for instance a panel regres-
sion models with roughly 100 countries between 1960
and 1990 with GDP growth rates (difference vari-
ables) over three periods (1965-75), (1975-85) and
(1985-90) as dependent variables in an instrumen-
tal variable estimation approach with amongst others
democracy as predictor. He also computed regres-
sion models with average democracy levels (1965-
74),(1975-84) and (1985-94) with amongst others
lagged GDP levels as predictors. Performing these
panel analysis, Barro concludes that while democ-
racy has no significant direct effect on GDP per capita
growth, GDP per capita has a significant positive ef-
fect on democracy (Barro, 1996).
As suggested by Figure 2 there is a general linear
growing tend for both GDP and democracy. How-
ever, from this general trend it is difficult to make any
reasonable conclusions about the dynamical interac-
tion of economy and democracy. More recent analy-
sis (Boix and Stokes, 2003; Krieckhaus, 2003) indeed
suggest that the relation between GDP and democracy
might be rather a non-linear and dynamic one. When
we create a phase portrait for GDP and democracy
the non-linearity and dynamics of their interaction be-
comes clear (see Figure 3).
Our analysis approach with data from 1980 to
2006 would result in these two best-fit mathematical
models for democracy’s change as a function of GDP
and democracy itself and for GDP’s change as a func-
tion of democracy and GDP itself:
dD
dt
= 0.0003G
2
− 0.4031
D
G
(5)
dG
dt
= 0.0246D+ 0.0017G− 0.0002G
2
(6)
ABayesianApproachtoModelingDynamicalSystemsintheSocialSciences
129
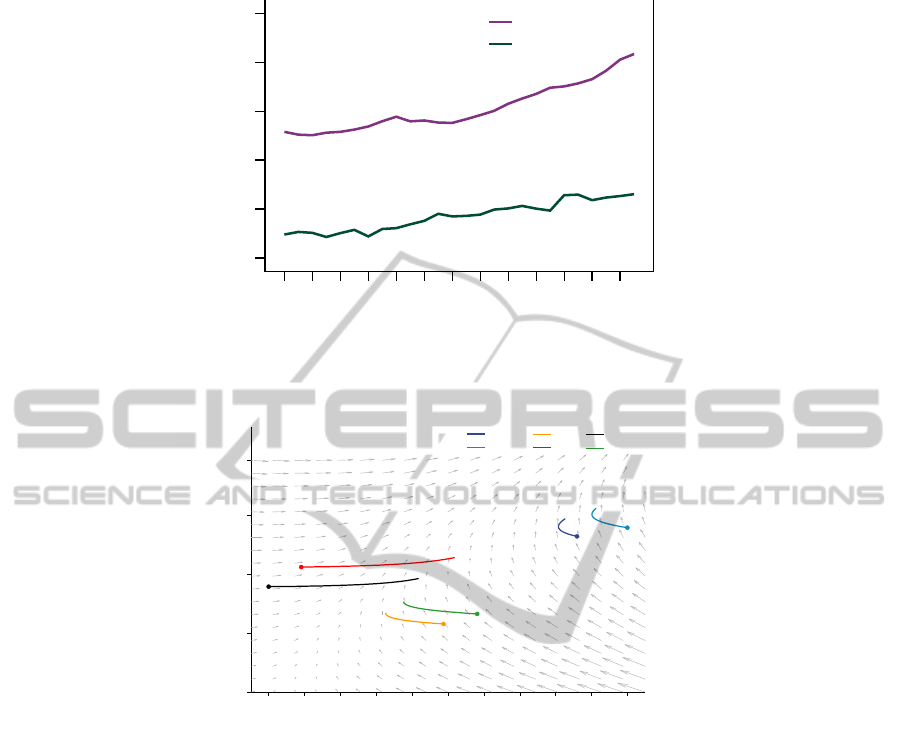
year
2005
2003
2001
1999
1997
1995
1993
1991
1989
1987
1985
1983
1981
Value
1.2
1.0
0.8
0.6
0.4
0.2
Democracy
GDP(rescaled)
Figure 2: Sequence chart with average (all countries) rescaled GDP and average (all countries) democracy in a time line
between 1981 and 2006.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
5
7
9
11
13
Democracy
GDP
Italia
Sweden
India
Chile
Albania
Nigeria
Figure 3: Visualisation of a phase portrait: changes in democracy values (x-axis) against log GDP (y-axis). The vector field
shows average change according to the model, while the coloured lines give changes in representative countries as predicted
by the model given initial conditions in 1980. Specifically, the ODE model is integrated forward to 2006 for each country
starting with the actual initial condition for the corresponding country in 1980. The democracy index is based on Freedom
House civil and political rights scores weighted for the actual human rights situation (based on Cingranelli/Richards Human
Rights data project) in the respective countries.
The symbiotic interaction of these two variables,
economy and democracy, produces an interesting de-
velopment pattern in the phase-portrait figure (see
Figure 3). It seems countries typically head towards,
what in dynamical systems is called, a stable man-
ifold. Countries begin either side of this manifold,
some with high democracy and low GDP, others with
low democracy and high GDP. Over time the coun-
tries move to a common trajectory moving from bot-
tom left to top right of the phase plane. These results
can explain the sometimes apparently contradictory
patterns previously seen in relating GDP and democ-
racy. If a country starts with high democratic levels
but a GDP that is rather low, the democratic level is
unstable and regresses to the point where it reaches
the stable manifold that then allows both democracy
and GDP to grow again.
4 CONCLUSIONS
Our method provides social scientists with a tool to
study complex and dynamic phenomena. Unlike clas-
sic panel analysis, where a decision is usually made
to study a particular time frame, our methods takes in
to account all of the available temporal data. In the
application example, we are able to capture dynami-
cal interplays of variables. We expect that the method
will be able to detect more complex phenomena, such
as amplification, growth limitation, glacial effects or
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
130

tipping effects. The analysis procedure results in best-
fit models that explicitly depict precise and dynamic
mechanisms. Equations such as 5 and 6 provide the
researcher with rich information beyond correlation
coefficients, since they express how variables change
with respect to each other’s state. In future studies, we
will show how the same mechanisms can be used to
look at three and more variables(Ranganathan et al.,
2013).
A key feature of our approach is that no prede-
fined model is imposed on the data. Instead the data
itself is used to find the best model. The same ap-
proach of calculating Bayes factor can of course be
used to test theoretically informed model specifica-
tions. Such testing can tell us how the best fit data-
driven model compares in terms of statistical fit, to
a model based on theoretical reasoning. There may
well be strong grounds to accept a theoretically jus-
tified model with a slightly worse fit, over a purely
data-driven model with the best fit. Indeed, we do not
suggest that social scientists should forget about the-
ories and always adopt the statistically best models.
No doubt, theories are useful to interpret results and
to evaluate models. But we think that social scientists
should be equally open to finding meaningful patterns
and mechanisms beyond established theories. If the
detected patterns and models are plausible and help to
understand social reality or give a new insight into a
phenomenon, then even new theoretical mechanisms
could be formulated or older theoretical mechanisms
revised, based on these findings.
REFERENCES
Allison, P. (2005). Fixed Effects Regression Methods for
Longitudinal Data. SAS Publishing.
Amemiya, T. (1985). Advanced econometrics. Blackwell,
Oxford.
Andersen, R. (2007). Modern Methods for Robust Regres-
sion. SAGE, London.
Ashimov, A. A., Sultanov, B. T., Adilov, Z. M., Borovskiy,
Y. V., Novikov, D. A., Nizhegorodtsev, R. M., and
Ashimov, A. A. (2011). Macroevonomic Analysis
and Economic Policy Based on Parametric Control.
Springer.
Barro, R. J. (1996). Democracy and growth. Journal of
Economic Growth, 1.
Barro, R. J. (1999). Determinants of democracy. Journal of
Political Economy, 107.
Bishop, C. M. (2006). Pattern recognition and machine
learning. Springer.
Boix, C. and Stokes, S. (2003). Endogenous democratisa-
tion. World Politics, 55.
Coleman, J. S. (1964). Introduction to Mathematical Soci-
ology. Free Press of Glencoe/Collier Macmillan.
de Marchi, S. (2005). Computation and Mathematical Mod-
eling in the Social Sciences. Cambridge University
Press.
Diamond, L. and Marks, G. (1992). Reexamining Democ-
racy. SAGE.
Garson, G. D. (2013). Two-Stage Least Square Regression.
Statistical Associates Publishers.
Gelman, A. (2004). Exploratory data analysis for com-
plex models. Journal of Computational and Graph-
ical Statistics, 13 (4).
Krieckhaus, J. (2003). The regime debate revisited: A sensi-
tive analysis of democracy’s economic effect. British
Journal of Political Science, 34.
Laird, N. M. and Ware, J. H. (1982). Random-effects mod-
els for longitudinal data. Biometrics, 38 (4).
Lewis-Beck, M. S. (1995). Data Analysis: An Introduction.
SAGE, London.
Ley, E. and Steel, M. F. (2009). On the effect of prior as-
sumptions in bayesian model averaging with applica-
tions to growth regression. Journal of Applied Econo-
metrics, 24:651–674.
Lipset, S. M. (1959). Some social requisites of democ-
racy: Economic development and political legitimacy.
American Political Science Review, 53.
Menard, S. (2001). Applied Logistic Regression Analysis.
SAGE, London.
Ostrom, C. W. (1990). Time Series Analysis: Regression
Techniques. SAGE, London.
Ranganathan, S., Mann, R. P., Nikolis, S. C., Swain, R. B.,
and Sumpter, D. J. (2013). A dynamical systems ap-
proach to modeling human development. Economet-
rica. submitted.
Robert, C. P. (1994). The Bayesian Choice: a decision-
theoretic motivation. Springer-Verlag, New York.
Saperstein, A. M. (2000). Dynamical Modeling of the Onset
of War. World Scientific Publishing Company.
Stebbins, R. A. (2001). Exploratory Research in Social Sci-
ences. SAGE, London.
Strogatz, S. H. (2000). Nonlinear Dynamics and Chaos:
With Applications to Physics, Biology, Chemistry and
Engineering. Westview Press.
Treiman, D. L. (2009). Quantitative Data Analysis: Doing
Social Research to Test Ideas. Jossey-Bass.
Tukey, J. (1977). Exploratory Data Analysis. Addison-
Wesley.
Weber, L. (2012). Demographic Change and Economic
Growth: Simulation on Growth Modeling. Physica.
Welzel, C. (2013). Freedom Rising. Human Empowerment
and the Quest for Emancipation. Cambridge Univer-
sity Press.
Wooldridge, J. M. (2010). Econometric Analysis of cross
section and panel data. MIT Press.
ABayesianApproachtoModelingDynamicalSystemsintheSocialSciences
131
