
Uncertainty Analysis of the LOCA Break Size Prediction Model using
GMDH
Soon Ho Park, Jae Hwan Kim, Dae Seop Kim
and Man Gyun Na
Department of Nuclear Engineering, Chosun University, 309 Pilmun-daero, Dong-gu, Gwangju, Republic of Korea
Keywords: Group Method of Data Handling (GMDH), Uncertainty Analysis, LOCA (Loss of Coolant Accidents),
Prediction of Break Size.
Abstract: When transients or accidents occur in the nuclear power plants, the plant operators and technical staffs are
provided with only partial information and faced with a number of signals and alarms. Therefore, providing
information such as a break size in case of LOCA is essential to control these events successively. In this
paper, in order to predict the LOCA break size, a prediction model was developed by using group method of
data handling (GMDH) algorithm, and we have conducted its uncertainty analysis. The proposed prediction
model was verified using the acquired data from the OPR1000 nuclear power plant.
1 INTRODUCTION
After the Fukushima nuclear power plant accident,
the public concern about the safety of nuclear power
plants (NPPs) has been growing.
If accidents or transients occur in NPPs, it is
important to check short time trend of major
parameters. However, if it is a severe accident, it is
very difficult to find out the initial event, since the
plant operators and technical staffs are offered with
only partial information or not have sufficient time
to analyze the accident in the urgent situation.
During the accident, operators and technical staffs
will be faced with a number of signals and alarms.
Therefore, providing information such as a break
size is important to control this event successively.
This study aims to predict the break size of loss
of coolant accidents (LOCA) and steam generator
tube rupture (SGTR) which may lead to severe
accident conditions by applying a group method of
data handling (GMDH). Additionally, the accuracy
of the proposed prediction model is verified by its
uncertainty analysis.
2 PREDICTION OF THE LOCA
BREAK SIZE USING GMDH
In order to solve the system problem such as control,
monitoring, prediction, diagnosis and so on, a lot of
mathematical methods have been studied.
The GMDH method is one of them. The GMDH
method which is one of the data-driven models such
as ANN (Artificial Neural Network) can be used for
LOCA break size prediction in this paper. Data-
driven models have many advantages of easy
implementation and accuracy, and famous for
superior capability in modelling complex systems.
In this paper, the GMDH method has been used
to develop a model for LOCA break size prediction.
2.1 Basic GMDH Algorithm
The GMDH algorithm is a way of finding a function
that well expresses a dependent variable from
independent variables. This method can find a
correlation in the data automatically to improve the
prediction accuracy and select the optimal structure
of the model. The GMDH algorithm is similar to
multiple regression model, but it uses the data
structure. The data set is divided into three subsets.
The reason of dividing is to prevent over-fitting and
maintain model regularization through cross-
validation. Figure 1 shows the data structure of the
GMDH algorithm.
The GMDH model uses a self-organizing
algorithm that can select nonlinear forms of the
basic inputs. Figure 2 shows the branch architecture
of the GMDH model. It shows the branch structure
of the GMDH model to start with the basic inputs in
the first step.
221
Ho Park S., Hwan Kim J., Seop Kim D. and Gyun Na M..
Uncertainty Analysis of the LOCA Break Size Prediction Model using GMDH.
DOI: 10.5220/0004481002210226
In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2013), pages 221-226
ISBN: 978-989-8565-70-9
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

11 12 1 1
21 22 2 2
12
12
training data set
verification data set
m
m
ll lm l
nn nm n
xx x y
xx x y
xx x y
xx x y
12
12
development data
test data set
KK Km K
NN Nm N
xx x
y
xx x y
Figure 1: GMDH data structure.
Figure 2: GMDH structure.
The original GMDH method employed the
following general form at each level of the
successive approximation:
22
(, )
ij i j i j ij
yfxx ABxCxDxExFxx
(1)
The coefficient parameters of the reference function
which is written above such as
, ,...,
A
BF
can be
obtained by using a least square method in an
arbitrary pair (
,
ij
x
x
) from independent variables
12
(, , , )
m
x
xxx
. This method takes a form of
hierarchical polynomial regression network to model
various complex input-output relationships.
However, more complicated function forms can be
used such as ratio terms (
ij
x
x ), trigonometric terms
(
sin( )cx , cos( )cx ), exponential terms ( exp( )cx )
and so on in accordance with complexity of the
system. The GMDH algorithm uses the
Kolmogorov-Gabor form of a high-order
polynomial. The Kolmogorov-Gabor form that is
called as Ivakhnenko polynomial can be expressed
as follows:
0
111 111
...
m mm mmm
i i ij i j ijk i j k
iij ijk
ya ax axx axxx
(2)
where
12
(, , , )
m
x
xxx
is an input vector and
0,
(,, , )
i ij ijk
aaaaa
is a coefficient vector that is a
weight vector of Kolmogorov-Gabor polynomial.
The GMDH algorithm can determine the structure of
the model and also calculate the system output of the
most important input simultaneously. This uses the
composition of the lower-order polynomials
mentioned above, which means that the GMDH
algorithm amalgamates lower order polynomials at
each generation to reach the subsequent generation.
This process continues until the GMDH model
begins to show over-fitting in training or exceeds the
maximum calculation time. If an evaluation value
(
R ) is greater than a reference value, the regression
equation is fallen behind. Otherwise, the regression
equation is survived. The survived regression
equation value is used as a training data of the new
generation. This process is conducted about all
possible pairs of independent variables. The
descendant with the smallest evaluation value in the
evaluation of this generation is selected as the
optimum fit. If the smallest evaluation value of the
current generation is smaller than that of the
previous generation, the above process is performed
repeatedly. When over-fitting of the evaluation
(
min
G
R
) value is found through alternation of
generation, the process is stopped. That is, if the
smallest evaluation value of the current generation is
larger than that of the previous generation, the
process is stopped.
As shown in Figure 3, if over-fitting is found, the
process of the algorithm is stopped and the optimum
fit of the previous generation is selected as the
optmized model that predicts the LOCA size.
*
11
z
*
12
z
1
*
1m
z
11
z
12
z
*
21
z
*
22
z
2
*
2m
z
*
1G
z
*
2G
z
*
G
Gm
z
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
222
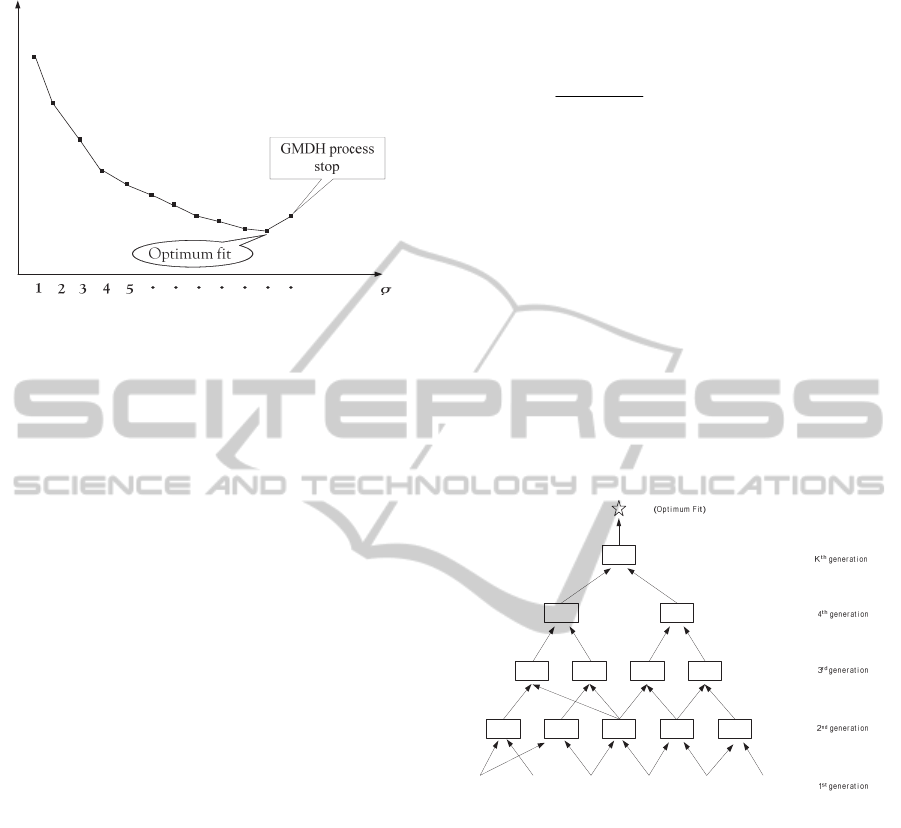
Figure 3: Value of each generation.
2.2 Main Implementation Steps
The GMDH algorithm generates and tests all input-
output combinations. Each element in the system
that is indicated as a rectangle box in Figure 2
executes a function of two inputs. The coefficient
parameters of Eq. (2) are decided by using a normal
least square method, and the variables of the
elements are calculated. A threshold value for
comparison with the evaluation value in each
generation decides whether the outputs of the
elements in a generation are acceptable. The output
of an element is eliminated in a current generation
when the result is larger than the threshold value.
Those variables or elements that are useful for
predicting the proper output are used at the next
generation. The generations are repeated until the
satisfactory results are obtained. This process is
similar to Darwin’s theory. The detailed main
implementation steps are given below.
First step, construct each of input and output
variable or data of the system. The data structure is
modeled and divided into the training and checking
data sets, and preprocess the data to normalize them.
Second step, choose the external inputs to the
GMDH network. Calculate the regression
polynomial parameters for each pair of input
variables involved in the training data set using the
least square method. Calculate the
(1)/2mm
high-order variables in place of the original input
variables
12
,,,
m
x
xx
in order to predict the output.
Third step, the algorithm designs a group of new
variables (
11
(1)/2
ggg
mmm
) in the previous
step. Here,
g
m
is the number of input variables for
generation
g
. A criterion is used to evaluate the
new variables in the generation
g
and is related
with the error for the checking data, which is defined
as follows:
2
2
1
2
1
1, 2, ,
n
iij
il
j
g
n
i
il
yz
rforjm
y
(3)
Last step, when over-fitting is found through
checking, the above mentioned process is stopped. If
the generation continues, the model will become
over-fitted. The polynomial with the minimum error
criterion is selected as the final approximate model.
Otherwise, the above steps are repeated.
At the end of the GMDH algorithm, regression
parameters are stored. The estimated coefficient for
the high-order polynomial is determined by tracing
back the GMDH structure until it reaches the
original variables
12
,,,
m
x
xx
. As shown in Figure
4, the tree structure with the optimum fit at the top is
called an Ivakhnenko Tree.
Figure 4: Ivakhnenko tree.
3 UNCERTAINTY ANALYSIS
The data-based model has several sources of
uncertainty in the predicted values such as selection
of training data, model structure including
complexity, and noise in the input and output
variables. The data-based model is developed by
using a given training data set. Each of the training
data set selected from entire data group will generate
a different model and have a distribution of
predicted values for a given observation data.
Furthermore, inappropriate model causes a bias.
This paper uses statistical uncertainty analysis
methods.
min
g
R
1
x
2
x
3
x
4
x
5
x
6
x
UncertaintyAnalysisoftheLOCABreakSizePredictionModelusingGMDH
223

3.1 Statistical Method
The statistical uncertainty analysis generates many
bootstrap samples of the training data set and is
conducted through training of data-based model
parameters. After sampling and training repeatedly,
the result of the prediction provides a distribution for
output value. In this paper, the bootstrap pairs
sampling algorithm, which is one of the statistical
methods was used. Figure 5 shows the bootstrap
pairs algorithm structure.
Figure 5: Bootstrap pairs sampling algorithm structure.
The detailed bootstrap pairs sampling algorithm
is given below.
First step, generate samples
J
(the number of
bootstrap samples) through sampling with
replacement from the development data pool.
Second step, the data-based model is obtained for
each bootstrap sample.
Last step, calculate the variance and the bias of
an observation data output
o
y
by using following
equation:
2
000
1
1
ˆ
1
ˆ
ˆ
J
j
j
Var y
J
yy
(4)
where
00
1
1/2
2
11
1
11
ˆˆ
ˆ
J
j
j
KJ
jj
kk
kj
J
bias
KJ
yy
yy
(5)
The estimate with a 95% confidence for an arbitrary
test input
0
x
can be expressed as follows:
0
2
00
ˆ
ˆ
ˆ
2()
y Var y bias y
(6)
3.2 Application to the LOCA Break
Size Prediction
In this paper, the proposed prediction model was
verified by applying to a number of numerical
simulations of OPR1000 NPPs. The number of 810
accident simulations were conducted using the
MAAP4 code to acquire the data. The data were
composed of 270 hot-leg LOCA, 270 cold-leg
LOCA and 270 SGTR, and were divided into
development data and test data. Each accident
simulation data is selected into 30 test data, 190
training data and 50 checking data.
Table 1: Performance of the proposed GMDH algorithm.
Event type Data type
MAX. error
(%)
RMS error
(%)
Hot-leg
LOCA
Training data 25.5019 3.1061
Verification data 10.4794 2.6101
Test data 15.8917 3.5650
Cold-leg
LOCA
Training data 9.2525 1.9933
Verification data 16.6147 3.1979
Test data 8.6985 2.5440
SGTR
Training data 15.3771 2.8586
Verification data 13.8253 2.7114
Test data 9.8385 2.6438
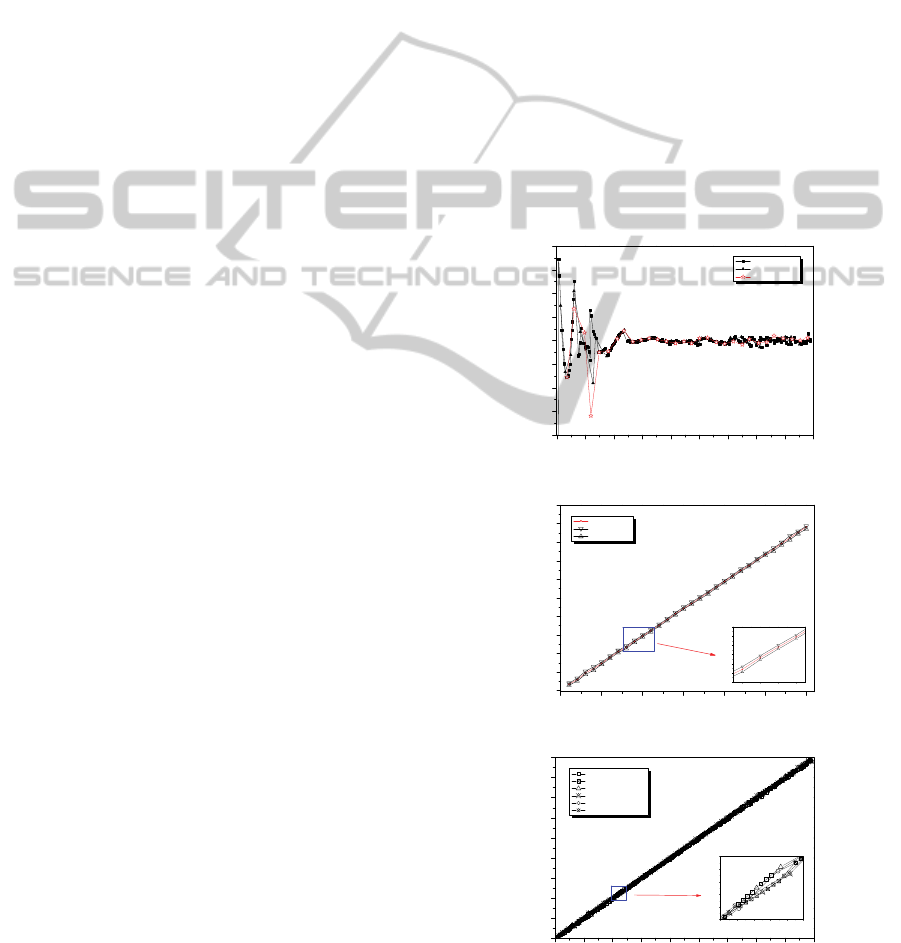
Table 1 summarizes the performance results of
the proposed GMDH algorithm, and Figure 6-8
shows a result of each prediction interval,
calculation errors, and uncertainty analysis. As
shown in Figures 6-8, the prediction interval is very
small which means that the model is accurate.
4 CONCLUSIONS
In this paper, a prediction model was developed to
estimate the LOCA break size of NPPs using the
GMDH algorithm. The proposed GMDH model was
applied and verified using the acquired real plant
data of OPR1000. Additionally, the prediction
interval was calculated by using the statistical
uncertainty analysis.
As a result of simulation, the performance of the
GMDH model was very well. The RMS errors of
test data in hot-leg LOCA, cold-leg LOCA and
SGTR are 3.5650%, 2.5440% and 2.6438%,
respectively. The proposed prediction model of
LOCA break size using the GMDH model fits very
well.
If the GMDH model is optimized by using a
variety of data, it is possible to predict the NPP
LOCA size more accurately.
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
224
REFERENCES
S. W. Cheon and S. H. Chang, May 1993, Application of
neural networks to connectionist expert system for
transient identification in nuclear power plants, Nucl.
Technol., vol. 102, no. 2, pp. 177-191.
Y. Bartal, J. Lin, and R. E. Uhrig, June 1995, Nuclear
power plant transient diagnostics using artificial neural
networks that allow “don’t-know” classifications, Nucl.
Technol., vol. 110, no. 3, pp. 436-449.
M. G. Na, S. M. Lee, S. H. Shin, D. W. Jung, S. P. Kim, J.
H. Jeong, and B. C. Lee, April. 2004, Prediction of
major transient scenarios for severe accidents of
nuclear power plants, IEEE Trans. Nucl. Sci., vol. 51,
no. 2, pp. 313-321.
M. G. Na, W. S. Park, and D. H. Lim, Feb. 2008,
Detection and diagnostics of loss of coolant accidents
using support vector machines, IEEE Trans. Nucl. Sci.,
vol. 55, no. 1, pp. 628-636.
S. H. Lee, Y. G. No, M. G. Na, K.-I. Ahn and S.-Y. Park,
Feb. 2011, Diagnostics of loss of coolant accidents
using SVC and GMDH models, IEEE Trans. Nucl.
Sci., vol. 58, no. 1, pp. 267-276.
I.-Y.Seo, B.-N. Ha, S.-W. Lee, C.-H. Shin, and S.-J. Kim,
2010, Principal components based support vector
regression model for on-line instrument calibration
monitoring in NPPs, Nucl. Eng. Technol., vol. 42, no.
2, pp. 219-230.
E. Zio and R. Bazzo, Aug. 2010, Optimization of the test
intervals of a nuclear safety system by genetic
algorithms, solution clustering and fuzzy preference
assignment, Nucl. Eng. Technol., vol. 42, no. 4, pp.
414-425.
Bo-Suk Yang, Won-Woo Hwang, M.-H. Ko, and S.-J. Lee,
Oct. 2005, Cavitation detection of butterfly valve
using support vector machines, J. Sound Vibr., vol.
287, nos. 1-2, pp. 25-43.
D. F. Specht, 1990, Probabilistic Neural Networks, Neural
Networks, vol. 3, no. 1, pp. 109-118.
A. G. Ivakhnenko, 1968, The group method of data
handling; a rival of method of stochastic
approximation, Soviet Automatic Control, vol. 1, no. 3,
pp. 43-55.
S.J. Farlow, 1984, Self-Organizing Methods in Modeling:
GMDH Type Algorithms, Marcel Dekker, New York.
C. R. Hild, 1998, Development of The Group Method of
Data Handling With Information-based Model
Evaluation Criteria: A New Approach to Statistical
Modeling, Ph.D. Dissertation, Univ. Tennessee,
Knoxville.
P. B. Ferreira and B. R. Upadhyaya, December 1999,
Incipient Fault Detection and Isolation of Sensors and
Field Devices, Nuclear Engineering Dept., Univ.
Tennessee, Knoxville, UTNE/BRU/99-02.
A. G. Ivakhnenko, 1971, Polynomial theory of complex
systems, IEEE Trans. Syst. Man & Cybern, SMC-1, pp.
364-378.
T. Takagi and M. Sugeno, Jan./Feb. 1985, Fuzzy
Identification of Systems and Its Applications to
Modeling and Control, IEEE Trans. Systems, Man,
Cybern., vol. SMC-1, no. 1, pp. 116-132.
S. L. Chiu, 1994, Fuzzy model identification based on
cluster estimation, J. Intell. Fuzzy Systems, vol. 2, pp.
267-278.
V. Kecman, 2001, Learning and Soft Computing,
Cambridge, Massachusetts: MIT Press.
V. Vapnik, 1995, The Nature of Statistical Learning
Theory, New York, Springer.
D. E. Goldberg, 1989, Genetic Algorithms in Search,
Optimization, and Machine Learning, Reading,
Massachusetts: Addison Wesley.
M. Mitchell, 1996, An Introduction to Genetic Algorithms,
Cambridge, Massachusetts: MIT Press.
R. E. Henry et al., 1990, MAAP4 – Modular Accident
Analysis Program for LWR Power Plants, User’s
Manual, Burr Ridge, IL: Fauske, vol. 1-4.
J.W. Hines, B. Rasmussen, Sept. 2005, Online sensor
calibration monitoring uncertainty estimation, Nucl.
Technol., vol. 151, pp. 281-288.
R. Tibshirani, 1996, A comparison of some error estimates
for neural network models, Neural Computation, vol.
8, pp. 152-163.
(a) relative error
(b) uncertainty analysis
(c) estimated break size
Figure 6: Prediction of hot-leg LOCA break size.
0.00.20.40.60.81.01.21.41.61.8
-20
-15
-10
-5
0
5
10
15
20
training data
verification data
test data
break size (m
2
)
relative error (%)
0 5 10 15 20 25 30
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
1.8
2.0
prediction size
upper interval
lower interval
test case
LOCA size (m
2
)
8 9 10 11
0.40
0.45
0.50
0.55
0.60
0.65
0.70
0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
1.8
0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
1.8
target (training)
estimated (training)
target (verification)
estimated (verification)
target (test)
estimated (test)
break size
(
m
2
)
estimated break size (m
2
)
0.40 0.42 0.44 0.46 0.48 0.50
0.40
0.42
0.44
0.46
0.48
0.50
UncertaintyAnalysisoftheLOCABreakSizePredictionModelusingGMDH
225

(a) relative error
(b) uncertainty analysis
(c) estimated break size
Figure 7: Prediction of cold-leg LOCA break size.
(a) relative error
(b) uncertainty analysis
(c) estimated break size
Figure 8: Prediction of SGTR break size.
0.0 0.2 0.4 0.6 0.8 1.0
-20
-15
-10
-5
0
5
10
15
20
training data
verification data
test data
break size (m
2
)
relative error (%)
0 5 10 15 20 25 30
0.0
0.2
0.4
0.6
0.8
1.0
prediction size
upper interval
lower interval
test case
LOCA size (m
2
)
891011
0.20
0.25
0.30
0.35
0.0 0.2 0.4 0.6 0.8 1.0
0.0
0.2
0.4
0.6
0.8
1.0
0.0 0.2 0.4 0.6 0.8 1.0
0.0
0.2
0.4
0.6
0.8
1.0
target (training)
estimated (training)
target (verification)
estimated (verification)
target (test)
estimated (test)
break size (m
2
)
estimated break size (m
2
)
0.20 0.22 0.24
0.20
0.22
0.24
0.00 0.02 0.04 0.06 0.08 0.10 0.12
-20
-15
-10
-5
0
5
10
15
20
training data
verification data
test data
break size (m
2
)
relative error (%)
0 5 10 15 20 25 30
0.00
0.02
0.04
0.06
0.08
0.10
0.12
prediction size
upper interval
lower interval
test case
LOCA size (m
2
)
24 25 26 27
0.086
0.088
0.090
0.092
0.094
0.096
0.098
0.100
0.102
0.00 0.02 0.04 0.06 0.08 0.10 0.12
0.00
0.02
0.04
0.06
0.08
0.10
0.12
0.00 0.02 0.04 0.06 0.08 0.10 0.12
0.00
0.02
0.04
0.06
0.08
0.10
0.12
target (training)
estimated (training)
target (verification)
estimated (verification)
target (test)
estimated (test)
break size (m
2
)
estimated break size (m
2
)
0.020 0.021 0.022 0.023 0.024
0.020
0.021
0.022
0.023
0.024
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
226
