Computational Experience in Solving Continuous-time Algebraic Riccati

Equations using Standard and Modiﬁed Newton’s Method

Vasile Sima

Advanced Research, National Institute for Research & Development in Informatics,

Bd. Mares¸al Averescu, Nr. 8–10, Bucharest, Romania

Keywords:

Algebraic Riccati Equation, Numerical Methods, Optimal Control, Optimal Estimation.

Abstract:

Improved algorithms for solving continuous-time algebraic Riccati equations using Newton’s method with or

without line search are discussed. The basic theory and Newton’s algorithms are brieﬂy presented. Algorith-

mic details the developed solvers are based on, the main computational steps (ﬁnding the Newton direction,

ﬁnding the Newton step size), and convergence tests are described. The main results of an extensive perfor-

mance investigation of the solvers based on Newton’s method are compared with those obtained using the

widely-used MATLAB solver. Randomly generated systems with orders till 2000, as well as the systems from

a large collection of examples, are considered. The numerical results often show signiﬁcantly improved accu-

racy, measured in terms of normalized and relative residuals, and greater efﬁciency than the MATLAB solver.

The results strongly recommend the use of such algorithms, especially for improving the solutions computed

by other solvers.

1 INTRODUCTION

The numerical solution of algebraic Riccati equations

(AREs) is an essential step in many computational

methods for model reduction, ﬁltering, and controller

design for linear control systems. Let A, E ∈ R

n×n

B ∈R

n×m

, and Q and R be symmetricmatrices of suit-

able dimensions. In a compact notation, the general-

ized continuous-time AREs (CAREs), with unknown

X = X

∈ R

n×n

, are deﬁned by

0 = Q+ op(A)

X op(E) + op(E)

X op(A) (1)

−L(X)R

−1

L(X)

=: R (X),

where E and R are assumed to be nonsingular, and

L(X):=L+ op(E)

XB ,

with L of suitable size. The operator op(M) repre-

sents either M or M

. Deﬁne also G := BR

−1

. An

optimal regulator problem involves the solution of an

ARE with op(M) = M; an optimal estimator problem

involves the solution of an ARE with op(M) = M

input matrix B replaced (by duality) by the transpose

of the output matrix C ∈ R

p×n

, and m replaced by

p. (This means that L should be n× p in this case.)

In practice, often Q and L are given as C

QC and

L = C

L, respectively. The solutions of an ARE are

the matrices X = X

for which R (X) = 0. Usually,

what is needed is a stabilizing solution, X

, for which

the matrix pair (op(A − BK(X

)), op(E)) is stable

(in a continuous-time sense), where op(K(X

)) is the

gain matrix of the optimal regulator or estimator, and

K(X) := R

−1

L(X)

(2)

(with X replaced by X

There is a vast literature concerning AREs and

their use for solving optimal control and estimation

problems; see, e.g., the monographs (Anderson and

Moore, 1971; Mehrmann, 1991; Lancaster and Rod-

man, 1995) for many theoretical results. The op-

timization criterion for linear control systems is a

quadratic performance index in terms of the system

state and control input. By minimizing this criterion,

a solution to the optimal systems stabilization and

control is obtained, expressed as a state-feedback con-

trol law. Brieﬂy speaking, this control law achieves a

trade-off between the regulation error and the control

effort. The optimal estimation or ﬁltering problem,

for systems with Gaussian noise disturbances, can be

solved as a dual of an optimal controlproblem, and its

solution gives the minimum variance state estimate,

based on the system output. It is worth to say that the

results of an optimal design are often better suited in

practice than those found by other approaches. For

instance, pole assignment may deliver too large gain

Sima V..

Computational Experience in Solving Continuous-time Algebraic Riccati Equations using Standard and Modiﬁed Newton’s Method.

DOI: 10.5220/0004482500050016

In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2013), pages 5-16

ISBN: 978-989-8565-70-9

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

matrices, producing high-magnitude inputs, which

might not be acceptable. In both control and estima-

tion problems, including those stated in the H

∞

theory

(e.g., (Francis, 1987)), a major computational step is

the solution of an ARE. Due to their importance, nu-

merous numerical methods have been proposed for

solving AREs; see, for instance, (Mehrmann, 1991;

Sima, 1996). There are also several highly-used soft-

ware implementation, e.g., in MATLAB (MATLAB,

2011), or in the SLICOT Library (Benner et al., 1999;

Benner and Sima, 2003; Van Huffel et al., 2004; Ben-

ner et al., 2010).

Newton’s method for solving AREs has been con-

sidered by many authors, for instance, (Kleinman,

1968; Mehrmann, 1991; Lancaster and Rodman,

1995; Sima, 1996; Benner, 1997; Benner, 1998; Ben-

ner and Byers, 1998). Actually, the matrix sign func-

tion method for solving AREs, e.g., (Roberts, 1980;

Gardiner and Laub, 1986; Byers, 1987; Sima and

Benner, 2008), uses a specialized Newton’s method

to compute the square root of the identity matrix of

order 2n. This paper merely reports on implementa-

tion details and numerical results. In addition, there

are contributions compared to (Benner, 1998; Ben-

ner and Byers, 1998): improved stopping criteria, im-

proved functionality (regarding generality in the co-

efﬁcient matrices and options), a better routine for

computing the roots of a third order polynomial, etc.

The paper extends the results of (Sima and Benner,

2006) in some details, and by investigating the nu-

merical behavior of the current Newton-based ARE

solvers for high-order random systems, and for sys-

tems from the COMPl

ib collection (Leibfritz and

Lipinski, 2003; Leibfritz and Lipinski, 2004). (The

previous paper (Sima and Benner, 2006) used ran-

domly generated systems with n ≤ 40, and systems

from the CAREX benchmark collection (Abels and

Benner, 1999), where most problems have small size,

but may be very ill-conditioned.) It is worth mention-

ing that Newton’s method has been applied in (Penzl,

2000) for solving special classes of large-orderAREs,

using low rank Cholesky factors of the solutions of

the Lyapunov equations built during the iterative pro-

cess (Penzl, 1998). Additional numerical results, for

randomly generated systems with n ≤ 600, and com-

parison with MATLAB and SLICOT solvers are pre-

sented in (Sima, 2005). However, contrary to stan-

dard solvers, the specialized solvers used (

lp lrnm

and

lp lrnm i

) are not general solvers. In order to

use them advantageously,the following main assump-

tions must be fulﬁlled: 1) the matrix A is structured or

sparse; 2) the solution X has a small rank in compar-

ison with n. (These solvers use the possibly sparse

structure of the matrix A and operations of the form

Ab or A

−1

b, where b is a vector.) The solvers dis-

cusssed in this paper are general, and can be used to

solve large dense problems.

The paper compares the performance of the New-

ton solver with or without line search with the per-

formance of the state-of-the-art commercial solver

care

from MATLAB Control System Toolbox. The

MATLAB solver uses a different, eigenvalue ap-

proach, based on the results in, e.g., (Laub, 1979;

Van Dooren, 1981; Arnold and Laub, 1984). Rela-

tively recent research, including both theoretical and

numerical investigation, has been directed to exploit

the Hamiltonian-symplectic structure of the eigen-

problem associated to the ARE (Raines and Watkins,

1992; Benner et al., 2002; Benner et al., 2007; Sima,

2010; Sima, 2011).

A recursive method for computing the positive

deﬁnite stabilizing solution of an ARE with an in-

deﬁnite quadratic term has been recently proposed

in (Lanzon et al., 2008).

One drawback of the Newton’s method is its de-

pendence on an initialization, X

. When searching for

a stabilizing solution X

, the initialization X

should

also be stabilizing, i.e., (op(A − BK(X

)), op(E) )

should be stable. Except for stable systems, ﬁnding a

suitable initialization can be a difﬁcult task. Stabiliz-

ing algorithms have been proposed, mainly for stan-

dard systems, e.g., in (Kleinman, 1968; Varga, 1981;

Sima, 1981; Hammarling, 1982). However, often

these algorithms produce a matrix X

and/or the fol-

lowing several matrices X

, i = 1,2,... (computed by

the Newton method), with very large norms, and the

solver may encounter severe numerical difﬁculties.

For this reason, Newton’s method is best used for it-

erative improvement of a solution or as defect correc-

tion method (Mehrmann and Tan, 1988), delivering

the maximal possible accuracy when starting from a

good approximate solution. Moreover, it is preferred

in implementing certain fault-tolerant systems, which

require controller updating, see, e.g. (Ciubotaru and

Staroswiecki, 2009) and the references therein.

The organization of the paper is as follows. Sec-

tion 2 starts by summarizing the basic theory and

Newton’s algorithms for AREs. Algorithmic details,

computation of the Newton direction, computation of

the Newton step size, and convergence tests are dis-

cussed in separate subsections. Section 3 presents the

main results of an extensive performance investiga-

tion of the solvers basedon Newton’s method, in com-

parison with the MATLAB solver

care

. Randomly

generated systems with order till 1000 (but also a sys-

tem with order 2000), as well as systems from the

COMPl

ib collection (Leibfritz and Lipinski, 2003;

Leibfritz and Lipinski, 2004), are considered in the

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

two subsections. Section 4 summarizes the conclu-

sions.

2 BASIC THEORY AND

NEWTON’S ALGORITHMS

The following assumptions are made.

Assumptions A:

• Matrix E is nonsingular.

• Matrix pair (op(E)

−1

op(A), op(E)

−1

B) is stabi-

lizable.

• Matrix R = R

is positive deﬁnite (R > 0).

• A stabilizing solution X

exists and it is unique.

The algorithms considered in the sequel are enhance-

ments of Newton’s method, which employ a line

search procedure to minimize the residual along the

Newton direction.

The conceptual algorithm can be stated in the fol-

lowing form:

Algorithm N: Newton’s method with line search

for CARE

Input: The coefﬁcient matrices E, A, B, Q, R, and L,

and an initial matrix X

= X

Output: The approximate solution X

of CARE.

FOR k = 0, 1, . . . , k

max

, DO

1. If convergenceor non-convergenceisdetected, re-

turn X

and/or a warning or error indicator value.

2. ComputeK

:= K(X

) with (2) and op(A

), where

= op(A) −BK

3. Solve in N

the continuous-time generalized (or

standard, if E = I

) Lyapunov equation

op(A

)

op(E) + op(E)

op(A

) = − R (X

4. Find a step size t

which minimizes the squared

Frobenius norm kR (X

+ tN

(with respect to

t).

5. Update X

k+1

= X

+ t

END

Standard Newton’s algorithms are obtained by taking

= 1 at Step 4 at each iteration. When the initial

matrix X

is far from a Riccati equation solution, the

Newton’s method with line search often outperforms

the standard Newton’s method.

Basic properties for the standard and modiﬁed

Newton’s algorithms for CAREs can be stated as fol-

lows (Benner, 1997):

Theorem 2.1 (Convergence of Algorithm N, standard

case). If the Assumptions A hold, and X

is stabiliz-

ing, then the iterates of the Algorithm N with t

= 1

satisfy

(a) All matrices X

are stabilizing.

(b) X

≤ ··· ≤ X

k+1

≤ X

≤ ··· ≤ X

k→∞

= X

(d) Global quadratic convergence: There is a con-

stant γ > 0 such that

k+1

−X

k ≤ γkX

−X

, k ≥ 1.

Theorem 2.2 (Convergence of Algorithm N). If the

Assumptions A hold, X

is stabilizing, and, in addi-

tion, (op(E)

−1

op(A), op(E)

−1

B) is controllable and

≥t

> 0, for all k ≥0, then the iterates of the Algo-

rithm N satisfy

(a) All iterates X

are stabilizing.

(b) kR (X

k+1

≤ kR (X

and equality holds

if and only if R (X

) = 0.

k→∞

R (X

) = 0.

(d) lim

k→∞

= X

(e) In a neighbourhood of X

, the convergence is

quadratic.

(f) lim

k→∞

= 1.

Theorem 2.2 does not ensure monotonic convergence

of the iterates X

in terms of deﬁniteness, contrary

to the standard case (Theorem 2.1, item (b)). On

the other hand, under the speciﬁed conditions, The-

orem 2.2 states the monotonic convergence of the

residuals to 0, which is not true for the standard algo-

rithms. It is conjectured that Theorem 2.2 also holds

under the weaker assumption of stabilizability instead

of controllability. This is supported by the numerical

experiments.

2.1 Algorithmic Details

The essential steps of Algorithm N will be detailed

below.

Continuous-time AREs can be put in a simpler

form, which is more convenient for Newton’s algo-

rithms. Speciﬁcally, setting

A = A−BR

−1

Q = Q−LR

−1

, (3)

after redeﬁning A and Q as

A and

Q, respectively,

equation (1) reduces to

0 = op(A)

X op(E) + op(E)

X op(A)

− op(E)

XGX op(E) + Q =: R (X), (4)

or, in the standard case (E = I

), to

0 = op(A)

X + X op(A) −XGX + Q =: R (X). (5)

ComputationalExperienceinSolvingContinuous-timeAlgebraicRiccatiEquationsusingStandardandModifiedNewton's

Method

The transformations in (3) eliminate the matrix L

from the formulas to be used. It is more economical

to solve the equations (4) or (5), since otherwise the

calculations involving L must be performed at each

iteration. In this case, the matrix K

is no longer

computed in Step 2, and A

= op(A) −GX

op(E) (or

= op(A) −DD

op(E)).

Algorithm N was implemented in a Fortran

77 subroutine

SG02CD

following the SLICOT Li-

brary (Benner et al., 1999; Van Huffel and Sima,

2002; Van Huffel et al., 2004) implementation and

documentation standards

. The implementation deals

with generalized algebraicRiccati equations, possibly

for the discrete-time case, without inverting the ma-

trix E. This is very important for numerical reasons,

especially when E is ill-conditioned with respect to

inversion. Standard algebraic Riccati equations (in-

cluding the case when E is speciﬁed as I

, or even

[]

in MATLAB), are solved with the maximal possible

efﬁciency. Moreover, both control and ﬁlter algebraic

Riccati equations can be solved by the same routine,

using an option (“mode”) parameter, which speciﬁes

the op operator. The matrices A and E are not trans-

posed. It it possible to also avoid the transposition for

C and L, for the ﬁlter equation, but this is less impor-

tant and more difﬁcult to implement. (Some existing

lower-level routinesdo not coverthe transposed case.)

The implemented algorithm solves either the gen-

eralized CARE (4) or standard CARE (5) using New-

ton’s method with or without line search. The selec-

tion is made using another option. There is an op-

tion for solving related AREs with the minus sign re-

placed by a plus sign in front of the quadratic term.

Moreover, instead of the symmetric matrix G, G =

−1

, the n-by-m matrix B and the symmetric and

invertible m-by-m matrix R, or its Cholesky factor,

may also be given. The iteration is started by an ini-

tial (stabilizing) matrix X

, which can be omitted, if

the zero matrix can be used. If X

is not stabilizing,

and ﬁnding X

is not required, Algorithm N will con-

verge to another solution of CARE. Either the upper,

or lower triangles, not both, of the symmetric matrices

Q, G (or R), and X

need to be stored. Since the so-

lution computed by a Newton algorithm generally de-

pends on initialization, another option speciﬁes if the

stabilizing solution X

is to be found. In this case, the

initial matrix X

must be stabilizing, and a warning is

issued if this property does not hold; moreover, if the

computed X is not stabilizing, an error is issued. An-

other optionspeciﬁes whether to use standard Newton

method, or the modiﬁed Newton method, with line

search. The optimal size of the real working array

can be queried, by setting its length to −1. Then, the

See

http://www.slicot.org

solver returns immediately, with the ﬁrst entry of that

array set to the optimal size.

A maximum allowed number of iteration steps,

max

, is speciﬁed on input, and the number of itera-

tion steps performed, k

, is returned on exit.

If m ≤ n/3, the algorithm is faster if a factoriza-

tion G = DD

is used instead of G itself. Usually, the

routine uses the Cholesky factorization of the matrix

R, R = L

, and computes D = BL

−1

. The standard

theory assumes that R is positive deﬁnite. But the rou-

tine works also if this assumption does not hold nu-

merically, by using the UDU

or LDL

factorization

of R. In that case, the current implementation uses G,

and not its factors, even if m ≤ n/3.

The arrays holding the data matrices A and E are

unchanged on exit. Array

stores either B or G. On

exit, if B was given, and m ≤ n/3,

returns the ma-

trix D = BL

−1

, if the Cholesky factor L

can be com-

puted. Otherwise, array

is unchanged on exit. Array

stores matrix Q on entry and the computed solution

X on exit. If matrix R or its Cholesky factor is given,

it is stored in array

. On exit,

contains either the

Cholesky factor, or the factors of the UDU

or LDL

factorization of R, if R is found to be numerically in-

deﬁnite. In that case, the interchanges performed for

theUDU

or LDL

factorization are stored in an aux-

iliary integer array.

The basic stopping criterion for the iterative pro-

cess is stated in terms of a normalized residual, r

, and

a tolerance τ. If

:= r(X

) := kR (X

/max(1,kX

) ≤ τ, (6)

where X

is the currently computed approximate so-

lution (at iteration k), the iterative process is success-

fully terminated. If τ ≤ 0, a default tolerance is used,

deﬁned in terms of the Frobenius norms of the given

matrices, and relative machine precision, ε

. Specif-

ically, for given G, τ is computed by the formula

τ = min( ε

√



kEk

(2kAk

+ kGk

kEk

) + kQk



√

). (7)

When G is given in factorized form (see above), then

kGk

in (7) is replaced by kDk

. When E is identity,

the factors involving its norm are omitted. The sec-

ond operand of min in (7) was introduced to prevent

deciding convergence too early for systems with very

large norms for A, E, G, and/or Q.

The ﬁnally computed normalized residual is also

returned. Moreover, approximate closed-loop system

poles, as well as min( k

, 50 )+1 values of the resid-

uals, normalized residuals, and Newton steps are re-

turned in a working array, where k

is the iteration

number when Newton’s process stopped.

Several approaches have been tried in order to re-

duce the number of iterations. One of them was to

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

set t

= 1 whenever t

≤

√

. Often, but especially

in the ﬁrst iterations, the computed optimal steps t

are too small, and the residual decreases too slowly.

This is called stagnation, and remedies are used to

escape stagnation, as described below. The ﬁnally

chosen strategy was to set t

= 1 when stagnation is

detected, but also when t

< 0.5, ε

1/4

< r

< 1, and

R (X

≤10, if this happens during the ﬁrst

10 iterations; here,

R (X

) is an estimate of the

residual obtained using the formula (10).

In order to observe stagnation, the last computed

residuals are stored in the ﬁrst k

entries of an array

RES

. If k

R (X

> τ

kR (X

k−k

> 0, then

= 1 is used instead. The current implementation

uses τ

= 0.9 and sets k

= 2, but values as large as

= 10 can be used by changing this parameter. The

ﬁrst k

entries of array

RES

are reset to 0 whenever a

standard Newton step is applied.

Pairs of symmetric matrices are stored economi-

cally, to reduce the workspace requirements, but pre-

serving the two-dimensional array indexing, for ef-

ﬁciency. Speciﬁcally, the upper (or lower) trian-

gle of X

and the lower (upper) triangle of R (X

)

are concatenated along the main diagonals in a two-

dimensional n(n + 1) array, and similarly for G and a

copy of the matrix Q, if G is used. Array

itself is

also used for (temporarily) storing the residual matrix

R (X

), as well as the intermediate matrices X

and

the ﬁnal solution.

If G is to be used (since m > n/3), but the norm of

G is too large, then its factor D is used thereafter, in

order to enhance the numerical accuracy, even if the

efﬁciency somewhat diminishes.

2.2 Computation of the Newton

Direction

The algorithm computes the initial residual matrix

R (X

) and the matrix op(A

), where A

:= op(A) ±

op(E). If no initial matrix X

is given, we set

= 0, R (X

) = Q and op(A

) = A.

At the beginning of the iteration k, 0 ≤ k ≤ k

max

the algorithm decides to terminate or continue the

computations, based on the current normalized resid-

ual r(X

). If r(X

) > τ, a standard (if E = I

) or gen-

eralized (otherwise) Lyapunov equation

op(A

)

op(E) + op(E)

op(A

) = − σR (X

(8)

is solved in N

(the Newton direction), using SLICOT

subroutines. The scalar σ ≤ 1 is set by the Lyapunov

solver in order to prevent solution overﬂowing. Nor-

mally, σ = 1.

Another option is to scale the matrices A

and

E (if E is general) for solving the Lyapunov equa-

tions, and suitably update their solutions. Note that

the LAPACK subroutines

DGEES

and

DGGES

, (Ander-

son et al., 1999) which are called by the SLICOT

standard and generalized Lyapunov solvers, respec-

tively, to compute the real Schur(-triangular) form,

do not scale the cefﬁcient matrices. Just column and

row permutations are performed, to separate isolated

eigenvalues. For some examples, this fact created

troubles: the convergence was not achieved in a rea-

sonable number of iterations. This difﬁculty was re-

moved by the scaling included in the Newton code.

2.3 Computation of the Newton Step

Size

The next step is the computation of the optimal size

of the Newton step (line search). The procedure mini-

mizes the Frobeniusnorm of the residual matrixalong

the Newton direction, N

. Speciﬁcally, the optimal

step size t

is given by

= argmin

kR (X

+ tN

. (9)

It is proved (Benner, 1997) that, in certain standard

conditions,an optimalt

exists, andit is in the “canon-

ical” interval [0,2]. Computationally, t

is found as

the argument of the minimal value in [0,2] of a poly-

nomial of order 4. Indeed,

R (X

+ tN

) = (1−t)R (X

) −t

, (10)

where V

= op(E)

op(E). Therefore, the

minimization problem (9) reduces to the minimiza-

tion of the quartic polynomial (Benner, 1997)

(t) = trace(R (X

+ tN

)

= α

(1−t)

−2β

(1−t)t

+ γ

, (11)

where α

= trace(R (X

)

), β

= trace(R (X

= trace(V

In order to solve the minimization problem (9), a

cubic polynomial (the derivative of f

(t)) is set up,

whose roots in [0,2], if any, are candidates for the so-

lution of the minimum residual problem. The roots

of this cubic polynomial are computed by solving an

equivalent 4-by-4 standard or generalized eigenprob-

lem, following (J´onsson and Vavasis, 2004). Speciﬁ-

cally, let the cubic polynomial be deﬁned by

p(t) = a+ bt + ct

+ dt

Normally, a matrix pencil is built, whose eigenvalues

are the roots of the given polynomial, and they are

computed using the QR and QZ algorithms, depend-

ing on the magnitude of the polynomial coefﬁcients.

ComputationalExperienceinSolvingContinuous-timeAlgebraicRiccatiEquationsusingStandardandModifiedNewton's

Method

A candidate solution should satisfy the following

requirements: (i) it is real; (ii) it is in the interval [0,2];

(iii) the second derivative of the cubic polynomial is

positive. If no solution is found, then t

is set equal to

1. If two solutions are found, then t

is set to the value

corresponding to the minimum residual.

2.4 Convergence Tests and Updating the

Current Iterate

The next action is to check if the line search stagnates

and/or the standard Newton step is to be preferred. If

n > 1, k ≤ 10, t

< 0.5, ε

1/4

< r

< 1, and k

R (X

≤10, or k

R (X

> τ

kR (X

k−k

(i.e., stagnation is detected), then a standard Newton

step (t

= 1) is used.

Another test is to check if updating X

is mean-

ingful. The updating is done if t

> ε

If this is the case, set X

k+1

= X

+ t

, and compute

the updated matrices op(A

k+1

) and R (X

k+1

). Other-

wise, the iterative process is terminated and a warn-

ing value is set, since no further improvement can be

expected. Although the computation of the residual

R (X

+ t

) can be efﬁciently performed by updat-

ing the residual R (X

), the original data is used, since

the updating formula (10) could suffer from severe

numerical cancellation, and hence it could compro-

mise the accuracy of the intermediate results.

Then, kX

k+1

and r

k+1

are computed, and k =

k+ 1 is set. If the chosen step was not a Newton step,

but the residual norm increased compared to the pre-

vious iteration, i.e., kR (X

k+1

≥ kR (X

, but

it is less than 1, and the normalized residual is less

than ε

1/4

, then the iterative process is terminated and

a warning value is set. Otherwise, the iteration con-

tinues.

3 NUMERICAL RESULTS

This section presents some results of an extensiveper-

formance investigation of the solvers based on New-

ton’s method. The numerical results have been ob-

tained on an Intel Core i7-3820QMportable computer

at 2.7 GHz, with 16 GB RAM, with the relative ma-

chine precision ε

≈ 2.22×10

−16

, using Windows 7

Professional (Service Pack 1) operating system (64

bit), Intel Visual Fortran Composer XE 2011 and

MATLAB 8.0.0.783 (R2012b). The SLICOT-based

MATLAB executable MEX-functions have been built

using MATLAB-provided optimized LAPACK and

BLAS subroutines.

3.1 Randomly Generated Systems

A ﬁrst set of tests refer to CAREs (4) with initial

matrices E, A, B, L, Q, and R randomly generated

from a uniform distribution in the (0,1) interval, with

n and m set as n = 200 : 200 : 1000, m = 200 : 200 : n

(in MATLAB notation). The generated matrix E was

stabilized by subtracting 100·norm(E) from the diag-

onal. The generated matrices Q and R were modi-

ﬁed by adding n and m, respectively, to the diagonal

entries, and then each of them was symmetrized, by

adding its transpose. The generated matrix L was di-

vided by 100. We then used the MATLAB function

care

from the Control System Toolbox (MATLAB,

2011) with inputs A, B, Q, R, L, and E, and stabilized

A using A := A −BF, where F is the feedback gain

matrix returned by

care

. A new Riccati solution was

computed by

care

using the modiﬁed A and the other

matrices. This allowed us to set to zero the initial ma-

trix X

. For the Newton solver, we removed the effect

of L using the formulas (3). Fifteen CARE problems

havebeen generated. For each CARE, variousoptions

havebeen tried (e.g., use either the upper or lower part

of symmetric matrices, use the two values of op(M),

use either the matrices B and R, or the matrix G). The

default tolerance, computed by the solver when the

input value is non-positive, has been used.

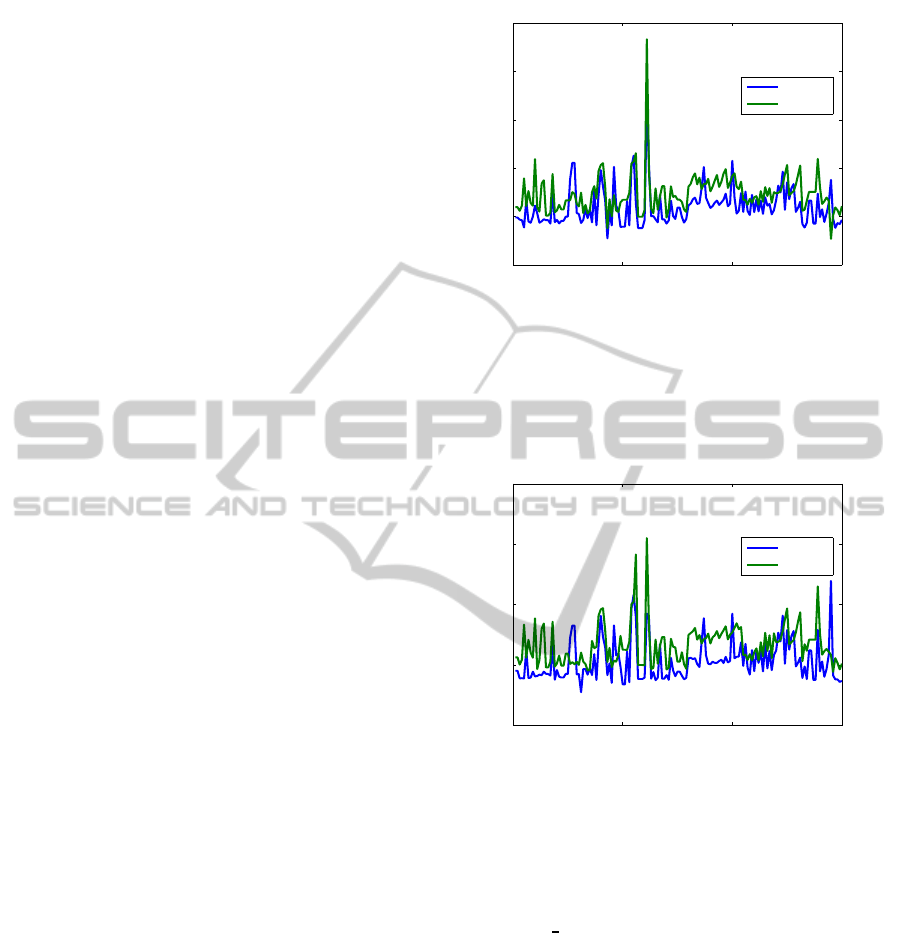
Fig. 1 presents the normalized residuals for the

random examples solved using Newton solver with

line search, and

care

. Fig. 2 presents the CPU times

(computed using the MATLAB pair functions

tic

and

toc

). The y-axis is scaled logarithmically, for

better clarity, since the CPU times vary signiﬁcantly.

For the largest example, the run time for the Newton

solver and op(M) = M is about half the run time for

care

0 5 10 15

−12

−10

−8

−6

−4

−2

Example #

Normalized residuals

Newton, op(M) = M

care, op(M) = M

Figure 1: The normalized residuals for random examples

using Newton solver with line search and

care

; n = 200 :

200 : 1000, m = 200 : 200 : n.

Similarly, Fig. 3 and Fig. 4 present the normalized

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

0 5 10 15

−1

Example #

CPU time

Elapsed CPU time

Newton, op(M) = M

care, op(M) = M

Figure 2: The CPU times for random examples using New-

ton solver with line search and

care

; n = 200 : 200 : 1000,

m = 200 : 200 : n.

residuals and the CPU times, respectively, when using

standard Newton solver and

care

. The large error for

an example with n = 600, m = 200 (and op(M) =

) is not typical.

0 5 10 15

−12

−10

−8

−6

−4

−2

Example #

Normalized residuals

Newton, op(M) = M

care, op(M) = M

Figure 3: The normalized residuals for random examples

using standard Newton solver and

care

; n = 200 : 200 :

1000, m = 200 : 200 : n.

For both variants, the Newton solver was almost

always faster than

care

. It was also (with one excep-

tion) signiﬁcantly more accurate. Note that for this set

of tests, the problems with op(M) = M

needed more

iterations and CPU time for Newton solver than those

with op(M) = M, especially for the standard Newton

solver. Indeed, the standard Newton solver was most

often over 50% faster than

care

for op(M) = M, but

often over 20% slower than

care

for op(M) = M

The Euclidean norm of the vectors of normalized

residuals (one normalized residual for each example)

and the mean number of iterations are shown in Ta-

ble 1 for the case op(M) = M.

We have also solved a problem with n = m =

2000, built as above. Newton solver with line search

needed 4 iterations when op(M) = M, and 7 iter-

0 5 10 15

−1

Example #

CPU time

Elapsed CPU time

Newton, op(M) = M

care, op(M) = M

Figure 4: The CPU times for random examples using stan-

dard Newton solver and

care

; n = 200 : 200 : 1000, m =

200 : 200 : n.

Table 1: Normalized residuals 2-norms and mean number

of iterations for random examples.

L. search Standard

care

1:15

2.98·10

−8

3.01·10

−8

1.55·10

−4

∑

5.6 5.33 −

ations when op(M) = M

. The CPU times were

about 793 and 1360 seconds, and the normalized

residuals were 8.41·10

−9

and 4.4·10

−9

, respectively.

MATLAB

care

needed about 1350 and 1530 sec-

onds, and the normalized residuals were 2.31 ·10

−7

and 3.66· 10

−7

, respectively. Similarly, when E =

, the results for the Newton solver were: 4 and

9 iterations, 68 and 469 seconds, and normalized

residuals 1.69· 10

−10

and 3.22 · 10

−13

, respectively.

MATLAB

care

needed 99.4 and 100 seconds, and

the normalized residuals were 1.61 ·10

−11

and 1.01·

−11

, respectively.

3.2 Systems from the COMPl

Collection

Other tests have been performed for linear systems

from the COMPl

ib collection (Leibfritz and Lipin-

ski, 2003; Leibfritz and Lipinski, 2004). This collec-

tion contains 124 standard continuous-time examples

(with E = I

), with several variations, giving a total of

168 problems. All but 16 problems (for systems of or-

der larger than 2000, with matrices in sparse format)

have been tried. The performance index matrices Q

and R have been chosen as identity matrices of suit-

able sizes. The matrix L was always zero. Most often

we used the default tolerance.

In a series of tests, we used X

set to a zero ma-

trix, if A is stable; otherwise, we tried to initialize the

Newton solver with a matrix computed using the al-

gorithm in (Hammarling, 1982), and when this algo-

ComputationalExperienceinSolvingContinuous-timeAlgebraicRiccatiEquationsusingStandardandModifiedNewton's

Method

rithm failed to deliver a stabilizing initialization, we

used the solution provided by the MATLAB function

care

. A zero initialization was used for 44 stable ex-

amples. Stabilization algorithm was tried on 107 un-

stable systems, and succeeded for 91 examples. Fail-

ures occurred for 16 examples. With default toler-

ance, the implementation of the Newton solver used

in the preliminary version of this paper did not im-

prove the

care

solution, returning with 0 iterations.

But, modifying the test at Step 1 of Algorithm N, in

order to continue the calculations at iteration k = 0,

enabled to improve the accuracy of

care

solution for

15 examples. (Only the solution for example ROC5

could not be improved.) The function

care

failed to

solve the Riccati equation for example REA4, with

the error message “There is no ﬁnite stabilizing solu-

tion”. This unstable example has been excluded from

our tests, because it could not be stabilized.

We tried both standard and modiﬁed Newton’s

method, with or without balancing the coefﬁcient ma-

trices of the Lyapunovequations. The modiﬁedsolver

needed more iterations than the standard solver for

10 examples only. The cumulative number of itera-

tions with modiﬁed and standard solver for all 150

examples was 1654 and 2289, respectively. With bal-

ancing, the total number of iterations was 1657 and

2279, respectively. The mean number of iterations

was about 11, for the modiﬁed solver, and 15.2, for

the standard solver. We tried also to use the stabiliza-

tion algorithm whenever possible, including for stable

A matrices. Doing so, the total number of iterations

without balancing was 1796 and 2208, respectively

(1784 and 2207, with balancing).

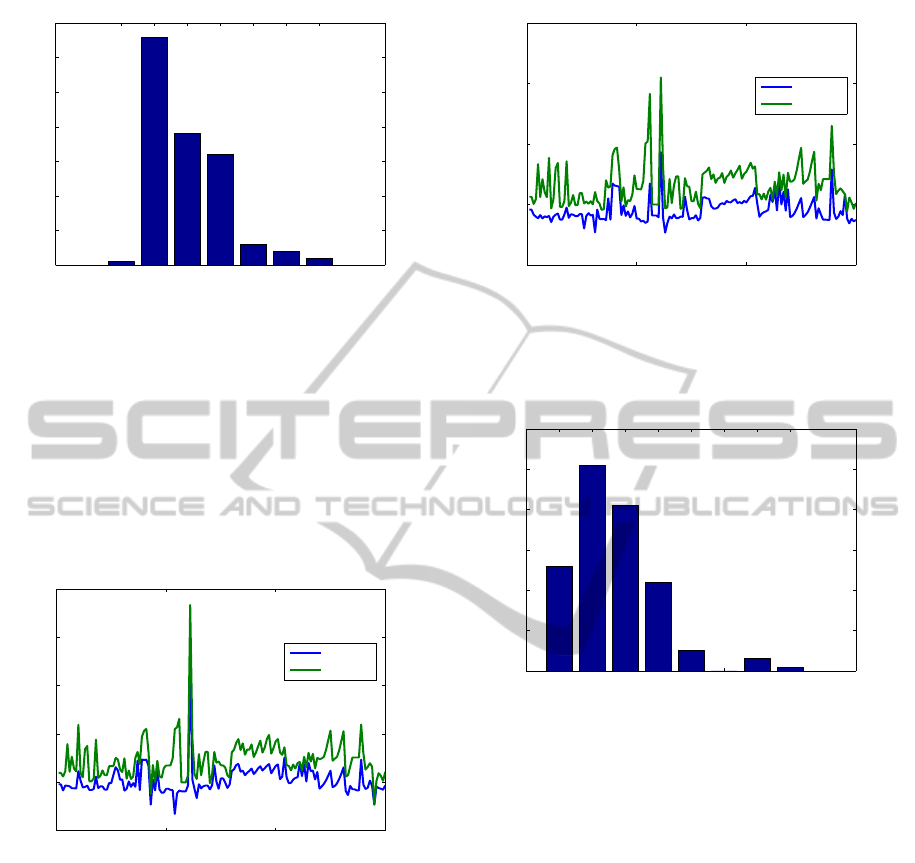
Fig. 5 shows the normalized residuals for the

COMPl

ib examples. For clarity, only the results for

Newton solver with line search without balancing and

for

care

are plotted. Note that the normalized resid-

ual is higher than 1 for the TL example when using

care

. (Its value is 2.13·10

for

care

, but 1.09·10

−3

for the Newton solver, and 1.32 ·10

−3

, using a stabi-

lizing X

6= 0.) The matrices A and B of this example

have norms of order 10

and are poorly scaled (the

minimum magnitude in A is of order 10

−4

). Omitting

example TL, the maximum normalized residual was

of order 10

−6

for the standard Newton solver, and of

order 10

−9

(10

−10

with balancing) for the modiﬁed

solver and

care

Similarly, Fig. 6 shows the relativeresiduals, com-

puted in a similar manner with that used in

care

. The

maximum value of these residuals is 8.98 ·10

−9

for

the modiﬁed Newton solver (for example ROC5), and

3.16·10

−5

for

care

(for example TL) . (Its value was

1 for the standard Newton solver and example TL!)

Omitting example TL, the maximum relative residual

0 50 100 150

−20

−15

−10

−5

Example #

Normalized residuals

Newton

care

Figure 5: The normalized residuals for examples from the

COMPleib collection, using Newton solver with line search

without balancing and

care

was of order 10

−7

for the standard Newton solver and

of order 10

−6

for

care

0 50 100 150

−20

−15

−10

−5

Example #

Relative residuals

Newton

care

Figure 6: The relative residuals for examples from the

COMPleib collection, using Newton solver with line search

and

care

Figure 7 shows the number of iterations of the

Newton solver with line search for the COMPl

ib ex-

amples. The largest number, 34, was applied for ex-

ample CM5

IS, with order n = 480, and m = 1.

Similarly, Fig. 8 shows the elapsed CPU times.

Although the modiﬁed Newton method was faster

than

care

for 100 examples, out of 150, the sum of

the CPU times was about 64% larger than for

care

This is mainly due to the fact that, with the chosen

initialization, some large examples (mainly, 15 exam-

ples in the HF2D class) required at least 19 iterations.

The standard Newton solver was globally over 25%

slower than the solver with line search. The balanc-

ing option increased the CPU times by less than 4%

in both cases. When using stabilizing X

6= 0, the

speed-up of the modiﬁed Newton solver increased by

about 30%; the main contribution came from solving

the ARE for example CM6 (n = 960, m = 1) in just

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

0 50 100 150

Example #

Number of iterations

Number of iterations (Newton with line search)

Figure 7: The number of iterations performed by the New-

ton solver with line search for examples from the COMPleib

collection.

one iteration, compared to 19 iterations needed when

= 0 was used. (Note that the stabilization algo-

rithm did not work for example CM6, so X

was set

to the

care

solution.) Clearly, a good initialization

could signiﬁcantly reduce the number of iterations.

0 50 100 150

−4

−2

Example #

CPU time

Elapsed CPU time

Newton

care

Figure 8: The elapsed CPU time needed by the Newton

solver with line search and MATLAB

care

for examples

from the COMPleib collection.

When the solution returned by

care

was used to

initialize the Newton solver variants for all COMPl

examples, with default tolerance and without the

modiﬁcation, mentioned before, of the test at Step 1,

the total number of iterations was 69, namely 50 it-

erations for TL, and one iteration for other 19 ex-

amples. The remaining examples were solved with-

out any iterations, since

care

results were accurate

enough with the default tolerance. The sum of the

CPU times for Newton solver was about 2.4 seconds,

compared to about 53.8 seconds for

care

. The nor-

malized residual decreased to 1.05·10

−3

for exam-

ple TL, but the relative residual slightly increased to

9.76·10

−6

. Omitting the example TL, the maximum

normalized residual decreased to 9.17·10

−10

(for ex-

ample EB6, with n = 160, m = 1), and the maximum

relative residual was 3.85·10

−10

(for example ISS2,

with n = 270, m = 3).

After modifying the test at Step 1 to force the

solver to try at least an update, and after adding a

test of relative residual, the total number of itera-

tions increased to 159, namely 11 iterations for ex-

ample TL, zero iterations for ROC5, and one itera-

tions for the other examples. The sum of the CPU

times for Newton solver was then about 8.3 sec-

onds. The normalized residual for example TL var-

ied in between 9.3 ·10

−4

and 1.3·10

−3

for the four

variants (with/without line search and with/without

balancing), and the relative residual varied between

1.61 ·10

−11

and 2.05·10

−11

. Omitting the example

TL, the maximum normalized residual decreased to

6.9·10

−13

for Newton solver, and 3.6·10

−9

for

care

(for example HF2D IS5, with n = 5, m = 2), and the

maximum relative residual was 8.42·10

−13

(for ex-

ample CBM, with n = 348, m = 1). The decision to

keep this modiﬁcation of the tests was based on these

improved results.

We used the same initialization provided by

care

with values for the tolerance parameter τ set to 10

−12

−14

, and relative machine precision, ε

For τ = 10

−12

, the behavior was identicalwith that

for the default τ. For τ = 10

−14

, example TL needed

50 iterations without convergence (the tolerance be-

ing too small), one example needed 6 iterations, 2 ex-

amples needed 5 iterations, 3 examples needed 4 iter-

ations, 14 examples needed 3 iterations, 9 examples

needed 2 iterations, 119 examples needed one itera-

tion, and ROC5 needed no iteration. The repartition

of the number of iterations for τ = ε

is shown in

the bar graph from Fig. 9, where TL example was ex-

cluded, for clarity. Only for ROC5 example, the New-

ton solver returned before ﬁnishing the ﬁrst iteration

(reporting 0 iterations); it found that no improvement

of X

is numerically possible, since the norm of the

correction t

, 3.07·10

−14

, was too small compared

to the norm of X

, which is 1.41 ·10

. (The normal-

ized residual value for X

was 4.88 ·10

−18

.) Omit-

ting TL, the maximum normalized residual reduced

to 6.9·10

−13

for τ = 10

−12

, and to about 3.5 ·10

−13

for smaller values of τ. Performance results are sum-

marized in Table 2.

Table 2: Summary of performance results for small toler-

ance τ and initialization by MATLAB

care

τ Total iterations Sum of CPU times

−12

198 10.83

−14

257 23.79

344 26.23

ComputationalExperienceinSolvingContinuous-timeAlgebraicRiccatiEquationsusingStandardandModifiedNewton's

Method

0 1 2 3 4 5 6

Repartition of the number of iterations

Number of examples

Number of iterations

Figure 9: Bar graph showing the repartition of the num-

ber of iterations for examples from the COMPleib collec-

tion, using Newton solver with line search without balanc-

ing, initialization using

care

and tolerance relative machine

precision.

Fig. 10 shows the normalized residuals for the New-

ton solver with line search, initialized by

care

, and

with tolerance τ = ε

. Clearly, Newton solver re-

duces the residuals by several orders of magnitude,

compared to

care

0 50 100 150

−20

−15

−10

−5

Example #

Normalized residuals

Newton

care

Figure 10: The normalized residuals for examples from the

COMPleib collection, using Newton solver with line search

without balancing, initialization using

care

and tolerance

relative machine precision.

Fig. 11 shows similarly the relative residuals. Ex-

cept for ROC5, Newton solver always reduces the

residuals, often by several orders of magnitude, com-

pared to

care

. Fig. 12 shows by a bar graph the size

of this improvement. Speciﬁcally, the improvement is

of seven orders of magnitude for one example, six or-

ders for three examples, four ordersfor ﬁve examples,

etc. For 114 examples, the improvement is between

one and three (inclusive) orders of magnitude.

0 50 100 150

−20

−15

−10

−5

Example #

Relative residuals

Newton

care

Figure 11: The relative residuals for examples from the

COMPleib collection, using Newton solver with line search

without balancing, initialization using

care

and tolerance

relative machine precision.

1 2 3 4 5 6 7 8

Improvement of relative residuals

Number of examples

Figure 12: Bar graph showing the improvement of the rela-

tive residuals for examples from the COMPleib collection,

using Newton solver with line search without balancing, ini-

tialization using

care

and tolerance relative machine preci-

sion. The height of the i-th vertical bar indicates the num-

ber of examples for which the improvement was between

i-1 and i orders of magnitude.

4 CONCLUSIONS

Basic theory and improved algorithms for solving

continuous-time algebraic Riccati equations using

Newton’s method with or without line search have

been presented. Algorithmic details for the devel-

oped solvers, the main computational steps (ﬁnding

the Newton direction, ﬁnding the Newton step size),

and convergence tests are described. The usefulness

of such solvers is demonstrated by the results of an

extensive performance investigation of their numeri-

cal behavior, in comparison with the results obtained

using the widely-used MATLAB function

care

. Ran-

domly generated systems with orders till 1000 (and

even a system with order 2000),as well as the systems

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

from the large COMPl

ib collection, are considered.

The numerical results most often show signiﬁcantly

improved accuracy (measured in terms of normalized

and relative residuals), and greater efﬁciency. The re-

sults strongly recommend the use of such algorithms,

especially for improving, with little additional com-

puting effort, the solutions computedby other solvers.

ACKNOWLEDGEMENTS

Part of this work was done many years ago in a

research stay at the Technical University Chemnitz,

Germany, during November 1 – December 20, 2005,

with the ﬁnancial support from the German Science

Foundation. The long cooperation with Peter Benner

from Technical University Chemnitz and Max Planck

Institute for Dynamics of Complex Technical Sys-

tems, Magdeburg, Germany, is much acknowledged.

Thanks are also addressed to Martin Slowik from In-

stitut f¨ur Mathematik, Technical University Berlin,

who worked out (till 2005) a preliminary version of

the SLICOT codes for continuous-timealgebraic Ric-

cati equations. The work has been recently resumed

by the author. Finally, the continuing support from

the NICONET e.V. is warmly acknowledged.

REFERENCES

Abels, J. and Benner, P. (1999). CAREX—A collec-

tion of benchmark examples for continuous-time al-

gebraic Riccati equations (Version 2.0). SLICOT

Working Note 1999-14, Katholieke Universiteit Leu-

ven, ESAT/SISTA, Leuven, Belgium. Available from

http://www.slicot.org.

Anderson, B. D. O. and Moore, J. B. (1971). Linear

Optimal Control. Prentice-Hall, Englewood Cliffs,

New Jersey.

Anderson, E., Bai, Z., Bischof, C., Blackford, S., Demmel,

J., Dongarra, J., Du Croz, J., Greenbaum, A., Ham-

marling, S., McKenney, A., and Sorensen, D. (1999).

LAPACK Users’ Guide: Third Edition. Software ·En-

vironments · Tools. SIAM, Philadelphia.

Arnold, III, W. F. and Laub, A. J. (1984). Generalized

eigenproblem algorithms and software for algebraic

Riccati equations. Proc. IEEE, 72(12):1746–1754.

Benner, P. (1997). Contributions to the Numerical So-

lution of Algebraic Riccati Equations and Related

Eigenvalue Problems. Dissertation, Fakult¨at f¨ur Math-

ematik, Technische Universit¨at Chemnitz–Zwickau,

D–09107 Chemnitz, Germany.

Benner, P. (1998). Accelerating Newton’s method for

discrete-time algebraic Riccati equations. In Beghi,

A., Finesso, L., and Picci, G., editors, Mathemati-

cal Theory of Networks and Systems, Proceedings of

the MTNS-98 Symposium held in Padova, Italy, July,

1998, pages 569–572. Il Poligrafo, Padova, Italy.

Benner, P. and Byers, R. (1998). An exact line search

method for solving generalized continuous-time alge-

braic Riccati equations. IEEE Trans. Automat. Contr.,

43(1):101–107.

Benner, P., Byers, R., Losse, P., Mehrmann, V., and

Xu, H. (2007). Numerical solution of real skew-

Hamiltonian/Hamiltonian eigenproblems. Technical

report, Technische Universit¨at Chemnitz, Chemnitz.

Benner, P., Byers, R., Mehrmann, V., and Xu, H. (2002).

Numerical computation of deﬂating subspaces of

skew Hamiltonian/Hamiltonian pencils. SIAM J. Ma-

trix Anal. Appl., 24(1):165–190.

Benner, P., Kressner, D., Sima, V., and Varga, A.

(2010). Die SLICOT-Toolboxen f¨ur Matlab. at—

Automatisierungstechnik, 58(1):15–25.

Benner, P., Mehrmann, V., Sima, V., Van Huffel, S., and

Varga, A. (1999). SLICOT — A subroutine library

in systems and control theory. In Datta, B. N., ed-

itor, Applied and Computational Control, Signals,

and Circuits, volume 1, chapter 10, pages 499–539.

Birkh¨auser, Boston.

Benner, P. and Sima, V. (2003). Solving algebraic Riccati

equations with SLICOT. In CD-ROM Proceedings

of The 11th Mediterranean Conference on Control

and Automation MED’03, June 18–20 2003, Rhodes,

Greece. Invited session IV01, “Computational Tool-

boxes in Control Design”, Paper IV01-01, 6 pages.

Byers, R. (1987). Solving the algebraic Riccati equa-

tion with the matrix sign function. Lin. Alg. Appl.,

85(1):267–279.

Ciubotaru, B. and Staroswiecki, M. (2009). Comparative

study of matrix Riccati equation solvers for paramet-

ric faults accommodation. In Proceedings of the 10th

European Control Conference, Budapest, Hungary,

pages 1371–1376.

Francis, B. A. (1987). A Course in H

∞

Control Theory,

volume 88 of Lect. Notes in Control and Information

Sciences. Springer-Verlag, New York.

Gardiner, J. D. and Laub, A. J. (1986). A generalization of

the matrix sign function solution for algebraic Riccati

equations. Int. J. Control, 44:823–832.

Hammarling, S. J. (1982). Newton’s method for solving the

algebraic Riccati equation. NPC Report DIIC 12/82,

National Physics Laboratory, Teddington, Middlesex

TW11 OLW, U.K.

J´onsson, G. F. and Vavasis, S. (2004). Solving polynomials

with small leading coefﬁcients. SIAM J. Matrix Anal.

Appl., 26(2):400–414.

Kleinman, D. L. (1968). On an iterative technique for Ric-

cati equation computations. IEEE Trans. Automat.

Contr., AC–13:114–115.

Lancaster, P. and Rodman, L. (1995). The Algebraic Riccati

Equation. Oxford University Press, Oxford.

Lanzon, A., Feng, Y., Anderson, B. D. O., and Rotkowitz,

M. (2008). Computing the positive stabilizing solu-

tion to algebraic Riccati equations with an indeﬁnite

quadratic term via a recursive method. IEEE Trans.

Automat. Contr., AC–50(10):2280–2291.

ComputationalExperienceinSolvingContinuous-timeAlgebraicRiccatiEquationsusingStandardandModifiedNewton's

Method

Laub, A. J. (1979). A Schur method for solving algebraic

Riccati equations. IEEE Trans. Automat. Contr., AC–

24(6):913–921.

Leibfritz, F. and Lipinski, W. (2003). Description of the

benchmark examples in COMPl

ib. Technical report,

Department of Mathematics, University of Trier, D–

54286 Trier, Germany.

Leibfritz, F. and Lipinski, W. (2004). COMPl

ib 1.0 – User

manual and quick reference. Technical report, Depart-

ment of Mathematics, University of Trier, D–54286

Trier, Germany.

MATLAB (2011). Control System Toolbox User’s Guide.

Version 9.

Mehrmann, V. (1991). The Autonomous Linear Quadratic

Control Problem. Theory and Numerical Solution,

volume 163 of Lect. Notes in Control and Infor-

mation Sciences (M. Thoma and A. Wyner, eds.).

Springer-Verlag, Berlin.

Mehrmann, V. and Tan, E. (1988). Defect correction meth-

ods for the solution of algebraic Riccati equations.

IEEE Trans. Automat. Contr., AC–33(7):695–698.

Penzl, T. (1998). Numerical solution of generalized Lya-

punov equations. Advances in Comp. Math., 8:33–48.

Penzl, T. (2000). LYAPACK Users Guide. Technical Report

SFB393/00–33, Technische Universit¨at Chemnitz,

Sonderforschungsbereich 393, “Numerische Simula-

tion auf massiv parallelen Rechnern”, Chemnitz.

Raines, III, A. C. and Watkins, D. S. (1992). A class of

Hamiltonian-symplectic methods for solving the alge-

braic Riccati equation. Technical report, Washington

State University, Pullman, WA.

Roberts, J. (1980). Linear model reduction and solution of

the algebraic Riccati equation by the use of the sign

function. Int. J. Control, 32:667–687.

Sima, V. (1981). An efﬁcient Schur method to solve the sta-

bilizing problem. IEEE Trans. Automat. Contr., AC–

26(3):724–725.

Sima, V. (1996). Algorithms for Linear-Quadratic Opti-

mization, volume 200 of Pure and Applied Mathemat-

ics: A Series of Monographs and Textbooks. Marcel

Dekker, Inc., New York.

Sima, V. (2005). Computational experience in solving

algebraic Riccati equations. In Proceedings of the

44th IEEE Conference on Decision and Control and

European Control Conference ECC’ 05, 12–15 De-

cember 2005, Seville, Spain, pages 7982–7987. Om-

nipress.

Sima, V. (2010). Structure-preserving computation of

stable deﬂating subspaces. In Kayacan, E., editor,

Proceedings of the 10th IFAC Workshop “Adapta-

tion and Learning in Control and Signal Process-

ing” (ALCOSP 2010), Antalya, Turkey, 26–28 Au-

gust 2010 (CD-ROM), 6 pages. IFAC-PapersOnLine,

Volume 10, Part 1, http://www.ifac-papersonline.net/

Detailed/46793.html.

Sima, V. (2011). Computational experience with structure-

preserving Hamiltonian solvers in optimal control. In

Ferrier, J.-L., Bernard, A., Gusikhin, O., and Madani,

K., editors, Proceedings of the “8th International

Conference on Informatics in Control, Automation

and Robotics” (ICINCO 2011), Noordwijkerhout, The

Netherlands, 28–31 July, 2011 (CD-ROM), volume 1,

pages 91–96. SciTePress—Science and Technology

Publications.

Sima, V. and Benner, P. (2006). A SLICOT imple-

mentation of a modiﬁed Newton’s method for alge-

braic Riccati equations. In Proceedings of the 14th

Mediterranean Conference on Control and Automa-

tion MED’06, June 28-30 2006, Ancona, Italy (CD-

ROM). Omnipress. Session FEA2: Control Systems

5, Paper FEA2-3.

Sima, V. and Benner, P. (2008). Experimental evaluation

of new SLICOT solvers for linear matrix equations

based on the matrix sign function. In Proceedings

of 2008 IEEE Multi-conference on Systems and Con-

trol. 9th IEEE International Symposium on Computer-

Aided Control Systems Design (CACSD), Hilton Pala-

cio del Rio Hotel, San Antonio, Texas, U.S.A., Septem-

ber 3–5, 2008, pages 601–606. Omnipress.

Van Dooren, P. (1981). A generalized eigenvalue approach

for solving Riccati equations. SIAM J. Sci. Stat. Com-

put., 2(2):121–135.

Van Huffel, S. and Sima, V. (2002). SLICOT and con-

trol systems numerical software packages. In Pro-

ceedings of the 2002 IEEE International Conference

on Control Applications and IEEE International Sym-

posium on Computer Aided Control System Design,

CCA/CACSD 2002, September 18–20, 2002, Scottish

Exhibition and Conference Centre, Glasgow, Scot-

land, U.K., pages 39–44. Omnipress.

Van Huffel, S., Sima, V., Varga, A., Hammarling, S., and

Delebecque, F. (2004). High-performance numeri-

cal software for control. IEEE Control Syst. Mag.,

24(1):60–76.

Varga, A. (1981b). A Schur method for pole assignment.

IEEE Trans. Automat. Contr., AC–26(2):517–519.

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics