
Mimicking Complexity
Automatic Generation of Models for the Development of Self-adaptive Systems
J
´
er
´
emy Boes, Pierre Glize and Fr
´
ed
´
eric Migeon
Institut de Recherche en Informatique de Toulouse, Universit
´
e Paul Sabatier, Toulouse, France
Keywords:
Complex Systems Modeling, Multi-Agent Systems, Self-tuning, Self-composition.
Abstract:
Many methods for complex systems control use a black box approach where the internal states and mecha-
nisms of the controlled process are not needed to be known. Usually, such systems are tested on simulations
before their validation on the real world process they were made for. These simulations are based on sharp
analytical models of the target process that can be very difficult to obtain. But is it useful in the case of black
box methods? Since the control system only sees inputs and outputs and is able to learn, we only need to
mimic the typical features of the process (such as non-linearity, interdependencies, etc) in an abstract way.
This paper aims to show how a simple and versatile simulator can help the design of systems that have to deal
with complexity. We present a generator of models used in the simulator and discuss the results obtained in
the case of the design of a control system for heat engines.
1 INTRODUCTION
More and more artificial systems have to deal with
real-world complex processes, like heat engines, bio-
processes or energy management. The design of such
systems usually requires the use of the relevant cor-
responding models so they can be tested on simula-
tions. Unfortunately, models for simulators are very
time consuming to design by the domain experts. This
is due to the great amount of parameters, their interde-
pendencies, the dynamics and the non linearities be-
tween their parts.
Relating our experience in the case of the design
of a heat engine controller, this paper aims to show
that the use of an accurate model is not always re-
quired to ensure the efficiency of a system before its
deployment in the real world. Indeed when the sys-
tem is able to learn during its lifetime and to adapt it-
self to the process, the tests concern the learning skills
and the adaptiveness, for which the simulation fidelity
to the domain is not crucial. Following this idea, we
designed simple and versatile abstract black-boxes to
test our system during its development phase. They
do not represent a specific real-world process, but
only replicate the important features from the adap-
tiveness point of view (such as non-linearity, interde-
pendencies, oscillations or latency). A generator has
been developped to easily build these black-boxes in
order to be able to perform every needed test.
Section 2 gives a short state of the art and explain
why such black-boxes can be adequate, then section 3
details the method to generate them. Section 4 relates
how we use the generated black-boxes and evaluates
their efficiency. Finally, we conclude in section 5 with
an analysis of our approach and future improvements.
2 CONTEXT
Our work on complex systems modeling was driven
by our needs in a research project on complex systems
control. This section gives a succinct state of the art
of this field before speaking about complex system
modeling and simulation.
2.1 Complex Systems Control
Controlling systems is a generic problem that can be
expressed as finding which modifications must be ap-
plied on the inputs in order to obtain the desired ef-
fects on the ouputs. The next paragraphs describe the
main approaches and challenges.
PID - Proportional-Integral-Derivative (PID) are
widely used in the industry. They base the control
on three terms related to the error between the cur-
rent state and the desired state of the process (As-
trom and Hagglund, 1995). PID controllers need a
353
Boes J., Glize P. and Migeon F..
Mimicking Complexity - Automatic Generation of Models for the Development of Self-adaptive Systems.
DOI: 10.5220/0004483003530360
In Proceedings of the 3rd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2013),
pages 353-360
ISBN: 978-989-8565-69-3
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)
heavy parametrization work to fit the controlled sys-
tem. Moreover they are not efficient with non-linear
systems and are difficult to deploy to handle more
than one input, which is a severe drawback for com-
plex systems control.
Adaptive Control - To deal with several inputs and
non-linearity, model-based approaches like Model
Predictive Control (MPC) (Nikolaou, 2001) use mod-
els to forecast the behavior of the process in order to
find the optimal control scheme. These approaches
are limited by the models they use. Building the mod-
els and finding the parameters that fit the actual con-
trolled system is an open problem. This will be de-
tailed in 2.2.
Intelligent Control - Intelligent control regroups ap-
proaches that use Artificial Intelligence methods to
enhance existing controllers and possibly avoid the
use of models. Among these methods we find fuzzy
logic (Lee, 1990), expert systems (Stengel, 1991),
neural networks (Hagan et al., 2002), bayesian con-
trollers (Colosimo and Del Castillo, 2007) and multi-
agent systems (Wang, 2001) or (Videau et al., 2011).
These methods often use a black-box approach where
only inputs and outputs values (but not internal vari-
ables and mechanisms) of the process are known by
the controller. Hence intelligent controllers mostly
rely on their learning skills to find the optimal con-
trol.
The main challenges in complex systems control
are to deal with interdependencies, non-linearity and
high dynamics. But they also include latency and
noise on the data.
2.2 Complex Systems Modeling
In the context of complex systems control, models can
be used in two ways. Either they are incorporated in
the controller to forecast the process behavior, or they
are used in simulators to test the controller before its
use on the real system.
For instance, many models of engines have been
proposed, such as (Borman, 1964) or the Turbo-
charged Diesel Engine (TDE) model (Jankovic and
Kolmanovsky, 2000). The TDE model has seven pa-
rameters. Using this model in a controller involves
to set them so the model fits the controlled engine.
This is a very difficult task, therefore control meth-
ods like NCGPC (Nonlinear Continuous-time Gen-
eralized Predictive Control) use a simplified version
with only three parameters (Dabo et al., 2008). How-
ever, finding the proper values of these parameters re-
mains time consuming and they might become inac-
curate when the engine wears out. The same simpli-
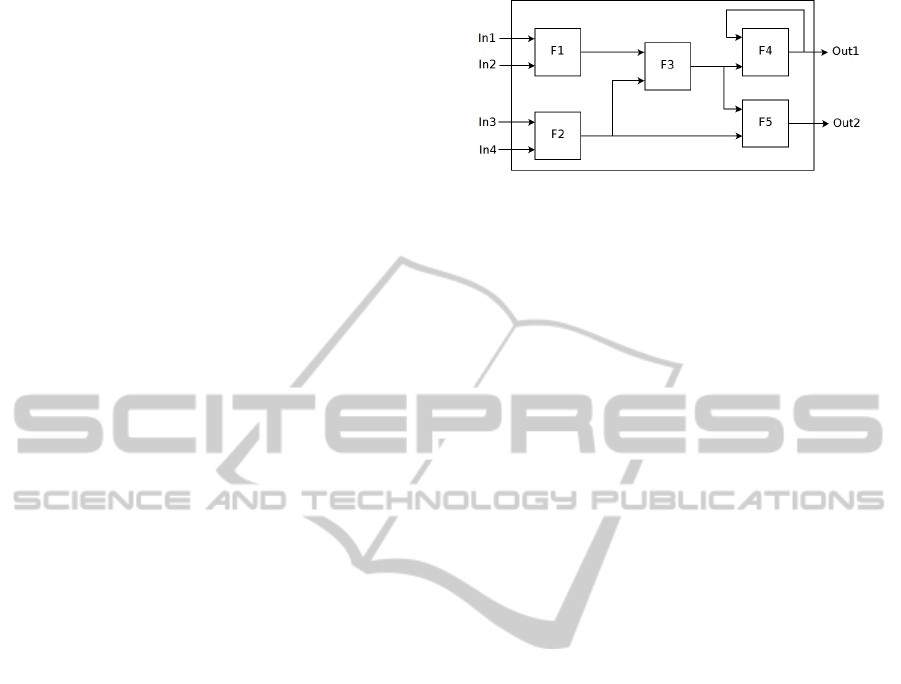
Figure 1: Inside an abstract black-box.
fied TDE model is implemented and used in a simula-
tor to test the NCGPC method, thus avoiding the task
of finding the parameters values.
Other simulation tools focus on different goals
such as finding optimal values of engine parame-
ters (Curto-Risso et al., 2009), comparing fuel per-
formances (Zhang et al., 2012) or leading studies on
the behavior of a specific type of engine (Zhao et al.,
2008). These models are highly specific and demands
a heavy work of implementation and parametrization.
2.3 Simulation Needs
Our needs in term of simulation come from the devel-
opment of a self-adaptive complex systems controller
meant to be applied on heat engines. We want to be
sure of the system’s adaptation skills before applying
it to real-world engines. Thus, we first identified the
challenging characteristics of engines complexity in
order to simulate them to test our system. In this con-
text, the simulation does not need to be accurate but
only to mimic the complexity of real-world engines.
In other words we want to check the behavior of our
system under various levels of interdependency, vari-
ous numbers of inputs and outputs, with linear or non-
linear outputs, with or without latency (or under any
combination of the previous features), regardless of
the relevance of the data relatively to the real engine.
We also need several instances of each case. None of
the existing heat engine models matches our required
degree of modularity.
Furthermore, existing black-box generation tech-
niques either focus on testing large software with a
discrete state-transitions behavior (Tahat et al., 2001)
or are meant to test software components and not the
whole system (Edwards, 2001). We need to run tests
on the system level with a continuous process.
Hence we use simple yet versatile black-boxes
that mimic the complexity of a real-world process and
that can be automatically generated. The models they
use and their generator are presented in the next sec-
tion.
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
354

Table 1: Input Agents: constraints and behavior.
Constraints Associated Behaviors
Bind Constraint: The agent must bind its output port to
at least one Function Agent. Critical level: 1.
Search for Function Agent with a free input port and bind
to it.
Table 2: Output Agents: constraints and behavior.
Constraints Associated Behaviors
Bind Constraint: The agent must bind its input port to
one (and only one) Function Agent. Critical level: 2.
Search for Function Agent and bind to it.
Path Constraint: The agent must link to every Input
Agents of a specified list, through a chain of Function
Agents. Output Agents are initialized with a Path con-
straint regarding to the user specifications. Critical level:
2*size of the list.
Search for a Function Agent linked to some of the tar-
geted Input Agents (if possible), bind to it, and delegate
the Path Constraint.
3 ABSTRACT BLACK-BOXES
In this section we present our abstract black-boxes:
how they are used, what they are made of, and how
they can be easily generated thanks to a multi-agent
system.
3.1 Utilization and Description
Abstract black-boxes are used to simulate a real-
world process in order to test the learning abilities of
an artificial system during its development. They al-
low to focus on a specific feature (or on a combination
of them) of complexity, and to make available a large
collection of different instances of the same feature.
They are composed of inputs, outputs and math-
ematical functions. Only inputs and outputs are ob-
servable from the outside. Each of the inputs are
linked to at least one output through a chain of one or
more functions, and vice versa. The chains of func-
tions can be intermingled and can presents cycles.
The role of inputs and outputs is obvious, they are
the link between the functions and the environment of
the black-box. At each timestep, inputs get a value
from the environment and forward it to their linked
functions, functions compute a value and forward it
to their linked neighbors (either other functions, it-
self or outputs), and outputs get the calculated value
of their linked function and forward it to the environ-
ment. To ease the automated generation presented in
3.2, it has been decided to limit the functions to two
arguments and one calculated value. Figure 1 shows
an example of a 4 inputs - 2 outputs generated black-
box, composed of five functions, containing one cycle
and where each of the four inputs impacts both of the
outputs.
3.2 Generation
A Multi-Agent System, based on the Adaptive Multi-
Agent System theory (Georg
´
e et al., 2011) and called
BACH (Builder of Abstract maCHines), has been
developped to easily and rapidly generate abstract
black-boxes given user-defined constraints. The user
gives the number of inputs, outputs and functions, de-
fines the variation range of each input and output, and
which input impacts which output. He also sets a loop
factor which determines the percentage of functions
that have to be in a cycle in the generated black box.
Then agents are created for each component of the
abstract black-box (Input Agents, Output Agents and
Function Agents). There are two main steps to the
generation. First, the self-composition is in charge of
the respect of the structural constraints (interdepen-
dencies and cycles). Then the self-tuning of the func-
tions ensures that the outputs stay in their specified
range. The self-composition and self-tuning phases
are explained in the next two paragraphs.
3.2.1 Self-Composition
BACH is initialized regarding to the user specifica-
tions: Inputs, Outputs and Functions Agents are cre-
ated and each of them is given a set of individual con-
straints. They have to cooperate and form links be-
tween them to solve these constraints. The resulting
organization is forwarded to the second step of the
generation. The next paragraphs describe the agents,
their constraints and how they solve them.
Architecture and Skills - Agents have inputs and/or
output ports. They can bind their output port to other
agents input ports (and the other way around) but in-
put ports can only be bound once while output ports
can be bound as many times as needed. Input Agents
MimickingComplexity-AutomaticGenerationofModelsfortheDevelopmentofSelf-adaptiveSystems
355

Table 3: Function Agents: constraints and behavior.
Constraints Associated Behaviors
Bind Constraint: The agent must bind its output port to
at least one agent and bind each of its input ports to one
agent. Critical level: 5.
First search a partner to bind the output port, then find a
partner for each of the input ports. Partners can be Input
Agents, Output Agents, Function Agents or itself.
Path Constraint: The agent must link to every Input
Agents of a specified list, either by direct binding or
through a chain of other Function Agents. Function
Agents are not initialized with Path Constraints, but they
eventually receive it from the binding partners on the out-
put port. Critical level: 4*size of the list.
If the agent’s input ports are both free and if the size of the
list is less than or equal to 2, then bind the input ports to
the specified Input Agents. The constraint is then solved.
Else, if the size of the list is greater than two, bind one of
the input port to another Function Agent, split the list in
half and send one of the half to the new partner, keep the
other. If both of the input ports are already bound, split
the list and send a half to each of the partners.
Cycle Constraint: The agent must be in a cycle. Critical
level: 7
Bind the output port to an agent of its input path, or bind
one of its input ports to an agent in its output path, or bind
one of the input port to its own output port.
do not have any input port and can bind their output
port to Function Agents only. Output Agents do not
have any output port and can bind their input port to
Function Agents only. Finally, Functions Agents have
two input ports, one output port and can bind them to
Input Agents, Output Agents or Function Agents (in-
cluding itself).
Constraints - There are three types of constraints with
which agents can be initialized: Bind Constraints rep-
resent the need for an agent to have all of its input and
output ports bound to another agent, Path Constraints
force agents to link to a specific list of Input Agents (if
needed through a chain of Function Agents), and Cy-
cle Constraints express the need for a Function Agent
to be part of a cycle.
Behavior - Each constraint has a critical level repre-
senting its relative significance. Agents try to solve
their most critical constraint first. They have a spe-
cific behavior for each type of constraint, described in
tables 1, 2 and 3.
The choice of a binding partner is based on two
main criteria: its usefulness and its critical level.
First, the agents are sorted between potential and non-
potential partners, whether they can fill the needs of
the selecting agent or not. Then the potential partner
for which the gain in terms of critical level will be
the best is selected. During the self-composition, an
agent may not find any potential partner. This hap-
pens when the user did not specified enough func-
tions regarding to the number of inputs and outputs
and their interdependencies. In other words the user
specified an overconstrained problem. In this case,
the system must release a constraint: the number of
functions. Hence the lonely agent creates a new Func-
tion Agent and they bind immediately.
3.2.2 Self-tuning
Once the structure of the black-box is set by the self-
composition phase, interdependencies and cycles an-
swer a part of the user requirements. Now the self-
tuning of the functions ensures that outputs stay in
the user-specified variation ranges.
Function Agents embed a matrix that is a discrete
representation of their function. The first row and the
first column are the axis (for the arguments) while
other cells contain the value of the function, thus are
called function cells. Table 4 shows an example of a
function f(x,y) where x varies from 1 to 10, y varies
from 0 to 70 and f from 0 to 100. A linear interpo-
lation is perfomed when needed for the computation
of a value. For instance in table 4, f(3.5,60)=4.5. The
self-tuning of the functions is merely the correct fill-
ing of the matrices.
To do so, each Output Agent sends to its bound
Function Agent a message containing its variation
range. The Function Agent randomly puts each bound
in one of the function cells of its matrix and calculates
the other function cells value v using the formula
v = a ∗ d + m (1)
where m is the value of the closest bound, d is the
Manhattan distance to this bound and a is a positive
coefficient if m is the minimum, negative otherwise.
If the computed v is out of bounds, the value of the
closest bound is affected to the cell instead of v. Once
the function cells are filled, the variation range of the
Output Agent is respected. Then, the Function Agent
sends a message containing this range to every Func-
tion Agent (possibly itself) bound to its output. Every
agent receiving this message will consequently adjust
the corresponding axis in its matrix. Finally, Input
Agents send their variation range to their bound Func-
tion Agents, who adjust their corresponding axis.
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
356

Table 4: A Function Agent’s function matrix: axis (grey) and function cells (white).
− 1 2 3 4 5 6 7 8 9 10
0 37 46 55 64 73 82 73 64 55 46
10 46 55 64 73 82 91 82 73 64 55
20 55 64 73 82 91 100 91 82 73 64
30 50 50 50 50 82 91 82 73 64 55
40 45 36 27 18 50 82 73 64 55 46
50 36 27 18 9 18 50 50 50 50 50
60 27 18 9 0 9 18 27 36 45 54
70 36 27 18 9 18 27 36 45 54 63
3.2.3 Generated Black-boxes
Figure 1 shows the result of the self-composition of
four Input Agents, two Output Agents and five Func-
tion Agents while table 4 shows the result of the self-
tuning process for a Function Agent. In addition to
the required characteristics of interdependency and
non-linearity, generated black-boxes exhibit oscilla-
tions (periodic or aperiodic), latency and progressive
stabilization, as shown in figure 2 where inputs are
manually controlled. We can see that the black-box
first takes some time to stabilize itself, then a modifi-
cation is applied on input In4. This causes perturba-
tions on outputs Out1 and Out2, then they eventually
stabilize until another modification applied on input
In3 causes them to move again.
The next section explains how we used the ab-
stract black-boxes during the development of a heat
engine controller, and compares the results of the tests
on generated black-boxes with those obtained on a
real engine.
4 CASE STUDY: THE DESIGN
OF A CONTROL SYSTEM
FOR HEAT ENGINES
Involved in a national project about heat engine con-
trol named Orianne
1
, our role was to develop a self-
calibration algorithm for the engine control unit. This
section explains how abstract black-boxes were used
and describes the results obtained both on simulators
and on real engines. In the following paragraphs ES-
CHER is the name of the self-adaptive controller be-
ing developed and tested, and stands for Emergent
Self-adaptive Control for Heat Engine calibRation.
4.1 Method
We defined a two phases process for the development
1
French acronym for Digital Tool for the Design of En-
gine Control Functions.
Figure 2: Inputs and outputs variations over time of a gen-
erated abstract black-box.
of ESCHER. During the first phase, ESCHER was de-
signed and implemented, and all tests were conducted
on abstract black-boxes. Then the second phase con-
sisted in replacing the black-boxes by a real 125cc
gasoline engine. The goal of this second phase is to
validate the use of abstract black-boxes. Indeed, our
software is able to learn the behavior of the generated
black-boxes to find the best actions to apply to their
inputs, hence being able to do the same with a real en-
gine would mean that the use of abstract black-boxes
is relevant.
4.2 Results
In this section, more information about ESCHER is
given before results on abstract black-boxes and on a
real engine are shown.
MimickingComplexity-AutomaticGenerationofModelsfortheDevelopmentofSelf-adaptiveSystems
357

4.2.1 ESCHER
ESCHER is a Multi-Agent System based on the Self-
Organizing Controller pattern (Boes et al., 2013).
Its function is to find the adequate values of a pro-
cess inputs in order to make the outputs fulfilling
user-defined objectives. These objectives are various
(thresholds, optimizations or setpoints), can change
over time and are expressed as criticality functions
that the system tries to lower. ESCHER has no previ-
ous knowledge about the process other than its inputs
and outputs and their variation ranges. It learns in
real-time from the effects of its actions to adjust itself
to the process and finds the most adequate actions to
apply. In our case, the process is an engine equipped
with its control unit (ECU): the inputs are some of
the parameters of the ECU and the outputs are values
measured on the engine.
In the next paragraphs, we show an example of
test we ran using abstract black-boxes.
4.2.2 Results on Abstract Black-boxes
For this example, we use a black-box with two inputs
(Var0 and Var1) and two outputs (Var2 and Var3). The
objective is to set Var2 and Var3 to the middle of their
range of variation, thus each of the outputs is associ-
ated with a criticality function. ESCHER must find
the value of the inputs for which both of the criticality
functions are at their minimum.
Figure 3 shows the critical levels of the outputs
and the values of the inputs over time. At first ES-
CHER increases only Var1. This causes the critical
levels to drop, so ESCHER keeps on this action until
the critical levels begin to increase. Then ESCHER
changes its behavior, modifying its actions (it starts
to increase Var0, lowers and stabilizes Var1, etc) to
maintain the lowering of the critical levels. Finally
both critical levels reach zero, which means the ob-
jectives have been reached. ESCHER now maintains
the black-box in this state.
We have seen that ESCHER is able to find the
most adequate values for the inputs of abstract black-
boxes (i.e. for which the critical levels are the lowest).
Now we see in the next paragraph how it behaves with
the real engine.
4.2.3 Results on the Real Engine
The following paragraphs describe an example of the
tests conducted on an engine and validated by do-
main experts. The engine is put in a steady operat-
ing point (defined by its rotational speed and its load).
Then ESCHER has to optimize the engine behavior
by modifying specific parameters of the ECU.
Figure 3: Test on an abstract black-box: outputs critical
levels (up) and inputs values (bottom).
ESCHER controls the injected fuel mass along
with the ignition advance. Its goal is to maximize the
torque. Figure 4 shows the torque critical level and
both of the controlled parameters. At first, ESCHER
decreases both of the controlled parameters, causing
the critical level to rise. It corrects this initial mistake,
increasing the injected fuel mass first, then the igni-
tion advance. It eventually finds the optimum value
for which the critical level is the lowest.
Before analysing these results, it is important to
note that alhough the test shown in 4.2.2 is simple and
easily explainable, BACH was used to generate heav-
ier black boxes that allowed us to enhance ESCHER.
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
358

Figure 4: Test on a real engine: torque critical level and
inputs values (injected fuel mass and ignition advance).
4.2.4 Analysis
ESCHER is able to adapt itself and to find an op-
timum for abstract black-boxes as well as for the
real engine. This means that the models used in the
black-boxes correctly replicate the main aspects of
the engine in terms of non-linearity and degree of in-
terdependency. The behavior of ESCHER faced to
these main aspects of complexity was properly tested
thanks to the generated abstract black-boxes. How-
ever, some adjustements in the way ESCHER inter-
acts with the process had to be made before obtaining
these results.
This was due to the fact that two important fea-
tures had not been tested with the black-boxes: the
noise on the perceived data, and the latency between
an action and its effects. As ESCHER reacts quickly
to correct its mistakes, the noise did not prevent the
system to work properly, it only made it make a few
more mistakes. But the latency caused more difficul-
ties, the system was not able to find the correlation
between its actions and its observations of the pro-
cess behavior. We overcomed this problem by slow-
ing down ESCHER, making it wait three seconds be-
tween its actions and its perceptions.
As most of the work had been done thanks to the
black-boxes, the second phase of development lasted
about three months (versus 12 months for the first
phase) and was only about minor modifications. In
conclusion, the abstract black-boxes were sufficient
for a very large part of the development of ESCHER
but still need some improvements to be more efficient.
This will be discussed in the next section.
5 CONCLUSIONS AND FUTURE
WORKS
In this paper, we presented models that replicate some
aspects of complexity and a way to simply generat-
ing them and use them as black-boxes. We showed
that they can be used during the development of self-
adaptive systems to test the adaptiveness skills be-
cause they properly imitate the main features of com-
plex systems. The easy generation allows to produce
tailored simulators. Interdependencies are ensured
by the slef-composition process while non-linearity
is provided by the self-tuning process. Latency can
be obtained by varying the number of functions in the
model. As abstract black-boxes only rely on general
properties of the real world processes they represent,
they remain generic and can be used in various do-
mains. They allowed us to abstract the specifics of
engines and thus to obtain a generic controller.
We claim that this approach avoids a time consum-
ing work: the creation of a fitted model of the system
we have to control. We show that the self-adaptive
control system tested on abstract black-boxes gives
interesting results when applied on a real heat engine.
Nevertheless abstract black-boxess are only interest-
ing when we have to develop a software able to learn.
Our future works will focus on two main draw-
backs: the absence of noise simulation and the lack
of control on the generation process. The first one
should be dealt by adding some classical noise gen-
eration algorithms on the Output Agents, such as
(Taralp et al., 1998). The second one leads to the
generation of models that are too intricate when the
MimickingComplexity-AutomaticGenerationofModelsfortheDevelopmentofSelf-adaptiveSystems
359

number of functions is too high. The outputs stay in
their user-defined variation range but are unable to re-
ally reach their minimum and maximum. This should
be handled by finding better behaviors for the agents
of BACH during the self-composition process. Fi-
nally, the self-tuning process can also be improved
by adding different methods for the calculation of
the matrices, such as b-splines surfaces (Catmull and
Clark, 1978).
REFERENCES
Astrom, K. J. and Hagglund, T. (1995). PID Controllers:
Theory, Design, and Tuning. Instrument Society of
America, Research Triangle Park, NC, second edition.
Boes, J., Migeon, F., and Gatto, F. (2013). Self-Organizing
Agents for an Adaptive Control of Heat Engine. In
International Conference on Informatics in Control,
Automation and Robotics (ICINCO), Reykjavik. IN-
STICC Press.
Borman, G. (1964). Mathematical simulation of inter-
nal combustion engine processes and performance in-
cluding comparison with experiment. PhD thesis,
Univ. of Wisconsin.
Catmull, E. and Clark, J. (1978). Recursively gener-
ated b-spline surfaces on arbitrary topological meshes.
Computer-Aided Design, 10(6):350 – 355.
Colosimo, B. M. and Del Castillo, E., editors (2007).
Bayesian Process Monitoring, Control and Optimiza-
tion. Taylor and Francis, Hoboken, NJ.
Curto-Risso, P. L., Medina, A., and Calvo Hernandez, A.
(2009). Optimizing the operation of a spark ignition
engine: Simulation and theoretical tools. Journal of
Applied Physics, 105(9):094904 –094904–10.
Dabo, M., Langlois, N., Respondek, W., and Chafouk, H.
(2008). NCGPC with dynamic extension applied to a
Turbocharged Diesel Engine. In Proceedings of the
International Federation of Automatic Control 17th
World Congress, pages 12065–12070.
Edwards, S. H. (2001). A framework for practical, au-
tomated black-box testing of component-based soft-
ware. Software Testing, Verification and Reliability,
11(2):97–111.
Georg
´
e, J.-P., Gleizes, M.-P., and Camps, V. (2011). Co-
operation. In Di Marzo Serugendo, G., editor,
Self-organising Software, Natural Computing Series,
pages 7–32. Springer Berlin Heidelberg.
Hagan, M. T., Demuth, H. B., and De Jesus, O. (2002). An
introduction to the use of neural networks in control
systems. International Journal of Robust and Nonlin-
ear Control, 12(11):959–985.
Jankovic, M. and Kolmanovsky, I. (2000). Constructive lya-
punov control design for turbocharged diesel engines.
IEEE Transactions on Control Systems Technology,
8(2):288 –299.
Lee, C. C. (1990). Fuzzy logic in control systems: Fuzzy
logic controller. IEEE Transactions on Systems, Man
and Cybernetics, 20(2):404–418.
Nikolaou, M. (2001). Model predictive controllers: A criti-
cal synthesis of theory and industrial needs. Advances
in Chemical Engineering, 26:131–204.
Stengel, R. F. (1991). Intelligent failure-tolerant control.
IEEE Control Systems, 11(4):14–23.
Tahat, L., Vaysburg, B., Korel, B., and Bader, A. (2001).
Requirement-based automated black-box test genera-
tion. In 25th Annual International Computer Software
and Applications Conference., pages 489 –495.
Taralp, T., Devetsikiotis, M., and Lambadaris, I. (1998). Ef-
ficient fractional gaussian noise generation using the
spatial renewal process. In IEEE International Con-
ference on Communications, pages 1456 –1460.
Videau, S., Bernon, C., Glize, P., and Uribelarrea, J.-L.
(2011). Controlling Bioprocesses using Cooperative
Self-organizing Agents. In Demazeau, Y., editor,
PAAMS, volume 88 of Advances in Intelligent and Soft
Computing, pages 141–150. Springer-Verlag.
Wang, H. (2001). Multi-agent co-ordination for the sec-
ondary voltage control in power-system contingen-
cies. Generation, Transmission and Distribution,
IEEE Proceedings, 148(1):61 –66.
Zhang, S., Broadbelt, L. J., Androulakis, I. P., and Ierapetri-
tou, M. G. (2012). Comparison of biodiesel perfor-
mance based on hcci engine simulation using detailed
mechanism with on-the-fly reduction. Energy and Fu-
els, 26(2):976–983.
Zhao, Z., Zhang, F., Zhao, C., and Chen, Y. (2008). Mod-
eling and simulation of a hydraulic free piston diesel
engine. SAE Technical Paper, pages 01–1528.
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
360
