Static Balance based Rescue Robot Navigation Algorithm in Random

Step Environment

Evgeni Magid and Takashi Tsubouchi

Intelligent Robot Laboratory, Department of Intelligent Interaction Technologies, University of Tsukuba, Tsukuba, Japan

Keywords:

Path Planning, USAR, Rescue Robot, Random Step Environment.

Abstract:

To increase safety and extend human rescuers capabilities during a rescue mission a robot is deployed at

a rescue site for exploration purposes. To improve a teleoperated rescue robot performance, we develop an

automatic pilot system which recommends an operator a safe path to a chosen target. We manage the proposed

path from static balance standpoint, based on our previous works. This paper concentrates on path search

algorithm in a simulated 3D debris environment, called Random Step Environment.

1 INTRODUCTION

Rescue robotics goal is to perform tasks in hazardous

or unreachable by humans environments. One par-

ticular domain is urban search and rescue (USAR)

which deals with trappy debris of collapsed construc-

tions, and often buried in unreachable locations vic-

tims. The catastrophe at Fukushima I nuclear power

plant emphasized the indispensability of rescue robots

in high radioactive contamination environments, pre-

venting human personal to perform any task.

During USAR mission a rescue robot explores a

post-disaster debris site, being operated by a human

teleoperator from a safe place outside the site. To de-

crease pressure on a teleoperator in a path planning

stage, we develop a pilot system which helps the op-

erator to select a fairly safe path to a chosen target.

Rough terrain navigation system must be able to

decide if a patch ahead is traversable, or it is an obsta-

cle to be circumnavigated (Ye and Borenstein, 2004).

To estimate a terrain patch, Gennery (Gennery, 1999)

ﬁts planes to the terrain and computes a driving cost,

an accumulating traveled distance, and a probability

that the slope or roughness may be too large to be

traversed. Seraji and Howard (Seraji and Howard,

2002) navigate using terrain local patch roughness,

slope, and discontinuity to represent the traversability.

Kelly (Kelly, 1995) constructs a 2.5D elevation map

and analyzes tip-over, collision, roll and pitch values

along a candidate path. Morphin system (Singh et al.,

2000) maps sensory data into a 25x25 cm cell size

grid, and the goodness of each cell is deﬁned with roll,

pitch, and roughness measures. Cell groups form a

goodness map used for evaluation of a predetermined

candidate arcs set to choose the best trajectory.

The above approaches are suitable for environ-

ments with smooth slopes mainly and are inappro-

priate for typical post-disaster debris scenes with a

signiﬁcant number of surface discontinuities, which

may result into drastic differences between two con-

sequent robot postures. In this paper we present a path

search algorithm created specially for the navigation

in Random Step Environment (RSE) – a standard-

ized by NIST 3D simulated debris environment (Ja-

coff et al., 2000). The uniqueness of our approach

is the management of a path search for a crawler ve-

hicle in RSE from a balance point of view which is

usually associated with legged locomotion (Zucker

et al., 2010; Belter and Skrzypczynski, 2012). To

make path search feasible we discretize robot move-

ment and state space before the search. The pilot sys-

tem predicts and categorizes a robot posture at each

step of the path with regard to robot static balance.

Next, we apply a modiﬁcation of Depth-First Search

algorithm for a path search and dynamically construct

a search tree using the rules which we had described

in (Magid et al., 2011).

The rest of the paper is organized as follows. In

Section 2 we describe our system and simulated en-

vironment model. Section 3 presents posture catego-

rization with regard to static stability. Section 4 deals

with transitions between consecutive states. The heart

of the paper is Section 5 which describes the path

search algorithm. Section 7 presents the discussion

of our future work. Finally, we conclude in Section 8.

251

Magid E. and Tsubouchi T..

Static Balance based Rescue Robot Navigation Algorithm in Random Step Environment.

DOI: 10.5220/0004483502510258

In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2013), pages 251-258

ISBN: 978-989-8565-70-9

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

2 SYSTEM SETUP

We assume a tractor-like crawler robot model with a

centroidal center of mass location (CoM) which cor-

responds to the basic conﬁguration of Kenaf robot

without the sub crawlers (Fig.1). Kenaf is developed

by NEDO project (Yoshida et al., 2007), and it is

admitted to have ”the best mobility in the world us-

ing NIST/ASTM rescue robot evaluation ﬁeld” (Ta-

dokoro, 2008).

XL

YL

Safe CoM

location

Rigid Surface (RSE)

Contact points

Safe inclination

ZG

XG

YG

X

Y

Figure 1: The safety requirements (Conditions A) on the

robot posture while operating in RSE.

For our research we use a Random Step Environ-

ment (RSE) - a standard NIST/ASTM environment

for robot mobility evaluation within RoboCup Res-

cue framework (Jacoff et al., 2011). We assemble

RSE from 85mm × 85mm size wooden blocks of 0,

90, 180, 270, or 360 mm height (Fig.1). We assume

that a small size local map of RSE is always available

to the robot

. To reduce the number of search direc-

tions, we discretize the robot movement and the state

space before the search. In (Magid and Tsubouchi,

2010) we showed that discretizing each 85x85 mm

RSE block (XY-coordinates) into 5x5 internal robot

map cells with 17x17 mm size is the best practical

choice for our framework. With this discretization, a

translation step is a one cell length step in the robot

local frame’s axis X

direction (Fig.1); a rotation step

is a 5 degrees change in the robot orientation θ, rotat-

ing clockwise (right) or counter clockwise (left). This

way we signiﬁcantly reduce the possibility of ending

in different from the expected poses when applying

small steps in the control.

Our application simulates a locally visible part of the

environment for a given robot posture, sensor range and

global map. For the explanation purposes only we show

full local maps.

3 POSTURE CATEGORIZATION

To guarantee reliable motion, a robot is required to be

stable at each posture. Using a linear projection ap-

proach for static stability estimation (Bretl and Lall,

2008), we deﬁne appropriate posture K of the robot

(Fig.1) with Conditions A:

1. Both crawlers contact terrain with no contacts in

the gap between them, thus avoiding getting stuck

2. Exist at least three distinct contact points

3. No slipping/overturning due to surface inclination

4. No overturning due to robot’s CoM displacement

If at least one of Conditions A is not satisﬁed at pos-

ture K, posture K is not appropriate.

(a)

CoM

Moving

direction

CoM

(b)

(c) (d)

(e)

(f)

O1

O2

Figure 2: Controlled balance loosing (CBL) at Orange state:

posture changes from O

(a) to O

(b). M-chain at climbing

up from (c) to (f).

From static stability standpoint we distinguish six

posture types, presented in Table 1. Red is a prohib-

ited posture. Cyan denotes a jump down. Normalized

Energy Stability Margin (NESM) (Hirose et al., 1998)

is applied to distinguish between two statically stable

states: high (Green) or fair quality balance (Yellow).

An unstable Orange posture affords to traverse obsta-

cles with loosing balance twice on a top: at a barrier

edge the robot changes its posture O

(Fig.2a) discon-

tinuously and reobtains a balance in a different body

orientation O

(Fig.2b) as a result of inertia. This

controlled balance loosing (CBL) state is indispens-

able for the path planning (Magid et al., 2010). Ma-

genta state denotes an ascend/descend on a vertical

RSE slope; we deﬁne M-chain as a sequence of Ma-

genta postures (Fig.2d,e) between two stable postures

(Fig.2c,f). The detailed explanations on the posture

categorization could be found in (Magid et al., 2008).

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

252

Table 1: The color labels explanation.

Label Balance quality Technical details

Red (R) The robot turns upside down OR Pitch >

OR Roll >

Gets stuck At least one of Conditions A is not satisﬁed

Orange (O) Controlled balance loosing (CBL) Two optional postures O

and O

exist

Magenta (M) The robot ascends OR descends Oscillations in posture estimation algorithm

a vertical slope of RSE

Cyan (C) The robot jump down CoM jump between two stable postures < 50mm

Yellow (Y) Fair balance (not (R, O, M or C)) AND (NESM parameter < 1)

Green (G) Good balance (not (R, O, M or C)) AND (NESM parameter ≥ 1)

4 TRANSITIONS BETWEEN

CONFIGURATIONS

To create a search tree, presented in the next sec-

tion, we provide a branch cutting function (BCF)

F(Args) = Res. Args are a current robot conﬁguration

and a local environment map. Res is a set of accessi-

ble within one step conﬁgurations, which are at most

three postures: go straight, rotate left or right. BCF

uses color categorization and estimation of a particu-

lar transition feasibility and quality in order to remove

all impossible search directions from the search tree

and to deﬁne the cost evaluation function.

To decide on legal transitions between two suc-

cessive states, we use a combination of pitch, roll,

and contact point quality parameter.

We built a large

set of RSEs and conﬁrmed experimentally the set of

rules on translational and rotational steps between

two successive postures to estimate particular tran-

sition feasibility (Magid et al., 2011). To obtain a

proper level of the real world approximation, we im-

plemented the rules in our simulator and executed ex-

haustive simulations followed by veriﬁcation exper-

iments. The loop rules-simulation-experiments was

repeated multiple times: the rules and the thresholds

were updated each time until the correlation between

the three stages became satisfactory. All possible

pairs of postures, connected with a translational or ro-

tational step, were divided into groups using color cat-

egories and pitch/roll/contact parameters. Each group

is labeled as possible, undesirable or prohibited cate-

gory transition with regard to the rules. Within each

of these three categories the quality of individual tran-

sitions may differ signiﬁcantly, and it is reﬂected in

path cost function g(v), presented in Section 5.2. A

path is formed mainly with possible category transi-

tions. Undesired transitions have a limited appearance

within the path, while the usage of prohibited ones is

totally prohibited.

Depends on the angle between robot crawlers and the

edges of RSE cells and affects the ability to ascend obsta-

cles, to lose balance at CBL, and to descend safely.

5 PATH PLANNING

To ﬁnd a good path in RSE we create a search tree by

means of our BCF. To speed up the search and provide

a fairly good solution, gaining computational perfor-

mance potentially at the cost of accuracy, heuristic

methods are used (Russel and Norvig, 2002). When

applied for a tree search, a selective at each decision

point heuristic focuses on paths that seem to push

the robot closer to the target conﬁguration rather than

exhaustively exploring all available options. For a

heuristic search algorithm the evaluation function of

node v is deﬁned as f(v) = g(v) + h(v), where cost

g(v) is the actual cost to reach node v from start S, and

heuristics h(v) is the estimated cost of reaching target

T. Next we present the search tree construction, cost

function deﬁnition and our search algorithm.

5.1 Search Tree

A naive branching function for each node opens all

three descendant nodes - go straight, turn left/right

(Fig.3a) - and the number of nodes explodes expo-

nentially with search depth D, where D≥dist(S, T) for

a discretized distance between start S and a chosen

within a visible patch of the environment target T.

t

t+1

t+2

t+3

t

t+1

t+2

t+3

(a)

(b)

Figure 3: (a) Naive algorithm search tree (NAT) and (b)

improved tree (IT) for depth D=3. White circle denotes a

translational step, red and blue denote rotation left and right

respectively.

At ﬁrst we create an improved tree (IT, Fig.3b)

saving one additional node opening at each rotational

StaticBalancebasedRescueRobotNavigationAlgorithminRandomStepEnvironment

253

Table 2: Good translational transitions cost (in points). P

and P

are the ﬁrst and the second postures of the pair.

Label P

Motion type g(v)

I G G Flat RSE patch 1

II O G CBL, ascend (A) 10

III G G Uniform ascend (UA) 5

G G Uniform descend (UD) 5

IV O G UA after CBL 12

O G UD after CBL 12

V G O CBL, A 10

VI G O CBL at descend 15

step by prohibiting oscillating rotations: immediately

after a rotation left a rotation right would be useless,

returning the robot to the previous conﬁguration. To

reduce further the number of nodes, BCF F(Args) is

applied to IT and F-tree (FT) is created – the search

tree utilized by our algorithm. At small search depth

D naive algorithm tree (NAT), IT and FT have simi-

lar number of explored nodes, but as D increases, the

difference becomes dramatic (Magid et al., 2011).

5.2 Evaluation Function

Let P

and P

denote a ﬁrst (current) and a second

(next) posture of a connected by a single step pair

respectively. At ﬁrst, color labels of P

and P

are

calculated, and a transition between P

and P

is cate-

gorized. For a prohibited transition the node is cut off

from the search tree with the entire branch that origi-

nates at P

. Next, for good and undesirable transitions

the step cost of transition P

→ P

is obtained from

Tables 2–5. A brief description of the transition type

is given in column ”Motion type”, while the detailed

explanations on each transition, including prohibited

ones, could be found in (Magid et al., 2011). Finally,

column ”g(v)” gives the transition cost.

Table 3: Undesirable translational transitions cost (points).

Label P

Motion type g(v)

VII G G CBL miss,descend(D) 15

VIII G G CBL miss, ascend (A) 10

IX G G M-chain miss, D 20

X G G M-chain miss, A 20

XI G G Non-uniform A 40

XII G O CBL, non-uniform D 100

XIII M O M-chain, D

followed by CBL 5000

XIV G G Non-uniform D 100

XV O M CBL followed by

M-chain, A 5000

XXIII M M M-chain, A 10

XXIV M M M-chain, D 10

Table 4: Good rotational transitions cost (points).

Label P

Motion type g(v)

XVI G G Flat patch 5

XVII G G Descending patch (DP) 15

XVIII G G Ascending patch (AP) 20

XIX G G DP with small body

orientation change 30

XX G G AP with small body

orientation change 40

Table 5: Undesirable rotational transitions cost (points).

Label P

Motion type g(v)

XXI M M Slide down 1000

XXII C G Jump down 3000

The transition cost was established empirically

through the experiment observations taking into an

account operational complexity, probability of failure

due to non-zero friction, sliding, power consumption,

etc. The most simple motion is traversing a ﬂat patch

of RSE (I). A uniform ascend/descend of a vertical

slope (III) and rotation on a ﬂat RSE patch (XVI) re-

quire some attention and are more energy consum-

ing. If CBL appears at ascend/descend explicitly

(II,V,VI) or implicitly (VII,VIII), a special attention

of the operator is needed. CBL at descending (VI,VII)

is more dangerous, making such transition to cost a

little more; an explicit appearance of CBL in uniform

ascend/descend (VI) costs somewhere in between.

Transitions XXIII and XXIV denote explicit ascend-

ing and descending M-chains respectively. Missed

M-chains at descend (IX) or ascend (X) mean faster

changes than explicit M-chains and have equal costs:

while a fast descend (sliding down) is more dangerous

for sensors, ascending a vertical wall consumes more

energy and may change robot orientation slightly after

completion. Non-uniform ascend (XI) and descend

(XIV) intend a CBL appearance; descend is less pre-

dictable, as well as an explicit CBL at non-uniform

descend (XII). The rotation step is more intuitive -

the more body orientation changes, the higher it costs.

Also a rotation on a descending slope is easier than

on an ascending. Sliding down (XXI) and jumping

down (XXII) while rotating are rather unpredictable

and thus have high costs in order to avoid their appear-

ances. Finally, two complicated translational transi-

tions XIII and XV receivean extremely high cost, rep-

resenting a sort of ”last chance” for the operator.

For the path planning transitions with cost 1–50

points are mainly used. A number of 100 points cost

transitions may postpone the further path exploration

for a while. Transitions with cost over 1000 points

leave rather small chances for the further exploration

of the current path. Yellow category postures are

treated in the same way as corresponding green pos-

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

254

tures and add 50% penalty to cost g(v). E.g. transla-

tion Y→G (UA) will cost 5+2.5 points, while Y→Y

will cost 1+0.5+0.5 points.

Heuristic for node v is deﬁned as h(v) = St

(v, T)

+ K×St

(v, T), where St

is a number of translation

steps from node v to target T on a straight line, and

is a number of necessary rotation steps to align

orientation θ at node v conﬁguration with the target

orientation. We varied heuristic functions from the

ones forcing the robot to search within a limited sec-

tor ﬁrst (i.e. concentrated on keeping direction to T)

with large parameter K to K=0 for distance impor-

tance only. Finally, to ensure that the heuristic func-

tion will be always admissible, we set K=0. Since for

the rescue task it is enough to arrive to the target des-

tination more or less precisely, the orientation is less

important if we converge in the terms of distance.

5.3 Path Search Algorithm

The most famous heuristic search algorithm is proba-

bly A

∗

- a best-ﬁrst search type algorithm (Hart et al.,

1968) which always ﬁnds an existing optimal path but

has exponential time and space requirements. Modi-

ﬁcations of A

∗

, like Iterative deepening A

∗

(IDA

∗

), re-

duce space requirements to linear (Korf, 1985), but

unfortunately, all variants of A

∗

at each step select

and expand a most high potential node in terms of

function f(v). Thus, successively expanded nodes v

and v

i+1

are not necessarily adjacent. The class of

graph search algorithms, which avoid such undesir-

able jumps, is Depth First Search algorithm (DFS).

DFS (Russel and Norvig, 2002) is the uninformed

search that progresses by expanding the search tree in

depth in the ﬁrst child node direction until a goal node

or a node without children is reached. In the later case

the search backtracks and returns to the most recent

node it did not ﬁnish.

We have chosen DFS algorithm for our applica-

tion since we strongly believe that it would converge

fast to the target if the path exists. However, to signal

that the path does not exist after exploring the entire

tree takes the same time as any other tree search al-

gorithm. Often the search graph is too large for the

entire exploration, and in such cases DFS would suf-

fer from non-termination. Therefore, when the ap-

propriate depth limit is not known in advance, the

search may be performed by iterative deepening, ap-

plying DFS repeatedly with a sequence of increasing

depth limits. In addition, DFS is much easier to in-

tegrate with heuristic methods of choosing a prospec-

tive search direction. We make two improvements to

iterative deepening DFS and call it MDFS-R - a Mod-

iﬁed DFS for Rescue:

• Switch a search direction when the current path

becomes unsatisfactory

• Use heuristics to ensure the preference of a more

promising search direction

5.4 MDFS-R Algorithm

Similarly to DFS, our algorithm at each node of FT

search tree expands 3 (or 2) descendant nodes and

chooses the most prospective descendant direction

with regard to evaluation function f(v) to continue

the exploration of the search tree.

(a)

Leaf

Opened node

Leaf

#1

#2 #4#3

#1

#2

#1

#2

#5 #7#6

#1

#2

#7

#8

#9

#10

Switch condition:

store #10 as Leaf

#1

#2

#7

#8

#9

#5

New branch:

Proceed from

here

Branch

cut off

Prohibited

node

(b)

(c)

(d)

(e)

VSw

Vnew

Figure 4: MDFS-R algorithm search tree with the encoun-

tered nodes distribution to Leaves (green), Open (yellow)

and Prohibit (red) lists.

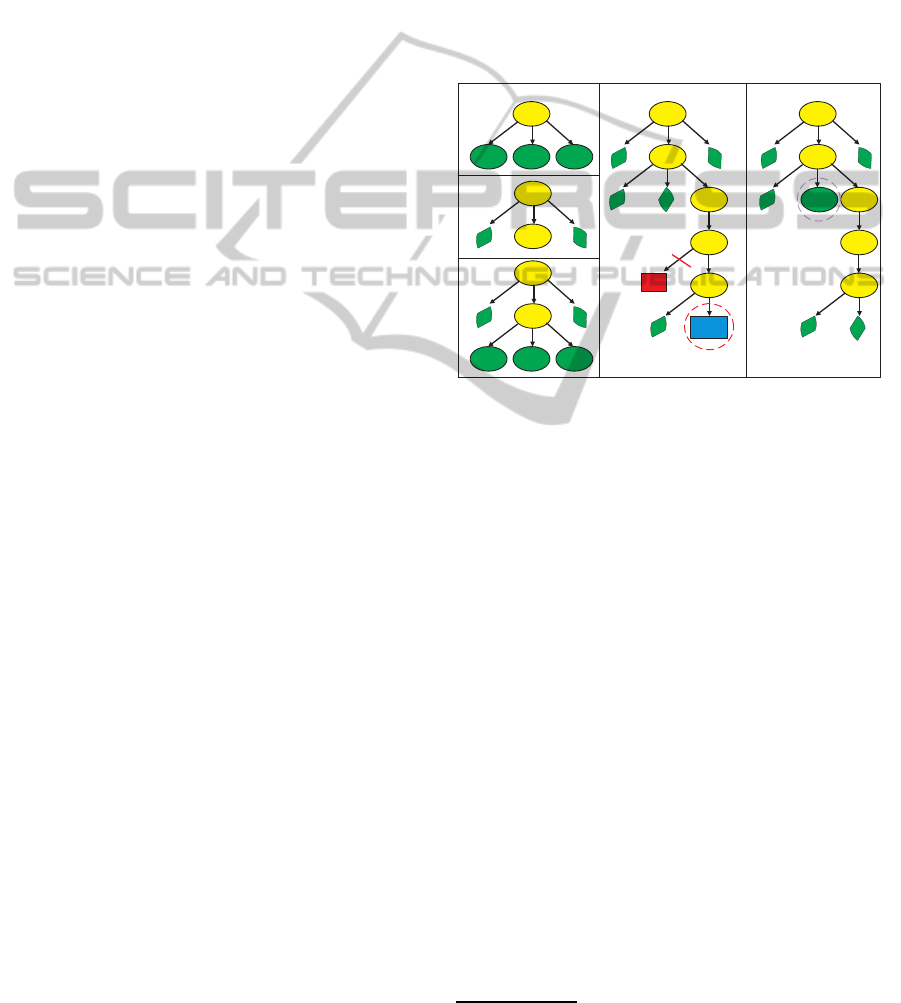
Figure 4 demonstrates MDFS-R algorithm. We

start at node #1, open and evaluate its 3 children -

Leafs (Fig.4a, green ovals). Nodes can have 1 (Fig.4d,

node #7), 2 (node #9) or 3 (node #1) children. Next,

the node is stored in Open list (yellow ovals). If a

child node is categorized as red during the evalua-

tion, it is cut off from the search tree and stored in

Prohibit list (Fig.4d, red rectangular). Among those

children a most promising in terms of minimal cost

and heuristics g(v)+h(v) node is chosen to continue

the search while others are stored as Leafs (Fig.4b).

This procedure is repeated (Fig.4c) until the target

is reached

or a switch condition (explained in the

next paragraph) is triggered (Fig.4d, node #10). The

node, which triggered the switch, is stored as a Leaf

(Fig.4e). The search continues in a different direction

starting at a most promising leaf v

new

(Fig.4e, node

#5), which minimizes the cost function with inﬂated

heuristic g(v)+10 × h(v). Arrival to a dead end acti-

vates a backtracking mechanism identical to the one

of DFS.

MDFS-R switches the search direction at node v

in the three following cases:

Or returning to the start if the path does not exist

StaticBalancebasedRescueRobotNavigationAlgorithminRandomStepEnvironment

255

1. Path cost g(v) becomes too high: the path be-

came too long or/and contains a large number of un-

desired transitions reﬂected in its cost. Exceeding

threshold signals that the robot seems to be on

a wrong path and has to change the search direction.

Initially we set Sw

= 1.5 × St

(S, T), where St

(S,

T) is a number of translational steps from Start to Tar-

get. After this switch is triggered, Sw

is reset to 1.5

× g(v

new

), where g(v

new

) is the path cost from Start

to the selected leaf v

new

. This switch condition is up-

dated throughout the search after every switch.

2. Signiﬁcant number of undesired transitions ap-

pears within the path; this threshold is set to Sw

20. It signals that the path became rather complicated

and a human teleoperator may have difﬁculties to re-

peat it.

3. The current search direction starts to move the

robot away from the desired target. We set this thresh-

old Sw

= 1.5 × St

(S, T).

When one of the three target variables exceeds its

threshold, the path becomes undesirable and its fur-

ther exploration is postponed. If all available choices

violate a switch constraint, after choosing the most

promising node the corresponding threshold is in-

creased. While Sw

and Sw

may only increase dur-

ing the path search, Sw

is reset to 1.5 × St

new

, T)

after every switch. MDFS-R can switch back to any

of the postponed pathes later.

Each node v of FT search tree contains key in-

formation [x, y, θ], posture information [z, θ

, θ

NESM, support polygon square, color], pointers to

ancestor node PF(v) and three children nodes - go

straight PS(v), rotate left PL(v) and right PR(v),

heuristic estimation h(v) from v to target T, path cost

g(v) from start S to v, and number of undesired tran-

sitions UN(v) within that path. We maintain 3 lists of

nodes: Opened, Prohibited, and Leaves. Opened list

stores explored nodes with expanded children; they

may be a part of the successful path. Nodes that were

categorized as ”red” are cut off from the tree without

further exploration of the forthcoming branch, stored

in Prohibited list, and do not appear in FT. If after ex-

ploration a leaf was evaluated as leading to a dead

end, it shifts from Opened list into Prohibited list.

Leaves which do not belong to any path yet, are ﬁlled

up with internal information and stored in Leaves list

with PS(v)=PL(v)=PR(v)=NULL. When a new node

is just opened its key is veriﬁed against Opened, Pro-

hibited, and Leaves lists to prevent multiple explo-

rations.

If during the search one of the three switching

conditions is triggered while comparing h(v) to Sw

g(v) to Sw

, and UN(v) to Sw

, the node of the

switch (ﬁg.4d, node #10) is stored in Leaves list and

the current candidate path explorationis postponed. A

better search direction with regard to the three switch

parameters is chosen (node #5) minimizing g(v)+10

× h(v), and a different candidate path exploration be-

gins. If no better node with regard to current Sw

threshold values exists in Leaves list, the violated

threshold(s) is(are) increased as was explained earlier.

When the target is reached, the path is backtracked

through PF(v) pointers.

6 SIMULATION

The search algorithm was implemented in MATLAB

environment. Figures 5 and 6 present two simple ex-

amples which demonstrate MDFS-R behavior in typ-

ical situations. For the demonstration purposes only

we assumed a full knowledge of a large local RSE

patch while usually for a real USAR task the patch

size is signiﬁcantly smaller. When the obstacle be-

tween S and T is passable but short, or on the contrary,

the obstacle is impassable – the algorithm decides to

get round instead of climbing up (Fig.5). When the

obstacle is passable but very long, or it cannot be cir-

cumvented for some reason, the algorithm chooses to

traverse the obstacle (Fig.6). Each cell of the XYZ-

grid corresponds to RSE cell. The blue rectangular

shows the robot at each distinct posture of the dis-

cretized path and the color dots (placed at the robot’s

CoM) denote static balance category labels.

0.5

Start

Tar get

Figure 5: The robot denoted with blue rectangular circum-

vents small size or impassable obstacles.

Avoiding a pole like obstacle (Fig.5) is a rather

trivial task for a human operator, especially under

perfect information simulations. The second task of

crossing a ridge line (Fig.6) doesn’t appear very chal-

lenging as well since there are a large number of

equally good paths to choose from. So these typical

tasks an experienced teleoperator would perform well

without any supporting pilot system.

Figures 7 and 8 present the map created with a

random generator and randomly chosen start and tar-

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

256

-1

Tar get

Start

Figure 6: The robot climbs the passable obstacle. The ob-

stacle cells are marked with the grey color: the darkest are

4 units high, the lightest are 1 unit. The 0 high white cells

correspond to free space.

get points. While after a number of trials a human

operator would probably end up with the robot tip-

over, our pilot system succeeded to ﬁnd a complicated

path in RSE with type I translation and type XVI rota-

tion steps only. Except few fair balance postures (yel-

low dots) within the path, good balance (green dots) is

guaranteed along the path and no changes in pitch and

roll are involved, preserving horizontal orientation of

the robot.

0 5 10 15 20 25 30 35 40 45

Start

Tar get

Figure 7: A complicated scenario in the random map (view

from above). The RSE cells have 2 (dark grey), 1 (light

grey), and zero (white) unit height.

7 FUTURE WORK

Due to the nature of debris scenarios, using in some

sense deterministic transitions based on discretized

controls is a strong assumption. The transition be-

tween states may become unreliable due to the kind

of terrain, drift, slippery, etc. As a part of our future

work we are going to model the possibility of ending

in different from the expected poses when applying

0.5

1.5

2.5

Start

Tar get

Figure 8: The robot succeeds to ﬁnd a path preserving hor-

izontal orientation along the path.

a control. Next, we plan to compare MDFS-R algo-

rithm effectiveness with a number of existing plan-

ners. While by construction MDFS-R is performing

better then classical BFS, DFS, and A

∗

in terms of

average number of opened nodes, we are interested

to compare MDFS-R and advanced modiﬁcations of

∗

, e.g. IDA

∗

(Korf, 1985) or ARA

∗

(Likhachev et al.,

2004), using different inﬂated heuristics.

MDFS-R algorithm is targeted to search a locally

suboptimal path to a target, which satisﬁes USAR

task, without reconstructing a global map of the en-

vironment, and the possibility that the constructed

search tree would be used once again for the next

stages of USAR mission is relatively small. Yet, if for

some reason the robot will have to return and replan,

some parts of previouslyconstructed search tree could

be reused if we continuously construct and maintain

the global map of the rescue scene.

The presented in this work results strongly depend

on the considered hardware of KENAF robot, but the

proposed approach may be reused at some degree

with a different hardware setup. As a part of our long

term goal we are interested to apply the proposed re-

search framework for the assistant path selection sys-

tem developmentwith several other robotic platforms.

We plan to build system prototypes followed by real

time application development, including global map

construction and sensory input treatment.

8 CONCLUSIONS

In this paper we presented static balance based path

search algorithm in Random Step Environment for a

crawler robot. To make the search feasible, we dis-

cretized robot movement and state space before the

search. Our modiﬁcation of Depth-First Search al-

StaticBalancebasedRescueRobotNavigationAlgorithminRandomStepEnvironment

257

gorithm, targeting specially for path planning tasks of

USAR scenarios, dynamically constructs a search tree

and provides a fairly safe path to a chosen by the op-

erator target. The simulations showed that while in

simple scenarios an experienced operator can manage

the path planning process easily, our assistant pilot

system is critical in complicated scenarios.

Even though the presented solution deals only

with a static stability of the vehicle and suffers from

a number of drawbacks and limitations like strong as-

sumptions on rigid and stable RSE, absence of slip-

pery and external disturbances, centroidal location of

robot’s CoM, etc., we believe that our unique ap-

proach to the crawler robot path planning from static

stability standpoint makes a signiﬁcant contribution

to the rescue robotics domain. While the presented

results strongly depend on the considered hardware,

the proposed approach may be reused at some degree

with a different hardware setup. This way we cre-

ated a complete framework which could guide assis-

tant system development for any typical crawler vehi-

cle operating in USAR scenario.

ACKNOWLEDGEMENTS

This work was partially supported by NEDO Project

for Strategic Development of Advanced Robotics Ele-

mental Technologies, High-Speed Search Robot Sys-

tem in Conﬁned Space. Special thanks are extended

to Leave a Nest Co. Ltd., Japan, for the generous ﬁ-

nancial support of this work.

REFERENCES

Belter, D. and Skrzypczynski, P. (2012). Posture optimiza-

tion strategy for a statically stable robot traversing

rough terrain. In IEEE Int. Conf. on Intelligent Robots

and Systems.

Bretl, T. and Lall, S. (2008). Testing static equilibrium for

legged robots. IEEE Trans. on Robotics, 24(4).

Gennery, D. B. (1999). Traversability analysis and path

planning for a planetary rover. Autonomous Robots,

6(2).

Hart, P. E., Nilsson, N. J., and Raphael, B. (1968). A formal

basis for the heuristic determination of minimum cost

paths. IEEE Trans. on Systems Science and Cybernet-

ics, 4(2).

Hirose, S., Tsukagoshi, H., and Yoneda, K. (1998). Nor-

malized energy stability margin: generalized stability

criterion for walking vehicles. In The 1st Int. Conf. on

Climbing and Walking Robots.

Jacoff, A., Messina, E., and Evans, J. (2000). A stan-

dard test course for urban search and rescue robots.

In Performance Metrics for Intelligent Systems Work-

shop’00.

Jacoff, A., Virts, A., and Downs, T. (2011).

RoboCup Rescue Robot League Arenas: Ma-

jor component descriptions. Available online:

http://www.isd.mel.nist.gov/projects/USAR/.

Kelly, A. J. (1995). Predictive control approach to the high-

speed cross-country autonomous navigation problem.

PhD thesis, Carnegie Mellon University.

Korf, R. E. (1985). Depth-ﬁrst iterative-deepening: An op-

timal admissible tree search. Artiﬁcial Intelligence,

27.

Likhachev, M., Gordon, G., and Thrun, S. (2004). ARA*:

Anytime A* with Provable Bounds on Sub-Optimality.

Advances in NIPS, MIT Press, Cambridge, MA.

Magid, E., Ozawa, K., Tsubouchi, T., Koyanagi, E., and

Yoshida, T. (2008). Rescue robot navigation: Static

stability estimation in Random Step Environment. In

Int. Conf. on Simulation, Modeling and Programming

for Autonomous Robots.

Magid, E. and Tsubouchi, T. (2010). Static balance for

rescue robot navigation: Translation motion discreti-

zation issue within Random Step Environment. In

Int. Conf. on Informatics in Control, Automation and

Robotics.

Magid, E., Tsubouchi, T., Koyanagi, E., and Yoshida, T.

(2010). Static balance for rescue robot navigation:

Losing balance on purpose within Random Step En-

vironment. In IEEE Int. Conf. on Intelligent Robots

and Systems.

Magid, E., Tsubouchi, T., Koyanagi, E., and Yoshida, T.

(2011). Building a search tree for a pilot system of

a rescue search robot in a discretized Random Step

Environment. J. of Robotics and Mechatronics, 23(4).

Russel, S. J. and Norvig, P. (2002). Artiﬁcial intelligence:

A modern approach. Prentice Hall.

Seraji, H. and Howard, A. (2002). Behavior-based robot

navigation on challenging terrain: a fuzzy logic ap-

proach. IEEE Trans. on Robotics and Automation,

18(3).

Singh, S., Simmons, R., Smith, T., Stentz, A., Verma, V.,

Yahja, A., and Schwehr, K. (2000). Recent progress

in local and global traversability for planetary rovers.

In IEEE Int. Conf. on Robotics and Automation.

Tadokoro, S. (2008). Rescue Robotics in Japan. DHS Uni-

versity Network Summit’2008.

Ye, C. and Borenstein, J. (2004). A method for mobile robot

navigation on rough terrain. In IEEE Int. Conf. on

Robotics and Automation.

Yoshida, T., Koyanagi, E., Tadokoro, S., Yoshida, K., Na-

gatani, K., Ohno, K., Tsubouchi, T., Maeyama, S.,

Noda, I., Takizawa, O., and Hada, Y. (2007). A high

mobility 6-crawler mobile robot Kenaf. In The 4th

International Workshop on Synthetic Simulation and

Robotics to Mitigate Earthquake Disaster.

Zucker, M., Bagnell, J. A., Atkeson, C. G., and Kuffner,

J. (2010). An optimization approach to rough terrain

locomotion. In IEEE Int. Conf. on Robotics and Au-

tomation.

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

258