About Optimization Techniques in Application

to Symbolic-Numeric Optimal Control Seeking Aproach

Ivan Ryzhikov, Eugene Semenkin and Vladimir Okhorzin

Institute of Computer Sciences and Telecommunication, Siberian State Aerospace University,

Krasnoyarskiy Rabochiy ave., 31, Krasnoyarsk, 660014, Russia

Keywords: Optimal Control Problem, Evolutionary Strategies, Differential Evolution, Partial Swarm Optimization.

Abstract: The optimal control problem for nonlinear dynamic systems is considered. The proposed approach is based

on the both partially analytical and partially numerical techniques of the optimal control problem solving.

Using the maximum principle the system with the state and co-state variables can be determined and after

closing up the initial optimal control problem, it can be reduced to unconstrained extremum problem. The

extremum problem is related to seeking for the initial point for the co-state variables that would satisfy the

boundaries. To solve the optimization problem, well-known global optimization techniques are suggested

and compared. The settings of the algorithms were varied. Also, the new modified hybrid evolutionary

strategies algorithm was compared to common techniques and in the current study it was more efficient.

1 INTRODUCTION

The optimal control problem for dynamic systems

with one control input and integral functional is

considered. Since the problem is old and it originates

from the practical needs, there exist many

techniques to solve the optimal control problem in

different problem definitions and for different

systems. But the developing of the modern

technologies creates new optimal control problems

that cannot be solved via well-known and classical

approaches. The main problem is nonlinearity of the

system model or the criterion. In general case, there

is no universal analytical technique that guarantees

the solution of nonlinear differential equation to be

found. But using the maximum principle, we can

always determine the characteristics of the function

that is suspected to be the solution of the optimal

control problem.

On the other hand, the numerical approaches are

useful and efficient but only for some problems that

they were designed for. Any control function

approximation technique that is being used to

determine the solution for the initial optimal control

problem is related with reduction of the problem to

extremum seeking on the real vector field. And the

problem reduction uses a convolution of different

objective functions and penalty functions for all the

constraints, and it requires more computational

resources and more efficient optimization

algorithms. There is no doubt that the direct method

based techniques are efficient, but increasing of

accuracy of the function approximation leads to

increasing of extremum problem dimension.

The indirect method of solving the optimal

control problem is related with solving the extremely

difficult boundary-value problem, but the found

solution gives us the proper control function with the

known structure. In the given study the shooting

method is based on the modified evolutionary

optimization algorithm.

It is important to highlight that there is a

sufficient benefit of using the information science

techniques of solving the complex optimization

problems. The modern methods and algorithms from

the fields of informatics, bioinformatics and

cybernetics are reliable, flexible and highly efficient

techniques. And it is possible to improve them for

every distinct optimization problem with unique

characteristics via modifying the schemes, operators

or hybridizing the algorithms.

Many works on optimal control problem solving

for nonlinear dynamic systems are about some

specific tasks. Many works are about the approaches

to solve optimal control problems for affine

nonlinear systems, like the work mentioned before,

for example, (Popescu and Dumitrache, 2005) and

(Primbs et al., 1999). In the last article the studied

268

Ryzhikov I., Semenkin E. and Okhorzin V..

About Optimization Techniques in Application to Symbolic-Numeric Optimal Control Seeking Aproach.

DOI: 10.5220/0004488302680275

In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2013), pages 268-275

ISBN: 978-989-8565-70-9

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

problem is related to optimal control of nonlinear

systems via usage of the Lyapunov functions, but

only one boundary in problem definition is

considered. Also, in article (Chen et al., 2003) the

approach of predictive optimal control for nonlinear

systems is considered. There are plenty of numerical

techniques application examples, (Rao, 2009).

Actually, since the problem is complex and there are

many problems with unique features, and there are

many different problem definitions for optimal

control.

These techniques also require an analytical form

of the system state and fit only the considered

structures. And in our study, the proposed approach

with implementation of some efficient global

optimization technique is suggested to be applicable

and reliable for solving many optimal control

problems, as an effective analogue to shooting-based

techniques.

In the study (Bertolazzi et al., 2005) symbolic-

numeric indirect approach is considered, which is

based on Newton Affine Invariant scheme for

solving boundary value problem, which fits the

considered systems and is being different technique

of solution seeking. Following scheme can find also

a local optimum.

The evolutionary strategies algorithm was used

to solve the optimal control problem, but as a direct

method. In the paper (Cruz and Torres, 2007) the

control function was discretized and every part of it

was optimized via evolutionary strategies algorithm.

That means, that there a as many optimization

variables, as many discrete points are approximating

the control.

The method of semi-analytical and semi-

numerical optimal control problem solving is

considered. The first part of the method is based on

the Pontryagin’s maximum principle (Kirk, 1970),

after determination of the Hamiltonian, the system

with co-state variables can be used. For the new

system that is a transformation of the initial problem

it becomes possible to reduce the optimal control

problem to extremum seeking on a real vectors’

field. For the last problem the new optimization

technique is applicable. The Pontryagin’s principle

allows to close up the system of equations and to

determine the structure of the control function in

terms of other variables. The dimension of the field

is the same as the dimension of the system for the

considered problems. There are many suitable

algorithms for the proposed problem, based on

random search and evolution search, but the every

distinct optimal control problem origins its own

unique structure of criterion with its own features.

2 ANALYTICAL-NUMERICAL

APPROACH TO OPTIMAL

CONTROL PROBLEM

Let the system be described with nonlinear

differential equation

(,,)

xut



(1)

where

():

RRR R



 is a vector function of its

arguments;

R

is a vector of system state;



is a continuous control function;

n is the system dimension.

We need to find a control function u(t) that brings

the system from the initial point

(0)

x to the end

point

()



within finite time T, that delivers the

extremum to functional

(,) (,)



x u F x u dt extr

(2)

The Hamiltonian (Kirk, 1970), is defined by the

equation

(,,) (,) (,,)





xut F xu p f xut

(3)

therefore the system with co-state variables

can

be determined with equations

(,,)

xut





dp dH

dt dx

(4)

The given system (4) is completed with system state

and conjugated variables starting points

(0)



and

(0)



pp, respectively. It means that the

control function

()ut

can be determined with

some

p . Then, it is necessary to close up the system

with the following condition



(5)

Since the differentiation of the analytical expression

is not a common problem, the forming of the system

in the current study was not made automatically.

Anyway, some mathematic software is able to

operate with analytical problems, simplify

expressions and differentiate them. The method can

be implemented in future.

The structure of the control function is

determined by equation (5). After using of the

AboutOptimizationTechniquesinApplicationtoSymbolic-NumericOptimalControlSeekingAproach

269

transversability conditions, by changing the starting

point of the co-state variables, we change the control

function and the solution of the optimal control

problem.

Actually, it means that the proper vector of the

co-state variables initial point, which provides the

condition

()

Tx would give us the solution for

the whole problem, since the functional (2) and the

differential equation (1) are forming the system (4).

Initial point is the real vector and it could be

searched with some optimization technique.

Since the main problem is reduced to

optimization problem on the field

R , let the

(0)

(), ()



xt pt

be the solution for the system (4) in

case of

(0) pp. Now let us describe the

functional

(0)

() () min



 



Kp x xT

(6)

The proposed criterion is multimodal, complex

function of its arguments. It is not known, in

general, where any extremum is located. Moreover,

if the initial system (1) or functional (2) that forms

the Hamiltonian (3) is nonlinear, so there is no

analytical solution for the given criterion (6) and it

can be evaluated only numerically.

The given criterion (6) is being transformed into

fitness function for the evolutionary algorithms

()

1()





fitness p

so the fitness function is a mapping:

[0,1]

The greater fitness is, the better is current solution.

To prove the high complexity of the optimization

problem let the system be defined by equation

ln( ) cos( )

(,,)

sin( ) ( )













fxtu

txut

1T









()









(7)

and the integrand function for the functional of the

optimal control problem

(,) min

Fxu u

(8)

is considered. Then, it is necessary to define the

extended system (4),

00 01

ln( ) cos( )

sin( )

(, ,) ,

sin( ) cos( )















 









Fxpt

pt xp

since we closed up the system with condition (5),

0()

 

pdH

Now, having the system with co-state variables and

the structure of the control function it is possible to

form an optimization problem for initial point of co-

state variables, so the end point of the system state

would be achieved at time

As one can see, the nonlinear differential

equation consists of logarithm function,

trigonometric functions and the system itself is

nonstationary.

The mapping (6) for the given problem is shown

on the figure 1. The surface was made via evaluating

numerically the nonlinear differential equation for

extended system, varying the initial point of the co-

state variables. As it can be shown on the current

surface some extremum problems that are reduced

from the optimal control problems have a lot of

local maximums that are less than 1 and so do not

satisfy two-point problem, and among them there

could be closed sets or distinct points, that delivers

extremum to criterion (6) and it equals 1.

Figure 1: The surface of the criterion (6) for optimal

control problem (7)-(8).

Let us describe the next optimal control problem for

the plant with inverted pendulum, which movement

is determined with system of nonlinear differential

equation

()

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

270

10 0

(,,)

sin( ) ( ) cos( )







  



fxtu

xut x

5T

















(9)

and functional

(,) min

Fxu u x

(10)

to be considered. Then, it is necessary to define the

extended system (4),

01 0

cos ( )

sin( )

(, ,) ,

sin(2 )

2cos()









 











   







Fxpt

xp x

because we closed up the system with condition (5),

cos( )

0()



 

The mapping (6) for current problem is shown on

the figure 2.

Every optimal control problem reduced to

extremum problem for vector function with

unknown characteristics and behavior of the

criterion.

Figure 2: The surface of the criterion (6) for optimal

control problem (9)-(10).

As it can be seen on figures, the problem is complex.

Moreover, there is no any information about the

location of the extremum.

To sum up, seeking for the solution of the

reduced problem, in general, is associated with the

optimization technique that works on the vector field

without any constraints. In other words, the

techniques of extremum seeking on

R should be

used. Anyway, it is possible to use the optimization

techniques, which works on the compact, but then

the special procedure of extending the compact or

switching to different one should be implemented.

Since many optimization techniques are suitable

for the considered problem and deal with its

features, it was suggested to compare these well-

known techniques: evolutionary strategies,

differential evolution and particle swarm

optimization.

To provide the efficiency growth evolutionary

strategies algorithm was modified. The basis of the

algorithms and modifications proposed is described

below.

3 EXTREMUM SEEKING

TECHNIQUES

As it has been mentioned before, the features of the

problem lead using the efficient global optimization

techniques that works on the real vector field. One

of the most sufficient characteristic of the algorithms

is that the search can proceed in any direction and

without any without any constrains.

Thus, the optimal control problem was reduced

to extremum problem for the real numbers and the

objective function cannot be evaluated analytically.

Now the techniques of extremum seeking are to be

described.

The main principle of evolutionary strategies

(ES) is described in (Schwefel, 1995). It was

extended via adding the operations of selection,

borrowed from the genetic algorithm. Proposed ES-

based optimization algorithm besides the selection

uses recombination, mutation and hybridized with

local optimization technique. The number of parents

which recombine to produce an offspring in the

current investigation was set to 2. Then the offspring

is mutating and the mutation operand is also

modified. The population size is constant for all

generations. Let every individual be represented

with a tuple

______

,, (),1,

ii i

Id op sp fitness op i N

where

()

1()





fitness op

is the fitness function for

criterion (6);

____

,1,

op R j k

is the set of objective parameters;

____

,1,

pRj k





is the set of method strategic

()

AboutOptimizationTechniquesinApplicationtoSymbolic-NumericOptimalControlSeekingAproach

271

parameters;

is the size of population.

There are a lot of different ways to transform the

criterion of optimization problem to the evolutionary

algorithm’s fitness function, but since the criterion

(6) is nonnegative the simple transformation can be

used.

Now we have to modify the mutation operation

for the ES adapting to the given problem. Let

[0,1]

m  be the mutation probability for every

gene and

be the Bernoulli distributed random

value with

(1)

zm . Then

_______________

(0, ), , 1, ( )

ii i i

op op z N sp op R i card op 

;

_______________

(0,1) , 1, ( ) 

pspzN i cardsp.

Another modification of the evolutionary strategies

algorithm suggested is the CMA-ES, which is

described in (Hansen, 2006) and uses the covariance

matrix adaptation.

As the next optimization technique the

differential evolution (DE) algorithm is suggested,

which main principle is described in (Storn, Price,

1997). Let every individual in the current algorithm

be represented with a tuple

______

,(),1,

Id op fitness op i N

where

____

,1,

op R j k

are the variables to be optimized;

()

1()





fitness op

is the fitness function for

the criterion (6).

The Algorithm uses two settings, the first is





0, 1

and the other is





0, 2F

, as it is

recommended. On every iteration for every

individual three different individuals are to be

randomly chosen, but they must differ from the

current individual. Then the random number





1, ...,

Nn is generated, as the random vector

with coordinates

___

(0,1), 1,

rand U i n . For every

individual the trial vector is generated

,1,

(),0,









  



ide

trial

abc

iiide

op f

op F op op f

where

___

,,,1,

abc

iii

op op op i n

are the coordinates of the

randomly chosen individuals;

1, ,

0, ,













ir r

if rand C or i N

if rand C and i N

is the special

indicator function.

If inequality

() ()

trial i

itness op fitness op

satisfied, the individual changes to the trial



itrial

op op

The last considered method of extremum seeking

is the partial swarm optimization (PSO), which is

described in (Kennedy, Eberhart, 2001). Let every

individual be represented with a tuple

______

,, ( ), 1,

ii i

Id op v fitness op i N

____

,1,

op R j k

are the variables to be optimized;

____

,1,

vRj k

are the velocities for each coordinate

of an every particle;

()

1()





fitness op

is the fitness function for

the criterion (6).

After every algorithm’s iteration the variable

best

op is to be refreshed. It is the vector that has the

highest fitness. There are also variables that store the

best found position that every individual ever had,

op . For every individual, the random values

,(0,1)rr U are generated and the velocity and

new individual’s position, for

____

1,jk

11 2 2

()( ),        

best

jj jj jj

vv ropop ropop





op op v

The random coordinate-wise real-valued genes

optimization has been implemented for the

algorithms performance improvement. The

optimization is fulfilled in the following way. For

every

N randomly chosen real-valued genes for

N randomly chosen individuals

N steps in

random direction with step size

h are executed.

For the numerical experiments in our study, the

parameters of the hybridization for ES-based

optimization procedure were set as followed: the

recombination probability is 0.8, the mutation

probability for every gene was set to

. Local

improvement parameters were set as

2Nop

Nop and

0.1



N with 0.05

h  . The

proposed algorithm performance has been evaluated

on twenty test problems and was found to be

promising.

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

272

4 OPTIMAL CONTROL

PROBLEM AND ALGORITHMS

EFFICIENCY INVESTIGATION

Unfortunately, it is impossible for the described

initial optimal control problem to determine the most

efficient settings of every algorithm, since every

different control problem leads to different criterion

(6). There is another important thing to be

mentioned, that there can be no control functions

available for some nonlinear system and boundaries.

Let us consider optimal control problems

described earlier to make the efficiency investigation

of optimization techniques listed above. To simplify

the representation of the results the following names

of algorithms are suggested: evolutionary strategies

– ES; differential evolution – DE; particle swarm

optimization – PSO; for hybrid evolutionary

strategies algorithm - ES+LO; ES with covariance

matrix adaptation – CMA-ES. For problems that

were described above: (7)-(8), (9)-(10), we set the

maximum numbers of criterion evaluation to 8000,

and tested different setting of the given algorithms.

The number of algorithms’ iterations and the size of

populations were varied too: 1600 and 5, 800 and

10, 400 and 20, 200 and 40, 100 and 80,

respectively.

Since the proposed optimization techniques have

different natures and their settings were varied

regarding to the features of algorithms. For the

evolutionary strategies techniques the selection was

varied: proportional, rank, tournament; crossover

operator was varied: intermediate, weighted

intermediate and discrete; mutation: classical and

modified, with mutation probability equals to

1 k .

For differential evolution technique the settings were

chosen due to recommendation given:

0.5



C and





0.2 : 10, 

aiiiN

. For the particle

swarm optimization settings were taken from the

followig sets:





0.5 : 4,   ii i N





1,2

0.4 : 6,   ii i N. The initial population

was randomly generated,

(0,10)

op N , (0,1)

sp N and (0,1)

vN . For

the ES+LO technique, the settings for LO and the

number of individuals and populations were chosen

as the numbers, which sum is equal to maximum

number evaluation. The settings for the CMA-ES

algorithm were set as it is recommended in

reference, for this technique the only numbers of

populations and individuals were varied.

For the problem (9)-(10) sometimes are about to

stagnate, the average of the fitness function for every

population and the fitness of the best individual are

shown on the figure 3.

On the figure 3 there are next measurements:

dotted thin line is the best solution found by PSO at

the current iteration; dotted thick line is the average

fitness function value for the population; the same

with dashed lines for differential evolution and dot

dashed lines for ES. These lines are the averaging of

the presented variables after 20 restarts of algorithms

with the same settings. The horizontal axis is the

number of iteration for every algorithm; vertical axis

is the fitness function value. As one can see, the

PSO technique efficiency is more dependent on its

settings, because the whole population can fall to the

best solution found fast enough without possibility

to leave local extremum.

0 50 100 150 200

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Figure 3: Behaviour of average fitness function value and

fitness of the best individual. Thick lines are the average

fitness and thin lines are the best fitness.

In table 1 the average values of the fitness function

for the found solution are presented. In every

column the efficiency with the best settings of every

technique are shown.

Table 1: Average values of the fitness function for

different techniques with the most efficient settings.

Algorithm

Problem ES DE PSO CMA-ES ES+LO

(7)-(8) 0.97 0.98 0.95 0.99 0.99

(9)-(10) 0.93 0.95 0.96 0.94 0.97

In table 2 the probability estimation of

1 ( *) 0.05



fitness op

is considered, since that is

the measurement of how the technique handle with

the complexity of objective function for the problem

(9)-(10).

AboutOptimizationTechniquesinApplicationtoSymbolic-NumericOptimalControlSeekingAproach

273

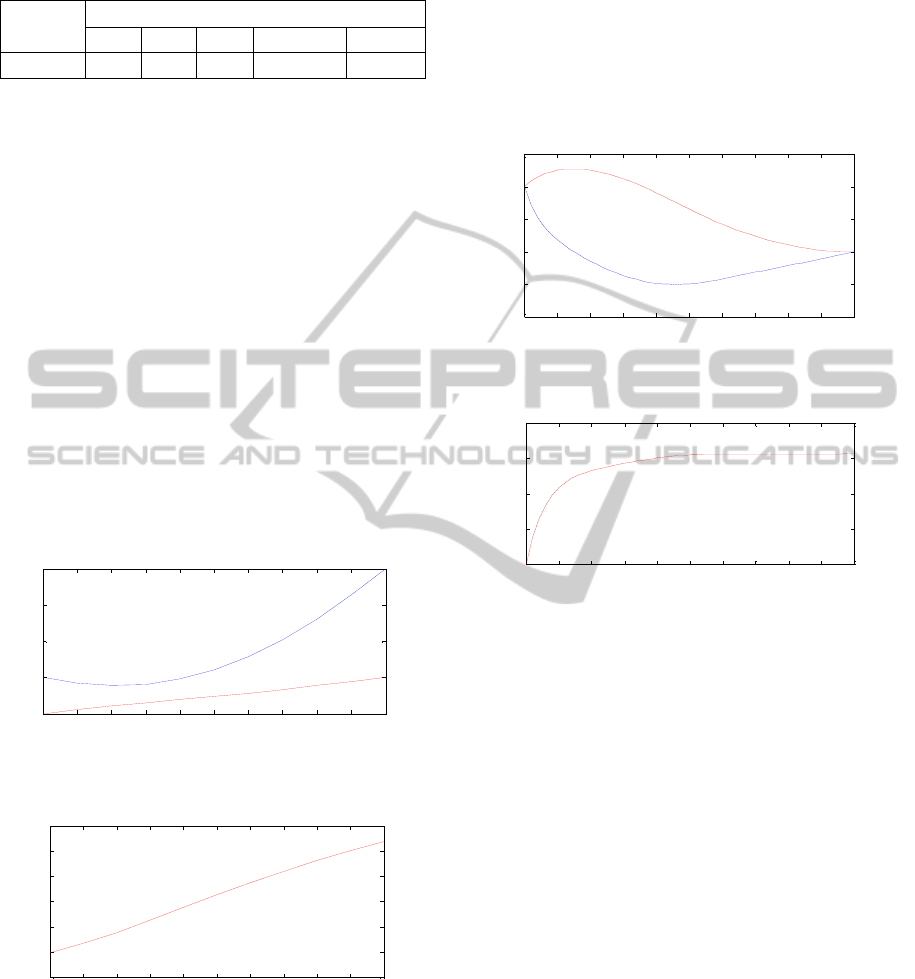
Table 2: The estimation of probability to return solution

that is close to the global optimum.

Algorithm

ES DE PSO CMA-ES ES+LO

Problem

0.3 0.5 0.6 0.35 0.65

In the current investigation, all the algorithms’

settings and population, individual numbers were

varied. Due to given problems, the hybrid

evolutionary strategies algorithm was the most

effective in searching the extremum and reliable in

case of the problems with objective function that

have a surface as it is shown on figure 2. After all

the runs, the best settings were estimated as

following ones: 20 individuals for 200 populations,

tournament selection (10%), discrete crossover,

modified mutation (mutation probability 0.75) and

/2

NNN ,

0.1N , with evaluations

number limitation equal to 8000.

For every of the proposed algorithms the most

efficient settings were estimated too. The balance

between the number of populations and size of

population differs from one method to another. For

example, PSO shows better results with increasing

the number of individuals, but DE does not.

0 0.1 0. 2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

Figure 4: The system output for the control problem (7)-

(8),

(), ()

txt.

0 0. 1 0. 2 0. 3 0. 4 0. 5 0. 6 0. 7 0. 8 0. 9 1

-4

-2

Figure 5: Function ()ut . Control problem (7)-(8).

Let us consider the optimal control problem (7)-(8)

again. It has been shown earlier how we analytically

transformed the initial problem and closed the

system with state and co-state variables. The

modified hybrid evolutionary strategies algorithm

was applied for this control problem. After 20 runs

of the algorithm, the best solution was taken. The

state variables are shown on the Figure 4 and the

control function is shown on the Figure 5. As one

can see, system state with the given control reaches

the desired end point at time T.

For the problem (9)-(10), another 20 runs of the

ES+LO algorithm gave us solution that is shown on

the Figures 6 and 7.

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

-1

-0.5

0.5

1.5

Figure 6: The system output for the control problem (9)-

(10),

(), ()

txt.

0 0.5 1 1. 5 2 2.5 3 3.5 4 4.5 5

-6

-4

-2

Figure 7: Function ()ut . Control problem (9)-(10).

As it is shown in the given examples, the proposed

algorithm effectively solves the unconstrained

optimal control problem for nonlinear dynamic

systems. The initial point for co-state variables is to

be found, because after closing up the extended

system with state and co-state variables, regarding to

the maximum principle, the control function is fully

determined with them. As one can see, the proposed

approach does not guarantee that any optimal control

problem can be solved, but if the solution exists,

there is a chance for it to be found. Also, the

proposed approach fits only the optimal control

problems that can be analytically transformed and

the control function can be expressed via state and

co-state variables after closing the system.

The proposed approach is suitable for the

optimal control problems with different definitions,

only criterion for extremum problem on the real

vector field would be different.

5 CONCLUSIONS

In this study the analytically-numerical algorithm of

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

274

the optimal control problem solving for nonlinear

dynamic systems with one input and many outputs is

considered. The initial two-point optimal control

problem with integral functional was reduced to

extremum problem on real vectors field. With all the

transformations, listed above, the system with state

and co-state variables can be closed and the control

function structure can be defined in terms of the co-

state variables and system state. The seeking of

initial point for the co-state variables brings the

solution for the optimal control problem and

suggested to be based on stochastic or evolution

unconstrained global optimization algorithms.

As the optimization techniques evolutionary

strategies, differential evolution, particle swarm

optimization and their modifications were suggested

and investigated on the given optimal control

problems set. It is suggested that optimization

techniques with special features are required and

future works are related with designing hybrid

algorithms that allow both the extremum seeking

and surface scouting.

Since, there are plenty of different optimal

control problems, as the system equations and

functional differs from task to task, the mapping to

be optimized has different characteristics and there

is no set of the problems that allows making a

complete investigation of the optimization

algorithms efficiency. All in all, the investigation of

efficiency for heuristic techniques proceeds in the

same way, techniques are testing on the well-known

set of the objective functions. The proposed

approach leads to investigate the efficiency of

techniques with different extremum problem

definition, and it seems to be the only way to find

the most suitable algorithm by testing it on some set

of the control problems.

In the current investigation the hybrid

evolutionary strategies approach was the most

effective.

The aim of the further investigation is to design

the critique program agent, which will be the

controller for the optimization technique, via

analysing the data: fitness function set and its

history, the topology of the individuals and its

dynamics. The algorithms with implementation of

this agent probably will be more efficient for global

extremum problems.

REFERENCES

Popescu, M., Dumitrache, M., 2005: On the optimal

control of affine nonlinear systems. Mathematical

Problems in Engineering (4): pp. 465–475.

Chen, W. H., Balance, D. J., Gawthrop, P. J., 2003:

Optimal control of nonlinear systems: a predictive

control approach. Automatica 39(4): pp. 633-641.

Primbs, J. A., Nevistic, V., Doyle, J. C., 1999: Nonlinear

optimal control: a control Lyapunov function and

receding horizon perspective. Asian Journal of

Control, Vol. 1, No. 1: pp. 14-24.

Rao, A. V., 2009: Survey of Numerical methods for

Optimal Control, AAS/AIAA Astrodynamics

Specialist Conference, AAS Paper 09-334, Pittsburg,

PA.

Bertolazzi, E., Biral, F., Lio, M., 2005, Symbolic-Numeric

Indirect Method for Solving Optimal Control

Problems for Large Multibody Systems: The Time-

Optimal Racing Vehicle Example. Multibody System

Dynamics, Vol. 13, No. 2., pp. 233-252

Cruz, P., Torres, D., 2007, Evolution strategies in

optimization problems, Proc. Estonian Acad. Sci.

Phys. Math., 56, 4, pp. 299–309

Kirk, D. E., 1970: Optimal Control Theory: An

Introduction. Englewood Cliffs, NJ: Prentice-Hall.

Schwefel, H-P, 1995: Evolution and Optimum Seeking.

New York: Wiley & Sons.

Hansen, N., 2006: The CMA evolution strategy: a

comparing review. Towards a new evolutionary

computation. Advances on estimation of distribution

algorithms, Springer, pp. 1769–1776

Storn, R. Price, K.,1997: Differential Evolution - A Simple

and Efficient Heuristic for Global Optimization over

Continuous Spaces, Journal of Global Optimization,

11: pp. 341–359.

Kennedy, J., Eberhart, R., 2001: Swarm Intelligence.

Morgan Kaufmann Publishers, Inc., San Francisco,

CA.

AboutOptimizationTechniquesinApplicationtoSymbolic-NumericOptimalControlSeekingAproach

275