
Highly Scalable Sort-merge Join Algorithm for RDF Querying
Zbynˇek Falt, Miroslav
ˇ
Cerm´ak and Filip Zavoral
Faculty of Mathematics and Physics, Charles University, Prague, Czech Republic
Keywords:
Merge Join, Parallel, Bobox, RDF.
Abstract:
In this paper, we introduce a highly scalable sort-merge join algorithm for RDF databases. The algorithm is
designed especially for streaming systems; besides task and data parallelism, it also tries to exploit the pipeline
parallelism in order to increase its scalability. Additionally, we focused on handling skewed data correctly and
efficiently; the algorithm scales well regardless of the data distribution.
1 INTRODUCTION
Join is one of the most important database opera-
tion. The overall performance of data evaluation en-
gines depends highly on the performanceof particular
join operations. Since the multiprocessor systems are
widely available, there is a need for the parallelization
of database operations, especially joins.
In our previous work, we focused on paralleliza-
tion of SPARQL operations such as filter, nested-
loops join, etc. (Cermak et al., 2011; Falt et al.,
2012a). In this paper, we complete the portfolio of
parallelized SPARQL operations by proposing an ef-
ficient algorithm for merge and sort-merge join.
The main target of our research is the area of
streaming systems, since they seem to be appro-
priate for a certain class of data intensive prob-
lems (Bednarek et al., 2012b). Streaming systems
naturally introduce task, data and pipeline paral-
lelism (Gordon et al., 2006). Therefore, an efficient
and scalable algorithm for these systems should take
these properties into account.
Our contribution is the introduction of a highly
scalable merge and sort-merge join algorithm.
The algorithm also deals well with skewed data
which may cause load imbalances during the par-
allel execution (DeWitt et al., 1992). We used
SP
2
Bench (Schmidt et al., 2008) data generator and
benchmark to show the behaviour of our algorithm in
multiple test scenarios and to compare our RDF en-
gine which uses this algorithm to other modern RDF
engines such as Jena (Jena, 2013), Virtuoso (Virtuoso,
2013) and Sesame (Broekstra et al., 2002).
The rest of the paper is organized as follows. Sec-
tion 2 examines relevant related work on merge joins,
Section 3 shortly describes Bobox framework that is
used for a pilot implementation and evaluation of the
algorithm. Most important is Section 4 containing a
detailed description of the sort-merge join algorithm.
Performance evaluation is described in Section 5, and
Section 6 concludes the paper.
2 RELATED WORK
Parallel algorithms greatly improve the performance
of the relational join in shared-nothing systems (Liu
and Rundensteiner, 2005; Schneider and DeWitt,
1989) or shared memory systems (Cieslewicz et al.,
2006; Lu et al., 1990).
Liu et al. (Liu and Rundensteiner, 2005) investi-
gated the pipelined parallelism for multi-join queries.
In comparison, we focus on exploiting the paral-
lelism within a single join operation. Schneider et
al. (Schneider and DeWitt, 1989) evaluated one
sort-merge and three hash-based join algorithms in a
shared-nothing system. In the presence of data skews,
techniques such as bucket tuning (Schneider and De-
Witt, 1989) and partition tuning (Hua and Lee, 1991)
are used to balance loads among processor nodes.
Family of non-blocking algoritms, i.e. (Ming
et al., 2004; Dittrich and Seeger, 2002) is introduced
to deal with pipeline processing where blocking be-
haviour of network traffic makes the traditional join
operators unsuitable (Schneider and DeWitt, 1989).
The progressive-mergejoin (PMJ) algorithm (Dittrich
and Seeger, 2002; Dittrich et al., 2003) is a non-
blocking version of the traditional sort-merge join.
For our parallel stream execution, we adopted the idea
of producing join results as soon as first sorted data
293
Falt Z.,
ˇ
Cermák M. and Zavoral F..
Highly Scalable Sort-merge Join Algorithm for RDF Querying.
DOI: 10.5220/0004489702930300
In Proceedings of the 2nd International Conference on Data Technologies and Applications (DATA-2013), pages 293-300
ISBN: 978-989-8565-67-9
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

are available, even when sorting is not yet finished.
(Albutiu et al., 2012) introduced a suite of new
massive parallel sort-merge (MPSM) join algorithms
based on partial partition-based sorting to avoid a
hard-to-paralellize final merge step to create one com-
plete sort order. MPSM are also NUMA
1
-affine, as
all sorting is carried on local memory partitions and it
scales almost linearly with a number of used cores.
One of the specific areas of parallel join compu-
tations are semantic frameworks using SPARQL lan-
guage. In (Groppe and Groppe, 2011) authors pro-
posed parallel algorithms for join computations of
SPARQL queries, with main focus on partitioning of
the input data.
Although all the above mentioned papers deal
with merge join parallelization, none of them focuses
on streaming systems and exploiting data, task and
pipeline parallelism and data skewness at once.
3 Bobox
Bobox is a parallelization framework which simplifies
writing parallel, data intensive programs and serves
as a testbed for the development of generic and es-
pecially data-oriented parallel algorithms (Falt et al.,
2012c; Bednarek et al., 2012a).
It provides a run-time environment which is used
to execute a non-linear pipeline (we denote it as
the execution plan) in parallel. The execution plan
consists of computational units (we denote them as
the boxes) which are connected together by directed
edges. The task of each box is to receive data from
its incoming edges (i.e. from its inputs) and to send
the resulting data to its outgoing edges (i.e. to its out-
puts). The user provides the execution units and the
execution plan (i.e. the implementation of boxes and
their mutual connections) and passes it to the frame-
work which is responsible for the evaluation of the
plan.
The only communication between boxes is done
by sending envelopes (communication units contain-
ing data) along their outgoing edges. Each envelope
consists of several columns and each column contains
a certain number of data items. The data type of
items in one column must be the same in all envelopes
transferred along one particular edge; however, differ-
ent columns in one envelope may have different data
types. The data types of these columns are defined
by the execution plan. Additionally, all columns in
one envelope must have the same length; therefore,
we can consider envelopes to be sequences of tuples.
1
Non-Uniform Memory Access
The total number of tuples in an envelope is cho-
sen according to the size of cache memories in the
system. Therefore, the communication may take
place completely in cache memory. This increases the
efficiency of processing of incoming envelopes by a
box.
In addition to data envelopes, Bobox distinguish
so called posioned envelopes. These envelopes do not
contain any data and they just indicate the end the of
a stream.
Currently, only shared-memory architectures are
supported; therefore, only shared pointers to the en-
velopes are transferred. This speeds up operations
such as broadcast box (i.e., the box which resends
its input to its outputs) significantly since they do not
have to access data stored in envelopes.
Although the body of boxes must be strictly
single-threaded, Bobox introduces three types of par-
allelism:
1. Task parallelism - independent streams are pro-
cessed in parallel.
2. Pipeline parallelism - the producer of a stream
runs in parallel with its consumer.
3. Data parallelism - independent parts of one
streams are processed in parallel.
The first two types of parallelism are exploited im-
plicitly during the evaluation of a plan. Therefore,
even an application which does not contain any ex-
plicit parallelism may benefit from multiple proces-
sors in the system. Data parallelism must be explicitly
stated in the execution plan by the user; however, it is
still much easier to modify the execution plan than to
write the parallel code by hand.
Due to the Bobox properties and especially its
suitability for pipelined stream data processing we
used the Bobox platform for a pilot implementation
of the SPARQL processing engine.
4 ALGORITHMS
Contemporary merge join algorithms mentioned in
Section 2 do not fit well into the streaming model
of computation (Gordon et al., 2006). Therefore,
we developed an algorithm which takes into account
task, data and pipeline parallelism. The main idea of
the algorithm is splitting the input streams into many
smaller parts which can be processed in parallel.
The sort-merge join consists of two independent
phases – sorting phase that sorts the input stream by
join attributes and joining phase. We have utilized
the highly scalable implementation of a stream sorting
algorithm (Falt et al., 2012b); it is briefly described in
Section 4.2
DATA2013-2ndInternationalConferenceonDataManagementTechnologiesandApplications
294

4.1 Merge Join
Merge join in general has two inputs – left and right.
It assumes that both inputs are sorted by the join at-
tribute in an ascending order. It reads its inputs and
finds sequences of the same values of join attributes
in the left and right input and then performs the cross
product of these sequences. The pseudocode of the
standard implementation of merge join is as follows:
while left.has
next ∧ right.has next do
left
tuple ← left.current
right
tuple ← right.current
if le ft
tuple = right tuple then
append left
tuple to left seq
left.move
next()
while left.has
next ∧left.current=left tuple do
append left.current to left
seq
left.move
next()
end while
append right
tuple to right seq
right.move
next()
while right.has
next∧right.current=right tuple do
append right.current to right
seq
right.move
next()
end while
output cross product(left
seq, right seq)
else if le ft
tuple < right tuple then
left.move
next()
else
right.move
next()
end if
end while
If we take any value V of the join attribute, then
all tuples less than V from both inputs can be pro-
cessed independently on the tuples which are greater
or equal to V. A common approach to merge join par-
allelization is splitting the inputs into multiple parts
by P − 1 values V
i
and process them in parallel in P
worker threads (Groppe and Groppe, 2011).
However, there are two problems with the selec-
tion of appropriate values V
i
:
1. The inputs of the join are data streams; therefore,
we do not know how many input tuples are there
until we receive all of them. Because of the same
reason, we do not know the distribution of the in-
put data in advance. Therefore, we cannot easily
select V
i
in order that the resulting parts have ap-
proximately the same size.
2. The distribution of data could be very non-
uniform (Li et al., 2002); therefore, it might be
impossible to utilize worker threads uniformly.
For the sake of simplicity, we first describe a sim-
plified algorithm for joining inputs without duplicated
join attribute values in Section 4.1.1. Then we extend
the algorithm to take duplicities into account in Sec-
tion 4.1.2.
4.1.1 Parallel Merge Join without Duplicities
In this section, we describe the algorithm which as-
sumes that the input streams do not contain duplicated
join attributes. The execution plan of this algorithm is
depicted in Figure 1.
The algorithm makes use of the fact that the
streams are represented as a flow of envelopes. The
task of preprocess box is to transform the flow of
input envelopes into the flow of pairs of envelopes.
The tuples in these pairs can be joined independently
(i.e., in parallel). Dispatch boxes dispatch these pairs
among join boxeswhich perform the operation. When
join box receives a pair of envelopes, it joins them
and creates the substream of their results. Therefore,
the outputs of join boxes are sequences of such sub-
streams which subsequently should be consolidated in
a round robin manner by consolidate box.
Now, we describe the idea and the algorithm of the
preprocess box. Consider the first envelope left
env
from the left input and the first envelope right env
from the right input. Denote the last tuple (the high-
est value) in left
env as last left and the last tuple in
right
env as last right.
Now, one of these three cases occurs:
1. last
le ft is greater than last right. In this case,
we can split le ft
env into two parts. The first
part contains tuples which are less or equal to
last
right and the second part contains the rest.
Now, the first part of left env can be joined with
the right
env.
2. last left is less than last right. In this case, we
can do analogous operation as in the former case.
3. last
le ft is equal to last right. This means, that
the whole le ft env and the whole right env might
be joined together.
The pseudocode of preprocess box is as follows:
left
env ← next envelope from left input
right
env ← next envelope from right input
while left
env 6= NIL∧ right env 6= NIL do
last
left ← left env[left env.size− 1]
last
right ← right env[right env.size− 1]
if left
last > right last then
split left
env to left first and left second
send right
env to the right output
send left
first to the left output
left
env ← left second
right
env ← next envelope from right input
else if left
last < right last then
split right
env to right first and right second
send right
first to the right output
send left
env to the left output
left
env ← next envelope from left input
right
env ← right second
else
send right
env to the right output
send left
env to the left output
HighlyScalableSort-mergeJoinAlgorithmforRDFQuerying
295

join
0
consolidate
dispatch
dispatch
join
1
join
2
join
3
preprocess
Le
Right
Figure 1: Execution plan of parallel merge join.
left
env ← next envelope from left input
right
env ← next envelope from right input
end if
end while
close the right output
close the left output
The boxes preprocess, dispatch and consolidate
might seem to be bottlenecks of the algorithm. Dis-
patch and consolidate do not access data in envelopes,
they just forward them from the input to the out-
put. Since the envelope typically contains hundreds
or thousands of tuples, these two boxes work in sev-
eral orders of magnitude faster than join box.
On the other hand, preprocess box accesses data
in the envelope since it has to find the position where
to split the envelope. This can be done by a binary
search which has time complexity O(log(L)) where L
is the number of tuples in the envelope. However, it
does not access all tuples in the envelope; therefore, it
is still much faster than join box.
4.1.2 Join with Duplicities
Without duplicities, preprocess box is able to gener-
ate pairs of envelopes which can be processed inde-
pendently. However, the possibility of their existence
complicates the algorithm. Consider a situation de-
picted in Figure 2.
2
2
2
1
2
3
3
3
3
3
3
3
4
5
3
3
3
4
5 6
Le
Right
1
st
pair
2
nd
pair
Figure 2: Duplicities of join attributes.
If join box receives the pair number 2, it needs to
process also the pair number 1. The reason is, that
it has to perform cross products of parts which are
denoted in the figure.
Therefore, join boxes have to receive all pairs of
envelopes for the case when there are sequences of the
same tuples across multiple envelopes. This compli-
cates the algorithm of join box, since each join has to
keep track of such sequences. When we processed an
envelope (from either input), there is a possibility that
its last tuple is a part of such sequence. Therefore, we
have to keep already processed envelopes for the case
they will be needed in the future. When the last tuple
of the envelope changes, the new sequence begins and
we can drop all stored envelopes except the last one.
The execution plan for the algorithm is the same
as in the previous case, the only difference is that dis-
patch box does not forward its input envelopes in a
round robin manner but it broadcasts them to all its
outputs. Since a box receives and sends only shared
pointers to the envelopes, the overhead of the broad-
cast operation is negligible in comparison to the join
operation and therefore it does not limit the scalabil-
ity.
Because of this modification, all boxes receive the
same envelopes. Therefore, the algorithm should dis-
tinguish among them so that they generate the output
in the same manner as in Section 4.1.1. Each join box
gets its own unique index P
i
, 0 ≤ P
i
< P. If we denote
each pair of envelopes sequentially by non-negative
integers j; then join box with index P
i
processes such
pairs j for which it holds j mod P = P
i
. This concept
of parallelization is described in (Falt et al., 2012a)
in more detail.
The complete pseudocode of join box is as fol-
lows:
left
env ← next envelope from left input
right
env ← next envelope from right input
j ← 0
left
seq ← empty
right
seq ← empty
while left
env 6= NIL∧ right env 6= NIL do
if j mod P = P
i
then
do the join of le ft
env and right env
end if
j ← j + 1
if left
env.size > 0 then
last
left ← left env[left env.size− 1]
if last
left 6= left seq then
left
seq ← last le ft
drop all left envelopes except left
env
else
store left
env
end if
DATA2013-2ndInternationalConferenceonDataManagementTechnologiesandApplications
296

end if
if right
env.size > 0 then
last
right ← right env[right env.size− 1]
if last
right 6= right seq then
right
seq ← last right
drop all right envelopes except right
env
else
store right
env
end if
end if
left
env ← next envelope from left input
right
env ← next envelope from right input
end while
The performance evaluation in Section 5.1.3
shows that such concept of parallelization allows bet-
ter scalability than other contemporary solutions.
4.2 Sort
If one or both input streams need to be sorted, we use
the approach based on algorithm described in (Falt
et al., 2012b). Basically, the sorting of the stream is
divided into three phases:
1. Splitting the input stream into several equal sized
substreams,
2. Sorting of the substreams in parallel,
3. Merging of the sorted substreams in parallel.
The algorithm scales very well; moreover, it starts
to produce its output very shortly after the reception
of the last tuple. Therefore, the consecutive merge
join can start working as soon as possible which en-
ables pipeline processing and increases scalability.
However, the memory becomes indispensable bot-
tleneck when sorting tuples instead of scalars, since a
tuple typically contains multiple items. Thus, the sort-
ing of tuples needs more memory accesses especially
when sorting in parallel.
Therefore, we replaced the merge algorithm (used
in the second and the third phase) by a merge algo-
rithm used in Funnelsort (Frigo et al., 1999). We used
the implementation available on (Vinther, 2006). This
algorithm utilizes cache memories as much as possi-
ble in order to decrease the number of accesses to the
main memory. According to our experiments, this al-
gorithm speeds up the merging phase by 20–30%.
5 EVALUATION
Since one of the main goals is efficient evaluation
of SPARQL (Prud’hommeaux and Seaborne, 2008)
queries, we used a standardized SP
2
Bench benchmark
for the performance evaluation of our algorithm in
a parallel environment. Moreover, in order to show
skewness resistance of our algorithm, we used addi-
tional synthetic queries.
All experiments were performed on a server run-
ning Redhat 6.0 Linux; server configuration is 2x In-
tel Xeon E5310, 1.60Ghz (L1: 32kB+32kB L2: 4MB
shared) and 8GB RAM. Each processor has 4 cores;
therefore, we used 8 worker threads for the evalua-
tion of queries. The server was dedicated specially to
the testing; no other applications were running during
measurements.
5.1 Scalability of the Algorithm
In this set of experiments we examined the behaviour
of the join algorithm in multiple scenarios. We used
5M dataset of SP
2
Bench.
We measured the performance of the queries in
multiple settings. The setting ST uses just one worker
thread and the execution plan uses operations with-
out any intraoperator parallelization (i.e., joining and
sorting was performed by one box). The setting MT1
uses also one worker thread; however, the execution
plan uses operations with intraoperator parallelization
(we use 8 worker boxes both for joining and sorting).
The purpose of this setting is to show the overhead
caused by the parallelization. The MT2, MT4 and
MT8 are analogous to the setting MT1; however, they
use 2, 4 and 8 worker threads respectively. These set-
tings show the scalability of the algorithm.
5.1.1 Scalability of the Merge Join
The first experiment shows the scalability of the
merge join algorithm when its inputs contain long se-
quences of tuples with the same join attribute (i.e., the
join produces high number of tuples) and with the join
condition with very high selectivity (i.e., the number
of resulting tuples is relatively low). Since both inputs
of the join are sorted by join attribute, this algorithm
shows only the scalability of merge join and does not
include eventual sorting.
For this experiment, we used this query E1:
SELECT ?article1 ?article2
WHERE {
?article1 swrc:journal ?journal .
?article2 swrc:journal ?journal
FILTER (STR(?article1) = STR(?article2))
}
The query generates all pairs of articles which
were published in the same journal and then selects
the pairs which have the same URI (in fact, it returns
all articles in the dataset). The execution plan of the
query is depicted in Figure 3. The numbers in the bot-
tom of boxes denote the numbers of tuples produced
by the them.
HighlyScalableSort-mergeJoinAlgorithmforRDFQuerying
297
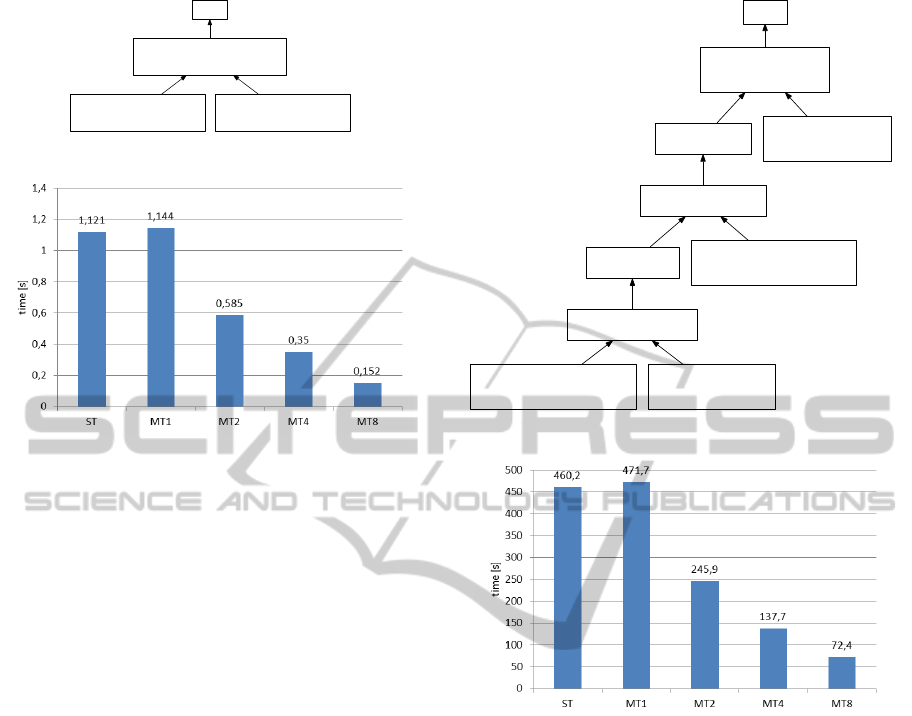
Select
MergeJoin by ?journal
(STR(?article1) = STR(?article2) )
207818
IndexScan [POS]
?article1 swrc:journal ?journal
207818
IndexScan [POS]
?article2 swrc:journal ?journal
207818
Figure 3: Query E1 execution plan.
Figure 4: Results for query E1.
The settings MT1 is slightly slower than ST, since
the query plan contains in fact more boxes (see Fig-
ure 1) which causes higher overhead with their man-
agement. Moreover, the preprocess box does use-
less job in this setting. However, when increasing
the number of worker threads, the algorithm scales
almost linearly with the number of threads.
5.1.2 Scalability of the Sort-merge Join
The scalability of the sort-merge join is shown in the
following experiment. In the contrast to the previ-
ous experiment, the inputs of merge joins (the second
phase of sort-merge join) need to be sorted.
For this experiment, we used this query E2:
SELECT ?article1 ?article2
WHERE {
?article1 swrc:journal ?journal .
?article2 swrc:journal ?journal .
?article1 dc:title ?title1 .
?article2 dc:title ?title2
FILTER(?title1 < ?title2)
}
This plan generates a large number of tuples
which have to be sorted before they can be finally
joined with the second input. The execution plan is
depicted in Figure 5.
We measured the runtime in the same settings as
the previous experiment and the results are shown in
Figure 6.
In this experiment, the difference between ST and
MT1 setting is bigger than in the previous experiment.
This is caused by the fact that the parallel sort al-
gorithm has some overhead (see (Falt et al., 2012b)
Select
MergeJoin on ?article2
(?title1 < ?title2)
4913461
Sort by ?article2
10034740
MergeJoin on ?journal
10034740
Sort by ?journal
209387
MergeJoin on ?article1
207818
IndexScan [PSO]
?article1 swrc:journal ?journal
207818
IndexScan [PSO]
?article1 dc:title ?title1
475059
IndexScan [POS]
?article2 swrc:journal ?journal
207818
IndexScan [PSO]
?article2 dc:title ?title2
475059
Figure 5: Query E2 execution plan.
Figure 6: Results for query E2.
for more information). However, the more worker
threads are used, the bigger speed-up we gain. The
scalability is not as linear as in the previous exper-
iment since the number of memory accesses during
sorting is much higher than during merging. There-
fore, the memory becomes the bottleneck with higher
number of threads.
5.1.3 Data-skewness Resistance
To show the resistance of the algorithm to the non-
uniform distribution of data, we used this query E3:
SELECT ?artcl1 ?artcl2 ?artcl3 ?artcl4
WHERE {
?artcl1 rdf:type bench:PhDThesis .
?artcl1 rdf:type ?type .
?artcl2 rdf:type ?type .
?artcl3 rdf:type ?type .
?artcl4 rdf:type ?type
}
The execution plan for this query is shown in
Figure 7. The variable
?type
has just one value
DATA2013-2ndInternationalConferenceonDataManagementTechnologiesandApplications
298

Select
MergeJoin on ?type
3208542736
MergeJoin on ?type
13481272
MergeJoin on ?type
56644
Sort by ?type238
MergeJoin on ?artcl1
238
IndexScan
?artcl1 rdf:type bench:PhDThesis
238
IndexScan
?artcl1 rdf:type ?type
911482
IndexScan
?artcl4 rdf:type ?type
911482
IndexScan
?artcl2 rdf:type ?type
911482
IndexScan
?artcl3 rdf:type ?type
911482
Figure 7: Query E3 execution plan.
Figure 8: Results for query E3.
(
bench:PhDThesis
); therefore, all joins on that vari-
able are impossible to be parallelized by partitioning
their inputs. Despite this fact, our algorithm accord-
ing to the results (Figure 8) scales very well and al-
most linearly.
5.2 Comparison to other Engines
The last set of experiments compares the Bobox
SPARQL engine which uses new sort-merge join
algorithm to other mainstream SPARQL engines,
such as Sesame v2.0 (Broekstra et al., 2002), Jena
v2.7.4 with TDB v0.9.4 (Jena, 2013) and Virtuoso
v6.1.6.3127-multithreaded (Virtuoso, 2013). They
follow client-server architecture and we provide a
sum of the times of client and server processes. The
Bobox engine was compiled as a single application.
We omitted the time spent by loading dataset to be
comparable with a server that has the data already pre-
pared.
We evaluated queries multiple times over datasets
5M triples and we provide the average times. Each
test run was also limited to 30 minutes (the same time-
out as in the original SP
2
Bench paper). All data were
stored in-memory, as our primary interest is to com-
pare the basic performance of the approaches rather
than caching etc.
Table 1: Results of SP
2
Bench benchmark.
ST MT8 Jena Virtuoso Sesame
Q1 0.01 0.01 0.01 0.00 0.54
Q2 1.32 0.39 242.80 39.03 16.11
Q3a 0.01 0.01 20.84 7.00 2.09
Q3b 0.00 0.00 1.89 0.04 0.54
Q3c 0.00 0.00 1.31 0.03 0.55
Q4 43.69 6.48 TO 1740.84 TO
Q5a 3.08 0.77 TO 30.89 TO
Q5b 1.23 0.23 38.97 28.03 11.02
Q6 TO 1119.3 TO 61.53 TO
Q7 54.89 6.99 TO 23.06 TO
Q8 6.73 1.21 0.26 0.24 17.37
Q9 3.19 0.50 12.25 16.56 7.58
Q10 0.00 0.00 0.30 0.03 1.28
Q11 0.42 0.12 1.50 3.12 0.53
The results are shown in Table 1 (TO means time-
out, i.e., 30 min). Queries Q1, Q3a, Q3b, Q3c and
Q10 operate on few tuples and they all fit into several
envelopes. Therefore, the parallelization is insignif-
icant. However, the important feature is that despite
the more complex execution plans in settings MT8,
the run time is not higher than for non-parallelized
version.
Queries Q8 and Q6 are slower than other frame-
works, since our SPARQL compiler does not perform
some optimizations useful for these queries.
The most important result is that queries Q2, Q3a,
Q3b, Q3c, Q4, Q5a, Q5b, Q9 and Q11 significantly
outperform other engines. All these queries benefit
from extensive parallelization; therefore, much larger
data can be processed in reasonable time. The signif-
icant slowdown of Virtuoso in Q4 is probably caused
by extensive swapping, since the result set is too big.
6 CONCLUSIONS AND FUTURE
WORK
In the paper, we proposed a new method of paral-
lelization of sort-merge join operation for RDF data.
Such algorithm is especially designed for streaming
systems; moreover, the algorithm behaves well also
with skewed data. The pilot implementation within
the Bobox SPARQL engine significantly outperforms
other RDF engines such as Jena, Virtuoso and Sesame
in all relevant queries.
In our future research we want to focus on fur-
ther optimizations such as the influence of granular-
ity of data stream units (envelopes) on overall perfor-
HighlyScalableSort-mergeJoinAlgorithmforRDFQuerying
299

mance. Additionally, the other research direction is to
use these ideas for other than RDF processing, e.g.,
SQL.
ACKNOWLEDGEMENTS
The authors would like to thank the GACR 103/13/
08195, GAUK 277911, GAUK 472313, and SVV-
2013-267312 which supported this paper.
REFERENCES
Albutiu, M.-C., Kemper, A., and Neumann, T. (2012).
Massively parallel sort-merge joins in main memory
multi-core database systems. Proc. VLDB Endow.,
5(10):1064–1075.
Bednarek, D., Dokulil, J., Yaghob, J., and Zavoral, F.
(2012a). Bobox: Parallelization Framework for Data
Processing. In Advances in Information Technology
and Applied Computing.
Bednarek, D., Dokulil, J., Yaghob, J., and Zavoral, F.
(2012b). Data-Flow Awareness in Parallel Data Pro-
cessing. In 6th International Symposium on Intelligent
Distributed Computing - IDC 2012. Springer-Verlag.
Broekstra, J., Kampman, A., and Harmelen, F. v. (2002).
Sesame: A generic architecture for storing and query-
ing RDF and RDF schema. In ISWC ’02: Proceed-
ings of the First International Semantic Web Confer-
ence on The Semantic Web, pages 54–68, London,
UK. Springer-Verlag.
Cermak, M., Dokulil, J., Falt, Z., and Zavoral, F. (2011).
SPARQL Query Processing Using Bobox Framework.
In SEMAPRO 2011, The Fifth International Confer-
ence on Advances in Semantic Processing, pages 104–
109. IARIA.
Cieslewicz, J., Berry, J., Hendrickson, B., and Ross, K. A.
(2006). Realizing parallelism in database operations:
insights from a massively multithreaded architecture.
In Proceedings of the 2nd international workshop on
Data management on new hardware, DaMoN ’06,
New York, NY, USA. ACM.
DeWitt, D. J., Naughton, J. F., Schneider, D. A., and Se-
shadri, S. (1992). Practical skew handling in parallel
joins. In Proceedings of the 18th International Con-
ference on Very Large Data Bases, VLDB ’92, pages
27–40, San Francisco, CA, USA. Morgan Kaufmann
Publishers Inc.
Dittrich, J.-P. and Seeger, B. (2002). Progressive merge
join: A generic and non-blocking sort-based join al-
gorithm. In VLDB, pages 299–310.
Dittrich, J.-P., Seeger, B., Taylor, D. S., and Widmayer, P.
(2003). On producing join results early. In Proceed-
ings of the twenty-second ACM SIGMOD-SIGACT-
SIGART symposium on Principles of database sys-
tems, PODS ’03, pages 134–142, New York, NY,
USA. ACM.
Falt, Z., Bednarek, D., Cermak, M., and Zavoral, F. (2012a).
On Parallel Evaluation of SPARQL Queries. In
DBKDA 2012, The Fourth International Conference
on Advances in Databases, Knowledge, and Data Ap-
plications, pages 97–102. IARIA.
Falt, Z., Bulanek, J., and Yaghob, J. (2012b). On Parallel
Sorting of Data Streams. In ADBIS 2012 - 16th East
European Conference in Advances in Databases and
Information Systems.
Falt, Z., Cermak, M., Dokulil, J., and Zavoral, F. (2012c).
Parallel sparql query processing using bobox. Inter-
national Journal On Advances in Intelligent Systems,
5(3 and 4):302–314.
Frigo, M., Leiserson, C. E., Prokop, H., and Ramachandran,
S. (1999). Cache-Oblivious Algorithms. In FOCS,
pages 285–298.
Gordon, M. I., Thies, W., and Amarasinghe, S. (2006). Ex-
ploiting coarse-grained task, data, and pipeline paral-
lelism in stream programs. SIGARCH Comput. Archit.
News, 34(5):151–162.
Groppe, J. and Groppe, S. (2011). Parallelizing join com-
putations of sparql queries for large semantic web
databases. In Proceedings of the 2011 ACM Sympo-
sium on Applied Computing, SAC ’11, pages 1681–
1686, New York, NY, USA. ACM.
Hua, K. A. and Lee, C. (1991). Handling data skew in mul-
tiprocessor database computers using partition tuning.
In Proceedings of the 17th International Conference
on Very Large Data Bases, VLDB ’91, pages 525–
535, San Francisco, CA, USA. Morgan Kaufmann
Publishers Inc.
Jena (2013). Jena – a semantic web framework for Java.
Available at: http://jena.apache.org/, [Online; Ac-
cessed February 4, 2013].
Li, W., Gao, D., and Snodgrass, R. T. (2002). Skew han-
dling techniques in sort-merge join. In Proceedings of
the 2002 ACM SIGMOD international conference on
Management of data, pages 169–180. ACM.
Liu, B. and Rundensteiner, E. A. (2005). Revisiting
pipelined parallelism in multi-join query processing.
In Proceedings of the 31st international conference
on Very large data bases, VLDB ’05, pages 829–840.
VLDB Endowment.
Lu, H., Tan, K.-L., and Sahn, M.-C. (1990). Hash-based
join algorithms for multiprocessor computers with
shared memory. In Proceedings of the sixteenth in-
ternational conference on Very large databases, pages
198–209, San Francisco, CA, USA. Morgan Kauf-
mann Publishers Inc.
Ming, M. M., Lu, M., and Aref, W. G. (2004). Hash-merge
join: A non-blocking join algorithm for producing fast
and early join results. In In ICDE, pages 251–263.
Prud’hommeaux, E. and Seaborne, A. (2008). SPARQL
Query Language for RDF. W3C Recommendation.
Schmidt, M., Hornung, T., Lausen, G., and Pinkel, C.
(2008). Sp2bench: A sparql performance benchmark.
CoRR, abs/0806.4627.
Schneider, D. A. and DeWitt, D. J. (1989). A performance
evaluation of four parallel join algorithms in a shared-
nothing multiprocessor environment. SIGMOD Rec.,
18(2):110–121.
Vinther, K. (2006). The Funnelsort Project. Available
at: http://kristoffer.vinther.name/projects/funnelsort/,
[Online; Accessed February 4, 2013].
Virtuoso (2013). Virtuoso data server. Available at:
http://virtuoso.openlinksw.com, [Online; Accessed
February 4, 2013].
DATA2013-2ndInternationalConferenceonDataManagementTechnologiesandApplications
300
