Light Scattering Device for Measuring Finest Particles

in the Exhaust of Diesel Engines

Harald Axmann

and Bernd Eichberger

AVL DiTEST Fahrzeugdiagnose GmbH, Alte Poststraße 152, 8020 Graz, Austria

Institute of Electronics, University of Technology, Inffeldgasse 12, 8010 Graz, Austria

Keywords:

Light Scattering, Periodical Technical Inspection, Diesel Engine, Particle Emissions.

Abstract:

Recent developments in engine technologies and exhaust aftertreatment systems signiﬁcantly reduced the par-

ticle emissions of diesel engines. This also demands new measurement devices for the periodical emission

checks, which shall ensure unchanged low emissions over the vehicles’ lifetime. As the current light transmis-

sion technique has reached its detection limit, a new device based on light scattering is presented. This paper

gives a short overview of scattering theory, followed by a description of the measurement system. An emphasis

is placed on the control mechanism for achieving a stable light source. Furthermore ﬁrst measurement results

are presented. Finally the issue of correlation between scattering and established measures is discussed.

1 INTRODUCTION

Particle emissions of internal-combustion engines are

a severe problem for health and environment (Mol-

lenhauer and Tsch¨oke, 2007; Nickel et al., 2013; Ris-

tovski et al., 2012). Just recently a study of the World

Health Organization found diesel soot to be cancero-

genic (IARC, World Health Organization, 2012). In

road trafﬁc, particles are mainly produced by diesel

engines due to incomplete combustion. Many gov-

ernments have reacted by introducing limits for the

allowed exhaust emissions of newly built vehicles. In

Europe these are the European Emission Standards,

which have been tightened repeatedly since their cre-

ation in 1992. In other countries like Japan or the

USA similar regulations have been established (Mol-

lenhauer and Tsch¨oke, 2007). To fulﬁll the require-

ments new motor technologies and above all com-

pletely new aftertreatment systems like the diesel

particle ﬁlter (DPF) have been developed (Mamakos

et al., 2013; Swanson et al., 2013).

To ensure the compliance of the vehicles with

those limits over their lifetime they have to undergo

periodic emission checks. In the European Union

these are regulated by the directive 2010/48/EU (Eu-

ropean Commission, 2010). As an indication of the

particle emissions the opacity of the exhaust fumes

at free acceleration of the engine to cut-off speed is

used. The according measurement device is the opac-

ity meter, which measures the turbidity by means of

light transmission. For old diesel vehicles, known to

emit black clouds of soot, this method was by far sat-

isfactory. Modern vehicle generations have exhaust

gases which are effectively invisible, so this tech-

nique reaches its detection limit (Giechaskiel et al.,

2013). Due to the poor resolution of the device and

the wide measurement tolerances, the limits at the pe-

riodic emission checks cannot be tightened. Elevated

emissions resulting from damaged DPFs are not de-

tected with the current measurement device, or the

cars still pass the check, because the limits are too

loose (Boulter et al., 2011; German Association of

manufacturers and importers of Automobile Service

Equipment, 2010; VdT

UV and DEKRA, 2010).

Consequently new devices for measuring the par-

ticle emissions in garages and vehicle inspection in-

stitutions are necessary. While providing the neces-

sary sensitivity they also need to fulﬁll the require-

ments for the usage in the garages. These are for

example simple operation and maintenance, mobility

and robustness. In a comparison of different meth-

ods for particle measurement another optical princi-

ple showed up as most promising: light scattering.

Instead of quantifying the attenuation of the transmit-

ted light the portion scattered into a distinct direction

is measured (see ﬁgure 1). By use of optimized sig-

nal processing this method can achieve a sensitivity

which surpasses that of opacity meters by two orders

of magnitude. The theory behind light scattering shall

be explained brieﬂy in the following chapter.

457

Axmann H. and Eichberger B..

Light Scattering Device for Measuring Finest Particles in the Exhaust of Diesel Engines.

DOI: 10.5220/0004490704570462

In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2013), pages 457-462

ISBN: 978-989-8565-70-9

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

Light source

Incident

light beam

Particles

Scattered

light

Detector

Figure 1: Light scattering principle.

2 LIGHT SCATTERING THEORY

Light scattering is the deﬂection of light rays due to

heterogeneities in the lit medium. The ﬁrst models for

describing the effect of light scattering go back to the

century. The simplest of these models was de-

veloped by Lord Rayleigh and deals with very small

particles compared to the wavelength of the incident

light. This so called Rayleigh scattering produces the

blue color of the sky (Bohren and Huffman, 1998;

van de Hulst, 1981). For such small particles the scat-

tered light only depends on their size in relation to

the wavelength, the polarization, the scattering angle

and the optical properties (the scattering index) of the

particle. The shape of the particles does not play any

role here. The upper limit for the application of the

Rayleigh model is reached for particle sizes between

one sixth and one tenth of the wavelength.

For bigger particles the shape has an inﬂuence on

the scattering behavior, too. For the simplest geo-

metric object, the sphere, a complete description of

the scattering properties was found in 1908 by Gus-

tav Mie (Mie, 1908). The mathematic functions used

herein are by far more complex than the Rayleigh for-

mulas and cannot be calculated in closed form. For

small particles both give the same results. Further

mathematical models exist for some selected geomet-

ric objects like cubes or cylinders, for which the ori-

entation adds as a variable.

For an ensemble of particles with arbitrary shape

a point is reached, where exact calculations become

too complex and therefore impractical. As the par-

ticles are typically randomly oriented, the approach

via approximation by spheres can be found in the lit-

erature (G¨orner et al., 1995; Hull et al., 2004). For

a random distribution of the particles in space, inter-

ference can be neglected and the total scattering can

be calculated as the sum of scattering from spherical

objects with adequate equivalent diameters. However

the shape of soot particles differs considerably from

spheres. They are chain-like aggregates of almost

spherical monomers, the so-called primary particles

(see ﬁgure 2). Hence the approximation via spheres

must be regarded critically. Although there are meth-

ods to exactly calculate the scattering of such aggre-

gates with known structure, this becomes impossible

for many particles with various structures and orien-

tations (Chakrabarty et al., 2007). Forrest and Witten

found a simpler mathematical description using frac-

tal theory based on the work of Mandelbrot (Forrest

and Witten, 1979). The scattering of these fractal-like

aggregates has been investigated by Sorensen in ex-

tensive studies (Sorensen, 2001). The following cen-

tral equation relates the number of primary particles

N to the geometric aggregate size R

N = k

/a)

(1)

is a root-mean-square radius called radius of

gyration, a is the radius of the primary particles, k

a proportionality constant in the order of 1 and D

the fractal dimension. The latter is a measure of the

space ﬁlling capacity of objects. Small values mean

sparse long chains, whereas values near 3 mean dense

sphere-like structures. Soot particles typically have

≈ 1.78 or D

≈ 1.95, depending on the creation

process (Lapuerta et al., 2006).

Figure 2: Soot particle from a propane ﬂame under a trans-

mission electron microscope (Reinisch, 2009).

On the basis of equation (1) a structure factor can

be calculated for the particle, which describes the in-

terference between the scattering contributions of the

primary particles. It is assumed that all monomers

are of the same size and see the same incident light

wave. Then the total scattering is the sum of the N

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

458

single scattering contributions of the monomers mul-

tiplied by the structure factor. The scattered light of

an ensemble of particles can again be calculated by

summation, because of the random distribution of the

particles.

8 × 10

−17

◦

210

◦

240

◦

270

◦

120

◦

150

◦

330

◦

180

◦

Mie

Rayleigh

Fractal

Figure 3: Calculated scattering intensity for a 100nm parti-

cle using various mathematical models.

Figure 3 shows the radial scattering intensity in

W/(m

sr) of a typical soot aggregate from combus-

tion processes using different mathematical models.

The size of the particle (diameter or 2R

respectively)

is 100 nm, its complex scattering index is assumed

as 1.5 + 1i. The incident light ray with wavelength

660 nm and an irradiance of 1W/m

is directed along

the positive abscissa. In the diagram one can nicely

see the starting deviation of the scattering between

Rayleigh and Mie model. For this size there is just a

little bit more forward scattering (i.e. in direction of

◦

). Forward scattering will become more and more

dominant for bigger particles. Furthermore ripples

from interferences appear. In comparison the scatter-

ing intensity of the fractal is smaller by two thirds,

because it is practically just the sum of the dispropor-

tionately weaker scattering of all the small primary

particles. In contrast to the Mie model there are no

ripples for any particle size. This is due to the fact that

the fractal model is based on the mean of the various

possible structures and orientations of a fractal-like

aggregate with the given parameters.

3 TECHNICAL REALISATION

Light scattering devices are used in non-exhaust re-

lated applications, e.g. for air quality monitoring

and for basic research (G¨orner et al., 1995; Hull

et al., 2004). However, for the use in the periodic

technical inspection special requirements have to be

fulﬁlled. These are robustness, resistance against

the sometimes tough environmental conditions in the

garages (temperature, humidity), mobility, high dy-

namic range (suitable for both low and high emitters),

low maintenance, short preparation time (e.g. heat-

ing up), compatibility with currently used measuring

units and ﬁnally low costs, to be affordable for the

garages.

Light scattering has an essential disadvantage:

The intensity of the scattered light is very small com-

pared to the incident intensity. Even if a wide angle

area is covered the ratio can be 1: 10

or more. Hence

strong light sources combined with sensitive detec-

tors are necessary to achieve the desired resolution.

Such components, especially strong lasers, are typi-

cally rather expensive. In comparison to light from

other sources laser light has the advantage to be very

well focusable, which is helpful for reducing the stray

light. Theoretically in light scattering the sensitivity

only depends on the absolute intensity of the incident

light, as there should ideally be no scattered light in

the absence of particles. In practice stray light and

reﬂections from the interior of the measurement cell

will produce some background light. That means that

the stability of the light source will directly inﬂuence

the lower detection limit, too. Noise or drift of the

light intensity degrade the performance considerably,

and increasing the intensity does not have a positive

effect (see ﬁgure 4). Therefore the control of the light

source is a crucial issue.

Sum of scattered

and background light

BG light

BG noise/drift

Detection limit

Real detection limit

due to source light

drift and noise

Particle concentration [a. u.]

Detector signal [a. u.]

Figure 4: Degraded detection limit due to noise and drift of

the background (BG) light in arbitrary units (a.u.).

For diode lasers the intensity is controlled via the

current through the diode. There are two principle

ways to operate them (Webb and Jones, 2004):

1. Automatic Current Control (ACC) operates the

diode with a constant current which is known to

LightScatteringDeviceforMeasuringFinestParticlesintheExhaustofDieselEngines

459

provide the desired intensity.

2. Automatic Power Control (APC) uses a monitor

diode to measure the laser optical output power

and to adjust the current accordingly.

APC is a simple solution to produce a more or less

constant intensity, which is ideally independent of the

ambient temperature. However depending on the cur-

rent and the temperature mode hopping may occur.

Mode hopping is the abrupt switching from one lon-

gitudinal mode in the laser to another (Heumier and

Carlsten, 1993; Pralgauskait˙a et al., 2013). It leads

to a small change in wavelength and intensity and can

even cause variationsin the direction of the laser light.

Best stability can be achieved with ACC and precise

temperature control. Though, for a bad combination

of case temperature and current, mode hopping may

still occur (Ascente, 2007). Furthermore precise tem-

perature stabilization is costly, so one might not want

to integrate it into a garage device.

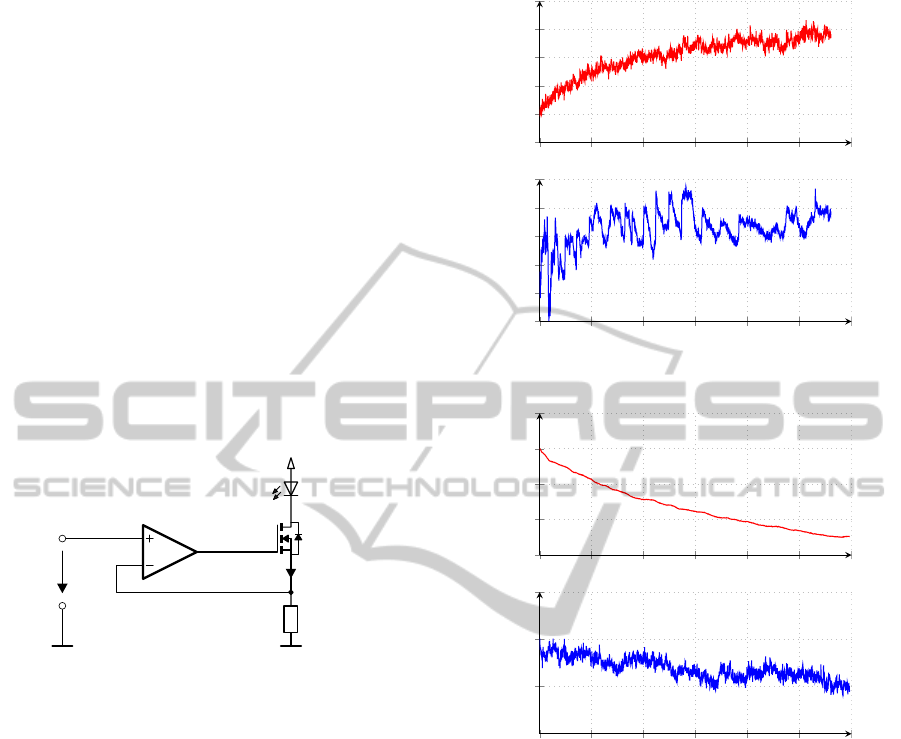
Laser diode

I U R= /

CTL S

CTL

Figure 5: Simpliﬁed analog ACC control loop without sta-

bility measures.

Several test runs showed that the best results in

terms of background light stability can be achieved

when using ACC with a constant average current and

an AC modulation superimposed (see ﬁgure 6). A fre-

quency of a few MHz and a modulation amplitude of

50 % are a good choice. Due to warming of the laser

diode in continuous operation the laser intensity de-

creases with constant current. This leads to a smaller

scattering signal and a drop in the signal background

and has to be corrected by postprocessing. The ef-

fective laser power can be determined via the moni-

tor diode. This information can be used in the micro

processor to correct both the scattering and the back-

ground signal accordingly. As the stray light might

not be directly proportional to the intensity in the fo-

cus, zero correction might not work optimally. Still

sufﬁciently stable background light levels could be

achieved.

For the actual system red diode lasers with a wave-

length of 660 nm and optical powers of 5-15mW

are used. The wavelength is relatively big in com-

parison to the exhaust particles. The accumulation

mode, which contains most of the particle mass, has

0 5 10 15 20 25 30

−2

·10

−3

Laser power P

[%]

0 5 10 15 20 25 30

−1

Time t [min]

Background V

[%]

(a)

0 5 10 15 20 25 30

−3

−2

−1

Laser power P

[%]

0 5 10 15 20 25 30

−2

−1

Time t [min]

Background V

[%]

(b)

Figure 6: Normalized laser power and background signal

in the measurement cell for different laser operation modes

without temperature control. (a) APC: The laser power is

held almost perfectly constant, the background signal shows

drift and spontaneous changes due to mode hopping though.

(b) ACC with modulation: The background signal is much

smoother and its drift is very small.

its peak around 100 nm (Kittelson, 1998; Liu et al.,

2012). This is already near the Rayleigh limit at

this wavelength. For particles below this size limit

scattering will decrease with the sixth power of the

size, quickly reaching the detection limit. Lasers

with shorter wavelength are still very expensive. The

gain in scattering is furthermore partly suspended by

the low spectral efﬁciency of photo diodes for these

wavelengths. Since the soot particles have a very

broad size distribution there are still many particles

that can be nicely detected using red light.

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

460

For detection a small photodiode with 1mm

sensitive area is used. It is thermally isolated from the

measurement cell to reduce temperature inﬂuences.

The current generated by the photo diode is in the pi-

coampere range and below. It is ampliﬁed in a sophis-

ticated circuit using special shielding measures to re-

duce electromagnetic interferences. Precision analog

digital converters typically feature a differential input

structure. The single ended current signal of the diode

is converted to such a differential voltage as exactly

as possible. For this purpose a new ampliﬁer circuit

design is used (Axmann and Eichberger, 2012, Euro-

pean patent pending). The photo diode is connectedto

two symmetric transimpedance ampliﬁers leading to a

differential signal around a center voltage. Noise on

the supply line will merely inﬂuence this center volt-

age resulting in a common mode interference, which

is suppressed by the analog digital converter.

In combination with a high ampliﬁcation over-

sampling is used to achieve a higher resolution. The

analog signal is sampled at a rate of 1 MHz, whereas

the data output rate is 100 Hz. Test measurements

conﬁrmed that this temporal resolution is sufﬁcient to

completely trace the exhaust emissions of combustion

engines. It is noteworthy that in the measurement cir-

cuit a dynamic range of 120dB is attained with only

one ampliﬁer stage. The lowest measurable currents

are approximately 250fA, which is equivalent to ap-

proximately 500 fW of optical power.

4 CORRELATION TO

ESTABLISHED MEASURES

Measurements conﬁrmed that the new device is com-

parable to much more expensivetest bench equipment

in terms of sensitivity. Thus it is capable of reliably

detecting smallest defects in the DPF. However, for

type approval of the new measurement technique a

conversion of the scattering signal to established mea-

sures is necessary. For Germany this is the opacity

N in percent or the equivalent absorption coefﬁcient

k in 1/m. Such a conversion is not straight forward,

because there is no direct physical relation between

scattering and opacity. A look at the mathematic for-

mulas illustrates that properties like used wavelength

or shape, size and optical properties of the particles

have an essential impact on the result.

Moreover the measurement principles differ in

their sensitivities. For example light transmission is

notably sensitive to NO

. This is a brown gaseous

exhaust component, which also attenuates the inci-

dent light (Giechaskiel et al., 2013; Mollenhauer and

Tsch¨oke, 2007; Norris, 2005). A series of measure-

ments at DPF equipped vehicles revealed that opac-

ity from NO

can even be the major part. For light

scattering there is no such inﬂuence because the gas

molecules are below the detection limit. Accordingly

light scattering is a pure particle measurement tech-

nique. With this in mind a conversion of the scatter-

ing signal to a particle mass concentration in mg/m

seems reasonable. Photo acoustic soot sensors have

proven to be a good reference for real time measure-

ments of the mass concentration. They are based

on the resonant measurement of acoustic waves cre-

ated by periodically absorbing particles. The mea-

sured signal is proportional to the soot mass concen-

tration with minimal cross sensitivity (Mollenhauer

and Tsch¨oke, 2007). The limitation to soot however

makes direct comparison to scattering signals some-

times difﬁcult, e. g. when abrasion particles are in-

volved.

Those considerations lead to the conclusion that

a fundamental conversion of the scattering signal to

the said measures is impossible. Instead one has

to rely on empirical formulas. A series of studies,

e.g. (VdT

UV and DEKRA, 2010), and measure-

ments demonstrated that there is a good overall com-

parability between scattering, opacity and mass con-

centration. In ﬁgure 7 the comparison of a device

based on scattering to an opacity meter for soot parti-

cles from propane combustion is shown. A good cor-

relation exists in the depicted range. Based on the

used conversion formulas the detection limit of light

scattering can be derived. It is below k = 0.0001/m.

This is an improvement of two orders of magnitude

compared to currently available garage opacity me-

ters (Norris, 2005).

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

Opacity meter: absorption k [1/m]

Light scattering: absorption k [1/m]

Measured data

Ideal

Figure 7: Correlation of the absorption coefﬁcient between

an opacity meter and a light scattering device (k ≤ 1 /m).

LightScatteringDeviceforMeasuringFinestParticlesintheExhaustofDieselEngines

461

5 CONCLUSIONS

A particle measurement method for periodic emis-

sion tests based on light scattering has been presented.

Care must be taken that noise from the incident light

(e.g. due to mode hopping for laser sources) is min-

imized to achieve highest possible resolutions. In

combination with a sensitive detection system reso-

lutions 100 times better than that of current garage

opacity meters can be achieved at comparable costs.

The temporal resolution (100 Hz) is by far sufﬁcient

for tracing exhaust emissions. Thus light scattering

devices are suitable for the exhaust measurement of

vehicles with state-of-the-art aftertreatment systems.

Further work will focus on the conversion of these re-

sults to established measures like opacity in order to

ensure the applicability of the determined formulas.

REFERENCES

Ascente, T. (2007). Laser diode intensity noise induced by

mode hopping. Rom. Rep. Phys., 59(1):87–92.

Axmann, H. and Eichberger, B. (2012). Circuit conﬁgura-

tion for evaluating photoelectric measurements. Euro-

pean Patent Application EP2501036A1.

Bohren, C. F. and Huffman, D. R. (1998). Absorption and

scattering of light by small particles. Wiley, New

York.

Boulter, P., Buekenhoudt, P., Stricker, P., et al. (2011). TED-

DIE – A new roadworthiness emission test for diesel

vehicles involving NO, NO

, and PM measurements.

Final report, CITA.

Chakrabarty, R. K., Moosm¨uller, H., Arnott, W. P., et al.

(2007). Light scattering and absorption by fractal-like

carbonaceous chain aggregates: comparison of theo-

ries and experiment. Appl. Optics, 46(28):6990–7006.

European Commission (2010). Commission Directive

2010/48/EU of 5 July 2010 adapting to technical

progress Directive 2009/40/EC of the European Par-

liament and of the Council on roadworthiness tests for

motor vehicles and their trailers. OJ L 173:42-72.

Forrest, S. R. and Witten, T. A. (1979). Long-range correla-

tions in smoke-particle aggregates. J. Phys. A: Math.

Gen., 12(5):L109–L117.

German Association of manufacturers and importers of Au-

tomobile Service Equipment (2010). Diesel-AU: Die

Endrohrpr¨ufung ist unerl¨asslich. Press Info. 4/10.

Giechaskiel, B., Schiefer, E., Schindler, W., Axmann, H.,

et al. (2013). Overview of soot emission measure-

ments instrumentation: From smoke and ﬁlter mass

to particle number. SAE Int. J. Engines, 6(1):10–22.

G¨orner, P., Bemer, D., and Fabri´es, J. (1995). Photometer

measurement of polydisperse aerosols. J. Aerosol Sci.,

26(8):1281–1302.

Heumier, T. A. and Carlsten, J. L. (1993). Detecting mode

hopping in semiconductor lasers by monitoring inten-

sity noise. IEEE J. Quantum Elect., 29(11):2756–

2761.

Hull, P., Shepherd, I., and Hunt, A. (2004). Modeling

light scattering from diesel soot particles. Appl. Opt.,

43(17):3433–3441.

IARC, World Health Organization (2012). Diesel engine

exhaust carcinogenic. Press Release No. 213.

Kittelson, D. B. (1998). Engines and nanoparticles: A re-

view. J. Aerosol Sci., 29(5/6):575–588.

Lapuerta, M., Ballesteros, R., and Martos, F. (2006). A

method to determine the fractal dimension of diesel

soot agglomerates. J. Colloid Interface Sci., 303:149–

158.

Liu, Z., Swanson, J., Kittelson, D. B., and Pui, D. Y. H.

(2012). Comparison of methods for online measure-

ment of diesel particulate matter. Environ. Sci. Tech-

nol., 46(11):6127–6133.

Mamakos, A., Martini, G., and Manfredi, U. (2013). As-

sessment of the legislated particle number measure-

ment procedure for a euro 5 and a euro 6 compliant

diesel passenger cars under regulated and unregulated

conditions. J. Aerosol Sci., 55:31–47.

Mie, G. (1908). Beitr¨age zur Optik tr¨uber Medien, speziell

kolloidaler Metall¨osungen. Ann. Phys., 25(3):377–

445.

Mollenhauer, K. and Tsch¨oke, H. (2007). Handbuch Diesel-

motoren. Springer, Berlin Heidelberg, 3

edition.

Nickel, C., Kaminski, H., Hellack, B., Quass, U., et al.

(2013). Size resolved particle number emission fac-

tors of motorway trafﬁc differentiated between heavy

and light duty vehicles. Aerosol. Air Qual. Res.,

13(2):450–461.

Norris, J. O. W. (2005). Low emission diesel research

CP17/18/770. Phase 3 – Report, Vehicle and Oper-

ator Services Agency (VOSA).

Pralgauskait˙a, S., Palenskis, V., Matukas, J., et al. (2013).

Analysis of mode-hopping effect in Fabry-P´erot

multiple-quantum well laser diodes via low frequency

noise investigation. Solid State Electron., 79:104–110.

Reinisch, T. (2009).

Uber die Morphologie von Rußpar-

tikeln von Verbrennungskraftmotoren im Hinblick auf

Partikelanzahlmessung. Bachelor Thesis, Graz, Uni-

versity of Technology.

Ristovski, Z. D., Miljevic, B., Surawski, N. C., Morawska,

L., et al. (2012). Respiratory health effects of diesel

particulate matter. Respirology, 17(2):201–212.

Sorensen, C. (2001). Light scattering by fractal aggregates:

A review. Aerosol Sci. Technol., 35(2):648–687.

Swanson, J. J., Watts, W. F., Newman, R. A., et al. (2013).

Simultaneous reduction of particulate matter and NO

emissions using 4-way catalyzed ﬁltration systems.

Environ. Sci. Technol., 47(9):4521–4527.

van de Hulst, H. C. (1981). Light scattering by small parti-

cles. Dover Publications, New York.

VdT

UV and DEKRA (2010). Emission Check 2010 Teil 2

– Diesel.

Webb, C. E. and Jones, J. D. C., editors (2004). Hand-

book of Laser Technology and Applications, volume

I: Principles. Institute of Physics Publishing, Bristol,

Philadelphia.

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

462