From State-transition Models to DEVS Models
Improving DEVS External Interoperability using MetaDEVS - A MDE Approach
Stéphane Garredu, Evelyne Vittori, Jean-François Santucci and Paul-Antoine Bisgambiglia
Department of Computer Science, University of Corsica, Campus Grimaldi, Corte, France
Keywords: M&S, DEVS, MDE, MDA, M2M, Interoperability, EMF, ATL.
Abstract: In this paper, the issue of the “external” interoperability of DEVS models is discussed. Scientists often need
to simulate non-DEVS models using a DEVS-oriented framework, in order, for instance, to make their
DEVS and non-DEVS modes interoperate. The source formalisms we propose to transform onto DEVS
models are those which are based on the “family” of states and transitions. A general and model-oriented
approach called MetaDEVS is presented in this article. MetaDEVS is also the name given to the DEVS
metamodel we use. This metamodel allows creating platform-independent DEVS models. This paper shows
how models which belong to the state and transitions “family” can be mapped onto DEVS, and more
exactly onto MetaDEVS-based DEVS models, following the MetaDEVS approach. Then, the approach is
applied to a concrete case: we transform Finite-State Machine (FSM) models into MetaDEVS models, using
ATL, a hybrid language (which mixes both declarative and imperative rules), within the Eclipse Modelling
Framework. A metamodel to describe the FSM formalism is also proposed.
1 INTRODUCTION
The study of complex systems and natural
phenomenons is usually done using approaches and
techniques which directly come frome the science of
modelling and simulation (M&S). In the area of
event-based systems, Discrete EVent system
Simulation (DEVS) (Zeigler et al. 2000) appears to
be one of the most popular formalisms used by the
scientists. It has many advantages such as a good
extensibility, a clear separation between models and
their simulators, and strong simulation protocol and
algorithms implemented on several DEVS-oriented
platforms using various object-oriented languages.
However, these several platforms decrease the
interoperability of DEVS models (Wainer et al.
2010), because a model has to be rewritten in order
to be used on another platform than the one for
which it was originally created. This illustrates that
there is a lack of interoperability which can be called
“internal”.
Moreover, there exist other formalisms used in
M&S which rely on the same concepts as DEVS
such as states, and transitions. The DEVS simulation
protocol can be used as an “universal simulator”,
enabling one to integrate a non-DEVS model within
a DEVS framework. Indeed, scientists sometimes
need to reuse non-DEVS models in order to simulate
them with DEVS models. To do so, they have to
rewrite their non-DEVS models in order to create
DEVS models, and usually do a “mental
translation” to reach their goal. This lack of
interoperability can be called “external”.
In the domain of Software Engineering, a fairly
recent research area named Model-Driven
Enginnering (MDE) has proposed several concepts
and techniques which aim to improve the lifecycle
of the models. The final code is no longer seen as
the most important element of the model lifecycle,
but as one of its elements. It is always the result of
one or more transformations. The most important
element in MDE is the model itself and every
element of the process, including the transformations
themselves, is considered as a model.
The main idea of MDE is to maintain a
separation between the concepts and their
implementation. Many MDE approaches, including
the famous Object Management Group (OMG)
Model-Driven Architecture (MDA), focus on
metamodelling.
A metamodel describe a way to describe models
using the concepts of the domain under study,
regardless of the implementation. For instance, a
DEVS-oriented meta-model enables one to specify
186
Garredu S., Vittori E., Santucci J. and Bisgambiglia P..
From State-transition Models to DEVS Models - Improving DEVS External Interoperability using MetaDEVS - A MDE Approach.
DOI: 10.5220/0004494401860196
In Proceedings of the 3rd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2013),
pages 186-196
ISBN: 978-989-8565-69-3
Copyright
c
 2013 SCITEPRESS (Science and Technology Publications, Lda.)

DEVS models, which can be called Platform-
Independent Models (PIMs). MetaDEVS is such a
meta-model (Garredu et al., 2012).
The main idea of our work is to improve DEVS
internal and external interoperability using MDE
techniques and tools.
This article deals with a generic approach which
can be used to transform non-DEVS models into
DEVS models. To do so, both of the metamodels
(source and destination) are required, beacause the
transformation rules take place at the metamodel
level. We already have the DEVS metamodel, it is
named MetaDEVS.
This generic approach is also named after the
metamodel we use : MetaDEVS.
Here, we chose to apply the MetaDEVS
approach to a well-known formalism : the Finite-
State Machines (FSM). In other words, we illustrate
the generic approach presented here by providing
transformation rules from FSM to DEVS: such a
transformation is called a “Model-To-Model”
(M2M) transformation.
This article starts with a background section, in
which we explore the DEVS formalism, the FSM
formalism, and the key concepts of Model-Driven
Engineering. This section ends with a short state-of-
the-art of other approaches which combine MDE
and DEVS, and introduces the the MetaDEVS
approach and metamodel.
Then, the third section is dedicated to the design
of a metamodel for the FSM formalism.
After that, we put together in the fourth section
the ideas presented in the previous sections and we
present the MetaDEVS approach applied to our
problem (M2M transformations), begining with the
global aspects of the approach, and ending with its
application to the transformation between FSM and
MetaDEVS. This section is concluded by an
example of such a transformation: we present a
simple FSM model and show how we automatically
transformed it into a MetaDEVS platform
independent model.
Finally, we conclude this paper after having
discussed the results of the transformation from
FSM to MetaDEVS.
2 BACKGROUND
This background section is dedicated to the concepts
used in the MetaDEVS approach; we start with an
overview of the DEVS formalism and the two kinds
of DEVS models (atomic and coupled). We also
make a brief recall of the well-known
FSM formalism.
2.1 Classic DEVS Formalism
Since the 1970s, formal tasks have been performed
to develop the theoretical foundations of modelling
and simulating discrete event dynamic systems.
One of the most popular discrete-event
formalisms is the DEVS formalism (Discrete Event
system Specification) (Zeigler, 1989) (Zeigler et al.
2000). The DEVS formalism may be defined as a
universal and general methodology, which provides
tools to model and simulate systems, the behaviour
of which is based on the notion of events.
This formalism is based on the systems theory
and the notion of the model and permits the
specification of complex discrete event systems in
modular and hierarchical form. Major efforts have
been made to adapt this formalism to various
domains and situations (Barros, 1997) (Bisgambiglia
et al., 2009) (Wainer et al., 2011).
DEVS has been implemented on several
platforms, such as PowerDEVS (Kofman et al.,
2003), which uses C++, JDEVS (Filippi, 2003),
which uses Java, DEVSimPy (Capocchi et al.,
2011), based on PyDEVS (Bolduc et al., 2001),
which both use Python. This leads to a lack of
interoperability between DEVS models.
At this time, there is no standard and platform-
independent representation of DEVS models, but
there exist several approaches, which try to reach
this goal.
DEVS is composed of two kinds of models: the
atomic models and the coupled models.
Since they are not used in this paper, coupled
models are not described here.
The smallest element in DEVS is the atomic
model. It is specified as follows :
AM = < X, Y, S, ta, δ
int
, δ
ext
, λ >
where
- X = {(p,v)|p ∈ InputPorts, v∈X
p
} is the input events
set, through which external events are received;
InputPorts is the set of input ports and X
p
is the set
of possible values for those input ports;
- Y = {(p,v)|p
∈ OutputPorts, v∈Y
p
} is the output
events set, through which external events are sent;
OutputPorts is the set of output ports and Y
p
is the
set of possible values for those output ports;
- S is the states set of the system;
- ta: S → R
0
+
∪ +∞ is the time advance function (or
lifespan of a state);
- δ
int
: S → S is the internal transition function;
- δ
ext
: Q × X → S with Q = {(s,e)/s∈S, e∈[0,ta(s)]} is
FromState-transitionModelstoDEVSModels-ImprovingDEVSExternalInteroperabilityusingMetaDEVS-AMDE
Approach
187

the external transition function;
- λ: S → Y, with Y = {(p,v)|p
∈ OutputPorts, v∈Y
p
}
is the output function.
The most simple transition is called the internal
transition: at a given moment, a system is in a state
s∈S. Unless an external event occurs on an input
port, the system remains in the s state for a duration
defined by ta(s). When ta(s) expires, the model
sends the value defined by λ(s) on an output port
y
∈Y , and then it changes to a new state defined by
δ
int
(s). Such a transition, which occurs because of the
expiration of ta(s), is an internal transition.
The other transition type is the external
transition; it is triggered by an external event. In this
case, it is the δ
ext
(s,e,x) function which defines which
state is the next one (s is the current state, e is the
elapsed time since the last transition, and x∈X
is the
event received).
In both cases, the system is now in a new state s’
for a new duration d’ = ta(s’) and the algorithm
restarts.
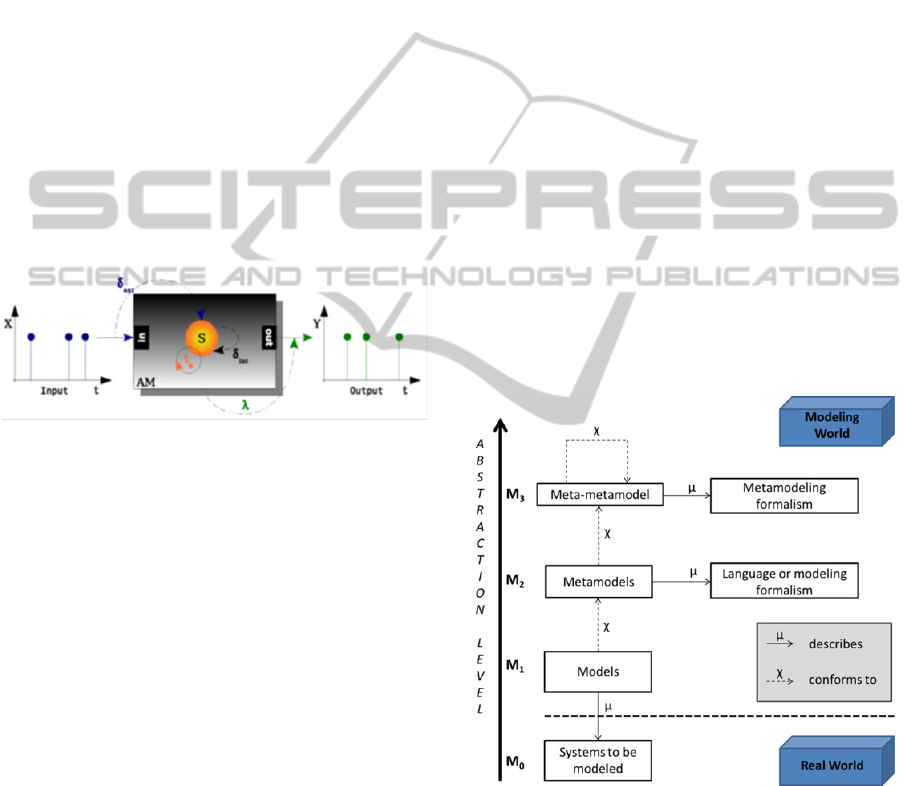
Figure 1: A DEVS atomic model.
The time advance function can take particular
values. If its value is +∞, the state s is passive: the
system will remain in this state unless an external
event occurs. When implementing the time advance
function for a passive state, +∞ will have to be
translated into a keyword (or a particular value)
known by the programming language.
On the other hand, if its value is zero, the state s
is a transient state: it instantaneously triggers the
δ
int
(s) function. Figure 1 shows a representation of a
DEVS atomic model.
2.2 Finite-State Machines
The Finite-State Machine is a well-known formalism
based on the set theory (Glushkov, 1961) (Hopcroft
et al., 1976). It is widely used for the modelling of
protocols, processes, and the description of
compilers, regular grammars.
A FSM (or automaton) is described as follows :
A = < S, Ʃ, δ, I, F >
where:
- S is a finite state set;
- Ʃ is a finite alphabet (and ε is its « empty word »);
- δ is the set of the transitinos : δ ⊆ ( Q × ( Σ∪{ε} )
× Q );
- I is the set of the initial states : I ⊆ Q;
- F is the set of the final states : T ⊆ Q.
The most used FSM are deterministic. In this case,
Card(I) = 1 and for a given state s and a given letter
a, there exists at most one transition starting from s
with the label a : ∀ s∊S, ∀ a∊Ʃ, Card(δ(s,a)) ≤ 1
2.3 Model-Driven Engineering
Model Driven Engineering is a software
development generic methodology that focuses on
creating and exploiting domain models.
Metamodels, models and transformations are the
most important concepts of MDE.
2.3.1 Models and Metamodels
The models, which describe the real world, conform
to a metamodel, located at a higher abstraction level.
The metamodel conforms to a meta-metamodel, or
metaformalism, itself located at a higher abstraction
level. A metaformalism conforms to itself (self-
description).
Figure 2: MDE meta levels.
The concepts of conformance and description are
discussed in (Bézivin, 2004). Figure 2 depicts the
relationships between the several abstraction levels
of MDE.
Each MDE-oriented approach is located in a
given technological space (Kurtev, 2002). The
nature of the technological space depends on the
metaformalism used at the top of the approach. For
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
188

instance, MDE’s most famous incarnation is the
Model Driven Architecture, owned by the OMG,
located in the object-oriented technological space,
because MDA’s metaformalism is the Meta-Object
Facility (MOF), a subset of Unified Modelling
Language (UML) (OMG, 2013). A MDE approach,
which uses the metaformalism XML Schema, would
be located in the XML technological space.
The purpose of a MDE approach is to list the
domain concepts and express them, their attributes,
their relationships, in a metamodel, without being
tied to any implementation platform. Such a
metamodel allows creating platform-independent
models, called PIM in the MDA approach.
Those PIMs can be transformed into platform-
specific models (PSMs), or even into code.
2.3.2 Transformations
The purpose of a transformation is to transform a
source model into a destination model.
A “Model-To-Model” (M2M) transformation
involves two models, while a “Model-To-Text”
(M2T) transformation involves a source model
which will be transformed into code (the code is
considered as a particular model).
A transformation is made by following several
transformation rules, which can be declarative,
imperative, and even hybrid (mixing declarative and
imperative aspects) (QVT, 2013). For the
implementation of our transformation, we use a
language able to express such hybrid rules: ATLas
Transformation Language (ATL) (Jouault et al.,
2006). This language is available as a plugin within
the EMF framework (Steinberg et al., 2009).
2.4 DEVS and MDE
In this section, we will only focus on the approaches
that propose a metamodel for DEVS formalism. The
main drawback of many of them is that the states set
has only one dimension (e.g. one state variable) and
the states are only qualitatitative. However,
(Cetinkaya et al., 2012) and (Garredu et al., 2012)
propose metamodels that allow to handle in their
atomic functions multi-dimensional states with
quantitative state variables. Other approaches aim to
let the programmer fill in empty code blocks (Song,
2006) (Touraille et al., 2010).
2.4.1 Existing Non-MOF DEVS Metamodels
Many approaches use XML to specify the DEVS
basic elements, such as (Mittal et al., 2007) which
can be considered as a “hybrid” approach as it uses
SOA in order to perform the simulation. DTDs are
used to describe the structure of a DEVS component.
A DEVS framework named SimStudio uses a
similar specification language named DML
(Touraille et al., 2010). It also has its own simulation
engine called DEVS-MS. In this approach, the XML
schema (and not the DTD) gives the structure of a
DEVS component. This approach fully complies
with OMG MDA specifications.
Two DEVS meta-models were also specified
using Entity-Relationship diagrams, the meta-meta-
formalism used by AToM
3
(Posse et al., 2003)
(Song, 2006).
2.4.2 DEVS Meta-Models in MOF
This category refers to the metamodels located in the
object-oriented technical space. The implementation
of the MOD-like approaches often uses Ecore as a
metaformalism. Ecore is the metaformalism used by
EMF, and it is a subset of MOF. Approaches of this
family are more recent than the other ones. Some
examples of them are EMF-DEVS (Sarjoughian et
al., 2012), MDD4MS (Cetinkaya et al., 2012) and
MetaDEVS (Garredu et al., 2012). The latter is
briefly presented in the following section.
2.4.3 The MetaDEVS Approach
This approach focuses on three main ideas:
- The central idea is the creation of a metamodel for
DEVS named MetaDEVS. This metamodel allows
creating platform-independent DEVS models, it is
able to handle quantitative state variables and
specify DEVS atomic functions (see 2.4.4).
- The issue of DEVS “external” interoperability.
Thanks to M2M transformations, DEVS formalism
can be used as a target for other formalisms. The
purpose of this paper is to illustrate that.
- The issue of DEVS “internal” interoperability.
This part of MetaDEVS approach is not detailed in
this article : it provides a code generation method
from a MetaDEVS model towards a DEVS-
oriented simulation code (“Model-To-Text”, or
M2T approach) using templates.
To solve the external interoperability issue, we
will use the MetaDEVS metamodel and the second
idea mentionned above.
The approach falls into 3 parts : in the first one,
we globally identify the concepts shared in common
by DEVS and the state/transition formalisms. In the
second one, we use a pseudo-language to express,
for each concept, the transformation from the source
formalisms to MetaDEVS. Those two first steps
have to be achieved only once. The third part is the
FromState-transitionModelstoDEVSModels-ImprovingDEVSExternalInteroperabilityusingMetaDEVS-AMDE
Approach
189

application of the MetaDEVS approach to a
particular source formalism, and the creation of its
metamodel (if it does not exist). The generic rules
previously defined will be refined and adapted to the
transformation context. This third step, which is the
hardest one, has to be achived for every new source
formalism.
2.4.4 The MetaDEVS Metamodel
This metamodel is detailed in (Garredu et al., 2012).
It is fully compliant with MDE and in particular
MDA specifications.
We chose to represent a state by what we call a
state variable or StateVar. It takes a new value when
the state changes (i.e. each new state change will
lead to a change of the value of the state variable).
A state variable must be named, and must be
typed. It can also be affected a literal value (initial
value).
State variables and types are included in a larger
set which name is DEVSXpression. It is one of the
basis of the MetaDEVS metamodel. As a StateVar is
a DEVSExpression, a LitteralBasicValue (LBV) is
also a simpler one, in fact the simplest one because it
is composed of a unique typed value. Even the Ports
(not detailed here) have an inheritance link with
DEVSXpression, but for clarity reasons (the DEVS
concepts must appear clearly in order to be easily
handled) they own their own package.
In spite of the differences between the four
DEVS atomic functions, we can notice that every
function describes a test, an action on a variable, or a
message. Those descriptions follow a sort of pattern,
which is often the same: a set of enumerations. We
call those enumerations DEVS Rules.
The purpose of a rule is to represent a set of
operations on specific elements. To be more
accurate, these are not exactly operations but
descriptions. A DEVS function is composed of one
or several rules. A rule is always composed of a
condition and an action. Table 1 sums this up.
A Condition is described by a test: a left
member, a comparator, and a right member. It can
be a test on an input port (in the case of an external
transition function) or on a state variable (in every
DEVS atomic function, there is a test on a state
variable). There exist two kinds of Condition: the
StateVarComparison, described by a StateVar, a
comparator, and a DEVSXpression, and the
InputPortComparison, described by an InputPort, a
comparator and a DEVSXpression.
An action is in fact the description of an action:
an output action (on a port), or a state change action
(in the case of a transition function). There exist two
kinds of Action: the OutputAction and the
StateChangeAction.
Table 1: DEVS atomic functions and their associated
operations.
An OutputAction is described by a port and a
message (a DEVSXpression), while a
StateChangeAction, used in the transition functions,
is described by the StateVar to be changed, and a
new value (DEVSXpression). Finally, we present the
DEVSModel package, which contains the basic
hierarchy of DEVS models in MetaDEVS (see
figure 3). There is a link between DEVSXpression
and AtomicDEVS: an AtomicDEVS contains
references to the DEVSXpression it handles.
Figure 3: The DEVSModel package.
Note that StateVar, even if it is a DEVSXpression, is
the basis of the state of a model, according to the
DEVS principles. Hence, it appears clearly in the
metamodel.
3 A FSM METAMODEL
In this small section, we shortly present our proposal
of a metamodel for the FSM formalism (restricted to
deterministic automata).
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
190

A FSM model must have one initial state, and at
least one final state. Two states cannot have the
same identifier. A transition involves one source
state and one target state. Two transitions with the
same source state cannot have the same label. A
state cannot be both initial and final.
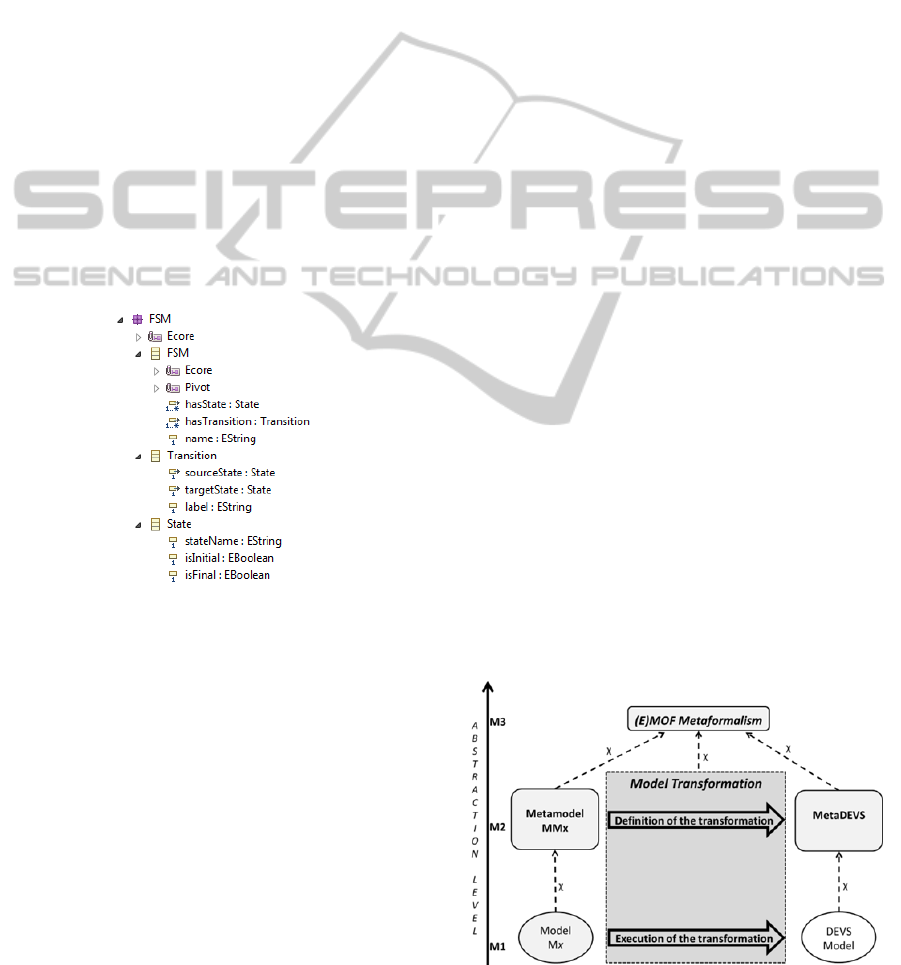
The metamodel we propose is shown in figure 5.
Some of the constraints mentioned above are not
shown here: they are expressed with OCL.
This metamodel is a screenshot of the EMF
Ecore editor; it is an equivalent view as a classic
UML class diagram, and can be used for very simple
metamodels. To create a FSM model, three very
simple steps have to be followed:
- create the model and give it a name
- create the model’s states. Each state has an
identifier (string). A state can be initial or final.
The default value of the attributes isInitial and
isFinal is set to false.
- create the transitions between the states. Each
transition has a source state, a target state, and a
label. The label symbolizes the letter read by the
automaton.
Figure 4: The FSM metamodel (EMF screenshot).
4 DEVS EXTERNAL
INTEROPERABILITY
We have presented in 2.4.4 an overview of the
MetaDEVS approach. In this section, we focus on a
part of this approach: the issue of the external
interoperability of the DEVS formalism. We and
provide a general and practical method, based on
MDE and M2M transformations, to transform any
formalism based on states and transitions onto
DEVS formalism, described in our case by the
MetaDEVS metamodel.
This method starts from the need scientists have
to simulate non-DEVS models within DEVS-
oriented platforms, in order to take advantage of the
DEVS simulation algorithms, to simulate their
models with DEVS models, and also to reuse those
previous models without rewriting them into DEVS
terms. This method lies on the fact that DEVS and
other formalisms share concepts in common. Those
formalisms can be untimed (e.g. Finite-State
Machines) or timed (e.g. Timed Petri Nets).
Moreover, it has been formally proved
(Vangheluwe, 2000) that for every model based on
discrete-events, and even every model based on
states and transitions, a DEVS model exists.
4.1 M2M Transformations in DEVS
Context
In this section, we detail the transformation process
from a language which belongs to the state-transition
family, towards DEVS concepts, in particular those
handled by the MetaDEVS.
4.1.1 Overview of a M2M Transformation
towards DEVS
If we apply to DEVS the ideas exposed before, we
obtain the basis of the MetaDEVS approach
regarding the DEVS external interoperability. The
transformation from a non-DEVS model into a
DEVS model is described at the M2 (metamodel)
level, then executed at the M1 (model) level. Figure
5 shows the basis of the approach.
Note that both of the metamodels, which will be
used to illustrate such a transformation (MetaDEVS
and the FSM metamodel), conform in our case to
EMOF (Ecore).
4.1.2 Concepts
Here, we look deeper into the definition of a
transformation. As we said before, the proposed
Figure 5: A basic M2M transformation towards DEVS.
FromState-transitionModelstoDEVSModels-ImprovingDEVSExternalInteroperabilityusingMetaDEVS-AMDE
Approach
191

method is made possible by the sharing of some key
concepts between DEVS and other formalisms based
on states and transitions.
Those concepts are the model, the state (and the
notion of initial state), the transition, and sometimes,
the port. They are shown in table 2, which also gives
the DEVS “incarnation” of those concepts.
Table 2: General concepts shared by DEVS and
formalisms based on states and transitions.
4.1.3 Generic Rules
The definition of a transformation always starts with
rules. As, at this stage, we do not know what will
exactly be the source formalism, we need to make
our rules be as generic as possible. A rule usually
looks for an element in the source model (optional),
then creates an element in the target model.
A rule can take arguments, call another rule, or
be called by another one. We use this mechanism
(“coupled” rules) to reuse most of the rules we
created: for instance, a rule, which creates a
LitteralBasicValue in the target model, will always
have the same form, whatever the source formalism
is (“immutable” rule). On the other hand, the rule
that calls it behaves as an “intermediate rule”. It will
change every time the source formalism changes.
We write our rules with a pseudo-language, close
to the OMG QVT specification.
The first rule to set up is the one that browses the
source model in order to recreate its hierarchy (if the
source formalism has one) into the target model.
This rule is particular, because it is at the top of the
transformation definition, and does not create
(directly) anything in the target model. Its pseudo-
code has the following form :
rule createHierarchy(s : SMM!Model)
if s.containsModels()
createCoupledDEVS(s);
else
createAtomicDEVS(s);
where SMM is the source metamodel, Model the
meta-element which designates a model in the
source formalism, and s its current instance (i.e. the
source model). Dev is the instance of AtomicDEVS
which is being created.
The rules called by this first rule will create
elements in the target model. In this paper, we will
assume that the source formalism does not have the
ability to specify a hierarchy. Hence, we will focus
on the second rule.
The rule
createAtomicDEVS() has the
following (simplified) form :
rule createAtomicDEVS(s : SMM!Model)
to dev : DEVS!AtomicDEVS
dev.name=s.name;
dev.handles = collectLBV(s);
DEVS!DeltaInt;
DEVS!DeltaExt ;
DEVS!Lambda ;
DEVS!TA ;
dev.InputPort=collectInputPorts(s)
dev.outputPort=collectOutputPorts(s)
We suppose here that the source model is named
(attribute name). Then the four DEVS behavioral
(atomic) functions are each one instantiated once.
Finally, the rule calls two rules in order to collect the
source model’s input and output ports. Then, those
rules will be in charge with the creation of the two
kinds of ports in the target model, by calling port
creation rules. This combination of rules is not
detailed here.
The four atomic functions have now to be filled
in. To do so, the first step is to collect all the values
handled by the source model. We propose once
again a combination of two rules, one will collect
each value handled by the source model and then
call the other one which will create the
corresponding LitteralBasicValue in the destination
model, passing as parameter the retrieved value.
Those rules have the following form:
rule collectLBV(s : SMM!Model)
foreach (s.handledValues)
createLBV(s.valeursManipulées)
rule createLBV(m : value)
to lbv : DEVS!LitteralBasicValue
lbv.isAlwaysTyped=<manually>
lbv.(int/str/char/…)val=m.value
Note that the harvest of the values depends on the
source formalism; we suppose here that it is done
with “handleValues” and that the type is verified.
Also note that in the second rule, the value type is
not known, and will be manually filled. It is possible
to write a function which does it automatically.
Finally, the values must be linked to the target
model, using a reference in the target model (see
rule
createAtomicDEVS()):
Transition DeltaIntorDeltaExt
SOURCE TARGET
Model AtomicDEVSorCoupledDEVS
State
OneormoreLitteralBasicValue
linkedtooneormoreStateVar
Port InputPortorOutputPort
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
192

dev.handles = collectLBV(s)
The second step is to create the StateVar(s) handled
by the target atomic model. The number of StateVar
depends on the nature of the source metamodel, for
instance, a FSM will be transformed into a DEVS
atomic model that will have only on state variable.
The initial value of the StateVar will be chosen
among the previously created LBVs.
The third step is to create some very important
and immutable rules: the rules, which will be in
charge with the creation of the two Condition kinds
(StateVarComparison and InputPortComparison),
and the two Action kinds (OutputAction and
StateChangeAction). Those “immutable” rules will
be called during the filling of the DEVS atomic
functions in the target model.
We give an example of each kind of rules, the
createSVC() rule creates a StateVarComparison,
and the rule
createSCA() creates a
StateChangeAction()(used in the transition
functions).
rule createSVC(s: SMM!State, sv:
DEVS!StateVar)
to sv : DEVS!StateVarComparison
left_member <- sv,
right_member<-select(DEVS!LBV,
s.value)
rule createSCA(t: SMM!Transition,
sv: DEVS!StateVar)
to sv : DEVS!StateChangeAction
state_to_be_changed <- sv
new_value<-select(DEVS!LBV,
t.targetState)
The fourth step consists in filling the atomic
functions. For instance, the DeltaInt function needs
to be filled in with Rules, composed of a
StateVarComparison and a StateChangeAction.
rule createDintRule(t:SMM!Transition
, sv: DEVS!StateVar)
to sv : DEVS!DeltaIntRule
tests <- createSVC(t.source,sv)
changes_state <- createSCA(t,sv)
The three other functions are not detailed here. The
major difficulty with MetaDEVS approach is to
create the rules of the fourth step, by taking into
account the specifications of the source metamodel,
in order to find the best way to represent it in DEVS
terms.
4.2 From FSM Models to MetaDEVS
Models
In this section, we apply the generic rules to a
concrete case: the transformation of a FSM model
into a MetaDEVS model, using the part of the
MetaDEVS approach dedicated to the M2M
transformations.
4.2.1 Discussion
First of all, we need to think about the basic
requirements of the transformation, by asking
ourselves a few questions, which are common to all
the MetaDEVS transformations: they must be linked
to the ideas presented in 4.1.2.
Those questions are: what DEVS concepts are
not represented in the source metamodel (FSM)?
How can we translate them into DEVS terms
without modifying the behaviour of the input model?
How does the destination model have to behave?
4.2.1 Proposal
A FSM evolves by reading letters. Even if it doesn’t
have any input, the resulting DEVS model needs to
read those letters on its input port. Hence, we need
to create an input port in the destination model.
If we reason even further, we notice that reading
a letter which arrives on an input port will trigger, in
DEVS terms, an external transition function. A first
proposal for the basic behaviour of the target model
can be the following one: while nothing happens on
the input port, stay in the current state for an infinite
time.
There is no internal transition and no temporized
state in the basic FSM formalism. However, a DEVS
atomic model needs its DeltaInt function not to be
empty. What particular transitions in the source
model may correspond to DeltaInt in DEVS terms?
If the basic transitions in the target model are, as we
said, triggered by letters read by the input port, we
can assume that all the states of the target model
have an infinite duration. If we do so, we will never
know when a word has been recognized.
To solve this, a possible solution is to assign, to
every final state:
- a lifespan with value below infinity, but above the
“arrival frequency” of the letters on the input port;
- an internal transition function, the target state of
which is not important: our purpose is to trigger
Lambda;
- a Lambda rule which, when the lifespan of the
state expires, send a message on the output port in
order to warn that the word has been recognized
(so, we also need an output port in the target
model).
This helpful global reasoning is to be applied for
each MetaDEVS M2M transformation.The general
rules presented above have to be specialized and
FromState-transitionModelstoDEVSModels-ImprovingDEVSExternalInteroperabilityusingMetaDEVS-AMDE
Approach
193

adapted to the current case: this is the last step (not
shown here) of MetaDEVS, it is illustrated by table
3 sums our discussion up and can be seen as a
specialization of table 2.
Table 3: MetaDEVS approach applied to FSM: a guideline
for the M2M transformation rules.
4.3 Example
Let us take the following FSM as an example It is
able to recognize the words described by the regular
expression:
mi[[ui]*[m]*]* .
Let us call it the “MIU” automaton. It is
composed of three states, the first is the initial state,
and the last is the final state.
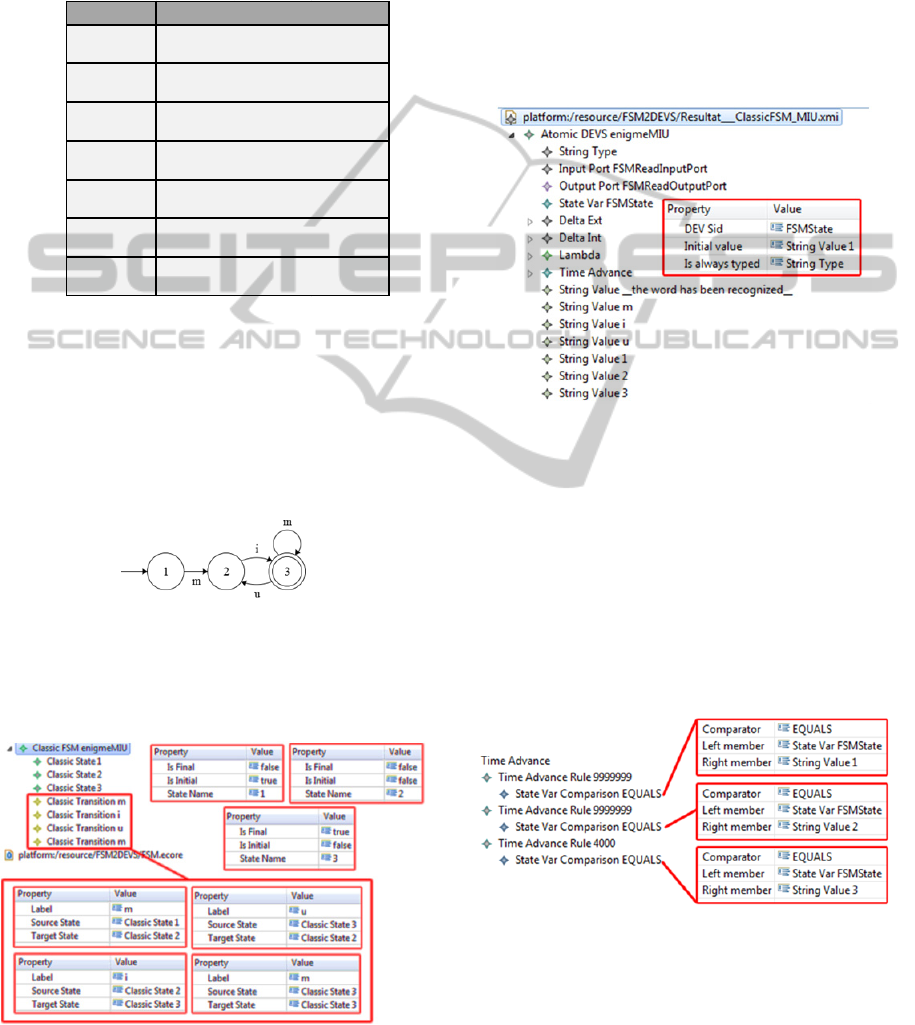
Figure 6: The automaton designed following the FSM
metamodel specifications.
Figure 7 shows an EMF screenshot of the
corresponding instance created within the FSM
Figure 7: EMF screenshot of the “MIU” automaton.
metamodel presented in 3. The transformation
definition was implemented within EMF using ATL
language. The rules are based on the ones we
previously presented.
The result of the automatic transformation is
partially shown here. The resulting model is an
AtomicDEVS model, with an InputPort, an
OutputPort, a StateVar named “FSMState”, seven
StringValue : “m”, “i”, “u”, “1”, “2”, “3”, “word
recognized”, and the four behavioral atomic
functions (figure 8).
Figure 8: The target model generated by the execution of
the transformation.
The initial state has been preserved by the
transformation.
If we look at the TimeAdvance function, we can
see it is conform to our proposal made in 4.2.1. The
final state as a lifespan which is below infinity (we
assume that it is above the “arrival frequency” of the
letters). The two other states have an infinite
lifespan. Figure 9 shows a screenshot of this
function.
Figure 9: The generated TimeAdvance function.
The DeltaInt function also conforms to our
expectations. It takes into account the two transitions
which are fired towards the target state (from state 2
to state 3, from state 3 to itself). This function is
shown on figure 10.
‐ 1InputPortand1OutputPort
Transition
D
eltaExtRulebasedonthenameofthe
stateandtheinputletterread
Transition
C
reateasmuchasLambdaRuleasther
e
aretransitionstowardsfinalstates
‐
C
reateasmuchasDeltaIntRuleasther
e
existfinalstates
SOURCE TARGET
FSM AtomicDEVS
StateList
SeveralStringValueinonlyone
StateVar(DEVSid="FSMState")
StateList
T
imeAdvanceRule>"arrivalfrequency
"
iffinalstate,elseequalstoinfinity
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
194

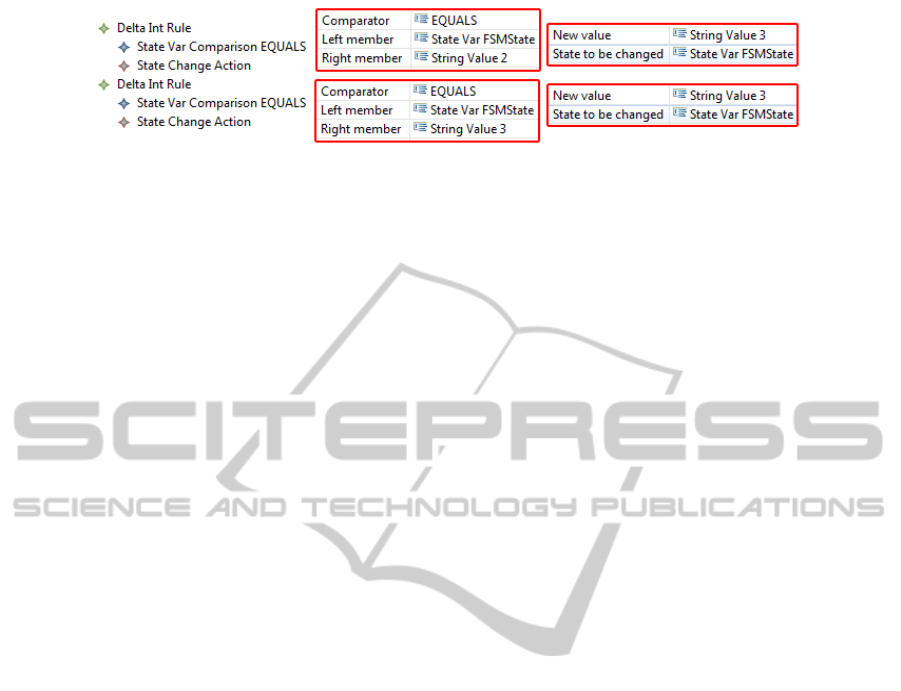
Figure 10: The generated DeltaInt function.
According to our expectations, the generated
Lambda function definition follows the DeltaInt
specifications, and describes an OutputAction which
will be triggered if the lifespans of the states 2 or 3
expire (not shown here).
Finally, the DeltaExt function definition shows
that the transitions of the source FSM model and the
generated MetaDEVS model match: the four FSM
transitions are preserved, they have been turned into
four DeltaExt rules (state “1” to state “2”, state “2”
to state “3”, state “3” to state “2”, state “3” to state
“3”).
This example shows that with what we know
about the source possible formalism, we can
establish generic rules in order to transform non-
DEVS models onto DEVS formalism, represented
by the MetaDEVS metamodel. This approach for
M2M transformations is a part of a larger approach
also named MetaDEVS. The generic rules,
expressed with a pseudo language, were applied to a
concrete case: a transformation between a simple
FSM and MetaDEVS. The results are those we
expected. The FSM model has now become a DEVS
model, fully specified without any code line.
The implementation was made within the EMF
framework, where both of the metamodels we used
were designed. We also used the ATL plugin. The
approach we followed is fully compliant with
MDE/MDA.
5 CONCLUSIONS
In this paper, we have proposed a MDE-oriented
approach, based on M2M transformations, in order
to increase the external interoperability of DEVS
formalism. This approach, named MetaDEVS, is
based on a DEVS target metamodel named
MetaDEVS. This model allows specifying DEVS
models without any reference to any simulation
platform. In other words, the MetaDEVS metamodel
is able to specify platform-independent models.
Our approach is based on the concepts, which are
shared by DEVS, and other formalisms based on
states and transitions. It has been validated by a
transformation definition between FSM and
MetaDEVS. The generated MetaDEVS model is
ready to be connected to a letter generator (i.e. used
in a coupled MetaDEVS model).
Another part of the MetaDEVS proposes a
solution to the “internal” interoperability of DEVS
models: having shown that MetaDEVS was a
solution to describe DEVS models in a platform-
independent way, we propose a method to generate
object-oriented code directly from MetaDEVS
models, using a template-driven approach (M2T
transformations).
However, the power of expression of MetaDEVS
is still limited, as long as it does not allow the
specification of complex conditions (complex
logical structures with Boolean operators), nor
complex actions (incremental structures, loops…).
The next step is to increase the ability of
MetaDEVS to specify complex functions, always in
a platform-independent way.
REFERENCES
Barros, F. J., 1997. Modeling formalisms for dynamic
structure systems. ACM Transactions on Modeling
and Computer Simulation 7, 501–515.
Bézivin J., « Sur les principes de base de l’ingénierie des
modèles », RSTI-L’Objet, 10(4):145–157, 2004.
Bisgambiglia, P.-A., Gentili, E. de, Bisgambiglia, P.A.,
Santucci, J.-F., 2009. Fuzz-iDEVS: Towards a fuzzy
toolbox for discrete event systems, in: ACM (Ed.),
Proceedings of the SIMUTools’09, Rome (Italy).
Bolduc, J. S., Vangheluwe, H. A modelling and simulation
package for classical hierarchical DEVS. MSDL
technical report MSDL-TR-2001-01, McGill
University, June 2001
Capocchi L., Santucci J. F., Poggi B., Nicolai C.,
DEVSimPy: A Collaborative Python Software for
Modeling and Simulation of DEVS Systems, 2nd
International Track on Collaborative Modeling &
Simulation - CoMetS'11, Paris : France (2011)
Cetinkaya Deniz, Verbraeck Alexander et Seck Mamadou
D., Model transformation from BPMN to DEVS in the
MDD4MS framework, Proceedings of the 2012
Symposium on Theory of Modeling and Simulation -
DEVS Integrative M&S Symposium, Orlando,
FromState-transitionModelstoDEVSModels-ImprovingDEVSExternalInteroperabilityusingMetaDEVS-AMDE
Approach
195

Floride, 2012
Filippi, J. « Une architecture logicielle pour la multi-
modélisation et la simulation à évènement discrets de
systèmes naturels complexes », PhD Thesis,
Université de Corse, 2003
Garredu, S., Vittori, E., Santucci, J.-F., and Bisgambiglia,
P.-A., A Meta-Model for DEVS - Designed following
Model Driven Engineering Specifications,
Proceedings of the 2nd International Conference on
Simulation and Modeling Methodologies,
Technologies and Applications, Rome, Italy, 28 - 31
July, 2012.
Glushkov, Victor M. « The abstract theory of automata »,
dans Russian Math. Surveys, vol. 16, 1961, p. 1–53
Hopcroft, J. E. and Ullman, J. D. Introduction to Automata
Theory, Languages, and Computation, Addison-
Wesley, Reading, MA, 1976.
Jouault J., Kurtev I., «On the Architectural Alignment of
ATL and QVT», In Proceedings ofthe 2006 ACM
symposium on Applied computing, session Model
transformation, Dijon, 2006, New York, ACM Press,
p. 1188-1195.
Kofman, E., M. Lapadula, and E. Pagliero, PowerDEVS:
A DEVS-based Environment for Hybrid System
Modeling and Simulation, Technical Report LSD0306,
LSD, Universidad Nacional de Rosario, Argentina,
2003
Kurtev, I., Bézivin, J. et Akşit, M. (2002) Technological
Spaces: An Initial Appraisal. In: International
Conference on Cooperative Information Systems
(CoopIS), DOA'2002 Federated Conferences,
Industrial Track, 30 Oct - 1 Nov 2002, Irvine, USA.
pp. 1-6.
Mittal S., Martín J. L. R., Zeigler B.P. « DEVSML:
automating DEVS execution over SOA towards
transparent simulators », Proceedings of the 2007
ACM Spring Simulation Multiconference, March 25-
29, 2007, Norfolk, VA, USA, Vol. 2, pp. 287-295.
OMG, Object Management Group website, www.omg.org,
2013
Posse E., Bolduc J.-S., « Generation of DEVS Modelling
& Simulation Environments », Proceedings of the
2003 SCS Summer Computer Simulation Conference,
July 2003, Montréal, Canada, pp. 295-300.
QVT, Object Management Group website,
http://www.omg.org/spec/QVT/1.1/PDF, 2013
Sarjoughian, Hessam et Markid, Abbas Mahmoodi, EMF-
DEVS modeling, Proceedings of the 2012 Symposium
on Theory of Modeling and Simulation - DEVS
Integrative M&S Symposium, Orlando, Florida, 2012
Song, H., Infrastructure for DEVS Modelling and
Experimentation. Master's thesis. McGill University.
School of Computer Science. (2006)
Steinberg, D., Budinsky F., Paternostro M., and Merks E.,
Eclipse Modeling Framework 2
nd
Edition, Addison
Wesley, 2009
Touraille L., Traoré M.K., Hill D., « SimStudio : une
Infrastructure pour la Modélisation, la Simulation et
l’Analyse de Systèmes Dynamiques Complexes », UMR
CNRS 6158, LIMOS/RR-10-13, 2010, 12 p. (2010)
Vangheluwe H. L. M., « DEVS as a Common
Denominator for Multi-formalism Hybrid Systems
Modelling », IEEE International Symposium on
Computer-Aided Control System Design, 25-27
September, 2000, Anchorage, Alaska, USA, pp. 129-
134.
Wainer, Gabriel A., Al-Zoubi, Khaldoon, Mittal, Saurabh,
Risco Martín, Jose Luis, Sarjoughian, Hessam,
Zeigler, Bernard P., Dalle, Olivier, Hill, David R.C.
(2010). Standardizing DEVS Simulation Middleware.
In: Discrete-Event Modeling and simulation: Theory
and Applications, edited by Wainer, G., and
Mosterman, P., CRC Press, Taylor and Francis, pp.
459-493
Wainer, G., Liu, Q., Jafer, S., 2011. Parallel Simulation of
DEVS and Cell-DEVS Models in PCD++, in: Wainer,
G., Mosterman, P. (Eds.), Discrete-Event Modeling
and Simulation. CRC Press, pp. 223–270.
Zeigler, B. P. 1989. "DEVS Representation of Dynamical
System", in Proceedings of the IEEE, Vol.77, pp. 72-
80
Zeigler, B. P., Praehofer, H., Kim, T. G. "Theory of
Modeling and Simulation: Integrating Discrete and
Continuous Complex Dynamic Systems", 2nd Edition,
Academic press 2000, ISBN 0-12-778455-1.
SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
196