Dispersion Analysis within a Measured 1,4 km MIMO Multimode

Channel

Andreas Ahrens, Steffen Schr¨oder and Steffen Lochmann

Hochschule Wismar, University of Technology, Business and Design, Philipp-M¨uller-Straße 14, 23966 Wismar, Germany

Keywords:

Multiple-Input Multiple-Output System, Optical Fibre Transmission, Multimode Fiber (MMF), Modal

Dispersion, Chromatic Dispersion.

Abstract:

In this contribution a signal theoretic Multiple Input Multiple Output (MIMO) system model for estimat-

ing modal and chromatic dispersion is developed. Based on channel measurements within a 1,4 km MIMO

multimode channel parameters for modal and chromatic dispersion are estimated. Furthermore, taking given

parameters of the dispersion into account, the introduced signal theoretic MIMO system model enables a

reconstruction of the MIMO speciﬁc impulse responses.

1 INTRODUCTION

The increasing desire for communication and infor-

mation interchange has attracted a lot of research

since Shannon’s pioneering work in 1948.

A possible solution was presented by Teletar and

Foschini in the mid 90’s, which revived the MIMO

(multiple-input multiple-output) transmission philos-

ophy introduced by van Etten in the mid 70’s (Telatar,

1999; Foschini, 1996; van Etten, 1975; van Etten,

1976).

Since the capacity of wireless multiple-input

multiple-output (MIMO) systems increases linearly

with the minimum number of antennas at both,

the transmitter as well as the receiver side, MIMO

schemes have attracted substantial attention (Zhou

et al., 2005; Mueller-Weinfurtner, 2002) and can be

considered as an essential part of increasing both

the achievable capacity and integrity of future gen-

erations of wireless systems (K¨uhn, 2006; Zheng

and Tse, 2003). MIMO transmission has inﬂuenced

nearly any standard of wireless communication.

However, the MIMO principle is not limited to

wireless communication channel and a lot of scenar-

ios can be described by the MIMO technology (K¨uhn,

2006; B¨ulow et al., 2011; Singer et al., 2008).

Within the last years, the concept of MIMO (mul-

tiple input multiple output) transmission over mul-

timode and multicore ﬁbers has attracted increasing

interest in the optical ﬁber transmission community,

e. g. (B¨ulow et al., 2010; B¨ulow et al., 2011; Singer

et al., 2008), targeting at increased ﬁber capacity.

Usually, the ﬁbre capacity is limited by the dis-

persion. In multimode ﬁbres the modal dispersion

dominates the chromatic dispersion by orders. Only

systems with Restricted Mode Launching (RML),

e.g. the 10 Gbit Ethernet system standard 10GBASE-

SR, focus on the description of both dispersion ef-

fects(Pimpinella et al., 2011; Castro et al., 2012).

Since the modal and the chromatic dispersion are

considered to be independent, the system impulse re-

sponse is given by the convolution of these individual

impulse responses.

Against this background, the novel contribution of

this paper is that based on channel measurement with

a 1,4 km multimode ﬁbre, a signal theoretic MIMO

system model for estimating modal and chromatic

dispersion is developed.

By taking given parameters of the dispersion into

account, the introduced system model enables a re-

construction of the MIMO speciﬁc impulse responses.

Thus, a fundamental algorithm for further studies on

the impact of dispersion and for a comparison of dif-

ferent MIMO systems utilizing different wavelengths

is presented.

The remaining part of this contribution is orga-

nized as follows: Section 2 introduces our system

model. The measurement setup for estimating the

channel impulse responses is presented in section 3.

In section 4 our signal theoretic system model is in-

troduced and discussed. The associated performance

results are presented and interpreted in section 5. Fi-

nally, section 6 provides our concluding remarks.

391

Ahrens A., Schröder S. and Lochmann S..

Dispersion Analysis within a Measured 1,4 km MIMO Multimode Channel.

DOI: 10.5220/0004495203910397

In Proceedings of the 4th International Conference on Data Communication Networking, 10th International Conference on e-Business and 4th

International Conference on Optical Communication Systems (OPTICS-2013), pages 391-397

ISBN: 978-989-8565-72-3

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

2 MULTIMODE MIMO

CHANNEL

In order to form the optical MIMO channel, different

sources of light have to be launched into the multi-

mode ﬁbre. In this work a (2×2) optical multimode

MIMO channel is studied. The corresponding elec-

trical MIMO system model is highlighted in Fig. 1.

s 1

(t)

s 2

(t)

k 1

(t)

k 2

(t)

Figure 1: Electrical MIMO system model (example: n = 2).

In Fig. 2 the optical MIMO setup is shown

schematically. On the left side the transmitter side

is represented for launching different sources of light

into the ﬁbre. By coupling light in the center of the

multimode core, described by TX

, low-order mode

groups are activated (e.g. fundamental mode). For

activating high order mode groups, described by TX

light has to be launched into the ﬁbre with an given

eccentricity.

At the receiver side, different spatial ﬁlters are

used to separate the different mode groups. For low-

order mode groups the spot ﬁlter (described by RX

)

and for higher order mode groupsthe ring ﬁlter is used

(described by RX

). Together with the mode group

coupling along the 1,4 km long ﬁbre, the MIMO sys-

tem model according to Fig. 1 can be formed (Pankow

et al., 2011).

3 MEASUREMENT SETUP

In order to evaluate the potential of MIMO in the

ﬁeld of optical multimode communication channels,

a good knowledge of the MIMO speciﬁc impulse re-

sponses and their corresponding dispersion parameter

is needed. For analyzing the MIMO speciﬁc impulse

responses, the measurement setup depicted in Fig. 3

is used. For measuring the impulse responses, the in-

put impulse was generated by using the Picosecond

Diode Laser System (PiLas). For the measurement

10µm

Figure 2: Forming the optical MIMO channel (left: light

launch positions at the transmitter side with a given eccen-

tricity δ, right: spatial conﬁguration at the receiver side as a

function of the mask diameter r).

campaign two different laser diodes are used: The

spectral properties of each laser diode are determined

by measurement. The ﬁrst laser diode has a center

wave length (CWL) of 1326 nm and a spectral half

width of approximately 8 nm. The second laser diode

has a CWL of 1576 nm and a spectral half width of

approximately 10 nm. Fig. 4 shows exemplarily the

Pulse

Generator

SM 10/125

Positioner (Alignment Unit)

GI 50/125

Fixed

GI-Fiber

Moveable

SM-Fiber

50/125

ring

center

Spatial Filter Characteristic

Oscilloscope

Analysis

Figure 3: Measurement setup for measuring the MIMO spe-

ciﬁc impulse responses.

measured spectrum of the 1576 nm Fabry-Perot laser

with the typical modal structure.

1565 1570 1575 1580 1585

Operating Wavelength (innm) →

Power (innW) →

Figure 4: Spectrum of used Fabry-Perot Laser (resolution

bandwidth (RBW) of optical spectrum analyzer 0,07 nm).

For generating a MIMO system, different sources

of light have to be launched into the multimode ﬁ-

bre. For the measurement campaign the laser light

will be launched through a single mode waveguide

OPTICS2013-InternationalConferenceonOpticalCommunicationSystems

392

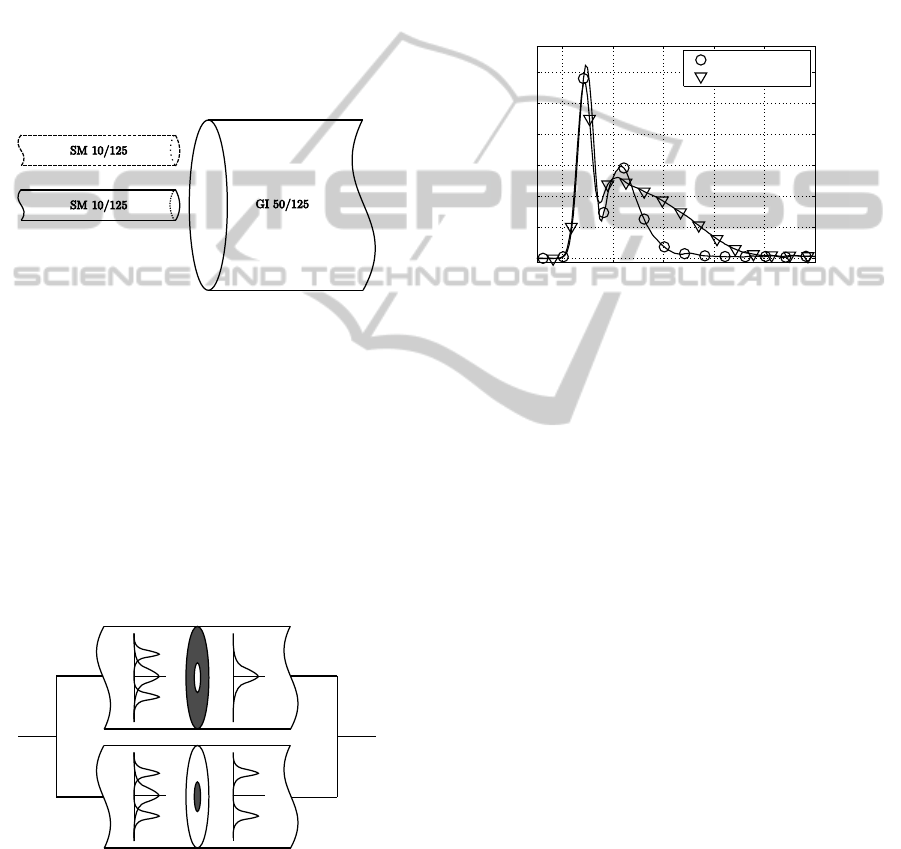
into the core of a multimode waveguide. For the

(2×2) MIMO System two different sources of light

are needed. This part is realized by the ﬁrst coupler

component using a splicer. In a splicer the end of

the transmitter waveguide and the beginning of the

transmission path are clamped together where they

are aligned exactly to each other (Fig. 5). By using the

center launch condition only the fundamental mode is

stimulated, represented by the signal u

(t) in Fig. 1.

The signal u

(t) in Fig. 1 represents the offset launch

condition for activating higher order mode groups.

For the measurements an eccentricity of 10µ m was

chosen. As a transmission channel a graded-index ﬁ-

bre of 1,4 km length was chosen. At the receiver side,

Figure 5: Transmitter side conﬁguration with center and

offset light launch condition.

for separating the different optical channels, different

spatial ﬁlters (i. e, the spot ﬁlter with a diameter of

r = 15µm for low order mode groups and the cor-

responding ring ﬁlter for higher order mode groups)

are used (Fig. 6). These spatial ﬁlters have been pro-

duced by depositing a metal layer at ﬁbre end-faces

and subsequent ion milling (Pankow et al., 2011; Aust

et al., 2012). To determine the appropriate impulse re-

sponse for the respective channel, the particular trans-

mitter/receiver combination has to be chosen.

Figure 6: Receiver side ﬁlter conﬁguration for separating

the different channels.

Fig. 7 highlights the electrical impulse for measur-

ing the MIMO-speciﬁc impulse responses. The pulses

are chosen in a way that the same optical power is

coupled into the multimode ﬁbre core. Theoretically,

an impulse like a dirac delta pulse has to be chosen in

order to measure the channel impulse response unaf-

fectedly from the input impulse. However, in this case

the optical power is no longer sufﬁcient to make the

modal structure measurable. Thus, the input impulses

shown in Fig. 7 are a good compromise to an impulse

like a dirac delta impulse at a reasonable amount of

coupled transmit power. The MIMO-speciﬁc impulse

responses are obtained after deconvolution with the

measured impulse responses.

0 0.1 0.2 0.3 0.4 0.5

t (inns) →

(t) (inmV) →

λ = 1326 nm

λ = 1576 nm

Figure 7: Input impulse for calculating the MIMO-speciﬁc

impulse responses at different operating wavelength.

4 SIGNAL THEORETIC SYSTEM

MODEL

The limiting factor in transmitting high speed data

over single input single output (SISO) multimode

ﬁbers is modal and chromatic dispersion. In order to

be able to study the effect of modal and chromatic dis-

persion especially in MIMO communication, a sim-

pliﬁed SISO system model is developed, which takes

the modal as well as the chromatic dispersion of a

multimode ﬁbre into account. Thereby the individual

mode groups, which propagate along the ﬁbre with

different speed, are modeled as a Gaussian impulse

sequence as highlighted in Fig. 8. This sequence is

described mathematically as

g(t) =

q−1

∑

ℓ=0

ℓ

δ(t −τ

ℓ

) (1)

by taking q dominant mode groups into account

which propagate along the ﬁbre. The delay time of

each mode group is described τ

ℓ

and the mode group

dependent weighting factor by a

ℓ

Since the modal as well as the chromatic disper-

sion are independent from each other, the gaussian

impulse sequence can be decomposed into two parts:

a weighted dirac delta impulse response g

(t) for the

DispersionAnalysiswithinaMeasured1,4kmMIMOMultimodeChannel

393

g(t)

Figure 8: Approximated impulse responses.

description of the modal dispersion (Fig. 9) and a

common gaussian part g

(t) for the description of the

chromatic dispersion (Fig. 10). The resulting SISO

speciﬁc impulse response can be obtained by convo-

lution of g

(t) and g

(t) and results in:

g(t) = g

(t) ∗g

(t) . (2)

Fig. 8 shows an exemplarily impulse response de-

(t)

m 0

m 3

m 2

m 1

Figure 9: Weighted Dirac delta impulse pulse response for

the description of the SISO speciﬁc mode dispersion.

composed into individual gaussian impulses. In this

work it is assumed that all mode groups are de-

scribed by Gaussian impulses with individual delay

and spread parameters. This sequence of weighted

Gaussian pulses can now be decomposed into a se-

quence weighted dirac impulses (Fig. 9), for the de-

scription of the modal dispersion, and into a Gaussian

pulse (Fig. 10), for the description of the chromatic

dispersion.

(t)

√

Figure 10: Gaussian pulse to describe chromatic dispersion.

Fig. 9 and 10 also highlights the parameters of the

presented SISO system model. The parameter τ

ℓ

de-

scribes the average delay time for the mode group ℓ,

mℓ

is the amplitude of ℓth mode group and σ

de-

scribes the spread of each mode group, which is as-

sumed to be the same for all mode groups.

4.1 Modal Dispersion

When launching light into the ﬁbre, different mode

groups will be activated which propagate along the

ﬁbre with different speed and different attenuation.

This effect can be described by a sum of weighted

dirac delta impulses as shown in Fig. 9. Taking the q

dominant mode groups into account, the mode disper-

sion is described by the following impulse response

(t) =

q−1

∑

ℓ=0

mℓ

δ(t −τ

ℓ

) (3)

with the parameter τ

ℓ

as the delay time and the param-

eter g

mℓ

as the weighting coefﬁcient of the ℓ-th mode

group.

The amount of modal dispersion included in the

measured impulse response can now be described ac-

cording to wireless transmission channels by a delay

spread parameter σ

(P¨atzold, 2002). The parame-

ter σ

describes the spread of the whole impulse re-

sponse and can be used as a reference value for the

modal dispersion. The delay spread is given by:

q−1

∑

ℓ=0

(τ

ℓ

mℓ

)

−(

)

. (4)

Therein, the average delay of all modal groups

(i.e.t

) results in

q−1

∑

ℓ=0

ℓ

mℓ

)

(5)

with normalization parameter A =

∑

q−1

ℓ=0

mℓ

)

. With

this normalization parameter, the mode-group depen-

dent weighting coefﬁcients fulﬁl the boundary condi-

tion

q−1

∑

ℓ=0

mℓ

)

= 1 . (6)

4.2 Chromatic Dispersion

Theoretically, in the absent of chromatic disper-

sion, each mode group can be described by a sin-

gle dirac delta impulse with a mode dependent de-

lay and weighting factor. However, as the operat-

ing wavelength increased, the modes within a mode

group travel with different speed and therefore the de-

lay time between the different modes within a mode

group become visible. This results in a broadening of

the beforehand analyzed individual mode group dirac

delta impulses. The parameter for this widening is the

spread parameter σ

. However, through the widening

of the mode group dependent dirac delta impulses, the

amplitude of impulse response is also weighted, i.e.,

OPTICS2013-InternationalConferenceonOpticalCommunicationSystems

394

the amplitude of impulse response a

ℓ

and the modal

dependent weighting factors g

mℓ

depend on the pa-

rameter σ

The chromatic dispersion of each mode group is

described by a normalized Gaussian impulse (Fig. 10)

and is given as

(t) =

√

2π

−

2σ

(7)

The parameter b in Fig. 10 represents the normaliza-

tion factor of the Gaussian impulse and results in

b =

√

2π

. (8)

4.3 Spread Parameters

For the SISO system model, modal and chromatic dis-

persion are described by their corresponding spread

parameters. Assuming that the individual mode

groups are described as Gaussian pulses

g(t) =

q−1

∑

ℓ=0

ℓ

δ(t −τ

ℓ

) , (9)

the parameter a

ℓ

is obtained by combining (3) and (7)

and results in

ℓ

= g

mℓ

√

2π

. (10)

Taking this equation into account, the mode group de-

pendent weighting factor g

mℓ

can be obtained as

mℓ

= a

ℓ

√

2π (11)

by taking into account that the measured amplitude

ℓ

contains the information about the width of the

gaussian pulse (i.e. chromatic dispersion) as well

as the mode-dependent weighting factor. Therefore,

the weighting factor g

mℓ

can be determined with the

predetermined spread parameter σ

and the measured

amplitude a

ℓ

, i.e.

mℓ

= a

ℓ

√

2π . (12)

Since the weighting of each mode group is described

by the modal dispersion completely, the chromatic

dispersion corresponding spread parameter σ

can be

calculated by taking the measured amplitudes a

ℓ

into

account.

4.4 MIMO System Model

In this work a (2 × 2 MIMO system model is inves-

tigated and the beforehand introduced signal theo-

retic SISO system model has now to be extended to

the MIMO system model. The corresponding elec-

trical MIMO system model is highlighted in Fig- 1

with the four existing transmission paths g

νµ

(t) (with

ν = 1, 2,... ,n

and µ = 1,2,.. .,n

), which will be

measured and analyzed separately. The number of

transmitters is given by the n

and the number of re-

ceivers by n

, respectively. Therefore, the impulse

response is given by

νµ

(t) = g

(νµ)

(t) ∗g

(νµ)

(t) . (13)

According to equation (14) the modal dispersion can

be described by

(νµ)

(t) =

q−1

∑

ℓ=0

(νµ)

mℓ

δ(t −τ

(νµ)

ℓ

) (14)

with the delay of ℓth mode group τ

(νµ)

ℓ

and the corre-

sponding weighting factors g

(νµ)

mℓ

. The average delay

of the mode groups can be calculated by

(νµ)

q−1

∑

ℓ=0

(νµ)

ℓ



(νµ)

mℓ



(15)

with the normalization factor A =

∑

q−1

ℓ=0



(νµ)

mℓ



(P¨atzold, 2002). Finally, the modal dispersion results

in:

(νµ)

q−1

∑

ℓ=0



(νµ)

ℓ

·g

(νµ)

mℓ



−



(νµ)



(16)

Assuming that the same laser is used for measuring all

four impulse responses, the chromatic dispersion can

be considered to be same within all four transmission

path. Taking (7) into account, the following equation

holds

(νµ)

(t) = g

(t) . (17)

5 RESULTS

Within this paper, channel measurements within a 1,4

km (2 ×2) MIMO system are carried out. For the

investigated optical MIMO channel an eccentricity δ

of 10µm and a mask diameter r of 15µm were chosen

(Fig. 2). Fig. 11 shows the four impulse responses

for an operating wavelength of 1326 nm according to

Fig. 1. Compared to 1576 nm depicted in Fig. 12 the

inﬂuence of the chromatic dispersion is highly visible.

The impulse responses are obtained after deconvo-

lution with the input impulse depicted in Fig. 7. Fur-

thermore it is assumed that each optical input within

DispersionAnalysiswithinaMeasured1,4kmMIMOMultimodeChannel

395

0 1 2

0.2

0.4

0.6

0 1 2

0.2

0.4

0.6

t (inns) →

1 1

(t) →

1 2

(t) →

2 1

(t) →

2 2

(t) →

Figure 11: Measured electrical MIMO impulse responses

with respect to the pulse frequency f

= 1/T

= 5,00 GHz

at 1326 nm operating wavelength.

0 1 2 3

0.1

0.2

0 1 2 3

0.1

0.2

0 1 2 3

0.05

0.1

0 1 2 3

0.05

0.1

t (inns) →

1 1

(t) →

1 2

(t) →

2 1

(t) →

2 2

(t) →

Figure 12: Measured electrical MIMO impulse responses

with respect to the pulse frequency f

= 1/T

= 5,00 GHz

at 1576 nm operating wavelength.

the multimode ﬁber will be fed by a system with iden-

tical mean properties with respect to transmit ﬁltering

and pulse frequency f

= 1/T

. For numerical assess-

ment within this paper, the pulse frequency is chosen

to be f

= 5,00 GHz Taking the measured impulse

Table 1: Parameters of the calculated chromatic dispersion.

λ (in nm) σ

in (ps)

1326 15

1576 129

responses, depicted in Fig. 11 and 12, into account,

the obtained parameters for the chromatic dispersion

are presented in Tab. 1. For the same operating wave-

length, the chromatic dispersion is assumed to be the

same for all propagation paths and all individualmode

groups. For comparison reason, the chromatic disper-

sion can be approximated by the following equation

= D

ℓ . (18)

The impulse spread τ

can be described as the width

of each impulse or mode group, measured at a 50%

decay of the maximum amplitude and to be assumed

to be approximately twice as large as the calculated

spread parameter σ

. The dispersion parameter D

at the operating wavelength of 1576 nm can be as-

sumed to be 20 ps/(nmkm) (Senior, 2008). Together

with the length of the measured multimode ﬁbre of

ℓ = 1,4 km and the spectral width δ

(FWHW, Full

Width Half Maximum) of the laser diode of 10 nm,

an impulse spread τ

of approximately 280 ps is ob-

tained. With τ

≈ 2σ

the measured values of σ

can

be justiﬁed. At a operating wavelength of 1326 nm

the chromatic dispersion tends to be zero. At this par-

ticular operating wavelength no chromatic dispersion

appears. Therefore, at the operating wavelength of

1326 nm, the chromatic dispersion is not exactly zero,

but much lower compared with an operating wave-

length of 1576 nm.

The estimated parameters of the modal dispersion

are highlighted in Tab. 2.

Table 2: Parameters of the calculated modal dispersion.

λ (in nm) σ

(in ps)

- g

(t) g

(t)

1326 38 215 62 199

1576 159 424 185 353

Next to analyzed parameters of modal and chro-

matic dispersion, the introduced system model en-

ables a reconstruction of the MIMO speciﬁc impulses

responses by taking the estimated dispersion parame-

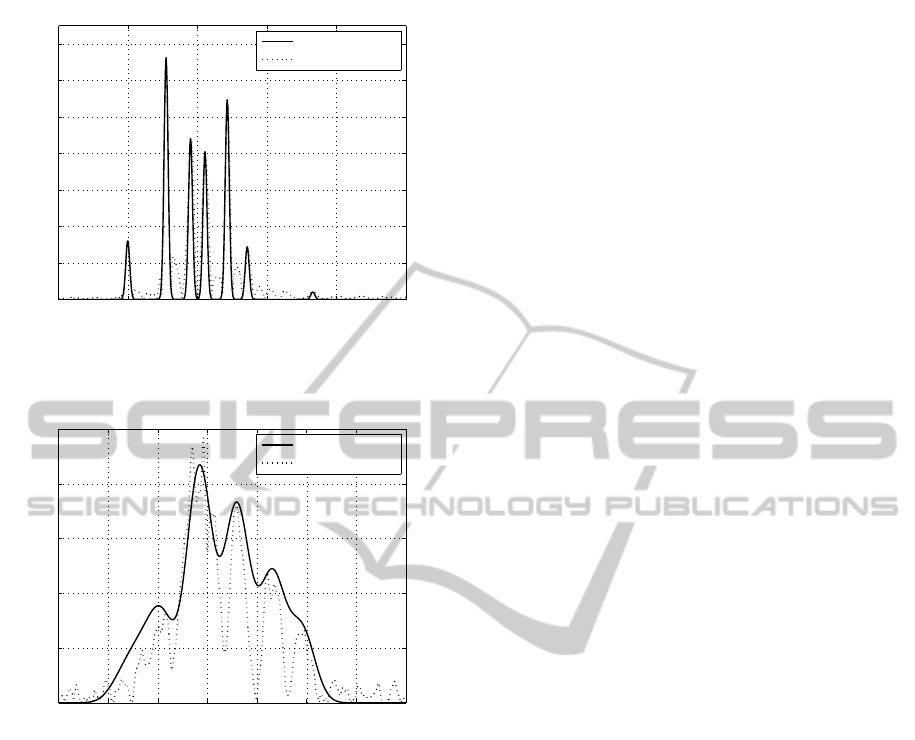
ters into account. In Fig. 13 and 14 the approximated

impulse response g

(t) is shown exemplarily at dif-

ferent operating wavelength by using the beforehand

introduced system model and the estimated parame-

ters of modal and chromatic dispersion. As shown by

Fig. 13 and 14 the approximated impulse responses

show a good correlation with the measured impulse

responses.

6 CONCLUSIONS

Based on channel measurements, in this work a signal

theoretic MIMO system model for estimating modal

and chromatic dispersion is introduced and parame-

ters for modal and chromatic dispersion for an 1,4 km

multimode MIMO channel are estimated.

OPTICS2013-InternationalConferenceonOpticalCommunicationSystems

396

−0.5 0 0.5 1 1.5 2

0.1

0.2

0.3

0.4

0.5

0.6

0.7

t (inns) →

2 2

(t) →

Measured

Calculated

Figure 13: Calculated and measured impulse response

(t) at 1326 nm operating wavelength.

−0.5 0 0.5 1 1.5 2 2.5 3

0.02

0.04

0.06

0.08

0.1

t (inns) →

2 2

(t) →

Measured

Calculated

Figure 14: Calculated and measured impulse response

(t) at 1326 nm operating wavelength.

ACKNOWLEDGEMENTS

The authors wish to thank their co-worker, Mr. Ralph

Bornitz, for supporting the measurement campaign.

REFERENCES

Aust, S., Ahrens, A., and Lochmann, S. (2012). Channel-

Encoded and SVD-assisted MIMO Multimode Trans-

mission Schemes with Iterative Detection. In Interna-

tional Conference on Optical Communication Systems

(OPTICS), pages 353–360, Rom (Italy).

B¨ulow, H., Al-Hashimi, H., and Schmauss, B. (2010). Sta-

ble Coherent MIMO Transport over Few Mode Fiber

Enabled by an Adiabatic Mode Splitter. In European

Conference and Exhibition on Optical Communica-

tion (ECOC), page P4.04, Torino, Italy.

B¨ulow, H., Al-Hashimi, H., and Schmauss, B. (2011).

Coherent Multimode-Fiber MIMO Transmission with

Spatial Constellation Modulation. In European Con-

ference and Exhibition on Optical Communication

(ECOC), Geneva, Switzerland.

Castro, J., Pimpinella, R., Kose, B., and Lane, B. (2012).

The Interaction of Modal and Chromatic Dispersion

in VCSEL based Multimode Fiber Channel Links and

its Effect on Mode Partition Noise. In 61th Interna-

tional Wire & Cable Symposium (IWCS), pages 724–

730, Providence, Rhode Island, USA.

Foschini, G. J. (1996). Layered Space-Time Architecture

for Wireless Communication in a Fading Environment

when using Multiple Antennas. Bell Labs Technical

Journal, 1(2):41–59.

K¨uhn, V. (2006). Wireless Communications over MIMO

Channels – Applications to CDMA and Multiple An-

tenna Systems. Wiley, Chichester.

Mueller-Weinfurtner, S. H. (2002). Coding Approaches for

Multiple Antenna Transmission in Fast Fading and

OFDM. IEEE Transactions on Signal Processing,

50(10):2442–2450.

Pankow, J., Aust, S., Lochmann, S., and Ahrens, A. (2011).

Modulation-Mode Assignment in SVD-assisted Op-

tical MIMO Multimode Fiber Links. In 15th Inter-

national Conference on Optical Network Design and

Modeling (ONDM), Bologna (Italy).

P¨atzold, M. (2002). Mobile Fading Channels. Wiley, Chich-

ester.

Pimpinella, R., Castro, J., Kose, B., and Lane, B. (2011).

Dispersion Compensated Multimode Fiber. In 60th In-

ternational Wire & Cable Symposium (IWCS), pages

410–418, Charlotte, North Carolina, USA.

Senior, J. (2008). Optical Fiber Communications: Princi-

ples and Practice. Prentice Hall, New Jersey.

Singer, A. C., Shanbhag, N. R., and Bae, H.-M. (2008).

Electronic Dispersion Compensation– An Overwiew

of Optical Communications Systems. IEEE Signal

Processing Magazine, 25(6):110 – 130.

Telatar, E. (1999). Capacity of Multi-Antenna Gaussian

Channels. European Transactions on Telecommuni-

cations, 10(6):585–595.

van Etten, W. (1975). An Optimum Linear Receiver

for Multiple Channel Digital Transmission Systems.

IEEE Transactions on Communications, 23(8):828–

834.

van Etten, W. (1976). Maximum Likelihood Receiver for

Multiple Channel Transmission Systems. IEEE Trans-

actions on Communications, 24(2):276–283.

Zheng, L. and Tse, D. N. T. (2003). Diversity and

Multiplexing: A Fundamental Tradeoff in Multiple-

Antenna Channels. IEEE Transactions on Information

Theory, 49(5):1073–1096.

Zhou, Z., Vucetic, B., Dohler, M., and Li, Y. (2005). MIMO

Systems with Adaptive Modulation. IEEE Transac-

tions on Vehicular Technology, 54(5):1073–1096.

DispersionAnalysiswithinaMeasured1,4kmMIMOMultimodeChannel

397