A Parity-based Error Control Method for Distributed Compressive

Video Sensing

Shou-ning Chen, Bao-yu Zheng and Liang Zhou

Institute of Signal Processing and Transmission, Nanjing University of Posts and Telecommunications,

Gulou Xin Mo Fan Road 66#, mailbox 214#, Nanjing, China

Keywords: Distributed Compressive Video Sensing (DCVS), Distributed Video Coding (DVC), Compressive Sensing

(CS), Parity-based Error Control (PEC).

Abstract: A novel framework called distributed compressive video sensing (DCVS), combining distributed video

coding (DVC) and compressive sensing (CS), directly capture the raw video data as measurements with

low-complexity and low-cost process. It meets the requirements of distributed system very well, because of

its resource consumption shifting from encoder to decoder. Nevertheless, the issue of measurements

transmission in bit error channel has not been considered yet in the previous work of DCVS. This paper

improved the existing DCVS codec scheme by adding the quantization and inverse quantization process,

and proposed a parity-based error control (PEC) method. This method is simple enough, and has high

coding efficiency. The proposed method is shown to increase video recovery quality greatly under binary

symmetric channel.

1 INTRODUCTION

In the framework of Wireless Media Sensor

Network (WMSN) (Akyildiz et al., 2007), the sensor

nodes must work under some resource constraints,

such as lower computational capability and limited

energy supply, so the problem of how to process the

considerable video information efficiently has been

brought into attention.

Compared with traditional compression standard

like H.264/MPEG, distributed video coding (DVC)

(Girod et al., 2005), which is developed from the

principle of distributed source coding (DSC) (Wyner

et al., 1976), was proposed to reduce the encoding

complexity via shifting the complicated motion

estimation work as the major encoding cost to

decoder.

Another popular theory, compressive sensing

(CS) (Candès and Wakin, 2008) also can shift the

encoder burden to decoder, which has the similar

structure to DVC. The CS theory, which combined

sampling with compression, captures the abundant

raw image information efficiently with a small

amount of incoherent measurements at encoder, and

recovers the image faithfully via linear programming

at decoder. CS is particularly fit for the distributed

systems because of the significant cost reduction of

data acquisition.

Motivated by the common principle of the two

aforementioned theories, the framework of

distributed compressive video sensing (DCVS)

(Kang et al., 2009);

(Do et al., 2009) was proposed.

However, the previous researches just focus on the

codec scheme without much concerning about

compressed signal transmission problem. Based on

the CS theory, the structure of compressed signal,

which is composed of some incoherent

measurements, differs a lot from the conventional

source coding signal which is represented by the

signal coefficients in frequency domain. Therefore,

the transmission problem of CS signal in DCVS

deserves our attention. There already has been some

research on quantization of CS signal (Dai et al.,

2009). And measurements rate allocation for DCVS

(Chen et al., 2010) was also proposed to enhance the

recovered video quality. Moreover, we also do some

work on video quality evaluation for DCVS (Chen et

al., 2012). Main work in this paper is displayed as

follows: 1, provided a suitable quantization for

measurements of DCVS; 2, proposed a parity-based

error control method for DCVS; 3, employed the

proposed method for quantized measurements to

alleviate the affect of binary symmetric channel.

The organization of this paper proceeds as

105

Chen S., Zheng B. and Zhou L..

A Parity-based Error Control Method for Distributed Compressive Video Sensing.

DOI: 10.5220/0004495901050110

In Proceedings of the 10th International Conference on Signal Processing and Multimedia Applications and 10th International Conference on Wireless

Information Networks and Systems (SIGMAP-2013), pages 105-110

ISBN: 978-989-8565-74-7

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

follows. Section 2 gives the basic aspects of DVC

and CS, section 3 describes the specific example of

DCVS and proposed parity-based error control (PEC)

method for DCVS, section 4 discusses the

simulation results and section 5 is the conclusion

and future directions of research.

2 RELATIVE WORKS

2.1 Distributed Video Coding (DVC)

In distributed source coding (DSC), assumed that W

and S are two statistically dependent discrete

signals, which are encoded independently but

decoded jointly. Slepian-Wolf theorem (Wyner et al.,

1976) asserted the achievable rate region for lossless

coding is defined by Rw≥H(W/S), Rs≥H(S/W), and

Rw+Rs≥H(W,S), where Rw and Rs are the encoding

rates for W and S, respectively, H(W/S) and H(S/W)

are the conditional entropy of W and S, respectively,

and H(W,S) is the joint entropy of W and S.

Additionally, S is known as the side information (SI)

of W.

In distributed video coding (DVC) (Girod et al.,

2005), the kinds of frames in a group of pictures

(GOP) are divided into Key frame and WZ frame

(Wyner-Ziv frame). The Key frames are intra-coded

an intra-decoded like I-frame in conventional video

compression standards. And some information

derived from Key frame is viewed as side

information (SI) at decoding end. At encoder,

without motion estimation, the compression of WZ

frame is achieved as parity bits (also called Wyner-

Ziv bits) by channel-encoding like turbo coding or

LDPC coding. Decoder receives the parity bits of

WZ frame viewed as W, and uses the SI S viewed as

noisy version of W to perform channel decoding for

reconstruction of WZ frame.

2.2 Compressive Sensing (CS)

In recent years, compressive sensing (CS) (Donoho,

2006); (Candès, 2006); (Candès and Tao, 2006)

provides a theory about broadband analog signals

sampling. The CS as a new research focus gives a

novel set of theoretical framework about signal

representation, signal sampling and signal

reconstruction. It points out that, if the signal x is

sparse in time domain or sparse in some transform

basis Ψ, then we can employ global measurement

instead of local sampling with sampling speed far

below the Nyquist frequency, get measurements y

less than original sampling number through the

measurement matrix Φ which is not coherent with

sparse transform basis Ψ. After that, original high-

dimensional signal x can be

recovered accurately

with appropriate reconstruction algorithm from low-

dimensional measurements y. Unlike Nyquist

sampling theory, the sampling rate is not dependent

on bandwidth of signal,

but on two basic criteria:

sparsity and the restricted isometry property (RIP)

(Candès and Tao, 2006). Theoretical framework of

compressive sampling is shown in Figure 1.

Figure 1: Compressive sampling framework.

CS contains the following four steps based on the

study of theory, shown as Figure 1.

 Assume that the original N-dimensional signal

can be sparse on the basis Ψ (N×N), then get the

sparse signal θ. If the original signal is sparse

already, skip this step.





(1)

 Devise the measurement matrix Φ (M×N) to

acquire measurements y, where A=ΨΦ called the

sensing matrix.





ΦΦΨ

(2)

 Solve the problem of minimum l

norm as

follows known Φ, Ψ and y, and reconstruct θ

from measurements y.

arg min || || s.t. =y





 A

(3)

 Obtain the original signal

using the inverse

transform of basis

Ψ.



 Ψ

(4)

Sparsity, measurement matrix and reconstruction

algorithm in the above steps are three key parts of

CS theory.

Sparse signal in compressive sampling is defined

as follows: if a signal only has finite number of non-

zero sample point (the number is K), and other

sample point is zero or similar to zero, this signal is

claimed as K-sparse and the sparsity is K. Ref

(Baraniuk, 2007) shows that the original signal may

be reconstructed accurately in large probability

under the condition that the relation between

measurements M and sparsity K should satisfies

M≥K·log(N), in other words, the signal recovery

quality will be affected quitely if the measurements

M is less than a certain number.

SIGMAP2013-InternationalConferenceonSignalProcessingandMultimediaApplications

106

According to the above characteristics of

compressive sensing, it has following advantages for

video transmission: (1) The correlation of adjacent

signal sampling points obtained by traditional

method is robust, on the contrary, the redundancy of

measurements observed by CS is in a very low state,

it is in favor of large amount of data information

processing like video transmission to avoid the

waste of a lot of redundant information (Barakat et

al., 2008); (2) The CS is suitable for distributed or

portable terminal video transmission particularly due

to resource consumption of computing and storage

transferred from sender to receiver; (3) Because CS

signal is unstructured presentation of image, and

reconstruction algorithms leave far from the

statistical radio channel interference constraints, so it

possesses good characteristics of resistance to

random channel errors.

3 IMPROVED DCVS SCHEME

AND PROPOSED PEC

METHOD

3.1 DCVS Codec Scheme

In the Kang’s DCVS codec scheme (Kang et al.,

2009) shown in Figure 2, a video sequence consists

of several GOPs, where GOP consists of a key frame

and some followed CS frames. At the encoder, each

frame x

, including Key frame and CS frame, is

compressed via CS measurement process as:



yx

(5)

where y

is the measurement vector with size M

, and

Φ is the scrambled block Hadamard ensemble

(SBHE) matrix described in (Do et al., 2008). The

sparse basis matrix

Ψ used in the scheme is DWT.

The significant difference between Key frame and

CS frame is that the measurement vector size M

Key frame should be larger than that of CS frame, to

guarantee the recovery video quality at decoder. The

measurement rate for each frame can be defined as:

RMN

(6)

where N is the size of video frame.

At the decoder, each Key frame x

reconstructed via Gradient projection for sparse

reconstruction algorithm (GPSR) (Figueiredo et al.,

2007), which solve the convex unconstrained

optimization problem described as:

min || || || ||







(7)

where y

is a vector with size M

, y

=Φx

, A= ΦΨ is

a M

×N matrix, and



is a non-negative parameter.

GPSR is essentially a gradient projection algorithm

applied to a quadratic programming formulation of

Eq.(7), in which the search path for each iteration is

acquired by projecting the negative-gradient

direction onto the feasible set, and the default initial

solution for θ

is a zero vector.

Before reconstructing a CS frame x

, the decoder

will generate its SI S

by motion-compensated

interpolation from the reconstructed neighboring

Key frames first, which can be viewed as a noisy

version of x

. In the same scene, the successive

frames should have a certain similarity. Hence, the

SI derived from the neighboring Key frame, should

be similar to this CS frame. So, each CS frame is

reconstructed via the modified GPSR with the initial

solution set by SI. To get a good quality for CS

frame, it is required to have a good initialization

derived from Key frame which is served as reference

frame. That is why the measurement vector size M

of Key frame should be much larger than that of CS

frame.

3.2 Quantization for Measurements

The measurements of DCVS frame is discrete in

time but continuous in amplitude. Hence, the

quantization is the indispensable part of codec

scheme. In order to improve the above-mentioned

DCVS codec scheme, the uniform quantization and

inverse quantization are added to the system for

digital transmission. Scale quantization is employed

on account of complexity of encoder. Quantizing

process is described as:

round(2 )





(8)

where y

is the measurements vector of a frame, z

the quantized measurements vector, Q bits refers to

the number of bits per measurement, also implies the

quantitative accuracy, and 2

-(Q-1)

refers to

quantization step. Define the quantization noise as:

ez y





(9)

In addition, we need one bit to represent the sign of

measurement. Then we can get the number of bits

ratio per frame of DCVS, shown as:

(1)

RQ MRN



 

(10)

AParity-basedErrorControlMethodforDistributedCompressiveVideoSensing

107

Figure 2: DCVS codec scheme.

where R

is the number of bits ratio per frame, MRt

the measurement rate for each frame, and N is the

size of a frame.

Currently, we only know the value of Q is just

the trade-off between reconstructed video quality

and compression ratio, and how to quantize the

measurements more efficiently, which will be left

for our future work.

3.3 PEC Method for DCVS

The dequantized measurements y

constitute a

random and incoherent combination of the original

frame pixel, which has been already studied in

(Chen et al., 2012). That is also to say, no individual

measurement is more important than any other

measurement for frame reconstruction. This means

that, the number of correctly received measurements

is the main factor in determining the quality of video

recovery. For this characteristic of measurements,

discarding a small amount of measurement will not

cause quality decline greatly, which will be shown in

next section. There will be badly impact on quality if

the measurements containing some error bit are used

for the reconstruction.

With the limitation of channel resource and

energy constraint, traditional ARQ (Automatic

Repeat re-Quest) error control scheme can’t be

adopted. And other FEC (Forward Error Correction)

methods such as LDPC, Turbo coding are also

inapplicable to the DCVS due to the additional

encoding complexity, even though the FEC scheme

shows stronger error correction capabilities. For the

above reasons, we proposed a simple parity-based

error control (PEC) method for resistance of random

channel error in DCVS. It is realized by using an

even parity bit added after each measurement at

encoder. If the parity check is failed, than dropped

this measurement immediately at receiver or at an

intermediate node. This method has the following

two benefits: 1, it is simple enough to adapt to the

requirements in the codec; 2, parity-based coding

efficiency is high extremely with low coding

redundancy. The coding efficiency of a frame can be

defined as:

(1)

QMRN

QMRNMRN

 







(11)

where MR

×N presents the number of parity bits.

Improved DCVS system is shown in Figure 3.

4 SIMULATIONS RESULTS

In this paper, we choose the ‘coastguard’ CIF video

sequence with frame size 352×288as the test video,

and GOP size is set to 3. The MR

of Key frame

equals to 70%, and MR

of CS is 30%. In the CS

measurement process, SBHE matrix is used as

sensing matrix

Φ, and DWT is employed as sparse

basis matrix

Ψ. GPSR algorithm is used for video

reconstruction at decoder. Quantitative accuracy Q is

set to 8 bit. Random channel error is simulated by

Binary Symmetric Channel (BSC). Ultimately, we

choose conventional Peak Signal to Noise Ratio

(PSNR) to evaluate the quality of recovery video.

Figure 4 shows the first Key frame of video

sequence in DCVS. (a) is the original frame, (b) is

the recovery frame without channel error. (c) is the

recovery frame which employ our PEC method

under channel bit error rate (BER) 10

-2

. (d) is the

recovery frame without any error control method

under BER 10

-2

We pick up 1-7 frames in the video sequence to

present the video reconstruction quality under

channel BER 10

-2

,10

-3

,10

-4

, and the ideal channel

without error, which is shown in Figure 5 and Figure

6. 1st, 4th, 7th frame are Key frames and 2nd, 3rd,

5th, 6th frame are CS frames. Figure 5 shows the

quality with our proposed method, and Figure 6

shows the quality without error control. Figure 7

shows PSNR of recovery the 4th frame which is Key

SIGMAP2013-InternationalConferenceonSignalProcessingandMultimediaApplications

108

Figure 3: Improved DCVS codec scheme.

Figure 4: 1st Key frame of test video sequence: (a) original frame; (b) the recovery frame without channel error; (c) the

recovery frame under 10

-2

BER with our PEC method; (d) the recovery frame under 10

-2

BER without any error control

method.

frame under the different BER and Figure 8 shows

PSNR of recovery the 3rd frame which is CS frame

under the different BER. For all reasonable BER,

our proposed method achieved the better

performance. Figure 9 shows that under different

BER, the true measurement ratio of Key frame and

CS frame in fact are received at decoder end.

5 CONCLUSIONS AND FUTURE

WORKS

Nowadays compressive sensing is on its growing

stage and we still have long way to go before putting

it into practice. How to convert analog information

into digital compressive information (Analog-

Information Converter) by the method of

compressive sensing is a tough issue. But

compressive sensing system has already been proved

to be feasible technically, and we firmly believe that

it shall be another important way for information

acquisition in the near future. In this paper, we

described a whole framework of DCVS, proposed a

parity-based error control method for CS

measurement of DCVS frame. Its good performance

has been shown in simulation results. Next, in

DCVS, we will focus on the measurement

quantization and entropy coding, alterable

measurement rate allocation, and video recovery

quality evaluation. These also attracted a lot of

attentions of many researchers in this field.

Figure 5: Recovery quality of 1st-7th frame in test video

under different BER with our PEC method.

Figure 6: Recovery quality of 1st-7th frame in test video

under different BER without error control method.

AParity-basedErrorControlMethodforDistributedCompressiveVideoSensing

109

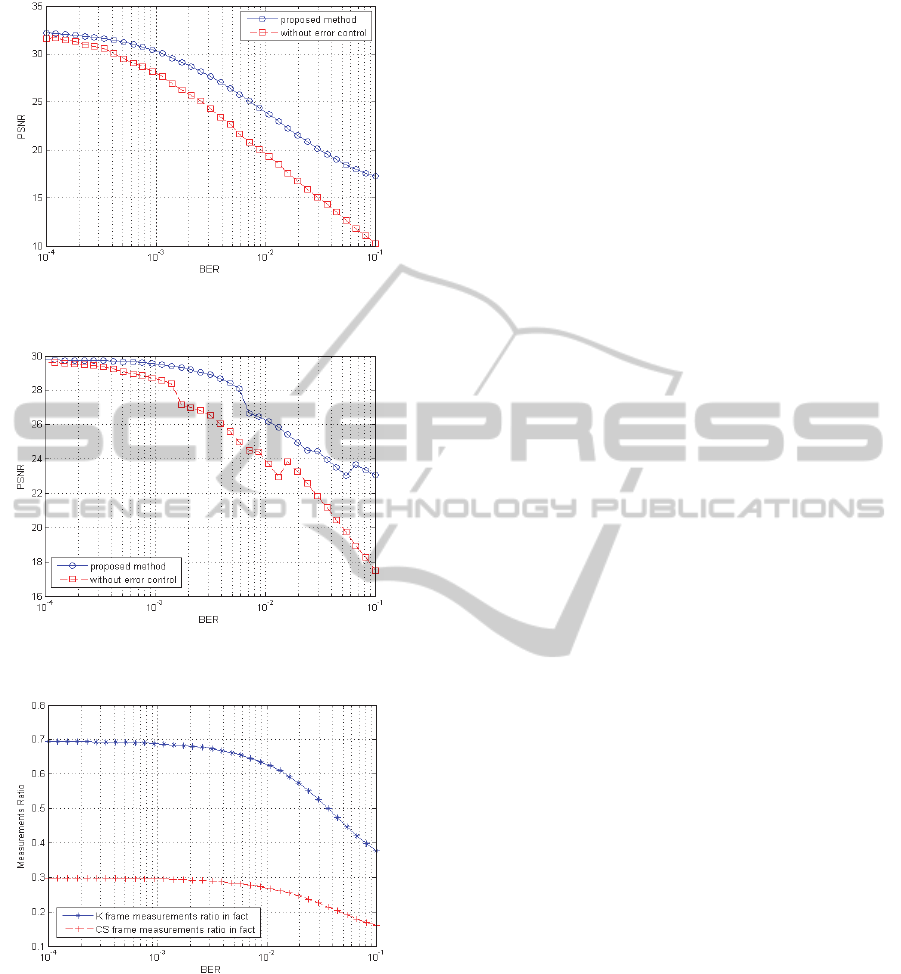
Figure 7: PSNR of recovery the 4th frame (Key frame)

under the different BER.

Figure 8: PSNR of recovery the 3rd frame (CS frame)

under the different BER.

Figure 9: the true measurement ratio of Key frame and CS

frame in fact under different BER.

REFERENCES

Akyildiz, I. F., Melodia, T., & Chowdhury, K. R. (2007).

A survey on wireless multimedia sensor networks.

Computer networks, 51(4), 921-960.

Barakat, W., Saliba, R., & Evans, B. L. (2008).

Compressive Sensing for Multimedia

Communications in Wireless Sensor Networks.

Baraniuk, R. G. (2007). Compressive sensing [lecture

notes]. Signal Processing Magazine, IEEE, 24(4),

118-121.

Candès, E. J., & Wakin, M. B. (2008). An introduction to

compressive sampling. Signal Processing Magazine,

IEEE, 25(2), 21-30.

Candès, E. J. (2006). Compressive sampling. In

Proceedings of the International Congress of

Mathematicians: Madrid, August 22-30, 2006: invited

lectures (pp. 1433-1452).

Candès, E. J., & Tao, T. (2006). Near-optimal signal

recovery from random projections: Universal encoding

strategies?. Information Theory, IEEE Transactions on,

52(12), 5406-5425.

Chen, H. W., Kang, L. W., & Lu, C. S. (2010, July).

Dynamic measurement rate allocation for distributed

compressive video sensing. In Visual Communications

and Image Processing 2010 (pp. 77440I-77440I).

International Society for Optics and Photonics.

Chen, S., Zheng, B., & Li, J. (2012). A method of image

quality assessment for compressive sampling video

transmission. Journal of Electronics (China), 29(6),

598-603.

Dai, W., Pham, H. V., & Milenkovic, O. (2009).

Quantized compressive sensing. arXiv preprint

arXiv:0901.0749.

Do, T. T., Chen, Y., Nguyen, D. T., Nguyen, N., Gan, L.,

& Tran, T. D. (2009, November). Distributed

compressed video sensing. In Image Processing

(ICIP), 2009 16th IEEE International Conference on

(pp. 1393-1396). IEEE.

Do, T. T., Tran, T. D., & Gan, L. (2008, March). Fast

compressive sampling with structurally random

matrices. In Acoustics, Speech and Signal Processing,

2008. ICASSP 2008. IEEE International Conference

on (pp. 3369-3372). IEEE.

Donoho, D. L. (2006). Compressed sensing. Information

Theory, IEEE Transactions on, 52(4), 1289-1306.

Figueiredo, M. A., Nowak, R. D., & Wright, S. J. (2007).

Gradient projection for sparse reconstruction:

Application to compressed sensing and other inverse

problems. Selected Topics in Signal Processing, IEEE

Journal of, 1(4), 586-597.

Girod, B., Aaron, A. M., Rane, S., & Rebollo-Monedero,

D. (2005). Distributed video coding. Proceedings of

the IEEE, 93(1), 71-83.

Kang, L. W., & Lu, C. S. (2009, April). Distributed

compressive video sensing. In Acoustics, Speech and

Signal Processing, 2009. ICASSP 2009. IEEE

International Conference on (pp. 1169-1172). IEEE.

Wyner, A., & Ziv, J. (1976). The rate-distortion function

for source coding with side information at the decoder.

Information Theory, IEEE Transactions on, 22(1), 1-

10.

SIGMAP2013-InternationalConferenceonSignalProcessingandMultimediaApplications

110