
Efficient Simultaneous Privately and Publicly Verifiable Robust Provable
Data Possession from Elliptic Curves
Christian Hanser and Daniel Slamanig
Institute for Applied Information Processing and Communications (IAIK),
Graz University of Technology (TUG), Inffeldgasse 16a, 8010 Graz, Austria
Keywords:
Provable Data Possession, Proofs of Retrievability, Remote Data Checking, Simultaneous Public and Private
Verifiability, Outsourced Storage, Elliptic Curves, ECDLP, Provable Security.
Abstract:
When outsourcing large sets of data to the cloud, it is desirable for clients to efficiently check, whether all
outsourced data is still retrievable at any later point in time without requiring to download all of it. Provable
data possession (PDP)/proofs of retrievability (PoR), for which various constructions exist, are concepts to
solve this issue. Interestingly, by now, no PDP/PoR scheme leading to an efficient construction supporting both
private and public verifiability simultaneously is known. In particular, this means that up to now all PDP/PoR
schemes either allow public or private verifiability exclusively, since different setup procedures and metadata
sets are required. However, supporting both variants simultaneously seems interesting, as publicly verifiable
schemes are far less efficient than privately verifiable ones. In this paper, we propose the first simultaneous
privately and publicly verifiable (robust) PDP protocol, which allows the data owner to use the more efficient
private verification and anyone else to run the public verification algorithm. Our construction, which is based
on elliptic curves, achieves this, as it uses the same setup procedure and the same metadata set for private and
public verifiability. We provide a rigorous security analysis and prove our construction secure in the random
oracle model under the assumption that the elliptic curve discrete logarithm problem is intractable. We give
detailed comparisons with the most efficient existing approaches for either private or public verifiability with
our proposed scheme in terms of storage and communication overhead, as well as computational effort for
the client and the server. Our analysis shows that for choices of parameters, which are relevant for practical
applications, our construction outperforms all existing privately and publicly verifiable schemes significantly.
This means, that even when our construction is used for either private or public verifiability alone, it still
outperforms the most efficient constructions known, which is particularly appealing in the public verifiability
setting.
1 INTRODUCTION
Cloud storage is an increasingly popular means for
archiving, backup, sharing of data, synchronization
of multiple devices and it is also envisioned for fu-
ture primary storage of (enterprise) data. Despite the
advantages of cloud storage being among others ubiq-
uitous access to data, immediate scalability and the
pay-per-usage billing model, there are still concerns,
which hinder a widespread adoption. These concerns
are mainly devoted to missing or inadequate security
and privacy related features, requiring customers to
fully trust in the integrity of the cloud provider as well
as the provider’s security practices. Among these is-
sues is the availability of outsourced data. Recent in-
cidents (Cloud Outages, 2011) indicate that, despite
the assumed high availability guarantees of the cloud,
outages occur in practice. One way to mitigate this
problem is to introduce redundancy in order to im-
prove availability (Slamanig and Hanser, 2012). An-
other crucial aspect in the context of availability is to
verify whether all outsourced data is still retrievable
and intact. A naive solution to this problem would be
to download all outsourced data and, thereby, check
the completeness from time to time. However, for
large data sets this is apparently not feasible. Thus,
the concepts of provable data possession (PDP) and
proofs of retrievability (PoR) have been introduced.
The goal of the aforementioned approaches is that a
client can regularly challenge the storage server to
provide a proof that assures that the outsourced data
is still retrievable without having access to the data
itself locally. In contrast to the naive approach, this
strategy aims at reducing the communication as well
15
Hanser C. and Slamanig D..
Efficient Simultaneous Privately and Publicly Verifiable Robust Provable Data Possession from Elliptic Curves.
DOI: 10.5220/0004496300150026
In Proceedings of the 10th International Conference on Security and Cryptography (SECRYPT-2013), pages 15-26
ISBN: 978-989-8565-73-0
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

as the computational overhead significantly. Ideally,
such proofs are of constant length (independent of the
size of the data) and the verification of these proofs
requires only a small and constant number of compu-
tations at the client. Such schemes are said to support
private verifiability, if only the client, who has pre-
viously outsourced the data (the data owner), is able
to verify proofs of data possession from the storage
server using a private key. In contrast, one speaks of
public verifiability if the data owner provides addi-
tional parameters into the public key, such that any
third party is able to request and verify proofs of data
possession without the client giving away its private
key. Consequently, no third party is able to compute
valid verification metadata for the data and, thus, can-
not modify outsourced data such that valid proofs can
still be given. It should be noted that publicly verifi-
able PDP schemes in general are far more expensive
than privately verifiable schemes.
The first construction tailored for the use within
outsourced storage denoted as provable data posses-
sion (PDP) was presented in (Ateniese et al., 2007;
Ateniese et al., 2011). A PDP protocol works by con-
structing homomorphic verifiable tags (HVTs), which
are computed by the client prior to outsourcing the
data and are stored as metadata in addition to the
data at the server. Typically, the proof then requires
the storage server (prover) to prove the knowledge
of a linear combination of randomly challenged data
blocks. It can be efficiently verified by the client by
using compact verification data sent by the verifier,
whose size is independent of the data size. Although
elegant, this RSA-style construction imposes a rather
large computational burden on the verifier (client),
i.e., a number of large integer exponentiations and in-
versions linear in the number of challenged blocks.
Independently to PDP, proofs of retrievability (PoR)
(Juels and S. Kaliski Jr., 2007) were introduced, fur-
ther refined in (Bowers et al., 2009) and generalized
as well as studied from a coding theoretic point of
view in (Dodis et al., 2009; Paterson et al., 2012).
PORs, in their original sense, pursue another ap-
proach, namely, check-values (so called sentinels) are
inserted in random positions into the data and then
the entire file is encrypted and permuted before out-
sourcing. A proof amounts to requiring the server to
send some of these sentinels to the client, who can
then check them locally. While PORs are restricted to
a limited number of challenges for given data, PDPs
usually support an unlimited number of challenges,
which is clearly desirable. We note that by using pri-
vate information retrieval (PIR) in order to hide the
exact positions of the accessed sentinels, one can also
realize PoR schemes supporting an unlimited number
of challenges. However, this approach is of theoreti-
cal interest only, since PIR requires the storage server
to access the entire data, which is clearly undesirable,
and the computational effort for the server as well as
the client renders this approach impractical.
Furthermore, PORs typically employ a coding
theoretic approach, i.e., a file is encoded prior to out-
sourcing, whereas PDPs initially were not concerned
with encoding (and thus corrections of minor corrup-
tions), but only to handle the detection of corruptions
of larger parts of the outsourced file. While PORs
come with an explicit knowledge extraction algorithm
Extract to retrieve the file from a sequence of chal-
lenges, PDPs only implicitly require such a knowl-
edge extractor in the course of their security proofs.
Therefore, the security guarantees made by the origi-
nal PDP constructions are slightly weaker than those
of a POR. However, we note that in recent works both
approaches seem to converge to a single unified ap-
proach as it is quite straightforward to combine PDPs
with suitable codes and thus obtain robustness against
small corruptions as well. What we denote as robust
PDP also refers to this converged model and thus also
may be seen as a “modern” PoR.
1.1 Related Work
In (Ateniese et al., 2009), the authors provide a
generic construction of PDP protocols from any ho-
momorphic identification protocol. The authors of
(Shacham and Waters, 2008) present a privately ver-
ifiable PDP construction from pseudo-random func-
tions in the standard model and a publicly verifiable
construction from BLS signatures (Boneh et al., 2001)
in the random oracle model. Based on this approach,
the authors of (Wang et al., 2013) introduce a pub-
lic auditing scheme, which extends the classical pub-
licly verifiable PDP/PoR model with the properties
of privacy-preservation and batch auditing. The for-
mer means that an auditor (verifier) can not learn any-
thing about the stored data during the auditing pro-
cess. The latter means that a third party perform-
ing the challenges on behalf of several clients is able
to batch all single challenges in order to obtain im-
proved performance. Recently, (Xu and Chang, 2012)
introduced a new privately verifiable PDP protocol
based on polynomial commitments in the standard
model. Another scheme based on polynomial com-
mitments for public verifiability has been introduced
in (Yuan and Yu, 2013). There are also constructions
for a distributed storage setting, that is, considering
multiple storage servers (Curtmola et al., 2008; Zhu
et al., 2012). The original PDP setting applies only to
static (or append-only) files or only supports limited
SECRYPT2013-InternationalConferenceonSecurityandCryptography
16

updates with a bounded number of challenges (Ate-
niese et al., 2008). Dynamic provable data posses-
sion (DPDP), in contrast, extends the PDP model to
support provable updates to stored data (Erway et al.,
2009; Chen and Curtmola, 2012; Cash et al., 2013)
including insertions at arbitrary positions, updates on
existing blocks, revision control (Zhang and Blanton,
2013), etc.
1.2 Contribution
By now no PDP leading to an efficient construction
supporting both private and public verifiability simul-
taneously is known. In particular, this means that by
now all PDP either allow public or privateverifiability
only, since different setup procedures and metadata
sets are required. However, supporting both variants
simultaneously seems interesting, as publicly verifi-
able schemes are far less efficient than privately veri-
fiable ones. In this paper, we propose the first simul-
taneous privately and publicly verifiable (robust) PDP
protocol, which allows the data owner to use the more
efficient private verification and anyone else to run
the public verification algorithm. Our construction,
which is based on elliptic curves, achieves this, as it
uses the same setup procedure and the same metadata
set for private and public verifiability. To the best of
our knowledge, this is the only construction support-
ing both features at the same time. Clearly, a triv-
ial alternative to the feature of providing private und
public verifiability in parallel would be to use a pri-
vately verifiable PDP protocol resulting in one set of
metadata (tags) and a second publicly verifiable PDP
protocol resulting in a second set of metadata (tags)
and to store both metadata sets at the storage site.
Then, the data owner could run the protocol on the
first set of metadata and all other parties on the sec-
ond set. However, besides inducing a doubled storage
overhead for the metadata, which may be quite signif-
icant, this trivial solutions suffers from additional de-
ficiencies. Namely, one needs to rely on differentPDP
schemes likely requiring a different setting, e.g., the
used groups, and providing security under potentially
unrelated cryptographic assumptions, the data owner
has to maintain more private key material as well as
public parameters and the data owner has to run the
computation of metadata twice. The latter issue does
not only apply to the preprocessing when outsourc-
ing data but also for the recomputation of tags when
updating any already stored data. Clearly, this also
results in an unnecessary computational overhead for
the data owner.
In contrast, our construction relies on a single
well-established cryptographic assumption and re-
quires none of the aforementioned overheads. We
provide a construction, which supports efficient pri-
vately und publicly verifiable robust PDP on the same
set of metadata and based on the same setup proce-
dure. Both versions can be shown to be secure in
the random oracle model under the assumption that
the ECDLP is intractable. Moreover, we give de-
tailed comparisons of the most efficient existing ap-
proaches for either private or public verifiability (Ate-
niese et al., 2011; Shacham and Waters, 2008; Xu
and Chang, 2012) with our proposed construction in
terms of storage and communication overhead as well
as computational effort for the client and the server.
Our analysis shows that our construction outperforms
all existing privately and publicly verifiable schemes
significantly. This means, that even when our con-
struction is used for either private or public verifiabil-
ity alone, it still outperforms the most efficient con-
structions known, which is particularly appealing in
the public verifiability setting.
1.3 Outline
Section 2 discusses the mathematical and crypto-
graphic preliminaries. Section 3 introduces the for-
mal model of provable data possession and the cor-
responding security model. Then, Section 4 details
our construction for simultaneous private and public
verifiability. In Section 5, we compare our results to
related approaches, and, finally, Section 6 concludes
the paper and lists open issues for future work.
2 PRELIMINARIES
In this section, we give an overview of required math-
ematical and cryptographic preliminaries.
2.1 Elliptic Curves and Pairings
An elliptic curve E over the finite field F
q
is a plane,
smooth algebraic curve usually defined by a Weier-
strass equation. The set E(F
q
) of points (x,y) ∈
F
2
q
satisfying this equation plus the point at infinity
O, which is the neutral element, forms an additive
Abelian group, whereas the group law is determined
by the chord-and-tangent method (Silverman, 1986).
Furthermore, if G is a cyclic group and p a divi-
sor of its group order, then there exists a subgroup of
order p, which we subsequently denote by G[p].
Definition 1 (Bilinear Map). Let G
1
,G
2
,G
T
be three
cyclic groups of the same prime order p, where G
1
,G
2
are additive groups and G
T
is a multiplicative group.
EfficientSimultaneousPrivatelyandPubliclyVerifiableRobustProvableDataPossessionfromEllipticCurves
17

We call the map e : G
1
× G
2
→ G
T
a bilinear map or
pairing, if the following conditions hold:
Bilinearity. For all P
1
,P
2
∈ G
1
and P
′
1
,P
′
2
∈ G
2
we
have:
• e(P
1
+ P
2
,P
′
) = e(P
1
,P
′
) · e(P
2
,P
′
) for all P
′
∈
G
2
,
• e(P,P
′
1
+ P
′
2
) = e(P,P
′
1
) · e(P,P
′
2
) for all P ∈ G
1
.
Non-degeneracy. If P is a generator of G
1
and P
′
a generator of G
2
, then e(P,P
′
) is a generator of
G
T
, i.e., e(P,P
′
) 6= 1
G
T
.
Efficiently Computable. e can be computed effi-
ciently.
If G
1
= G
2
, then e is called symmetric and asym-
metric otherwise. The former type is also called Type-
1 pairing, whereas in case of the latter we distinguish
between Type-2 and Type-3 pairings. For Type-2 pair-
ings there is an efficiently computable isomorphism
Ψ : G
2
→ G
1
(Chatterjee and Menezes, 2011) and
for Type-3 pairings such an efficiently computable
isomorphism does not exist. Furthermore, let G
T
=
F
∗
q
k
[p], which is an order p subgroup of F
∗
q
k
. Note
that k, the so called embedding degree, is defined as
k = min{ℓ ∈ N : p | q
ℓ
− 1}.
Definition 2 (Elliptic CurveDiscrete Logarithm Prob-
lem (ECDLP)). Let E(F
q
)[p] be an elliptic curve
group of prime order p generated by P ∈ E(F
q
)[p].
Given elements P,aP ∈ E(F
q
)[p] compute a ∈ Z
p
.
2.2 Erasure Codes
An (n,k,d)-erasure code is a code that transforms
a message of k symbols into a codeword of n sym-
bols, such that the minimum Hamming distance of
any two codewords is d. In general, this allows to
detect up to d − 1 and to correct up to (d − 1)/2 er-
roneous symbols per codeword. A standard choice
for erasure codes, are Reed-Solomon codes (Reed
and Solomon, 1960), which are based on polynomials
over finite fields F
q
= F
p
n
. For this particular erasure
code, we have n = q − 1 and a minimum distance of
d = n − k + 1. Consequently, up to n − k erroneous
symbols can be detected and up to (n − k)/2 can be
corrected.
3 PROVABLE DATA POSSESSION
The goal of a provable data possession scheme is that
a client C can outsource data to some storage server S
(typically a cloud provider), then delete the local copy
of the data while being able to regularly challenge S to
provide a proof that the outsourced data is still retriev-
able. Ideally, such proofs are of constant length (inde-
pendent of the size of the data) and the verification of
these proofs requires only a small and constant num-
ber of computations at C. This is achieved by requir-
ing C to compute verification metadata (tags) for the
data prior to outsourcing and storing the data together
with the tags at S. Furthermore, S should not need
to access the entire data for generating a proof and,
therefore, a probabilistic spot checking approach is
used. This means thatC challenges S to provethe pos-
session of a randomly sampled subset of data blocks,
such that the best strategy S can follow is to store the
entire data. Otherwise, C will detect this misbehavior
with high probability (see Section 3.1 for a discus-
sion of the choice of parameters). Furthermore, the
data is encoded prior to outsourcing to obtain robust-
ness against minor corruptions, which would not be
detected by means of spot checking. Subsequently,
we give a formal definition of such a provable data
possession scheme and in the remainder we denote an
outsourced data unit as file.
3.1 Spot Checking and Robustness
Spot checking means that the client asks the server to
prove the possession of a subset of c randomly sam-
pled file blocks of the entire file. This allows a client
to detect, whether the server has corrupted a larger
portion of the file. Now, one can ask how the choice
of c should be made when a file consists of ℓ blocks
and that the server has corrupted/deleted β blocks. As
discussed in (Ateniese et al., 2011), the probability
P that at least one of c blocks sampled by the client
matches one of the blocks corrupted/deleted by the
server can be analyzed by an urn experiment and can
be shown to be bounded by
1−
1−
β
ℓ
c
≤ P ≤ 1−
1−
β
ℓ − c+ 1
c
.
For instance, let us assume that we have a file consist-
ing of ℓ = 10
6
file blocks (of t elements each) and we
assume that the server has corrupted β = 10
3
of these
blocks, i.e., 0.1% of all blocks, then to achieve P ≈
0.99 we have to set the challenge size to |I | = 4600.
However, when the server only corrupts a very
small fraction of the file , e.g., a single block, this
can not be efficiently recognized via spot checking.
Therefore, erasure codes can be applied to a file be-
fore outsourcing in order to resolve this problem (cf.
(Ateniese et al., 2011; Juels and S. Kaliski Jr., 2007)
for a discussion). PDP schemes that also take re-
sistance against small corruptions into account, typ-
ically by means of erasure codes, are called robust
PDP schemes (Chen and Curtmola, 2012).
SECRYPT2013-InternationalConferenceonSecurityandCryptography
18

3.2 PDP Protocol and Security Model
Definition 3 (Provable Data Possession Scheme
(PDP)). A PDP scheme is a tuple of polynomial-time
algorithms (KeyGen,Tag, Prove, Verify) so that:
KeyGen(κ): This probabilistic algorithm gets the se-
curity parameter κ ∈ N and returns a public and
private key pair (pk,sk).
Tag(pk,sk, id, i, ~m
i
): This deterministic algorithm
takes a key pair (pk,sk), a file identifier id, the
index i of the file block ~m
i
as input and returns a
verification tag T
i
.
Prove(pk,M ,T , C ): This deterministic algorithm
gets as input the public key pk, a file M (whose id
is determined by C ), the sequence of correspond-
ing tags T , and the challenge C . It returns a proof
of possession π for the blocks determined by the
challenge C .
Verify(pk,sk,C ,π): This deterministic algorithm
takes as input a key pair (pk,sk), a challenge
C and a proof of data possession π. It returns
accept if π is a correct proof of possession for the
blocks determined by the challenge C and reject
otherwise.
A PDP scheme is called correct, if for any hon-
estly generated proof of possession π using honestly
generated tags T , the probability that the verify al-
gorithm accepts is 1. Using the definition of a PDP
scheme, we can now specify the interaction between
a client C and a server S by means of the following
generic PDP protocol.
Definition 4 (Provable Data Possession Protocol). A
PDP protocol is a tuple of interactive polynomial-
time algorithms (Setup,Store,Challenge) so that:
Setup. The clientC obtains a key pair (pk,sk) by run-
ning KeyGen(κ), publishes pk and keeps sk pri-
vate.
Store. Given a file F identified by id, encode the file
using a suitable erasure code and obtain the file
M . Then, divide it into ℓ = n/t elements and ex-
ecute Tag(pk,sk, id, i, ~m
i
) on every file block ~m
i
of
t elements in M = (M
1
,...,M
⌈
n
t
⌉
). Finally, send
(id,M ,T ) to the server S.
Challenge. The challenger V (not necessarily the
client C) generates a challenge C = (id,I,l),
where id is the file identifier, I is a subset of block
indexes I ⊆ {1,...,⌈
n
t
⌉} and l is a randomly cho-
sen coefficient. V sends the challenge C to S and
S runs Prove(pk,M , T ,C ) to generate the proof
π. S sends π back to V and V checks the proof via
Verify(pk,sk, C ,π).
We emphasize that in a privately verifiable PDP
protocol Store and Challenge can only be run by the
data owner, while in a publicly verifiable PDP pro-
tocol Challenge can be run by any (third) party and
Store only by the data owner.
Now, we state the security for a PDP protocol us-
ing a game that captures what we require for this pro-
tocol to be secure. Loosely speaking, a server should
only be able to provide a valid proof, if it holds all
challenged data and corresponding tags and can only
forge valid proofs for files he does not possess with
at most negligible probability. Our security model
adopts the security model of (Xu and Chang, 2012).
Definition 5 (Data Possession Game). The data pos-
session game is comprised of the following consecu-
tive phases:
Setup. The challenger V executes KeyGen(κ), gives
pk to the adversary B and keeps sk private.
Query. The adversary B makes adaptive tagging
and verification queries. B can perform tag-
ging queries for potentially different file id’s,
i.e., B chooses a file block ~m
i
, sends it to the
challenger, who returns T
i
obtained by running
Tag(pk,sk, id, i, ~m
i
). Per file id, B is only allowed
to query consecutive file blocks. For each id the
adversary stores these blocks and the sequence of
corresponding tags. B is restricted to query only
unique (id,i) pairs.
Retrieve. V challenges B λ times for some previ-
ously queried file M
∗
identified by id
∗
, where the
challenged indexes have been queried before and
sends it to B. B computes the according proofs
π
1
,...,π
λ
for the file M
∗
identified by id
∗
and
challenge C
i
and returns them to V. From the file
blocks obtained in these proofs, V extracts a file
M
′
using some PPT knowledge extractor. B wins
the game if M
′
6= M
∗
.
An adversary is called ε-admissible, if the proba-
bility that it is able to convince V to accept a proof in
the retrieve phase of the above game is at least ε.
Now, we state what constitutes a secure PDP pro-
tocol:
Definition 6. A PDP protocol (Setup, Store,
Challenge) built upon a PDP scheme (KeyGen,Tag,
Prove,Verify) guarantees robust provable data
possession, if it is correct and if for any ε-admissible
PPT adversary there is a value λ for the number of
queries in the retrieve phase, which is bounded by
some polynomial in the number of file blocks, such
that the probability that B wins the data possession
game is negligibly small in the security parameter κ.
EfficientSimultaneousPrivatelyandPubliclyVerifiableRobustProvableDataPossessionfromEllipticCurves
19

4 CONSTRUCTION
In this section, we present our construction for simul-
taneous private and public verifiability. The intuition
behind our protocol in general is that S is required to
prove the knowledge of a linear combination of file
blocks (indicated by the challenge), where the coef-
ficients are based on a value randomly chosen by the
client in each protocol run. This makes storing lin-
ear combinations of file blocks instead of file blocks
impractical. Along with this linear combination, S ag-
gregates the tags corresponding to the challenged file
blocks, which enable verification at C without having
access to the actual file blocks.
In the following, we identify each file block with
a vector. Therefore, as it is common, we split the
file M = (m
1
,...,m
n
) represented as elements of Z
p
into ℓ =
n
t
consecutive vectors ~m
i
= (m
i,1
,...,m
i,t
) for
1 ≤ i ≤ ℓ of t subsequent elements of Z
p
, where t is
a parameter chosen by the user to adjust the storage
overhead. We assume that the length n of M is a mul-
tiple of t, whereas M is padded with an appropriate
number of elements of the form 0 ∈ Z
p
if this condi-
tion is not satisfied. Doing so, we obtain a represen-
tation M
′
of M such that
M
′
=
~m
1
.
.
.
~m
i
.
.
.
~m
n
t
=
m
1,1
··· m
1,t
.
.
.
.
.
.
m
i,1
··· m
i,t
.
.
.
.
.
.
m
n
t
,1
··· m
n
t
,t
.
For each vector ~m
i
, we compute a tag T
i
, i.e., every tag
aggregates t elements of Z
p
. We emphasize that the
challenge in designing PDP protocols, which aggre-
gate vectors into single tags, is to prevent the storage
server from storing the sum of the vectors components
instead of all components thereof.
Scheme 4.1 shows the detailed construction of our
scheme for simultaneous private and public verifiabil-
ity, which is used as building block for Protocol 4.1.
Note that for the data owner it is considerably cheaper
to run the private verification, since it, firstly, does
not involve pairing evaluations and, secondly, saves
a considerable amount of scalar multiplications and
point additions, as the data owner has access to the
private key.
4.1 Security Analysis
For Protocol 4.1 we are able to prove the following
statement.
Theorem 1. Assuming the hardness of the ECDLP,
Protocol 4.1 guarantees robust provable data posses-
sion in the random oracle model.
KeyGen: On input κ, choose an elliptic curve E(F
q
)
with a subgroup of large prime order p gener-
ated by P ∈ E(F
q
)[p], such that the bitlength
of p is κ. Choose an asymmetric pairing
e : E(F
q
)[p] × G
2
→ F
∗
q
k
[p] with G
2
being a p-
order elliptic curve subgroup over (an extension of)
the field F
q
with generator P
′
, where the choice
of G
2
depends on the specific instantiation of the
pairing. Now, let elements s
1
,s
2
,α ∈
R
Z
p
, let
Q
′
1
= s
1
P
′
, Q
′
2
= s
2
P
′
, compute αP,. .., α
t
P, choose
two cryptographic hash functions h : {0,1}
∗
→ Z
p
and H : {0,1}
∗
→ E(F
q
)[p] and output pk =
(E(F
q
),G
2
,e, p,P,P
′
,Q
′
1
,Q
′
2
,αP, ... ,α
t
P,h,H) as
well as sk = (s
1
,s
2
,α).
Tag: Given pk, sk, a file identifier id, a vector index i and
a vector ~m
i
= (m
i, j
)
t
j=1
, compute the corresponding
tag as T
i
= (s
1
H(idki)+s
2
h(idki)
∑
t
j=1
m
i, j
α
j
P) and
output T
i
.
Prove: On input pk, M = ( ~m
1
,.. ., ~m
n
t
), T and chal-
lenge C = (id, I,l), compute
µ = (µ
j
)
t
j=1
=
h(idki)
∑
i∈I
m
i, j
l
i
t
j=1
and τ =
∑
i∈I
l
i
T
i
,
where m
i, j
is the element with index (i, j) in the rep-
resentation M
′
of M . Return π = (µ,τ) ∈ Z
t
p
×
E(F
q
).
Verify
Priv
: Given pk, sk, challenge C and proof π, check
whether the relation
s
1
∑
i∈I
l
i
· H(idki) + (s
2
t
∑
j=1
µ
j
α
j
)P = τ
holds and return accept on success and reject other-
wise.
Verify
Pub
: Given pk,sk = null, challenge C and proof
π, check whether the relation
e(
∑
i∈I
l
i
· H(idki),Q
′
1
) · e(
t
∑
j=1
µ
j
(α
j
P),Q
′
2
) = e(τ, P
′
)
holds and return accept on success and reject other-
wise.
Scheme 4.1: PDP scheme with simultaneous private and
public verifiability.
The proof of Theorem 1 can be found in Ap-
pendix 6.1.
4.2 On Efficient Implementations
In our construction, we make use of a hash func-
tion H : {0,1}
∗
→ E(F
q
)[p], which maps to an ellip-
tic curve group. We note that there are well-known
strategies to hash into elliptic curve groups (Icart,
2009). However, in our concrete scenario, we are able
to choose H to be of a partic-
SECRYPT2013-InternationalConferenceonSecurityandCryptography
20

Setup: C runs KeyGen(κ) and obtains
the key pair (pk,sk), where pk =
(E(F
q
),G
2
,e, p,P,P
′
,Q
′
1
,Q
′
2
,αP, ... ,α
t
P,h,H)
and sk = (s
1
,s
2
,α). C publishes pk in an authentic
way and keeps sk private.
Store: Apply a Reed-Solomon code (Reed and
Solomon, 1960) to the file F and obtain an encoded
file M . For every vector ~m
i
of t elements in M
identified by id, C invokes Tag(pk,sk,id,i, ~m
i
)
to build the sequence of tags T . Then, C sends
(id,M ,T ) to the server S and removes M and T
locally.
Challenge
Priv
: C requests a proof of possession for file
M with identifier id by spot checking c vectors of
M as follows:
• C picks an index set I ⊆ {1,.. .,
n
t
} of c elements,
a random element l ∈ Z
p
and sends the challenge
C = (id,I, l) to the server S.
• On receiving C , S runs Prove(pk,M ,T ,C ) to ob-
tain π and sends it to C.
• Finally, C runs Verify
Priv
(pk,sk,C ,π).
Challenge
Pub
: V requests a proof of possession for file
M with identifier id by spot checking c vectors of
M as follows:
• V picks an index set I ⊆ {1,. .. ,
n
t
} of c ele-
ments, a random l ∈ Z
p
and sends the challenge
C = (id,I, l) to S.
• On receiving C , S runs Prove(pk,M ,T ,C ) to ob-
tain π and sends it to V.
• Finally, V runs Verify
Pub
(pk,null,C ,π).
Protocol 4.1: PDP protocol with simultaneous private and
public verifiability.
ular form, which allows us to obtain very efficient
implementations of our construction. In particular,
we choose H in such a way that H(x) = h(0kx) · P,
whereas h is the cryptographic hash function map-
ping to the integers modulo the group order used in
Scheme 4.1. Note that prepending 0 to the input of
h yields a hash function, which is independent from
h itself. This is necessary to prevent tags from being
malleable.
The above hash function instantiation allows us to
simplify Scheme 4.1 as follows:
Tag:
T
i
= (s
1
h(0kidki) + s
2
h(idki)
t
∑
j=1
m
i, j
α
j
)P
Verify
Priv
:
(s
1
∑
i∈I
h(0kidki)l
i
+ s
2
t
∑
j=1
µ
j
α
j
)P = τ
Verify
Pub
:
e((
∑
i∈I
h(0kidki)l
i
)P,Q
′
1
) · e(
t
∑
j=1
µ
j
(α
j
P),Q
′
2
) =
e(τ,P
′
)
As one can see, this allows us to trade expen-
sive elliptic curve scalar multiplications for inexpen-
sive field multiplications in Z
p
. Furthermore, us-
ing Horner’s method for the polynomial evaluations,
the number of field multiplications in the algorithms
Prove, Verify
Priv
and Verify
Pub
can be kept at a min-
imum. Moreover, note that the algorithms Prove and
Verify
Pub
are well-suited for the application of si-
multaneous multiple point multiplication (Hankerson
et al., 2003), which improves their computational ef-
ficiency considerably.
Notice, that we can use such an instantiation of
the hash function H without sacrificing the security of
the overallconstruction, as we incorporate the random
and unknown value s
1
in the computation of the tags.
An implication of this particular choice of H is that e
needs to be a Type-3 pairing, in order to prevent Q
′
1
and Q
′
2
to be mapped to the group E(F
q
)[p], as, oth-
erwise, the tag construction is no longer secure. Nev-
ertheless, Type-3 pairings are the best choice from a
security and performance perspective (Chatterjee and
Menezes, 2011).
Finally, we emphasize that after applying these
optimizations, the data owner still benefits signif-
icantly from using the private verification relation,
which will be clear from the analysis in Section 5.
4.3 Remarks
• In our challenge, we have included the index set
I. For sake of reduced communication bandwidth,
it can be generated by the server from a com-
pact seed by using the (δ,γ)-hitter construction
given by Goldreich (Goldreich, 1997) or by using
pseudo-random functions (PRFs) as in (Ateniese
et al., 2011).
• We suggest point compression for all transmitted
and stored curve points.
• Note that the proposed scheme can be easily
adapted to batch challenges (Wang et al., 2013)
over multiple files, which yields a constant com-
munication overhead independent of the number
of challenged files.
5 COMPARATIVE ANALYSIS
In this section we draw a comparison between exist-
EfficientSimultaneousPrivatelyandPubliclyVerifiableRobustProvableDataPossessionfromEllipticCurves
21
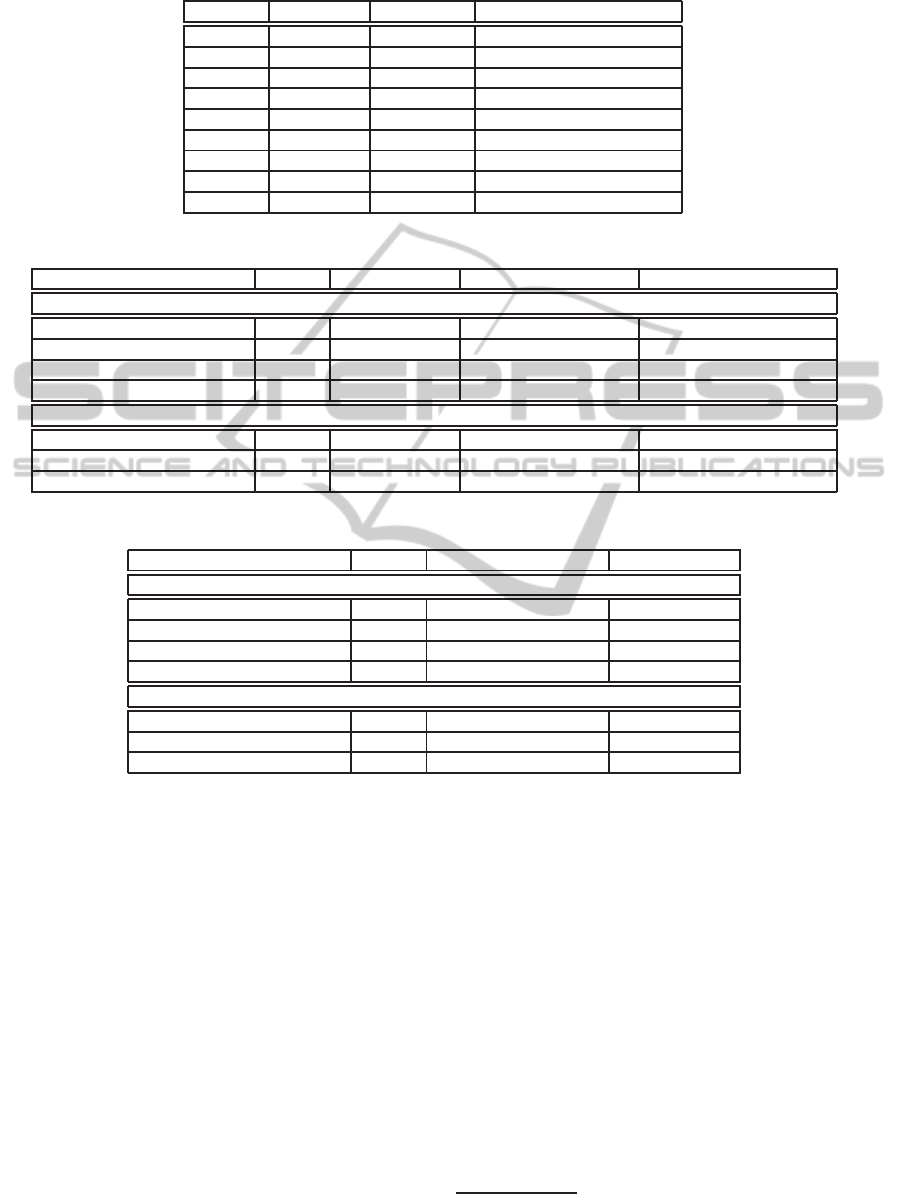
Table 1: Symbols for costs of arithmetical operations.
Operation Semantics Operand Size Description
P e(P
1
,P
′
2
) 224 Pairing computation
E b
d
2048 Large integer exponentiation
S d·P 224 Scalar multiplication
A P
1
+P
2
224 Point addition
I b
−1
(mod N) 2048 Large integer modular inversion
M b
1
·b
2
2048 Large integer multiplication
i b
−1
224 Field inversion
m b
1
·b
2
224 Field multiplication
H H(m) 224 Hash or PRF function evaluation
Table 2: Comparison of computational complexity of PDP schemes with private and public verifiability.
Scheme Key Size Tagging Server Client
Private Verifiability
S-PDP (Ateniese et al., 2011) κ=2048 ℓ(2κE+2M+H) (2ct+c)E+2(c−1)M+H (c+2)E+I+cM+(c+1)H
SPOR (Shacham and Waters, 2008) κ=2048 ℓtM+(ℓ+1)H c(t+1)M (c+t)M+(c+1)H
EPOR (Xu and Chang, 2012) κ=224 ℓ(t+1)m+ℓH (t−1)(S+A)+(ct+c+t)m 2S+i+(c+1)m+cH
Scheme 4.1 κ=224 ℓ(S+(t+3)m+2H) cS+(c−1)A+c(t+2)m+cH S+(c+t+2)m+cH
Public Verifiability
P-PDP (Ateniese et al., 2011) κ=2048 2n(κE+M+H) cE+2(c−1)M (c+2)E+I+2(c−1)M+2cH
PPOR (Shacham and Waters, 2008) κ=224 ℓ((t+1)S+tA+H) cS+(c−1)A+ctm 2P+(c+t)S+(c+t−1)A
Scheme 4.1 κ=224 ℓ(S+(t+3)m+2H) cS+(c−1)A+c(t+2)m+cH 3P+(t+1)S+(t−1)A+cm+cH
Table 3: Comparison of communication and storage overhead of PDP schemes with private and public verifiability.
Scheme Key Size Communication Overhead Storage Overhead
Private Verifiability
S-PDP (Ateniese et al., 2011) κ=2048 (c+1)κ+h ℓκ
SPOR (Shacham and Waters, 2008) κ=2048 (2t+c+1)κ+h ℓκ+tκ
EPOR (Xu and Chang, 2012) κ=224 (c+3)κ ℓκ
Scheme 4.1 κ=224 (t+1)κ ℓκ
Public Verifiability
P-PDP (Ateniese et al., 2011) κ=2048 (c+2)κ ≥nκ
PPOR (Shacham and Waters, 2008) κ=224 (2t+c+2)κ ℓκ+(t+1)κ
Scheme 4.1 κ=224 (t+1)κ ℓκ
ing approaches and our construction in terms of stor-
age and communication overhead as well as computa-
tional effort. We point out that existing literature typi-
cally uses far too small security parameters for the in-
tended use of provable data possession, i.e., outsourc-
ing large datasets for long-term storage. In particu-
lar, all works we are aware of suggest parameter sizes
of 1024 bits for RSA-based/DL-based approaches and
160 bits for ECDL-based approaches. However, hav-
ing the long-term characteristic in mind, it is more
natural to choose at least 2048 and 224 bits security,
respectively, as suggested by NIST in (Barker et al.,
2007). Subsequently, κ, t and ℓ stand for the security
parameter, the number of file elements, which are ag-
gregated into one tag and ℓ = n/t the number of file
blocks (vectors), respectively. Furthermore, let the
challenged index set of file blocks (vectors) I be of
size c.
5.1 Computational Effort
In Table 2, we compare our proposed scheme with
existing approaches in terms of computational effort.
The symbols for the operands and their respective
meanings are illustrated in Table 1.
Figure 1 illustrates the performance comparison
of our proposed scheme with existing approaches.
We conducted the experiments on an Intel Core i5-
2540M equipped with 8GB RAM running Ubuntu
12.10/amd64 and OpenJDK 6/amd64. For the 2048-
bit integer arithmetics we use the standard Java
TM
Big-
Integer class. Furthermore, we were using the jPBC
library
1
version 1.2.1. We have chosen an MNT
curve (Miyaji et al., 2001) with a group size of 224
bits and embedding degree k = 6 over a prime field
1
http://gas.dia.unisa.it/projects/jpbc
SECRYPT2013-InternationalConferenceonSecurityandCryptography
22
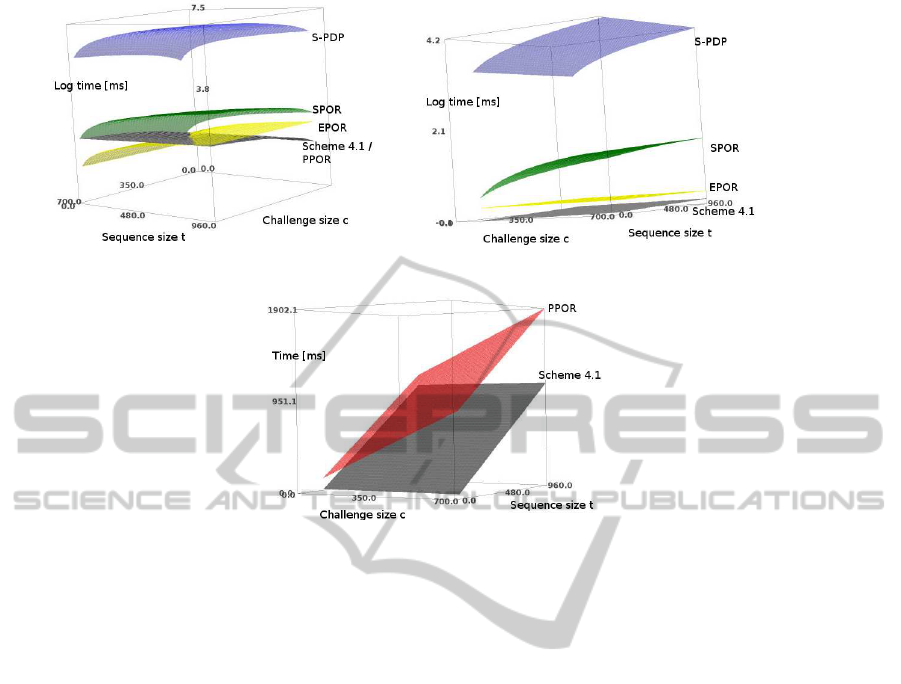
(a) Computational costs for Prove in the case of public and
private verifiability.
(b) Computational costs for Verify in the case of private veri-
fiability.
(c) Computational costs for Verify in the case of public verifi-
ability.
Figure 1: Figure 1(a) illustrates the computational costs of the Prove algorithms of all schemes in Table 2 by varying both
parameters c and t. Figure 1(b) illustrates the computational costs of the Verify algorithms of all privately verifiable schemes
in Table 2 by varying both parameters c and t. The time is in logarithmic scale with radix 10. Figure 1(c) illustrates the costs
of the Verify algorithms of the publicly verifiable schemes PPOR and Scheme 4.1 in Table 2 by varying both parameters c and
t. Furthermore, we set H = 0.
and used the Tate pairing in order to perform our
benchmarks. In order to guarantee fairness and sim-
plicity for the comparisons illustrated in Figure 1, we
have omitted the costs of hash function evaluations in
our benchmarks. Figure 1 shows that our scheme is
the most efficient scheme for private and public veri-
fiability with respect to server and client computations
for reasonable values of the challenge size c and vec-
tors size t. It is important to note that an efficient Ver-
ify algorithm, as achieved by our scheme, is the most
important aspect with respect to practicality. This is
due to the fact that the client can be assumed to be far
more resource constraint than the server (the cloud),
since the client could, for instance, be a smart phone.
In Table 2, one can see that for the data owner it
is considerably cheaper to run the private verification,
as the data owner has access to the private key. More
precisely, the data owner can trade three pairing eval-
uations, t scalar multiplications and t −1 additions for
t + 2 cheap multiplications in Z
p
.
5.2 Storage Overhead
In Table 3, we give an analysis of the storage and com-
munication overhead of our scheme compared to ex-
isting approaches. In the following, h stands for the
output length of a hash function or HMAC of suit-
able size. As one can see from Table 3, our proposed
scheme is as efficient as the most efficient previous
schemes, which either support only private or public
verifiability with respect to communication and stor-
age overhead. Here, we need to note that when one
wants to have private and public verifiability simul-
taneously than for all other schemes except ours the
storage overhead will be the sum of the storage over-
heads of the respective privately and publicly verifi-
able PDP schemes.
6 CONCLUSIONS
In this paper we have presented a novel construction
for privately and publicly verifiable robust provable
data possession. Our construction is based on ellip-
tic curves and is provable secure in the random oracle
model assuming the intractability of the elliptic curve
discrete logarithm problem. We have shown that our
scheme is the most efficient (robust) scheme with re-
EfficientSimultaneousPrivatelyandPubliclyVerifiableRobustProvableDataPossessionfromEllipticCurves
23

spect to server and client computations for reason-
able values of challenge and block size for private as
well as public verifiability. To the best of our knowl-
edge our construction is the first to support the use
of simultaneous private and public verifiability on the
same set of metadata. This means that the data owner
can use the more efficient scheme with private verifi-
cation, while any other party can run the publicly ver-
ifiable variant at the same time without having access
to the owner’s private key. Thereby, both versions use
the same parameters as well as metadata (tag) sets.
6.1 Future Work
The original PDP setting applies only to static (or
append-only) files or only supports limited updates
with a bounded number of challenges (Ateniese et al.,
2008). Dynamic provable data possession (DPDP),
in contrast, extends the PDP model to support prov-
able updates to stored data (Erway et al., 2009; Chen
and Curtmola, 2012; Cash et al., 2013) including
insertions at arbitrary positions, updates on existing
blocks, revision control (Zhang and Blanton, 2013),
etc. Future work includes investigating our construc-
tion in the DPDP model.
ACKNOWLEDGEMENTS
We thank the anonymous reviewers for their helpful
feedback on the paper. This work has been supported
by the Austrian Research Promotion Agency (FFG)
through project ARCHISTAR, grant agreement num-
ber 832145.
REFERENCES
Ateniese, G., Burns, R., Curtmola, R., Herring, J., Khan,
O., Kissner, L., Peterson, Z., and Song, D. (2011).
Remote data checking using provable data possession.
ACM Trans. Inf. Syst. Secur., 14(1):12:1–12:34.
Ateniese, G., Burns, R. C., Curtmola, R., Herring, J., Kiss-
ner, L., Peterson, Z. N. J., and Song, D. X. (2007).
Provable data possession at untrusted stores. In ACM
CCS, pages 598–609.
Ateniese, G., Kamara, S., and Katz, J. (2009). Proofs of
storage from homomorphic identification protocols.
In ASIACRYPT, pages 319–333.
Ateniese, G., Pietro, R. D., Mancini, L. V., and Tsudik, G.
(2008). Scalable and efficient provable data posses-
sion. In SecureComm 2008.
Barker, E., Barker, W., Burr, W., Polk, W., and Smid, M.
(2007). NIST SP800-57: Recommendation for Key
Management Part 1: General(Revised). Technical re-
port.
Boneh, D., Lynn, B., and Shacham, H. (2001). Short sig-
natures from the weil pairing. In ASIACRYPT, pages
514–532.
Bowers, K. D., Juels, A., and Oprea, A. (2009). Proofs of
retrievability: theory and implementation. In CCSW,
pages 43–54.
Cash, D., K¨upc¸ ¨u, A., and Wichs, D. (2013). Dynamic
Proofs of Retrievability via Oblivious RAM. In EU-
ROCRYPT 2013, LNCS. Springer.
Chatterjee, S. and Menezes, A. (2011). On crypto-
graphic protocols employing asymmetric pairings -
the role of ψ revisited. Discrete Applied Mathemat-
ics, 159(13):1311–1322.
Chen, B. and Curtmola, R. (2012). Robust dynamic prov-
able data possession. In ICDCS Workshops, pages
515–525.
Cloud Outages (2011). http://www.crn.com/slide-shows/
cloud/231000954/the-10-biggest-cloud-outages-of-
2011-so-far.htm.
Curtmola, R., Khan, O., Burns, R. C., and Ateniese, G.
(2008). Mr-pdp: Multiple-replica provable data pos-
session. In ICDCS 2008, pages 411–420.
Dodis, Y., Vadhan, S. P., and Wichs, D. (2009). Proofs of re-
trievability via hardness amplification. In TCC, pages
109–127.
Erway, C. C., K¨upc¸¨u, A., Papamanthou, C., and Tamassia,
R. (2009). Dynamic provable data possession. InCCS,
pages 213–222.
Goldreich, O. (1997). A sample of samplers - a computa-
tional perspective on sampling (survey). ECCC,4(20).
Hankerson, D., Menezes, A. J., and Vanstone, S. (2003).
Guide to Elliptic Curve Cryptography. Springer-
Verlag New York, Inc., Secaucus, NJ, USA.
Icart, T. (2009). How to hash into elliptic curves. In
CRYPTO, pages 303–316.
Juels, A. and S. Kaliski Jr., B. (2007). Pors: proofs of re-
trievability for large files. In ACM CCS, pages 584–
597.
Miyaji, Nakabayashi, and Takano (2001). New Ex-
plicit Conditions of Elliptic Curve Traces for FR-
Reduction. TIEICE: IEICE Transactions on Commu-
nications/Electronics/Information and Systems.
Paterson, M. B., Stinson, D. R., and Upadhyay, J. (2012).
A coding theory foundation for the analysis of
general unconditionally secure proof-of-retrievability
schemes for cloud storage. Cryptology ePrint Archive,
Report 2012/611. http://eprint.iacr.org/.
Reed, I. and Solomon, G. (1960). Polynomial codes over
certain finite fields. Journal of the Society for Indus-
trial and Applied Mathematics, 8(2):300–304.
Shacham, H. and Waters, B. (2008). Compact proofs of
retrievability. In ASIACRYPT, pages 90–107.
Silverman, J. (1986). The Arithmetic of Elliptic Curves, vol-
ume 106 of Graduate Texts in Mathematics. Springer.
Slamanig, D. and Hanser, C. (2012). On Cloud Storage and
the Cloud of Clouds Approach. In ICITST-2012, pages
649 – 655. IEEE.
Wang, C., Chow, S. S. M., Wang, Q., Ren, K., and Lou, W.
(2013). Privacy-preserving public auditing for secure
cloud storage. IEEE Trans. Computers, 62(2):362–
375.
SECRYPT2013-InternationalConferenceonSecurityandCryptography
24

Xu, J. and Chang, E.-C. (2012). Towards efficient proofs of
retrievability. In AsiaCCS. ACM.
Yuan, J. and Yu, S. (2013). Proofs of retrievability with
public verifiability and constant communication cost
in cloud. In International Workshop on Security in
Cloud Computing. ACM.
Zhang, Y. and Blanton, M. (2013). Efficient dynamic prov-
able possession of remote data via balanced update
trees. In AsiaCCS, pages 183–194. ACM.
Zhu, Y., Hu, H., Ahn, G.-J., and Yu, M. (2012). Coopera-
tive provable data possession for integrity verification
in multicloud storage. IEEE Trans. Parallel Distrib.
Syst., 23(12):2231–2244.
APPENDIX
Proof of Theorem 1
Proof. This proof consists of three parts addressing
the correctness, the unforgeability of the tags, via a
reduction to the ECDLP in E(F
q
)[p], and the retriev-
ability of the file F .
At first, we show the correctness of Scheme 4.1. From
the verification relation in Verify
Priv
we get:
s
1
∑
i∈I
l
i
· H(idki) + (s
2
t
∑
j=1
µ
j
α
j
)P =
s
1
∑
i∈I
l
i
· H(idki) + (s
2
t
∑
j=1
∑
i∈I
l
i
h(idki)m
i, j
α
j
)P =
∑
i∈I
l
i
· (s
1
H(idki) + s
2
t
∑
j=1
h(idki)m
i, j
α
j
P) =
∑
i∈I
l
i
T
i
= τ
Furthermore, from the verification relation in
Verify
Pub
we get:
e(
∑
i∈I
l
i
· H(idki),Q
′
1
) · e(
t
∑
j=1
µ
j
(α
j
P),Q
′
2
) =
e(s
1
∑
i∈I
l
i
· H(idki),P
′
) · e(s
2
t
∑
j=1
µ
j
(α
j
P),P
′
) =
e(s
1
∑
i∈I
l
i
· H(idki) + s
2
t
∑
j=1
µ
j
(α
j
P),P
′
) =
e(s
1
∑
i∈I
l
i
· H(idki) + s
2
t
∑
j=1
∑
i∈I
l
i
h(idki) · m
i, j
· α
j
P,P
′
) =
e(
∑
i∈I
l
i
(s
1
· H(idki) + s
2
t
∑
j=1
h(idki) · m
i, j
· α
j
P),P
′
) =
e(
∑
i∈I
l
i
T
i
,P
′
) = e(τ,P
′
)
This demonstrates the correctness of both verification
relations.
Secondly, we prove that the tags in our scheme are
unforgeable. We do so by showing that any PPT ad-
versary B winning the data possession game for a file
not equal to the original file, can be turned into an ef-
ficient PPT algorithm A that solves arbitrary instances
of the ECDLP in E(F
q
)[p]. In the following, we de-
scribe how this algorithm simulates the environment
of the challenger when interacting with the adversary.
Algorithm A is given an arbitrary instance (P,R =
rP) of the ECDLP in E(F
q
)[p]. Then, A sets the
public and private keys as (E(F
q
), p, P,H), where A
chooses α
j
P = (φ
j
P+ ψ
j
R) for φ
j
,ψ
j
∈
R
Z
p
, as well
as sk = (s
1
,s
2
) and givespk to B. Note that this choice
of the values α
j
P in the simulation is indistinguish-
able from the values chosen in the real game. It will
be clear from the simulation of the hash function why
we use values α
j
P of this particular form.
Furthermore, A simulates the tagging and hash or-
acle queries for B, whereas B is allowed to run the
public verification algorithm for all generated tags.
Now, if A receives a tagging query for a file block
~m
i
identified by (id,i), A checks whether a previous
query has already been made for (id,i). If so, A re-
trieves the recorded tuple (id,i, ~m
i
,t
i
,T
i
). Otherwise,
A chooses an element t
i
∈
R
Z
p
and computes the tag
as the point T
i
= t
i
P ∈ E(F
q
)[p] and records the tu-
ple (id,i, ~m
i
,t
i
,T
i
). In both cases A returns T
i
. A an-
swers B’s hash oracle queries for the hash function
h as follows. If A receives a hash query for some
value idki, then A checks whether a previous query
has already been made for idki. If so, A retrieves the
recorded tuple (idki,x
id,i
) and otherwise A chooses a
value x
id,i
∈
R
Z
p
and records the tuple (idki,x
id,i
). In
both cases A returns x
id,i
. A answers B’s hash ora-
cle queries for the hash function H as follows. If
A receives a hash query for some value idki, then A
checks whether a previous query has already been
made for idki. If so, A retrieves the recorded tuple
(idki,H(idki)). Otherwise, A retrieves (id,i, ~m
i
,t
i
,T
i
)
from the list of recorded tagging queries and the re-
quired tuples (idki,x
id,i
) from the list of recorded hash
queries for the hash function h and computes
H(idki) = s
−1
1
(t
i
P− s
2
x
id,i
t
∑
j=1
m
i, j
(α
j
P)) ∈ E(F
q
)[p]
and records the tuple (idki,H(idki)). In both cases, A
returns the recorded value H(idki).
In the retrieve phase, A generates challenges C
i
=
(id
∗
,I,l) for 1 ≤ i ≤ λ for a file M
∗
identified by id
∗
.
Now, if B delivers proofs π
i
= (µ,τ) for file M
′
6= M
∗
and challenge C
i
then A proceeds as follows. W.l.o.g.
we demonstrate the reduction by means of a single
proof π with µ = (µ
j
)
t
j=1
=
∑
i∈I
l
i
h(id
∗
ki) · m
∗
i, j
t
j=1
and τ =
∑
i∈I
l
i
T
i
. Recall that the verification relation,
after substituting the simulated hash function values,
EfficientSimultaneousPrivatelyandPubliclyVerifiableRobustProvableDataPossessionfromEllipticCurves
25

looks as follows:
∑
i∈I
l
i
· (t
i
P− s
2
x
id,i
t
∑
j=1
m
i, j
(α
j
P)) + s
2
t
∑
j=1
µ
j
(α
j
P) = τ
By replacing the values α
j
P, we obtain:
∑
i∈I
l
i
· (t
i
P− s
2
x
id,i
t
∑
j=1
m
i, j
(φ
j
P+ ψ
j
R))+
s
2
t
∑
j=1
µ
j
(φ
j
P+ ψ
j
R) = τ
Simplifications of the left-hand-side yield:
∑
i∈I
l
i
(t
i
P− s
2
x
id,i
t
∑
j=1
m
i, j
(φ
j
P+ ψ
j
R))+
s
2
t
∑
j=1
µ
j
(φ
j
P+ ψ
j
R) =
∑
i∈I
l
i
(t
i
P− s
2
x
id,i
t
∑
j=1
m
i, j
(φ
j
P+ ψ
j
R)+
s
2
x
id,i
t
∑
j=1
m
∗
i, j
(φ
j
P+ ψ
j
R)) =
∑
i∈I
l
i
(t
i
P+ s
2
x
id,i
t
∑
j=1
(m
∗
i, j
− m
i, j
)(φ
j
P+ ψ
j
R)) =
∑
i∈I
l
i
(t
i
P+ s
2
x
id,i
t
∑
j=1
δ
i, j
(φ
j
P+ ψ
j
R)) =
∑
i∈I
l
i
(t
i
P+ s
2
x
id,i
t
∑
j=1
δ
i, j
φ
j
P)+
∑
i∈I
l
i
(t
i
P+ s
2
x
id,i
t
∑
j=1
δ
i, j
ψ
j
R)
where δ
i, j
= m
i, j
− m
∗
i, j
. Equating the so obtained
simplification with the right-hand-side and subtract-
ing the right-hand-side, we get:
∑
i∈I
l
i
(t
i
+ s
2
x
id,i
t
∑
j=1
δ
i, j
φ
j
)P+
(
∑
i∈I
l
i
s
2
x
id,i
t
∑
j=1
δ
i, j
ψ
j
)R = O
From this it follows that
R = rP = −
∑
i∈I
l
i
(t
i
+ s
2
x
id,i
∑
t
j=1
δ
i, j
φ
j
)
(
∑
i∈I
l
i
s
2
x
id,i
∑
t
j=1
δ
i, j
ψ
j
)
P.
Consequently, if B provides a forged proof, i.e., if
there is at least one pair m
i, j
6= m
∗
i, j
implying that
∑
t
j=1
(m
i, j
− m
∗
i, j
) 6= 0, then A can compute r ∈ Z
p
,
which is the solution to the given instance (P,R = rP)
of the ECDLP in E(F
q
)[p]. A returns (P,R,r).
Note that the reduction can be performed analo-
gously using the public verification relation, which
would lead to the following relation:
g
r
= g
−
∑
i∈I
l
i
(t
i
+s
2
x
id,i
∑
t
j=1
δ
i, j
φ
j
)
(
∑
i∈I
l
i
s
2
x
id,i
∑
t
j=1
δ
i, j
ψ
j
)
.
A returns (P,R,r) which is a valid solution to the
ECDLP, since E(F
q
)[p] ≃ F
∗
q
k
[p] ≃ Z
p
and g =
e(P,P
′
) is a generator of F
∗
q
k
[p].
Finally, we need to show that for sufficiently large
λ the original file F can be reconstructed. As shown
in (Dodis et al., 2009), it suffices to prove that if the
encoding of the file (primary encoding) as well as the
response from the server (secondary encoding) are ef-
ficiently erasure-decodable, then the original file can
be efficiently reconstructed. The primary encoding of
the file is done using a Reed-Solomon code and is,
thus, efficiently erasure decodable. By looking at the
server’s response, in particular at the value
µ = (µ
j
)
t
j=1
=
h(idki)
∑
i∈I
m
i, j
l
i
t
j=1
it is clear that the verifier can eliminate the values
h(idki) giving the sequence
∑
i∈I
m
i, j
l
i
t
j=1
, whose
elements constitute Reed-Solomon encodings of the
sequences (m
i, j
)
i∈I
. This means that our secondary
encoding is also efficiently erasure decodable. Con-
sequently, by applying Lemma 6 and then applying
Lemma 7 of (Dodis et al., 2009), the desired result
follows.
SECRYPT2013-InternationalConferenceonSecurityandCryptography
26
