Linear Software Models

Vector Spaces for Design Pattern Modules

Iaakov Exman

Software Engineering Dept., The Jerusalem College of Engineering, POB 3566, Jerusalem, 91035, Israel

Keywords: Linear Software Models, Vector Spaces, Modularity Matrix, Software Design Patterns, Pattern Modules,

Additivity.

Abstract: Software Design Patterns have an important role for software development and reuse within the object

oriented design paradigm. But the commonly used set of design patterns has remained arbitrary and lacking

a well-founded theoretical basis. This work offers algebraic Vector Spaces for software design patterns as a

theoretical framework based on Linear Software Models. It starts with modularity matrices of design

patterns made of software modules additively composed. The elements of the Vector Space are exactly the

pattern modules, upon which operates a direct sum operator. Design pattern modularity matrices are used to

extract typical modules, frequently used and often found in more than a single pattern. This leads to the

ultimate goal of sets of generic pattern modules serving as bases for the vector space. Design patterns and

larger sub-systems are additively built from the bases modules. Software design patterns’ case studies are

carefully analysed to demonstrate the approach.

1 INTRODUCTION

Software Design Patterns – see e.g. the well-known

GoF book (Gamma et al., 1995) – attained along the

years the status of a standard starting point to

approach software development problems. But since

their introduction there has not been a systematic

effort to give design patterns a theoretical basis.

They still are an ad hoc, more or less frequently

used, set of patterns.

This work offers the heretofore lacking

theoretical basis: Vector Spaces. We wish to obtain a

set of design pattern modules having properties of

necessity and sufficiency. To this end we base

ourselves on Linear Software Models. This work is

an application of these models to software Design

Patterns.

1.1 Linear Software Models

Linear Software Models were proposed as a theory

of software system composition from COTS

(Commercial Off-The-Shelf) components. Linear

Software Models, based on plain Linear Algebra, are

shortly reviewed here. For the detailed theory, please

see the original reference (Exman, 2012a), and

(Exman, 2012b).

In Linear Software Models, the architecture of a

software system is expressed by two kinds of basic

entities: structors and functionals.

Structors – which remind us of vectors – are

architectural units, from the structural viewpoint.

Structors generalize structural units to a diversity of

types (e.g. structs, classes, interfaces, aspects) and

collections (sets of classes, as design patterns).

Functionals are architectural system units from a

behavioral viewpoint. These are potential functions

that may be, but are not necessarily invoked.

Typically these are, Java methods, function families

(e.g. hyperbolic functions) or roles which define the

functionality of a design pattern (Riehle, 1996).

Modules are architectural units in a higher

hierarchical level of a system. Modules are

composed of grouped structors and their

corresponding functionals.

Linear models are usually formulated in terms of

matrices. The Modularity Matrix is a Boolean matrix

with columns standing for structors and rows for

functionals. A matrix element is 1-valued for a

functional-structor link and 0-valued for no link.

A central concept in Linear Software Models is

linear independence. Linear independence is the

formal algebraic equivalent to the informal software

engineering concept of uncoupling.

520

Exman I..

Linear Software Models - Vector Spaces for Design Pattern Modules.

DOI: 10.5220/0004496605200527

In Proceedings of the 8th International Joint Conference on Software Technologies (ICSOFT-PT-2013), pages 520-527

ISBN: 978-989-8565-68-6

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

A software structor is defined to be independent

of other structors in the system, if it provides a non-

empty proper sub-set of functionals of the system,

given by the links in the respective column, and is

linearly independent of other columns in the

Modularity Matrix. A similar statement is true for

independent functionals.

It has been demonstrated – see ref. (Exman,

2012) – that if all structors and all functionals of a

Modularity Matrix are respectively linearly

independent, the matrix is square. Moreover, if a

given functionals’ subset is disjoint to other subsets,

the matrix can be put in a block-diagonal form.

Therefore, if software design patterns are indeed

canonical building blocks for larger software

systems, we expect their Modularity Matrix to obey

the Linear Software Models. Thus, their modularity

matrices should be square and block-diagonal.

1.2 Mediator Modularity Matrix:

An Introductory Example

For design patterns the modularity matrix structor

columns refer to classes, while the matrix functional

rows refer to the respective class methods.

An example modularity matrix for the Mediator

design pattern is seen in Fig. 1. It contains the

generic pattern classes – Abstract and Concrete

mediator, Abstract and Concrete colleague. Here we

disregard any specific application classes.

The respective functionals – WidgetChanged,

Maintain Widgets, Changed and

SetActionByMediator – fit the list of participants

and sample code for the pattern in the GoF book

(Gamma et al., 1995). The functionals' names,

referring to Widget, hint to a GUI – graphical user

interface – application in the sample code.

The two diagonal blocks correspond to the

mediator module (upper-left) and to the colleague

Figure 1: Mediator Modularity Matrix – shows structor

columns and functional rows. Zero values are left blank,

while those within diagonal blocks are hashed.

module (lower-right). Even though one could have

several colleagues in the system only one is

represented in the matrix.

In Fig. 1 and all subsequent figures, 1-valued

matrix elements are explicit (orange colored), while

0-valued elements are omitted for simplicity. 0-

valued elements within blocks are hashed. 0-valued

elements outside blocks are left blank.

1.3 The Goal: Pattern Module Bases

for Vector Spaces

The goal of this work is a basis of design patterns in

which the different patterns are equally important

and cover the entire vector space of software design

patterns in a uniform way.

Design patterns not in the basis should be easily

expressed in term of one or more patterns belonging

to the basis.

Here we introduce the big idea: instead of

directly using design patterns in the basis, one

should use design pattern modules as the basis.

Different pattern modules are selected to be in

the vector space basis in order to not overlap in a

trivial way, i.e. they should be orthogonal.

The remaining of the paper is organized as

follows. Section 2 introduces vector spaces for

design pattern modules. Section 3 deals with the

choice of pattern modules for vector space bases.

Section 4 describes design pattern composition from

basis pattern modules. Section 5 concludes with a

discussion.

2 VECTOR SPACES FOR DESIGN

PATTERN MODULES

The aim of this section is to describe Vector Spaces

for design pattern modules. We propose here a three-

valued Vector Space.

2.1 Three-valued Vector Space

with Direct Sum

A vector space – see e.g. (Lang, 2002) – is defined

by a set of elements, together with two operations,

an addition and a multiplication by a scalar, obeying

a specified set of algebraic properties.

The elements in the set are square matrices – the

module sub-matrices of the modularity matrix –

defined for software design patterns as seen in the

introduction.

The addition operation is chosen to be the matrix

LinearSoftwareModels-VectorSpacesforDesignPatternModules

521

direct sum – see e.g. (Weisstein, 2006) – which

constructs a block diagonal matrix from a set of

square matrices. In general, for i=1,…,n square

matrices A

the direct sum is written

⊕

i=1

= diag(A

, A

, … , A

)

(1)



where ⊕ stands for direct sum, and diag means

block diagonal.

The choice of the matrix direct sum is motivated

by its ability to construct standard modularity

matrices from existing modules. Thus a modularity

matrix is viewed as a vector in terms of the defined

vector space.

The multiplication by a scalar operation is just

plain number multiplication, but the scalars in this

case are three-valued, i.e. only 1, 0 and -1. Three-

valued scalars imply respectively addition/no-

change/subtraction of given modules to/from a

modularity matrix.

The direct sum is easily shown to obey the

required associative and commutative properties.

The zero element and an inverse operation must be

defined and added to these properties.

The zero element for the direct sum, denoted by

(), the matrix with an empty set of elements, has

the property:

⊕ () = A

(2)

The inverse operation for the direct sum is the

matrix direct subtraction, denoted by ⊖,defined as:

Ai ⊖ Ai = () (3)

The meaning of the direct subtraction A

⊖ A

is a

binary operation used to remove the square matrix

(the second argument of the binary operator ⊖

from the preceding block diagonal matrix A

(the

first argument of the binary operator).

The multiplication by a scalar also obeys the

required simple properties, viz. distributive

regarding square matrices, distributive regarding the

scalar coefficient and associative regarding scalar

coefficients. The identity scalar coefficient has value

Simple consequences of the above properties are:

0 * A

= ()

(4)

 * () = ()

(5)



where A

is any square matrix and  is any scalar

coefficient. Finally, with the same conventions, one

formally has

 * A

= ⊖*A







meaning that multiplying by -1 is equivalent to the

creation of a 2

argument of the matrix direct

subtraction. These formal properties are needed for

the complete characterization of the vector space.

3 A BASIS FOR THE PATTERN

MODULES VECTOR SPACE

In this section we propose a basis for the GoF

pattern modules vector space.

We first propose selection criteria. Then use the

criteria to make an actual basis proposal. Finally we

ask about the dimension of this basis.

3.1 Vector Space Basis Selection

Criteria

Based upon the design pattern statistics of usage, not

all patterns have equal importance. This seems to

imply that we should not expect that all the design

pattern modules will appear in the vector space

bases.

Thus, reasonable selection criteria for pattern

modules to appear in vector space bases should

include:

 Relative usage – modules in widely used patterns

should be included, in contrast to scarcely used or

too specific patterns;

 Role uniqueness – include pattern modules with a

unique role, do not include modules with similar

roles;

The overall idea is to attain a representative and

orthogonal basis set. Relative usage discards

irrelevant patterns. Role uniqueness contributes to

orthogonality.

If one looks for usage statistics of the GoF patterns,

one finds a significant variance. For instance in

reference (Shi and Olsson, 2006) a tool was applied

to recover pattern instances from several large

software packages written in the Java language.

Results show that in four software packages

certain patterns were very frequent (Mediator up to

500 instances, Bridge more than 100 instances,

Façade close to 100 instances), while other patterns

were not frequent (Abstract Factory around 30

instances, Strategy around 60 instances) and still

others totally negligible (Singleton, Template

Method, Visitor). This means that in terms of usage

frequency the proposed design patterns are very non-

uniform, in other words with very unequal relative

importance.

The GoF book itself – in the Guide to Readers –

proposes a selection of most common patterns,

which differs from the above results.

ICSOFT2013-8thInternationalJointConferenceonSoftwareTechnologies

522

A truly representative statistics may not be easy

to obtain.

3.2 A Basis Set of Design Pattern

Modules

The Vector Space in this work is intended to cover

only Design Pattern modules. But, often these

modules are composed with classes of other

modules. These are either supplementary classes

needed for the design pattern execution – typically a

client – or just application classes.

Therefore, pattern modules can be classified as:

a- Essential – modules with an essential role

defining the design pattern;

b- Accessory – modules with an accessory role

needed to execute the design pattern.

We have analysed the GoF patterns to extract a basis

set for the Vector Space, according to the criteria in

the previous sub-section. The proposed basis set is

seen in Table 1.

Table 1 displays the chosen 16 essential modules

and their semantics.

A list of most common accessory modules in

GoF Design Patterns includes: Client, Target,

Abstraction, Implementor, Sub-system, Invoker,

Receiver, Originator, Context, Element, Class,

Expression and Aggregate. These can be seen to

have a quite generic character, not defining a

specific Design Pattern.

Table 1: GoF Pattern Modules Basis Set.

Module

Name

Module Semantics

1 Factory

Constructs instances of another class

2 Product

Class that may be repeatedly constructed

3 Director

Construction Recipe

4 Prototype

Construction Clone to be copied

Numbered

Factory

Factory with Predefined Instances’ number

6 Adapter

Interface converter into another interface,

7 Adaptee

Interface being converted

8 Component

Part from Hierarchy

9 Mediator

Unifying point of Abstraction

10 Colleague

End-point of Abstraction

11 Handler

Intermediate point of Abstraction

12 Subject

Unifying source of communication

13 Observer

End-point of communication

14 Strategy

Dynamic Alternative role

15 Command

Action that may be repeatedly invoked

16 State

State worth signalling by means of a class

An example of an essential module occurring in two

different design patterns is Numbered Factory. It

occurs in the Singleton pattern, with at most one

instance, and in the Flyweight Factory with maximal

instances number being application dependent.

3.3 Dimension of Pattern Module

Vector Spaces

An important issue concerning the Vector Space for

GoF design pattern modules is its dimension, in

other words what is the size of its bases. The

following Lemma aims at providing an upper bound

to the space dimension.

A proof sketch is as follows. An upper bound to the

space dimension is given by two conditions:

 The number of essential pattern modules – this is a

small constant m that was proposed above to be

16 modules;

 The number of accessory modules needed per

essential module – assumed to be k;

The sought dimension upper bound is D=m*k.

Is the assumption that k is a small constant

reasonable? By empirical observation, the maximal

overall number of classes in design pattern class

diagrams in the GoF book is of the order of ten.

Specifically, the Abstract Factory pattern has 10

classes and the Façade pattern has 15 classes.

4 ADDITIVE COMPOSITION

FROM BASIS MODULES

Here we describe case studies of design pattern

composition from basis modules. This also

illustrates the additive composition above the level

of individual patterns.

4.1 Single GoF Patterns

Frequently used behavioral design patterns include,

e.g. the Mediator and the Observer.

The Mediator pattern, shown in Fig. 1 is

represented in terms of the matrix direct sum, by the

following equation:

Lemma 1 – Dimension of Pattern Modules

Vector Space

Assuming that the number of the accessory

modules needed by each essential module is at

most a constant k, the dimension of the vector

space of GoF design pattern modules is finite

and bounded.

LinearSoftwareModels-VectorSpacesforDesignPatternModules

523

Mediator-Pattern

= A

mediator

⊕ A

colleague

(7)

This equation makes explicit that the block diagonal

modularity matrix of the Mediator pattern is

composed of a mediator module and a colleague

module, by means of the matrix direct sum. The

equation also reflects the intuition that modules in

Linear Software Modules are additively composed.

The order of the modules in equation (7) is

arbitrary. This arbitrariness is a consequence of the

way of computation of diagonality, i.e. only the

distance of a module matrix element from the

diagonal is important, not its specific position. It

does not matter whether the mediator module is the

upper-left block and the colleague is the lower-right

block in the matrix or vice-versa.

Figure 2: Observer Modularity Matrix – the same

conventions used in Fig.1 and in all subsequent figures

containing modularity matrices for a given pattern.

Thus, although the matrix direct sum in general is

not commutative, for the particular case of module

composition we use a commutative version and

therefore it is a true vector space.

For details about the choice of functionals in the

Observer pattern see ref. (Exman, 2012). The

Observer pattern, shown in Fig. 2 is represented

similarly, by the following equation:

Observer-Pattern

= A

subject

⊕ A

observer

(8)

4.2 Pairs of Patterns

The first example of composition of a couple of

design patterns is found in the GoF book (Gamma et

al., 1995) itself, viz Observer and Mediator.

The original purpose of this composition is to

encapsulate in the mediator a complex graph of

dependencies – a DAG, Directed Acyclic Graph – of

large numbers of observer instances possibly

connected to more than a single subject.

The Observer-Mediator composition of patterns

is represented in terms of the matrix direct sum of

modules, by the following equation:

Obs-Med-Composition

= A

subject

⊕ A

mediator

⊕ A

observer

(9)

The direct sum terms are in the same order as the

modules in the modularity matrix shown in Fig. 3.

Note that the composition does not include the

colleague module, since this is the role of the subject

and the observer in this composition.

The composition clear additivity justifies well

the choice of the direct sum as the operation of the

Vector Space.

Figure 3: Observer-Mediator Composed Modularity

Matrix – the mediator is the central module between the

upper-left subject and the bottom-right observer.

4.3 Triplets of Patterns

The next example adds to the previous composition

the Singleton pattern – also suggested in the GoF

book – since it is reasonable to expect the Mediator

to behave as a Singleton for this kind of system.

Here we do not use fully expanded modules as in

Fig 3, since their classes are already known. We

collapse each of the Observer-Mediator modules

into upper level black-boxes leaving one matrix

element per module, as seen in Fig. 4. The resulting

modularity matrix is strictly diagonal.

The added Singleton pattern is a special case

containing just one class. Thus, its expanded and

collapsed square matrices coincide.

The Observer-Mediator-Singleton composition

of patterns is represented by the following equation:

Obs-Med-Singlet

= A

subject

⊕ A

mediator

⊕ A

singleton



⊕ A

observer

(10)

The modules’ order in this equation is the same as in

the matrix in Fig. 4. The Singleton module is close

to the Mediator since its purpose is to add the single

instance property to the Mediator module.

ICSOFT2013-8thInternationalJointConferenceonSoftwareTechnologies

524

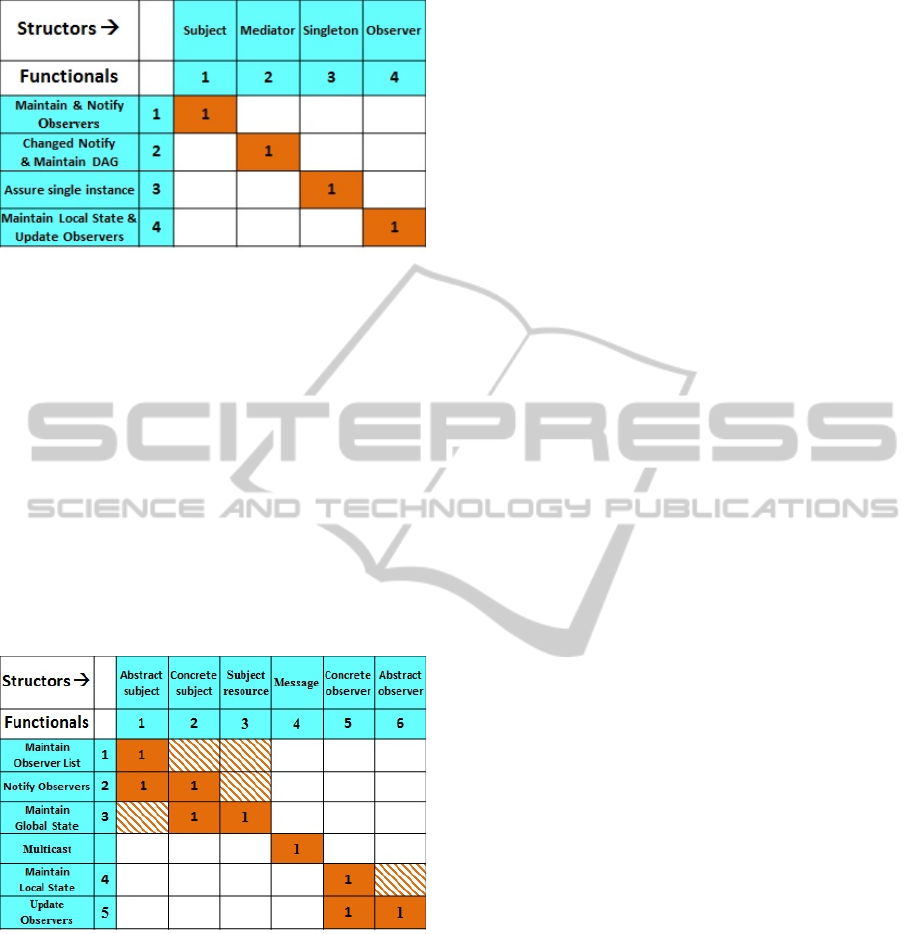
Figure 4: Observer-Mediator-Singleton Modularity Matrix

– this is a strictly diagonal matrix, as each module is

collapsed into an upper-level black-box. Expanded white-

boxes would recover classes with additional 1-values per

module as seen in Fig. 3.

4.4 Expressing Any Pattern in Terms

of Basis Modules

The current example shows how to derive one

pattern from another one. In particular we obtain the

Multicast (Vlissides, 1997) pattern from the

Observer pattern.

The derivation implies that Observer modules are

in the basis of GoF pattern modules. On the other

hand the Multicast pattern is viewed as a derived

pattern.

Figure 5: Multicast derived pattern Modularity Matrix –

this pattern is derived from the Observer pattern modules,

with the addition of the Message module.

We disregard the renaming issues – say attach

instead of register – and other specific structural

differences, as long as the pattern desired behavior is

attained.

The essential difference between the Multicast

and the Observer is the additional module with a

Message class. This enables more specific

characterization of message instances as deemed

necessary.

It should be clear that the Message module is an

accessory module, in the sense of sub-section 3.2.

This is justifiable since messages are ubiquitous in

software systems. Whether the Message is part of

another pattern and not just an independent module,

is a decision that could be taken, but is out of the

scope of this paper.

The Multicast pattern in terms of the Observer

pattern modules is represented by the following

equation:

Multicast

= A

subject

⊕ A

message

⊕ A

observer

(12)

The Multicast derived pattern modularity matrix is

seen in Fig. 5.

4.5 Multi-pattern Composition

The above examples give a flavour of pattern

composition by means of the direct sum operator in

the Vector Space. They also clarify the potential

meaning of bases for this kind of vector space.

Additional multi-pattern composition can be

done in similar ways.

Nonetheless, it should be clarified that such

matrices are only relevant for cases of actual

interaction among the respective design patterns.

Design patterns may occur in disjoint parts of

large systems. In such cases there is no sense in

depicting them in a common modularity matrix

independent of the other modules of the large

system.

5 DISCUSSION

5.1 Vector Spaces

Vector spaces have linear independence as a

fundamental concept. This is a formal concept

corresponding to the informal notion of decoupling

in Software Engineering. Therefore, vector spaces

are perfectly suitable to deal with design patterns,

where decoupling is a main purpose.

The matrix direct sum operation is neatly defined

and suitable for additive pattern composition. Some

minor additions and modifications needed for this

operation were introduced, such as the inverse

operation matrix direct subtraction.

The vector space is the central algebraic structure

proposed in this work as a theoretical base for GoF

design pattern modules.

The issue of bases for this vector space was dealt

with. Lemma 1 stated that the vector space is finite

and bounded. On the other hand, no specific sizes or

LinearSoftwareModels-VectorSpacesforDesignPatternModules

525

very tight bounds for the vector space size were

offered yet.

Modules are preferable to whole patterns as the

bases elements, since various modules appear as

common units in several patterns, obtaining a

desirable uniformity at the module level. This

uniformity facilitates understanding and additive

usability of pattern composition.

5.2 Related Work

Patterns were first proposed by Beck and

Cunningham – see ref. (Beck and Cunningham,

1987).

After the publication of the GoF design patterns,

many other compilations of design patterns

appeared, some of them specialized for specific

purposes, among them for Networks (Buschmann et

al., 1996) and J2EE (Alur et al., 2003).

Different formal approaches were proposed to

deal theoretically with design patterns. To our best

knowledge none of them pursues an algebraic

structure approach similar to ours.

Mikkonen (Mikkonen, 1998) used high-level

abstractions of communications combined with a

Temporal Logic of actions.

Yehudai and collaborators (Eden et al., 1998,

1999) proposed LePUS a system based on predicate

logic, also displaying a readable diagrammatic

representation.

Cechich and Moore (Cechich and Moore, 1999)

use RSL a specification language to formally decide

whether a given design conforms to an intended

design pattern.

Wang and Huang (Wang and Huang, 2008) use

RTPA – real-time process algebra – as a

specification of design patterns. Despite the

algebraic name, it is a formal language oriented

approach.

Most of these approaches solve particular

problems. Our approach is generic, and displays the

power and clarity of an algebraic structure.

5.3 Future Work

The Three-valued Vector Space can certainly be

extended to more general spaces, say real vector

spaces. This will allow, among other possibilities,

consistent treatment of expanded and collapsed

modules in equal foot.

For instance, in ref. (Exman, 2012) collapsed

modules were marked with the trace and diagonality

integers – instead of just Boolean values – to provide

information about the underlying collapsed modules

and to enable their recovery.

The current Linear Software Model and its

vector space may possibly be refined to deal not

only with functionals, but also in a finer scale with

attributes.

5.4 Main Contribution

The main contribution of this paper is the use of

Vector Spaces as a formal tool for analysis of GoF

Design Patterns, based upon Linear Software

Models, a generic theoretical framework for

software composition.

Its practical application is additive composition

of software sub-systems, design patterns and

upwards, from the basis modules.

REFERENCES

Alur, D., Crupi, J., and Malks, D., 2003. Core J2EE

Patterns: Best Practices and Design Strategies, 2

edition, Prentice-Hall, Upper Saddle River, NJ, USA.

Beck, K. and Cunningham, W., 1987. “Using Pattern

Languages for Object-Oriented Programs”, in

OOPSLA-87 Workshop on the Specification and

Design for Object-Oriented Programming.

Borndorfer, R., Ferreira, C.E., and Martin, A., 1998.

“Decomposing Matrices into Blocks”, SIAM J.

Optimization, Vol. 9, Issue 1, pp. 236-269.

Buschmann, F., Meunier, R., Rohnert, H., Sommerlad, P.,

and Stal, M., 1996. Pattern-Oriented Software

Architecture - A System of Patterns. Wiley and Sons.

Cechich, A., and Moore, R., 1999. “A Formal Basis for

Object-Oriented Patterns”, in Proc. 6

APSEC Asia

Pacific Software Engineering Conf., pp. 284-291.

Eden, A. H., Gil, J., Hirshfeld, Y. and A. Yehudai, 1999.

“Towards a Mathematical Foundation for Design

Patterns”, Tel-Aviv University, Technical Report,

1999

Eden, A.H., Hirshfeld, Y. and A. Yehudai, 1998.

“Multicast - Observer ≠ Typed Message”. C++

Report, SIGS Publications.

Exman, I., 2012. “Linear Software Models for Well-

Composed Systems”, in S. Hammoudi, M. van

Sinderen and J. Cordeiro (eds.), Proc. 7

ICSOFT’2012 Conference, pp. 92-101, Rome, Italy.

Exman, I., November 2012. “Linear Software Models”,

Extended Abstract, in Ivar Jacobson, Michael

Goedicke and Pontus Johnson (eds.), Proc. GTSE

2012, SEMAT Workshop on a General Theory of

Software Engineering, pp. 23-24, KTH Royal Institute

of Technology, Stockholm, Sweden.

http://semat.org/wp-content/uploads/2012/10/GTSE_

2012_Proceedings.pdf. See also video presentation:

http://www.youtube.com/watch?v=EJfzArH8-ls

Gamma, E., Helm, R., Johnson, R., and Vlissides, J.,

1995. Design Patterns: Elements of Reusable Object-

ICSOFT2013-8thInternationalJointConferenceonSoftwareTechnologies

526

Oriented Software, Addison-Wesley, Boston, MA,

USA.

Lang, S., 2002. Algebra, Springer Verlag, 3

edition, New

York, USA.

Mikkonen, T., 1998. “Formalizing Design Patterns”, in

Proc. ICSE’98, pp. 115-124, IEEE Computer Society

Press.

Mitchell, B. S., and Mancoridis, S., 2006. “On the

Automatic Modularization of Software Systems Using

the Bunch Tool”, IEEE Trans. Software Engineering,

Vol. 32, pp. 193-208, (3).

Riehle, D., 1996. “Describing and Composing Patterns

Using Role Diagrams”, in K-U. Mutzel & H-P. Frei.

(eds.) Proc. Ubilab Conf., Universitatsverlag

Konstanz, pp. 137-152.

Shi, N., and Olsson, R.A., 2006. “Reverse Engineering of

Design Patterns from Java Source Code”, in Proc.

ASE’06 21

Int. Conf. Automated Software

Engineering, pp. 123-134.

Vlissides, J., 1997. “Multicast”. C++ Report, Sep. 97.

SIGS Publications.

Wang, Y., and Huang, J., 2008. “Formal Modeling and

Specification of Design Patterns using RTPA”, Int. J.

Cognitive Informatics and Nat. Intelligence, vol. 2, pp.

100-111, 2008.

Weisstein, E. W., 2006. "Matrix Direct Sum" from

MathWorld – a Wolfram Web Resource.

http://mathworld.wolfram.com/MatrixDirectSum.html.

LinearSoftwareModels-VectorSpacesforDesignPatternModules

527