
Modulation-mode and Power Assignment
in SVD-assisted MIMO Systems
with Transmitter-side Antennas Correlation
Andreas Ahrens
1
, Francisco Cano-Broncano
2
and C´esar Benavente-Peces
2
1
Hochschule Wismar, University of Technology, Business and Design, Philipp-M¨uller-Straße 14, 23966 Wismar, Germany
2
Universidad Polit´ecnica de Madrid, Ctra. Valencia. km. 7, 28031 Madrid, Spain
Keywords:
Multiple-Input Multiple-Output System, Singular-Value Decomposition, Bit Allocation, Power Allocation,
Antennas Correlation, Wireless Transmission.
Abstract:
Multiple-input multiple-output (MIMO) systems can provide a noticeable improvement in channel perfor-
mance. Nevertheless some perturbances affect the capability of this technique to get the expected improve-
ment. Due to the use of multiple antennas at the same front-end and their close spacing the so called antennas
correlation effect appears. Antennas correlation can drastically affect the channel behaviour by increasing the
bit-error rate (BER) and dropping its capability. This paper analyses the impact of transmitter-side antennas
correlation on the MIMO system performance. The singular value decomposition (SVD) is used to transform
the MIMO channel into independent layers. Afterwards bit and power allocation techniques are applied in
order to obtain the best performance.
1 INTRODUCTION
MIMO communication systems have been studied
along the last two decades and incorporated in com-
munication standards due to their ability of increasing
the channel capabilities (lower bit-error rate (BER)
and larger data rates) without requiring additional
transmit power and bandwidth. In order to obtain the
full advantages promised by MIMO techniques, addi-
tional signal processing should be applied. Singular-
value decomposition (SVD) is a popular techniques
which allows removing the inter-antenna interfer-
ences due to the multiple antennas arrangements both
at the transmitter and the receiver sides (Haykin,
2002). The SVD transforms the MIMO channel
into multiple independent layers (single-input single-
output channels, SISO). In order to get the full ben-
efits of using the SVD, perfect channel state infor-
mation should be available both at the transmit and
receive front-ends. Once the SVD has been applied
each layer is characterized by a singular value (gain
factor). The ideal set-up is that in which after SVD
all the layers behave in the same way, that is, all the
singular values take the same value. Usually this sit-
uation does not take place and layers have different
performances. MIMO systems benefit from scattered
environments where multipath is present and take ad-
vantage of the multipath effect by using signal pro-
cessing techniques (as the aforementioned singular-
value decomposition) (K¨uhn, 2006).
MIMO wireless channels are affected by the vari-
ous disturbances influencing regular wireless commu-
nication systems. Additionally, due to the use of mul-
tiple antennas at both the transmit and receive sides,
and the typical close spacing of the antennas due to
physical limitations, the so called antennas correla-
tion effect arises (Lee, 1973; Salz and Winters, 1994;
Shiu et al., 2000).
Therefore, MIMO scenarios with uncorrelated
channel coefficients have reached a state of maturity.
By contrast, MIMO scenarios with correlated channel
coefficients require substantial further research.
Antennas correlation diminishes multipath reach-
ness, essential to MIMO techniques. Due to that ef-
fect the various paths from each transmitter-side an-
tenna to each receiver-side antenna become similar.
Under this condition applying the SVD deals to sin-
gular values which are quite different and the ratio be-
tween the layers having largest and smallest singular
values becomes high. This means that predominant
layers arise, some with large singular values which
have a pretty good performance and others with quite
225
Ahrens A., Cano-Broncano F. and Benavente-Peces C..
Modulation-mode and Power Assignment in SVD-assisted MIMO Systems with Transmitter-side Antennas Correlation.
DOI: 10.5220/0004497102250232
In Proceedings of the 10th International Conference on Signal Processing and Multimedia Applications and 10th International Conference on Wireless
Information Networks and Systems (WINSYS-2013), pages 225-232
ISBN: 978-989-8565-74-7
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

low singular values which have a poor performance.
In consequence this paper analyzes and charac-
terizes the antennas correlation effect focussing our
attention on the transmitter-side. The analysis re-
marks the parameters affecting the correlation effect
and their influence on the overallsystem performance.
Additional techniques can be applied to improve
the MIMO system performance. Some of these tech-
niques are bit and power allocation (Zhou et al., 2005;
Mutti and Dahlhaus, 2004). Based on the MIMO lay-
ers performance various transmission modes can be
defined by allocating a different number of bits per
symbol along the various layers while maintaining the
overall data rate. Through the analysis of some exem-
plary transmission modes this paper shows that not
all the layers should be activated in order to obtain
the best results.
Power allocation techniques distribute the trans-
mit available power along the different transmit an-
tennas. One of the most popular techniques is the so
called water-filling. Based on the layers quality it is
determined the layers which should be activated and
hence the total available transmit power is appropri-
ately distributed.
Against this background, the novel contribution of
this paper is that we demonstrate the benefits of amal-
gamating a suitable choice of activated MIMO layers
and number of bits per symbol together with the ap-
propriate allocation of the transmit power under the
constraint of a given fixed data throughput. Our re-
sults showthat under the constraint of correlation only
a few layer should be used for the data transmission
when minimizing the overall bit-error rate.
The remaining part of this paper is organized as
follows. Section 2 describes the MIMO system model
including the antennas correlation characterization.
The bit- and power assignment in correlated channel
situation is discussed in section 3. The obtained re-
sults are presented and interpreted in section 4. Fi-
nally section 5 remarks the main results obtained in
this investigation.
2 MIMO SYSTEM MODEL
This section is aimed to establish the MIMO system
model affected by transmitter-side antennas correla-
tion effect. First, the correlation coefficients are de-
fined and characterized in order to finally describe the
overall MIMO system model.
2.1 Transmitter-side Correlation
Coefficients Characterization
The correlation effect is described by the correla-
tion coefficients. Transmitter-side antennas correla-
tion coefficients describe the similitude between paths
corresponding to a pair of antennas (at the transmit-
ter side) with respect to a reference antenna (at the
receiver side). Fig. 1 describes the basic set-up for
obtaining the correlation coefficient, where d is the
transmitter-side antennas spacing, d
1
is the distance
between transmit antenna #1 and the receiver-side an-
tenna (taken as reference) and d
2
is the distance from
transmit antenna #2 to the reference receive antenna
(it is assumed d << d
1
,d
2
); φ is the departure an-
gle. In consequence two paths are described and the
correlation coefficient describes how like they are.
When analyzing the system configuration, presented
d
1
d
2
d/2
d/2
antenna #1
Transmitter side
Receiver side
antenna #1
antenna #2
φ
Figure 1: Antennas’ physical disposition: two transmit and
one receive antennas.
in Fig. 1, the correlation between the signal s
r1
(t), i. e.
the signal arriving at the receive antenna from trans-
mit antenna #1, and the signal s
r2
(t), i. e. the signal
arriving at the receive antenna from transmit antenna
#2, is given by
ρ
(TX)
1,2
=
E{s
r1
(t) ·s
∗
r2
(t)}−E{s
r1
(t)}·E{s
r2
(t)}
p
E{s
r1
(t) ·s
∗
r1
(t)}·
p
E{s
r2
(t) ·s
∗
r2
(t)}
(1)
and simplifies as shown in (Cano-Broncano et al.,
2013) to
ρ
(TX)
1,2
= e
−j2π
(d
1
−d
2
)
λ
. (2)
The transmit antenna separation d
λ
= d/λ given in
wavelengths units can be expressed as
d
2
−d
1
λ
= d
λ
·cos(φ) . (3)
Inserting (3) in (2), the transmitter-side correlation
coefficient is given by
ρ
(TX)
1,2
= e
j2πd
λ
cos(φ)
. (4)
The antennas path correlation coefficient for line of
sight (LOS) trajectories depends on the antennas sep-
aration d
λ
and the transmit antennas reference axis
WINSYS2013-InternationalConferenceonWirelessInformationNetworksandSystems
226
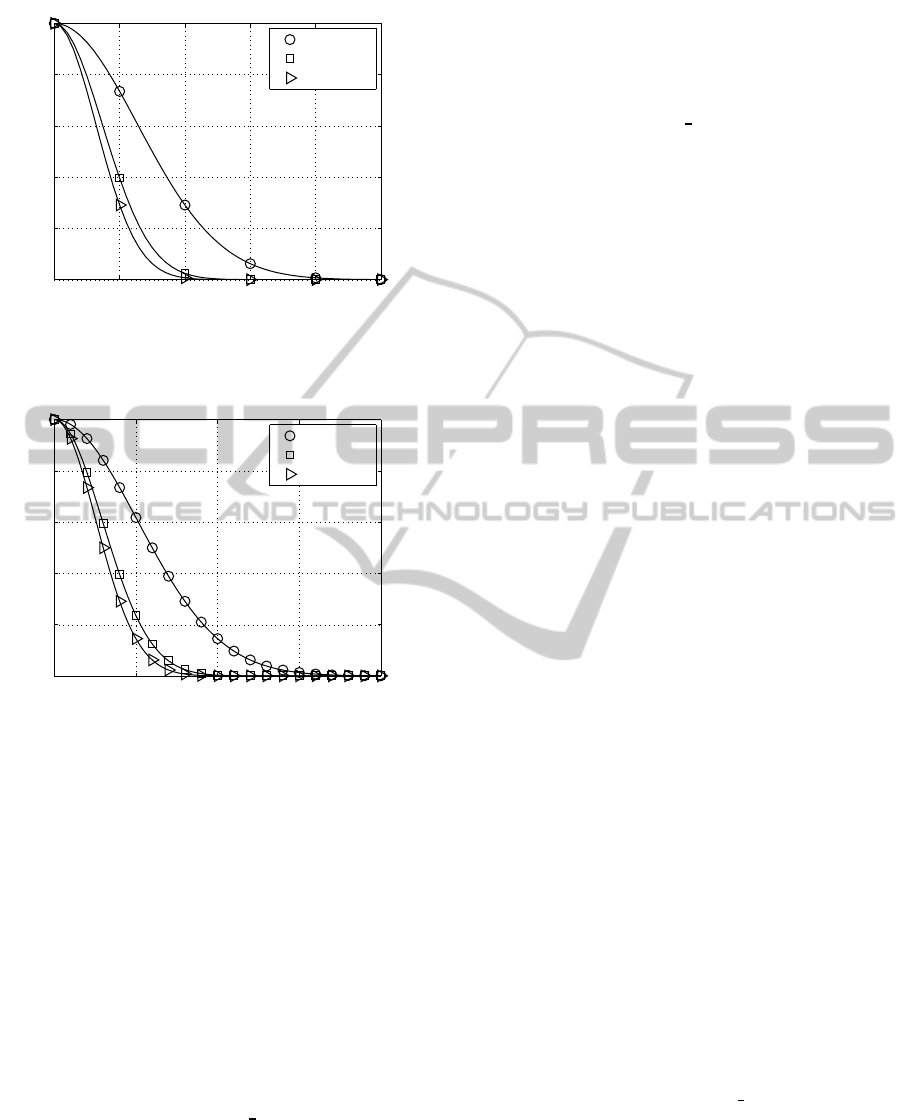
0 1 2 3 4 5
0
0.2
0.4
0.6
0.8
1
|ρ
(TX)
1,2
(φ,σ
ξ
)| →
σ
ξ
→
φ = 30
◦
φ = 60
◦
φ = 90
◦
Figure 2: Dependency of |ρ
(TX)
1,2
(φ,σ
ξ
)| as a function of σ
ξ
and φ assuming an antennas separation in wavelengths of
d
λ
= 1/4.
0 5 10 15 20
0
0.2
0.4
0.6
0.8
1
|ρ
(TX)
1,2
(φ,σ
ξ
)| →
σ
ξ
→
φ = 30
◦
φ = 60
◦
φ = 90
◦
Figure 3: Dependency of |ρ
(TX)
1,2
(φ,σ
ξ
)| as a function of σ
ξ
and φ assuming a wavelength specific antenna separation of
d
λ
= 1/16.
rotation angle φ (or signals angle of departure). By
taking the scattered environment of wireless chan-
nels into consideration, the transmit antennas refer-
ence axis rotation angle φ becomes time-variant and
(4) results in:
ρ
(TX)
1,2
= E{e
j2πd
λ
cos(φ+ξ
i
)
} . (5)
The parameter ξ
i
in (5) expresses the randomness of
the angles for the various scatters and is described by
a Gaussian distribution with zero mean and variance
σ
2
ξ
. Calculating the expectation under this assumption
leads to the following equation:
ρ
(TX)
1,2
(φ,σ
ξ
) = e
j2πd
λ
cos(φ)
e
−
1
2
(2πd
λ
sin(φ)σ
ξ
)
2
. (6)
When analyzing Fig. 2 and Fig. 3, high coefficients
correlation appears for small parameters of φ and σ
ξ
.
Additionally, in case of a small antenna separation,
i. e. reducing d
λ
, the received signals s
r1
(t) and s
r2
(t)
become even more similar.
2.2 Correlated MIMO System Model
The (n
R
×n
T
) system matrix H of a correlated MIMO
system model is given by
vec(H) = R
1
2
HH
·vec(G) (7)
where G is a (n
R
×n
T
) uncorrelated channel matrix
with independent, identically distributed complex-
valued Rayleigh elements and vec(·) is the opera-
tor stacking the matrix G into a vector column-wise
(Oestges, 2006). Based on the quite common assump-
tion that the correlation between the antenna elements
at the transmitter side is independent from the correla-
tion between the antenna elements at the receiverside,
the correlation matrix R
HH
can be decomposed into a
transmitter side correlation matrix R
TX
and a receiver
side correlation matrix R
RX
following the Kronecker
product ⊗. Under this assumption the matrix R
HH
is
formulated as
R
HH
= R
TX
⊗R
RX
. (8)
In this paper, no correlation at the receiver side is as-
sumed. Therefore, the (n
R
×n
R
) receiver-side corre-
lation matrix R
RX
simplifies to
R
RX
= I (9)
with the matrix I describing the identity matrix. The
(n
R
×n
R
) correlation matrix R
TX
for the investigated
(4×4) MIMO system is finally given by:
R
(4×4)
TX
=
1 ρ
(TX)
12
ρ
(TX)
13
ρ
(TX)
14
ρ
(TX)
21
1 ρ
(TX)
23
ρ
(TX)
24
ρ
(TX)
31
ρ
(TX)
32
1 ρ
(TX)
34
ρ
(TX)
41
ρ
(TX)
42
ρ
(TX)
43
1
.
(10)
Therein, the correlation coefficient ρ
(TX)
k,ℓ
describes
the transmitter side correlation between the transmit
antenna k and ℓ. Taking line-of-sight conditions into
account, the correlation coefficient results according
to (4) in
ρ
(TX)
k,ℓ
= e
−j2π(k−ℓ) d
λ
cos(φ)
for k < ℓ . (11)
Extending these results to scattered conditions, the
transmitter side correlation coefficient results accord-
ing to (5) for k < ℓ in
ρ
(TX)
k,ℓ
(φ,σ
ξ
) = e
−j2π(k−ℓ)d
λ
cos(φ)
e
−
1
2
(2π(k−ℓ)d
λ
sin(φ)σ
ξ
)
2
(12)
For the calculation of the transmitter-side correlation
coefficient for values of k > ℓ it can be exploited that
the values of the correlation coefficients are complex
conjugated. This is due to the sign change when com-
puting the distance difference between antennas with
Modulation-modeandPowerAssignmentinSVD-assistedMIMOSystemswithTransmitter-sideAntennasCorrelation
227
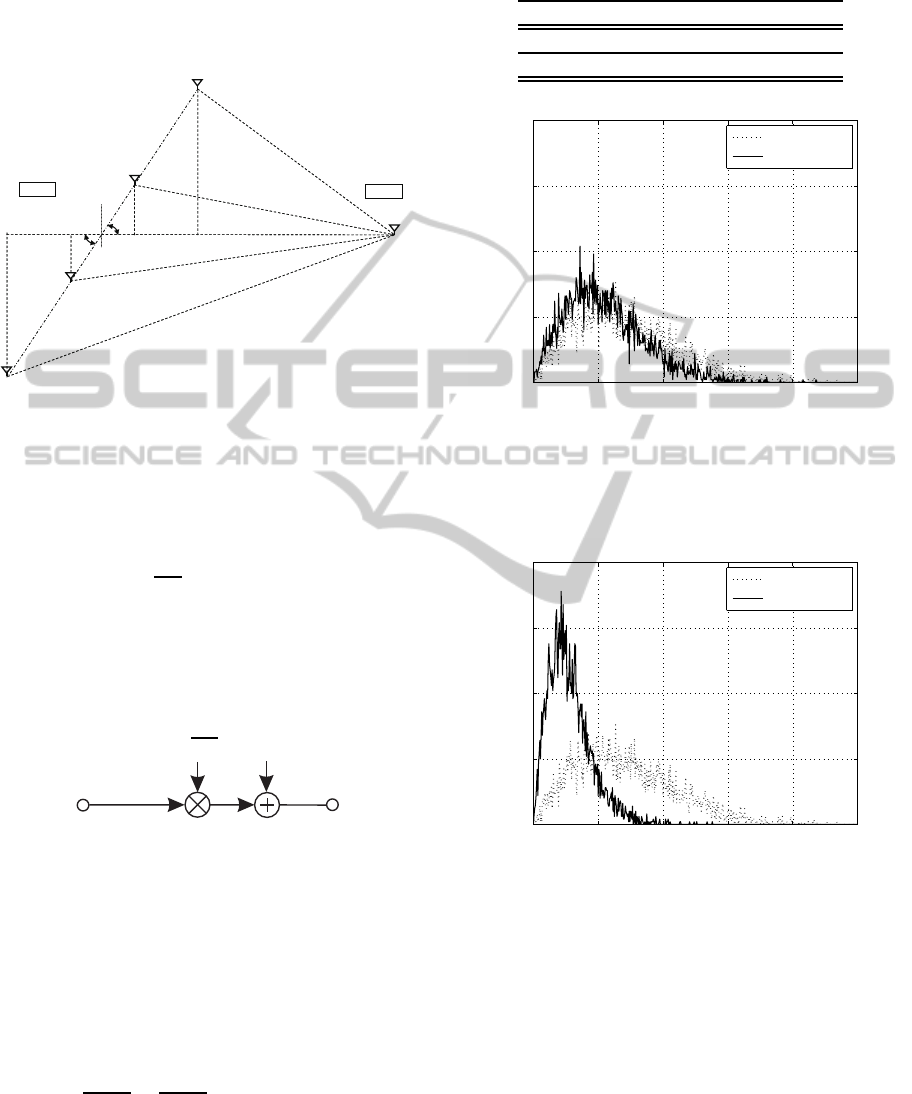
different antenna reference (see Fig. 4). Finally, the
following equation can be used to calculate the corre-
lation coefficient for values of k > ℓ
ρ
(TX)
ℓ,k
= ρ
∗(TX)
k,ℓ
. (13)
d
1
d
2
d/2
d/2
antenna #2
antenna #3
d
antenna #1
antenna #1
d
antenna #4
d
3
d
4
Tx
Rx
φ
Figure 4: Antennas’ physical disposition: four transmit and
one receive antennas.
Having frequency non-selective MIMO channels,
the whole MIMO system can be decomposed into a
number of independent, non-interfering layers. Us-
ing singular-value decomposition (SVD), the result-
ing system model is depicted in Fig. 5, where the
weighting factor
p
ξ
ℓ,k
represents the positive square
roots of the eigenvalues of the system matrix per
MIMO layer ℓ and per transmitted data block k. The
transmitted complex input symbol per MIMO layer
ℓ is described by c
ℓ,k
and the additive, white Gaus-
sian noise (AWGN) by w
ℓ,k
, respectively. In gen-
c
ℓ,k
y
ℓ,k
w
ℓ,k
p
ξ
ℓ,k
Figure 5: Resulting system model per MIMO layer ℓ and
transmitted data block k.
eral, correlation influenced the unequal weighting of
the different layers. In order to carefully study the
influence of the correlation, two channel constella-
tions are chosen as highlighted in Tab. 1. The cor-
responding unequal weighting of the different lay-
ers is shown in Fig. 6 and Fig. 7 for an exemplarily
studied (4 ×4) MIMO system. Therein, the differ-
ence in the layer-specific fluctuations is described by
the probability density function (pdf) of the parame-
ter ϑ =
p
ξ
ℓ=4,k
/
p
ξ
ℓ=1,k
, which shows the unequal
weighting of the different layers within the MIMO
system.
The ratio between the smallest and the largest sin-
gular values is an appropriate way to infer the anten-
Table 1: Parameters of the of the investigated channel con-
stellations.
Description φ σ
ξ
d
λ
Weak correlation 30
◦
1 1
Strong correlation 30
◦
1 0,25
0 0.1 0.2 0.3 0.4 0.5
0
0.005
0.01
0.015
0.02
uncorrelated
correlated
pdf →
ϑ →
Figure 6: PDF (probability density function) of the ratio
ϑ between the smallest and the largest singular value for
weakly correlated (solid line) as well as uncorrelated (dot-
ted line) frequency non-selective (4 ×4) MIMO channels
(d
λ
= 1, φ = 30
◦
and σ
ξ
= 1,0).
0 0.1 0.2 0.3 0.4 0.5
0
0.005
0.01
0.015
0.02
uncorrelated
correlated
pdf →
ϑ →
Figure 7: PDF (probability density function) of the ratio
ϑ between the smallest and the largest singular value for
strongly correlated (solid line) as well as uncorrelated (dot-
ted line) frequency non-selective (4 ×4) MIMO channels
(d
λ
= 1/4, φ = 30
◦
and σ
ξ
= 1,0).
nas correlation effects. When this parameter ϑ ap-
proaches the unity the MIMO channel is close to the
best performance which is reached when all the layers
have the same performance (assuming the same noise
power at the receiver-side). In this particular case the
layer-specific weighting factors, i.e., the singular val-
ues, are very similar. For weak antennas correlation,
as depicted in Fig. 6, this parameter decreases which
means some layers performs better than others and the
WINSYS2013-InternationalConferenceonWirelessInformationNetworksandSystems
228
overall MIMO channel performance drops. When an-
tennas correlation is significantly high, the parameter
ϑ becomes smaller, meaning a noticeable difference
in the performance of the various layer. Now, pre-
dominant strong and weak layers appear which de-
creases the overall channel performance (by increas-
ing the BER).
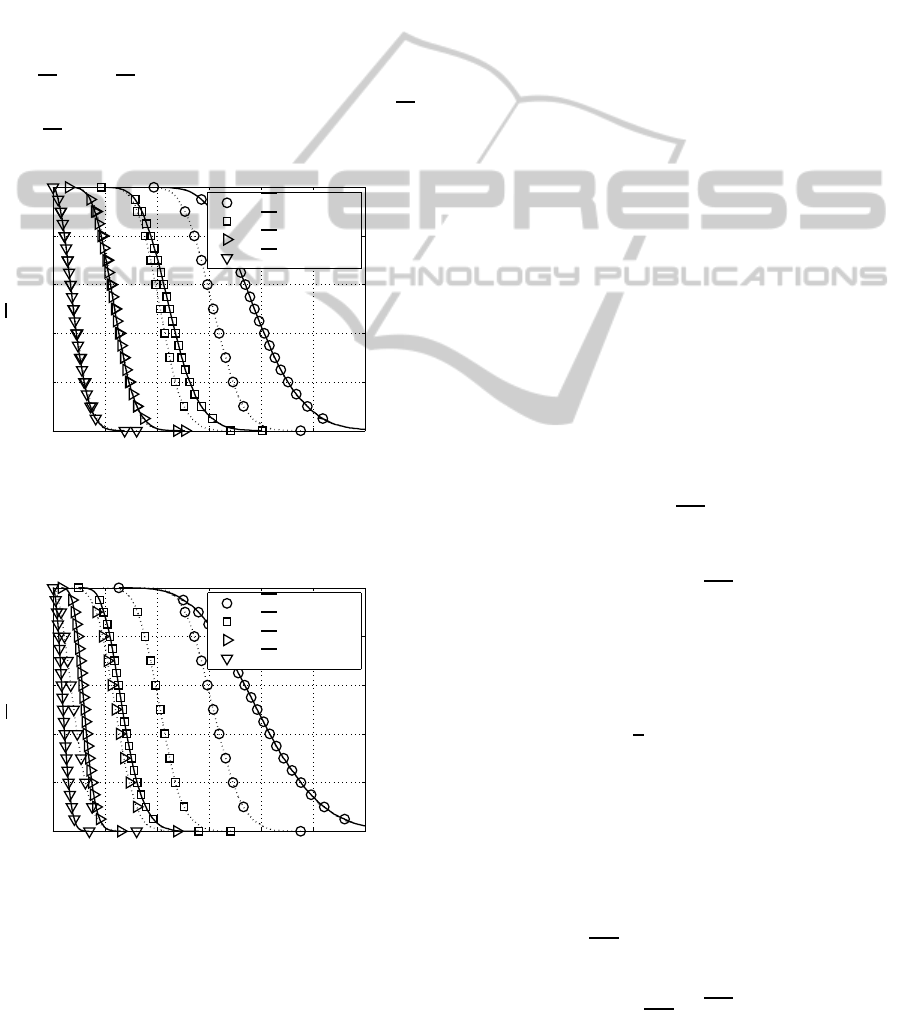
The distribution of the layer-specific characteris-
tic can be studied when analyzing the CCDF (com-
plementary cumulative distribution function) for the
different degrees of correlation as shown in Fig. 8 and
Fig. 9. The antennas correlation increases the prob-
ability of having layers with larger values (see lay-
ers
p
ξ
1
and
p
ξ
2
) and increases for weak layers the
probability of having lower values (see layers
p
ξ
3
and
p
ξ
4
).
0 1 2 3 4 5 6
0
0.2
0.4
0.6
0.8
1
p
ξ
1
(1st layer)
p
ξ
2
(2nd layer)
p
ξ
3
(3rd layer)
p
ξ
4
(4th layer)
Prob{
p
ξ
ℓ
≥U} →
U →
Figure 8: CCDF of the layer-specific distribution for weakly
correlated (solid line) as well as uncorrelated (dotted line)
frequency non-selective (4 ×4) MIMO channels (d
λ
= 1,
φ = 30
◦
and σ
ξ
= 1,0).
0 1 2 3 4 5 6
0
0.2
0.4
0.6
0.8
1
p
ξ
1
(1st layer)
p
ξ
2
(2nd layer)
p
ξ
3
(3rd layer)
p
ξ
4
(4th layer)
Prob{
p
ξ
ℓ
≥U} →
U →
Figure 9: CCDF of the layer-specific distribution for
strongly correlated (solid line) as well as uncorrelated (dot-
ted line) frequency non-selective (4 ×4) MIMO channels
(d
λ
= 1/4, φ = 30
◦
and σ
ξ
= 1,0).
The inspection of the CCDF also provides rele-
vant information to predict the MIMO channel per-
formance. Increasing antennas correlation spreads the
singular values CCDF curves. For the non-correlated
case, the various layers CCDF seem to be more con-
centrated. In the ideal case all of them overlap and
the best performance is obtained. Weak correlation
spreads the curves by right shifting those correspond-
ing to the highest singular values increasing the prob-
ability of getting large values in contrast to the small-
est singular values. Under strong antennas correlation
the CCDF curve for the largest singular values are in-
deed more right shifted while the smallest ones are
left shifted. In consequence, in this case the probabil-
ity of the largest singular value to obtain a high value
increases while the probability of taking the smallest
singular values a lower value also increases dealing to
the MIMO channel worse performance.
3 BIT- AND POWER
ASSIGNMENT
Assuming M-ary Quadrature Amplitude Modulation
(QAM), the argument ρ = U
2
A
/U
2
R
of the complemen-
tary error function (Kalet, 1987; Proakis, 2000) can
be used to optimize the quality of a data communi-
cation system by taking the half-vertical eye-opening
U
A
and the noise power per quadrature componentU
2
R
at the detector input into account (Ahrens and Lange,
2008). The half-vertical eye-opening per MIMO layer
ℓ and per transmitted symbol block k results in
U
(ℓ,k)
A
=
q
ξ
ℓ,k
·U
sℓ
, (14)
where U
sℓ
denotes the half-level transmit amplitude
assuming M
ℓ
-ary QAM and
p
ξ
ℓ,k
represents the pos-
itive square roots of the eigenvalues of the matrix
H
H
H. The average transmit power P
sℓ
per MIMO
layer ℓ determines the half-level transmit amplitude
U
sℓ
and is given by
P
sℓ
=
2
3
U
2
sℓ
(M
ℓ
−1) . (15)
Activating L ≤ min(n
T
,n
R
) MIMO layers, the overall
transmit power P
s
=
∑
L
ℓ=1
P
sℓ
can be calculated.
Power Allocation (PA) can be used to balance the
BER in the different numbers of activated MIMO lay-
ers (Ahrens and Lange, 2008). The resulting layer-
specific system model including power allocation is
highlighted in Fig. 10. The layer-specific power allo-
cation factors
√
p
ℓ,k
adjust the half-vertical eye open-
ing according to
U
(ℓ,k)
APA
=
√
p
ℓ,k
·
q
ξ
ℓ,k
·U
sℓ
. (16)
Modulation-modeandPowerAssignmentinSVD-assistedMIMOSystemswithTransmitter-sideAntennasCorrelation
229

replacements
c
ℓ,k
y
ℓ,k
w
ℓ,k
p
ξ
ℓ,k
√
p
ℓ,k
Figure 10: Resulting layer-specific system model including
MIMO-layer PA.
This results in the layer-specific transmit power per
symbol block k
P
(ℓ,k)
sPA
= p
ℓ,k
P
sℓ
. (17)
Taking all activated MIMO layers into account, the
overall transmit power per symbol block k is obtained
as
P
(k)
sPA
=
L
∑
ℓ=1
P
(ℓ,k)
sPA
= P
s
. (18)
In order to balance the BER in the different numbers
of activated MIMO layers, solutions for the so far un-
known PA parameters are needed.
A simplified PA solution can be found when guar-
anteeing that the signal-to-noise-ratio at the detector
input is the same for all activated MIMO layers per
data block k. In this particular case, the following
condition should be ensured for the signal-to-noise ra-
tio at the detector input
ρ
(ℓ,k)
PA
=
U
(ℓ,k)
APA
2
U
2
R
= constant ℓ = 1, 2,··· ,L .
(19)
When assuming an identical detector input noise vari-
ance U
2
R
for each channel output symbol the before-
hand introduces Equal-SNR criteria requires the same
half vertical eye opening of each channel output sym-
bol
U
(ℓ,k)
APA
= constant ℓ = 1, 2,··· ,L . (20)
The power to be allocated to each activated MIMO
layer ℓ and transmitted data block k can be shown to
be calculated as follows:
p
ℓ,k
=
1
U
2
sℓ
·ξ
ℓ,k
·
L
L
∑
ν=1
1
U
2
sν
·ξ
ν,k
(21)
and guarantees for each channel output symbol (ℓ =
1,··· ,L) the same half vertical eye opening of
U
(ℓ,k)
APA
=
√
p
ℓ,k
·
q
ξ
ℓ,k
·U
sℓ
=
v
u
u
u
t
L
L
∑
ν=1
1
U
2
sν
ξ
ν,k
(22)
Together with the identical detector input noise vari-
ance for each channel output symbol, the above-
mentioned equal quality scenario is encountered.
Table 2: Investigated QAM transmission modes.
throughput layer 1 layer 2 layer 3 layer 4
8 bit/s/Hz 256 0 0 0
8 bit/s/Hz 64 4 0 0
8 bit/s/Hz 16 16 0 0
8 bit/s/Hz 16 4 4 0
8 bit/s/Hz 4 4 4 4
4 RESULTS
In this work a (4×4) MIMO system with transmitter-
side antennas correlation is studied.
In order to transmit at a fixed data rate while
maintaining the best possible integrity, i. e., bit-error
rate, an appropriate number of MIMO layers has to
be used, which depends on the specific transmission
mode, as detailed in Tab. 1.
The choice of fixed transmission modes regardless
of the channel quality can be justified when analyz-
ing the probability of choosing a specific transmis-
sion mode by using optimal bitloading (Wong et al.,
1999). As highlighted in Table 3 for uncorrelated
MIMO channels, it turns out that only an appropri-
ate number of MIMO layers has to be activated, e.g.,
the (16,4,4,0) QAM configuration. However, when
Table 3: Probability of choosing specific transmission
modes at a fixed data rate by using optimal bitloading
(10·log
10
(E
s
/N
0
) = 10 dB).
mode (64,4,0,0) (16,16,0, 0) (16,4, 4,0) (4, 4,4,4)
pdf 0.0116 0.2504 0.7373 0.0008
the correlation effect appears as illustrated in Table 4
for weakly correlated as well as in Table 5 for highly
correlated MIMO channels, the importance of using
layers with large singular values increases.
The optimization results when using PA are shown
in Fig. 11 and Fig. 12: The BER becomes minimal
in case of an optimized bit loading with highest bit
loading in the layer with largest singular values.
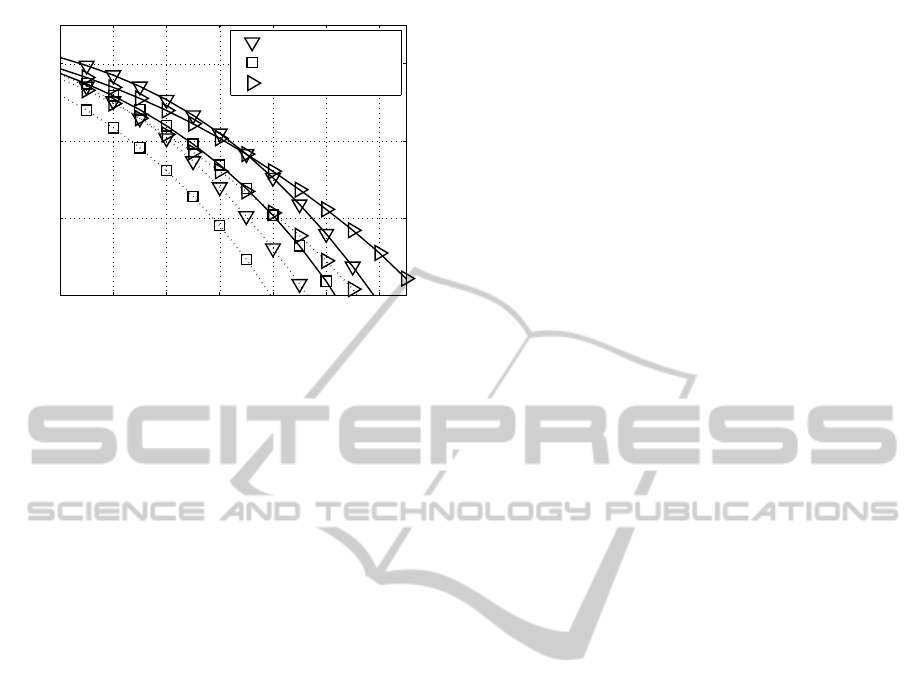
Fig. 13 and 14 show the MIMO system perfor-
mance when using fixed transmission modes and hav-
ing different degrees of correlation. As highlighted by
the BER curves, in case of high correlation only the
layers with the largest singular values should be used
for the data transmission.
WINSYS2013-InternationalConferenceonWirelessInformationNetworksandSystems
230
Table 4: Probability of choosing specific transmission
modes in weakly correlated MIMO channels at a fixed data
rate by using optimal bitloading (10 · log
10
(E
s
/N
0
) = 10
dB).
mode (64,4,0,0) (16,16,0, 0) (16,4, 4,0) (4, 4,4,4)
pdf 0.1274 0.3360 0.5366 0.0
Table 5: Probability of choosing specific transmission
modes in strongly correlated MIMO channels at a fixed data
rate by using optimal bitloading (10 · log
10
(E
s
/N
0
) = 10
dB)
mode (64,4,0,0) (16,16,0, 0) (16,4, 4,0) (4, 4,4,4)
pdf 0.8252 0.1087 0.0605 0.0
12 14 16 18 20 22 24
10
−8
10
−6
10
−4
10
−2
10 ·lg(E
s
/N
0
) (indB) →
bit-error rate →
(256,0,0,0) QAM
(64,4,0,0) QAM
(16,16,0,0) QAM
(16,4,4,0) QAM
(4,4,4, 4) QAM
Figure 11: BER with optimal PA (dotted line) and without
PA (solid line) when using the transmission modes intro-
duced in Tab. 2 and transmitting 8 bit/s/Hz over frequency
non-selective (4×4) MIMO channels (d
λ
= 1, φ = 30
◦
and
σ
ξ
= 1,0) with weak transmitter-side correlation.
5 CONCLUSIONS
This paper has shown the correlation coefficients
characterization of transmitter-side correlated MIMO
channels as well as their performance on the pres-
ence of correlation. The correlation coefficients de-
pend on paths physical parameters describing the an-
tennas arrangement. Antennas spacing, angle of de-
parture and the scattering angle affect the paths cor-
relation degree and hence the MIMO performance.
The singular-value decomposition (SVD) is a signal
processing technique that having perfect channel state
information at both the transmit and receive sides in-
volves pre- and post-processing at the transmit and
receive sides respectively which converts the MIMO
channel into independent layers characterized by the
layer gain given by the singular values. Antennas cor-
12 14 16 18 20 22 24
10
−8
10
−6
10
−4
10
−2
10 ·lg(E
s
/N
0
) (indB) →
bit-error rate →
(256,0,0,0) QAM
(64,4,0,0) QAM
(16,16,0,0) QAM
(16,4,4,0) QAM
(4,4,4, 4) QAM
Figure 12: BER with optimal PA (dotted line) and without
PA (solid line) when using the transmission modes intro-
duced in Tab. 2 and transmitting 8 bit/s/Hz over frequency
non-selective (4×4) MIMO channels (d
λ
= 1/4, φ = 30
◦
and σ
ξ
= 1,0) with strong transmitter-side correlation.
12 14 16 18 20 22 24
10
−8
10
−6
10
−4
10
−2
10 ·lg(E
s
/N
0
) (indB) →
bit-error rate →
no Correlation
weak Correlation
strong Correlation
Figure 13: BER with optimal PA (dotted line) and without
PA (solid line) when using the (16,16,0,0 QAM transmis-
sion mode and transmitting 8 bit/s/Hz over frequency non-
selective (4×4) MIMO channels with different degrees of
correlation.
relation affects the SVD dealing to dispersed singular
values: some with large values and others with low
values, in contrast to the ideal case. This singular val-
ues dispersion yields a poor MIMO channel perfor-
mance due to those layers with low singular values
which present a low reliability. The overall anten-
nas correlation effect is described by the correlation
matrix which relates the channel uncorrelated matrix
to the correlated one. The analysis has demonstrated
that the representation of the PDF of the ratio be-
tween the smallest and the largest singular values pro-
vides a useful mean to predict the channel behavior
and the appropriateness of activating all the MIMO
layers. Besides, the singular values CCDF gives rel-
evant information concerning the probability of ob-
Modulation-modeandPowerAssignmentinSVD-assistedMIMOSystemswithTransmitter-sideAntennasCorrelation
231
12 14 16 18 20 22 24
10
−8
10
−6
10
−4
10
−2
10 ·lg(E
s
/N
0
) (indB) →
bit-error rate →
no Correlation
weak Correlation
strong Correlation
Figure 14: BER with optimal PA (dotted line) and without
PA (solid line) when using the (64,4,0, 0 QAM transmis-
sion mode and transmitting 8 bit/s/Hz over frequency non-
selective (4×4) MIMO channels with different degrees of
correlation.
taining predominant (strong and weak) layers and in-
fer the MIMO channel behaviour. The best perfor-
mance is obtained when all CCDF coincide (are the
same) or are quite close. CCDF curve dispersion re-
veals the existence of predominant layer lowering the
MIMO performance. Additionally, in order to miti-
gate correlation effects the investigation has analyzed
the effect of bit and transmit power allocation along
the various MIMO layers as techniques for improv-
ing channel performance even in the presence of an-
tennas correlation. Regarding the power allocation,
a basic technique has been applied in order to obtain
the same quality along the different activated layers,
i.e., the same SNR at each detector. This technique
allows obtaining a higher performance. Moreover, bit
loading has been studied through the description of
some profiles (transmission modes) dealing to differ-
ent constellation per layer (bit per symbol interval)
but maintaining the overall transmission rate. A re-
markable conclusion is that activating all the MIMO
layers not necessarily provides the best performance
as highlighted in the results where the transmission
modes (64,4,0, 0) and (16,16, 0,0) present the best
performance. In order to highlight the importance of
this fact the probability of using each transmission
mode was analyzed and the previous conclusion was
remarked.
REFERENCES
Ahrens, A. and Lange, C. (2008). Modulation-Mode and
Power Assignment in SVD-equalized MIMO Sys-
tems. Facta Universitatis (Series Electronics and En-
ergetics), 21(2):167–181.
Cano-Broncano, F., Benavente-Peces, C., Ahrens, A.,
Ortega-Gonzalez, F. J., and Pardo-Martin, J. M.
(2013). Analysis of MIMO Systems with Transmitter-
Side Antennas Correlation. In International Con-
ference on Pervasive and Embedded Computing
and Communication Systems (PECCS), Barcelona
(Spain).
Haykin, S. S. (2002). Adaptive Filter Theory. Prentice Hall,
New Jersey.
Kalet, I. (1987). Optimization of Linearly Equalized
QAM. IEEE Transactions on Communications,
35(11):1234–1236.
K¨uhn, V. (2006). Wireless Communications over MIMO
Channels – Applications to CDMA and Multiple An-
tenna Systems. Wiley, Chichester.
Lee, W.-Y. (1973). Effects on Correlation between two Mo-
bile Radio Base-Station Antennas. IEEE Transactions
on Vehicular Technology, 22(4):130–140.
Mutti, C. and Dahlhaus, P. (2004). Adaptive Power Load-
ing for Multiple-Input Multiple-Output OFDM Sys-
tems with Perfect Channel State Information. In Joint
COST 273/284 Workshop on Antennas and Related
System Aspects in Wireless Communications, pages
93–98, Gothenburg.
Oestges, C. (2006). Validity of the Kronocker Model for
MIMO Correlated Channels. In Vehicular Technology
Conference, volume 6, pages 2818–2822, Melbourne.
Proakis, J. G. (2000). Digital Communications. McGraw-
Hill, Boston.
Salz, J. and Winters, J. H. (1994). Effect of Fading Correla-
tion on adaptive Arrays in digital Mobile Radio. IEEE
Transactions on Vehicular Technology, 43(4):1049–
1057.
Shiu, D., Foschini, G., Gans, M., and Kahn, J. (2000). Fad-
ing Correlation and its Effect on the Capacity of Mul-
tielement Antenna Systems. IEEE Transactions on
Communications, 48(3):502–513.
Wong, C. Y., Cheng, R. S., Letaief, K. B., and Murch, R. D.
(1999). Multiuser OFDM with Adaptive Subcarrier,
Bit, and Power Allocation. IEEE Journal on Selected
Areas in Communications, 17(10):1747–1758.
Zhou, Z., Vucetic, B., Dohler, M., and Li, Y. (2005). MIMO
Systems with Adaptive Modulation. IEEE Transac-
tions on Vehicular Technology, 54(5):1073–1096.
WINSYS2013-InternationalConferenceonWirelessInformationNetworksandSystems
232
