
Minimizing the Inter-vehicle Distances of the Time Headway Policy for
Platoon Control on Highways
Alan Ali
1,2
, Gaetan Garcia
2
and Philippe Martinet
1,2
1
IRCCYN, Ecole Central de Nantes, rue No ¨e, Nantes, France
2
Ecole Central de Nantes, rue No ¨e, Nantes, France
Keywords:
Platoon, Control, Time Headway, Constant Spacing, String Stability, Inter-vehicle Distance, Highways.
Abstract:
Heavy traffic on highways requires the optimization of inter-distances between vehicles in order to reach
time performance and to provide safety solution in transport. Variable spacing and constant spacing are the
two policies for the longitudinal control of platoon. Variable spacing doesn’t require a lot of data (position,
speed...) from other vehicles, and string stability using only on-board information is obtained. However, inter-
vehicle distances are very large, and hence traffic density is low. Constant spacing can offer string stability with
high traffic density, but it requires at least data from the leader. In this paper, a novel expression of the variable
spacing policy has been proposed. It is effective to decrease the distance between the cars, to become nearly
equal to the constant spacing policy. It also enables increasing the string stability and the robustness of the
control regarding to unmodeled lags, and it can avoid control torque saturation. This novel approach doesn’t
require heavy communication between the cars. The new control law has been evaluated by simulation with
perfect system using Matlab, and with imperfect system using TORCS. The good results have demonstrated
the effectiveness of the novel approach.
1 INTRODUCTION
Nowadays, traffic congestion, pollution, and people
safety problems become more and more important
due to the explosion in the number of cars.
Treatments of these problems on highways dif-
fer from those in urban areas. In highways environ-
ment and normal condition, we usually travel at high
speeds, cars move faster, the roads are less curved and
there are less obstacles compared with the urban ar-
eas.
Some proposed ideas impose some changes to the
infrastructure (automatic speed limits, roads monitor-
ing, reversible lanes...). Others ideas depend on the
automated vehicles to increase the traffic density and
to avoid the oscillation. Driving in platoon has many
advantages, It increases traffic density and security,
at the same time it decreases fuel consumption and
driver tiredness (Ricardo, 2009).
From the modeling and control point of view, it is
possible to decouple the longitudinal behavior from
lateral one, considering that road have low curva-
ture, or using techniques like chained system theory
(Thuilot and Martinet, 2004). Lateral control can be
done using different modalities like 3D laser (like it
is used in the famous Google car), magnetic markers
(PATH project), vision sensor (Royer et al., 2005)...
So in highways environment, it is common to con-
centrate on longitudinal behavior including modeling
and control.
Platoon models can be found in (Swaroop, 1997)
any communications to full communications between
all the vehicles. Others has modeled the platoon us-
ing physics-inspired models, (Franck et al., 2004)
treated the platoon as multi agents system, the agents
(vehicles) interact according to physical phenom-
ena or mimicking animal interaction behaviors, oth-
ers modeled the interaction as virtual spring-dumper
(Yanakiev and Kanellakopoulos, 1996), or as Newton
forces (Khatir and Davison, 2004).
String stability means that the errors must not am-
plify as they propagate through the platoon, and the
errors must have the same sign to avoid collision, The
definition is given in the time domain in (Swaroop,
1997) and in frequency domain in (Rajamani, 2006).
Local control depends on data from adjacent ve-
hicles, while global control depends on data at least
from leader. In local control, the car is totally au-
tonomous, it does not require sophisticated sensors,
and can be used in all environments, but trajectory
417
Ali A., Garcia G. and Martinet P..
Minimizing the Inter-vehicle Distances of the Time Headway Policy for Platoon Control on Highways.
DOI: 10.5220/0004497704170424
In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2013), pages 417-424
ISBN: 978-989-8565-71-6
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)
tracking and inter-vehicles distance keeping is not
very accurate. In the other hand the global control are
more accurate, but it needs more sophisticated sen-
sors, and sometimes it needs adaptation in the envi-
ronment where we use it, and finally it needs very re-
liable communication systems.
The spacing between vehicles differ according to
two control policies (Constant spacing and variable
spacing). Variable spacing, usually, doesn’t require
a lot of data from other vehicles, whats more, it can
ensure string stability just by using on-board informa-
tion (Ioannou and Chien, 1993), but the inter-vehicle
distances is very large (function of velocity), and
hence traffic density is low. Constant spacing can get
string stability with high traffic density, but it requires
inter-vehicle communications.
Constant Time Headway (CTH) is the simplest
and most common variable spacing policy (Swaroop
and Rajagopal, 2001; Yanakiev and Kanellakopou-
los, 1996). Variable time headway can vary linearly
with the velocity, with relative velocity (Yanakiev and
Kanellakopoulos, 1995), or even with the vehicle dy-
namics and the road conditions (Huppe et al., 2003).
In this work, we will concentrate on the longitu-
dinal control of platoons in highways. We will pro-
pose a new modification to the time headway pol-
icy, develop the corresponding dynamic control law,
study the stability and the control robustness of the
platoon and demonstrate the effectivness of the novel
approach. The new control law will be a mixture of
local and global decentralized control. Security will
not be discussed in this paper.
The paper is organized as follows. Section 2 will
describe the vehicle and platoon models. The control,
string stability, and control robustness will be pre-
sented in section 3. Section 4 will explain the simula-
tions results obtained with Matlab and TORCS (The
Open Racing Car Simulator) (Onieva et al., 2009). Fi-
nally, section 5 will discuss the most important advan-
tages of the proposed approach, and we will make a
comparison with other existing approaches.
2 MODELING AND CONTROL
As we are dealing with highways with small curva-
ture, in this paper we will only address the longitudi-
nal control:
2.1 Longitudinal Dynamic Model
of the Vehicle
According to Newton’s law, we can write the dynamic
equation (Sheikholeslam and Desoer, 1989) of the i-th
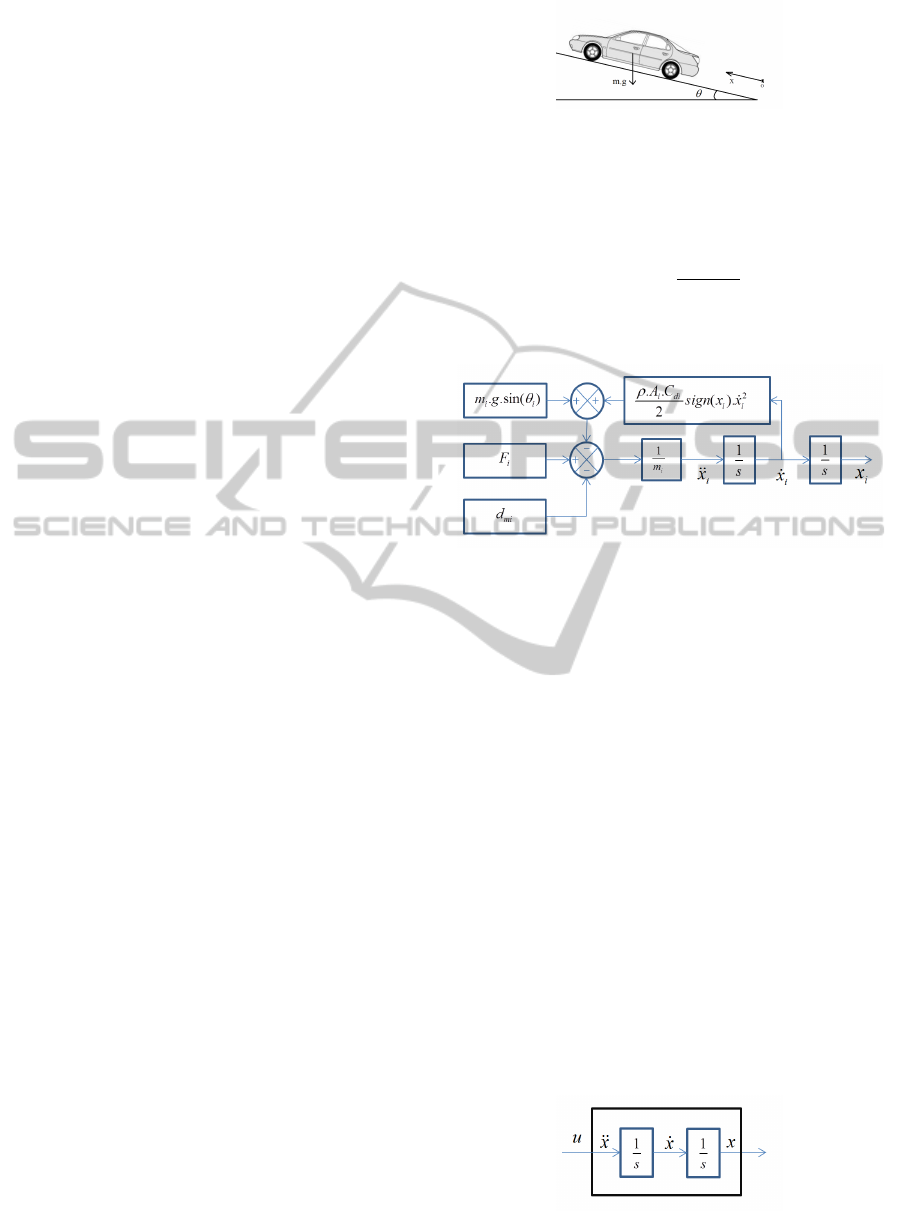
Figure 1: i-th car.
vehicle in the platoon shown in figure (1) as:
m
i
¨x
i
= F
i
+ F
i,g
+ F
i,aero
+ F
i,drag
m
i
¨x
i
= F
i
−m
i
g sin(θ) −
ρ A
i
C
di
2
˙x
2
i
sgn( ˙x
i
) −d
mi
(1)
which can be represented in figure (2):
Figure 2: Dynamical car model.
where:
• x
i
: Position of the i-th vehicle in X axis.
• F
i
: Force produced by the i-th vehicle engine.
• F
i,g
, F
i,aero
, F
i,drag
: Gravitational, aero dynamical
and Mechanical drag force respectively.
• g: Acceleration of gravity.
• θ: Angle between the road surface and a horizon-
tal.
• ρ: Specific mass of air, A
i
, C
di
Cross-sectional
area and drag coefficient of the i-th vehicle.
• d
mi
: Mechanical drag of the i-th vehicle
We can use exact linearization to linearize the previ-
ous system to obtain a linear model of the car longi-
tudinal dynamics by taking:
F
i
= −F
i,g
−F
i,aero
−F
i,drag
+ m
i
u
i
(2)
Then, we get: where u
i
is the new command input
for the linearized system show in figure (3).
Figure 3: Linearized car model.
¨x
i
= u
i
(3)
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
418
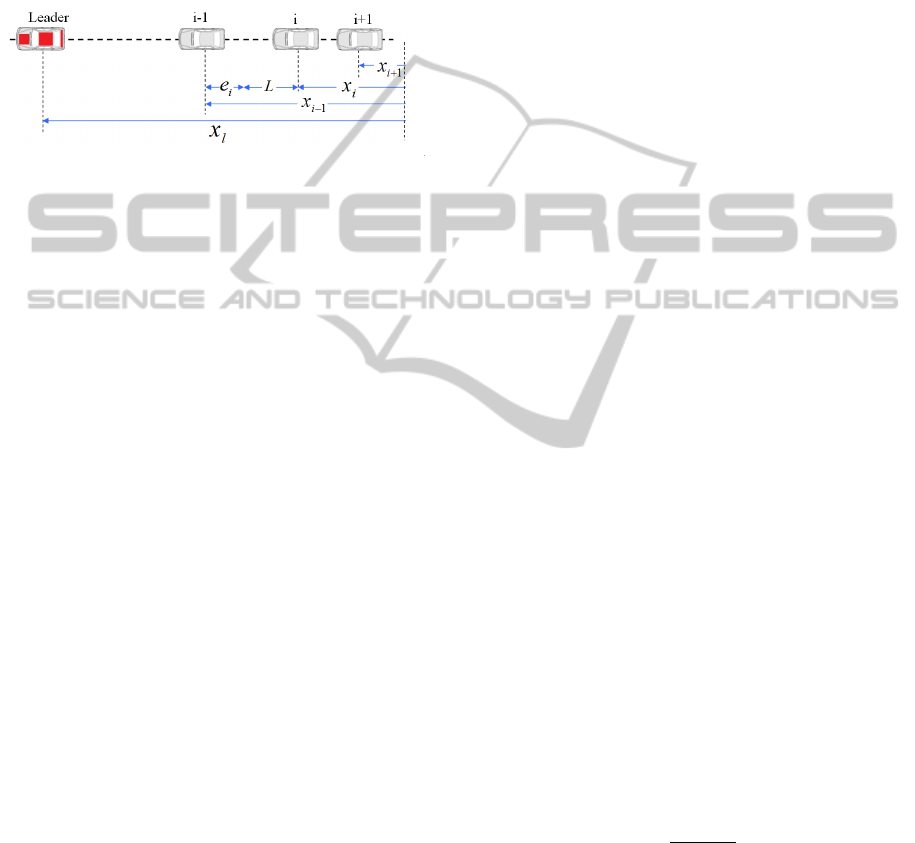
2.2 Platoon Definitions
Figure (4) shows a platoon which consists of N vehi-
cles moving at the same speed v
d
with a desired in-
ter distance L between each set of two vehicles. The
leader of the platoon can be driven by a human or au-
tonomously. The followers are controlled to maintain
a desired inter-distance.
Figure 4: Platoon.
We define the constant spacing error of the ith vehicle
by:
e
i
= ∆X
i
−La (4)
where
• ∆X
i
= x
i−1
−x
i
: real spacing between i-th car and
its predecessor (i-1-th car).
• x
i
: position of i-th vehicle.
• La = L + D
min
: actual desired distance.
• L: desired inter-vehicle distance (bumper-to-
bumper).
• D
min
: minimum distance between two vehicles to
prevent bumper-to-bumper collision, equal or big-
ger than vehicle’s length.
In the following, we will assume a point mass
model for the vehicles and we will ignore D
min
, so
e
i
= ∆X
i
−L. The kinematic evolution of the spacing
error is given by:
˙e
i
= ˙x
i−1
− ˙x
i
= v
i−1
−v
i
where v
i
represents the velocity of the i-th vehicle.
3 PLATOON CONTROL
AND STABILITY
3.1 Control Objectives
The main objectives of the control law are to:
1. Keep the inter-vehicle distance equal to L, and
to make all vehicles move at the same speed so
˙e
i
= 0.
2. Assure the string stability of the platoon (the
spacing error does not increase as it propagates
through the platoon).
3. Increase the traffic density.
4. Keep the system stable in case of total loss of
communication.
5. Accommodate the instability produced by the ac-
tuation and sensing lags (robustness).
3.2 Control Law
In constant spacing control, the control law will make
e
i
→0 so the inter-vehicle distance will become equal
to L, but this requires, at least, information from the
leader to assure the string stability of the platoon and
robustness.
In time headway policy, a new term is added to the
previous error, which will eliminate the communica-
tion with the leader and increase the string stability.
A new spacing error is defined as:
δ
i
= e
i
−h v
i
= ∆X
i
−L −h v
i
In this case the control law makes δ
i
→ 0, so the
steady state of the inter-vehicle distance will be equal
to ∆X
i
= L + h v
i
, which is proportional to vehicle
speed and can become very large when the vehicle
travels at high speed.
Adding the time headway term (h v
i
) improves the
stability. This improvement is not due to enlarging
inter-vehicle distance, but to the fact that it is a func-
tion of the velocity. So, the main idea of this paper
is to propose a novel spacing error defining the time
headway term proportional to the difference between
the velocity of the vehicle and some value V shared
between all other vehicles in the platoon. We will dis-
cuss later how to set the parameter V . In this case, we
define the novel error as:
δ
i
= e
i
−h (v
i
−V) = ∆X
i
−L −h (v
i
−V)
where V is the same velocity value shared between
all the vehicles at the same sampling time.
The new control law is defined by:
u
i
=
˙e
i
+ λ δ
i
h
which is represented in figure (5) for the i-th vehi-
cle.
The dynamic error becomes:
h ¨e
i
+ (1 + λ h) ˙e
i
+ λ e
i
= ˙e
i−1
+ λ e
i−1
(5)
For the first car, we have:
h ¨e
1
+ ˙e
1
+ λ e
1
= h ¨x
L
+ λ ( ˙x
1
−V) (6)
MinimizingtheInter-vehicleDistancesoftheTimeHeadwayPolicyforPlatoonControlonHighways
419

Figure 5: Control scheme of the i-th vehicle.
where ¨x
L
is leader acceleration.
Then, at equilibrium it comes:
e
i
= e
i−1
, i = 1...N
and
e
1
= h ¨x
L
+ λ ( ˙x
1
−V) = h u
L
+ λ ( ˙x
1
−V)
where u
L
is the leader input.
So we get :
e
1
= e
2
= ... = e
N
= h u
L
+ λ ( ˙x
1
−V) (7)
To verify the effectiveness of the new law, the
string stability of the platoon and the robustness of
this control law must be analyzed.
3.3 String Stability Analysis
General string stability definition is given in (Swa-
roop, 1997), which means that, all the states are lim-
ited if the initial states (position and velocity errors)
are limited and summable.
A sufficient condition for string stability is given
in (Rajamani, 2006):
k
e
i
k
∞
≤
k
e
i−1
k
∞
which means
that the spacing error must not increase as it propa-
gates through the platoon. To verify this condition,
the spacing error propagation transfer function is de-
fined by:
G
i
(s) =
e
i
(s)
e
i−1
(s)
A sufficient condition for string stability is given by:
k
G
i
(s)
k
∞
≤ 1 and g
i
(t) > 0 i = 1, 2..N (8)
where g
i
(t) is the error propagation impulse response
of the i-th vehicle.
So to verify the string stability of a platoon using
the novel spacing error, the spacing error propagation
transfer function H(s) must be computed:
G
i
(s) =
e
i
(s)
e
i−1
(s)
=
1
h.s + 1
(9)
After some development, it can be shown that:
|
G
i
(ω)
|
=
1
√
h
2
ω
2
+1
≤ 1
g
i
(t) =
e
−t
h
h
> 0
(10)
In other words, at all frequencies, the spacing er-
rors do not increase as they propagate through the pla-
toon, so the system is string stable.
3.4 Robustness to unmodeled Actuation
and Sensing Lags
All realistic systems have actuation and sensing lags.
Usual approximate models of the non linear actuation
systems ignore some actuation dynamics, this unmod-
eled dynamics may produce lag in the actuator re-
sponse. Sensing lags is due to the sampling time or
filtering time. So we have to take the problem of the
lag into consideration and verify the robustness of the
control system to unmodeled actuation and sensing
lags, which can be taken in consideration as follows
(Swaroop and Rajagopal, 2001):
¨x
i
= u
c,i
τ ˙u
c,i
+ u
c,i
= u
i
where τ is a small unknown constant which represents
lag time constant, u
c,i
is the real acceleration of the i
th vehicle, and u
i
is the control law. All the sensing
and actuation lags in the system have been modeled
in the second equation in an aggregate manner.
The new spacing error propagation transfer func-
tion becomes:
G
p
(s) =
e
i
(s)
e
i−1
(s)
G
p
(s) =
s + λ
τ h s
3
+ h s
2
+ (1 + λ.h) s + λ
(11)
The subscript p in the transfer function H
p
(s) has
been used to indicate that it describes the error prop-
agation transfer function for the disturbed system. To
assure the string stability for this disturbed system,
|
H
p
( j.ω)
|
≤ 1 for all ω must be verified. So it comes:
ω
2
+ λ
2
≤ (λ −h ω
2
)
2
+ (1 + λ h −τ h ω
2
)
2
ω
2
which is equivalent to :
τ
2
h
2
ω
4
+ (h
2
−2 τ h (1 + λ h)) ω
2
+ λ
2
h
2
≥ 0
The above inequality holds only if the discrimi-
nant is negative or if the coefficient of ω
2
is positive.
Both conditions are satisfied (Swaroop, 1997) only if
τ ≤
h
2
(12)
This means the sum of all unmodeled lags must be
less than or equal to half the time headway employed.
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
420

3.5 Unmodeled Vehicle Motor and
Static Spacing Error
Equation 7 shows that the static spacing error is the
same for all the vehicles, and it is equal to the leader
input u
L
multiplied by h, in addition to λ.( ˙x
1
−V ).
The second term, as it will become equal to zero at
equilibrium, will be ignored. So the steady state error
becomes:
e
1
= e
2
= ... = e
N
= h u
L
At equilibrium all the vehicles have the same ve-
locity v
d
. In this case the input u
L
of the double in-
tegrator model of the leader, ¨x
L
= u
L
, must be zero,
hence the steady state spacing error will become equal
to zero.
But as the motor model has not been taken into
account, the actual car model will be not equivalent
strickly to a double integrator. For instance, if the
model for vehicle velocity is given by:
V
L
(s)
u
L
(s)
=
K
m
1 + T
m
s
in this case the system input will not be zero at equi-
librium. It will be equal to u
L
=
V
d
K
m
, so the spacing
error will be given by the following:
e
1
= e
2
= ... = e
N
=
h V
d
λ K
m
(13)
Obviously, the model of the motor must be defined
and take into account. It was out of scope of this pa-
per.
4 SIMULATIONS
The control law have been checked under Matlab, and
using TORCS to get more realistic results (as it takes
more phenomena into account) and to have visual out-
put when applying the novel spacing error.
All the simulations will be done on a straight road
in Matlab and with small curvatures in TORCS. The
desired speed of the leader of the platoon is changed
three times (see figure 6) to check the transit response
and the stability of the platoon. The desired inter-
vehicle distance (bumper-to bumper distance, so we
omit all the cars lengths from all following figures)
is fixed to L = 5 m. We have chosen λ = 1, h = 1
which give good compromise between stability and
inter-vehicle distance.
Figure 6: Leader’s velocity profile.
4.1 Matlab Results
The linearized car model given in equation (3) has
been used in simulation, which is ideal situation to
check the validity of the control law without any dis-
turbances.
Figure 7 shows the reduction in inter-vehicle dis-
tance using the novel control law, compared to the
classical time headway control law. Inter-vehicle dis-
tances are greatly reduced and become equal to the
desired L at equilibrium. In addition, to assure the pla-
toon string stability during the dynamic changes, the
desired distance changes. The system is string stable
(the error e
i
decreases as i increases).
Figure 7: Inter-vehicle distance using CTH law and the new
control law (in Matlab).
Figure 8: Inter-vehicle distance after taking lags into ac-
count.
MinimizingtheInter-vehicleDistancesoftheTimeHeadwayPolicyforPlatoonControlonHighways
421

Then, robustness of the new control law by taking
the actuation and sensing lags into account has been
checked. A lag time equal to τ = 0.25 s satisfying
the condition given in equation (12) has been chosen,
and the corresponding results are given by the figure
8: the system is still string stable.
As said before, the car model used under Matlab
is very simple (i.e. ideal model). To be more realistic
and to take more physical phenomena, new simulation
have done done using TORCS environment.
4.2 TORCS Results
The Open Racing Car Simulator (Onieva et al., 2009)
is one of the most popular car racing simulators. It
is written in C++ and is available under GPL license
from its web page. TORCS presents several advan-
tages for academic purposes, such as:
1. It lies between advanced simulators, like recent
commercial car racing games, and a fully cus-
tomizable environment, like the ones typically
used by computational intelligence researchers for
benchmark purposes.
2. It features a sophisticated physics engine (aerody-
namics, fuel consumption, traction...) as well as
a 3D graphics engine for the visualization of the
races.
3. It was not conceived as a free alternative to com-
mercial racing games, but it was specifically de-
vised to make it as easy as possible to develop
your own controller.
Same simulations as under Matlab have been per-
formed, but using a road with small curvatures, taking
the car model in equation (1), linearized using equa-
tion (2). As explain in the subsection 3.5, the motor
model has not been taken into account in the novel
control law.
In figure 9, the same results have been obtained in
TORCS as in Matlab concerning the stability and re-
duction of the inter-vehicle distances. It can be seen
that the inter-vehicle distance at equilibrium isn’t ex-
actly equal to the desired distance L=5m, as it was
explain in subsection 3.5.
In the same way, immunity of the control law to
actuation and sensing lags has been evaluated: the
platoon remains string stable even if actuation and
sensing lags equal to τ = 0.25 s have been added. The
results are shown in figure 10, where the system is
string stable. So, the novel control is robust to lag
errors.
Again we tried to check the immunity of the con-
trol law to actuation and sensing lags, we also found
here that the platoon still string stable even if we add
Figure 9: Inter-vehicle distances using CTH law and our
law (in TORCS).
Figure 10: Inter-vehicle distances after taking lags into ac-
count.
actuation and sensing lags equal to τ = 0.25 s. The
results is shown in figure(10), where we can see that
the system is string stable, so the control is robust to
lag errors.
5 DISCUSSION
the proposed approach greatly reduces the inter-
vehicle distances required to assure the stability. This
is obtained by making the distance proportional, not
to velocity, but to the difference between the vehicle
velocity and a common velocity value shared by all
vehicles of the platoon.
5.1 Advantages and Comparison
Using the new spacing error and the correspond-
ing new control law, the advantages are the following:
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
422

String Stability: The propagation function H(s), cor-
responding to the new control law, is not related to
V , so its value will not affect the platoon stability. It
can be noticed, that it is exactly the same propagation
transfer function for the classical time headway spac-
ing policy (Swaroop and Rajagopal, 2001; Yanakiev
and Kanellakopoulos, 1996), so with this modifica-
tion the system remains string stable.
Inter-vehicle Distance: The most important effect of
the proposed modification is on the inter-vehicle dis-
tances. At equilibrium it comes ∆X
i
= L +h (v
L
−V ),
by choosing V = v
L
the inter-vehicle distance be-
comes ∆X
i
= L, and during dynamic changes the
inter-vehicle distance becomes ∆X
i
= L + h (v
i
−V
L
).
The inter-vehicle distance has been decreased
from ∆X
i
= L + h v
i
(which might be very large at
high speeds) in the case of the classical time headway
policy (Swaroop and Rajagopal, 2001; Xiao and Gao,
2011), to become ∆X
i
= L + h (v
i
−V ) (which is ex-
actly equal to L at equilibrium and a little bit larger
than it during transient phase). So during transient
phase, the length of the platoon will be little different
from the length of a platoon using constant spacing
policy (Yanakiev and Kanellakopoulos, 1996; Swa-
roop, 1997).
Another important thing is the effect of increas-
ing the h parameter (which has many positive effects
on stability...). In CTH it has a big negative effect on
the inter-vehicle distance; as this distance increases
proportionally to h, and hence the traffic density de-
creases. In our case, the inter distance is also pro-
portional to h but with a smaller coefficient (v
i
−V ),
so the inter distance changes will be smaller than the
changes in CTH.
Collision: it is very clear that the possibility of col-
lision between the vehicles is increased, as the inter
distance between them is reduced. The problem of
collision can be addressed separately from the prob-
lem of stability by adding a new term for the security.
Communication: adding V to the equation means
that data must be exchanged. The amount of ex-
changed data between the vehicles by updating the
value of V every many sample times (depending on
the rate of changes of the platoon velocity) can be re-
duced changing the value smoothly to avoid jumps in
the inter distance.
Stability without Communication: The string sta-
bility can be preserved even if the communication
with the leader is totally lost, by switching to the clas-
sical time headway policy V = 0 (full autonomous
mode). In this case there is no need to communicate
with the leader. So this law can keep the platoon sta-
ble even if communication is lost, on the contrary, it
has been proved that the constant spacing policy can
not be string stable, for homogeneous platoon with
homogeneous control (all the gains are equals), with-
out using any information from other vehicles (Seiler
et al., 2004).
Hand checking protocol, between the leader and
other vehicles, is very important to detect any loss of
communication. If any loss is detected the leader will
transmit an order to all vehicles to switch to full au-
tonomous mode V = 0, while the vehicle, which has
lost the communication, will automatically switch to
this mode.
Robustness: The condition for stability in the pres-
ence of lags τ has been found:
h ≥ 2 τ
It is difficult to increase h in the classical time head-
way policy. But in the novel approach, it can be eas-
ily increased to accommodate the instability produced
even by large lags, without large changes to the inter-
vehicle distance. On the other hand, some simple con-
stant spacing laws are not totally robust or only stable
for small values of lags (Swaroop, 1997).
Control torque Saturation: The control effort is in-
versely proportional to the desired headway time h
(Swaroop and Rajagopal, 2001), so decreasing h may
saturate the brake and engine torques. For the clas-
sical time headway, it is not possible to increase h
very much, but in the novel approach, it can be in-
creased: this will prevent the control effort saturation,
with only slight increase in the inter-vehicle distance.
Simplicity and Type of required Data: The new
control has the same simplicity of CTH law. It use
the same variables of CTH in addition to a low rate
updating of common speed (may be the leader or pla-
toon speed). This last variable is the only difference
with the classical time headway policy, while the con-
stant spacing policy is always more complicated, as
it may need the acceleration or other information, at
least from the leader.
5.2 Supervision of the Parameter V
As seen previously, the unique condition when adding
V to keep the platoon stable is to make it the same for
all the vehicles at the same sample time. So, any value
for V (e.g. leader’s velocity, the medium velocity of
the platoon or the minimum velocity in the platoon...)
can be chosen.
To increase the security and to prevent the colli-
sion, one can choose V = min(v
Leader
, v
1
, v
2
...., v
N
).
This will always make h.(v
i
−V ) > 0. In that case, the
inter vehicle distance becomes ∆X
i
= L+h (v
i
−V ) >
L but of course it will enlarge the inter-vehicle dis-
tance during velocity changes.
MinimizingtheInter-vehicleDistancesoftheTimeHeadwayPolicyforPlatoonControlonHighways
423

Changing V quickly may has negative effect on
the control and hence on the performance. So V must
not change quickly, or it must be interpolated to get
smooth changes.
6 CONCLUSIONS
In this paper, the design of longitudinal control of
platoons in highways has been addressed. A novel
modification of CTH control law has been proposed
in order to improve the large inter-vehicle distance
(the main shortcoming of this control law). It also
enables to increase the stability, the robustness, and
avoid torque saturation. These benefits are obtained
without the need for high rate data from other vehi-
cles. Moreover, the platoon can still be stable even if
the communication link is totally lost. All this results
have been tested under Matlab and TORCS to check
the validity of the novel approach.
This novel approach will enable us to apply the
CTH law in real applications because the inter-vehicle
distance becomes nearly equal to constant spacing
policy.
REFERENCES
Franck, G., Vincent, C., and Francois, C. (2004). A re-
active multi-agent system for localization and track-
ing in mobile robotics. In Tools with Artificial Intel-
ligence, 2004. ICTAI 2004. 16th IEEE International
Conference, pages 431 – 435.
Huppe, X., de Lafontaine, J., Beauregard, M., and Michaud,
F. (2003). Guidance and control of a platoon of vehi-
cles adapted to changing environment conditions. In
Systems, Man and Cybernetics, 2003. IEEE Interna-
tional Conference, volume 4, pages 3091 – 3096 vol.4.
Ioannou, P. and Chien, C. (1993). Autonomous intelligent
cruise control. Vehicular Technology, IEEE Transac-
tions on, 42(4):657 –672.
Khatir, M. and Davison, E. (2004). Decentralized control
of a large platoon of vehicles using non-identical con-
trollers. In American Control Conference, 2004. Pro-
ceedings of the 2004, volume 3, pages 2769 –2776
vol.3.
Onieva, E., Pelta, D., Alonso, J., Milanes, V., and Perez,
J. (2009). A modular parametric architecture for the
torcs racing engine. In Computational Intelligence
and Games, 2009. CIG 2009. IEEE Symposium on,
pages 256 –262.
Rajamani, R. (2006). Vehicle dynamics and control.
Springer Science, 1 edition.
Ricardo (2009). Cars that drive themselves can become
reality within ten years. http://www.ricardo.com/en-
GB/News–Media/Press-releases/News-
releases1/2009/Cars-that-drive-themselves-can-
become-reality-within-ten-years/.
Royer, E., Bom, J., Dhome, M., Thuilot, B., Lhuillier, M.,
and Marmoiton, F. (2005). Outdoor autonomous nav-
igation using monocular vision. In Intelligent Robots
and Systems, 2005. (IROS 2005). 2005 IEEE/RSJ In-
ternational Conference, pages 1253–1258.
Seiler, P., Pant, A., and Hedrick, K. (2004). Disturbance
propagation in vehicle strings. Automatic Control,
IEEE Transactions on, 49(10):1835 – 1842.
Sheikholeslam, S. and Desoer, C. A. (1989). Longitudinal
control of a platoon of vehicles i: Linear model. Tech-
nical Report UCB/ERL M89/106, EECS Department,
University of California, Berkeley.
Swaroop, D. (1997). String stability of interconnected sys-
tems: An application to platooning in automated high-
way systems. UC Berkeley: California Partners for
Advanced Transit and Highways (PATH).
Swaroop, D. and Rajagopal, K. (2001). A review of con-
stant time headway policy for automatic vehicle fol-
lowing. In Intelligent Transportation Systems, 2001.
Proceedings. 2001 IEEE, pages 65 –69.
Thuilot, B. Bom, J. M. F. and Martinet, P. (2004). guid-
ance of an urban electric vehicle relying on a kine-
matic gps sensor. In 5th IFAC Symposium on Intelli-
gent Autonomous Vehicles (IAV04), Lisboa (Portugal),
July 2004.
Xiao, L. and Gao, F. (2011). Practical string stability of
platoon of adaptive cruise control vehicles. Intelli-
gent Transportation Systems, IEEE Transactions on,
12(4):1184 –1194.
Yanakiev, D. and Kanellakopoulos, I. (1995). Variable time
headway for string stability of automated heavy-duty
vehicles. In Proc. 34th IEEE CDC, pages 4077–4081.
Yanakiev, D. and Kanellakopoulos, I. (1996). A simplified
framework for string stability analysis in ahs. In In
Proceedings Of The 13th IFAC World Congress, pages
177–182.
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
424
