Fuzzy Model-based Algorithm for 3-D Bone Tumour Analysis

Joanna Czajkowska

Media Systems Group, Institute for Vision and Graphics, University of Siegen, Hoelderlinstr. 3, Siegen, Germany

Department of Biomedical Engineering, Silesian University of Technology, ul. Akademicka 16, Gliwice, Poland

Keywords:

Model based Analysis, Fuzzy Interference System, Fuzzy Connectedness Analysis, Gaussian Mixture Model.

Abstract:

In this paper, a new fuzzy model based algorithm for 3-D bone tumour segmentation in MR series is intro-

duced. The presented segmentation procedure is based on a modiﬁed fuzzy connectedness method. The there

required fuzzy afﬁnity values are estimated using a fuzzy inference system, whose fuzzy membership func-

tions are structured on the basis of gaussian mixture model of analyzed image regions. The 3-D fuzzy tumour

model is generated using different MR modalities acquired during a single examination. The segmentation

abilities of prototype system have been tested on a MR database consisting of 27 examinations composed of

two different sequences each.

1 INTRODUCTION

According to (Davies et al., 2009; Husband and

Reznek, 2004), bone tumour is an abnormal growth of

cells within a single bone, spreading to another one,

muscles or soft tissue in their surroundings. They

are usually found in children and young adults and

their early diagnosis can be crucial for the treatment

applied. The diversity of bone tumours in children

still features many diagnostic and therapeutic prob-

lems. Determination of their nature requires experi-

ence and close collaboration of specialists from vari-

ous areas. Despite the signiﬁcant progress of imaging

techniques, many cases are diagnosed too late.

The bone tumours diagnostics is mostly based on

Magnetic Resonance (MR) imaging, where during a

single examination, series in different MR modalities

are acquired. However, different tumour types vary in

their appearance even in the same modality. Largely

only the comparative radiological analysis taking into

consideration several acquired series enables a reli-

able diagnosis.

Due to the fact, that bone tumours are quite rare,

the problem of their segmentation is not often dis-

cussed in literature. Varied intensity levels in MR se-

quences constituting different tumours cause the de-

scribed segmentation methods (Ma et al., 2005; Zhao

et al., 2004; Pan and Li, 2003) to be dedicated to

one tumour type only. A wide range of currently

available imaging techniques differentiates the seg-

mentation procedure to dynamic MR based (Zhao

et al., 2004; Zhao et al., 2003) as well as static MR

based (Ma et al., 2005; Pan and Li, 2003) techniques.

All the procedures presented in the mentioned papers

combine the information coming from different MR

modalities. The segmentation algorithm proposed

in (Ma et al., 2005) is based on fuzzy connected-

ness analysis developed by (Rosenfeld, 1979; Udupa

and Samarasekera, 1996) and is commonly used in

different medical applications (Pednekar et al., 2008;

Udupa et al., 2002). The fuzzy connectedness princi-

ples have been tested in dozens of studies in past 15

years.

There exist different fuzzy logic based techniques

dedicated to medical applications described in litera-

ture (Yamaguchi et al., 2010; Hata et al., 2000; Tolias

and Panas, 1998). The fully automated fuzzy topol-

ogy method used for brain image analysis is proposed

in (Mari and Dellepiane, 1996). Brain analysis inves-

tigating its morphological changes based on a combi-

nation of Bayesian classiﬁcation with Gaussian Mix-

ture Model (GMM) and fuzzy active surface is pre-

sented in (Yamaguchi et al., 2010).

The differences in grey intensity levels building

bone tumours areas depending on their location in

the human body make reliable automatic segmenta-

tion and direct application of mentioned procedures

impossible. Therefore, this paper presents a new

segmentation algorithm combining GMM and fuzzy

inference systems in the fuzzy connectedness pro-

cedure, insensitive to tumour type and location in

the body. The developed 3-D segmentation method,

185

Czajkowska J..

Fuzzy Model-based Algorithm for 3-D Bone Tumour Analysis.

DOI: 10.5220/0004498301850192

In Proceedings of the 5th International Joint Conference on Computational Intelligence (FCTA-2013), pages 185-192

ISBN: 978-989-8565-77-8

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

based on the previously segmented tumour as well as

surrounding tissues regions on a single slice, adopts

the fuzzy inference system parameters to enable the

analysis of the whole study.

Radiological diagnostic of bone tumours relies

on comparative analysis of different MR images ac-

quired during one examination. With this in mind, in

the presented methodology a parallel analysis of two

different MR series is applied.

In the following section, a short introduction to

the fuzzy connectedness-based segmentation proce-

dure is given. In section 3 the membership functions

structured based on GMM are described. Section 4

introduces the used fuzzy inference system and sec-

tion 5 presents the developed algorithm. Discussion

concerning performed experiments and obtained seg-

mentation results is given in section 6. Then, the last

section (section 7) concludes the work and presents

some plans for the future.

2 FUZZY CONNECTEDNESS

BASED SEGMENTATION

The idea of fuzzy connectedness analysis in image

processing and image segmentation has been given

in works (Rosenfeld, 1979; Udupa and Samarasek-

era, 1996). The there presented methodology oper-

ates on multidimensional, multifeature sets of data,

being connected and ordered. The points classiﬁed

into an object are strongly connected with some rela-

tions having relatively lower values, when it comes to

points outside the object. In medical image segmen-

tation a multifeature data set often consists of grey

intensity levels of pixels (or voxels – in volumetric

data) in acquired CT, MR, US etc. studies. The image

fusion methods applied afterwards make it possible

to simultaneously analyse them all. In the presented

study only MR data of bone tumours are collected,

however the multifeature dataset is constructed with

different MR modalities, namely T2-weighted, T1-

weighted, T1-weighted contrast enhanced, etc.

Then, the segmentation procedure takes into con-

sideration local similarities of the analyzed voxels,

exploring their position e = (e

) and gray in-

tensity levels I

(e), where d = {1,...,D} is the di-

mensionality of feature space.

Fuzzy connectedness of two image points is es-

timated on the basis of their fuzzy relation – fuzzy

afﬁnity κ

κ = {((e, d),µ

(e,d)) : (e, d) ∈ C ×C}, (1)

where µ

∈ [0, 1] is the fuzzy afﬁnity membership

function of spels (spatial elements) e and d. The

reﬂexive: µ

(e,e) = 1 and symmetric: µ

(e,d) =

(d, e) fuzzy afﬁnity is mostly given as

(e,d) = µ

(e,d) ·g(µ

(e,d), µ

(e,d)), (2)

where µ

is the functional form of adjacency rela-

tion α and µ

, µ

are intensity-based and intensity

gradient-based components of the afﬁnity, respec-

tively. There are different forms of (2) discussed

in (Udupa et al., 2002), from which the most popu-

lar in medical applications is the weighted gaussian

variant

(e,d) = µ

· (w

(e,d) + w

(e,d)), (3)

with parameters w

and w

denoting positive con-

stants fulﬁlling

+ w

= 1. (4)

Components H

and H

are deﬁned as:

(e,d) = exp



−

2σ



I(e)+I(d)

− λ





(e,d) = exp



−

2σ

(|I(e) − I(d)| − λ

)



(5)

Pairs λ

, σ

and λ

, σ

are the expected parameters

of the segmented object, describing its gray intensity

and gradient.

To determine the relations of spels e and d the

concept of digital path has been introduced (Udupa

and Samarasekera, 1996). A nonempty path p

from

e = e

(1)

to d = e

(m)

is any sequence of elements

⟨e

(1)

(2)

,...,e

(m)

⟩, such that for any i ∈ [1, m − 1]

pair ⟨e

(i+1)

⟩ a link exists. The strength of a path

is given by the strength of its weakest link (with the

smallest afﬁnity). The strength of the ”strongest”

paths between two image points (spels) e and d de-

scribes their connectedness.

Finally, the fuzzy κ-connectedness relation K be-

tween two image points e and d is given as follows

(e,d) = max

∈P

[µ

)], (6)

where

) = min

{µ

(i)

(i+1)

)}. (7)

Fuzzy afﬁnity scene ℓ

with respect to object’s

starting point o is then given by

ℓ

(e) = µ

(o,e). (8)

Then, the segmented fuzzy object O(o) containing

starting point o is obtained using the thresholding pro-

cedure on scene ℓ

. The problem of threshold se-

lection is solved by introducing the second object,

treated as a background region with its own seed

point b. Therefore, spel e belongs to object O(o) if

(o,e) > µ

(b,e). The already described approach

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

186

is called the Relative Fuzzy Connectedness method

and it is discussed in detail in (Udupa et al., 2002;

Udupa and Samarasekera, 1996). To solve the short-

est path problem the authors use the dynamic pro-

gramming approach, which in (Carvalho et al., 1999)

has been replaced by the Dijkstra’s Algorithm. In the

later FC applications (Saha and Udupa, 2001) also the

single seed points belonging to the object as well as

the background have been replaced by the seed points

sets.

In cases of clearly visible tissues and sharp enough

edges the already described FC-based segmentation

method yields very good results. Based on the se-

lected seed points areas the required intensity and in-

tensity gradient parameters are there easy to estimate.

The pathologies, like soft tissue tumours, with a more

complex structure can be segmented applying a clus-

tering based FC analysis presented in (Badura et al.,

2011). The analysed image data are ﬁrst clustered and

the obtained clusters parameters are then utilised in

the FC step.

The idea introduced in this paper is to adopt the

fuzzy connectedness approach to multifeature bone

tumour analysis. The presented methodology is based

on two different MR modalities. Two exemplary im-

ages of a bone cyst on coronal Short Time Inver-

sion Recovery (STIR) and Fast Spin-Echo (FSE) T1-

weighted series are shown in Figure 1. In the radio-

logical diagnosis the comparative analysis of both the

series is utilised. Due to this fact, ﬁrst, different 3-

D multifeature clustering procedures (McLachlan and

Peel, 2000; Heo and Gader, 2010) have been applied.

However, none of the implemented multifeature algo-

rithms has yielded satisfactory ﬁnal segmentation re-

sults. Therefore, a fuzzy inference system simulating

experts reasoning, described in the following sections,

has been developed.

Figure 1: A bone cyst visualised on a single slice coming

from two different MR coronal series: left – STIR, right –

FSE T1-weighted.

Let us assume that there are two reference regions

selected on a single slice: tumour area and the back-

ground, respectively. The areas are then transferred

into both the analyzed modalities. Let the already

given regions constitute the expert knowledge. Due to

the fact that the grey intensity levels constructing the

tumours areas vary depending on the analyzed lesion

and its location in the patients body, the fuzzy rules

and dictionary are adaptively created for each single

tumour case. The varying grey intensity levels build-

ing tumour as well as background areas on both MR

sequences are described using the Gaussian Mixture

Model. The obtained models are then used both in a

fuzzy system dictionary and the rules base. The crisp

value at the output of the developed fuzzy inference

system is the fuzzy afﬁnity value µ

(o,e).

3 GAUSSIAN MIXTURE MODEL

Gaussian Mixture Model (GMM) is a semi-

parametric technique, which enables estimating a

probability density function with a mixture distribu-

tion (McLachlan and Peel, 2000; Dempster et al.,

1977), deﬁned as a weighted sum of its components.

Let be a set of N vectors x

= [x

,...,x

]

n ∈ {1, . . . , N}, where D is the dimensionality of fea-

ture space. Consider a mixture model with K(K > 1)

components in R

for n ≥ 1. The probability density

function of vector x in the mixture is given as

p(x) =

∑

k=1

(x), (9)

where p

(x) is the density of k-th component and

∈ [0, 1] are the mixing proportions coefﬁcients ful-

ﬁlling

∑

k=1

= 1. (10)

In the Gaussian Mixture Model each group of the

data is assumed to be generated by a normal probabil-

ity distribution

(x) =

(2π)

det(Σ

)

exp



−

(x − λ

)

−1

(x − λ

)



(11)

where λ

and Σ

are the parameters of D-dimensional

normal probability distribution N(λ

,Σ

), mean val-

ues vector and covariance matrix, respectively.

The maximum likelihood estimator of parameter

Θ = {Θ

,Θ

,...,Θ

}, where Θ

= {λ

,Σ

}, of a

parametric probability distribution is found using the

Expectation-Maximization (EM) algorithm (Demp-

ster et al., 1977). Since the EM procedure is dedicated

to incomplete data sets analysis, it iteratively alter-

nates between ﬁnding the greatest lower bound to the

likelihood function, making guesses about the com-

plete data and then maximizing this bound by ﬁnding

the Θ that maximizes p(x|Θ) over Θ.

FuzzyModel-basedAlgorithmfor3-DBoneTumourAnalysis

187

The EM algorithm requires starting points as well

as clusters number selection. The required parame-

ters are estimated applying the unsupervised cascade

clustering procedure and Kernelised CS cluster valid-

ity measure discussed in detail in (Czajkowska et al.,

2012).

In the proposed segmentation procedure the adap-

tively generated bone tumour as well as background

model constitute the basis for fuzzy inference system.

The obtained components parameters are used in the

fuzzy dictionary, which deﬁnes the membership func-

tions of fuzzy rules. The combination of different

components building particular image regions is the

basis for fuzzy rules generation.

4 FUZZY INFERENCE SYSTEM

There exist different fuzzy reasoning systems de-

scribed in literature (Yamaguchi et al., 2010; Hata

et al., 2000; Siler and Buckley, 2005) and also applied

to medical tasks. The basic structure of such systems

consists of three components: dictionary deﬁning the

membership functions, base of fuzzy IF-THEN rules

and reasoning mechanism.

Historically the ﬁrst fuzzy control system, based

on Zadeh’s formulations from 1973, was introduced

by Mamdani in 1976. The input numbers are there

translated into linguistic terms and the fuzzy rules

map them onto linguistic terms describing the system

output. Then, the output linguistic terms are trans-

lated back into the numbers. The procedures of trans-

lations are known as fuzziﬁcation and defuzziﬁcation,

respectively. A typical fuzzy rule in such a system is

constructed as follows:

IF input1 is A

AND input2 is A

T HEN out put is B

(12)

It tries to formulate the expert knowledge using some

linguistic rules. An exemplary rule dedicated to the

task of bone tumour segmentation can be simply de-

scribed as:

”IF the intensity level o f the area

in T 2 − weighted series is very high

AND the intensity level o f the area

in T 1 − weighted series is very low

THEN the analyzed region

might be a tumour”

(13)

There are different combinations of grey intensity lev-

els suggestive of bone tumour deﬁned by the experts

and consequently different linguistic rules connected

with them. Simultaneously, there exists a set of lin-

guistic rules deﬁning the healthy tissues. The devel-

oped fuzzy inference system attempts to describe the

majority of them.

Let the fuzzy sets in the fuzzy premises of i-th rule

be given as A

and A

, respectively and the fuzzy set

in the conclusion of i-th rule is denoted as B

. In the

exemplary radiologist reasoning rule, the fuzzy sets

and A

are given as ”high” and ”low” and B

”might be tumour”.

The fuzzy control algorithm developed by Mam-

dani is based on two concepts: fuzzy implication and

compositional rule of inference (Kickert and Mam-

dani, 1978). Assume two fuzzy sets: A of the uni-

verse of discourse X and B of Y deﬁned by their fuzzy

membership functions µ

and µ

. The membership

function of a fuzzy implication S: ”IF A then B” is

then deﬁned as

(x,y) = min[µ

(x);µ

(y)], x ∈ X, y ∈ Y. (14)

For such given implication S, fuzzy set B

′

of the uni-

verse of discourse Y inferred by a given fuzzy set A

′

of X, has a membership function estimated as

′

(y) = max

min[µ

′

(x);µ

(x, y)], x ∈ X, y ∈ Y.

(15)

In fuzzy systems found in research applications

there are different rules describing one phenomenon.

When the rules conditions are matched, a set of ac-

tions will be activated. Each rule, with the antecedent

non-zero matching degree, contributes an output with

the activation value equal to it. The ﬁnal system out-

put taking into consideration all the activated rules is

constructed using an aggregation operation. Its most

common implementation is operator max, however

there exist different aggregation operators found in

real applications, like algebraic sum or the bounded

product.

Coming back to the bone tumours analysis, the

already described fuzzy system is used in the fuzzy

connectedness analysis in order to estimate the fuzzy

afﬁnity value of the spels connection, instead of the

functions given by (4) and (5).

5 ALGORITHM

Before the segmentation procedure begins, thanks to

the positioning information provided by the DICOM

header, the positions of voxels belonging to the two

analysed MR series are matched.

The segmentation procedure starts on

the basis of exemplary region selection

performed by an expert. The automated

part of analysis begins with the adaptive

3-D ﬁltering method (Perona et al., 1994). The

there required parameters are adaptively estimated

based on the assumptions given in (Positano et al.,

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

188

2000). The goal of this analysis step is ﬁrstly the

reduction of noise and thereby an increase in the

signal-to-noise or contrast-to-noise ratios while

maintaining the edge lines. Secondly, as a result of

smoothing the objects areas the number of groups

in the clustering procedure, being the next step,

decreases and the analysis is not sensitive to outliers.

The main part of performed analysis constitutes of

four steps discussed in previous sections, whose com-

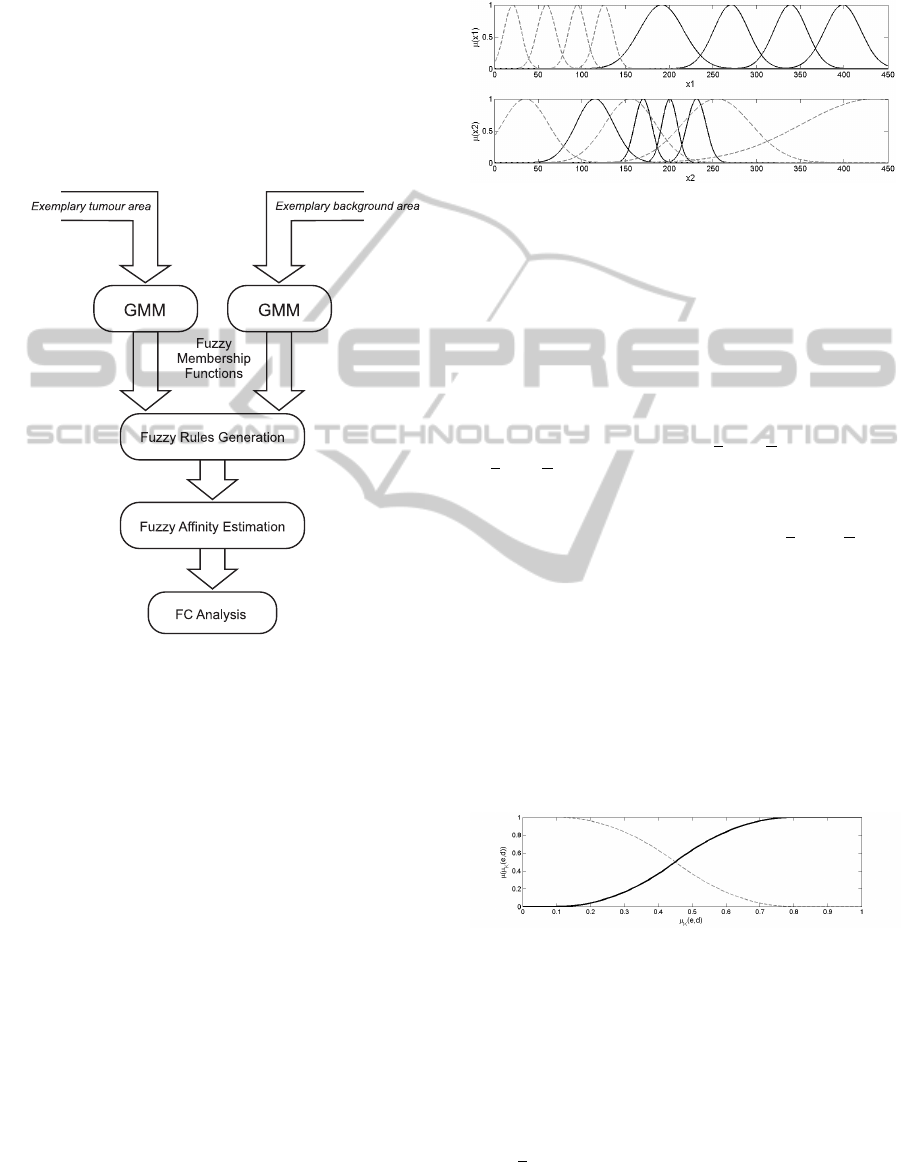
bination is shown on the block diagram in Figure 2.

Figure 2: The ﬂow chart of 3-D bone tumours segmentation

procedure

First, based on the reference expert selections,

personalized GMMs of bone tumour and background

areas are generated. The detailed discussion of the al-

gorithm is given in section 3. Let the obtained GMMs

of tumour area be given as G

1,2

and of the background

as G

1,2

, respectively. Both GMM pairs are the sets of

mixture components parameters θ and voxels C clas-

siﬁed into each of K

or K

groups

= (θ

),(θ

),...,(θ

= (θ

),(θ

),...,(θ

(16)

where index i = {1,2} refers to two simultaneously

analysed MR sequences.

Based on them, the input membership functions

describing the intensity levels constituting tumour as

well as background areas are deﬁned. An exemplary

set of membership functions obtained for a bone cyst

in STIR and T1-weighted sequences (Figure 1) is vi-

sualised in Figure 3. The membership functions de-

ﬁned for the tumour area are marked with the black

solid lines and the membership functions deﬁned for

the background are given by the grey dashed lines.

Figure 3: An exemplary set of membership functions gener-

ated for a bone cyst in STIR (top) and T1-weighted (down)

sequences. The membership functions deﬁned for the tu-

mour area are marked with the black solid lines and the

membership functions deﬁned for the background are given

by the grey dashed lines.

Since the fuzzy connectedness analysis is used in

the segmentation step, the system inputs should cause

two adjacent spels to obtain their afﬁnity value. The

functions given by (4) and (5) take into consideration

the mean intensity value 0.5(I(e)+I(d)) and gradient

|I(e)−I(d)|. Since the attempts of modelling gradient

values characterising tumour or healthy tissues have

not provided any useful information, the inputs to the

fuzzy system are deﬁned as x

= 0.5(I

(e) + I

(d)).

Two membership functions in the conclusions of

rules are shown in Figure 4. The output of the system

is the afﬁnity value of two adjacent spels. The mem-

bership function visualised using the black solid line

deﬁnes the ”high” afﬁnity and the dashed line deﬁnes

the ”low” afﬁnity of spels connection. Moreover, to

reduce the computation time associated with the rela-

tive FC analysis, the meaning of ”big” afﬁnity value is

”it might be tumour”. Based on the graph of the func-

tions in Figure 4, the threshold deﬁning the tumour

area can be set to 0.45.

Figure 4: An exemplary set of membership functions on the

output of the fuzzy inference system. The black solid line

deﬁnes the tumour and the grey dashed line represents the

background.

Let the fuzzy sets in premises referring to G

1,2

and G

1,2

are given as A

and A

, and the fuzzy sets in

conclusions as B

– ”high” and B

– ”low”. Then, on

the basis of sets G

1,2

and G

1,2

and all the positions of

voxel c the unique fuzzy rules R

, l ∈ {1, 2,...L} and

, p ∈ {1, 2, . . . P} deﬁning tumour and non-tumour

FuzzyModel-basedAlgorithmfor3-DBoneTumourAnalysis

189

areas, respectively, are generated as follows:

1: if c ∈ T and c ∈ C

and c ∈ C

, where T is the set

of reference tumour voxels then

: IF x 1 is A

AND x2 is A

T HEN µ

(e,d) is B

(17)

3: end if

4: if c ∈ T and c ∈ C

and c ∈ C

, where T is the set

of reference background voxels then

: IF x1 is A

AND x2 is A

T HEN µ

(e,d) is B

(18)

6: end if

For each pair of the adjacent voxels the output linguis-

tic value is then translated into their fuzzy afﬁnity. In

the defuzziﬁcation step the center of gravity method is

employed. Using the precomputed afﬁnity tables, the

multiseeded FC algorithm described in (Badura et al.,

2011) is performed.

To reduce the false positive regions in the case

when the tumour is connected with the healthy tissues

having similar characteristics, a convex hull-based

postprocessing technique is applied. Starting from the

reference slice the there obtained tumour convex hull

is then mapped into the adjacent slices. The compar-

ison of areas of tumour like regions covered and un-

covered by the convex hull provides the information

concerning the ﬁnal segmentation results.

6 EXPERIMENTS AND RESULTS

To evaluate the ability of developed methodology, the

database consisting of 27 examinations of 18 patients

studies has been used. The therein contained cases

have included 5 types of bone tumours: chondromas,

Ewing’s sarcomas, osteosarcomas, bone cysts and

chondrosarcomas. In total, 413 pairs of slices have

been analysed. An individual pair have consisted of

T1-weighted, T1-weighted contrast enhanced and fat

saturated, T2-weighted or STIR sequences in differ-

ent MR projections: axial, sagittal and coronal. The

FC threshold values have been set to 0.45 and 0.5.

All the obtained results have been discussed with

an expert, who jugged them on each slice in each ex-

amination. As a result the obtained image regions

have been divided into three classes: true positive

(TP) – the coherent areas containing a correctly indi-

cated tumour, false positive (FP) – a coherent region

containing healthy tissues incorrectly classiﬁed as tu-

morous, false negative (FN) – a coherent region con-

taining tumour areas incorrectly classiﬁed as healthy

tissue.

The accuracy of presented segmentation proce-

dure has been estimated based on the following simi-

larity coefﬁcient

DV =

FP + FN

T P + FN

, (19)

yielding the value equal 0 when the segmentation re-

sults are fully correct. The obtained DV value for the

bone tumours database has been equal to 0.12, which

is sufﬁcient for computer assisted diagnosis systems.

Exemplary results for 3 different types of bone tu-

mours are shown in Figures 5 - 7.

The original fuzzy connectedness algorithm (FC1)

described in (Udupa et al., 2002) as well as its modiﬁ-

cation (FC2) developed in (Badura et al., 2011) were

used to compare the obtained results, which were cat-

egorized into two groups: the segmentation results

in the homogeneous and in-homogeneous image se-

ries. The numerical results (DV values) are summa-

rized in the Table 1, where the last column (FIS) pro-

vides the results obtained using the proposed method-

ology. The ﬁrst row of Table 1 shows that the segmen-

tation results obtained for homogeneous image data

are comparable with other methods. The second row

proves a superiority of the proposed method over an-

other approach described in literature, which results

are insufﬁcient for computer assisted diagnosis sys-

tems and not acceptable by a radiologist.

Table 1: Accuracy of different segmentation procedures –

DV coefﬁcient.

FC1 FC2 FIS

Homogeneous

Series (22) DV 0.16% 0.13% 0.13%

In-homogeneous

Series (5) DV 0.6% 0.5% 0.11%

Figure 5: Final segmentation results of knee Enchondroma

visualised on a single slices of axial MR series: left – T2

Blade FS, right – T1 TSE.

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

190

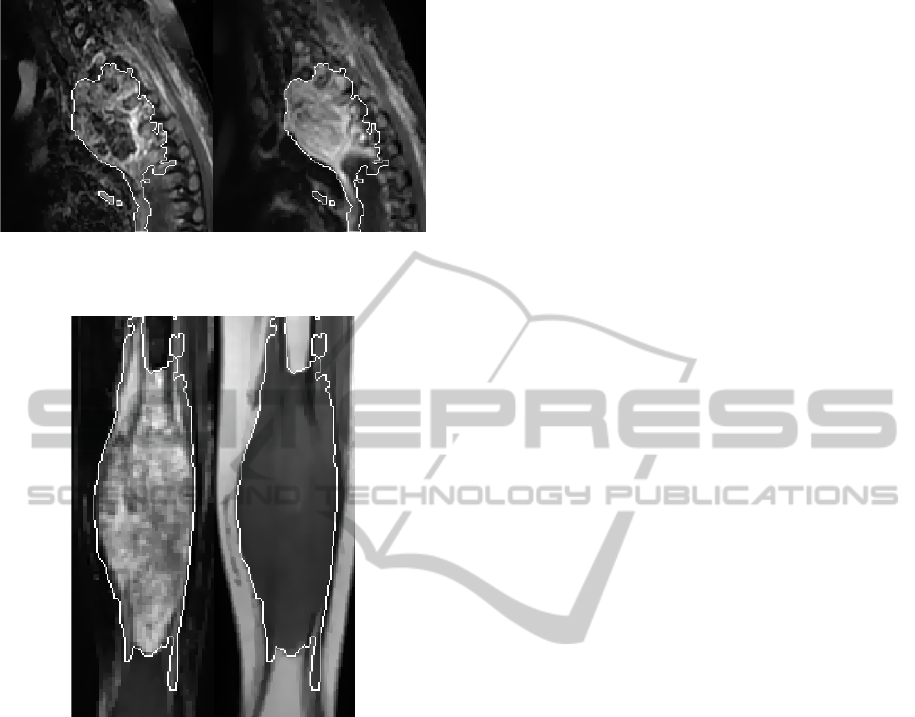
Figure 6: Final segmentation results of spines Ewing’s sar-

coma visualized on a single slices of sagittal MR series: left

– T1+C SE FS, right – STIR.

Figure 7: Final segmentation results of tibias Osteosarcoma

visualized on a single slices of coronal MR series: left – T2

FRFSE FS, right – T1 FSE.

7 CONCLUSIONS

This paper introduces a 3-D multifeature bone tu-

mours segmentation method in MR images. The in-

sensitive to bone tumour location and type algorithm

combines Gaussian Mixture Model and fuzzy infer-

ence system in the fuzzy connectedness analysis. The

proposed procedure has been tested on the database

of real bone tumour cases consisting of 27 exami-

nations of 18 patients, a single examination contain-

ing two different MR series. The obtained segmenta-

tion results encourage to further develop this method.

The presented system provides a basis for develop-

ing an adaptively learning algorithm, training being

based on the currently analysed and veriﬁed cases.

The problem still remaining to be solved is the nor-

malisation of MR sequences so that they can be com-

pared. The plans for further work take into consider-

ation expanding the database with new tumour cases

and involving in the analysis new features like tex-

ture. The detailed radiological consultation will en-

able developing fuzzy IF-THEN rules base and rea-

soning mechanism. In order to improve the segmen-

tation results some fuzzy rules interpolation technique

is also planned to be introduced.

REFERENCES

Badura, P., Kawa, J., Czajkowska, J., Rudzki, M., and

Pietka, E. (2011). Fuzzy connectedness in segmen-

tation of medical images. In International Conference

of Fuzzy Computation Theory and Applications, pages

486–492.

Carvalho, B. M., Joe Gau, C., Herman, G. T., and

Yung Kong, T. (1999). Algorithms for fuzzy segmen-

tation. Pattern Analysis & Applications, 2:73–81.

Czajkowska, J., Bugdol, M., and Pietka, E. (2012). Ker-

nelized fuzzy c-means method and gaussian mixture

model in unsupervised cascade clustering. In Inter-

national Conference of Information Technologies in

Biomedicine, Lecture Notes in Bioinformatics, Gli-

wice, Poland, pages 58–66.

Davies, A. M., Sundaram, M., and James, S. L. J. (2009).

Imaging of Bone Tumors and Tumor-Like Lesions,

Techniques and Applications. Medical Radiology, Di-

agnostic Imaging, Springer-Verlag Berlin Heidelberg,

Berlin.

Dempster, A. P., Laird, N. M., and Rubin, D. B. (1977).

Maximum likelihood from incomplete data via the em

algorithm. Journal of the Royal Statistical Society. Se-

ries B (Methodological), 39(1):1–38.

Hata, Y., Kobashi, S., Hirano, S., Kitagaki, H., and Mori,

E. (2000). Automated segmentation of human brain

mr images aided by fuzzy information granulation and

fuzzy inference. Systems, Man, and Cybernetics, Part

C: Applications and Reviews, IEEE Transactions on,

30(3):381 – 395.

Heo, G. and Gader, P. (2010). An extension of global fuzzy

c-means using kernel methods. In IEEE International

Conference on Fuzzy Systems.

Husband, J. E. and Reznek, R. H. (2004). Imaging in On-

cology, volume 1. Taylor & Francis, London.

Kickert, W. J. M. and Mamdani, E., H. (1978). Analysis

of a fuzzy logic controller. Fuzzy Sets and Systems,

1(1):29 – 44.

Ma, J., Li, M., and Zhao, Y. (2005). Segmenta-

tion of multimodality osteosarcoma mri with vec-

torial fuzzy-connectedness theory. Fuzzy Systems

and Knowledge Discovery, Lecture Notes in Com-

puter Science, Springer-Verlag Berlin Heidelberg,

36(14):1027–1030.

Mari, M. and Dellepiane, S. (1996). A segmentation method

based on fuzzy topology and clustering. In Pattern

Recognition, 1996., Proceedings of the 13th Interna-

tional Conference on, volume 2, pages 565 –569 vol.2.

FuzzyModel-basedAlgorithmfor3-DBoneTumourAnalysis

191

McLachlan, G. and Peel, D. (2000). Finite Mixture Model.

Wiley Series in Probability and Statistics.

Pan, J. and Li, M. (2003). Segmentation of mr osteosar-

coma images. In International Conference on Com-

putational Intelligence and Multimedia Applications

(ICCIMA03), IEEE .

Pednekar, A., Kakadiaris, I. A., and Kurkure, U. (2008).

Adaptive fuzzy connectedness-based medical image

segmentation. In Proceedings of the Indian Confer-

ence on Computer Vision, Graphics, and Image Pro-

cessing.

Perona, P., Shiota, T., and Malik, J. (1994). Anisotropic dif-

fusion. Geometry-Driven Diffusion in Computer Vi-

sionKluwer Academic Publishers, 3:73–92.

Positano, V., Santarelli, M. F., Landin, L., and Benassi, A.

(2000). Nonlinear anisotropic ﬁltering as a tool for

snr enhancement in cardiovascular mri. Computers in

Cardiology, IEEE, pages 707–710.

Rosenfeld, A. (1979). Fuzzy digital topology. Information

and Control, 40(1):76–87.

Saha, P. K. and Udupa, J. K. (2001). Fuzzy connected ob-

ject delineation: Axiomatic path strength deﬁnition

and the case of multiple seeds. Computer Vision and

Image Understanding, 83(3):275–295.

Siler, W. and Buckley, J. J. (2005). Fuzzy Expert Systems

and Fuzzy Reasoning. Wiley.

Tolias, Y. and Panas, S. (1998). On applying spatial

constraints in fuzzy image clustering using a fuzzy

rule-based system. Signal Processing Letters, IEEE,

5(10):245 –247.

Udupa, J. K., Saha, P. K., and Lotufo, R. A. (2002). Rel-

ative fuzzy connectedness and object deﬁnition: The-

ory, algorithms, and applications in image segmenta-

tion. IEEE Transaction on Pattern Analysis and Ma-

chine Intelligence, 24(11):1485–1500.

Udupa, J. K. and Samarasekera, S. (1996). Fuzzy con-

nectedness and object deﬁnition: Theory, algorithms,

and applications in image segmentation. Graphical

Models and Image Processing, 58(3):246–261.

Yamaguchi, K., Fujimoto, Y., Kobashi, S., Wakata, Y.,

Ishikura, R., Kuramoto, K., Imawaki, S., Hirota, S.,

and Hata, Y. (2010). Automated fuzzy logic based

skull stripping in neonatal and infantile mr images. In

Fuzzy Systems (FUZZ), 2010 IEEE International Con-

ference on, pages 1 –7.

Zhao, Y., Hong, F., and Li, M. (2003). Multimodality mri

information fusion for osteosarcoma segmentation. In

Biomedical Engineering, 2003. IEEE EMBS Asian-

Paciﬁc Conference on, pages 166 – 167.

Zhao, Y., Hong, F., and Li, M. (2004). Segmentation of os-

teosarcoma based on analysis of blood-perfusion epi

series. In International Conference on Communica-

tions, Circuits and Systems, ICCCAS 2004, IEEE, vol-

ume 2.

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

192