
Privacy-preserving SVANETs
Privacy-preserving Simple Vehicular Ad-hoc Networks
Jan Hajny, Lukas Malina, Zdenek Martinasek and Vaclav Zeman
Dpt. of Telecommunications, Brno University of Technology, Technicka 12, Brno, Czech Republic
Keywords:
Security, Cryptography, Privacy, Digital Signature, Authentication, Protocols.
Abstract:
The paper deals with the cryptographic design and experimental implementation of a scheme for (but not
limited to) vehicular ad-hoc networks (VANETs). In contrast to existing solutions, our scheme does not
need any complex infrastructure (like costly road-side units or special on-board devices) and is based just on
users’ smart-phones and Internet connection. We call this simplified concept SVANETs (Simple Vehicular
Ad-Hoc Networks). In addition, our cryptographic scheme supports drivers’ privacy by employing advanced
cryptographic constructions like Σ-protocols and proof of knowledge protocols. Our scheme is computa-
tionally efficient and practically implementable on current hardware. To prove the efficiency and practical
implementability, we provide the first implementation results, which were obtained from our experimental
implementation on the Android platform.
1 INTRODUCTION
Vehicular ad-hoc networks (VANETs) provide, so far
only theoretically, mechanisms for the communica-
tion among cars in daily traffic. By implementing
VANETs, it would be possible to share information
about traffic accidents, road conditions, traffic density
or road closures. Moreover, VANETs would also al-
low easier monitoring of traffic in cities and on high-
ways. This would improve route planning. Improved
traffic monitoring would significantly improve the ef-
ficiency, time demands and ecology of traveling.
VANETs allow the communication among cars,
which are equipped with special devices called On-
Board Units (OBUs). These built-on-purpose de-
vices are wirelessly connected to stationary devices
along roads called Road-Side Units (RSUs). Addi-
tionally to vehicles with OBUs and RSUs, many ex-
isting schemes also use additional third party entities
(e.g., registration authorities, revocation authorities,
etc.). We consider this concept too complex and im-
practical for a real-world implementation. It would
be too demanding (both financially and logistically)
to equip roads with special electronic devices on side
(RSUs). Also, it would be very difficult to equip
all cars with new, built-on-purpose devices (OBUs).
Thus, we propose a new concept called SVANETs
1
in
this paper, which needs only smart-phones in partici-
1
We chose SVANETs name because they provide the
pating cars. By simplifying the concept of VANETs,
we hope that these communication networks will be-
come more efficient and subsequently more commer-
cially interesting and easier to deploy.
The security of VANETs plays a crucial role in the
whole system. First, it is necessary to provide confi-
dentiality and authenticity of messages. In addition to
classical security requirements, like the confidential-
ity and authenticity of messages, the VANETs must
also provide new means of privacy protection. Many
security problems of existing VANETs are connected
to the privacy of users. It must be assured that drivers
are not traceable by attackers or by any other entity
in the system. The protection of users’ privacy plays
an important role when the system is about to be de-
ployed commercially and in a large scale. A system
which allows the monitoring of drivers and their un-
wanted tracing would be surely rejected by drivers.
In this paper, we propose a novel cryptographic
scheme which is bothhighly computationallyefficient
and supporting all security requirements. It provides
both the authenticity of messages and the privacy of
users. The cryptographic scheme described in this pa-
per is a practical representation of the SVANET con-
cept and uses cryptographic techniques from attribute
authentication systems (Hajny and Malina, 2013).
same functionality as VANETs, though over Internet.
267
Hajny J., Malina L., Martinasek Z. and Zeman V..
Privacy-preserving SVANETs - Privacy-preserving Simple Vehicular Ad-hoc Networks.
DOI: 10.5220/0004498802670274
In Proceedings of the 10th International Conference on Security and Cryptography (SECRYPT-2013), pages 267-274
ISBN: 978-989-8565-73-0
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

1.1 Related Work
Many existing VANET schemes (e.g., (Plossl et al.,
2006; Raya et al., 2006; Haas et al., 2009)) pro-
vide basic security features like message confidential-
ity, authenticity and non-repudiation by using simple
cryptographic methods. Some schemes add the pro-
tection of drivers’ privacy. It is becoming an impor-
tant requirement on modern VANETs to provide the
prevention against the observing of geographic po-
sition of cars and driver’s daily routes. In existing
VANETs, privacy is usually ensured by two main ap-
proaches, i.e., pseudonyms and group signatures.
Privacy preserving solutions based on
pseudonyms have been proposed in (Gerlach
et al., 2007). The work (Raya and Hubaux, 2007)
uses anonymous certificates which are stored in
vehicles (usually in a tamper-proof device). This ap-
proach uses a set of short-lived pseudonyms and fast
changing of these pseudonyms provides the privacy
of vehicles. Nevertheless, in dense urban VANETs,
this approach is burdened by the preloading and
storing of a large number of anonymous certificates
with pseudonyms. For low-performance devices
like mobile phones, the management of pseudonyms
becomes a too complex operation.
The second approach is based on Group Signa-
tures (GS). They provide user anonymity by pro-
ducing message signatures on behalf of a group in
VANETs. Generally, GS guarantee the anonymity
of honest users and the traceability of misbehav-
ing users. The group signature scheme called BBS
scheme (Boneh et al., 2004) serves as a crucial build-
ing block for many security solutions in VANETs
(e.g., (Lin et al., 2007) and (Zhang et al., 2008)).
Nevertheless, these schemes need several expensive
operations like bilinear pairings, modular exponentia-
tions and multiplications during the verification phase
and are not appropriate for dense VANETs where tens
or hundreds of signatures must be verified in short
time. The work (Malina et al., 2012) speeds up multi-
ple group signatures by using short linkability which
provides categorized batch verification. Also this so-
lution is based on the BBS scheme and therefore it
needs slow bilinear pairing operations.
Based on the analysis of existing schemes, we lack
a practical scheme which is able to provide both basic
security features (message confidentiality and authen-
ticity) as well as advanced privacy-preserving fea-
tures (like anonymity, untraceability and unlinkablity
of drivers, no trusted third parties, all defined in Sec-
tion 3.1). Even though some schemes come very close
to our requirements, these schemes are currently too
complex for smart-phone implementation.
1.2 Our Contribution
In our proposal, we get rid of costly Road-Side
Units (RSU) and replace On-Board Units (OBUs)
with users’ smart-phones. We call the new concept,
described in Section 3.2 in detail, Simple VANETs
(SVANETs). Our concept supports both the ba-
sic security features, such as message confidential-
ity and authenticity, and advanced privacy-enhancing
features. Still, the scheme remains highly practical on
mobile devices.
2 PRELIMINARIES
The SVANET scheme proposed in this paper is based
on advanced cryptographic constructions. Most con-
structions are well know and their description can be
found in the cited literature. The SVANETs scheme is
the practical application of the attribute authentication
technology presented in (Hajny and Malina, 2013)
where further cryptographic details can be found.
2.1 Assumptions
The Generalized Discrete Logarithm Problem
(GDLP) Assumption. Based on (Menezes, 1996) it
is assumed that given a finite cyclic group G of order
q, a generator g and an element β ∈ G it is hard to find
an integer 0 ≤ x ≤ q− 1 such that g
x
≡ β.
Factorization Hardness Assumption. Based on
(Okamoto and Uchiyama, 1998) it is assumed that it is
hard to factor n = r
2
s, where r,s are large safe primes.
2.2 Cryptographic Primitives
Discrete Logarithm Commitment Schemes. A
cryptographic commitment scheme can be used in
scenarios where a user (U) is required to bind to a
number without disclosing it. Therefore, there are
two properties which must be fulfilled. They are the
hiding property and the binding property. A practi-
cal example of using the commitment schemes is the
situation where a user generates a random number w
and computes a commitment c = commit(r,w) using
a randomness r. Then, the user can disclose c to some
verifier (V). Although c is disclosed, the verifier is un-
able to learn w from it (hiding property) and the user
is unable to change his w without changing c (binding
property).
SECRYPT2013-InternationalConferenceonSecurityandCryptography
268

DL Proof of Knowledge (PK) Protocols. The
Proof of Knowledge of Discrete Logarithm (PKDL)
protocol can be used by a Prover to give a proof about
the knowledge of a discrete logarithm of some pub-
lic value c with respect to a generator g and modulus
p. Using PKDL, the Prover is able to convince V that
he knows w = log
g
c mod p without actually disclos-
ing it. More information about these protocols can
be found in (Cramer, 1996; Quisquater et al., 1989;
Cramer et al., 2000; Fiat and Shamir, 1987; Damg˚ard
and Fujisaki, 2002; Camenisch and Stadler, 1997; Ha-
jny and Malina, 2013).
DL Proof of Representation Protocols. In crypto-
graphic constructions, it is very common to compute
multi-exponentiations in multiplicative groups. The
Pedersen commitment (Pedersen, 1992) is the typical
example of multi-exponentiation where two genera-
tors are used. Using k generators and exponents, the
multi-exponentiation can be denoted as
c =
∏
1≤i≤k
g
w
i
i
mod p, (1)
where (w
1
,w
2
,...,w
k
) is called the representation
of c with respect to generators (g
1
,g
2
,...,g
k
) in
modp. With (g
1
,g
2
,...,g
k
),q, p,c being public,
the Verifier might ask the Prover to give a proof
of knowledge of (w
1
,w
2
,...,w
k
). In our pro-
posal, a proof of representation for k = 2 is used. PK
protocols can be used for proofs of representation too.
Group Signatures from PK Protocols. In the
proof of knowledge (resp. proof of representation)
protocols introduced above, the Prover always proves
the knowledge of some secret value with respect to
some public value to the Verifier. In these protocols,
the Prover always has to compute a correct answer to
some challenge. These protocols can be easily con-
verted to group signature schemes (Fiat and Shamir,
1987). The public value (value c in our examples)
can be considered a public key, the secret (value w
in our examples) can be considered a private key and
the challenge e can be replaced by the message (or its
hash) being signed. We denote the group signatures
constructed using the proof of knowledge (representa-
tion) protocols as SPK(message), thus for our exam-
ples and message we get SPK{w : c = g
w
}(message)
and SPK{w
1
,w
2
: c = g
w
1
1
g
w
2
2
}(message).
Okamoto-Uchiyama Trapdoor One-way Function.
Let n = r
2
s and r,s be large primes. Pick g ∈ Z
n
such that g mod r
2
is a primitive element of Z
∗
r
2
.
Then c = g
x
mod n is a trapdoor one-way function
with r as a trapdoor (Okamoto and Uchiyama, 1998).
Value x can be computed using the trapdoor as x =
((c
r−1
mod r
2
) − 1)/r
((g
r−1
mod r
2
) − 1)/r
mod r. The function is secure
if the factorization of n is hard. Size recommenda-
tions for n are the same as for RSA scheme.
2.3 Notation
A Discrete Logarithm (DL) commitment c to a value
w is denoted as c = commit(w). For various proofs of
knowledge or representation, the efficient notation in-
troduced by Camenisch and Stadler (Camenisch and
Stadler, 1997) is used. Thus, a PKDL protocol can
be denoted as PK{w : c = g
w
}. The proof of knowl-
edge of representation is denoted as PK{w
1
,w
2
: c =
g
w
1
1
g
w
2
2
}. The proof of discrete log equivalence with
respect to different generators g
1
,g
2
is denoted as
PK{w : c
1
= g
w
1
∧ c
2
= g
w
2
}. A group signature on
message is denoted as SPK{w : c = g
w
}(message).
All these protocols can be realized by Σ-protocols
(Cramer, 1996). A digital signature using some exist-
ing scheme (e.g., RSA) by a user U on some message
is denoted as Sig
U
(message). The symbol “:” means
“such that”, “|” means “divides”, “a||b” is the con-
catenation of strings a and b, “|x|” is the bitlength of
x and “x ∈
R
{0,1}
l
” is a randomly chosen bitstring of
maximum bitlength l. “x ∈
R
Z
q
” denotes a randomly
chosen integer less than q. “Z
∗
q
” denotes an integer
multiplicative group modulo q.
3 SCHEME DESCRIPTION
3.1 Requirements
In the Introduction and Related Work sections, we
identified the major problems of existing solutions
for inter-vehicular communication. In particular, we
stated that it is very difficult to provide both authentic-
ity of messages and user anonymity, both in a single
efficient VANET scheme. Therefore, our goal is to
design a scheme providing both message authenticity
and privacy-enhancing features. Namely, we provide
following privacy-enhancing features.
• Anonymity of Users: in VANETs, a large num-
ber of messages is shared among cars. To pre-
vent privacy violation, the messages cannot dis-
close the identity of drivers.
• Untraceability of Users: to protect drivers’ pri-
vacy, it must be impossible to trace vehicles by
intercepting VANET messages.
Privacy-preservingSVANETs-Privacy-preservingSimpleVehicularAd-hocNetworks
269
• Unlinkability of Signatures: all valid messages
in a VANET are signed to limit fraud messages.
The signatures from a particular car cannot be mu-
tually linkable as it would allow unwanted tracing
of cars.
• Revocation: in case of policy violation, it must be
possible to revoke malicious drivers (cars) from
the system.
3.2 SVANETs
In our proposal, we get rid of all built-on-purpose de-
vices. By this, we significantly reduce the cost of the
vehicular network and make the penetration to the real
world much easier. We use only smart-phones and
their connection to the Internet through anonymous
routing protocols (Reed et al., 1998). The SVANET
is based on a mobile phone application which is able
to share all traffic information in a privacy-preserving
manner. The registration of users as well as the man-
agement of the network is done by cloud services. In
contrast to classical VANETs or mobile phone traffic
applications, we propose a cryptographic protection
which prevents all entities (including service admin-
istrators and cloud-based management) from break-
ing the privacy of drivers (i.e., tracing, identification
or monitoring). Thus, we do not need any trusted ser-
vice as many existing proposals do. Our SVANET
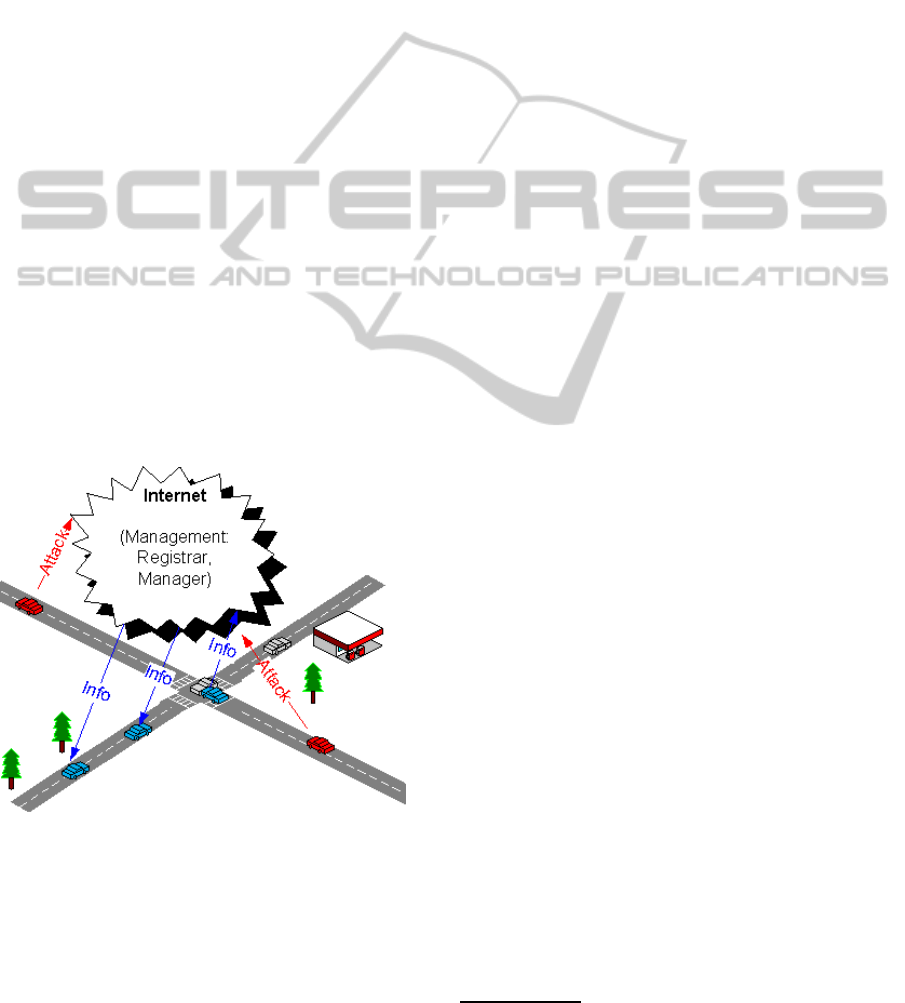
concept is depicted in Figure 1.
Figure 1: SVANET concept.
In the Figure 1, there are cars equipped with
smart-phone devices. These devices are used for
sending and receiving traffic information. The in-
formation about, for example, road conditions, traf-
fic jams or accidents can be shared. The information
is shared among cars using the Internet connection,
based on the cellular data communication (GPRS,
EDGE, 3G etc.) and the anonymous routing proto-
cols (Reed et al., 1998)
2
. For Android, there is al-
ready an implementation called Orbot available, thus
we do not deal with anonymous routing in this pa-
per but rather use it as a service. All the management
of the network is done using Internet cloud services,
thus it is not necessary to use any road-side devices or
services. In contrast to existing solutions, we employ
strong cryptographic techniques to protect all privacy-
sensitive data of users.
3.3 Entities
The SVANET scheme is composed of following enti-
ties.
• Users: entities which communicate in SVANETs.
They can sign messages and verify signatures
broadcasted in SVANET using their public and
private keys. There can be more roles in the sys-
tem, e.g., drivers, police, ambulance, firefight-
ers etc. The signature assures that the sender is
from a particular authorized group but does not re-
lease any other privacy-sensitiveinformation (like
user’s identity).
• Registrar: the entity who registers new users and
verifies their qualification for joining the system.
• Manager: the entity who is able to manage users
(revoke invalid users, attackers, malicious users
etc.).
3.4 Protocols
The scheme is composed of 5 cryptographic proto-
cols. They are the
Setup
,
Register
,
Sign
,
Verify
and
Revoke
.
The
Setup
protocol is run by the Manager and
Registrar to establish all system parameters.
The
Register
protocol is run between the User
and the Registrar with Manager and outputs a keypair
for signing/verifying of SVANET messages. Dur-
ing the registration, the User provides his identity
and all data required by the Registrar (e.g., ID card,
driving licence etc.). This information disclosure
does not limit User’s privacy since the registration is
completely unlinkable to subsequent message sign-
ing/verification. Also, the User is assigned a role
in the SVANET (general driver, police, ambulance,
etc...).
The
Sign
protocol is used for signing messages.
By the signature, the User certifies to the authenticity
and integrity of the message. Only the group origin is
2
TOR can add to the complexity of the protocol.
SECRYPT2013-InternationalConferenceonSecurityandCryptography
270

revealed by the signature, User’s concrete identity is
hidden.
The
Verify
protocol is used for the verification
of messages. The authenticity and integrity of mes-
sages can be verified by the
Verify
protocol. Only
the group origin is disclosed (for example, the ver-
ifier learns that the message is coming from police,
ambulance etc.), the concrete sender’s identity stays
hidden. All messages of a single particular driver are
mutually unlinkable.
The
Revoke
protocol is used only in cases where
some policy violation is detected. In that case, the
User’s signing key can be revoked. In most severe
violation cases, even the identity of senders can be
revealed, but only if the Registrar and Manager coop-
erate. By such a distribution of power, we limit the
privacy violation opportunities of single entities.
3.4.1 Cryptographic Specification of Protocols
Setup Protocol. (params,K
M
,K
R
) ←
Setup
(k,l,m)
protocol: the goal of the protocol is to generate sys-
tem parameters params, Manager’s key K
M
and Reg-
istrar’s key K
R
. The protocol inputs security param-
eters k, l, m (k is the bitlength of the hash function
used, l relates to the bitlength of Users’ secrets, and
m is the verification error parameter). The Registrar
generates a group H defined by a large prime mod-
ulus p, generators h
1
,h
2
of prime order q : |q| = 2l
and q|p − 1. The Manager generates group G for the
Okamoto-Uchiyama Trapdoor One-Way Function. G
is defined by the modulus n = r
2
s with r,s large
primes (|r| > 360,|r| > 4.5l,|n| ≥ 1024, r = 2r
′
+ 1,
s = 2s
′
+1, r
′
,s
′
are primes), generator g
1
∈
R
Z
∗
n
of or-
der ord(g
1
mod r
2
) = r(r − 1) in Z
∗
r
2
and ord(g
1
) =
rr
′
s
′
in Z
∗
n
. The Manager also randomly chooses
its secrets S
1
,S
2
,S
3
: |S
1
| = 2.5l, |S
2
| = l, |S
−1
3
mod
φ(n)| = l and GCD(S
1
,φ(n)) = GCD(S
2
,φ(n)) =
GCD(S
3
,φ(n)) = 1. Finally, Manager computes
group public key G
PK
= g
S
1
1
mod n (public, com-
mon for all group members, linked to a specific de-
scription, e.g. ”general drivers”) and values g
2
=
g
S
2
1
mod n,g
3
= g
S
3
1
mod n. There might be more
public group keys (different G
PK
i
’s and S
1
i
’s) related
to different groups of users in the SVANET. In that
case, each unique G
PK
i
represents one group
3
. In the
rest of the paper, we consider for simplicity only one
group with one public key G
PK
.
The values q, p, h
1
,h
2
,n,g
1
,g
2
,g
3
,G
PK
are made
public as system parameters params, while r,s,
S
1
,S
2
,S
3
are securely stored by the Manager as
K
M
key. Additionally, we use a traditional digital
3
A public list of groups and their assigned keys G
PK
i
’s
is maintained by the Manager.
signature scheme (e.g., RSA). Registrars and Users
are equipped with a private/public key-pair for digital
signatures. This can be accomplished by existing
techniques for PKI. The Registrar’s private key is
denoted as K
R
.
Register Protocol. SK
U
←
Register
(params,K
R
,
K
M
) protocol: the first part of the
Register
proto-
col runs between User’s smart-phone and the Regis-
trar. The communication is not anonymous here, thus
the Registrar can physically check the identity of the
User, his licence etc. Then, User’s smart-phone gen-
erates User’s contribution to his private key (w
1
,w
2
)
and commits to these values. The commitment C
R
is digitally signed
4
by the User and sent with an ap-
propriate construction correctness proof PK{w
1
,w
2
:
C
R
= h
w
1
1
h
w
2
2
} to the Registrar. The Registrar checks
the proof, the signature and replies with his digital
signature on the commitment. In this phase, the User
generated and committed to his private key contribu-
tion. It will be used in all his future signatures. The
Registrar approved a new User by signing the com-
mitted key contribution.
The second part of the protocol runs between
the User’s smart-phone and the Manager. In this
phase, the Manager checks the signature of the
Registrar on User’s commitment C
R
and computes
his contribution w
M
to User’s private key such that
G
PK
= g
w
1
1
g
w
2
2
g
w
M
3
mod n holds. As a result, the
User’s smart-phone learns all parts of the private
key SK
U
, namely User’s part (w
1
,w
2
) and M’s
part w
M
. This triplet forms the discrete logarithm
representation of the group public key G
PK
such
that G
PK
= g
w
1
1
g
w
2
2
g
w
M
3
mod n. This representation
can be computed only in cooperation with M (who
knows the factorization of n). Although G
PK
is
shared among all group members, the private key
(w
1
,w
2
,w
M
) is unique for each user, since (w
1
,w
2
) is
randomly generated by each User’s smart-phone and
w
M
is generated by M. Due to the discrete logarithm
assumption, Users are stuck to their keys and they are
unable to compute other valid keys without knowing
K
M
. The private key SK
U
never leaves the smart-
phone and is stored in phone’s hardware-protected
memory. All operations involving (w
1
,w
2
,w
M
) are
computed in the phone. The
Register
protocol is
depicted in Figure 2.
Sign Protocol. signature ←
Sign
(params,SK
U
,
message) protocol: the protocol is used by User’s
smart-phone to construct a signature on message
message. In the protocol, the User proves the
4
Here, we rely on already established PKI, e.g., RSA
signatures.
Privacy-preservingSVANETs-Privacy-preservingSimpleVehicularAd-hocNetworks
271

Manager User Registrar
w
1
∈
R
{0,1}
2l−1
, w
2
∈
R
{0,1}
l−1
C
R
= commit(w
1
,w
2
) = h
w
1
1
h
w
2
2
mod p
PK{w
1
,w
2
: C
R
= h
w
1
1
h
w
2
2
},Sig
U
(C
R
)
−−−−−−−−−−−−−−−−−−−−−−−−−−→
Store (C
R
,Sig
U
(C
R
))
Sig
R
(C
R
)
←−−−−−−−−−−−−−−−−−−−−−−−
G
′
PK
= g
w
1
1
g
w
2
2
mod n
G
′
PK
,C
R
,Sig
R
(C
R
),
PK{(w
1
,w
2
) :C
R
= h
w
1
1
h
w
2
2
∧ G
′
PK
= g
w
1
1
g
w
2
2
}
←−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
w
M
: G
PK
= g
w
1
1
g
w
2
2
g
w
M
3
mod n
−−−−−−−−−−−−−−−−−−−−−−−−−−→
User private key for G
PK
: SK
U
= (w
1
,w
2
,w
M
)
Figure 2:
Register
Protocol.
User 1 User 2
G
PK
= g
w
1
1
g
w
2
2
g
w
M
3
mod n
K
S
∈
R
{0,1}
l
A = G
K
S
PK
mod n
C
1
= g
K
S
w
M
3
mod n
C
2
= g
K
S
3
mod n
SPK{(K
S
,K
S
w
1
,K
S
w
2
,K
S
w
M
) : A = g
K
S
w
1
1
g
K
S
w
2
2
g
K
S
w
M
3
∧A = G
K
S
PK
∧C
1
= g
K
S
w
M
3
∧C
2
= g
K
S
3
}
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−→
(message)
Figure 3:
Sign
Protocol in Camenisch-Stadler Notation.
User 1 User 2
G
PK
= g
w
1
1
g
w
2
2
g
w
M
3
mod n
K
S
∈
R
{0,1}
l
A = G
K
S
PK
mod n
C
1
= g
K
S
w
M
3
mod n
C
2
= g
K
S
3
mod n
r
1
,r
2
∈
R
{0,1}
m+k+3l
r
3
∈
R
{0,1}
m+k+4.5l
r
S
∈
R
{0,1}
m+k+l
¯
G
PK
= g
r
1
1
g
r
2
2
g
r
3
3
mod n
¯
A = G
r
S
PK
mod n
¯
C
1
= g
r
3
3
mod n
¯
C
2
= g
r
S
3
mod n
e = H (params,message,A,
¯
A,
¯
G
PK
,C
1
,C
2
,
¯
C
1
,
¯
C
2
)
z
1
= r
1
− eK
S
w
1
z
2
= r
2
− eK
S
w
2
z
3
= r
3
− eK
S
w
M
z
S
= r
S
− eK
S
message,A,C
1
,C
2
,e,z
1
,z
2
,z
3
,z
S
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−→
Figure 4:
Sign
Protocol in detail.
knowledge of his private key SK
U
= (w
1
,w
2
,w
M
).
The session is randomized by a session key K
S
. User
creates a commitment C
2
to the session key K
S
and
proves its correctness. The protocol transcript forms
the signature. The protocol is illustrated in Figure
3 in CS notation. The
Sign
protocol follows the
standard mechanisms specified in Section 2.2, thus
can be implemented as shown in Figure 4.
Verify Protocol. The
Verify
protocol is the veri-
fication of the SPK protocol transcript generated by
the
Sign
protocol. Following the standard verifica-
tion equations (see paper (Hajny and Malina, 2013)
for more cryptographic details), the
Verify
protocol
consists of equations (2-6) which are evaluated by the
recipient. The last equation (7) checks whether the
User is revoked or not.
¯
G
PK
= A
e
g
z
1
1
g
z
2
2
g
z
3
3
mod n (2)
¯
A = A
e
G
z
S
PK
mod n (3)
¯
C
1
= C
e
1
g
z
3
3
mod n (4)
¯
C
2
= C
e
2
g
z
S
3
mod n (5)
e
?
= H (params,message,A,
¯
A,
¯
G
PK
,C
1
,C
2
,
¯
C
1
,
¯
C
2
) (6)
C
1
?
6≡ C
rev
2
mod n (7)
Revoke Protocol. rev ←
Revoke
(params,signature,
K
M
,K
R
) protocol: the protocol is only executed if a
User needs to be revoked from the system or if the
Manager wants to reveal malicious users (and has a
strong evidence for doing so). The transcript of the
Sign
protocol can be forwarded to the Manager in
case of policy violations. The Manager can decide
about the type of revocation. User revocation or
identification are available.
User Revocation. The Manager knows the factoriza-
tion of n thus he knows the trapdoor to the Okamoto-
Uchiyama trapdoor function. From C
2
, he learns the
session key K
S
and from C
1
, his contribution w
M
to
the User private key SK
U
. The Manager can publish
revocation information rev = w
M
on a public black-
list of revoked keys. Then, each User is able to check
if the keys used for message signing are blacklisted
or not by checking C
1
?
≡ C
rev
2
mod n. The equation
holds only for revoked Users. In dense urban areas,
the blacklist has to be periodically reset to limit its
size. In that case, the user keys have a temporal valid-
ity only. Using this type of revocation, no identity is
revealed and no valid users have to update their keys.
The revocation does not influence non-revoked users
in any sense. Users only need to periodically down-
load the blacklist with short rev values. Also Regis-
trars can initiate the revocation, by sending C
R
to the
Manager who is able to linkC
R
to w
M
. The revocation
information rev is then published by the Manager in
the same way as if revocation is initiated by Users.
Identification. Sometimes, it is necessary to iden-
tify malicious users. In that case, the Manager re-
veals w
M
and finds corresponding C
R
since both val-
ues are linked by the
Register
protocol. C
R
is then
forwarded to the Registrar who can de-anonymize the
User since he has a database of digitally signed C
R
’s.
SECRYPT2013-InternationalConferenceonSecurityandCryptography
272

The identification is non-repudiable since C
R
is dig-
itally signed and perfectly binds the User to the key
inside.
4 SECURITY ANALYSIS
We provide the security analysis of the proposed
SVANET scheme in this section. The scheme is
built using well-established cryptographic protocols.
These protocols, defined in Section 2.2, provide prov-
able security features. Since all protocols are from the
Σ-protocol family (Cramer, 1996), they provide fol-
lowing features (the proofs of features can be found
in (Cramer et al., 2000)).
• Completeness: honest users who know the pri-
vate keys are always accepted by the verification
protocol.
5
• Soundness: dishonest users who do not know pri-
vate keys are always rejected by the verification
protocol.
6
• Zero-knowledge: all protocols have the Zero-
Knowledge property which mathematically
proves that no secret information about user
private keys is released by the signatures.
7
Using the above specified features of Σ-protocols,
it is straightforward, that group signatures can be con-
structed only by honest group members who know
private keys. Now, we prove privacy-enhancing fea-
tures stated in Section 3.1.
• Anonymity of Users: by having the ZK property,
it is possible to provethat the signatures release no
informationexcept that they belong to some group
member. Thus, signer’s identity is not released.
• Untraceability of Users: no entity (including
Registrar and Manager) can trace a particular user
since they cannot de-anonymize signatures alone
due to the DL assumption. Furthermore, they can-
not link the
Register
and
Sign
protocols without
cooperating.
• Unlinkability of Signatures: all signatures are
randomized by a secret value K
S
, thus all signa-
tures are mutually unlinkable.
5
This is proven by the design of the protocol - hon-
est users can always construct correct responses z
1
,z
2
,z
3
,z
S
during the
Sign
protocol.
6
This is proven by the existence of the knowledge ex-
tractor, see (Cramer et al., 2000) for more information.
7
This is proven by the existence of the Zero-Knowledge
simulator, see (Cramer et al., 2000) for more information.
• Revocation: in case of policy violation, the Reg-
istrar and the Manager can join their secret infor-
mation to identify signature owners. No entity
can misuse its secret knowledge to de-anonymize
users alone.
5 IMPLEMENTATION RESULTS
Recently, many VANET schemes with privacy-
enhancing features were proposed. Unfortunately,
many solutions are based on cryptographic primi-
tives which require bilinear pairing operations. These
operations are much more demanding than classical
operations (more than 100 times slower, based on
(Caro, 2012)). The computational demands are the
main reasons why existing proposals remain theoret-
ical only. Currently, it is unfeasible to implement
schemes which use bilinear pairing on mobile devices
such as smart-cards or mobile phones (Caro, 2012).
The signing operation would take seconds which is
unacceptable for real-life applications.
The SVANET scheme proposed in this paper is
based on plain modular arithmetic. The signing algo-
rithm needs only 8 modular exponentiations, 6 mod-
ular multiplications and 4 subtractions. Since mod-
ular operations are fast on current hardware (usually
provided by dedicated libraries or default APIs), we
consider the signing phase to be very efficient. The
complexity of a signature verification is very similar
- 8 modular exponentiations are needed if nobody is
revoked. Each revoked vehicle adds to the complexity
by 1 exponentiation. Our next goal is to limit this lin-
ear dependencyby using batch verification techniques
(Malina et al., 2012).
We implemented all the required operations on
two Android devices. One represents an older mobile
phone (Samsung Galaxy S i9000) and the second rep-
resents a new smart-phone (Samsung Galaxy Nexus
I9250M). The time of signature generation using our
scheme and 1024 b group is presented in Table 1 in
milliseconds. The numbers represent the average of
100 measurements. Based on these results, the time
of signing on an average smart-phone is under 100 ms
which we consider very practical.
6 CONCLUSIONS
In this paper, we proposed a novel concept called
SVANETs. This concept makes inter-vehicular com-
munication efficient and affordable because it elimi-
nates all the costly hardware devices, replacing them
Privacy-preservingSVANETs-Privacy-preservingSimpleVehicularAd-hocNetworks
273

Table 1: Signing Performance in Milliseconds.
Operation Samsung
Galaxy S1
Nexus
i9250
Random Num. Gen. (160b) 0,05 0,04
Random Num. Gen. (560b) 0,12 0,08
Hash SHA1 0,11 0,02
Modular Power (160b) 6,13 4,30
Modular Power 14,83 9,69
Modular Multiplication 0,16 0,14
Multiplication 0,03 0,03
Subtraction 0,01 0,02
Total 102,38 ms 67,58ms
by drivers’ smart-phones. In addition, we pro-
pose a new cryptographic scheme which makes these
SVANETs both secure and privacy-friendly. With the
proposed cryptographic scheme, it is possible to re-
tain both authenticity of messages and anonymity of
drivers. The proposed scheme allows smart-phones to
send digitally signed messages on behalf of a particu-
lar group of drivers. Our implementation results show
that the scheme is highly practical and implementable
on today’s smart-phones.
ACKNOWLEDGEMENTS
This research work is funded by projects SIX
CZ.1.05/2.1.00/03.007; the Technology Agency of
the Czech Republic projects TA02011260 and
TA03010818; the Ministry of Industry and Trade of
the Czech Republic project FR-TI4/647.
REFERENCES
Boneh, D., Boyen, X., and Shacham, H. (2004). Short
group signatures. In Proc. Adv. Cryptology-Crypto 04,
ser. LNCS 3152, pages 41–55. Springer-Verlag.
Camenisch, J. and Stadler, M. (1997). Proof systems for
general statements about discrete logarithms. Techni-
cal report.
Caro, A. D. (2012). The java pairing based cryptogra-
phy library (jpbc): Benchmark. http://gas.dia.unisa.it/
projects/jpbc/benchmark.html#testbed3.
Cramer, R. (1996). Modular Design of Secure, yet Practical
Cryptographic Protocols. PhD thesis, University of
Amsterdam.
Cramer, R., Damgrd, I., and MacKenzie, P. (2000). Effi-
cient zero-knowledge proofs of knowledge without in-
tractability assumptions. In Public Key Cryptography,
volume 1751 of Lecture Notes in Computer Science,
pages 354–372. Springer Berlin Heidelberg.
Damg˚ard, I. and Fujisaki, E. (2002). A statistically-hiding
integer commitment scheme based on groups with
hidden order. In Proceedings of the 8th International
Conference on the Theory and Application of Cryptol-
ogy and Information Security: Advances in Cryptol-
ogy, ASIACRYPT ’02, pages 125–142, London, UK.
Springer-Verlag.
Fiat, A. and Shamir, A. (1987). How to prove your-
self: Practical solutions to identification and signature
problems. In Odlyzko, A., editor, Advances in Cryp-
tology - CRYPTO 86, volume 263 of Lecture Notes in
Computer Science, pages 186–194. Springer Berlin /
Heidelberg.
Gerlach, M., Festag, A., Leinmuller, T., Goldacker, G., and
Harsch, C. (2007). Security architecture for vehicular
communication. In The 5th International Workshop
On Intelligent Transportation.
Haas, J., Hu, Y.-C., and Laberteaux, K. (2009). Real-world
VANET security protocol performance. In Global
Telecommunications Conference, 2009. GLOBECOM
2009. IEEE, pages 1 –7.
Hajny, J. and Malina, L. (2013). Unlinkable attribute-
based credentials with practical revocation on smart-
cards. In Proceedings of the 11th international confer-
ence on Smart Card Research and Advanced Applica-
tions, CARDIS’12, pages 62–76, Berlin, Heidelberg.
Springer-Verlag.
Lin, X., Sun, X., han Ho, P., and Shen, X. (2007). Gsis: A
secure and privacy preserving protocol for vehicular
communications. In IEEE Transactions on Vehicular
Technology, volume 56, pages 3442–3456.
Malina, L., Castella-Roca, J., A., V.-G., and Hajny, J.
(2012). Short-term linkable group signatures with cat-
egorized batch verification. In the FPS, pages 1 –17.
Menezes, A. J. (1996). Handbook of Applied Cryptography.
CRC Press.
Okamoto, T. and Uchiyama, S. (1998). A new public-
key cryptosystem as secure as factoring. In Advances
in Cryptology - EUROCRYPT 98, volume 1403 of
Lecture Notes in Computer Science, pages 308–318.
Springer Berlin / Heidelberg.
Pedersen, T. P. (1992). Non-interactive and information-
theoretic secure verifiable secret sharing. In Proceed-
ings of the 11th Annual International Cryptology Con-
ference on Advances in Cryptology, CRYPTO ’91,
pages 129–140, London, UK, UK. Springer-Verlag.
Plossl, K., Nowey, T., and Mletzko, C. (2006). Towards
a security architecture for vehicular ad hoc networks.
In Availability, Reliability and Security, 2006. ARES
2006. The First International Conference on, page 8.
Quisquater, J.-J., Guillou, L., Annick, M., and Berson, T.
(1989). How to explain zero-knowledge protocols to
your children. In Proceedings on Advances in cryp-
tology, CRYPTO ’89, pages 628–631, New York, NY,
USA. Springer-Verlag New York, Inc.
Raya, M. and Hubaux, J.-P. (2007). Securing vehicular ad
hoc networks. J. Comput. Secur., 15:39–68.
Raya, M., Papadimitratos, P., and Hubaux, J.-P. (2006). Se-
curing vehicular communications. Wireless Commu-
nications, IEEE, 13(5):8 –15.
Reed, M., Syverson, P., and Goldschlag, D. (1998). Anony-
mous connections and onion routing. IEEE Journal on
Selected Areas in Communications, 16(4):482–494.
Zhang, C., Lu, R., Lin, X., Ho, P.-H., and Shen, X. (2008).
An efficient identity-based batch verification scheme
for vehicular sensor networks. In INFOCOM, pages
246–250. IEEE.
SECRYPT2013-InternationalConferenceonSecurityandCryptography
274
