An Interactive Evaluation Method of Decentralized Procurement

Plan by Multi-Objective Genetic Algorithm

Ryoji Kobayashi

, Masakatsu Mori

, Masaki Samejima

and Norihisa Komoda

Graduate School of Information Science and Technology, Osaka University, 2-1, Yamadaoka, Suita, Osaka, Japan

Yokohama Research Laboratory, Hitachi, Ltd., 292 Yoshida-cho, Totsuka-ku, Yokohama, Kanagawa 244-0817, Japan

Keywords: Supply Chain, Decentralized Procurement Plan, Multi-Objective Genetic Algorithm, Interactive Evaluation.

Abstract: This paper addresses evaluation of a decentralized procurement plan for the support of the discussion among

decision-makers with considering a catastrophic disaster. For the evaluation of the decentralized

procurement plan, we have formulated the decentralized procurement planning problem as 3-objective

optimization problem. However, multiple-objective genetic algorithms (MOGA) to solve the problem take

several minutes and display many Pareto solutions. We propose the interactive evaluation method of the

decentralized procurement plan that is an expanded interactive MOGA (iMOGA) with loss evaluation

simulator and solution selection by characteristics of the decentralized procurement plan. Experimental

results show that the proposed method can allow the decision-makers to find their preference solutions with

38% fewer interactions than the basic iMOGA can.

1 INTRODUCTION

Supply chain is a sequence of operations such as

procurement, production, logistics and sale for

supplying products from suppliers to final

consumers. Retailers in the supply chain procure

products from suppliers and sell products to the

consumers. In supply chain, there is a problem that

catastrophic disasters such as earthquakes may

interrupt the procurement from suppliers. The

retailers suffer losses because they can not sell the

products along with the consumers' demand. In

order to decrease the losses, the retailer increases the

stock of the products and decentralizes procurement

of the product from geographically distributed

multiple suppliers (Chopra and Sodhi, 2004),

(Kleindorfer and Saad, 2005). However, there are so

many plans of decentralizing procurement with

inventory stock that the decision-makers in the

retailers can not find the appropriate plan. In this

paper, we address evaluating the decentralized

procurement plans for the decision making.

For evaluating the decentralized procurement

plans, we formulate the decentralized procurement

planning problem. Decentralizing procurements can

decrease the losses because surviving suppliers from

the catastrophic disasters can keep supplying

products to the retailers. And the increase of the

stock is also available for decreasing the losses. But,

the retailers have to cost in the decentralizing

procurement and the control of the increased stock.

This discussion leads us to formulate the

decentralizing procurement planning problem as a 3-

objective optimization problem to decrease the loss,

the cost for the decentralization, and the cost for the

stock.

Through the formulation, the decision makers

can discuss the plans based on the evaluation by

solving the 3-objective optimization problem by

computer. For more efficient discussion, it is

possible to solve the problem by the Multiple

Objective Genetic Algorithm (MOGA) that is one of

the meta heuristics. However, the computational

time by MOGA is not so short as the decision

makers can use in their discussion because MOGA

is the method for finding many Pareto solutions. The

decision makers can not understand many Pareto

solutions and rather hope to select about 10

representative Pareto solutions based on their

preferences in short time. In this paper, we apply

the interactive MOGA (iMOGA) to decentralizing

procurement planning problem and propose the

method to display the representative solutions with

fewer interactions.

361

Kobayashi R., Mori M., Samejima M. and Komoda N..

An Interactive Evaluation Method of Decentralized Procurement Plan by Multi-Objective Genetic Algorithm.

DOI: 10.5220/0004507203610368

In Proceedings of the 4th International Conference on Data Communication Networking, 10th International Conference on e-Business and 4th

International Conference on Optical Communication Systems (ICE-B-2013), pages 361-368

ISBN: 978-989-8565-72-3

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

2 DECENTRALIZED

PROCUREMENT PLANNING

PROBLEM

2.1 Target Supply Chain Model

First, we introduce a basic supply chain model that

consists of a retailer and multiple suppliers. In order

to consider that a catastrophic disaster hits the

supplier, we have expanded such the basic supply

chain model. Fig.1 shows the target supply chain

model.

Figure 1: The target supply chain model.

Unless the catastrophic disaster happens, the retailer

makes a procurement plan to replenish the stock I up

to the safety stock SS. The stock I is remained

products when the products for demand D is shipped

from safety stock SS;. The amount of

replenishment M is decided by the following:





 





As the above formula shows, because the time

for delivery to the customer from the retailer is 0, the

replenishment M is equal to D. The demand D

follows the Gaussian distribution. And the retailer

has design the strategy of the procurement; what

percent of the amount of the replenishment is

assigned to each supplier. We call the rate of the

assignment “order rate: o

”. In the procurement plan,

the retailer orders (



 products to supplier s.

When the catastrophic disaster hits some

suppliers, the supplier can not supply their products

at the rate of the probability of the breakdown 



;





0 for 



days. In order to make up the lacking

products, the retailer place the orders to the

surviving suppliers. Then, the supplier can supply

additional products up to a ceiling of the additional

procurement rate ( 



) of the order rate. Furthermore,

the retailer can store the urgent stocks U up to a

ceiling of the capacity Cap. When the total stock

(I+U) is below the demand D, the loss L (=D-I-U)

happens.

2.2 Problem Formulation

The decision-makers in the retailer make a

decentralized procurement plan P that indicates both

of each order rate o

and the urgent stock U. So, the

decision variables of this problem are P as shown in

the following:





,



,…,



,

The decision-makers decide the procurement plan P

to decrease the loss L. But the decrease of the loss

by decentralization carries cost E for orders to the

suppliers that supply the high price c

products. Here,

decentralized ordering costs E is defined as the

increased cost compared to the cheapest plan.









min













Furthermore, the urgent stocks U also cost in being

stored in the warehouse. Therefore, we formulate the

decentralized procurement planning problem as the

following 3-objectives optimization problem:

 Objective functions





  Loss → minimize











 Decentralizedorderingcosts

→ minimize





  Urgentstocks → minimize

 Constraints











1

where the above described constraints are only the

constraints that represent the decentralized

procurement planning problem.

2.3 Research Purpose

In the multi-objective optimization problem, it is

impossible to decide the optimal solution; some

solutions indicate low loss and high cost, but the

others indicate high loss and low cost. General

approaches derive Pareto optimal solutions whose

one or more objective functions’ values are not

worse than the other solutions, and has the decision-

makers to select solutions that they prefer. The

Pareto optimal solution is decided by Pareto ranking

method shown in Fig. 2. Fig. 2 assumes two kinds of

the objective functions (



, 



) to be minimized. The

most inner coordinates indicate the value of Pareto

optimal solutions. The evaluation values of Pareto

optimal solutions shape a Pareto curve. Generally, in

ICE-B2013-InternationalConferenceone-Business

362

order to solve such a multi-objective optimization

problem, the multi-objective genetic algorithm

(MOGA) has been applied (Murata and Ishibuchi,

1995), (Fonseca and Fleming, 1993). MOGA is the

method to derive Pareto optimal solutions efficiently

by the weighting sum of objective functions (Murata

1995) or ranking the solutions (Fonseca and

Fleming, 1993). In this paper, MOGA with Pareto

ranking method (Fonseca and Fleming, 1993) is

applied to the problem. The basic idea of MOGA is

shown in Fig. 3. MOGA is performed based on the

following steps:

(1) Initialize: generate some P

(2) Crossover: generate two solutions from a pair of

(3) Mutation: generate a solution from P

(4) Selection: select generated P based on Pareto

rank

Pareto rank indicates the rank of the solution in

generated P. In order to decide Pareto rank, MOGA

count the number of non-dominated solutions x

whose all objective functions’ values are better than

P. Let n(x, P) denote the number of x for P. Pareto

rank is decided as n(x, P)+1. In this paper, we

assume that only the solutions have Pareto rank of

1are selected.

Figure 2: Pareto ranking method.

Figure 3: Basic idea of MOGA.

Because MOGA is the method for deriving many

different Pareto optimal solutions, there are

following problems in the use of MOGA for the

support of the decision-makers’ discussion.

 The decision-maker has their preferences of the

solutions, e.g. the loss is more important than the

cost for the stock. But they can not select the

preference solution from many Pareto optimal

solutions.

 MOGA takes several minutes to solve the

decentralized procurement planning problem.

The decision-makers have to wait the response from

MOGA in their discussion.

So, our research purpose is to allow the decision-

makers to find preference solution in a minute.

3 INTERACTIVE EVALUATION

METHOD

OF DECENTRALIZED

PROCUREMENT PLAN

3.1 Outline of the proposed Method

Because many Pareto optimal solutions are hard for

decision-makers to select and are derived in several

times, we introduce the interactive MOGA

(iMOGA) that stops the crossover and the mutation

in a short time and displays about 10 representative

solutions to the decision-makers (Ishibashi, 2011),

(Hiroyasu, 2008), (Takagi, 2001). Fig. 4 shows the

outline of the interactive evaluation method by

iMOGA.

Figure 4: Outline of the interactive evaluation method by

iMOGA.

iMOGA executes MOGA with fewer crossovers and

mutations several times in order to display the

solutions in a short time. The proposed method uses

the general crossovers and mutations method: blend

crossover (Takahashi and Kita, 2001) and mutation

to exchange randomly selected two o

each other.

Because the decision-makers can watch only about

Pareto optimal solutions

Pareto curve

AnInteractiveEvaluationMethodofDecentralizedProcurementPlanbyMulti-ObjectiveGeneticAlgorithm

363

10 solutions, iMOGA makes about 10 clusters of the

solutions by MOGA. In this method, we apply k-

means method as a typical clustering algorithm

(Hearst, 2006). And, the decision-makers select the

preferable solution from the displayed representative

solutions that are closest to the center of each cluster.

Basic iMOGA uses the solutions in the cluster that

the decision-maker selects for the next GA. By

repeating MOGA and the decision-makers’ selection,

the preference solution appears in iMOGA.

Furthermore, in order to display the preference

solutions through fewer times of the interaction, the

proposed method has the following two functions:

 Loss evaluation simulator

Because the breakdown happens at random and the

demand changes with following the Gaussian

distributions, it is impossible to evaluate loss L

uniquely. The loss evaluation simulator can

evaluate the distribution of the loss L by Monte

Calro Method.

 Solution selection based on decentralized

procurement plan

iMOGA uses the solutions in the cluster that the

decision-makers select. However, if the preference

solution is not in the cluster, it becomes difficult to

search the preference solution by the crossover and

the mutation.

3.2 Loss Evaluation Simulator

The outline of the loss evaluation simulator is shown

in Fig. 5. As shown in Fig. 5, the probability of the

distribution is not Gaussian distribution. A survey in

Japan reports that the catastrophic earthquake

happens below 1%. So, it is not appropriate to

evaluate the loss as the expectation of the probability

distribution of the loss because there is potential for

underestimating the loss (Azaron et al., 2008), (Wu

et al., 2010).

Figure 5: Outline of loss evaluation simulator.

In order to evaluate such the catastrophic disaster

that causes great loss but rarely happens, we

introduce the index of Value at Risk (VaR)

(Johnathan, 2010). By integrating the probability

density from the largest loss in the distribution to the

smaller, the loss when the value of integral is a

certain rate (0.001 in Fig.5) is VaR of the rate (0.001

VaR in Fig.5).

It is necessary to decide the distribution of the

loss for deciding VaR. Therefore, the proposed

method uses Monte Carlo method that samples form

the distribution of the demand and the probability of

the breakdown and decide the loss (Johnathan, 2010).

In order to evaluate the loss for the recovery time r

days, the proposed method uses the time-series

simulation with a set of sampled values shown in Fig.

Figure 6: Time-series loss simulation.

After sampling by Monte Carlo method, the time-

series simulator evaluates the loss by using the

sample set of the demand. As shown in Fig. 6, there

no losses before the breakdown. When the

breakdown happens, the supply from the supplier

that is broken down is 0. Then the retailer places

orders to the other suppliers additionally. But, if the

demand is larger than the supply, the stock is

decreased day by day. Finally, the stock is exhausted

and the demand is regarded as the loss until the

supplier is recovered.

3.3 Solution Selection based

on decentralized Procurement

Plans

In order to search the preference solution that is not

in the cluster selected by the decision-makers, the

proposed method selects not only the solutions in the

selected cluster but also a part of the other solutions.

From the other solutions, it is necessary to select the

solutions that tend to generate the preference

solutions by crossover. In the decentralized

procurement planning problem, there are the

relations between the plan and the preference. Fig. 7

shows the relation and our approach to decide which

ICE-B2013-InternationalConferenceone-Business

364

Figure 7: Approach to select solutions.

solutions to be used in addition to the solutions in

the selected cluster.

As described in section 3.2, the retailer places

orders to surviving suppliers when the catastrophic

disaster prevents some suppliers to supply products.

As Fig. 7 shows, when the retailer plans the

decentralized ordering to many suppliers, the loss

and the urgent stock can be decreased by additional

orders. This plan is preferred by those who think that

the loss and the cost for stock are important. On the

other hand, when the retailer does not decentralize

the orders, the loss and the urgent stock can not be

decreased, but the cost for decentralized ordering is

decreased. This plan is preferred by those who think

that cost for decentralized ordering is important.

Therefore, the proposed method selects the solutions

that indicate either decentralized ordering or not-

decentralized ordering, and generate preference

solutions by crossover of the solutions.

In order to select such plans, the amount of the

additional orders is an effective index. The amount

of the additional orders is large in the decentralized

procurement plan. Here, the process of selecting

solution based on the amount of the additional

orders is shown in Fig. 8. The amounts of the

additional orders are calculated in the loss evaluation

simulator and follow the Gaussian distribution. By

using the amounts of the additional orders, the

proposed method selects the solutions that have

large amount or small amount of the additional

orders by the following:

(1) The proposed method calculates the frequency

distribution of average additional orders based on

the solutions by the loss evaluation simulator.

(2) From the distribution, the proposed method

selects the solutions whose average additional

orders in the top or bottom N%.

The selected solutions are used for next MOGA

together with the solutions in the cluster that the

Figure 8: Process of selecting solution based on the

amount of the additional orders.

decision-makers select.

4 EVALUATION EXPERIMENT

4.1 Target of Experiment

The target retailer deals with electronic device that

the retailer procures from 3 suppliers A, B and C

(Mitsukuni et al., 1997). The demand to the retailer

follows Gaussian distribution of N(1500, 250000).

The safety stock coefficient is 1.96 and the retailer

stores the safety stock SS:

  1500  

1.96

√

250000

=7960

The parameter setting of the suppliers is shown in

Table 1.

Table 1: Parameter setting of the suppliers.

Supplier

A B C

Price [yen] 1,000 1,010 1,020

Lead time [day] 4

Probability of

breakdown

0.83% 0.126% 0.06%

Recovery time

[day]

Additional

procurement

rate

20%

In this experiment, we use the agent to express the

decision-makers’ preferences and evaluate the

proposed method by simulating the decision-makers’

selection. The agent selects the representative

solution in the interaction based on the following

utility function (Shixin et al., 2006):

AnInteractiveEvaluationMethodofDecentralizedProcurementPlanbyMulti-ObjectiveGeneticAlgorithm

365

  





















1

By changing the weight 



randomly 250 times, we

have the 250 kinds of agents to find their preference

solution. The agent gives up the search when the

interaction is over 10 times. In order to compare the

proposed method, we applied the following methods

too:

 Brute force search method

Brute force search method searches Pareto optimal

solutions by evaluating all the solutions. The

preference solution is displayed but many Pareto

optimal solutions are also displayed. And the

computation time is so long that the decision-

makers can not use for the discussion.

 MOGA

As described in the section 2.3, MOGA is the

method to search efficiently Pareto optimal

solutions. As well as the brute force search method,

MOGA displays many Pareto optimal solutions.

 iMOGA

As described in the section 3.1, iMOGA repeats

short MOGA. iMOGA does not select the solution

based on the amount of the additional orders.

First, MOGA, iMOGA and the proposed method

generate the solutions through changing the order

rates by 10% or the urgent stock by Cap / Lead time

for the initialization of the solutions. And, MOGA,

iMOGA and the proposed method performs the

blend crossover; a new solution is generated from 2

solutions by selecting a supplier randomly and set

new order rate on the selected one as a uniform

random number based on the order rates of 2

solutions. MOGA and iMOGA performs mutations

to exchange order rates among supplier A, B and C.

The mutation rate is 1%. The proposed method does

not perform the mutation because the proposed

method selects solutions, described in section 3.3, to

diversify the solutions. In iMOGA and the proposed

method, 6 generations are generated in MOGA and

10 representative solutions by k-means clustering

are displayed for one interaction.

The computer used in this experiment has the

specification of Intel® Xeon® 2.1GHz 32 cores

and

128 GB Memory. The evaluation criteria are the

following:

 Response time

Response time indicates how long the decision-

Intel and Xeon are trademarks or registered trademarks of Intel

Corporation.

makers can wait the output from each method after

they execute the methods. The decision-maker can

wait about 10 or 20 seconds. Decision-making takes

several minutes, but the decision-makers have to

check as many solutions as possible. So the

decision-makers can wait only 10 or 20 seconds to

get the output.

 The number of the interactions

iMOGA and the proposed method have the

decision-makers to select the solutions

interactively. The better method can decrease the

number of the interactions by displaying the

preference solutions early.

 Rate of successful search

Because the decision-makers give up the search in

10 interactions, the rate of successful search

indicates the rate of the preference solutions to be

displayed within 10 interactions.

4.2 Experimental Result

The response time, the number of interactions and

the rate of the successful search are shown in Fig. 9,

Fig. 10, and Fig. 11, respectively.

Figure 9: Response time.

Figure 10: The number of the interactions.

Fig. 9 shows that brute force method and MOGA

takes over a few minutes, which is not available for

the decision-makers discussion. On the other hand,

ICE-B2013-InternationalConferenceone-Business

366

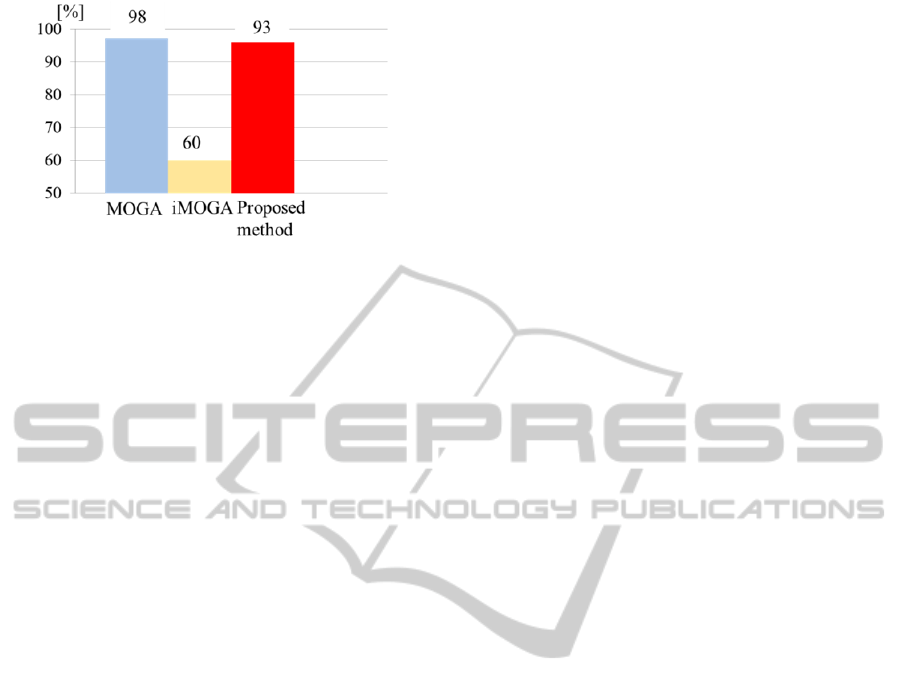
Figure 11: The rate of the successful search.

iMOGA can be executed in 9.3 seconds, and the

proposed method can be executed in 10 seconds.

Response time of proposed method is a little bit

longer than that of iMOGA because of selecting the

solution based on the amount of the additional

orders. But the increase of the computational time is

trivial for the decision-makers.

Fig. 10 shows the result of the interaction by 250

kinds of the agent. The proposed method can search

the preference solutions for the half of the agents

with 3 interactions. The more preference solutions

are searched up to 7 interactions. Finally, the

proposed method can not search 7% of the

preference solutions within 10 times of the

interactions. iMOGA can search the preference

solutions for 30% of the agents with 3 interactions

and also search more solutions up to 7 interactions.

iMOGA can not search 40% of the preference

solutions within 10 times of the interactions. As

shown in Fig. 10, the average of the interactions by

the proposed method is 3.9 and one by iMOGA is

6.3. So, the proposed method can succeed in

decreasing the number of the interactions by 38%

compared to iMOGA.

Focusing the rate of the successful searches

shown in Fig. 11, MOGA can search the preference

solutions for 98% of the agents within 10

interactions. The proposed method can search the

preference solutions for 93% of the agents within 10

interactions. This indicates that the proposed method

is as available as MOGA from the viewpoint of the

accuracy of displaying the preference solutions.

Because iMOGA selects solutions for next MOGA

only from a selected cluster, iMOGA often fails to

search the preference solutions within 10

interactions.

From the experimental result, it is confirmed that

it is possible to search more preference solutions by

the proposed method with fewer interactions

compared to iMOGA. And the representative

solutions are displayed within 10 seconds, which is

short enough to support the discussion.

5 CONCLUSIONS

In this paper, we proposed an interactive evaluation

method of decentralized procurement plan by Multi-

objective genetic algorithm (MOGA). Although

MOGA has been applied to the multi-objective

optimization problem, the decision-maker can not

understand many Pareto optimal solutions by

MOGA. And, MOGA takes several minutes to solve

the multi-objective optimization problem. Our

proposed method displays the representative

solutions to the decision-makers and has them to

select one. By repeating this interaction, the

decision-maker can search their preference solutions

in a short time. In order to evaluate the loss that is

caused probabilistic catastrophic disaster, we

developed the loss evaluation simulator. This

simulator can evaluate the loss by simulating the

stock with Monte Carlo method. Furthermore, in

order to decrease the interaction, the proposed

method selects not only the solutions that are in the

selected cluster but also the solutions that tend to

generate the preference solutions based on the

amount of the additional orders. Through the

application of the proposed method to the supply

chain model, we confirmed that the proposed

method decreased the 38% of the interactions of

selecting solutions compared to iMOGA.

Our future work is to expand the versatility of

the proposed method to apply other supply chain

model. It will be necessary to analyse the sensitivity

of the parameters, especially the number of suppliers

and additional procurement rates. For practical use

of this method, we will implement the graphical user

interface to display the representative solutions to

support selecting solutions by the decision-maker.

REFERENCES

Azaron, M. A., Brown, K.N., Tarim, S.A., Modarres M.,

2008. “A multi-objective stochastic programming

approach for supply chain design considering risk,”

International Journal of Production Economics, Vol.

116, pp. 129-138.

Chopra, S., Sodhi, M. S., 2004. “Managing Risk to Avoid

Supply-Chain Breakdown,” MIT Sloan Management

Review, Vol. 46, No. 1 pp.53-61.

Fonseca C. M., Fleming, P. J., 1993. “Genetic Algorithms

for Multiobjective Optimization: Formulation,

Discussion and Generalization,” In Proceedings of the

International Conference on Genetic Algorithms,

pp. 416-423.

Hearst, M. A., 2006. “Clustering versus faceted categories

for information exploration,” Communications of the

AnInteractiveEvaluationMethodofDecentralizedProcurementPlanbyMulti-ObjectiveGeneticAlgorithm

367

ACM, Vol. 49, No. 4, pp.59-61.

Johnathan, M., 2010. Modeling Risk: Applying Monte

Carlo Risk Simulation, Strategic Real Options,

Stochastic Forecasting, and Portfolio Optimization,

John Wiley & Sons.

Kleindorfer, P. R., Saad, G. H., 2005. “Managing

Disruption Risks in Supply Chains,” Production and

Operations Management, Vol. 14, No. 1, pp.53-68.

Mitsukuni, K., Komiya, F., Sugiyama, K., Tomita, Y.,

Maki, H., Komoda, N., 1997. “Coupling point

production control system for quick response to orders

and minimum inventories”, In Proceedings of the 6th

International Conference on Emerging Technologies

and Factory Automation, pp. 154 – 159.

Murata, T., Ishibuchi, H., 1995. “MOGA: multi-objective

genetic algorithms,” In Proceedings of IEEE

International Conference on Evolutionary

Computation, vol. 1, pp. 289.

Shixin, L., Jiafu, T., Jianhai, S., 2006. “Order-planning

model and algorithm for manufacturing steel sheets,”

International Journal of Production Economics, Vol.

100, No. 1, pp. 30-43

Takagi, H., 2001. “Interactive evolutionary computation:

Fusion of the capabilities of EC optimization and

human evaluation,” In Proceedings of the IEEE, Vol.

89, No. 9, pp.1275-1296.

Ishibashi, K., 2011. “Proposal of Font Selection Method

using Interactive Genetic Algorithm and Similarity

Serch,” ITE Technical Report, Vol. 35, No. 39, pp.33-

36.

Hiroyasu, T., 2008. “Discussion of the Evaluation Method

of the Individual for interactive Genetic Algorithm, ”

IPSJ SIG Technical Report, Vol. 68, No. 29, pp.113-

116.

Takahashi M., Kita H., 2001. “A Crossover Operator

Using Independent Component Analysis for Real-

Coded Genetic Algorithm,” In Proceedings of the

2001 Congress on Evolutionary Computation, pp.

643-649.

Wu, D. D., Zhang, Y., Wu, D., Olson, L., 2010. “Fuzzy

multi-objective programming for supplier selection

and risk modeling: A possibility approach,” European

Journal of Operational Research, Vol. 200, pp. 774-

787.

ICE-B2013-InternationalConferenceone-Business

368