Partially Wildcarded Attribute-based Encryption and Its Efﬁcient

Construction

Go Ohtake

, Yuki Hironaka

, Kenjiro Kai

, Yosuke Endo

, Goichiro Hanaoka

, Hajime Watanabe

Shota Yamada

∗2,3

, Kouhei Kasamatsu

2,4

, Takashi Yamakawa

2,3

and Hideki Imai

2,5

Science & Technology Research Laboratories, Japan Broadcasting Corporation,

1-10-11 Kinuta, Setagaya-ku, Tokyo 157-8510, Japan

Research Institute for Secure Systems (RISEC), National Institute of Advanced Industrial Science and Technology (AIST),

1-1-1 Umezono, Tsukuba-shi, Ibaraki 305-8568, Japan

Graduate School of Frontier Sciences, The University of Tokyo, 5-1-5 Kashiwanoha, Kashiwa-shi, Chiba 277-8561, Japan

Security Solution Business Department, NTT Software Corporation,

Teisan Kannai Bldg. 209, Yamashita-cho, Naka-ku, Yokohama-shi, Kanagawa 231-8551, Japan

Faculty of Science and Engineering, Chuo University 1-13-27 Kasuga, Bunkyo-ku, Tokyo 112-8551, Japan

Keywords:

Attribute-based Encryption, Ciphertext Policy, Wildcard.

Abstract:

Many kinds of ciphertext-policy attribute-based encryption (CP-ABE) schemes have been proposed. In CP-

ABE, the set of user attributes is associated with his/her secret key whereas a policy is associated with a

ciphertext so that only users whose attributes satisfy the policy can decrypt the ciphertext. CP-ABE may be

applied to a variety of services such as access control for ﬁle sharing systems and content distribution ser-

vices. However, CP-ABE costs more for encryption and decryption in comparison with conventional public

key encryption schemes since it can handle more ﬂexible policies. In particular, wildcards, which mean that

certain attributes are not relevant to the ciphertext policy, are not essential for a certain service. In this paper,

we construct a partially wildcarded CP-ABE scheme with a lower decryption cost. In our scheme, the user’s

attributes are separated into those requiring wildcards and those not requiring wildcards. Our scheme hence

embodies a CP-ABE scheme with a wildcard functionality and an efﬁcient CP-ABE scheme without wild-

card functionality. We compare our scheme with the conventional CP-ABE schemes and describe a content

distribution service as an application of our scheme.

1 INTRODUCTION

1.1 Background

In attribute-based encryption (ABE), the set of user

attributes is associated with a secret key or a cipher-

text so that only users whose attributes satisfy the

policy can decrypt the ciphertext. ABE may be ap-

plied to a variety of services, e.g., access control for

ﬁle sharing systems and content distribution services.

The ﬁrst ABE scheme was proposed as an extension

of the identity-based encryption (IBE) scheme called

Fuzzy IBE (Sahai and Waters, 2005) and many kinds

of ABE schemes have been proposed. ABE scheme

∗

The seventh author is supported by a JSPS Research

Fellowship for Young Scientists.

is classiﬁed into two types: key-policy ABE (KP-

ABE) (Goyal et al., 2006; Ostrovsky et al., 2007) and

ciphertext-policy ABE (CP-ABE) (Bethencourt et al.,

2007; Cheung and Newport, 2007; Emura et al., 2009;

Katz et al., 2008; Lewko et al., 2010; Nishide et al.,

2008; Okamoto and Takashima, 2010; Waters, 2011).

In KP-ABE, ciphertexts are associated with attributes,

and users’ secret keys are associated with policies. If

the attributes satisfy the key policy, the user can de-

crypt the ciphertext successfully. On the other hand,

in CP-ABE, attributes are associated with secret keys

and policies are associated with ciphertexts. If the at-

tributes satisfy the ciphertext policy, the user can de-

crypt the ciphertext successfully. In this paper, we

focus on CP-ABE.

Bethencourt, Sahai, and Waters proposed the ﬁrst

CP-ABE scheme (Bethencourt et al., 2007), where ci-

339

Ohtake G., Hironaka Y., Kai K., Endo Y., Hanaoka G., Watanabe H., Yamada S., Kasamatsu K., Yamakawa T. and Imai H..

Partially Wildcarded Attribute-based Encryption and Its Efﬁcient Construction.

DOI: 10.5220/0004509303390346

In Proceedings of the 10th International Conference on Security and Cryptography (SECRYPT-2013), pages 339-346

ISBN: 978-989-8565-73-0

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

phertext policies are expressed by a tree structure in-

cluding AND-gates and OR-gates. This scheme al-

lows ciphertext policies to be very expressive, but it

has larger costs for encryption and decryption than

conventional public key encryption schemes. In con-

trast, Cheung and Newport proposed an efﬁcient CP-

ABE scheme (Cheung and Newport, 2007), where ci-

phertext policies are compactly expressed by AND-

gates and three types of attribute values: positive, neg-

ative, and don’t care. This scheme has much lower

costs for encryption and decryption than the scheme

in (Bethencourt et al., 2007). However, the expres-

sion of ciphertext policies is rather restricted: the size

of possible values for each attribute is only one bit.

On the other hand, Nishide, Yoneyama, and Ohta pro-

posed a CP-ABE scheme (Nishide et al., 2008) where

ciphertext policies are expressed by AND-gates and

a subset of possible values for each attribute and the

corresponding policies are hidden for the purpose of

guaranteeing the recipient’s anonymity. Both (Che-

ung and Newport, 2007) and (Nishide et al., 2008)

construct an efﬁcient CP-ABE scheme with limited

ciphertext policies by using only AND-gates. Fur-

thermore, in these schemes, encryptors can use wild-

cards to mean that certain attributes are not relevant

to the ciphertext policy. On the other hand, Emura,

Miyaji, Nomura, Omote, and Soshi proposed a CP-

ABE scheme (Emura et al., 2009) that is more efﬁ-

cient than those of (Cheung and Newport, 2007) and

(Nishide et al., 2008) by removing the wildcard func-

tionality. In this scheme, ciphertext policies are ex-

pressed by AND-gates and one of the possible values

for each attribute. This scheme has much lower costs

for decryption compared with the scheme presented

in (Nishide et al., 2008).

CP-ABE schemes with a wildcard functional-

ity (Cheung and Newport, 2007; Nishide et al.,

2008) are effective for services where certain at-

tributes might not be relevant to the ciphertext pol-

icy. However, this scheme is functionally redundant

if all attributes are relevant. In contrast, the CP-ABE

scheme without the wildcard functionality (Emura

et al., 2009) has much lower costs for decryption.

However, this scheme cannot be applied to services

where certain attributes are not relevant to the cipher-

text policy.

In particular, the decryption costs of broadcasting

services must be as small as possible, since the de-

vices in the user terminals are usually lower in per-

formance than personal computers and it is possible

that the decryption process is performed on tamper-

resistant devices such as smart cards.

1.2 Our Contributions

In this paper, we propose a partially wildcarded CP-

ABE scheme to reduce the decryption cost. (Emura

et al., 2009) shows that the presence or absence of

wildcard functionality has an inﬂuence on the efﬁ-

ciency of the CP-ABE scheme. In our scheme, an

user’s attribute list is separated into a list of attributes

which require wildcards and an list of attributes which

do not require wildcards. Our scheme embodies a CP-

ABE scheme with a wildcard functionality and an ef-

ﬁcient CP-ABE scheme without a wildcard function-

ality. Our idea is to split the master secret key into

two shares by using 2-out-of-2 secret sharing and to

use the shares as master secret keys of each CP-ABE

scheme. We compare our scheme with conventional

CP-ABE schemes and describe a content distribution

service as an application of our scheme. For example,

if there is only one attribute that requires wildcards

among four attributes, our scheme can reduce the de-

cryption cost by 40% in comparison with the conven-

tional CP-ABE schemes.

2 PRELIMINARIES

2.1 Model

A CP-ABE scheme consists of the following four al-

gorithms (Nishide et al., 2008).

Setup(1

): This algorithm takes the security parame-

ter k as input and generates a public key PK and a

master key MK.

KeyGen(MK, L): This algorithm takes MK and an at-

tribute list L as input and generates a secret key

associated with L.

Encrypt(PK, M, W): This algorithm takes PK, a mes-

sage M, and an ciphertext policy W as input and

generates a ciphertext CT.

Decrypt(CT, SK

): This algorithm takes CT and SK

associated with L as input. We use the no-

tation L |= W to mean that L satisﬁes W. If

L |= W, it returns the message M such that

Decrypt(Encrypt(PK,M,W), SK

) = M

2.2 Security Deﬁnition

We consider the following security game.

Init: The adversary A chooses the challenge cipher-

text policy W and gives it to the challenger B.

Setup: B runs Setup and gives PK to A .

SECRYPT2013-InternationalConferenceonSecurityandCryptography

340

Phase 1: A transmits an attribute list L for KeyGen

query to B . B returns SK

associated with L to A

iff L 6|= W.

Challenge: A transmits two messages M

and M

B. B chooses b ∈ {0,1} at random, generates a

ciphertext CT = Encrypt(PK,M

,W), and trans-

mits it to A.

Phase 2: Same as Phase 1.

Guess: A outputs a guess b

′

of b.

The security of the CP-ABE scheme is deﬁned as

follows:

Deﬁnition 1. We say that a CP-ABE scheme is se-

lective IND-CPA secure if Adv



Pr[b

′

= b] −



negligible in the above game.

2.3 Bilinear Maps

Let G,G

be multiplicative cyclic groups of prime

order p and g be a generator of G. A bilinear map is

a map e : G × G → G

with the following properties:

Bilinear: e(g

) = e(g,g)

∀a,b ∈ Z

Non-degenerate: e(g,g) 6= 1

We say that G is a bilinear group if the group action

in G can be efﬁciently computed and there exists a

group G

and an efﬁciently computable bilinear map

e : G × G → G

, as above.

2.4 Decisional Bilinear Difﬁe-Hellman

(DBDH) Assumption

Let z

∈ Z

∗

be chosen at random and g ∈ G

be a generator. Also, let Z be a random element

in G

. The DBDH assumption is that no prob-

abilistic polynomial-time algorithm can distinguish

the tuple [g,g

,e(g,g)

] from the tuple

[g,g

,Z] with a non-negligible advantage.

3 CONVENTIONAL SCHEMES

Here, we describe the CP-ABE algorithm with a wild-

card functionality that was proposed in (Nishide et al.,

2008) and the algorithm without a wildcard function-

ality that was proposed in (Emura et al., 2009).

3.1 CP-ABE with Wildcard (Nishide

et al., 2008)

In (Cheung and Newport, 2007), each attribute can

take two values: 1 (positive) and 0 (negative), but in

(Nishide et al., 2008), each attribute can take two or

more values, and eachW

in a ciphertext policyW can

be any subset of possible values for each attribute A

In this paper, the user’s attribute list is simply repre-

sented by indices correspondingto the possible values

for each attribute. Let S

= {1, 2, ..., n

} be the set of

possible values for A

where n

is the number of pos-

sible values for A

. Then, let L = [L

,...,L

] be the

attribute list where L

∈ S

and let W = [W

, W

, ...,

] be the ciphertext policy where W

⊆ S

. When the

encryptor speciﬁes a wildcard for A

, it corresponds

to specifying W

= S

for A

. The attribute list L satis-

ﬁes the ciphertext policy W; that is, L |= W iff L

∈ W

for all i ∈ [n].

Setup(1

): Choose multiplicative cyclic groups G

and G

of prime order p, a bilinear map e :

G × G → G

, and a random generator g ∈

G. Then, pick w, a

i,t

, b

i,t

∈ Z

∗

, A

i,t

∈

G at random for i ∈ [n], t ∈ [n

]. Compute

Y = e(g,g)

and output the public key PK =

hp,G,G

,e,g,Y, {{A

i,t

}

t∈[n

]

}

i∈[n]

i and the

master key MK = hw,{{a

i,t

}

t∈[n

]

}

i∈[n]

KeyGen(MK, L): Let L = [L

,...,L

] be the at-

tribute list for the user who will obtain the cor-

responding secret key. Pick random values s

∈

∗

for i ∈ [n], set s =

∑

i=1

, and compute

= g

w−s

. Then, pick random values λ

∈ Z

∗

for i ∈ [n] and compute {D

i,0

i,1

i,2

} = {g

i,L

)

i,L

}. Output the secret

key SK

= h D

∏

i=1

i,0

, {D

i,1

i,2

}

i∈[n]

i asso-

ciated with L.

Encrypt(PK, M, W): Let W = [W

,...,W

] be a ci-

phertext policy and M ∈ G

be a message. Pick

a random value r ∈ Z

∗

and compute

C = M ·Y

and C

= g

. Then, execute the following pro-

cess for all i ∈ [n]: pick random values r

i,t

∈ Z

∗

for t ∈ [n

]. If t ∈ W

, compute {C

i,t,1

i,t,2

} =

{(A

i,t

)

i,t

,(A

i,t

)

r−r

i,t

}. If t 6∈ W

, let {C

i,t,1

i,t,2

}

be random values in G. Output the ciphertext

CT = h

C,C

,{{C

i,t,1

i,t,2

}

t∈[n

]

}

i∈[n]

Decrypt(CT, SK

): Check whether the attribute list L

for the user satisﬁes the ciphertext policy W. If

L |= W, output the message,

M =

C·

∏

i=1

e(C

i,L

i,1

) · e(C

i,L

i,2

)

e(C

∏

i=1

i,0

)

3.2 CP-ABE without Wildcard (Emura

et al., 2009)

In (Emura et al., 2009), each attribute can take two or

more values, and eachW

in a ciphertext policyW can

PartiallyWildcardedAttribute-basedEncryptionandItsEfficientConstruction

341

be any one of the possible values for attribute A

. As

a result, the encryptor cannot specify a wildcard.

In this paper, an user’s attribute list is simply rep-

resented by indices corresponding to possible values

for each attribute. Let S

= {1, 2, ..., n

} be a set of

possible values for A

where n

is the number of the

possible values for A

. Then, let L = [L

,...,L

] be

the attribute list where L

∈ S

and let W = [W

, W

..., W

] be the ciphertext policy where W

∈ S

. The

attribute list L satisﬁes the ciphertext policy W, that

is, L |= W iff L

= W

for all i ∈ [n].

Setup(1

): Choose multiplicative cyclic groups G

and G

of prime order p, a bilinear map

e : G × G → G

, and random generators

g,h ∈ G. Then, pick y,t

i, j

∈ Z

at ran-

dom for i ∈ [n] and j ∈ [n

]. Compute Y =

e(g,h)

and T

i, j

= g

i, j

. Output the public key

PK = hp,G,G

,e,g,h,Y,{{T

i, j

}

j∈[n

]

}

i∈[n]

i and

the master key MK = hy,{{t

i, j

}

j∈[n

]

}

i∈[n]

KeyGen(MK, L): Let L = [L

,...,L

] be the at-

tribute list for the user who will obtain the cor-

responding secret key. Pick a random value

r ∈ Z

and output the secret key SK

= hh

∑

i∈[n]

i,L

)

i associated with L.

Encrypt(PK, M, W): LetW = [W

,...,W

] be a ci-

phertext policy and M ∈ G

be a message. Pick a

random value s ∈ Z

and compute C

= M · Y

= g

, and C

= (

∏

i∈[n]

i,W

)

= (g

∑

i∈[n]

i,W

)

Output the ciphertext CT = hW,C

Decrypt(CT, SK

): Check whether the attribute list L

for the user satisﬁes the ciphertext policy W. If

L |= W, output the message

M =

· e(C

)

e(C

· (g

∑

i∈[n]

i,L

)

4 PROPOSED SCHEME

We propose a partially wildcarded CP-ABE scheme

to reduce the decryption cost.

4.1 Overview of Proposed Scheme

In (Emura et al., 2009), it is found that a more ef-

ﬁcient CP-ABE scheme than the scheme in (Nishide

et al., 2008) can be constructed by removing the wild-

card functionality. Hence, the presence or absence of

the wildcard functionality has an inﬂuence on the ef-

ﬁciency of the CP-ABE scheme. In our scheme, the

user’s attribute list is separated into a list of attributes

requiring wildcards and a list of attributes not requir-

ing wildcards. Our scheme thus embodies schemes

with and without the wildcard functionality. Gen-

erally, a CP-ABE scheme without a wildcard func-

tionality has a smaller cost than one with a wildcard

functionality. Therefore, the larger the number of at-

tributes not requiring a wildcard functionality is, the

smaller the total cost of the CP-ABE scheme will be.

However, combining two schemes with and with-

out the wildcard functionality is not trivial. When

the secret key corresponding to the attributes requir-

ing wildcards and the secret key corresponding to the

attributes not requiring wildcards are generated, they

are associated with each other by using a random

number in order to prevent collusion attacks. Further-

more, the ciphertext size is reduced by the encryption

algorithms sharing another random number.

In (Nishide et al., 2008), the authors achieve re-

cipient anonymity by hiding the subsetW

for each A

speciﬁed in the ciphertext policy of the AND-gate of

all the attributes. However, ciphertext policies must

be revealed in certain services. For example, in a

content distribution service, users must know what at-

tributes are required for playing content. In this paper,

we construct a modiﬁed CP-ABE scheme by remov-

ing recipient anonymity from the CP-ABE scheme in

(Nishide et al., 2008) and use the modiﬁed scheme

as a CP-ABE scheme with a wildcard functionality.

Moreover, we combine it with the CP-ABE scheme

without the wildcard functionality in (Emura et al.,

2009).

4.2 Proposed Scheme

Let ˆn be the number of attributes

which re-

quire wildcards and ˇn be the number of attributes

which do not require wildcards. Moreover, let

= {1,2,..., ˆn

} be the set of possible values for at-

tribute

and

= {1,2,..., ˇn

} be the set of possi-

ble values for attribute

. The user’s attribute list L

is separated into one list

L = {

, ...,

ˆn

} which

requires wildcards, where

∈

, and another list

= {

, ...,

ˇn

} which does not require wildcards,

where

∈

. Also, the ciphertext policy W is sepa-

rated into a ciphertext policy

W = {

, ...,

ˆn

}

which requires wildcards, where

⊆

, and a policy

W = {

, ...,

ˇn

} which does not require wild-

cards, where

∈

Setup(1

, ˆn, ˇn, { ˆn

}

i∈[ ˆn]

, { ˇn

}

i∈[ ˇn]

): Choose multi-

plicative cyclic groups G and G

of prime order

p, a bilinear map e : G × G → G

, and a random

generator g ∈ G. Then, pick a random value

w ∈ Z

∗

, and compute Y = e(g,g)

. Also, pick a

random value A

i, j

∈ G for all i ∈ [ ˆn] and j ∈ [ ˆn

and pick a random value T

i, j

∈ G for all i ∈ [ˇn]

and j ∈ [ ˇn

]. Output the public key PK = h p, G,

SECRYPT2013-InternationalConferenceonSecurityandCryptography

342

, e, g, Y, {{A

i, j

}

j∈[ ˆn

]

}

i∈[ ˆn]

, {{T

i, j

}

j∈[ ˇn

]

}

i∈[ ˇn]

and the master key MK = w.

KeyGen(PK, MK,

L): Pick a random value ξ ∈ Z

∗

and a random value s

∈ Z

∗

for all i ∈ [ ˆn]. Set

s =

∑

ˆn

i=1

and compute D = g

w−s+ξ

. After that,

pick a random value λ

∈ Z

∗

for all i ∈ [ ˆn] and

compute {D

i,0

i,1

} = {g

·A

}. Also, pick

a random value u ∈ Z

∗

and compute {D

′

} =

−ξ

· (

∏

i∈[ ˇn]

)

}. Output the secret key

[

= h

L, D·

∏

i∈[ ˆn]

i,0

· D

′

, {D

i,1

}

i∈[ ˆn]

, D

′

i associated with the user’s attribute list

L and

Encrypt(PK, M,

W): Pick a random value r ∈

∗

and compute C

= M · Y

, C

= g

, C

(

∏

i∈[ ˇn]

)

. Then, compute C

i, j

= A

i, j

for all

i ∈ [ ˆn] and j ∈

. Output the ciphertextC

[

W, C

, C

, {C

i, j

}

i∈[ ˆn], j∈

Decrypt(SK

[

, C

[

): If

L |=

W and

L |=

W, out-

put the message,

M = C

∏

i∈[ ˆn]

e(C

i,1

) · e(C

′

)

e(D·

∏

i∈[ ˆn]

i,0

· D

′

)

4.3 Security Proof

Theorem 1. Our scheme is selective IND-CPA secure

if the DBDH assumption holds in G.

Proof. Let A be an adversary interested in thwarting

our scheme. We build an algorithm B that solves the

DBDH problem in G by using A. Pick random values

α,β,γ in Z

∗

and compute g

= g

, g

= g

, and g

. Then, pick a random bit δ ∈ {0,1}. If δ = 1, set

R = e(g,g)

αβγ

. If δ = 0, let R be a random value in

. B takes as input hg,g

,Ri and proceeds as

follows:

Init: A chooses the challenge ciphertext policies

∗

= (

∗

,...,

∗

ˆn

) and

∗

= (

∗

,...,

∗

ˇn

)

and gives them to B.

Setup: B receives

∗

and

∗

. It computes the pub-

lic key as follows: B computes Y = e(g

). After

that, it picks random values a

i, j

in Z

∗

for all i ∈ [ ˆn]

and j ∈ [ ˆn

]. If j ∈

∗

, it computes A

i, j

= g

i, j

If j 6∈

∗

, it computes A

i, j

= g

i, j

. Moreover, B

picks random values b

i, j

in Z

∗

for all i ∈ [ ˇn] and

j ∈ [ ˇn

]. If j =

∗

, it computes T

i, j

= g

i, j

. If

j 6=

∗

, it computes T

i, j

= g

i, j

. Finally, it returns

PK = hg,Y,{{A

i, j

}

j∈[ ˆn

]

}

i∈[ ˆn]

,{{T

i, j

}

j∈[ ˇn

]

}

i∈[ ˇn]

i to A.

Phase 1: When A transmits the attribute lists

L =

(

,...,

ˆn

) and

L = (

,...,

ˇn

) for the KeyGen

query to B, B returns the corresponding secret key as

follows: If (

L |=

∗

) ∧ (

L |=

∗

), B returns ⊥ to A .

Here, the query can be classiﬁed into three types. A

type 1 query satisﬁes (

L 6|=

∗

) ∧ (

L 6|=

∗

); a type

2 query satisﬁes (

L |=

∗

) ∧ (

L 6|=

∗

); and a type 3

query satisﬁes (

L 6|=

∗

) ∧ (

L |=

∗

• Type 1 or Type 2: B picks a random value ξ

′

∗

. After that, it picks a random value s

in Z

∗

for all i ∈ [ ˆn]. It computes s =

∑

ˆn

i=1

and D =

s−ξ

′

. It then picks random values λ

in Z

∗

for all

i ∈ [ ˆn] and computes D

i,0

= g

· A

and D

i,1

. In Type 1 and Type 2,

L 6|=

∗

is satisﬁed.

Therefore, B can set

∑

i∈[ ˇn]

= T

+ T

α, where

6= 0 (The probability of T

= 0 is negligible and

it has no inﬂuence on the security proof, so we

will omit this case. See (Emura et al., 2009).). B

can compute T

and T

by using {b

i, j

}

i∈[ ˇn],j∈[ ˇn

]

It picks a random value u

′

in Z

∗

and computes

′

= g

′

· g

′

· g

′

· g

−

and D

′

= g

′

· g

−

• Type 3: B picks random values ξ and u in Z

∗

and

computes D

′

= g

−ξ

· (

∏

i∈[ ˇn]

)

and D

′

= g

In Type 3,

L 6|=

∗

is satisﬁed. Therefore, there

exists the index k such that

6∈

. B picks

random values s

in Z

∗

for all i ∈ [ ˆn]\k. Then,

it picks random values λ

in Z

∗

and computes

i,0

= g

· A

and D

i,1

= g

. It picks random

values s

′

and λ

′

in Z

∗

for the index k such

that

6∈

and computes D = g

−s

′

−

∑

i∈[ ˆn]\k

+ξ

k,0

= g

′

· g

′

, and D

k,1

= g

′

· g

Finally, B computes SK

[

= h

L, D ·

∏

i∈[ ˆn]

i,0

′

, {D

i,1

}

i∈[ ˆn]

, D

′

i and returns SK

[

to A .

Lemma 1. SK

[

is distributed identically to that in

the real IND-CPA game.

We will prove Lemma 1 after showing the advantage

of B.

Challenge: A transmits two messages M

and M

to B . B picks a random bit η ∈ {0,1} and computes

= M

· R, C

= g

, and C

= g

∑

i∈[ ˇn]

∗

. It then

computes C

i, j

= g

i, j

for all i ∈ [ ˆn] and j ∈

∗

. It

returns the challenge ciphertext C

∗

= h

∗

, C

, {C

i, j

}

i∈[ ˆn], j∈

∗

i to A.

PartiallyWildcardedAttribute-basedEncryptionandItsEfficientConstruction

343

Lemma 2. If R = e(g,g)

αβγ

, C

∗

is distributed

identically to the challenge ciphertext in the real IND-

CPA game. Otherwise, A can obtain no information

about η.

this Lemma can be proved easily since A

i, j

= g

i, j

for

all i ∈ [ ˆn], j ∈

∗

and T

i, j

= g

i, j

for all i ∈ [ ˇn] if j =

∗

. Hence, we will omit the proof.

Phase 2: Same as Phase 1.

Guess: A outputs η

′

. B outputs δ

′

= 1 if η = η

′

Otherwise, B outputs δ

′

= 0.

B outputs δ

′

= 1 iff A can predict the value of η.

When R = e(g,g)

αβγ

, B completely simulates the

IND-CPA game for A . In contrast, when R is a ran-

dom element in G

, the value of η is information-

theoretically hidden, so the probability that A can pre-

dict the value of η is 1/2. Hence, Pr[δ

′

= 1|δ = 1] =

Adv

CPA

(k) +

and Pr[δ

′

= 1|δ = 0] =

. That is, the

advantage of B solving the DBDH problem is as fol-

lows:



Pr[δ

′

= 1|δ = 1] − Pr[δ

′

= 1|δ = 0]



= Adv

CPA

(k)

If Adv

CPA

(k) is non-negligible, B has non-negligible

advantage for the DBDH problem, which contradicts

the DBDH assumption. Therefore, in the selective

IND-CPA game for our scheme, the advantage of A

is negligible. Hence, Theorem 1 holds.

Proof. To prove Lemma 1, we show that SK

[

gen-

erated by B satisﬁes the following equations:

[

= h

L,D

′′

,{D

i,1

}

i∈[ ˆn]

′

i (1)

where D = g

w−s+ξ

(2)

i,0

= g

· A

for all i ∈ [ ˆn] (3)

i,1

= g

for all i ∈ [ ˆn] (4)

′

= g

−ξ

· g

u·

∑

i∈[ ˆn]

(5)

′

= g

(6)

′′

= D·

∏

i∈[ ˆn]

i,0

· D

′

(7)

where s =

∑

ˆn

i=1

and w = αβ.

• Type 1 or Type 2: By setting −ξ

′

= αβ + ξ, it be-

comes obvious that D, D

i,0

, and D

′

respectively

satisfy equations (2), (3), and (4). These computa-

tions do not require g

αβ

, so B can easily compute

them. Next, D

′

and D

′

can be computed as fol-

lows by setting −ξ = αβ + ξ

′

and u

′

= β + uT

′

= g

′

· g

′

· g

′

· g

−

= g

′

· g

αu

′

· g

′

−β

= g

′

· g

α(β+uT

)

· g

= g

(αβ+ξ

′

)

· g

u(T

α)

= g

−ξ

· g

u·

∑

i∈[ ˆn]

′

= g

′

· g

−

= g

β+uT

· g

−

= g

where

∑

i∈[ ˇn]

= T

+ T

α from the conditions

of Type 1 and Type 2. ξ

′

and u

′

are uniformly and

randomly chosen, so ξ and u are also uniformly

and randomly distributed, and D

′

and D

′

satisfy

the above equations. Therefore, D

′

and D

′

sat-

isfy equations (5) and (6). Hence, SK

[

gen-

erated by B satisﬁes equation (1), and Lemma 1

holds.

• Type 3: It is obvious that D

′

and D

′

satisfy equa-

tions (5) and (6) since their computations are sim-

ilar to equations (5) and (6) without g

αβ

. As a

result, it is obvious that {D

i,0

i,1

}

i∈[ ˆn]\k

, where

k is an index wherein

6∈

, satisﬁes equations

(3) and (4) since their computations are similar

to equations (3) and (4) without g

αβ

. D, D

k,0

and D

k,1

can be computed as follows by setting

−s

′

= αβ − s

, λ

′

= a

− β.

D = g

−s

′

−

∑

i∈[ ˆn]\k

+ξ

= g

αβ−s

−

∑

i∈[ ˆn]\k

+ξ

= g

w−s+ξ

k,0

= g

′

· g

′

= g

α(−β+a

)

· g

′

= g

−αβ+s

′

· g

= g

· A

k,1

= g

′

· g

= g

′

+β

= g

′

is uniformly and randomly chosen, so s

also uniformly and randomly distributed and D,

k,0

, and D

k,1

satisfy the above equations. There-

SECRYPT2013-InternationalConferenceonSecurityandCryptography

344

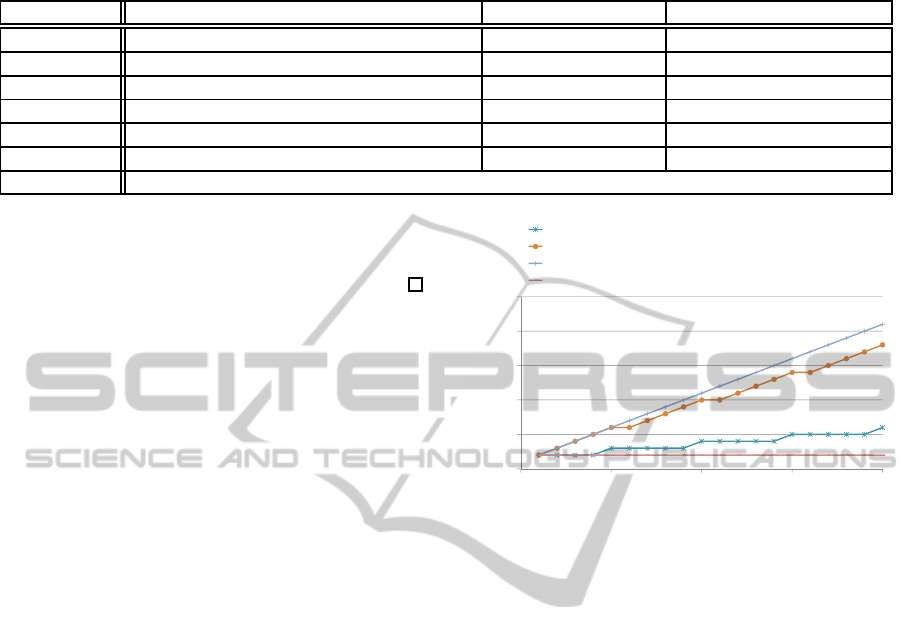
Table 1: Comparison of our scheme and conventional CP-ABE schemes. (See Section 5.1 for the notation.)

Modiﬁed scheme of (Nishide et al., 2008) (Emura et al., 2009) Our scheme

|PK| (n

+ 1)|G| + |G

| (n

+ 2)|G| + |G

| (n

+ 1)|G| + |G

|SK| (n+ 1)|G| 2|G| (θn+ 2)|G|

|CT| (m

+ 1)|G| + |G

| 2|G| + |G

| ( ˆm

+ 2)|G| + |G

Enc (m

+ 1)M

+ M

(n+ 1)M

+ M

(θn+ ˇm

+ 1)M

+ M

Dec (n+ 1)P 2P (θn+ 2)P

Wildcard yes (for all attributes) no yes (for partial attributes)

Assumption DBDH

fore, D, D

k,0

, and D

k,1

respectively satisfy equa-

tions (2), (3), and (4). Hence, SK

[

generated by

B satisﬁes equation (1), and Lemma 1 holds.

5 PERFORMANCE

5.1 Cost Comparison

Table 1 compares our schemes with the modiﬁed

scheme of (Nishide et al., 2008) and the scheme pre-

sented in (Emura et al., 2009). In this table, |PK| de-

notes the size of the public key, |SK| the size of the

secret key, |CT| the size of the ciphertext, Enc the en-

cryption cost, and Dec the decryption cost. |G| and

| denote the size of the elements in G and G

respectively. n is the number of attributes A, ˆn the

number of attributes

A that require wildcards, and ˇn

the number of attributes

A that do not require wild-

cards. θ denotes the proportion of attributes which

require wildcards, and 0 ≤ θ ≤ 1. n

∑

i=1

, where

denotes the number of possible values for attribute

. ˆn

∑

ˆn

i=1

ˆn

, where ˆn

denotes the number of

possible values for attribute

which require wild-

cards, and ˇn

∑

ˇn

i=1

ˇn

, where ˇn

is the number of

possible values for attribute

which do not require

wildcards. m

∑

i=1

, where m

means the number

of attribute values in a policy W

such that m

≤ n

ˆm

∑

ˆn

i=1

ˆm

, where ˆm

denotes the number of at-

tribute values in a policy

that require wildcards and

ˆm

≤ ˆn

. ˇm

∑

ˇn

i=1

ˇm

, where ˇm

denotes the number

of attribute values in a policy

that do not require

wildcards and ˇm

≤ ˇn

. M

and M

denote modulo

exponentiation in G and G

, respectively. P denotes

a pairing computation on an elliptic curve.

Figure 1 compares the processing times for de-

cryption. The number of attributes is the horizontal

axis and the processing time for decryption is the ver-

tical axis. We assume that the processing time for

one pairing computation is 10 (msec) (Zhang et al.,

2008). The graphs for our scheme correspond to the

case of θ = 0.2 and that of θ = 0.8. Figure 1 clearly

is also

satisfy the above equations. Therefore,

respectively satisfy equations

generated by

Table 1 compares our schemes with the modiﬁed

scheme of (Nishide et al., 2008) and the scheme pre-

ϮϬϬ

ϮϱϬ

WƌŽĐĞƐƐŝŶŐƚŝŵĞĨŽƌĚĞĐƌǇƉƚŝŽŶ;ŵƐĞĐͿ

KƵƌƐĐŚĞŵĞ;ɽсϬ͘ϮͿ

KƵƌƐĐŚĞŵĞ;ɽсϬ͘ϴͿ

DŽĚŝĨŝĞĚƐĐŚĞŵĞŽĨ;EŝƐŚŝĚĞĞƚĂů͕͘ϮϬϬϴͿ

;ŵƵƌĂĞƚĂů͕͘ϮϬϬϵͿ

ϱϬ

ϭϬϬ

ϭϱϬ

Ϭ ϱ ϭϬ ϭϱ ϮϬ

WƌŽĐĞƐƐŝŶŐƚŝŵĞĨŽƌĚĞĐƌǇƉƚŝŽŶ;ŵƐĞĐͿ

EƵŵďĞƌŽĨĂƚƚƌŝďƵƚĞƐ

Figure 1: Processing time for decryption in CP-ABE

schemes.

shows that the processing time for decryption in our

scheme is short when the proportion of attributes re-

quiring wildcards is small.

5.2 Application

A content distribution service is a potential applica-

tion of our scheme. Let us assume that users have

four attributes: residence, membership, contract in-

formation, and gender. First, the user’s attributes are

classiﬁed according to the need of wildcards as fol-

lows:

(Attribute with wildcard)

: residence

= {1, 2,...,47} = {Hokkaido, Aomori, ..., Oki-

nawa}

(Attribute without wildcard)

: membership

= {1, 2} = {general, premium}

: contract information

= {1, 2} = {payer, non-payer}

: gender

= {1, 2} = {male, female}

PartiallyWildcardedAttribute-basedEncryptionandItsEfficientConstruction

345

Our scheme can realize a regionally restricted con-

tent distribution service. In Japan, there are 47 pre-

fectures, so we assign them to possible values for

. We also allow two kinds of membership, general

and premium, as possible values for

, two kinds

of contract information, payer and non-payer, as pos-

sible values for

, and two genders, male and fe-

male, as possible values for

. For example, when

a service provider encrypts a piece of content with

the policy

= {Tokyo, Kanagawa, Saitama, Chiba,

Gunma, Tochigi, Ibaraki}, which means the Kanto

region, a user who has the attribute

= Tokyo can

decrypt the content but a user who has the attribute

= Osaka cannot decrypt the content. In this case,

n = 4 and θ = 0.25. Therefore, the decryption cost is

5P in the modiﬁed scheme of (Nishide et al., 2008)

and 3P in our scheme, respectively, which means that

our scheme can reduce the decryption cost by 40%

in comparison with the modiﬁed scheme of (Nishide

et al., 2008).

For attribute

, a service provider must encrypt

content with either

= general or

= premium.

If the service provider allows both general members

and premium members to decrypt a content, they must

transmit two corresponding ciphertexts to users (For

the other attributes

and

, the service provider

must do the same as the above.). If the number of

possible values for an attribute is large, the wildcard

functionality is effective. On the other hand, if the

number of possible values for an attribute is small, the

service provider should employ such a trivial scheme

rather than use wildcards to reduce total costs. That

is, the service provider should transmit as many ci-

phertexts as possible attribute values to users.

Table 2 is a numerical comparison of the schemes

described in Table 1. Several parameters are set

according to the above content distribution service:

|G| = 176 (bits), |G

| = 1056 (bits), M

= 5 (msec),

= 8 (msec), P = 10 (msec), n = 4, ˆn = 1, ˇn = 3,

θ = 0.25, n

= 53, m

= 10, ˆn

= 47, ˆm

= 7, ˇn

= 6,

and ˇm

= 3. As shown in Table 2, our scheme is more

efﬁcient than the modiﬁed scheme of (Nishide et al.,

2008).

6 CONCLUSIONS

We proposed a partially wildcarded CP-ABE scheme.

We compared our scheme with conventional CP-ABE

schemes and described a content distribution service

as an application of our scheme. The result showsthat

our scheme can reduce the decryption cost in compar-

ison with the conventional CP-ABE schemes.

Table 2: Numerical comparison of our scheme and conven-

tional CP-ABE schemes. M-NYO08 denotes the modiﬁed

scheme of (Nishide et al., 2008) and EMNOS09 denotes the

scheme in (Emura et al., 2009).

M-NYO08 EMNOS09 Ours

|PK| (bits) 10,560 10,736 10,560

|SK| (bits) 880 352 528

|CT| (bits) 2,992 1,408 2,640

Enc (msec) 63 33 33

Dec (msec) 50 20 30

REFERENCES

Bethencourt, J., Sahai, A., and Waters, B. (2007).

Ciphertext-policy attribute-based encryption. In IEEE

Symposium on Security and Privacy, pages 321–334.

Cheung, L. and Newport, C. (2007). Provably secure ci-

phertext policy abe. In ACMCCS’07, pages 456–465.

Emura, K., Miyaji, A., Nomura, A., Omote, K., and Soshi,

M. (2009). A ciphertext-policy attribute-based en-

cryption scheme with constant ciphertext length. In

ISPEC, pages 13–23.

Goyal, V., Pandey, O., Sahai, A., and Waters, B. (2006).

Attribute-based encryption for ﬁne-grained access

control of encrypted data. In ACMCCS, pages 89–98.

Katz, J., Sahai, A., and Waters, B. (2008). Predicate encryp-

tion supporting disjunctions, polynomial equations,

and inner products. In Eurocrypt, pages 146–162.

Lewko, A., Okamoto, T., Sahai, A., Takashima, K., and

Waters, B. (2010). Fully secure functional encryp-

tion: Attribute-based encryption and (hierarchical) in-

ner product encryption. In Eurocrypt, pages 62–91.

Nishide, T., Yoneyama, K., and Ohta, K. (2008). Attribute-

based encryption with partially hidden encryptor-

speciﬁed access structures. In ACNS, pages 111–129.

Okamoto, T. and Takashima, K. (2010). Fully secure func-

tional encryption with general relations from the deci-

sional linear assumption. In Crypto, pages 191–208.

Ostrovsky, R., Sahai, A., and Waters, B. (2007). Attribute-

based encryption with non-monotonic access struc-

tures. In ACMCCS, pages 195–203.

Sahai, A. and Waters, B. (2005). Fuzzy identity-based en-

cryption. In Eurocrypt, pages 457–473.

Waters, B. (2011). Ciphertext-policy attribute-based en-

cryption: An expressive, efﬁcient, and provably se-

cure realization. In PKC, pages 53–70.

Zhang, Y., Kanayama, N., and Okamoto, E. (2008). Java

implementation of pairing on elliptic curves over F

(in japanese). In CSS, pages D2–1.

SECRYPT2013-InternationalConferenceonSecurityandCryptography

346