
Limitations of Super Resolution Image Reconstruction
and How to Overcome them for a Single Image
Seiichi Gohshi
1
and Isao Echizen
2
1
Kogakuin University, 1-24-2 Nishi-Shinjuku, Shinjuku-ku, Tokyo,163-8677, Japan
2
National Institute of Informatics, 2-1-2, Hitotsubashi, Chiyoda-ku, Tokyo, 101-8430, Japan
Keywords:
Image Enhancement, Super Resolution Reconstruction, Frequency Domain, Real-time.
Abstract:
Super resolution image reconstruction (SRR) is a typical super resolution (SR) technology that has been re-
searched with varying results. The SRR algorithm was initially proposed for still images. It uses many
low-resolution images to reconstruct a high-resolution image. Unfortunately, in practice, we rarely have a suf-
ficient number of low-resolution images for SRR to work. Usually, there is only one (or a few) blurry images.
On the other hand, there is a need to improve blurry images in applications ranging from security and photo
restoration to zooming functions and countless other examples related to the printing industry. Recently, SRR
was extended to video sequences that have many similar frames that can be used as low-resolution images
to reconstruct high-resolution frames. In normal SRR, one reconstructs a high-resolution image from low-
resolution images sampled from one high-resolution image, but in the video application, the low-resolution
video frames are not taken from higher resolution ones. This paper proposes a novel resolution improvement
method that works without such a high- resolution image. Its algorithm is simple and can be applied to a single
image and real-time video systems.
1 INTRODUCTION
Methods of creating high-resolution images from
low-resolution images have been researched for many
years. These gimage restorationh methods were ini-
tially applied to still pictures. They were later ex-
tended in scope and are now called super resolu-
tion (SR)(Sung et al., 2003). One SR technique is
super resolution image reconstruction (SRR) (Farsiu
et al., 2004)(Adam et al., 2010)(Katsaggelos et al,,
2007)(Panda et al., 2011). SRR is at present the
only SR method among the many proposed to be in-
corporated in commercial products (Matsumoto and
Ida, 2008)(Matsumoto and Ida, 2010)(Matsumoto
and Ida, 2010)(Toshiba). However, the practical lim-
itations of SRR have not been discussed especially in
regard to real-time applications.
Display devices, such as LCDs, and ink jet print-
ers have advanced to such an extent that their reso-
lutions exceed those of pictures taken with film cam-
eras. Moreover, although most photographs are taken
with digital cameras these days, they are prone to be-
ing blurred because of focusing mistakes or the cam-
era being shaken while in operation. SRR is not a
good way to improve the resolution of individual pho-
tographs since it requires many low-resolution im-
ages; typically, only one blurry photograph is avail-
able. In contrast, video would seem to be a very good
application for SRR, since video consists of numer-
ous frames and adjacent frames that look similar. Not
surprisingly, therefore, many papers have been pub-
lished on the subject citeSR:Face (Katsaggelos et al,,
2007)(Protter et al., 2009). However, the methods
proposed so far are complex. Recently, SRR func-
tions with self congruency characteristics in a frame
have been incorporated in HDTV sets and BluRay
players (Matsumoto and Ida, 2008)(Matsumoto and
Ida, 2010). However, before we can evaluate the effi-
cacy of SRR for these devices, we must bear in mind
that video frames have different characteristics than
those of still images taken with still cameras.
A common form of video content is TV broad-
casting. Analogue broadcasting has been around for
more than 60 years, but it is being replaced with digi-
tal HDTV broadcasting in many countries. The ini-
tial cost of digital HDTV broadcasting is high for
most broadcasting companies. SRR for video would
be very useful if it could improve the resolution of
analogue video that has been converted into HDTV;
broadcasters could continue showing analogue pro-
71
Gohshi S. and Echizen I..
Limitations of Super Resolution Image Reconstruction and How to Overcome them for a Single Image.
DOI: 10.5220/0004518300710078
In Proceedings of the 10th International Conference on Signal Processing and Multimedia Applications and 10th International Conference on Wireless
Information Networks and Systems (SIGMAP-2013), pages 71-78
ISBN: 978-989-8565-74-7
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

ductions and thereby reduce their costs. Viewers who
own HDTVs with SRR functions for converting ana-
logue video into HDTV would be able to view po-
tentially all their programming at an HDTV level of
resolution. For manufacturers, this would mean that
HDTV receivers with SRR could be sold all over
the world. In fact, HDTV sets with SRR functions
are now on the market, and SRR has been deemed
a practical technology (Toshiba). However, despite
there having been many studies, no HDTVs equipped
with SRR functions for converting analogue broad-
casting have been developed. Recently, it was proven
that the resolution of HDTV with SRR is inferior to
the HDTV without SRR (Gohshi and Echizen, 2013).
This suggests that SRR cannot improve the resolution
of general TV content.
SRR has another issue. To improve resolution of a
still image, we need many low-resolution images with
different phases. This presents a problem if there is
only one low-resolution image. Although some tech-
nologies can improve resolution with a single image
(Glasner et al., 2009)(Panda et al., 2011), they need it-
erations and the processing time depends on the char-
acteristics of the image. In practice, the effectiveness
of SRR technologies should not be image dependent.
This paper is organized as follows. First, the lim-
itations of SRR are discussed in the frequency do-
main. Second, a non-linear signal processing (NLSP)
method that is free of the issues of SRR is introduced.
The basic idea behind this method was recently de-
scribed (Gohshi, 2012) . However, the theoretical
backgroundofNLSPin the frequencydomain was not
discussed in detail. This paper proposes another non-
linear function that gives better results and discusses
the algorithm of NLSP in the frequency domain. As
just one image simulation result is not sufficient for
practical applications, we give several simulation re-
sults to prove the validity of the method. In the same
way it is applied to still images, the NLSP method can
improve resolution of video sequences using a single
frame at a time, which is something that SRR cannot
do.
2 ISSUES OF SRR IN
FREQUENCY DOMAIN
SRR is usually discussed with regard to an original
image and the reconstructed image. Image quality is
a subjective assessment, and it is not easy to tell the
difference in image quality between similar images
printed on sheets of paper or in pdf files. Image qual-
ity can, however, be discussed in an objective way by
referring to spectra in the frequency domain. To see
how this is done, let us consider Figure 1. One of
LRIs shown in Figure 2 is created from Figure 1 by
subsampling. Figure 3 is the corresponding SRR im-
age generated from 16 LRIs and 100 iterations (Farsiu
et al., 2004). The sizes of the LRIs in this case were a
quarter that of the original HRI. Such a still image is
the best condition of SRR signal processing since the
still image has sufficient sharp edges for SRR. More
than 16 LRIs would be necessary to get a comparable
result for video since motion blur would smear out
such sharp edges (Gohshi, 2007). Although Figure
1 and Figure 3 look the same, their two-dimensional
fast Fourier transforms (FFTs) are different (Figure 4
and Figure 5). In Figure 5 showing the FFT of the
SSR, there is a rectangular null area without any fre-
quency components and the same repeated frequency
characteristics. This sort of phenomenon is due to
sub-sampling and the null area does not exist if SRR
can reconstruct the HRI perfectly.
Figure 1: Original image.
Figure 2: LRI.
Figure 3: SRR image.
Figure 6 shows the two-dimensional FFT of one
of the quarter-size LRIs from Figure 2. All the LRIs
have the same null areas in the frequency domain due
to the sampling theory. The white rectangle in Figure
6 is the Nyquist frequency (vertical and horizontal) of
SIGMAP2013-InternationalConferenceonSignalProcessingandMultimediaApplications
72
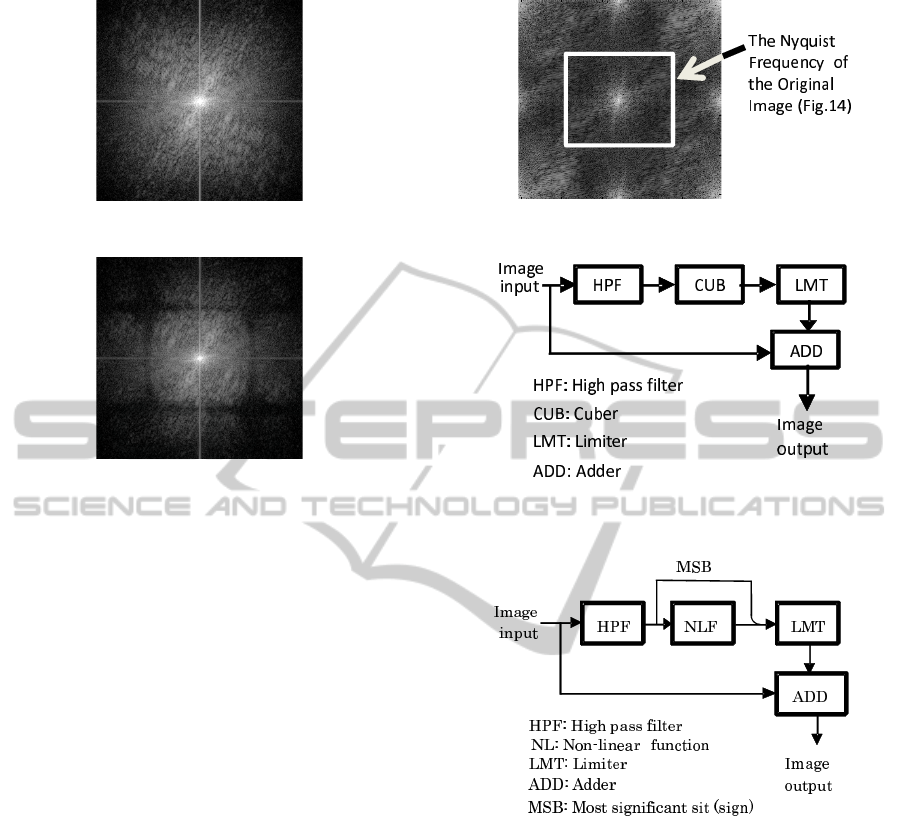
Figure 4: 2D FFT of Fig.1.
Figure 5: 2D FFT of Fig. 3.
the LRIs, and it is clear that the same frequency spec-
tra spread outside of the white rectangle. Compared
with Figure 5 and Figure 6, both of the vertical and
horizontal Nyquist frequencies are half those shown
in Figure 4. There are repeated frequency spectra in
Figure 5, and the repetition cycle is the same value in
cycles as the frequency of the white rectangle shown
in Figure 6. Although Figure 3 is reconstructed from
16 LRIs, Figure 5 has the same shape cycle as Figure
6. This means that SRR cannot reconstruct the origi-
nal image completely, and the SRR result is affected
by the size of the LRIs. Figure 3 was reconstructed
from 16 LRIs over 100 iterations. It was made under
the ideal conditions for SRR but it is not the same as
the original image. The rectangular null area shown
in Figure 5 appears at any factor of enlargement. The
null areas in Figure 5 are exactly the same as the
Nyquist frequencies of LRIs. The difference between
the two-dimensional frequency characteristics of Fig-
ure 4 and Figure 5 causes the difference in resolution
between in Figure 1 and Figure 3.
3 NON-LINEAR SIGNAL
PROCESSING METHOD
The non-linear signal processing (NLSP) algorithm
is simple (Figure 7). The basic idea is similar to
Unsharp Mask or Enhancer (Schreiber, 1970)(Lee,
1980)(Pratt, 2001). The difference between the pro-
posed method and Enhancer is the cubic function in
Figure 7. Enhancer detects edges with a high pass
filter (HPF) and a limiter (LMT) restricts the level
Figure 6: 2D FFT of one of 16 LRIs.
Figure 7: NLSP algorithm.
Figure 8: New NLSP algorithm.
of edges so as not to emphasize noise in the images.
However, Enhancer cannot create frequency elements
that the input image does not have. The proposed
method uses a non-linear cubic function (CUB). CUB
can generate higher frequency elements that the input
image does not have as follows.
In Figure 7, edges are detected with the HPF and
are added to the input image. It uses y = x
3
as the
non-linear function.
In Figure 7 edges are detected with HPF and are
added to the input image. It uses y = x
3
as the non-
linear function. However, y = x
3
creates three times
higher frequencyelements than the original frequency
elements. The output of the high pass filter has plus
and minus elements. Although y = x
3
can hold pos-
itive and negative values, it may create unnecessar-
ily high frequency elements. There is no feedback
LimitationsofSuperResolutionImageReconstructionandHowtoOvercomethemforaSingleImage
73

Figure 9: NLSP image.
Figure 10: 2D FFT of Fig. 9.
Figure 11: Comparison.
loop in Figure 7, which means that the NLSP is just
straightforward signal processing and iterations are
not necessary. NLSP uses just one LRI for the input.
The image is input at the left top and is enlarged with
a linear digital filter such as a Lanczos filter or bicu-
bic filter. The enlarged image is distributed to the high
pass filter (HPF) and the adder (ADD). The HPF de-
tects the edges in the image and the edges are cubed.
The cubed edges can create high-frequency elements
that the input image does not have. It is well known
that an image expanded by a Fourier series consists
of sin and cos functions. Edges are represented with
sinnω
0
and cosnω
0
functions. Here, ω
0
= 2π f
s
: f
s
is the sampling frequency, and n is an integer number
(n = 0, ±1, ±2, · · · ). The edge cuber (CUB) gener-
ates sin
3
nω
0
and cos
3
nω
0
from sinnω
0
and cosnω
0
.
sin
3
nω
0
andcos
3
nω
0
generate sin3nω
0
and cos3nω
0
. This means three times higher frequency elements
are generated and these high-frequency elements are
edges that the original image does not have. The
edges are added to the input image by ADD, and the
resulting high-resolution image is output. A new al-
gorithm shown in Figure 8 is proposed in this paper.
The output of HPF is the edge information that has
signs, which means plus or minus for each pixel. Af-
ter the HPF, the edges are processed with a non-linear
function (NLF). If an even function such as x
2
is ap-
plied, the sign information, plus or minus, is lost. The
most significant bit (MSB) is separated from the edge
information before NLF and restored to them after
NLF. Using this method, we can use even non-linear
functions. This method gives much more flexibility
than the previous algorithm shown in 7. A simple
non-linear function y = x
2
is used in this paper. Gen-
erally, non-linear functions can generate harmonics
that can create higher frequency elements, which the
original image does not have. NLSP with other non-
linear functions should also be able to create high-
frequency elements. Here, we propose y = x
2
for plus
edges and y = −x
2
for minus edges. They create two
times higher frequency elements and are for enlarg-
ing mages twice horizontally and vertically, such as
in the conversion from HDTV to 4K TV. The pro-
cessed image is shown in Figure 9. In this process,
just one LRI shown in Figure 2 is the input image.
In spite of the simple signal processing, the resolu-
tion is not worse than that of Figure 1 and Figure 3.
Figure 10 shows the two-dimensional FFT result of
Figure 9. Figure 10 does not have the null in-band
areas shown in Figure 5, and it means that the NLSP
does not generate null areas. Although the size of the
input image is just a quarter that of the output im-
age shown in Figure 1, NLSP can create the higher
frequency elements beyond the Nyquist frequency of
the input image. Figure 11 shows enlarged parts of
the original image, SRR image, and the NLSP image.
They are enlarged images and help to understand the
resolution difference of (b)SRR and (c)NLSP.
Three other simulation results are shown from
Figure 12 to Figure 29. Each simulation result
shows the original image (512x512), the quarter
size (256x256), enlarged and NLSP processed im-
age (512x512) and their two-dimensional FFT re-
sults. Figure 17, Figure 23, and Figure 29 show two-
dimensional FFT results of NLSP processed results.
These simulations show that NLSP produces good re-
sults even with enlarged images. There are no null
areas in the frequency domain characteristics. This
means NLSP does not have the issues that SRR has.
4 COMPARISON OF NLSP WITH
SRR
Figure 30 illustrates the signal processing of SRR.
The top and bottom images in Figure 30 are those
of Figure 1 and Figure 3. It is necessary to create
16 LRIs and iterate the procedure 100 times. The
SIGMAP2013-InternationalConferenceonSignalProcessingandMultimediaApplications
74

Figure 12: (512X512). Figure 13: (256X256.)
Figure 14: Lenna (512x512 NLSP image pro-
cessed from Fig. 13).
Figure 15: 2D FFT of Fig. 12. Figure 16: 2D FFT result of Fig.13. Figure 17: 2D FFT of Fig. 14.
Figure 18: (512X512). Figure 19: (256X256).
Figure 20: (512x512 NLSP image processed from
Fig. 19).
LimitationsofSuperResolutionImageReconstructionandHowtoOvercomethemforaSingleImage
75
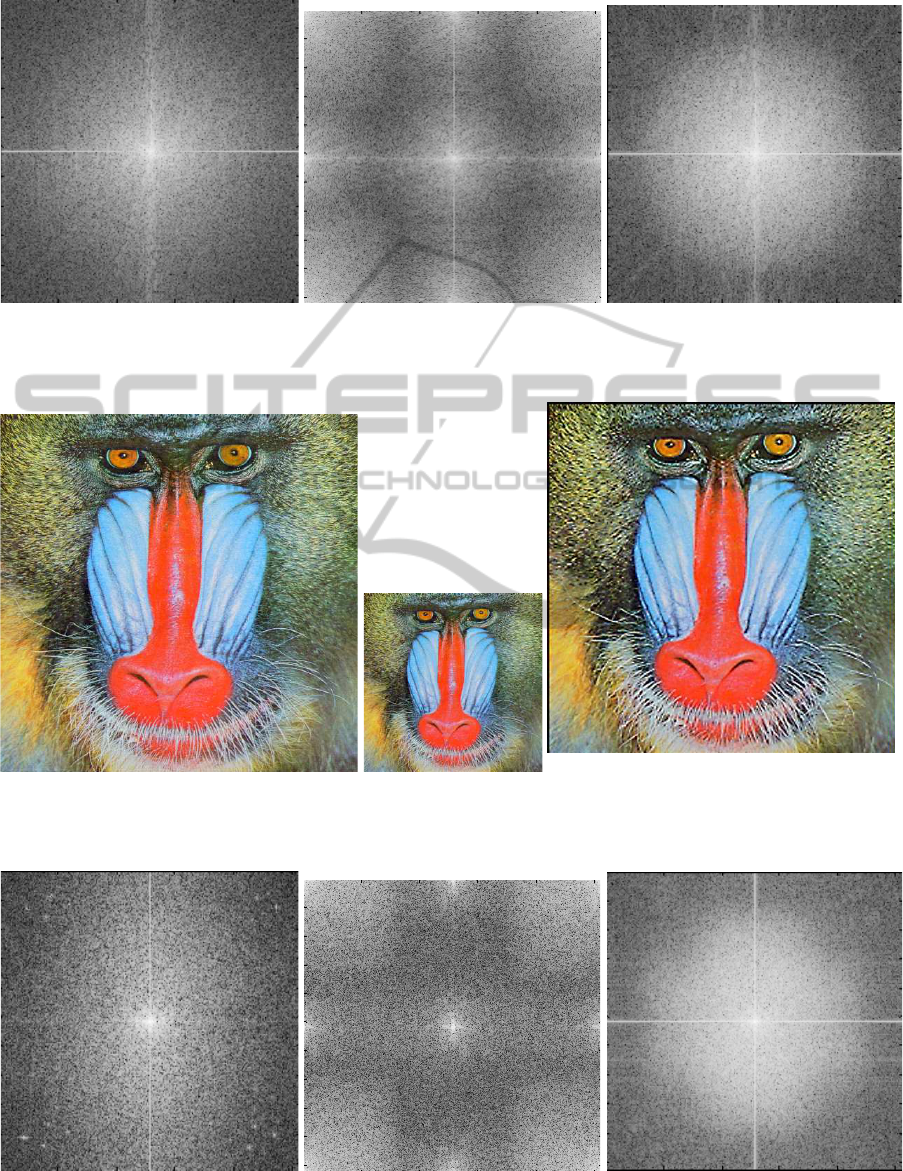
Figure 21: 2D FFT of Fig. 18. Figure 22: 2D FFT of Fig. 19. Figure 23: 2D FFT of Fig. 20.
Figure 24: (512X512). Figure 25: (256X256).
Figure 26: (512x512 NLSP image processed from
Fig. 25).
Figure 27: 2D FFT of Fig. 24. Figure 28: 2D FFT of Fig. 25. Figure 29: 2D FFT of Fig. 26.
SIGMAP2013-InternationalConferenceonSignalProcessingandMultimediaApplications
76
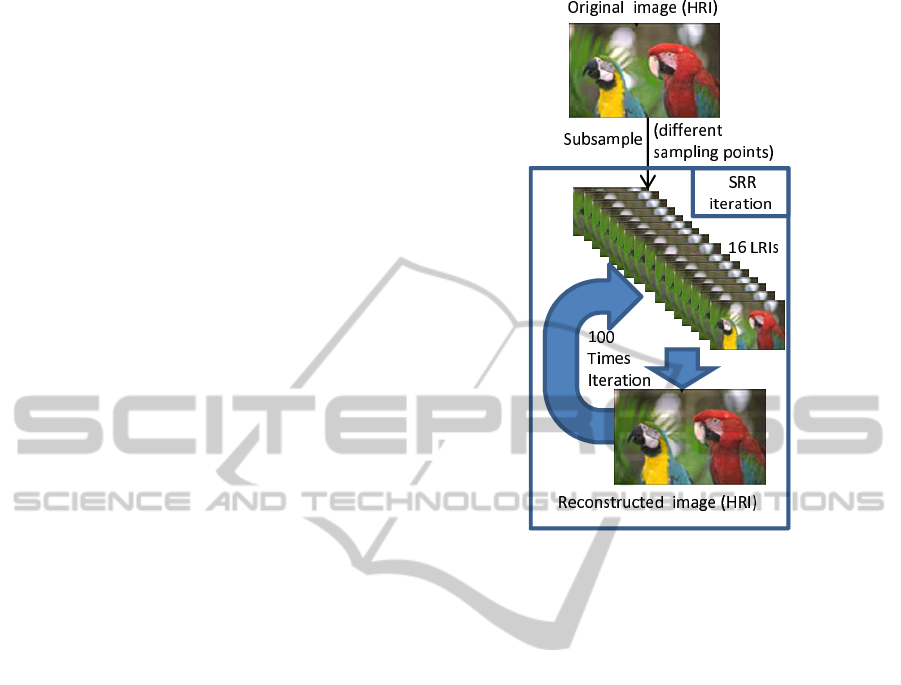
16 LRIs contain the same amount of information as
four original images, so the amount of information
in the 16 LRIs is four times the original image. The
reconstructed HRI image is stored in the frame mem-
ories. SRR thus uses five times the memory needed
to store the original image. Moreover, 100 iterations
are needed to create the SRR image. This means
SRR consumes a lot of resources in reconstructing the
image and its resolution is still not the same as the
original image because of the null in-band frequency
shown in Figure 4 and Figure 5.
On the other hand, the NLSP signal processing
is very simple: just straightforward signal process-
ing and no feedback processing, as shown in Figure
8. Moreover, NLSP needs only one quarter-size LRI.
The HPF part is just a digital filter in the frame, the
NLF part can be replaced by a look up table, and the
ADD part is very simple, which all means NLSP has
negligible frame delay when it is applied to video. It
is not difficult to embody a real-time NLSP method in
an inexpensive FPGA. Although a single frame mem-
ory type of SRR has been proposed for TV (Mat-
sumoto and Ida, 2008)(Matsumoto and Ida, 2010) and
there are HDTV sets equipped with it, the resolution
of HDTV sets with it is inferior to the HDTV sets
without it . The simulation results presented in this
paper show that SRR cannot give sufficient resolution
for enlarged images even if it is used under the ideal
condition, which means one high-resolution image is
reconstructed from all of the LRIs. In the simulation
results, the size of the LRIs was a quarter that of the
reconstructed image, which is the same ratio as the
image conversion from HDTV to 4K TV, and16 LRIs
were necessary to create one HRI from a still image.
Hence, it seems that an SSR technique would need 16
HDTV frames to convert HDTV into 4K TV. Besides
that, SRR faces other difficulties with motion vector
detection, motion blur, etc.
5 CONCLUSIONS
SRR is a useful tool only as long as the LRIs have
aliasing in them. That is, SRR can remove alias-
ing and create beautiful images, but it is useless if
the LRIs do not have aliasing in them. This means
SRR will not work if all we have is a single low-
resolution image. Moreover, SRR only works for
certain kinds of video sequences such as infrared-ray
video sequences with block noise and does not work
for general video TV and BluRay content. The prob-
lem is that most video sequences do not have aliasing,
except for interlaced aliasing or block noise, and SRR
cannot create higher frequency elements than what
Figure 30: SRR algorithm.
are in the original HRI. This means it is very difficult
to find video sequences taken with commercial video
cameras that would benefit from SRR. Although SRR
has been widely researched and has been touted as
a means of improving resolution for HDTV content,
its ability to improve video under practical circum-
stances turns out to be very limited.
The new NLSP method was compared with SRR,
and it was found to have better frequency characteris-
tics than those of SRR. NLSP can improve the reso-
lution of a single low-resolution image and can create
frequencyelements higher than the Nyquist frequency
of the original image. The four simulation results and
their frequency characteristics presented in this pa-
per prove that NLSP can create frequency elements
higher than the Nyquist frequency of the original im-
age.
The complexity and processing loads of NLSP
and SRR were also compared, and NLSP was found
to be light enough to be embodied in an FPGA. This
means it is possible to design a real-time NLSP device
for a real-time video system. There are many poten-
tial applications of NLSP including broadcasting, cin-
ema, security and medical fields. Two-dimensional
FFTs show that the resolution of NLSP is better than
that of SRR. However, subjective assessments with
NLSP and SRR with HDTV or 4K TV will have to
be made in the future. Several SR ideas have been
proposed for still images, and signal processing of
LimitationsofSuperResolutionImageReconstructionandHowtoOvercomethemforaSingleImage
77

still images is much more flexible in the sense that
real-time signal processing is not required. Thus, a
comparison of SR and NLSP for still images should
also be done. Further analysis is necessary before this
method can be implemented in an FPGA. An anal-
ysis of the high-frequency components generated by
the non-linear function used in the proposed method
and the original high-resolution image should also be
conducted.
REFERENCES
Sung Cheol Park, Min Kyu Park and Moon Gi Kang,
”Super-Resolution Image Reconstruction: A Techni-
cal Overview”, IEEE Signal Processing Magazine,
1053-5888/03, pp. 21-36, May, 2003.
S. Farsiu, D. Robinson, M. Elad, and P. Milanfar, ”Fast and
Robust Multi-frame Super-resolution”, IEEE Transac-
tions on Image Processing , vol. 13, no. 10, pp. 1327-
1344, October, 2004.
Adam W. M. van Eekeren, Klamer Schutte, and Lucas J.
van Vliet, ”Multiframe Super-Resolution Reconstruc-
tion of Small Moving Objects”, IEEE Transactions on
Image Processing, pp. 2901-2912, Vol. 19, No. 11,
November, 2010.
Aggelos Katsaggelos, Rafael Molina, and Javier Mateos,
”Super Resolution of Images and Video”, Synthesis
Lectures on Images, Video and Multimedia Process-
ing, Morgan& Clayppo Publishers, 2007.
Xianghua Houa and Honghai Liu, ”Super-resolution Image
Reconstruction for Video Sequence”, 2011 Interna-
tional Conference on Electronic & Mechanical Engi-
neering and Information Technology, pp. 4600-4603,
12-14 August, 2011.
Matan Protter, Michael Elad, Hiroyuki Takeda, and Pey-
man Milanfar, ”Generalizing the Nonlocal-Means to
Super-Resolution Reconstruction”, IEEE Transac-
tions on Image Processing, pp. 36-51, Vol. 18, No. 1,
Jan. 2009.
D. Glasner, S. Bagon, and M. Irani, ”Super-Resolution from
a Single Image”, International Conference on Com-
puter Vision (ICCV), October 2009.
S. Panda, R.S. Prasad, and G. Jena, ”POCS Based Super-
Resolution Image Reconstruction Using an Adaptive
Regularization Parameter”, IJCSI International
Journal of Computer Science Issues, Vol. 8, Issue 5,
No. 2, September 2011, ISSN (Online), 1694-0814.
N. Matsumoto and T. Ida, ”A Study on One Frame
Reconstruction-based Super-resolution Using Image
Segmentation”, IEICE Technical Report , SIP2008-
6,IE2008-6 (2008-04) (in Japanese).
N. Matsumoto and T. Ida, ”Reconstruction Based Super-
Resolution Using Self-Congruency around Image
Edges”, Journal of IEICE , Vol. J93-D, No. 2, pp.
118-126, Feb. 2010 (in Japanese).
http://www.toshiba.co.jp/regza/lineup/xs5/quality
4k2k.html
http://www.toshiba.co.jp/regza/detail/superresolution/reso
lution.html(in Japanese)
http://techon.nikkeibp.co.jp/english/NEWS
EN/20110906/
198008/
Seiichi Gohshi and Isao Echizen, ”Subjective Assessment
for HDTV with Super-Resolution function”, Sev-
enth International Workshop on Video Processing
and Quality Metrics for Consumer Electronics -
(VPQM2013), Jan. 2013.
Seiichi Gohshi, ”A New Signal Processing Method for
Video” ACM Multimedia Systems 2012, Feb.2012.
ACM Digital Library: MMSys ’12 Proceedings of the
3rd Multimedia Systems Conference, pp. 47-52 ACM
New York, NY, USA c2012.
W. F. Schreiber, ”Wirephoto Quality Improvement by Un-
sharp Masking”, J. Pattern Recognition, 2, 1970,
pp. 111-121.
J-S. Lee, ”Digital Image Enhancement and Noise Filtering
by Use of Local Statistics”, IEEE Trans. Pattern
Analysis and Machine Intelligence, PAMI-2, 2, March
1980, pp. 165-168.
W. K. Pratt, ”Digital Image Processing (3rd Ed)”, John
Wiley and Sons, 2001, pg. 278.
Seiichi Gohshi, ”Limitation of Super Resolution Image
Reconstruction for Video”, Computational In-
telligence, Communication and Networks (CICSyN),
Madrid, Jun. 2007.
T. Kurita and Y. Sugiura, Consideration on Motion Com-
pensated Deinterlacing and its Converter”, Tech-
nical Report of IEICE, CS93-148, IE93-85(1993-12).
(in Japanese)
SIGMAP2013-InternationalConferenceonSignalProcessingandMultimediaApplications
78
