Towards Cryptographic Function Distinguishers

with Evolutionary Circuits

Petr

Svenda, Martin Ukrop and Vashek Maty´aˇs

Masaryk University, Botanicka 68a, Brno, Czech Republic

Keywords:

eStream, Genetic Programming, Random Distinguisher, Randomness Statistical Testing, Software Circuit.

Abstract:

Cryptanalysis of a cryptographic function usually requires advanced cryptanalytical skills and extensive

amount of human labour. However, some automation is possible, e.g., by using randomness testing suites

like STS NIST (Rukhin, 2010) or Dieharder (Brown, 2004). These can be applied to test statistical proper-

ties of cryptographic function outputs. Yet such testing suites are limited only to predeﬁned patterns testing

particular statistical defects. We propose more open approach based on a combination of software circuits

and evolutionary algorithms to search for unwanted statistical properties like next bit predictability, random

data non-distinguishability or strict avalanche criterion. Software circuit that acts as a testing function is au-

tomatically evolved by a stochastic optimization algorithm and uses information leaked during cryptographic

function evaluation. We tested this general approach on problem of ﬁnding a distinguisher (Englund et al.,

2007) of outputs produced by several candidate algorithms for eStream competition from truly random se-

quences. We obtained similar results (with some exceptions) as those produced by STS NIST and Dieharder

tests w.r.t. the number of rounds of the inspected algorithm. This paper focuses on providing solid assessment

of the proposed approach w.r.t. STS NIST and Dieharder when applied over multiple different algorithms

rather than obtaining best possible result for a particular one. Additionally, proposed approach is able to

provide random distinguisher even when presented with very short sequence like 16 bytes only.

1 INTRODUCTION

The main motivation for this work is to provide a tool

with the crucial ability to automatically probe for un-

wanted properties of cryptographic functions that sig-

nalize ﬂaws in the function design. Although proper

and repeated cryptanalysis by a human cryptanalyst

(often assisted by automated tools) is by far the most

successful approach to assert function overall secu-

rity, one may want to automatically test for known sta-

tistical defects present in output produced by a func-

tion. Additionally, output testing for a given imple-

mentation of a particular cryptographic function is re-

quired to detect implementation errors.

Typical cryptanalytical approach against a new

cryptographic function is usually based on application

of various statistical testing tools (e.g., STS NIST,

Dieharder) as the ﬁrst step. Then follows applica-

tion of established cryptanalytical procedures (algo-

rithmic attacks, differential cryptanalysis, etc.) com-

bined with an in-depth knowledge of the inspected

function. The ﬁrst step can be at least partly auto-

mated and (relatively) easy to apply, but will detect

only the most visible defects in the function design or

apply only to a limited number of algorithm rounds.

The second approach usually yields much stronger in-

sight and detects more signiﬁcant defects, but usually

requires extensive human cryptanalytical labour. Ad-

ditionally, general statistical testing tools are limited

to a predeﬁned set of statistical tests. That on one

hand makes the follow-up analytical work easier if

the function fails a certain test, yet on the other hand

severely limits the potential to detect other defects.

We propose a novel approach based on combi-

nation of an automatically generated algorithm in

form of a hardware-like circuit designed by evolu-

tionary algorithms (more speciﬁcally, by genetic pro-

gramming). Evolutionary algorithms were previously

used to probe speciﬁc problems of a particular func-

tion (e.g., DES, TEA, XTEA), yet for their really

useful application, the identiﬁcation of speciﬁc sub-

problems like deviation of χ

Goodness of Fit tests

applied to statistic of least signiﬁcant bits (Castro and

Vi˜nuela, 2005) was required. Our approach may di-

rectly provide a distinguisher without prior identiﬁca-

tion of such sub-problems as well as be used when

135

Svenda P., Ukrop M. and Matyas V..

Towards Cryptographic Function Distinguishers with Evolutionary Circuits.

DOI: 10.5220/0004524001350146

In Proceedings of the 10th International Conference on Security and Cryptography (SECRYPT-2013), pages 135-146

ISBN: 978-989-8565-73-0

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

such a property was identiﬁed, providing a higher de-

gree of freedom when searching for a distinguisher.

We designed and tested an automated process that

can be used in a similar manner as general statistical

testing suites, but additionally provides the possibil-

ity to construct (again automatically) new tests. We

represent the “tests” as a hardware-like circuit emu-

lated in software that execute over given inputs and

computes outputs. Evolutionary algorithms (EAs)

are used to design the circuit layout (“wires” and

“gates”). Although such an automated tool will not

(at least for the moment) outperform a skilled cryp-

tographer, still it brings two major advantages:

• It can be applied automatically against multiple

different cryptographic functions with no addi-

tional human labour – working implementation of

the inspected function is sufﬁcient. Cryptographic

function competitions like AES (AES, 1997),

SHA-3 (SHA-3, 2007) or eStream (ECRYPT,

2004) are providing a particular advantage be-

cause candidate functions have to comply with

a standard programming interface (API), further

easing tests of numerous functions.

• It may discover and use other information leakage

“side channels” of the function than those usu-

ally assumed by cryptographers. The proposed

approach does not require pre-selection of partic-

ular parts of the function or input/output bits or to

deﬁne statistics used – this decision is left to the

evolutionary algorithm. Note that the proposed

approach may lead to even better results if a crypt-

analyst targets only a speciﬁc part of the inspected

function.

We implemented the proposed approach (more details

given in Section 3) and tested our idea on random

distinguishers of output from several eStream candi-

date functions (see Section 4). To assess the success

and usefulness of this method, we focused on func-

tions with inner structure containing repeated rounds.

By gradually increasing the number of rounds used

in a function, one can identify the maximum num-

ber of rounds where the approach still provides re-

sults (i.e., distinguisher with better probability than

random guessing). Results are very similar to those

obtained from STS NIST and Dieharder test suites

w.r.t. the number of rounds of the inspected function.

2 PREVIOUS WORK

Numerous works tackled the problem of distinguisher

construction between data produced by cryptographic

functions and truly random data, both with reduced

and full number of rounds. Usually, statistical testing

with battery of tests (e.g., STS NIST (Rukhin, 2010)

or Dieharder (Brown, 2004)) or additional custom tai-

lored statistical tests are performed. The STS NIST

battery was used to evaluate ﬁfteen AES (round 2)

candidates, demonstrating some deviation from ran-

domness in six candidates (Soto, 1999). In (Turan

et al., 2006), detailed examination of eStream Phase

2 candidates (full and reduced round tests) with STS

NIST battery and structural randomness tests was per-

formed, ﬁnding six ciphers deviating from expected

values. More recently, the same battery, but only a

subset of the tests, was applied to the SHA-3 candi-

dates (in the second round of competition, 14 in to-

tal) for a reduced number of rounds as well as only

to compression function of algorithm (Doganaksoy

et al., 2010). Additionally, custom-built statistical

tests based on strict avalanche criterion and others

were used, resulting in estimation of relative secu-

rity margins of candidates w.r.t. the number of rounds.

(Sulak et al., 2010) proposed a method to test statis-

tical properties of short sequences typically obtained

by block ciphers or hash algorithms for which some

from STS NIST can not be applied due to insufﬁcient

length. Probabilities expressed by p-values are calcu-

lated for each short subinterval and improved method

based on recalculation of expected probabilities is

provided. Example results applied to selected block

and hash functions are presented. 256-bit versions of

SHA-3 ﬁnalists were subjected to statistical tests us-

ing a GPU-accelerated evaluation (Kaminsky, 2012).

Both algorithms and selected tests from STS NIST

battery were implemented for the nVidia CUDA plat-

form. Because of massive parallelization, superpoly

tests introduced by (Dinur and Shamir, 2009) were

possible to be performed, detecting some deviations

in all but the Grøstl algorithm.

Stochastic algorithms were also applied in cryp-

tography to some extent, focusing initially mostly on

simple transposition and substitution ciphers or prob-

lems like efﬁcient knapsack algorithm. A nice re-

view of usage of genetic algorithms in cryptography

up to year 2004 can be found in (Delman, 2004), a

more recent review of evolutionary methods used in

cryptography is provided by (Picek and Golub, 2011).

TEA algorithm (Wheeler and Needham, 1995) with

a reduced number of rounds is a frequent target for

cryptoanalysis with genetic algorithms. In (Castro

and Vi˜nuela, 2005), a successful randomness distin-

guisher for XTEA limited to 4 rounds is generated

with genetic algorithms. The distinguisher gener-

ates a bit mask with high Hamming weight which

when applied to function input, resulting in devi-

ated χ

Goodness of Fit test of the output. Addi-

SECRYPT2013-InternationalConferenceonSecurityandCryptography

136

tionally, a special behaviour of the TEA algorithm

with full number of rounds was observed when XOR-

ing instead of adding the mask. However no distin-

guisher for full number of rounds was found. Subse-

quent work (Hu, 2010) improves an earlier attack with

quantum-inspired genetic algorithms, ﬁnding more

efﬁcient distinguishers for a reduced round TEA algo-

rithm and succeeding for the 5-round TEA. In (Gar-

rett et al., 2007) a comparison of genetic techniques

is presented, with several suggestions which genetic

techniques and parameters should be used to obtain

better results. We adopted the genetic programming

(Banzhaf et al., 1997) technique with steady-state re-

placement (Liu et al., 2008). An important difference

of our approach from previous work is the production

of a program (in the form of a software circuit) that

provides different results depending on given inputs.

Previous work produced a ﬁxed result, e.g., bit mask

in (Castro and Vi˜nuela, 2005; Hu, 2010) that is di-

rectly applied to all inputs.

Structure of a software circuit resembles artiﬁcial

neural networks (NN) to some extent. Notable dif-

ferences are in the learning mechanism and in a high

number of layers used in our software circuit (NN

usually use only three). Recently, deep belief neu-

ral networks (DBNN) were proposed (Hinton et al.,

2006) with the learning algorithm based on restricted

Boltzmann machines that also use 5 or even more

layers. Still, a software circuit uses mutation and

crossover to converge towards an optimum instead of

back propagation in case of classical NN or lay-by-

layer learning algorithm for DBNN. Also, different

functions may be computed inside every node in case

of software circuit instead of weighted sum of DBNN.

3 SOFTWARE CIRCUIT

Software circuit is a software representation of a

hardware-like circuit with nodes (“gates”) responsible

for computation of simple functions (e.g., AND, OR).

Nodes are positioned in layers where outputs from the

previous layer are provided as inputs to the nodes in

the following layer by connectors (“wires”). Input to

the whole circuit is simulated as an output of the ﬁrst

layer and output of last layer is taken as the output of

whole circuit. Connectors might connect a node to all

nodes from a previous layer, to only some of them, or

to none at all. Connectors in a software circuit may

also cross each other as they are emulated – in con-

trary to real single-layer hardware circuits. A simple

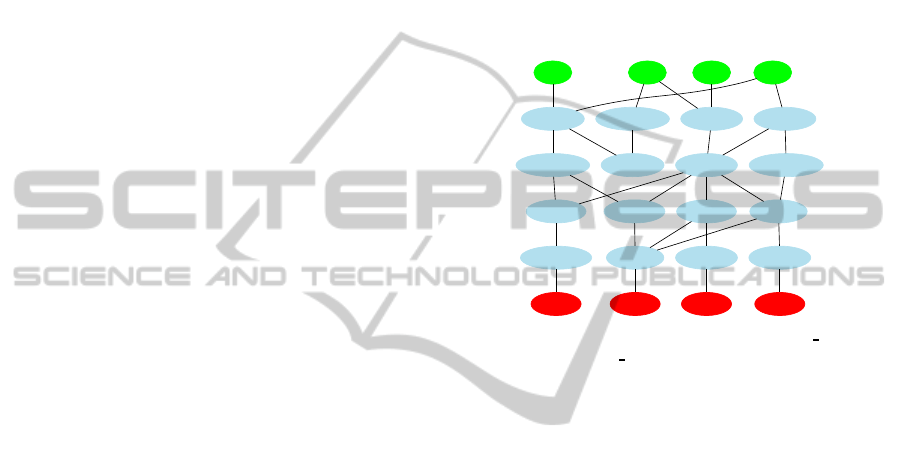
circuit can be seen in Figure 1.

Examples of such a circuit might be a Boolean

circuit where functions computed in nodes are lim-

ited to logical functions or artiﬁcial neural networks

where nodes compute the weighted sum of the inputs.

Besides studying complexity problems, these circuits

were used in various applications like construction of

a fully homomorphic scheme (Gentry, 2010) or in de-

sign of efﬁcient image ﬁlters (Sekanina et al., 2012).

Circuit evaluation can be performed by a software

emulator that propagatesinput values, computes func-

tions and collects outputs in nodes or possibly directly

in hardware when FPGAs are used (Sekanina et al.,

2012).

IN_0 IN_1 IN_2 IN_3

1_0_NOR 1_1_ROL_5 1_2_AND 1_3_NOP

2_0_ROL_0 2_1_SUM 2_2_ADD 2_3_ROR_6

3_0_SUB 3_1_OR_ 3_2_SUB 3_3_DIV

4_0_BSL_3 4_1_DIV 4_2_NAN 4_3_ADD

0_OUT 1_OUT 2_OUT 3_OUT

Figure 1: Software circuit with input nodes (IN x), inner

nodes, output nodes (x

OUT) and connectors. Note that not

all input or output nodes need to be used as well not all inner

nodes need to output any value.

3.1 How to Design Circuit Layout

Circuit design can be laid out by an experienced

human designer, automatically synthetized from the

source code or even automatically initialized and then

improved by an optimization algorithm. We use the

last approach and combine a software circuit evalu-

ated on a CPU (or also on GPUs) with evolutionary

algorithms (EAs). The main goal is to ﬁnd a circuit

that will reveal an unwanted defect in the inspected

cryptographic functions. For example, if a circuit is

able to correctly predict the n

bit of a key stream

generated by a stream cipher just by observing pre-

vious (n − 1) bits, then this circuit serves as a next-

bit predictor (Yao, 1982), breaking the security of the

given stream cipher. When a circuit is able to distin-

guish output of the tested function from a truly ran-

dom sequence, it serves as a random distinguisher

(Englund et al., 2007) providing a warning sign of

function weakness.

Note that a circuit need not provide correct an-

swers for all inputs – it is sufﬁcient if a correct answer

is provided with a probability signiﬁcantly better than

random guessing.

When combined with evolutionary algorithms, the

whole process of circuit design consists of the follow-

TowardsCryptographicFunctionDistinguisherswithEvolutionaryCircuits

137

ing steps:

1. Several software circuits are randomly initialized

(randomly selected functions in nodes, randomly

assigned existence of connectors between nodes)

forming population of candidate individuals. Ev-

ery individual is represented by one circuit. Note

that such a random circuit will most probably not

provide any meaningful output for given inputs

and can even have disconnected layers (no output

at all).

2. If necessary, generate new test vectors used later

by a so-called ﬁtness function for evaluation (see

Section 3.2 for discussion).

3. Every individual (circuit) in the population is em-

ulated and obtained outputs are evaluated. The

ﬁtness function assigns a rating based on each in-

dividual success in given task (e.g., what fraction

of inputs were correctly recognized as being out-

put of a stream cipher rather than a completely

random sequence, see Section 3.2 for details).

4. Based on the evaluation provided by the ﬁtness

function, a potentially improved population is

generated by mutation and crossover operators

from individuals taken from the previous gener-

ation. Design of every individual (circuit) may

be changed by changing operations computed in

nodes or adding/removing connectors between

nodes in subsequent layers.

5. Repeat from step 2. Usually hundreds of thou-

sands or more repeats are performed, therefore

the evaluation of a single circuit in step 3 must be

fast enough (currently, we are in the milliseconds

range).

3.2 How to Deﬁne Problems to be

Solved by Circuit

Evolutionary algorithms need to be supplied with a

metric of success (so-called ﬁtness function) that is

applied to measure quality of a candidate individual.

Proper deﬁnition of ﬁtness function is crucial to ob-

tain a working solution to the deﬁned problem. In this

work, we limit ourselves to randomness distinguisha-

bility as a target goal and devise the metric of success

based on a number of test vectors correctly identiﬁed

by the software circuit as the output from the crypto-

graphic function or the stream of random data. Other

goals like next-bit predictor (Yao, 1982) or defector of

strict avalanche criterion (Webster and Tavares, 1986)

can be used.

In this work, we aim to obtain a software circuit

capable of correctly distinguishing between a block

of bytes generated by a cryptographic function (eS-

tream candidate) with an unknown key and truly ran-

dom data. We worked with three scenarios with re-

spect to the frequency of key change:

1. Key is ﬁxed for all generated test sets and vectors.

Even when test sets change, new test vectors are

generated using the same key.

2. Every test set was generated using a different key.

All test vectors in a particular test set are gener-

ated with the same key.

3. Every test vector (16 bytes) was generated using

a different key.

The circuit input is a sequence of bytes produced ei-

ther by the inspected function (ﬁrst type) or generated

completely randomly (second type). The circuit out-

put is an encoding of the guessed source. Different

encodings are possible: single bit (e.g., 0 meaning

“random data” and 1 meaning “function output”) or

multiple bits (e.g., low versus high Hamming weight

of whole output byte). Results in this work use only

byte’s highest bit for easier interpretation, but Ham-

ming weight seems to be a better choice for later ex-

periments. Additionally, a circuit can be allowed to

make multiple guesses by producing multiple output

bytes. A circuit thus has the possibility to express its

own certainty in the predicted result (e.g., by setting 2

out of 3 outputs to predict random data and remaining

one to predict the function output) as well as to evolve

more than one predictor inside a single circuit.

A circuit is successful if able to distinguish func-

tion outputs from random sequences signiﬁcantly bet-

ter than by random guessing.

3.3 How to Evaluate Circuit

Performance?

For evaluation of a circuit performance, we use super-

vised learning with test sets containing pairs of inputs

and expected outputs generated by a “teacher” prior

to the evaluation. Since we generated the test sets, we

also know which vectors were generated from func-

tion output and which were taken from random data.

Outputs from a circuit for given inputs are compared

with expected outputs and circuit performance is then

rated as follows:

fitness =

#(correctly

predicted test vectors)

#(total test vectors)

For our experiments, we used the following settings

to maintain a good trade-off between the evaluation

time and statistics (inﬂuenced mainly by the number

of test vectors) and the ability to prevent overlearning

(inﬂuenced by the test set change frequency).

SECRYPT2013-InternationalConferenceonSecurityandCryptography

138

• Every test set contains 1000 test vectors with ex-

actly half taken from inspected function’s output

and second half taken from random data. Order

of test vectors in the set is not important as test

vectors are handled by circuit completely inde-

pendently.

• Every test vector has length of 16 bytes.

• Test set is periodically changed every 100

gen-

eration to prevent overlearning on a given test set.

3.4 Practical Implementation

We represent a software circuit by a two-dimensional

array with values in odd rows interpreted as nodes

and values in even rows as masks deﬁning existing

connectors. The circuit simulator takes this array to-

gether with input values, passes inputs to the ﬁrst

layer of nodes and propagates values modiﬁed by el-

ementary functions in nodes via connectors to the

following layer. After processing all layers of cir-

cuit, values provided by the last layer are returned

as the circuit output. For the start, we used the fol-

lowing elementary operations for nodes: no operation

(NOP), logical functions (AND, OR, XOR, NOR,

NAND), bit manipulating functions (ROTR, ROTL,

BITSELECTOR), arithmetic functions (ADD, SUBS,

MULT, DIV, SUM), read a speciﬁed input byte even

from an internal layer (READX) and produce a con-

stant value (CONST). The implementation is avail-

able as an open-source project EACirc (Ukrop and

Svenda, 2013).

As optimization requires many evaluations of can-

didate circuits, we use our computation infrastructure

with the BOINC control (Anderson, 2004) to per-

form distributed computation with more than thou-

sand CPU cores. EACirc is implemented to coordi-

nate computation based on logs of population of indi-

viduals and on the internal state, providing possibil-

ity to perform optimization with unlimited number of

generations even when a computation node itself lasts

only a limited time before reboot.

Truly random data used for test vectors were pro-

duced by the Quantum Random Bit Generator Service

(QRBG) (Stevanovi´c et al., 2008).

To ease understanding of our software circuits, we

implemented an automatic removal of nodes and con-

nectors that do not contribute to the resulting ﬁtness

value (pruning) and transformation into the Graphviz

dot format for easy visualization.

To independently replicate results provided by a

circuit emulator and to double check against possible

implementation bugs, EACirc allows to transform the

two-dimensional array with the circuit into the source

code of a plain C program. The resulting C program

can be compiled separately and computes only the

circuit from which it was generated, but completely

avoids the circuit emulator.

4 APPLICATION TO ESTREAM

CANDIDATES

The testing methodology described in Section 3 was

applied against candidate functions from the eStream

competition (ECRYPT, 2004). We considered the

availability of implementations with the same pro-

gramming interface (API) for all candidates, where

one can automatically test (both STS NIST/Dieharder

and software circuit distinguisher) on a large number

of functions with ease. Additionally, one can cherry-

pick only such functions where a well-working cir-

cuit is found for further analysis. In this work, we fo-

cused primarily on the goal to obtain at least the same

results as with STS NIST/Dieharder batteries. Previ-

ous works evaluated statistical properties of candidate

functions with the full number of rounds as well as

with a reduced number of rounds (Turan et al., 2006).

Testing full number of rounds usually provides only

limited information – either the function is very weak

and exhibits weaknesses even in the full number of

roundsor no defect at all is detected, even when an ex-

ploitable serious attack might exist for a limited num-

ber of rounds.

From 34 candidates in the eStream competition,

23 were potentially usable for testing (due to re-

named or updated versions, problems with compi-

lation, etc.). For the start, we limited ourselves to

7 of these (Decim, Grain, FUBUKI, Hermes, LEX,

Salsa20 and TSC) having a structure that allows for

a reduction of complexity by a decreased number of

rounds in a straightforward way.

4.1 Settings Used

For the Dieharder test battery, the following settings

were used:

• 250 MB of data generated from a given function

with 3 different key change frequencies;

• tests correspondingto the original Diehard battery

were used (except for the Diehard sums test);

• each test was run once, length of the data stream

actually used was decided by the test;

• based on the test results, sum over all tests

(pass=1, weak=0.5, fail=0) is displayed.

For the STS NIST, the following settings were used:

TowardsCryptographicFunctionDistinguisherswithEvolutionaryCircuits

139

IN_0IN_1 IN_2 IN_3 IN_4 IN_5

IN_6

IN_7

IN_8

IN_9 IN_10 IN_11

IN_12 IN_13

IN_14

IN_15

1_2_ROL_3 1_3_ROL_5 1_4_NOR 1_5_SUM

2_3_OR_ 2_5_NOP

3_3_OR_

4_0_SUM 4_3_NOP

5_0_NOP 5_1_OR_

0_OUT 1_OUT

IN_0IN_1 IN_2 IN_3IN_4IN_5 IN_6 IN_7

IN_8

IN_9 IN_10 IN_11 IN_12 IN_13 IN_14 IN_15

1_0_XOR1_1_XOR 1_3_NOP1_4_ADD 1_5_ADD 1_7_SUB

2_0_XOR 2_1_OR_ 2_3_NAN 2_4_AND 2_5_OR_

3_0_NAN 3_1_NOP 3_2_OR_ 3_3_MUL 3_5_NOP

4_0_MUL 4_2_NOP 4_3_NAN

5_0_NOR5_1_NOR

0_OUT1_OUT

Figure 2: Two example circuits found by evolution for distinguishing the Grain algorithm (limited to 2 rounds) from truly

random data (only nodes contributing to resulting success rate are shown). Although both circuits encode distinguishers with

the same success rate (strong 99%), their internal complexity is different. The right circuit uses all inputs but number 8 (IN

8),

whereas the left circuit ignores four more inputs. Additionally, the left circuit is performing distinguisher functionality only in

its ﬁrst three layers, remaining two are only propagating values to output layer. Notice also the SUM function in the 4

layer

0 SUM) – it has no other functionality than to pass the output from the 3

layer to the 5

(output) layer (equivalent of

NOP) – a simple example of equivalent functionality encoded in multiple ways typical for evolutionary algorithms. Finally,

observe nodes in the 5

layer of the right circuit – the same function (NOR) is performed over the same set of inputs from

the 4

layer, outputting the same value into 0

OUT and 1 OUT. Such a behaviour was observed in almost all evolved circuits

and is the consequence of circuit outputs interpretation (see Section 3.2).

• same source ﬁles with data as for Dieharder were

used;

• each test runs 100 times on 1 000 000 bits;

• some runs had problems (error during test exe-

cution) with tests RandomExcursions and Ran-

domExcursionsVariant. These tests are therefore

not included in the results.

Note that we will not discuss all results in details as

such discussion was already done several times before

(Soto, 1999; Turan et al., 2006; Doganaksoy et al.,

2010). We will focus only on the identiﬁcation of the

highest round where some defects are still detected

and the signiﬁcance of such detection – whether al-

most all tests fail or only a minority of them.

For the software circuit, we used the following set-

tings:

• 5 layers, 8 nodes in every internal layer, 16 input

nodes (corresponding to 16 input bytes in every

test vector) and 2 output nodes.

For evolutionary algorithms, we used the following

settings (based on our previous experience):

• Population consists of 20 individuals refreshed by

the steady-state replacement strategy (Liu et al.,

2008) with

/3 of individuals replaced every gen-

eration.

• 30000 generations were executed in a single evo-

lution run with 30 separate evolution runs running

in parallel.

• Mutation is applied with probability of 0.05 and

changes function in given node or connector mask

by addition or removalof connector to given node.

• Crossover is applied with probability of 0.5 and

performs single point crossoverwith the ﬁrst i lay-

ers taken from the ﬁrst parent and remaining lay-

ers from the second parent.

Around 2.3MB ((30000/100) · 500 · 16B) is re-

quired for evolution with 30000 generations and the

test set changed every 100

generation. If 30 runs

were executed in parallel (this was performed to ob-

tain reliable samples), around 68 MB of data pro-

duced by a given function is required. However, all

runs for eStream ended with the same success ra-

tio and were therefore unnecessary in principle (tests

with SHA-3 candidates provided more varying re-

sults).

We like to stress out that STS NIST and Dieharder

make decision on all such data processed together in

single pass. Our circuit will make decision on much

smaller sample of 16 bytes only.

4.2 Results for eStream Candidates

Tables 1–7 summarize results for selected eStream

candidates depending on a number of algorithm

rounds and also on the key change frequency. Visual-

ization of example circuit is shown at Figure 2 . In-

terpretation of values in tables 1–7 is the following:

both statistical tests have several tests in battery – 20

for Diehard, 162 for STS NIST (for STS NIST, two

groupsof tests were omitted as mentionedearlier, oth-

erwise the number of tests would be 188). Dieharder

provides three levels of evaluationfor a particular test:

pass, weak, fail. Values 1, 0.5, 0 were assigned to

these levels respectively and sum over all tests is com-

puted and displayed. For STS NIST, number of all

SECRYPT2013-InternationalConferenceonSecurityandCryptography

140

passed tests is displayed (this is deduced from the dis-

tribution of p-values across all 100 runs with respect

to the signiﬁcance level of α = 0.01).

For the software circuit (EACirc), the distin-

guisher success rate (ﬁtness value) is computed on a

fresh new test set never seen by a given circuit be-

fore. Two types of values are presented. When a

distinguisher with at least 99% success rate for 50

consecutive test sets was found (very strong distin-

guisher), average number of generations (from 30 in-

dependent runs) necessary to ﬁnd it is listed. When

no such strong distinguisher is found, the average suc-

cess rate is listed, computed as the average of averages

of maximum ﬁtness after test vector change (denoted

as AAM). The ﬁrst case provides a distinguisher that

is almost always right. The second case provides a

distinguisher sometimes giving a wrong answer, but

still better than random guessing.

To verify results provided by the proposed ap-

proach, we ﬁrst let circuits distinguish between two

groups of test vectors, but with both taken from truly

random data. Intuitively, our approach should fail

to ﬁnd a working distinguisher and should behave as

random guessing. The predicted behaviour was con-

ﬁrmed by an experiment with same settings as these

used for testing functions. All statistical tests from

Dieharder (20/20) and STS NIST (162/162) success-

fully passed on such data, and no stable distinguisher

was found. The average distinguisher success ratio

computed in the same manner as for tested functions

(AAM) was 0.52. Note that the value of 0.52 is

equivalent to random guessing, although bigger than

0.5. The reason is that more than one individual is

present in the population (20 individuals were used,

20 guesses instead of 1 are made, best one is used).

Changing the number of individuals or the number

of test vectors will inﬂuence the expected centre of

distribution – the distinguisher success ratio shifts to-

wards the value 0.5 when the number of individuals is

decreasing, as well as when the number of test vectors

is increasing, as intuitively expected. We also exper-

imentally veriﬁed this reasoning: for the population

ﬁxed to 20 individuals, setting the test set size to 200,

500, 1000, 2000, 5000 and 10000 vectors provide the

average success ratios of 0.544, 0.527, 0.520, 0.514,

0.509 and 0.506, respectively. For the test size ﬁxed

to 1000 vectors, setting the population size to 5, 10,

20, 50 and 100 individuals provide the average suc-

cess ratios of 0.509, 0.514, 0.520, 0.526 and 0.530,

respectively.

Let us take Grain limited to 1 round as an example

how to interpret data in Tables 1–7:

• For a key ﬁxed over all tests (the key is set only

once for the run), all tests from Dieharder and STS

NIST failed, therefore the displayed value is 0. A

software circuit found a strong 99% distinguisher

in the 221

generation (on average).

• For the key changed every test set, all tests from

Dieharder and STS NIST failed again, resulting

in value 0. The software circuit was unable to

ﬁnd a strong 99% distinguisher, but found a dis-

tinguisher with approximately 0.67 success rate

(AAM) – value (0.67) is displayed.

• For the key changed every test vector (every 16

bytes), Dieharder resulted in one fail and one

weak test (all other passed), therefore the sum is

18.5. For STS NIST, all tests passed, resulting

in value 162. The software circuit was unable to

ﬁnd any distinguisher better than random, having

AAM value equal to 0.52, therefore (0.52) is dis-

played.

4.3 Veriﬁcation of Separate Circuit

To cross-verify results found by the proposed ap-

proach, we took the source code representation of a

circuit found and executed it without the circuit em-

ulator directly over 100 000 test vectors. The results

conﬁrmed values obtained via circuit emulator.

5 DISCUSSION

Process of circuit optimization and circuits found can

be analysed to understand how EAs progress towards

a working solution and what makes circuit a working

distinguisher. The following behaviour was observed:

• Different circuits with the same distinguishing

success rate might be evolved, as is demonstrated

with the example of Grain-2 (Figure 2), possibly

with a signiﬁcant diversity. A deeper analysis of

shared components between different circuits may

provide a better understanding of statistical de-

fects detected in data.

• Fitness progress typical for evolutionary algo-

rithms was observed. Intermediate solutions tend

to overlearn on a particular testing set and sharply

decrease once the testing set is changed (occur-

ring every 100

generation), forming a jaw-like

graph (see Figure 3). Once a genuine progress

in the distinguisher success rate is achieved, over-

learning still takes place, but the subsequent drop

is not going down to random guessing.

• Not all nodes and connectors in input and inner

layers are utilized for prediction. As such nodes

and connectors can be automatically detected (no

TowardsCryptographicFunctionDistinguisherswithEvolutionaryCircuits

141

Table 1: Results for Grain.

# of rounds

IV and key reinitialization

once for run for each test set for each test vector

Dieharder

(x/20)

STS NIST

(x/162)

EACirc

Dieharder

(x/20)

STS NIST

(x/162)

EACirc

Dieharder

(x/20)

STS NIST

(x/162)

EACirc

1 0.0 0 n = 221 0.0 0 (0.67) 18.5 162 (0.52)

2 0.0 0 n = 471 0.5 0 (0.66) 20.0 162 (0.52)

3 19.5 160 (0.52) 20.0 162 (0.52) 20.0 162 (0.52)

13 20.0 162 (0.52) 20.0 161 (0.52) 19.5 162 (0.52)

Table 2: Results for Decim.

# of rounds

IV and key reinitialization

once for run for each test set for each test vector

Dieharder

(x/20)

STS NIST

(x/162)

EACirc

Dieharder

(x/20)

STS NIST

(x/162)

EACirc

Dieharder

(x/20)

STS NIST

(x/162)

EACirc

1 0.0 0 n = 2681 0.0 0 (0.85) 0.0 5 n = 1431

2 0.5 0 (0.54) 1.0 0 (0.54) 15.5 146 (0.52)

3 1.0 0 (0.53) 1.0 0 (0.53) 15.0 160 (0.52)

4 3.5 79 (0.52) 3.0 78 (0.52) 20.0 160 (0.52)

5 4.5 79 (0.52) 3.5 91 (0.52) 17.5 161 (0.52)

6 19.0 158 (0.52) 19.0 159 (0.52) 18.0 162 (0.52)

7 18.5 162 (0.52) 19.0 161 (0.52) 20.0 161 (0.52)

8 20.0 162 (0.52) 20.0 159 (0.52) 19.0 161 (0.52)

Table 3: Results for FUBUKI.

# of rounds

IV and key reinitialization

once for run for each test set for each test vector

Dieharder

(x/20)

STS NIST

(x/162)

EACirc

Dieharder

(x/20)

STS NIST

(x/162)

EACirc

Dieharder

(x/20)

STS NIST

(x/162)

EACirc

1 20.0 162 (0.52) 20.0 161 (0.52) 18.0 162 (0.52)

4 20.0 162 (0.52) 20.0 162 (0.52) 20.0 162 (0.52)

change to the ﬁtness value when temporarily re-

moved), a pruned version of the circuit is easier to

analyse.

5.1 Comparison of Software Circuit

with STS NIST/Dieharder Batteries

Based on results obtained with the proposed approach

(software circuits designed by genetic programming),

a comparison to statistical batteries like STS NIST

and Dieharder can be undertaken:

Advantages

• The proposed method is based on a completely

different approach than statistical tests used in

batteries, opening space for detecting dependen-

cies between solutions not covered by tests from

batteries.

• The proposed method offers possibility to con-

struct a distinguisher based on a dynamically con-

structed algorithm rather than a predeﬁned one

from batteries.

SECRYPT2013-InternationalConferenceonSecurityandCryptography

142

Table 4: Results for Hermes.

# of rounds

IV and key reinitialization

once for run for each test set for each test vector

Dieharder

(x/20)

STS NIST

(x/162)

EACirc

Dieharder

(x/20)

STS NIST

(x/162)

EACirc

Dieharder

(x/20)

STS NIST

(x/162)

EACirc

1 20.0 162 (0.52) 20.0 162 (0.52) 20.0 162 (0.52)

10 20.0 160 (0.52) 20.0 162 (0.52) 20.0 162 (0.52)

Table 5: Results for LEX. Note that the internal structure of LEX responds differently to the limitation of number of rounds

(when compared to other algorithms). LEX internally prepares 4 bytes of data during every round as output stream. Limitation

of the number of rounds will only limit number of bytes in the output, not the strength of output data. Since we are testing 16

bytes of input data, 4 rounds will generate enough internal output bytes to encrypt it as a full round version.

# of rounds

IV and key reinitialization

once for run for each test set for each test vector

Dieharder

(x/20)

STS NIST

(x/162)

EACirc

Dieharder

(x/20)

STS NIST

(x/162)

EACirc

Dieharder

(x/20)

STS NIST

(x/162)

EACirc

1 0.0 0 n = 148 0.0 0 n = 7274 3.0 1 n = 154

2 4.0 1 n = 221 4.0 1 n = 304 3.5 1 n = 254

3 0.5 1 n = 378 3.5 1 n = 491 4.0 1 n = 361

4 20.0 162 (0.52) 19.5 162 (0.52) 20.0 161 (0.52)

10 19.5 162 (0.52) 19.5 160 (0.52) 20.0 160 (0.52)

Table 6: Results for Salsa20.

# of rounds

IV and key reinitialization

once for run for each test set for each test vector

Dieharder

(x/20)

STS NIST

(x/162)

EACirc

Dieharder

(x/20)

STS NIST

(x/162)

EACirc

Dieharder

(x/20)

STS NIST

(x/162)

EACirc

1 5.5 1 (0.87) 8.5 1 (0.67) 17.5 161 (0.52)

2 5.5 1 (0.87) 7.0 1 (0.67) 19.5 162 (0.52)

3 20.0 162 (0.52) 20.0 162 (0.52) 19.5 161 (0.52)

12 20.0 162 (0.52) 19.5 161 (0.52) 19.0 161 (0.52)

• Once a working distinguisher is found, it requires

extremely short sequences (tested on 16 bytes

only) to detect function output. Statistical batter-

ies require at least several megabytes of data.

• Once a distinguisher is found (time intensiveoper-

ation), it can be used to quickly process additional

test vectors produced with different keys.

• Lower amount of data extracted from a given

function is necessary to provide a working dis-

tinguisher (at maximum, we used 2.2 MB). Data

required by STS NIST and Dieharder were larger

(more than 200 MB required for some Dieharder

tests). Note that some tests may provide indica-

tion of failure even when less data is available.

Disadvantages

• Because of very short sequences the circuit is

working on, subtle statistical defects may not be

detected. However, several modiﬁcations to the

proposed approach might be used to process large

sequences instead of 16 bytes only (e.g., circuit

with memory executed iteratively over large data

partitioned to 16 bytes chunks) – testing such

TowardsCryptographicFunctionDistinguisherswithEvolutionaryCircuits

143

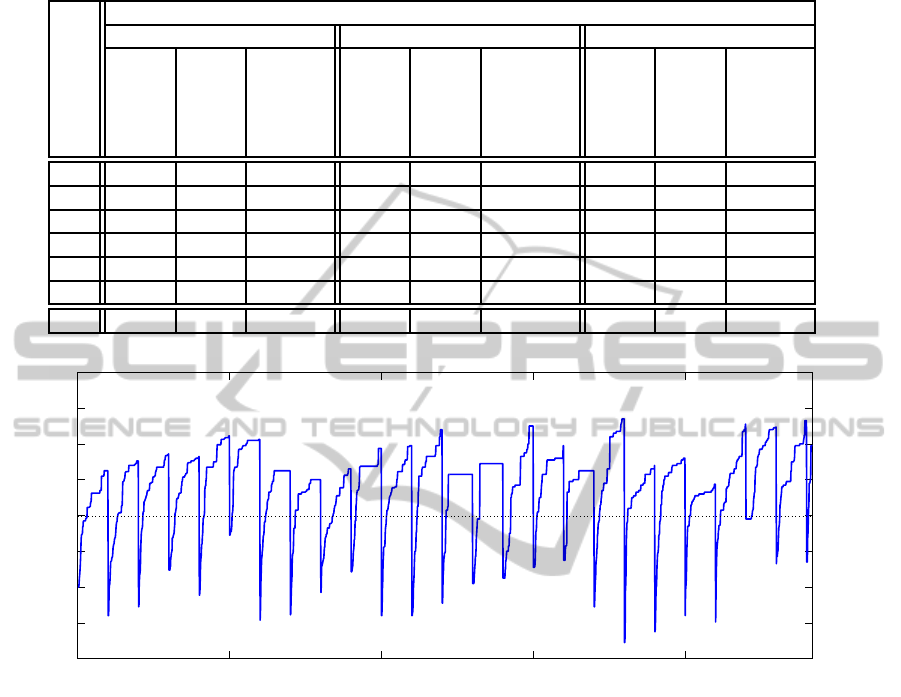
Table 7: Results for TSC. Note that the TCS algorithm does not ﬁll data into all output structures before round 9. During

the ﬁrst 8 rounds, only parts of memory are set by function output, leaving remaining memory ﬁlled with memory garbage

(values present in the memory before allocation).

# of rounds

IV and key reinitialization

once for run for each test set for each test vector

Dieharder

(x/20)

STS NIST

(x/162)

EACirc

Dieharder

(x/20)

STS NIST

(x/162)

EACirc

Dieharder

(x/20)

STS NIST

(x/162)

EACirc

1-8 0.0 0 n = 104 0 0 n = 4101 0.0 0 n = 104

9 1.0 1 n = 234 1.5 1 n = 491 2.0 1 n = 121

10 2.0 13 n = 188 3.0 13 n = 218 3.0 12 n = 158

11 10.0 157 (0.52) 11.5 157 (0.52) 14.0 159 (0.52)

12 16.0 162 (0.52) 17.0 161 (0.52) 17.5 162 (0.52)

13 20.0 162 (0.52) 20.0 162 (0.52) 19.0 162 (0.52)

32 20.0 161 (0.52) 20.0 162 (0.52) 20.0 161 (0.52)

0 500 1000 1500 2000

0.48

0.49

0.5

0.51

0.52

0.53

0.54

0.55

0.56

Distinguisher success rate

Random to random data distinguisher

Number of generations

Figure 3: Example of success rate for distinguisher evolution between two sets of random data, the data set changed every

100

generation (dotted line corresponds to average success of random guessing). Although no structure is present in data,

the circuit is overlearning on a particular data set and thus exhibiting better success rate then random guess (increasing part of

curve) before the test set is changed (a sudden drop in the success rate).

modiﬁcations is now on our agenda.

• The resulting distinguisher may be hard to analyse

– what is the weakness detected and what should

be ﬁxed in the function design?

• EA based approach may require signiﬁcantly

higher computational requirements to test the can-

didate function during the evolution phase of soft-

ware circuit. Evaluation of an evolved circuit

(e.g., distinguisher) is then very fast.

• A distinguisher found may be ﬁtted to a particular

candidate function (and possibly even a particular

key, if the key is not changed periodically in the

training set) instead of discovering generic defects

in the tested function.

To verify usability of the proposed methodology

against a wider set of functions than stream ciphers

from the eStream competition, we applied the de-

scribed methodology also against 18 selected func-

tions from the SHA-3 competition. As these algo-

rithms provide only ﬁxed and short sequences, hash

of value of randomly initialized counter is used to

obtain data from the algorithms passed to statistical

tests. Results obtained conﬁrmed the results against

eStream candidates (

Svenda et al., 2013).

6 CONCLUSIONS

We proposed a general design of a cryptoanalytical

tool based on genetic programming and applied it to

the problem of ﬁnding a random distinguisher for sev-

SECRYPT2013-InternationalConferenceonSecurityandCryptography

144

0 0.5 1 1.5 2 2.5 3

x 10

0.4

0.5

0.6

0.7

0.8

0.9

1.1

Salsa20 (2 rounds), fixed key for whole run

Number of generations

Distinguisher success rate

Figure 4: Fitness progress over 30000 generations for Salsa20 reduced to 2 rounds and with a ﬁxed key for all test sets.

Although sometimes the distinguishing success rate drops down to random guess when a key set was changed, the circuit is

quickly able to learn back to a high success rate. Such a behaviour motivated us to compute and display the AAM value rather

than a single value of the best individual from last round. Also, the circuit is (over-)learning very quickly to a particular data

set. Such a behaviour led us to inspect the overlearning speed as a potential metric of success instead of how well the circuit

is working after a test vector change.

eral stream ciphers (with a reduced number of rounds)

taken from the eStream competition. In general, the

proposed approach proved to be capable of closely

matching the performance of the NIST statistical test-

ing suite (except for the Decim algorithm) and with

several exceptions also to the Dieharder battery. A

robust evaluation was performed to obtain an aver-

age success rate over various scenarios w.r.t. the key

change frequency as well as the number of rounds to

which the target stream cipher is limited to.

The proposed approach provides a novel way of

inspecting statistical defects in cryptographic func-

tions and may provide a signiﬁcant advantage when

working with very short sequences (such as 16 bytes)

once the learning phase of evolution is completed.

Our future work will cover techniques that will en-

able providing signiﬁcantly more data as circuit in-

put to provide more fair comparison to STS NIST and

Dieharder batteries, which are making statistical ana-

lysis on tens (STS NIST) up to hundreds (Dieharder)

of megabytes of data.

Resources (data, source codes, conﬁguration ﬁles,

etc.) for the work discussed are provided at (

Svenda

et al., 2013).

ACKNOWLEDGEMENTS

This work was supported by the GAP202/11/0422

project of the Czech Science Foundation. The ac-

cess to computing and storage facilities owned by par-

ties and projects contributing to the National Grid In-

frastructure MetaCentrum, provided under the pro-

gramme Projects of Large Infrastructure for Re-

search, Development, and Innovations (LM2010005)

is highly appreciated.

REFERENCES

AES (1997). AES competition, announced 2.1.1997.

Anderson, D. P. (2004). BOINC: A system for public-

resource computing and storage. In Proceedings of

the 5th IEEE/ACM International Workshop on Grid

Computing, GRID ’04, pages 4–10, Washington, DC,

USA. IEEE Computer Society.

Banzhaf, W., Nordin, P., Keller, R. E., and Francone, F. D.

(1997). Genetic programming: An introduction: On

the automatic evolution of computer programs and its

applications.

Brown, R. G. (2004). Dieharder: A random number test

suite, version 3.31.1.

Castro, J. C. H. and Vi˜nuela, P. I. (2005). New results on

the genetic cryptanalysis of TEA and reduced-round

versions of XTEA. New Gen. Comput., 23(3):233–

243.

Delman, B. (2004). Genetic algorithms in cryptography.

PhD thesis, Rochester Institute of Technology.

Dinur, I. and Shamir, A. (2009). Cube attacks on tweak-

able black box polynomials. In Proceedings of the

28th Annual International Conference on Advances in

Cryptology: the Theory and Applications of Crypto-

graphic Techniques, EUROCRYPT ’09, pages 278–

299. Springer-Verlag.

Doganaksoy, A., Ege, B., Koc¸ak, O., and Sulak, F. (2010).

Statistical analysis of reduced round compression

TowardsCryptographicFunctionDistinguisherswithEvolutionaryCircuits

145

functions of SHA-3 second round candidates. Techni-

cal report, Institute of Applied Mathematics, Middle

East Technical University, Turkey.

ECRYPT (2004). Ecrypt estream competition, announced

November 2004.

Englund, H., Hell, M., and Johansson, T. (2007). A note

on distinguishing attacks. In Information Theory for

Wireless Networks, 2007 IEEE Information Theory

Workshop on, pages 1–4. IEEE.

Garrett, A., Hamilton, J., and Dozier, G. (2007). A compar-

ison of genetic algorithm techniques for the cryptanal-

ysis of tea. International journal of intelligent control

and systems, 12(4):325–330.

Gentry, C. (2010). Computing arbitrary functions of en-

crypted data. Commun. ACM, 53(3):97–105.

Hinton, G. E., Osindero, S., and Teh, Y.-W. (2006). A fast

learning algorithm for deep belief nets. Neural com-

putation, 18(7):1527–1554.

Hu, W. (2010). Cryptanalysis of TEA using quantum-

inspired genetic algorithms. Journal of Software En-

gineering and Applications, 3(1):50–57.

Kaminsky, A. (2012). GPU parallel statistical and cube test

analysis of the SHA-3 ﬁnalist candidate hash func-

tions. In 15th SIAM Conference on Parallel Process-

ing for Scientiﬁc Computing (PP12).

Liu, L., Li, M., and Lin, D. (2008). Replacement strate-

gies in steady-state multi-objective evolutionary algo-

rithm: A comparative case study. In Proceedings of

the 2008 Fourth International Conference on Natural

Computation, ICNC ’08, pages 645–649, Washington,

DC, USA. IEEE Computer Society.

Picek, S. and Golub, M. (2011). On evolutionary computa-

tion methods in cryptography. In MIPRO, 2011 Pro-

ceedings of the 34th International Convention, pages

1496 –1501.

Rukhin, A. (2010). A statistical test suite for the valida-

tion of random number generators and pseudo ran-

dom number generators for cryptographic applica-

tions, version STS-2.1. NIST Special Publication 800-

22rev1a.

Sekanina, L., Salajka, V., and Vaˇs´ıˇcek, Z. (2012). Two-step

evolution of polymorphic circuits for image multi-

ﬁltering. In IEEE Congress on Evolutionary Compu-

tation, pages 1–8.

SHA-3, N. (2007). SHA-3 competition, announced

2.11.2007.

Soto, J. (1999). Randomness testing of the AES candidate

algorithms. NIST.

Stevanovi´c, R., Topi´c, G., Skala, K., Stipˇcevi´c, M., and

Rogina, B. M. (2008). Quantum random bit generator

service for Monte Carlo and other stochastic simula-

tions. In Lirkov, I., Margenov, S., and Wa´sniewski, J.,

editors, Large-Scale Scientiﬁc Computing, pages 508–

515. Springer-Verlag.

Sulak, F., Do˘ganaksoy, A., Ege, B., and Koc¸ak, O.

(2010). Evaluation of randomness test results for

short sequences. In Proceedings of the 6th inter-

national conference on Sequences and their applica-

tions, SETA’10, pages 309–319. Springer-Verlag.

Turan, M. S., Doˇganaksoy, A., and C¸. C¸ alik (2006). De-

tailed statistical analysis of synchronous stream ci-

phers. In ECRYPT Workshop on the State of the Art of

Stream Ciphers (SASC’06).

Ukrop, M. and

Svenda, P. (2013). EACirc project,

https://github.com/petrs/eacirc.

Svenda, P., Ukrop, M., and Maty´aˇs, V. (2013).

SeCrypt2013 paper – supplementary data,

http://www.ﬁ.muni.cz/∼xsvenda/papers/secrypt2013/.

Webster, A. F. and Tavares, S. E. (1986). On the design of

S-boxes. pages 523–534. Springer-Verlag.

Wheeler, D. and Needham, R. (1995). TEA, a tiny encryp-

tion algorithm. In Fast Software Encryption, pages

363–366. Springer.

Yao, A. C. (1982). Theory and application of trapdoor

functions. In Proceedings of the 23rd Annual Sympo-

sium on Foundations of Computer Science, SFCS ’82,

pages 80–91, Washington, DC, USA. IEEE Computer

Society.

SECRYPT2013-InternationalConferenceonSecurityandCryptography

146