
Extending the Ciphertext-Policy Attribute Based Encryption Scheme
for Supporting Flexible Access Control
Bo Lang, Runhua Xu and Yawei Duan
School of Computer Science & Engineering, Beihang University, 37# Xueyuan Road, Beijing, China
Keywords: Ciphertext-Policy Attribute Based Encryption (CP-ABE), Extended CP-ABE, Attribute Based Access
Control, Cloud Computing.
Abstract: Ciphertext-Policy Attribute Based Encryption (CP-ABE) is recognized as an important data protection
mechanism in cloud computing environment for its flexible, scalable and fine-grained access control
features. For enhancing its security, efficiency and policy flexibility, researchers have proposed different
schemes of CP-ABE which have different kinds of access policy structures. However, as far as we know,
most of these structures only support AND, OR and threshold attribute operations. In order to achieve more
effective data self-protection mechanisms in open environments such as Cloud computing, CP-ABE needs
to support more flexible attribute based policies, most of which are described using operators of NOT, <, ,
>, . This paper proposed an Extended CP-ABE(ECP-ABE) scheme based on the existing CP-ABE scheme.
The ECP-ABE scheme can express any access policy represented by arithmetic comparison and logical
expressions that involve NOT, <, , >, operators in addition to AND, OR and threshold operators. We
prove the Chosen-plaintext Attack (CPA) security of our scheme under the Decisional Bilinear Diffie-
Hellman (DBDH) assumption in the standard model, and also discuss the experimental results of the
efficiency of ECP-ABE.
1 INTRODUCTION
In open computing environment such as cloud
computing, the protection mechanism of outsourced
data (sometimes just simply called data) attracts
much more attentions(Samarati et al., 2010);
(Vimercati et al., 2010). These data departs from the
control domain of its owner and is stored and
managed by unreliable service providers. Hence, the
self-protection capabilities of data become very
important. Traditionally, access control and
encryption are the two basic protection mechanisms
for achieving data integrity and confidentiality. Self-
protection of data means that data itself can ensure
its integrity and confidentiality without depending
on other parties.
Data encryption is the primary data self-
protection means at present. Traditional Public-Key
encryption and Identity Based Encryption schemes
(Shamir, 1985)
are designed for one-to-one
communication, which means the information
encrypted by a public key or identity can only be
decrypted by the specific private key. This situation
has been changed since Sahai and Waters proposed
the Attribute Based Encryption scheme (Sahai and
Waters, 2005), where ciphertexts are not necessarily
encrypted to one particular user. Both users’ private
keys and ciphertexts are associated with a set of
attributes or a policy over attributes. When the
attributes of a user’s private key can match the
attributes of the ciphertext in a certain extent, the
user can be able to decrypt the ciphertext. By
defining decryption attributes, ABE can dynamically
control the user group of the encrypted data.
Goyal et al. further developed this idea and
introduced two variants of ABE, namely key-policy
attribute based encryption(KP-ABE) and ciphertext-
policy attribute based encryption(CP-ABE). In KP-
ABE, whose first construction is given by (Goyal et
al., 2006), ciphertext is associated with a set of
attributes and the secret key is associated with the
access tree. A user will be able to decrypt if and only
if the attributes in the ciphertext satisfy his access
tree. In CP-ABE, the idea is reversed. The ciphertext
is associated with the access tree and the secret key
is associated with a set of attributes, and the
encrypting party determines the decryption policy.
147
Lang B., Xu R. and Duan Y..
Extending the Ciphertext-Policy Attribute Based Encryption Scheme for Supporting Flexible Access Control.
DOI: 10.5220/0004525801470157
In Proceedings of the 10th International Conference on Security and Cryptography (SECRYPT-2013), pages 147-157
ISBN: 978-989-8565-73-0
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

(Bethencourt et al., 2007) gave the initial
structure of CP-ABE. We refer to this scheme as
BSW07 in this paper. BSW07 is relatively
expressive and efficient, but the security argument is
based on generic group model, an artificial model
which assumes the attacker needs to access an oracle
in order to perform any group operation. After that,
many researchers have presented different schemes
for the less ideal security argument, trying to prove
the security based on a well-studied complexity-
theoretic problem. And also there are many people
worked at improving the efficiency or the flexibility
of access policy for the CP-ABE scheme. These
schemes mainly support three kinds of access policy
structure: AND-gates, tree structure and Linear
Secret Share Scheme (LSSS) matrix. Among them,
the tree structure and LSSS matrix are relatively
flexible, which supports AND, OR and threshold
operation. BSW07 uses “bag of bits” to express
policies containing <, , >, . However, this
approach is much complex and has poor scalability,
and is hard to be used in practical applications. For
NOT operator, BSW07 has no solution. To the best
of our knowledge, there is no efficient way to
express an access policy that contains operators such
as NOT, <, , > and in present CP-ABE schemes,
which makes CP-ABE only support simple attribute
policies.
Access control and encryption are the two key
techniques in data-centric protection, and CP-ABE
makes it possible to integrate these two techniques
seamlessly. However, the limited access policy
expression in CP-ABE restricts its access control
capability.
Our Contribution. In the area of access control,
Attribute-based Access Control (ABAC) model
(Junbeom and Dong Kun, 2011, Lang et al., 2009,
Wang et al., 2010) makes access control decisions
based on user attributes. The policies in ABAC are
defined as attribute expressions that contain
attributes, constants, and AND, OR, NOT, <, , >,
operators, and can express complex access control
rules. If the access policy structure of CP-ABE can
be enhanced to express complex attribute policies as
ABAC, CP-ABE will become an ideal scheme for
implementing data self-protection in open computing
environments. Following this idea, we proposed the
Extended CP-ABE scheme (ECP-ABE). In ECP-
ABE, by introducing extended leaf nodes, the access
tree of CP-ABE is enhanced to support all kinds of
logical and arithmetic comparison operators,
including <, , =, >, and NOT et al. Therefore,
ECP-ABE can realize powerful access control as
well as encryption, and data processed by ECP-ABE
will have strong self-protection capabilities. Our
scheme is proven to be chosen plaintext (CPA)
secure under the decisional Bilinear Diffie-Hellman
(DBDH) assumption in the standard model.
Organization. The remaining sections are organized
as follows. In Section 2, we introduce related work.
In Section 3, we review the concepts of access
structure, Shamir’s secret sharing scheme, bilinear
maps, DBDH assumption and the backgrounds of
the CP-ABE scheme. We present our extended CP-
ABE (ECP-ABE) scheme in Section 4. We then
discuss the performance of ECP-ABE from aspects
of security and efficiency in Section 5. Finally, we
conclude this paper in Section 6.
2 RELATED WORK
BSW07 expresses the access policy by a tree
structure which supports AND, OR and threshold
operations. At the same time, the length of the
ciphertext and the encryption or decryption time are
linearly related with the number of attributes of the
access structure tree. However, the security proof of
BSW07 is based on generic group model, rather than
the standard numerical theoretical assumptions. In
addition, as a result of using polynomial
interpolation to resume secret during the decryption
phase, BSW07 needs greater number of bilinear
mapping and exponentiation operation, and costs of
these operations are relatively high.
After that many scholars have proposed different
schemes (Su et al., 2011). Cheung and Newport first
gave the CP-ABE scheme (CN07)(Cheung and
Newport, 2007) under CPA security based on
DBDH assumption. However, the scheme only have
the AND and NOT operator in the access policy
structure, and the ability of policy expression is
poor. Moreover, the length of the ciphertext and the
key, and the time of encryption or decryption are
linearly related with the number of attributes, which
lead to the lower efficiency. Goyal et al raised the
Bounded Ciphertext Policy Attribute Based
Encryption scheme (Goyal et al., 2008) based on
DBDH assumption, which supported the AND, OR
and threshold operations. (Liang et al., 2009a);
(Liang et al., 2009b) shortened the system’s public
key, the user’s private key and the length of the
ciphertext and improved the efficiency of encryption
and decryption based on BCP-ABE. But it limited
the level of the access policy tree and the number of
child non-leaf nodes.
SECRYPT2013-InternationalConferenceonSecurityandCryptography
148

Nishide gave an Attribute-Based encryption scheme
(Nishide et al., 2008) with partially hidden
encryptor-specified access structures, which only
supported the AND operation and attributes have
more than one candidate value. Emura et al first
raised the CP-ABE with constant ciphertext length
based on Nishide’s scheme
(Emura et al., 2009),
which improved the efficiency of the algorithm. But
it also just supported the AND operation. Ibraimi et
al gave an efficient and provable secure CP-ABE
scheme (Ibraimi et al., 2009) based on DBDH
assumption using the threshold secret share
technology (Shamir, 1979), which supported AND,
OR and threshold operations. Its access structure
was an n-tree and the costs of key generation,
encryption and decryption are lower than the
BSW07 scheme. Waters has used the LSSS matrix
to express the access control policy and pointed out
that the ability of expression is not lower than the
tree structure(Waters, 2011). Lewko et al (Lewko et
al., 2010) also applied the LSSS matrix structure in
their scheme, which supported any monotone access
formula. Attrapadung and Imai (Attrapadung and
Imai, 2009) gave a revocable scheme which admits
ciphertext and private key sizes roughly the same as
the currently best (non-revocable) ciphertext-policy
ABE.
In order to support complex Boolean access
policies, Junod and Karlov (Junod and Karlov, 2010)
proposed an efficient public-key ABBE scheme
allowing arbitrary access policies, which is based on
a modification of the Boneh-Gentry-Waters
broadcast encryption scheme. Chen et al (Chen et al.,
2011)
presented two new CP-ABE schemes, which
have both constant-size and constant computation
costs for a non-monotone AND gate policy. Jin et al
(Li et al., 2011)
enhanced the attribute-based
encryption with attribute hierarchy and obtain a
provable secure HABE under tree hierarchy.
(Attrapadung et al., 2011); (Attrapadung et al., 2012)
proposed the first KP-ABE schemes allowing for
non-monotonic access structures and with constant
ciphertext size. Zhiguo et al (Zhiguo et al., 2012)
proposed a hierarchical attribute-set-based
encryption (HASBE) scheme which extended the
ciphertext-policy attribute-set-based encryption for
access control in cloud computing.
From the view of security and expressive ability
of access policy, only the W08 and ITHJ09 scheme
supported the AND, OR and threshold operation
under the theoretical assumptions of the standard
numerical. And the computation cost of encryption
and decryption of ITHJ09 is lower than W08’s.
Therefore, we choose ITHJ09 as the basic CP-ABE
scheme, and further expand the access policy tree of
ITHJ09 to construct an Extended CP-ABE scheme.
3 ANALYSIS OF CP-ABE
SCHEME
3.1 Preliminaries
We firstly give formal definition for access structure,
and then introduce the relevant background
information on Shamir secret sharing scheme,
bilinear maps and the Decision Bilinear Diffie-
Hellman(DBDH) assumption.
3.1.1 Access Structure
Definition 1. Access Structure (Beimel, 1996). Let
{}
1
2n
P
,P ,...,P
be a set of parties. A collection
{}
2A
1
2n
P
,P ,...,P
is monotone if
,
B
C
: if
B
A
and
BC
then
CA
. An access structure
(respectively, monotone access structure) is a
collection (respectively, monotone collection)
A
of
non-empty subsets
{}
12 n
P , P ,..., P
, i.e.,
{}
2A
12 n
P ,P ,...,P
\{∅}
。The sets in
A
are called the authorized sets, and
the sets not in
A
are called the unauthorized sets.
In ECP-ABE, the access structure
A
will contain
the set of authorized attributes.
3.1.2 Shamir Secret Sharing Scheme
In Shamir's secret sharing technique (Shamir, 1979)
a secret s is divided into n shares in such a way that
any subset of t shares, where t n, can together
reconstruct the secret; no subset smaller than t can
reconstruct the secret. The technique is based on
polynomial interpolation where a polynomial y =
f(x) of degree t-1 is uniquely defined by t points (x
i
,
y
i
). The details of the scheme are as follows:
1. Setup. The dealer D wants to distribute the secret
s 0 among t users.
a) D chooses a prime p max(s,n), and define a
0
= s.
b) D selects t-1 random coefficients a
1
,…,a
t-1
, 0
a
j
p-1, and define the random polynomial
over
p
:
1
0
()
t
j
j
j
f
xax
c) D computes s
i
=f(i) mod p, and sends securely
the share s
i
to user p
i
together with the public
ExtendingtheCiphertext-PolicyAttributeBasedEncryptionSchemeforSupportingFlexibleAccessControl
149

index i.
2. Pooling of shares. Any group of t or more users
pool their distinct shares (x,y)=(i,s
i
) allowing
computation of the coefficients a
j
of f(x) by
Lagrange interpolation,
1
01,
0
() () , ()
t
i
jj j
it i j
j
j
i
x
x
fx lxswherelx
x
x
The secret s is f(0) = a
0
.
3.1.3 Bilinear Maps
Let
and
T
be two multiplicative cyclic groups of
prime order p. Let g be a generator of and e be a
bilinear map, e:
T
, with the following
properties:
Bilinearity: for all x, y and a,b
p
, we have
e(x
a
,y
b
) = e(x,y)
ab
.
Non-degeneracy: e(g, g) ≠ 1
If the group operation in and the bilinear map e
are both efficiently computable, the multiplicative
cyclic group is a bilinear group. Notice that the
map e is symmetric since e(g
a
, g
b
) = e(g,g)
ab
= e(g
b
,
g
a
).
3.1.4 The Decisional Bilinear
Diffie-Hellman Assumption
Let a, b, c, z
p
be chosen randomly, Z be the
random element from
T
(Z= e(g, g)
z
), and g be a
generator of .
and
T
are two multiplicative
cyclic groups mentioned in 3.1.3. The decisional
BDH assumption(Boneh and Boyen, 2004); (Sahai
and Waters, 2005) is that no probabilistic
polynomial-time algorithm
can distinguish the
tuple <g
a
, g
b
, g
c
, e(g, g)
abc
> from the tuple <g
a
, g
b
,
g
c
, Z> with more than a negligible advantage
:
|Pr[(, , ,(,))0]Pr[(, , ,)0]|
abc abc abc
gggegg gggZ
Here the probability is over the random choice of Z
in
T
, the random choice of a, b, c in Z
p
, and the
random bits of
.
3.2 CP-ABE
3.2.1 Access Tree
Definition 2. Access Tree (Bethencourt et al., 2007).
Let
be a tree representing an access structure.
Each non-leaf node of the tree represents a threshold
gate, described by its children and a threshold value.
If num
x
is the number of children of a node x and k
x
is its threshold value, then 0<k
x
<num
x
. When k
x
=1,
the threshold gate is an OR gate and when k
x
=num
x
,
it is an AND gate. Each leaf node x of the tree is
described by an attribute and a threshold value k
x
=1.
We define tree functions over the tree. The
function parent(x) represents the parent of node x. If
x is a leaf node, we define the function attr (x) to
denote the attribute with the leaf node. As the access
tree has an ordering between the children of every
node, the function index(x) represents the index
number of each child node.
3.2.2 Satisfying an Access Tree
Definition 3. Satisfied Access Tree (Bethencourt et
al., 2007). Let
be an access tree with root r.
Denote by
x
the subtree of
rooted at the node x.
Thus,
is the same as
r
. If a set of attributes γ
satisfies the access tree
x
, we denote it as
x
(γ)=1.
We compute
x
(γ) recursively as follows. If x is a
non-leaf node, evaluate
x'
(γ) for all children x' of
node x.
x
(γ) returns 1 if and only if at least k
x
children return 1. If x is a leaf node, then
x
(γ)
returns 1 if and only if att(x) γ.
3.2.3 CP-ABE Algorithms
The ciphertext-policy attribute based encryption
scheme consists of four fundamental algorithms
(Bethencourt et al., 2007): Setup, Encrypt, Key
Generation, and Decrypt.
Setup (k). The setup algorithm takes no input other
than the security parameter k. It outputs the public
parameters PK and a master key MK.
Key-Generation (MK, S). The key generation
algorithm takes as input the master key MK and a set
of attributes S that describe the key. It outputs a
private key SK.
Encrypt (PK, M, A). The encryption algorithm takes
as input the public parameters PK, a message M, and
an access structure A over the universe of attributes.
The algorithm will encrypt M and produce a
ciphertext C
T
such that only a user that possesses a
set of attributes that satisfies the access structure will
be able to decrypt the message. We will assume that
the ciphertext implicitly contains A.
Decrypt (PK,C
T
, SK). The decryption algorithm
takes as input the public parameters PK, a ciphertext
C
T
which contains an access policy A, and a private
key SK. If the set S of attributes satisfies the access
structure A then the algorithm will decrypt the
ciphertext and return a message M, otherwise return
the error symbol .
SECRYPT2013-InternationalConferenceonSecurityandCryptography
150

4 ECP-ABE SCHEME
The ITHJ09 used Shamir secret sharing technique to
support AND, OR and of (threshold) nodes based on
CP-ABE scheme. The access policy tree is n-ary
tree. Each node has two attributes: the number of
child nodes n and threshold value t (1
t
n
). When t
=1, it’s an OR gate; when t = n, it’s an AND gate;
when 1<t<n, it’s an of gate. The leaf node associates
policy properties and its value t is 1. The ECP-ABE
scheme we proposed is based on the ITHJ09 scheme
and we extend the access tree to make it be able to
express the complex policies that contain arithmetic
and logical expressions.
4.1 Extended Leaf Node
The universal attribute set U is published by the
Trusted Authority. Each user has his or her attribute
set w which is used for key generation and we refer
to it as the basic attribute set. In Attribute Based
Access Control system, user’s access right could be
dynamically calculated according to his security
character and the resource he applied for. Inspired
by this, we extend the leaf node of the access policy
tree.
We replace the original leaf node with the
operator node and give it two children, which we
refer to as the attribute name node and the attribute
value node, as shown in Figure 1(a). The operator
node, the attribute name node and the attribute
value node compose an extended leaf node, and the
attribute expression described by an extended leaf
node is called an extended attribute, for instance, the
attribute “age>18” is an extended attribute.
Meanwhile, the range of threshold value t of the
extended leaf node is less than 0 from the original
value 1.
The operator node only has the threshold value t
(t<0). Different value of t denotes specific operator,
for instance, t = -1 for not operator, t = -2 for
operator. The attribute name/value node denotes the
attribute name and the attribute value respectively
that are associated with the operator. With this
structure, we can express policy attributes using
operators of not, , , , . Figure 1(b) is an
example of this structure, which express the policy
attribute “school not software-engineering”.
ECP-ABE scheme augments two kinds of
operators: comparison operators and logic operators.
Comparison operators:, , , .
Logic operators: not.
The values of t and the corresponding operator that
each value represents are defined in Table 1.
Table 1: Values of t and its corresponding operator.
Value t Operator
-1 not
-2 <
-3 >
-4
-5
4.2 Transforming an extended Policy
Tree to a Standard Tree
Now we define the extended policy tree as the
extended tree T
*
and the original tree is called the
standard tree T. An extended tree can be
transformed to an equivalent standard tree by
removing the attribute name/value node, converting
the operator node to the standard leaf node and then
assigning the attribute expression described by the
extended leaf node as an extended attribute to the
stand leaf node. The extended tree T
*
and the
standard tree T express the same access policy. For
example, the extended tree in Figure 2(a) can be
transferred into the standard tree in Figure 2(b).
The user expresses the access policy using the
extended tree and makes it the parameter for the
encryption. The encryption algorithm will firstly
transform the extended tree to a standard tree, and
then encrypts the message using the standard access
policy tree. Finally, we attach the extended tree in
the ciphertext.
To decrypt the ciphertext, the decryption party
needs to apply the secret key by giving PKG his
basic attribute set and the extended parts of the
access tree. At the PKG side, we use the attribute
verification algorithm as shown in Algorithm 1 to
verify and transform an extended leaf node.
Algorithm 1: Attribute Verification.
1:
Get the expression exp(N.O.V) of the extended leaf node,
where N, O and V denote the basic attribute name, the
operator and the attribute value respectively;
2:
Traverse the basic attribute set A’ to find the basic
attribute N and its value V’;
3:
Let N=V’, and calculate the expression exp(N.O.V);
4:
if the value of exp(N.O.V) is true
5: Convert exp(N.O.V) to string S=“N.O.V”
6:
return S;
7:
else
8:
return null;
9:
end if
ExtendingtheCiphertext-PolicyAttributeBasedEncryptionSchemeforSupportingFlexibleAccessControl
151
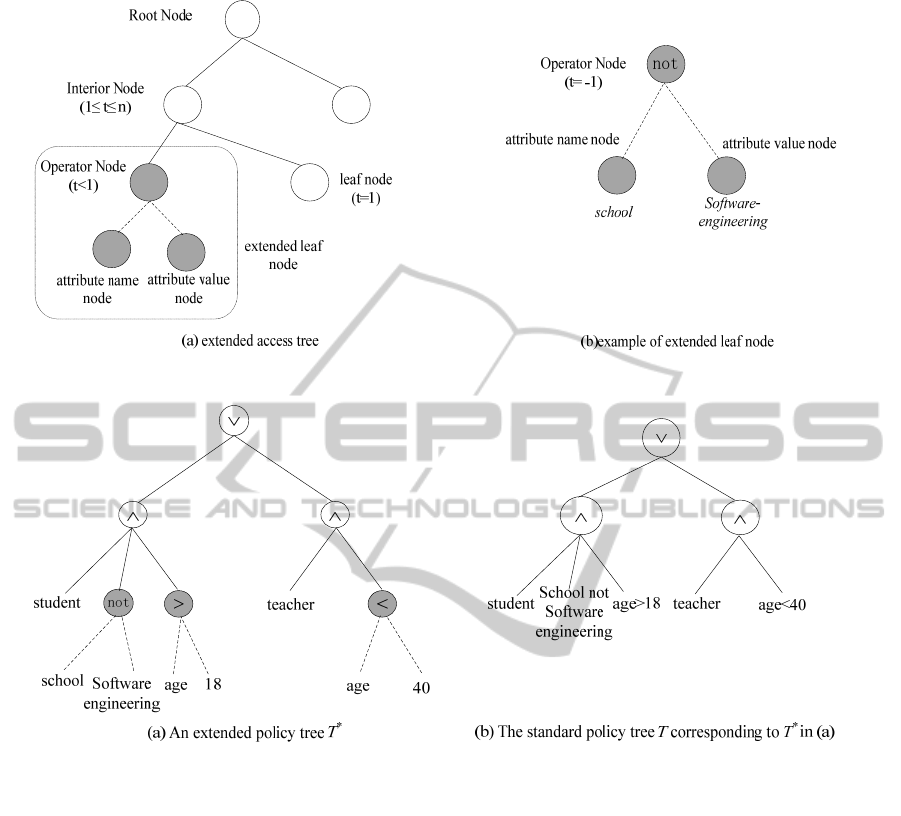
Figure 1: Extended access tree.
Figure 2: Examples of extended and standard access policy tree.
This algorithm will first get user’s basic attribute
set and then traverse the attribute set to check
whether or not the attribute N satisfies the
expression exp(N.O.V). If the answer is yes, it
returns the string form of exp(N.O.V), i.e. “attribute
name operator attribute value” which is regarded as
an extended attribute of the user. Otherwise it will
return null.
Here is an example of the transformation.
There is a file F in a campus network system and
the file has an access policy: “It can be accessed if
and only if the user is a teacher under age of 40 or an
older than 18-year-old student who is not in school
of software-engineering”. So, we can give the policy
“T* = (student school not software-engineering
age 18) (teacher age 40)”, and the extended
access tree for this policy is shown in Figure 2(a).
Figure 2(b) is the standard access tree which
converts from the extended tree in figure 2(a). The
encryption party encrypts the file F with T and
attaches T
*
in the ciphertext.
Suppose user A and user B wants to decrypt the
file F. The basic attributes of A is {student,
school=computer science, age=20}, and the basic
attributes of B is {student, school=computer science,
age=17}. Firstly, Both A and B need to extract the
extended parts of T
*
from the ciphertext and send
them with their basic attribute set to PKG. Then,
PKG verifies and generates the new attribute set
{student, school not software-engineering , age
18} for A, and the new attribute set { student,
school not software-engineering,age = 17} for B.
The corresponding private keys are generated using
these new attribute sets by PGK concurrently.
Obviously, user B’s attribute set doesn’t satisfy the
access policy, hence user A can decrypt the file F
while user B can’t.
SECRYPT2013-InternationalConferenceonSecurityandCryptography
152

4.3 Encryption and Decryption
Process of ECP-ABE
The encryption party expresses the access policy
with an extended tree and the tree in the ciphertext is
also in the extended structure. However, when
encrypts a message, the encryption algorithm will
first transform the extend tree to an equivalent
standard tree and encrypt the message using the
standard one. So in the encryption phase, we can use
the algorithm of ITHJ09 scheme. For ciphertexts that
encrypted under different extended access trees,
users have to apply for different secret keys, since
PKG need to verify and generate extended attributes
according to the extended tree and user’s basic
attributes. Detailed encryption and decryption
processes are described as follows.
a. Initialize: the system initializes and generates
public parameter pk and master key mk. It gives
pk to the encryption party. The description of
initialization algorithm Setup (k) is as follow.
i. Generate a bilinear group G of prime order p
with a generator g and a bilinear map e:G G
GT.
ii. Generate the attribute set U = {a1,a2,…,am},
for some integer m, and random elements ,
t1, t2,…,tm Zp*. Let y = e(g,g), Tj = gtj
(1 j m). The public key is pk = (e, g, y,
Tj(1 j m)), and the master key is mk = (,
tj (1 j m)).
b. Specify the Access Policy: the encryption party
specifies access policy, which is expressed by an
extended tree T
*
.
c. Encryption: the encryption party calls the
encryption algorithm Encrypt (m, T
*
, pk) with
plaintext m, the extended tree T
*
and the public
parameter pk. The encryption algorithm will first
transform T
*
to the equivalent standard tree T,
and then encrypt m under T using Shamir’s secret
sharing technique. Finally it returns the
ciphertext C
T
which contains T
*
, such that only
users who have the secret key generated from the
attributes that satisfy T
*
will be able to decrypt
the message. The detail description is as follows:
i. Convert the T
*
to the standard tree T;
ii. Select a random element s Z
p
*
and compute
c
0
= g
s
and c
1
= M
y
s
= M
e(g,g)
s
iii. Set the value of the root node of T to be s,
mark all child nodes as un-assigned, and
mark the root node assigned. Recursively, for
each un-assigned non-leaf node, do the
following:
If its child nodes are un-assigned,the secret
s is divided using (t,n)-Shamir secret sharing
technique. The relation of n and t is: if the
symbol is of then 1 t n; if the symbol is
AND, then t = n; if the symbol is OR, then t
= 1. To each child node a share secret s
i
= f(i)
is assigned. Mark this node assigned.
iv. For each leaf attribute a
j,i
T, compute c
j,i
=
T
j
si
, where i denote the index of the attribute
in the access tree.
v. Return the ciphertext: C
T
= (T, c
0
, c
1
, a
j,I
T:c
j,i
).
d. Secret Key Request: when a user gets C
T
and
wants to decrypt, he first needs to analyze the
structure of T
*
and find the extended parts, then
apply for the secret key by giving PKG his basic
attribute set w and the extended parts of the
access tree.
e. Secret Key Generation: PKG first verify the
user’s basic attribute. If the basic attributes of the
user are authenticated, PKG will extract the
attribute name, the attribute value and the
operator, and run Algorithm 1. Attributes in w
that satisfy the extended leaf node will be
replaced by the returned extended attributes.
Finally PKG gets the new attribute set w
*
and
generates the secret key sk
w*
corresponds to w
*
and sends it back to the user. The detailed
description is as follows:
i. Select a random value r Z
p
*
, d
0
= g
- r
.
ii. For each attribute a
j
in w, compute d
j
=
1
j
rt
g
.
iii. Return the secret key sk
w
=(d
0
,a
j
w:d
j
)
f. Decryption: the user calls the decryption
algorithm Decrypt(C
T
, sk
w
*
). The algorithm
returns message m if the smallest attribute set w’
w
*
that corresponds to sk
w
*
satisfies T.
Otherwise it returns an error symbol . More
details are as follows:
For every attribute a
j
w’, computing:
1
(0)
00 ,
'
(, ) ( , )
i
j
l
ji j
aw
c
m
ec d ec d
l
i
(0) is a Lagrange coefficient and can be computed
by everyone who knows the index of the attribute in
the access tree.
ExtendingtheCiphertext-PolicyAttributeBasedEncryptionSchemeforSupportingFlexibleAccessControl
153

Correctness Proof:
1
1
1
(0)
00 ,
'
(0)
(0)
'
'
(, ) ( , )
(, )
(, )( , )
(, )
(, ) ( , )
i
j
j
ii
ji j
i
j
l
ji j
aw
s
rt
sl
sr
j
s
ts rt
l
sr
aw
c
m
ec d ec d
megg
eg g eT g
megg
eg g eg g
(, ) (, )
(, )(,) (, )
ss
sr rs s
megg megg
m
eg g egg eg g
5 ECP-ABE PERFORMANCE
ANALYSIS
5.1 Security
The major contribution of ECP-ABE scheme is the
extension of the access tree. The core
encryption/decryption algorithm of ECP-ABE is
based on ITHJ09 scheme. In ITHJ09 scheme
semantic security under chosen-plaintext attack
(CPA) is modeled by IND-sAtt-CPA game. The
security model of ECP-ABE will still be based on
IND-sAtt-CPA game, but the challenging access tree
provided by the adversary in
Init phase will be an
extended tree instead of a standard tree. IND-sAtt-
CPA game of ECP-ABE security model is as
follows:
Init. The adversary A chooses the challenge
access tree T
*
and gives it to the challenger, T
*
is
an extended tree.
Setup. The challenger runs Setup to
generate(pk,mk) and gives the public key pk to
adversary A. The challenger also transforms T
*
to
the equivalent standard tree T.
Phase1. Adversary A makes a secret key request
to the Keygen oracle for any attribute set w = { a
j
| a
j
U}, with the restriction a
j
T
*
and a
j
does
not satisfy the policy attribute requirement
expressed by the extend part of T
*
. The
challenger runs Algorithm 1 to generate extended
attribute set w
*
and then returns Keygen(w
*
, mk).
Challenge. Adversary A sends to the challenger
two equal length messages m
0
, m
1
. The
challenger picks a random bit b {0,1} and
returns C
b
= Encrypt(m
b
, T
*
, pk).
Phase2. Adversary A can continue querying
Keygen oracle with the same restriction as in
Phase1.
Guesss. Adversary A outputs a guess b
’
{0,1}.
The advantage of A winning this game is defined as:
= |Pr[b’=b] – 1/2|.
Definition 1. ECP-ABE scheme is said to be secure
against an adaptive chosen-plaintext attack(CPA) in
the standard model if any polynomial-time adversary
has only a negligible advantage in the above IND-
sAtt-CPA game.
In the above game, adversary A uses an extended
tree to challenge instead of a standard tree. We have
the following analyse:
1.
The limitation for the basic attribute set w = { a
j
|
a
j
U } provided by adversary A in Phase1 is a
j
T
*
and a
j
does not satisfy the policy attribute
requirement expressed by the extended part of T
*
.
According to this limitation, we can infer that
b
j
*
w
*
, b
j
*
T. So in Phase1, changes of
access tree will not introduce any new security
problem, i.e. the secret key that A gets could not
decrypt the ciphertext C
b
.
2.
Although adversary A submits the extended tree
T
*
in Init phase, message m
b
is encrypted under
standard tree T. Transformation between T
*
and T
is public. In
Phase1, Challenge and Phase2,
adversary A could design the query and challenge
against T
*
. So the attacking ability of A keeps the
same.
Hence, we can conclude that in ECP-ABE scheme
the advantage of A in the IND-sAtt-CPA game
equals to the advantage of A in ITHJ09 scheme, i.e.
in ECP-ABE scheme any polynomial-time adversary
has only a negligible advantage in the IND-sAtt-
CPA game.
So ECP-ABE scheme is secure against an adaptive
chosen-plaintext attack(CPA) in the standard model.
Our extension for the access tree will not lower the
system security compared with ITHJ09.
5.2 Efficiency
In ITHJ09 scheme, encryption requires |
T
|+1
exponentiations in
and one exponentiation in
T
and |
T
| is the number of attributes in the access tree
T
. Key generation requires |w|+1 exponentiations in
, w is the attribute set the user has. Decryption
requires |w’|+1 pairing operations, |w’|
multiplications, w’ is the set of attributes satisfying
the access tree, w’ w.
SECRYPT2013-InternationalConferenceonSecurityandCryptography
154

Table 2: The test samples without repetitive same name attributes.
1-4 attribute nodes
(4 nodes for instance)
5-7 attribute nodes
(6 nodes for instance)
8-10 attribute nodes
(9 nodes for instance)
Standard attribute policy
security_ level=7
∧salary=7500
∧genderM
∧age24
(security_level=7
∧genderM
∧department=product
∧expired_date201301
∧age24
∧nameSk
y
(security_level =7
∧department=product
∧nameSky
∧genderM
∧officeBC‐1
∧projectT1
∧age24∧salary7
∧expired_date201301
Extended attribute policy
(id not Bob@gmail.com)
∧namenotTom
∧salary7000
∧security_level4
(age25)∧(salary9000)
∧(department not account)
∧idnotTom@gmail.com
∧namenotjack
∧security_level7
(age20)∧(salary5000)
∧(department not account)
∧namenottom
∧projectnotS1
∧idnotBob@gmail.com
∧officenotA1
∧professionalnotPA
∧security_level7
(a) The encryption time cost comparison of
ECP-ABE scheme and ITHJ09 scheme.
(b) The key application time cost
comparison of ECP-ABE scheme and
ITHJ09 scheme
(c) The decryption time cost comparison of
ECP-ABE scheme and ITHJ09 scheme
Figure 3: The efficiency comparison of ECP-ABE and ITHJ09 scheme without repetitive same name attributes.
ECP-ABE uses the encryption and decryption
algorithms of ITHJ09 scheme, so the calculation
expenses and the length of ciphertext are the same as
ITHJ09. The ECP-ABE scheme has two main
differences compared with ITHJ09 scheme: the
ECP-ABE has the conversion from an extended tree
to a standard tree during the encryption; it also has
the verification and transformation of extended
attributes during the key generation. Meanwhile, in
ECP-ABE, the attribute set used to generate the
private key will be expanded after the extended leaf
node transformation. Therefore, the added
calculation expense comes from the following three
factors:
ExtendingtheCiphertext-PolicyAttributeBasedEncryptionSchemeforSupportingFlexibleAccessControl
155

The transformation from the extended tree to the
standard tree during the encryption phase
The verification and transformation of the
extended attributes during the key generation
phase
The following experiments illustrate the impact of
the above factors on the actual efficiency.
We use two groups of policy file shown in Table
2 as test samples. One group only contains policies
with the standard attributes which are used as the
policies of the ITHJ09 scheme, and the other only
contains policies with the extended attributes which
are used as the policies of our ECP-ABE scheme.
Each group has 10 test policy files to test the
efficiency when the number of attribute node varies
from 1 to 10. The access tree is a two-tier structure
when there are 1-4 attribute nodes, a three-tier
structure when there are 5-7 attribute nodes, and a
four-tier structure when there are 8-10 attribute
nodes.
We run three times for each test policy file and
get the average cost as the result. Figure 3 is the
result of test.
Discussion: the verification of the extended leaf
nodes and the transformation from the extended tree
to the standard tree nearly have no effect on the
performance during the encryption and key
application phase. However, the ECP-ABE scheme
has greatly enhanced the access policy expression
capability.
6 CONCLUSIONS
The paper proposed an ECP-ABE scheme, which
introduces the extended leaf nodes into the access
policy tree to support access policy formulas
involving operators including
NOT, , , , in
addition to AND, OR and threshold operators.
Hence the scheme enhanced access control ability
prominently, which is important to data self-
protection in open computing environments.
ECP-ABE adopts the same implementation
mechanism as other CP-ABE schemes. Basing on
the experiments analysis, we can see that our scheme
has nearly the same expense compared with ITHJ09
scheme, and ECP-ABE scheme is proven chosen
plaintext (CPA) secure under the decisional Bilinear
Diffie-Hellman assumption in the standard model.
Hence, ECP-ABE can keep the security and
efficiency properties of the CP-ABE scheme which
it based on, but prominently improves the access
capability of the baseline scheme. Also, the policy
extension method used in ECP-ABE is not limited to
the ITHJ09 scheme; it can be used on other CP-ABE
schemes that utilize tree-based access policy
structures.
For future work, it would be interesting to probe
other more efficient way to enhance the access
control capability of CP-ABE schemes, such as
working on other access policy structures like LSSS,
or designing new encryption/decryption algorithms.
ACKNOWLEDGEMENTS
This work was supported by the National Natural
Science Foundation of China (Grant No.61170088)
and Foundation of the State Key Laboratory of
Software Development Environment (Grant No.
SKLSDE-2013ZX-05).
REFERENCES
Attrapadung, N., Herranz, J., Laguillaumie, F., Libert, B.,
De Panafieu, E. & Ràfols, C. 2012. Attribute-based
encryption schemes with constant-size ciphertexts.
Theoretical Computer Science, 422, 15-38.
Attrapadung, N. & Imai, H. 2009. Conjunctive Broadcast
and Attribute-Based Encryption. In: SHACHAM, H.
& WATERS, B. (eds.) Pairing-Based Cryptography –
Pairing 2009. Springer Berlin Heidelberg.
Attrapadung, N., Libert, B. & Panafieu, E. 2011.
Expressive Key-Policy Attribute-Based Encryption
with Constant-Size Ciphertexts. In: CATALANO, D.,
FAZIO, N., GENNARO, R. & NICOLOSI, A. (eds.)
Public Key Cryptography – PKC 2011. Springer
Berlin Heidelberg.
Beimel, A. 1996. Secure schemes for secret sharing and
key distribution. PhD thesis, Israel Institute of
Technology, Technion, Haifa, Israel.
Bethencourt, J., Sahai, A. & Waters, B. Ciphertext-Policy
Attribute-Based Encryption. Security and Privacy,
2007. SP '07. IEEE Symposium on, 20-23 May 2007
2007. 321-334.
Boneh, D. & Boyen, X. Efficient selective-ID secure
identity-based encryption without random oracles.
Advances in Cryptology-EUROCRYPT 2004, 2004.
Springer, 223-238.
Chen, C., Zhang, Z. & Feng, D. 2011. Efficient Ciphertext
Policy Attribute-Based Encryption with Constant-Size
Ciphertext and Constant Computation-Cost. In:
BOYEN, X. & CHEN, X. (eds.) Provable Security.
Springer Berlin Heidelberg.
Cheung, L. & Newport, C. 2007. Provably secure
ciphertext policy ABE. Proceedings of the 14th ACM
SECRYPT2013-InternationalConferenceonSecurityandCryptography
156

conference on Computer and communications security.
Alexandria, Virginia, USA: ACM.
Emura, K., Miyaji, A., Nomura, A., Omote, K. & Soshi,
M. 2009. A Ciphertext-Policy Attribute-Based
Encryption Scheme with Constant Ciphertext Length.
In: BAO, F., LI, H. & WANG, G. (eds.) Information
Security Practice and Experience. Springer Berlin
Heidelberg.
Goyal, V., Jain, A., Pandey, O. & Sahai, A. 2008.
Bounded Ciphertext Policy Attribute Based
Encryption. In: ACETO, L., DAMG RD, I.,
GOLDBERG, L., HALLD RSSON, M., ING LFSD
TTIR, A. & WALUKIEWICZ, I. (eds.) Automata,
Languages and Programming. Springer Berlin
Heidelberg.
Goyal, V., Pandey, O., Sahai, A. & Waters, B. 2006.
Attribute-based encryption for fine-grained access
control of encrypted data. Proceedings of the 13th
ACM conference on Computer and communications
security. Alexandria, Virginia, USA: ACM.
Ibraimi, L., Tang, Q., Hartel, P. & Jonker, W. 2009.
Efficient and Provable Secure Ciphertext-Policy
Attribute-Based Encryption Schemes. In: BAO, F., LI,
H. & WANG, G. (eds.) Information Security Practice
and Experience. Springer Berlin Heidelberg.
Junbeom, H. & Dong Kun, N. 2011. Attribute-Based
Access Control with Efficient Revocation in Data
Outsourcing Systems. Parallel and Distributed
Systems, IEEE Transactions on, 22, 1214-1221.
Junod, P. & Karlov, A. 2010. An efficient public-key
attribute-based broadcast encryption scheme allowing
arbitrary access policies. Proceedings of the tenth
annual ACM workshop on Digital rights management.
Chicago, Illinois, USA: ACM.
Lang, B., Foster, I., Siebenlist, F., Ananthakrishnan, R. &
Freeman, T. 2009. A Flexible Attribute Based Access
Control Method for Grid Computing. Journal of Grid
Computing, 7, 169-180.
Lewko, A., Okamoto, T., Sahai, A., Takashima, K. &
Waters, B. 2010. Fully Secure Functional Encryption:
Attribute-Based Encryption and (Hierarchical) Inner
Product Encryption. In: GILBERT, H. (ed.) Advances
in Cryptology – EUROCRYPT 2010. Springer Berlin
Heidelberg.
Li, J., Wang, Q., Wang, C. & Ren, K. 2011. Enhancing
Attribute-Based Encryption with Attribute Hierarchy.
Mobile Networks and Applications, 16, 553-561.
Liang, X., Cao, Z., Lin, H. & Shao, J. 2009a. Attribute
based proxy re-encryption with delegating capabilities.
Proceedings of the 4th International Symposium on
Information, Computer, and Communications Security.
Sydney, Australia: ACM.
Liang, X., Cao, Z., Lin, H. & Xing, D. 2009b. Provably
secure and efficient bounded ciphertext policy
attribute based encryption. Proceedings of the 4th
International Symposium on Information, Computer,
and Communications Security. Sydney, Australia:
ACM.
Nishide, T., Yoneyama, K. & Ohta, K. 2008. Attribute-
Based Encryption with Partially Hidden Encryptor-
Specified Access Structures. In: Bellovin, S., Gennaro,
R., Keromytis, A. & Yung, M. (eds.) Applied
Cryptography and Network Security. Springer Berlin
Heidelberg.
Sahai, A. & Waters, B. 2005. Fuzzy Identity-Based
Encryption. In: CRAMER, R. (ed.) Advances in
Cryptology – EUROCRYPT 2005. Springer Berlin
Heidelberg.
Sam
arati, P. & Di Vimercati, S. D. C. Data protection in
outsourcing scenarios: Issues and directions.
Proceedings of the 5th ACM Symposium on
Information, Computer and Communications Security,
2010. ACM, 1-14.
Shamir, A. 1979. How to share a secret. Commun. ACM,
22, 612-613.
Shamir, A. 1985. Identity-based cryptosystems and
signature schemes. Proceedings of CRYPTO 84 on
Advances in cryptology. Santa Barbara, California,
United States: Springer-Verlag New York, Inc.
Su, J., Cao, D., Wang, X., Sun, Y. & Hu, L. 2011.
Attribute-based Encryption Schemes. Journal of
Software, 22, 1299-1315.
Vimercati, S. D. C. D., Foresti, S., Jajodia, S., Paraboschi,
S. & Samarati, P. 2010. Encryption policies for
regulating access to outsourced data. ACM
Transactions on Database Systems (TODS), 35, 12.
Wang, G., Liu, Q. & Wu, J. 2010. Hierarchical attribute-
based encryption for fine-grained access control in
cloud storage services. Proceedings of the 17th ACM
conference on Computer and communications security.
Chicago, Illinois, USA: ACM.
Waters, B. 2011. Ciphertext-Policy Attribute-Based
Encryption: An Expressive, Efficient, and Provably
Secure Realization. In: Catalano, D., Fazio, N.,
Gennaro, R. & Nicolosi, A. (eds.) Public Key
Cryptography – PKC 2011. Springer Berlin
Heidelberg.
Zhiguo, W., Jun'e, L. & Deng, R. H. 2012. HASBE: A
Hierarchical Attribute-Based Solution for Flexible and
Scalable Access Control in Cloud Computing.
Information Forensics and Security, IEEE
Transactions on, 7, 743-754.
ExtendingtheCiphertext-PolicyAttributeBasedEncryptionSchemeforSupportingFlexibleAccessControl
157
