Security Evaluation and Optimization of the Delay-based Dual-rail

Pre-charge Logic in Presence of Early Evaluation of Data

Simone Bongiovanni, Giuseppe Scotti and Alessandro Trifiletti

Dipartimento di Ingegneria dell’Informazione, Elettronica e Telecomunicazioni, Sapienza Università di Roma, Rome, Italy

Keywords: Cryptography, Cryptographic Hardware, Smart Cards, Side Channel Attacks, Differential Power Analysis

(DPA), Dual-rail Pre-charge Logic (DPL), Hiding Countermeasure, Early Evaluation Effect, VLSI Design.

Abstract: Delay-based Dual-rail Pre-charge Logic (DDPL) has been introduced for counteracting power analysis

attacks. Basically DDPL allows to achieve a constant power consumption for each data transition even in

presence of capacitive load mismatches, thanks to an asynchronous two-phases evaluation. Unlikely other

secure logic styles, in DDPL the clock frequency does not fix the security level since it depends on the value

of the delay Δ between the complementary signals, which can be designed to be lower than 1ns using

current CMOS technologies. However no works exist in which the DPA-resistance of DDPL is tested in

presence of early evaluation, due to the different arrival times of the signals. The aim of this work is to

provide and validate through transistor level simulations a theoretical model of the variations of the delay Δ

during the evaluation phase for each possible data configuration in order to assess the effect of the early

evaluation in DDPL, and to design early evaluation free DDPL gates. Moreover a case study crypto-core

implemented both with basic and optimized DDPL gates has been designed in which a Correlation

Frequency Power Analysis (CFPA) attack is mounted so to detect any leakage on simulated current traces.

1 INTRODUCTION

A side-channel attack is an attempt to recover

confidential data, such as the secret key of a

cryptographic algorithm, by exploiting the

information leaked by the hardware implementation

during the execution of the algorithm (Kocher,

1996). For this reason they represent a critical issue

for cryptographic applications where a high level of

security is required. Side-channels are strongly

related to the existence of a physically observable

phenomenon, such as time, power, electromagnetic

radiations or noise emitted by the device.

Several countermeasures against side channel

attacks have been proposed in the technical

literature. At the physical level, shields, physically

unclonable functions (Tuyls et al., 2006), detectors,

and detachable power supplies (Shamir et al., 2000)

can be used to improve the resistance of a device

against physical attacks. At the algorithmic level,

time randomization (May et al., 2001), encryption of

the buses (Brier et al., 2001), masking (i.e., making

the leakage dependant of some random value)

(Goubin et al., 1999) are typical countermeasures.

At the technological level, Dual-rail Pre-charge

Logic (DPL) styles (as an alternative to CMOS)

have been proposed in various shapes to decrease

the data dependencies of the power consumption. At

all the previous levels, noise addition is the generic

solution to decrease the amount of information in the

side-channel leakages. Countermeasures also exist at

the protocol level, e.g. based on key updates.

However no single technique allows to provide

perfect security. Protecting implementations against

physical attacks consequently intends to make the

attacks harder. In this context, the implementation

cost of a countermeasure is of primary importance

and must be evaluated with respect to the obtained

additional security.

This paper focuses on power consumption which

is a frequently considered side-channel in practical

attacks. Power analysis attacks exploit the

dependence of the power consumption of a hardware

implementation on the switching activity and on the

state of internal gates, which are both correlated to

the processed data. Many techniques have been

introduced to promote and refine power analysis

attacks, such as Differential Power Analysis (DPA)

(Kocher et al., 1999), Correlation Power Analysis

(CPA) (Brier et al., 2004), Template Attacks (Chari

183

Bongiovanni S., Scotti G. and Triﬁletti A..

Security Evaluation and Optimization of the Delay-based Dual-rail Pre-charge Logic in Presence of Early Evaluation of Data.

DOI: 10.5220/0004526501830194

In Proceedings of the 10th International Conference on Security and Cryptography (SECRYPT-2013), pages 183-194

ISBN: 978-989-8565-73-0

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

et al., 2002), Mutual Information Analysis (MIA)

(Gierlichs et al., 2005), Leakage Power Analysis

(LPA) (Alioto et al., 2010) and Correlation Power

Analysis in frequency domain (CFPA) (Gebotys et

al., 2010), (Schimmel et al., 2010).

Between the above mentioned countermeasures,

DPLs are particularly suitable for thwarting power

analysis. Basically DPLs are new logic families

which aim at de-correlating power consumption

from the processed data by making it constant

irrespective to the input data statistics. DPLs are

adoptable for counteracting power analysis for

dedicated integrated circuits, and are also known as

anti-DPA logic styles. Sense Amplifier Based Logic

(Tiri et al., 2002) is one of the first full custom DPL

styles. Other DPL styles as WDDL (Tiri et al., 2004)

and MDPL (Popp et al., 2005) are based on CMOS-

composed standard cells and are also suitable for

FPGAs. However DPLs suffer on almost two well

known leakage factors (Suzuki et al., 2008) which

compromise their DPA resistance: the capacitive

load mismatches on the internal differential pairs,

and the early evaluation effect of data. Whereas the

former becomes more critical with the technology

scaling, forcing a perfect balance of the

interconnections by using for example a semi-

automatic routing (Tiri et al., 2004), the latter is

directly linked to the different propagation times of

the signals through a DPL gate (Suzuki et al., 2006).

The common side-effect of both is a data-dependent

variation of the switching time of gates which shows

up in the power-consumption pattern and can be

exploited in power analysis attacks. Early evaluation

and capacitive unbalance are caused by electrical

effects and thus are technology-dependent, therefore

a DPL design must count them.

Delay-based Dual-rail Pre-charge Logic (DDPL)

has been recently proposed for breaking the

dependence of the power consumption on the

capacitive load mismatches (Bucci et al., 2011).

DDPL is a particular DPL which counteracts power

analysis through a novel data encoding which is

based on a two-phase evaluation. This way

measurements of the current adsorbed from the

power supply line do not exhibit any data

dependence, which makes power analysis attacks

very difficult to succeed. Preliminary results (Bucci

et al., 2011) demonstrated that DDPL gates are very

effective for what concerns the ability of flattening

the power consumption for each data input

combination even in presence of capacitance

mismatches at the output of the complementary

lines. Moreover in DDPL the clock frequency does

not fix the security since it depends on the delay Δ

between DDPL complementary lines; on the

contrary in a standard pre-charge logic like SABL,

the operating frequency constraints the logic

synthesis of the design and determines, at the same

time, the achievable security level. For these reasons

DDPL is suitable to be used in a semi-custom design

as a standard dual-rail logic. However no work

exists where an analysis of the early evaluation

effect in DDPL, the other main leakage factor in

DPLs, is executed in order to assess how the

asynchronous evaluation can generate correlation

between the power consumption of the logic and the

random variations of the delay of dynamic signals.

The paper is organized as follows. After a review

of the leakage factor of the CMOS logic style which

is related to the data dependence of the dynamic

power consumption (Section 2), the working

principle of DDPL is described in Section 3. An in-

depth analysis and a model of the early evaluation

effect in DDPL combinatorial paths are discussed in

Section 4, where early evaluation free gates are

presented. Simulation results and model validation

are presented in Section 5. A correlation frequency

power analysis attack on a simple crypto core is

carried out in Section 6 both using the basic and

early evaluation insensitive DDPL logic. Finally

conclusions are reported in Section 7.

2 ORIGIN OF LEAKAGE IN

CMOS

In the static CMOS gates there are three distinct

dissipation sources (Rabaey, 2003): the leakage

currents of the transistors (P

leak

), the short-circuit

currents (P

), and the dynamic power consumption

dyn

). The latter is particularly relevant from a side-

channel point of view since it determines a

relationship between the processed data inside the

gate and its externally observable consumption. In

Figure 1 the model of power consumption is

presented for a CMOS inverter. The dynamic current

is depicted with a dotted arrow whereas the short

circuit current with a point arrow. In the case

depicted in Figure 1a, when a transition from 0 to

occurs on the output, capacitance C

is charged

and a visible peak appears in the pattern of the

current adsorbed by the power supply line due to the

sum of dynamic and short circuit currents.

SECRYPT2013-InternationalConferenceonSecurityandCryptography

184

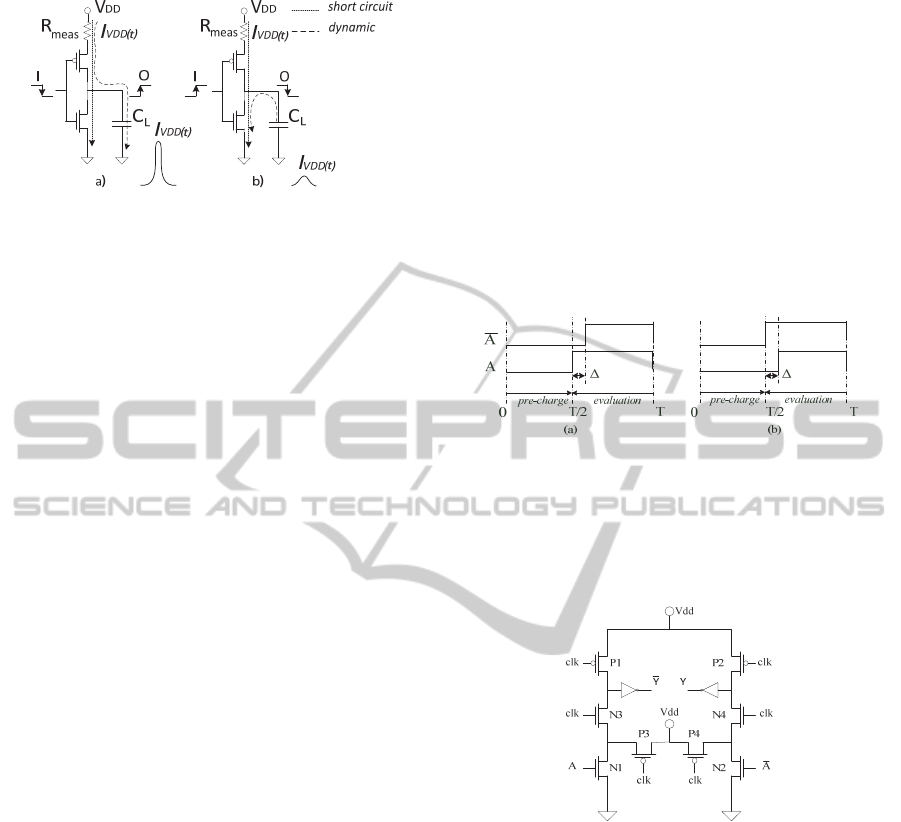
Figure 1: Model of power consumption of an inverter.

Conversely, when a transition from V

to 0

occurs as depicted in Figure 1b, C

is discharged and

the only visible contribution is due to the short

circuit current, which can be neglected being much

smaller than the dynamic contribution. The dynamic

power consumption is given by the integral of the

instantaneous power in a clock cycle, which leads to

the well known formula (Rabaey, 2003):



V





C





P

→

(1)

→

is the switching activity at the output line, and

can assume the value 1 if a transition from 0 to V

occurs or 0 if not. A similar analysis can be

conducted for the anti-DPA differential dynamic

logics. It is well known that even if DPLs help to

break any dependence of the dynamic power

consumption on the switching activity of the gate,

the inevitable mismatch of the capacitances at the

output nodes of the complementary lines can be

exploited for extracting information on the

processed data (Tiri et al., 2004).

3 BRIEF REVIEW OF THE DDPL

LOGIC STYLE

DDPL has been introduced in order to flatten the

power consumption irrespective of the data input

statistics even in presence of a unbalanced capacitive

load (Bucci et al., 2006). In DDPL the data encoding

is executed in the time domain, namely the

information is encoded in the same order as the lines

are charged. Each cell has a fully differential

complementary pair composed of an asserted and a

not asserted signal, according to which lines is the

first to be evaluated (i.e. the asserted signal). The

data encoding is characterized by two asynchronous

evaluation sub-phases, which occur after the rising

edge of the clock and are separated by an interval Δ

which is called dynamic delay of DDPL.

Figure 2 shows the two possible situations for a

DDPL data encoding. During the pre-charge phase

the differential lines are set to 0 and, in the

evaluation phase, they are both charged to V

after

the clock rising edge. For a logic-1 (Figure 2a), the

first line to be charged is A. Conversely, for a logic-

0 (Figure 2b), the first line to be charged is A



. Since

both lines are charged and discharged once over

each operating cycle, the switching activity is

always equal to 1 on each differential line for both

input data. Therefore the capacitive mismatches

between the complementary lines do not affect the

balanced distribution of the current because each

capacitance is always charged and discharged once

during a clock cycle, and the dynamic power

consumption over a cycle is made constant.

Figure 2: Time domain encoding. (a) Logic-1, (b) Logic-0.

A basic DDPL NOT/BUFFER gate is shown in

Figure 3. It is a DDPL n-type gate. We refer as n-

type (p-type) to a dynamic circuit topology in which

the evaluation network is the pull-down (pull-up).

Figure 3: A DDPL NOT/BUFFER gate.

In a DDPL n-type circuit all complementary

lines are forced to V

during the pre-charge phase.

Moreover the gate is a Domino-type logic and the

complementary outputs are pre-charged to 0. Note

that the output inverters present no data dependence

because in each clock cycle they perform the same

transitions (0  1 and 1 0 on complementary

outputs). With reference to the timing diagram

shown in Figure 4 for a logic-1, the DDPL data

operation is the following:

1) pre-charge: at the beginning of each cycle, clk is

low and P1 and P2 are closed, pre-charging both

output lines to 0. Since during this phase the input

lines are low (outputs from another DDPL gate), the

pull-down logic is open.

2) evaluation: the DDPL encoded input data



SecurityEvaluationandOptimizationoftheDelay-basedDual-railPre-chargeLogicinPresenceofEarlyEvaluationof

Data

185



, 





 ,  are presented to the circuit on the

rising edge of clk. Since A goes high before 



, the

output Y is charged after 



, thus



, 





 , .

Figure 4: Time diagram of the NOT/BUFFER signals.

4 EARLY EVALUATION EFFECT

4.1 The Early Evaluation Effect

in DPLs

The early evaluation is a transistor-level effect

which causes a logical gate to evaluate before all

inputs are valid. It is very critical for a DPL

combinatorial gate because it produces a dependence

of the adsorbed current on the arrival times of the

input signals. This effect is directly linked to the

logical function and translates to the physical

implementation. The early evaluation can result in a

data dependent power consumption even for DPA-

resistant circuits implemented with perfectly

balanced internal and output capacitances, and it

represents a well known leakage factor in DPLs as

anticipated in Section 1.

There is a number of papers in which authors

describe this vulnerability in the DPA-resistant logic

families, both theoretically (Kulikowski et al.,

2008), (Saeki et al., 2008) and experimentally

(Bhasin et al., 2010). In many cases the early

propagation must be eliminated through the design

of more complicated logics, with the drawback of an

additional hardware overhead, both for solution

based on existing standard cell (FPGA) and for full-

custom logic styles (ASIC).

In this section we discuss the impact of early

evaluation in the DDPL gates and present a model

for describing the variation of the delay Δ.

4.2 The Fluctuation Effect of Δ

As discussed in Section 3, the DDPL data encoding

is characterized by a two-phase evaluation for the

complementary lines which is needed in order to de-

correlate the power consumption from the input data

statistics even in presence of capacitive load

mismatches. In a typical current pattern two peaks

are visible in the evaluation phase (Bucci et al.,

2011). The value of the dynamic delay Δ represents

the distance between them (see Figure 2). Actually

the security level of a DDPL chip is fixed by the a

priori choice of Δ which poses a constraint on the

resolution required by a power analysis

measurement setup for discriminating separately the

two peaks of evaluation in order to extract

information on the data.

However even if the power consumption in a

given clock cycle is made constant, the evaluation

phase is asynchronous for each complementary half

sub-circuit in the pull down of a DDPL gate, and a

variation of the delay Δ between the complementary

lines is expected due to the different propagation

times on the complementary paths. This effect is

related to the above mentioned early evaluation,

which in a DDPL gate causes one half sub-circuit of

the differential cell to activate in a certain instant

without waiting for the evaluation of the

complementary network. For this reason the actual

delay Δ

on the output lines depends on the

propagation time of the gate which, in turns,

depends on the topology of the gate itself. In other

words a fixed delay Δ

between

a complementary pair

at the input of a gate is mapped into a not constant

delay Δ

between the complementary pair at the

output. This variation of the value of the dynamic

delay can be positive (Δ

> Δ) or negative (Δ

< Δ)

according to the circuit architecture. Note that in

DDPL logics the minimum value of Δ is set by the

propagation time of the critical path of the multi-

level logic between two DDPL flip-flops, whereas

the maximum allowed value is set by the level of

security chosen for the entire circuit (i.e. lowering

the maximum Δ increases the resolution required for

the attacking measurement setup) (Bucci et al.,

2011). Therefore we are interested in avoiding

positive variations. We name this phenomenon as

fluctuation effect of the delay Δ in a DDPL circuit.

Thus with the aim of investigating how the actual

level of security of DDPL changes due to early

evaluation, it must be guaranteed that the delay Δ

does not increase randomly or uncontrollably at the

output of each gate so to avoid the fluctuation effect

of Δ along a multi level logic.

4.3 A Theoretical Model of the Delay

In this section we provide an analysis for modelling

the random variations occurring on the dynamic

SECRYPT2013-InternationalConferenceonSecurityandCryptography

186

delay Δ in the real case of not synchronized DDPL

input pairs at the input of some typical combinatorial

cells. Without loss of generality assume that signal

B, B



 is delayed with respect to signal A, A



.

Moreover assume Δ

= Δ and Δ

 Δ, i.e. the

dynamic delay of B, B



 is lower or equal than Δ.

This is consistent with the assumption that the delay

between complementary input signals cannot be

greater than Δ, as required by a DDPL circuit where

no fluctuation effect of Δ is generated. We name t

and t

the delays between the rising edges of the

asserted and the not asserted lines of A, A



 and

B, B



, respectively, therefore t

 t

In the following schemes transistors sizes are

optimized for power, area and timing requirements,

and for obtaining equalized capacitances at the input

of the cells. We use a minimum length equal to L

min

in a given technology and aspect ratios W/L equal to

2 and 4 for all nMOS and pMOS respectively.

The purpose of this analysis is to verify how the

early evaluation effect may impact the value of Δ

and possibly to furnish a light circuit level solution

by re-designing a cell in order to guarantee that Δ

, Δ

for each input data combination.

4.3.1 Analysis of the AND/NAND Logic Gate

Figure 4 shows a basic DDPL AND/NAND gate.

The gate was designed with a n-type evaluation

network so to reduce the area overhead with respect

to the original p-type scheme (Bucci et al., 2011).

Figure 4: A basic DDPL AND/NAND gate with the

equivalent circuits of the evaluation network.

The evaluation network is composed of four

transistors, which is the minimum number for

implementing the logic function AND/NAND. In

fact the physical design of a gate is minimized by

exploiting the fact that, for some input combinations,

a gate can propagate its logical output early without

having to wait for all of the logical inputs. However

as explained in Section 4.1 this can represent a

drawback in an anti-DPA logic style because it

generates a power consumption dependent on the

arrival times of signals.

Figure 4 also shows the equivalent circuits of the

two dual pull-down networks during the evaluation

phase when the half sub-circuits are activated. For

the sake of simplicity consider C



C



C.

Actually the total capacitance at the node v

slightly smaller than the capacitance at v

due to the

parasitic capacitances of the stack transistor N3

(Rabaey, 2003). Anyway pass transistors P3 and P4

provide to charge both C



and C



at V

during the

pre-charge phase reducing each mismatch. Note also

that the Domino inverters decouple nodes v

and v

from possible unbalances at the output nodes.

The propagation time for the evaluation network

depends on how many transistors are simultaneously

activated. If we model the pull-down resistance of

each transistor with a resistor R

, then during the

evaluation phase the pull-down sub-circuits PD1 and

PD2 have a different time of discharge of the

capacitances C



and C



because the number of

simultaneously activated transistors is different. The

time constants satisfy relation (2).



R



Cτ



2R



C,

(2)

Capacitance C



discharges more slowly than C



and Y has a propagation time greater than Y



.We

name Δτ



 τ



 τ



the delay associated with the

difference between the two pull-down paths. The

analysis of the variation of Δ for different data

inputs is reported in equations (3a-d), which refer to

the time diagram in Figure 5.



,

 Δ t



t



 Δτ



(3a)



,

 Δ t



 Δτ



(3b)



,

 Δ t



 Δτ



(3c)



,

 Δ  Δτ



(3d)

Δ



,

indicates the output delay for the inputs A =



A, A





and B =



B, B





, where 1 stands for (1,0) and 0

stands for (0,1). Equations (3a-d) state that for this

implementation the actual delay on the output

complementary lines can result greater than the fixed

delay Δ. This increase of Δ adds up in a multi level

logic path according to the input statistics, lowering

the security level of the overall circuit (Section 5.2).

4.3.2 Analysis of the XOR/XNOR Logic

Gate

A similar analysis is carried out for the DDPL

XOR/NXOR gate. In Figure 6 a n-type DDPL

XOR/NXOR gate is shown. Note that XOR is a

symmetric logic function which is mapped into a

SecurityEvaluationandOptimizationoftheDelay-basedDual-railPre-chargeLogicinPresenceofEarlyEvaluationof

Data

187

Figure 5: Time diagram of the evaluated signals at the output of a basic DDPL AND/NAND cell for all possible inputs.

symmetric circuit topology, therefore both pull-

down sub-circuits can be represented by the

equivalent circuits PD1 or PD2 according to the

number of simultaneously evaluated inputs and the

delay between



A, A





and



B, B





. Again consider



C



, neglecting the contribution of the

parasitic capacitances of the other activated

transistors which would cause an increase of the

equivalent capacitance C. Thus the time for the

discharge of the capacitances C



and C



is τ



or τ



according to the input data. The time constants of

PD1 and PD2 satisfy equation (4).



2R



Cτ



R



(4)

Figure 6: A basic DDPL XOR/NXOR gate with the

equivalent circuits of the evaluation network.

We name Δτ



 τ



 τ



the delay associated

with the difference between the propagation times of

the two pull-down paths.

If input pairs are delayed so that the rising edges

of the not asserted signals are separated by t

> τ



(see Figure 7), the sub-circuit networks behave

always as PD1 due to the symmetry of the gate. This

leads to a constant value for the actual delay Δ

irrespective of the input data configuration (5):

Δ



 Δ  τ









 τ





 Δ t



 Δ

(5)

Thus the output delay Δ

is independent on Δτ



and not greater than Δ for all possible data

combinations. In other words the propagation time

along the pull-down network is equalized thanks to

the symmetric architecture of the gate which avoids

the fluctuation effect of Δ at the output.

Figure 7: Time diagram of the evaluated signals at the

output of a basic DDPL XOR/NXOR cell for each input.

Instead if the delay of signals



B, B





from



A, A





is negligible, that is if t

< τ



, the not asserted signal

propagates according to the time constant of the

circuit model PD2 where all transistors are

simultaneously activated. In this case the

propagation time reduces from τ



to τ



because the

pull down resistance path is lower (see equation 6),

and the output delay depends on the propagation

times of the pull-down networks entailing the

presence of early evaluation:



 Δ  τ









 τ





 Δ t



 Δτ

xor

 Δ

(6)

Anyway no increase of Δ in the DDPL XOR/NXOR

gate is caused. This allows to conclude that the

XOR/NXOR gate does not exhibit the fluctuation

effect of the delay at its output.

4.3.3 An Optimized AND/NAND Logic Gate

with no Early Evaluation

After having examined the XOR/NXOR gate, the

data-dependent behaviour of the DDPL

AND/NAND gate shown in Section 4.3.1 is

supposed to be caused by the asymmetry of the

evaluation paths. In (Tiri et al., 2005) authors

present a design methodology to create fully

connected differential pull-down networks so to

balance the propagation delays for any input

combination. Some dummy transistors are inserted

with the aim of equalizing the resistive path during

the evaluation phase. We used this methodology for

SECRYPT2013-InternationalConferenceonSecurityandCryptography

188

designing an optimized AND/NAND gate in which

the pull down network is made up of 8 n-MOS

transistors (Figure 8) and the propagation times of

the logic are balanced as in the XOR/NXOR gate.

Figure 8: An optimized DDPL NAND/AND gate with the

equivalent circuits of the evaluation network.

The analysis of this circuit is similar as in the

XOR/NXOR gate, but in this case the value of the

output delay is not expected to be constant due to the

asymmetry of the evaluation network. As seen in

Figure 8 the pull-down sub-circuit on the right can

be represented by the equivalent circuits PD1 or

PD2 according to the number of simultaneously

evaluated inputs and to the delay between



A, A





and



B, B





, whereas the other sub-circuit can be

represented only by PD1. Thus the time of discharge

of the capacitance C



can be τ



or τ



according to

the number of transistors simultaneously activated,

whereas for C



time constant is always τ



. The time

constants satisfy equation (7):



2R



Cτ











(7)

Again for the equivalent circuits we neglect the

contribution of the parasitic capacitances and

consider C



C



C. We name Δτ



 τ



 τ



the delay associated to the difference between the

propagation times of the two pull-down paths. If

input pairs are delayed so that the rising edges of the

not asserted signals are separated by t

> τ



, the sub-

circuit networks behave always as PD1 (see Figure

9). This is described by equations (8a-d):

Δ



,

 Δ t



t



(8a)

Δ



,

 Δ t



t



(8b)

Δ



,

 Δ t



(8c)

Δ



,

 Δ t



(8d)

Instead if the delay of signals



B, B





from



A, A





negligible, that is if t

< τ



, the not asserted signal

propagates according to the time constant of the

circuit model PD2 where all transistors are

simultaneously activated. In this case the

propagation time of the rising edges of the not

asserted line reduces from τ



to τ



because the pull

down resistance path of the network on the right is

lower. The output delay is calculated in (9a-d):



,

Δt



 Δτ





(9a)



,

Δt





(9b)



,

Δt



 Δτ





(9c)



,

Δt



 Δτ





(9d)

Equations (8a-d) and (9a-d) show that unlike the

XOR/NXOR gate, the asymmetry of the pull-down

network of the AND/NAND gate causes the actual

delay to be not constant. However this is not an issue

because the actual delay Δ

is always less than the

input delay Δ for each input data combinations,

thanks to the balanced evaluation network in which

all resistance paths are equalized.

4.3.4 Design of Multi Level DDPL Gates

with No Early Evaluation

The previously presented analysis allows to

conclude that by carefully designing the evaluation

network, the early propagation effect in the DDPL

combinatorial gates can be controlled as in other

dual-rail dynamic logic styles even if an

asynchronous two phase evaluation occurs and even

if the logic function to be implemented is

asymmetric. The guideline is to guarantee a good

balance of the resistive paths of the evaluation

network by inserting dummy transistors if needed.

This way the propagation times of the asserted and

the not asserted signals, which in turns depend on

the time constants associated to the capacitances at

the respective internal node, are constant irrespective

of the input data combination and their arrival times.

In Figure 10 a further reduced implementation of

an early evaluation free AND/NAND gate is

reported. The pull down network requires only 6

transistors instead of 8 transistors, lowering the area

overhead.

The OR/NOR gate can be implemented by

swapping the input and output wires of the

AND/NAND cell. By adopting a set of basic DDPL

early evaluation free gates (i.e. BUFFER/NOT,

AND/NAND, OR/NOR, XOR/NXOR) it is possible

to build any DDPL combinatorial gates and multi

level logics which do not suffer on early evaluation.

SecurityEvaluationandOptimizationoftheDelay-basedDual-railPre-chargeLogicinPresenceofEarlyEvaluationof

Data

189

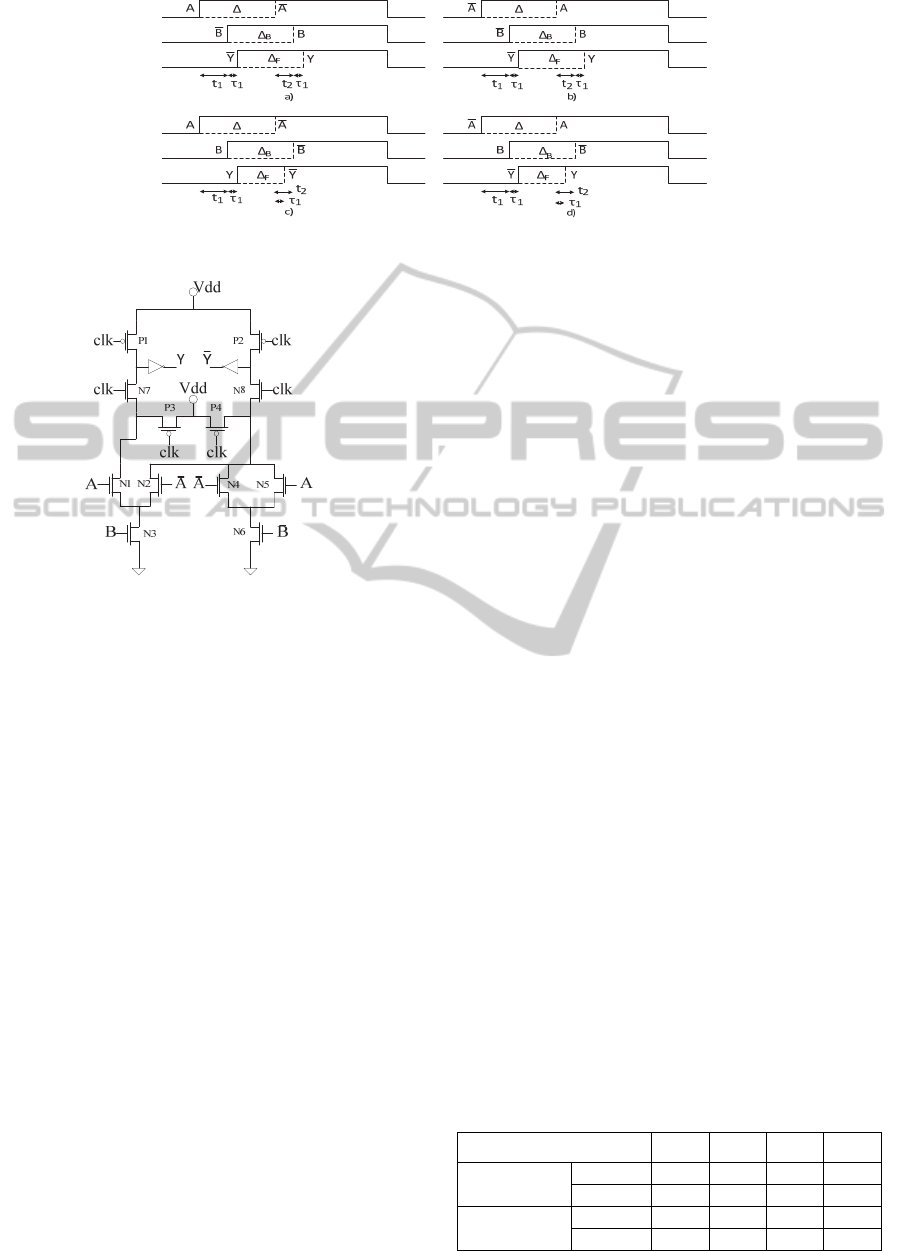
Figure 9: Time diagram of the evaluated signals at the output of an optimized DDPL AND/NAND cell for each input.

Figure 10: An optimized implementation of an early

evaluation free DDPL AND/NAND gate.

5 SIMULATION RESULTS AND

MODEL VALIDATION

In this section we prove the accuracy of the

theoretical model by performing simulations on

simple combinatorial case studies. Simulations were

performed in Cadence Analog Design Environment

adopting standard-V

BSIM4 transistor models with

nominal values (@Temp = 25°C). The circuits were

Microelectronics. Moreover the followings

parameters are used: Δ

= Δ

= 500ps, clock

frequency f

= 100MHz and supply voltage V

1V. The aim of the simulations is to measure the

variations of the output delay in some combinational

case studies and verify if results are in agreement

with the model discussed in Section 4.

5.1 A Single Combinational Gate

The basic and the optimized AND/NAND gates

have been compared in simulation under balanced

and unbalanced load conditions. Input signals have

been delayed each other with t

= t

≈ 120ps.

5.1.1 Balanced Capacitive Load

The gates were loaded with balanced capacitances of

1fF. In Figure 11 the current pattern in the

evaluation phase for all input combinations and the

clock signal are shown. Current peaks are associated

to the asserted and the not asserted signals

respectively, and are separated from a time interval

equal to Δ



. For the basic cell the random variations

of Δ



highlight the dependence of the current trace

on the applied inputs. Moreover the fluctuation

effect is visible being Δ

> Δ, as predicted by the

model. On the contrary, for the optimized cell the

current peaks are nearly superimposed (a slight

deviation of Δ

less than 50ps is visible) and the

relation Δ

< Δ holds for all data.

5.1.2 Unbalanced Capacitive Load

Simulations were repeated by loading the gates with

unbalanced capacitances on the complementary lines

in order to test if a mismatch on the output load can

reduce the effectiveness of the model. The output

capacitances were chosen to be equal to 1fF and 5fF

on the NAND and the AND output respectively,

with a mismatch factor of 5.

Results are summarized in Table I for both cases

and for both load conditions. It is worth noting that a

capacitive mismatch increases the range of variation

of Δ

, anyway the optimized cell still exhibits an

output delay Δ

< Δ. Simulation results are in

agreement with the model also for the XOR/NXOR

gate, and show that if the evaluation network is

optimized, not even an output unbalanced load can

generate fluctuation effect.

Table 1: Output delay in the AND/NAND gates (in ps).

AND/NAND



,

Δ



,

Δ



,



,

No EE

Bal 422 400 420 375

Unbal 453 354 460 418

With EE

Bal 649 357 526 524

Unbal 688 315 571 567

SECRYPT2013-InternationalConferenceonSecurityandCryptography

190

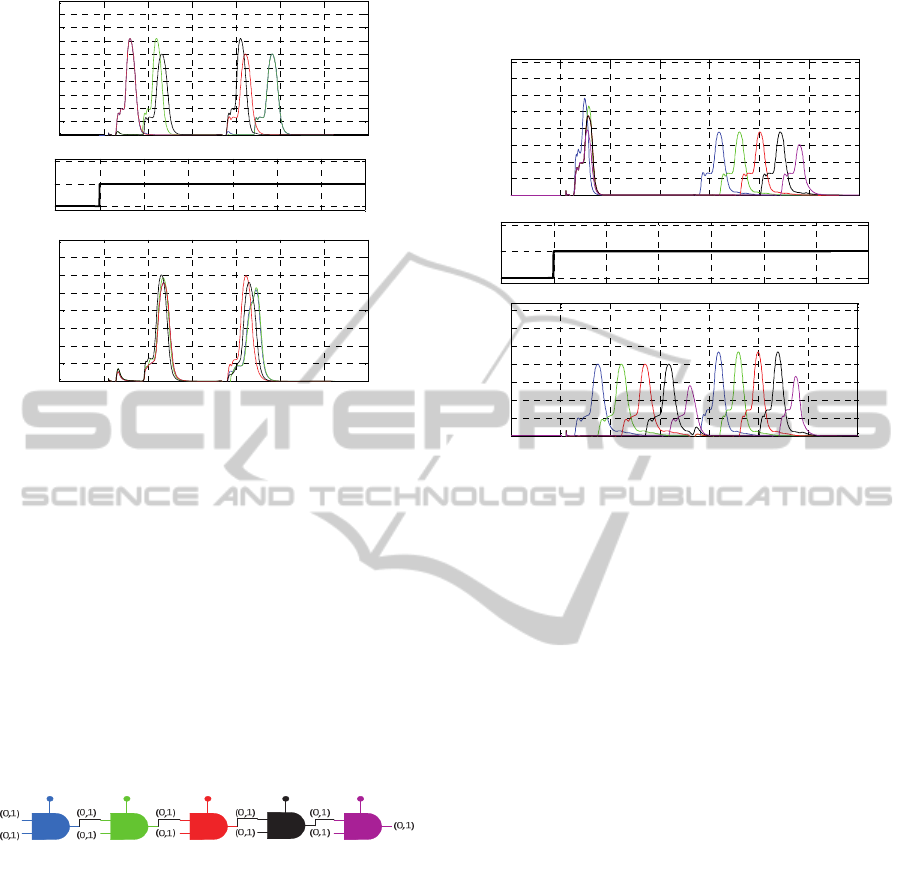
Figure 11: Superimposition of current traces for a basic

(upper) and an optimized (lower) AND/NAND gate.

5.2 Combinational Multi-level Logic

In the previous section simulations demonstrated

that the early evaluation effect combined to the

different propagation times of the DDPL

complementary signals at the input of a single gate

generates random variations of the output delay and

in particular a fluctuation effect of Δ. Analysis is

now generalized for a combinatorial multi-level

logic made up of five cascaded AND/NAND gates

in order to compare the timing behaviour of the

basic and the optimized AND/NAND gate when

inserted in a real combinatorial path (Figure 12).

Figure 12: A combinatorial multi-level logic case study.

According to the analysis reported in Section 4, the

critical path (from the viewpoint of early evaluation

effect) is associated to the data transition which

causes the output delay of the gate i to be greater

than its input delay. This particular data

configuration just corresponds to the case



A, A









B, B





0,1 when the fluctuation of Δ is

maximum, as described by equation (3b). Thus the

AND output of a gate is connected to the input of the

following gate and each cell is stimulated with

signals (0,1) as input so to simulate the critical path.

In Figure 13 the evaluation current peaks are

coupled according to the colour in Figure 12: the

peaks in blue represent the two-phase evaluation of

the first gate in Figure 12, whereas the peaks in

violet are associated to the last gate.

Figure 13: Superimposition of current traces for the multi

level logic implemented with basic (upper) and optimized

(lower) AND/NAND gates.

The upper part of Figure 13 refers to the current

pattern of the logic suffering on early evaluation.

The current peaks of the first gate exhibit a delay Δ

equal to 540ps, whereas the current peaks of the last

gate exhibit a delay Δ

equal to 860ps, which is

almost 60% greater than the original value of Δ.

Thus each stage is characterized by an output DDPL

delay almost 80ps greater than its input delay.

Relation (10) holds for each gate (





Δ:





Δ





Δ.

(10)

It is worth noting that the output delay of the last

gate is greater than the original delay of a quantity

directly proportional to the number N of stages and

Δτ



. Maximum can be estimated by (11) and

represent the worst case for this specific logic path

in terms of fluctuation of Δ:





ΔΔτ



⋅NΔ

(11)

On the contrary when the optimized AND/NAND

gate with no early evaluation is used, the output

delay, as depicted in the lower part of Figure 13,

gradually decreases as expected in a DDPL

combinatorial path. Even if the current pattern is

dependent on the propagation time of signals along

the logic, no fluctuation is visible, and Δ

stays

within the originally fixed resolution Δ.

We can conclude that in the AND/NAND

implementation which suffers on the early

evaluation effect the fluctuation introduced by a

4800 5000 5200 5400 5600 5800 6000 6200

0.5

1.5

2.5

3.5

4.5

x 10

-5

time [ps]

Curr ent [ A]

A = (0,1), B = (0,1)

A = (1,0), B = (0,1)

A = (0,1), B = (1,0)

A = (1,0), B = (1,0)

4800 5000 5200 5400 5600 5800 6000

time [ps]

Voltage [V]

evaluation

precharge

4800 5000 5200 5400 5600 5800 6000 6200

0.5

1.5

2.5

3.5

x 10

-5

time [ps]

Curr ent [ A]

A = (0,1), B = (1,0)

A = (1,0), B = (1,0)

A = (0,1), B = (0,1)

A = (1,0), B = (0,1)

4800 5000 5200 5400 5600 5800 6000 6200

0.5

1.5

2.5

3.5

x 10

-5

time [ps]

Current [A]

540ps 700ps

780ps

860ps

620ps

4800 5000 5200 5400 5600 5800 6000

time [ps]

Voltage [V]

evaluation

precharge

4800 5000 5200 5400 5600 5800 6000 6200

0.5

1.5

2.5

3.5

x 10

-5

time [ps]

Current [A]

500ps

480ps

460ps

440ps

420ps

SecurityEvaluationandOptimizationoftheDelay-basedDual-railPre-chargeLogicinPresenceofEarlyEvaluationof

Data

191

single gate actually adds up to the output delay,

whereas using optimized gates the skew is equally

distributed both on the asserted and the not asserted

DDPL lines and the value of the output delay Δ

always lower than the initial value which fixes the

maximum resolution for solving the evaluation

current peaks in DDPL circuits.

It is worth noting that by using current CMOS

technologies the delay Δ can be designed to be in the

range of a few hundreds of picoseconds which

forces a mesurement setup to have a bandwidth in

the range of some GHz in order to make a power

analysis attack effective. Moreover it has to be

pointed out that the simple low pass filtering action

of the on-chip power supply distribution network

can make these differences not easily detectable out

of the chip. Successful attacks have been performed

in the literature which exploit some nano seconds of

skew due to the early evaluation in a combinatorial

paths (Popp et al., 2007).

6 CASE STUDY: ATTACK ON A

SIMPLE CRYPTO CORE

In this section we validate the model on a real

cryptographic case study. We implemented a crypto

core by using both basic and optimized DDPL

AND/NAND gates. The circuit under test is the S-

box S

from the Serpent algorithm (Anderson et al.,

1998) (see Figure 14) which takes as input the XOR

between a 4 bit input word and the 4 bit key (0000)

Figure 14: Cryptographic circuit used as case study.

Simulation parameters were set to the same

values used in Section 4, except Δ

and Δ

which

were fixed to 1ns according to the maximum delay

associated to the critical path of the logic. A number

of 1000 randomly generated binary data were given

as inputs to the circuit, and the current adsorbed

from the power supply line of the S-box logic was

measured with an acquisition time of 1ps.

Rather than using a power analysis attack in the

time domain which can unlikely detect the leakage

associated to the fluctuation effect in DDPL in a

simulation attack scenario, we chose a power

analysis in the frequency domain. Frequency

analysis was introduced in (Gebotys et al., 2010). In

(Schimmel et al., 2010) a multi-step procedure for

implementing a simulated Correlation Frequency

Power Analysis (CFPA) attack on an AES S-box is

presented. Authors demonstrated that a power

analysis in frequency domain can be more effective

than a power analysis in time domain in exploiting

the leakage when time shifts or misalignments occur

in the traces. Therefore CFPA is a good candidate as

attack strategy for detecting timing mismatches due

to early evaluation in a DDPL circuit.

We adopt the basic attack procedure presented in

(Schimmel et al., 2010). The latter involves the use

of the Fast Fourier Transform (FFT), which is

related to the energy distribution of the measured

current traces for each frequency component (Power

Spectrum Density, PSD). Thus correlating the

leakage model (i.e. the Hamming weight of the S-

box output) to the PSD of the current traces can help

to detect some information on the correct key as in a

standard CPA attack.

In Figure 15 a superimposition of the current

traces is shown for the two case studies. The upper

part of the figure refers to the S-box implemented

with basic logic gates where the early evaluation

effect causes an irregular pattern. Instead in the

current pattern of the early evaluation free logic

(lower), traces are nearly superimposed.

Figure 15: Superimposition of the current traces for the

S-Box with (upper) and without (lower) early evaluation.

Simulated traces are noise free, and were

windowed around the evaluation phase according to

a 2048-points FFT. CFPA results are shown in

Figure 16 and Figure 17. In the current pattern of the

early evaluation free S-box (Figure 16) no peaks are

visible in the correlation trace of the correct key

(black line). Instead in the other case (Figure 17)

some current peaks are detected for the correct key

trace, with a correlation coefficient equal to 0.8,

demonstrating the successful of the attack. A basic

0 200 400 600 800 1000 1200 1400 1600 1800 2000

x 10

-4

time [ps]

Current [A]

0 200 400 600 800 1000 1200 1400 1600 1800 2000

x 10

-4

time [ps]

Current [A]

SECRYPT2013-InternationalConferenceonSecurityandCryptography

192

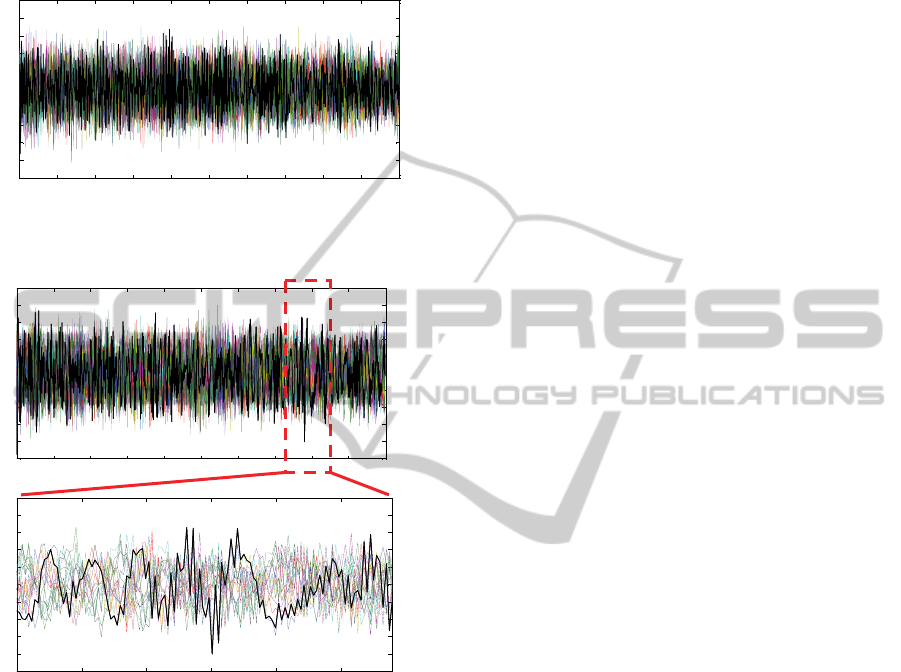
CFPA shows that the fluctuation effect is a leakage

factor which reduces the level of security of a DDPL

cryptographic circuit because it propagates along the

logic, and must be taken into account in the design.

Figure 16: Correlation frequency power analysis on a

DDPL S-box without early evaluation (N = 1000).

Figure 17: Correlation frequency power analysis on a

DDPL S-box with early evaluation (N = 1000).

7 CONCLUSIONS

In this paper we presented a deep analysis of the

early evaluation effect on DDPL combinatorial gates

when asynchronously evaluating dynamic data are

given as input. An analytical model based on a fine-

grain circuit analysis has been presented. This

highlights that DDPL gates can suffer on the early

evaluation effect on the data due to an asynchronous

two-phase evaluation which causes a non-constant

shift of the value of the dynamic delay Δ in gates

with asymmetric evaluation networks. In particular a

positive variation of Δ, named fluctuation effect, can

reduce the level of security of a DDPL circuit under

the perspective of a power analysis attack, because it

reduces the resolution required from a measurement

setup for solving the two asynchronous evaluation

peaks in a current pattern.

The model was validated by performing current

measurements on multi level logics. Moreover a

simulated correlation power analysis attack in the

frequency domain has been mounted on a case study

crypto-core. CFPA proves to be a powerful tool for

exploring the leakage of a transistor level

countermeasure in presence of time mismatches.

This analysis allows to conclude that the

asynchronous behavior of the DDPL style does not

reduce the level of security of the circuit provided

that the DDPL combinatorial cells are adequately

designed. This way it is possible to build a standard-

cell library composed of early evaluation free DDPL

gates, with a reasonable area overhead, unlike other

DPLs which requires a lot of additive logic for

resynchronizing signals before the evaluation phase

at the input of each cell.

REFERENCES

Alioto, M.; Giancane, L.; Scotti, G.; Trifiletti, A.; 2010.

Leakage Power Analysis Attacks: A Novel Class of

Attacks to Nanometer Cryptographic Circuits. In IEEE

Transactions on Circuits and Systems I. IEEE, vol. 57

, no. 2, pp. 355-367.

Anderson, R.; Biham, E.; Knudsen, L.; 1998. Serpent: A

proposal for the advanced encryption Standard. NIST

AES proposal, 1998. Online:

http://www.cl.cam.ac.uk/ftp/users/ria14/serpent.pdf.

Bhasin, S.; Guilley, S.; Flament, F.; Selmane, N.; Danger,

J.; 2010. Countering early evaluation: an approach

towards robust dual-rail precharge logic. In WESS '10,

5th Workshop on Embedded Systems Security,

Scottsdale, AZ, USA..

Brier, E.; Clavier, C.; Olivier, F.. Correlation Power

Analysis with a Leakage Model. In the Workshop on

Cryptograpghic Hardware and embedded Systems

(CHES) 2004, Lecture Notes of Computer Science

(LNCS), Springer-Verlag, vol. 3156, pp. 16-29.

Brier, E.; Handschuh, H.; Tymen, C.; 2001. Fast

Primitives for Internal Data Scrambling in Tamper

Resistant Hardware. In CHES 2001, LNCS, Springer-

Verlag, vol. 2162, pp. 16–27, Paris, France.

Bucci, M.; Giancane, L.; Luzzi, R.; Scotti, G.; Trifiletti,

A.; 2011. Delay-Based Dual-Rail Precharge Logic. In

IEEE Transactions on Very Large Scale Integration

(VLSI) Systems, vol. 19, no. 7, 2011, pp. 1147-1153.

Chari, S.; Rao J.; Rohatgi, P.; 2002. Template Attacks. In

CHES 2002. LNCS, Springer, vol. 2523, pp. 13-28.

Gierlichs, B.; Batina, L.; Tuyls, P.; Preneel, B.; 2005.

Mutual information analysis. In CHES 2005. LNCS,

Springer, vol. 5154, pp. 426–442.

Goubin, l.; Patarin, J.; 1999. DES and Differential Power

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5

-1

-0.8

-0.6

-0.4

-0.2

0.2

0.4

0.6

0.8

Normalized frequency

Correlation coefficient

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5

-1

-0.8

-0.6

-0.4

-0.2

0.2

0.4

0.6

0.8

Normalized frequency

Correl ation coefficient

0.36 0.37 0.38 0.39 0.4 0.41

-1

-0.8

-0.6

-0.4

-0.2

0.2

0.4

0.6

0.8

Normalized frequency

Correlation coefficient

SecurityEvaluationandOptimizationoftheDelay-basedDual-railPre-chargeLogicinPresenceofEarlyEvaluationof

Data

193

Analysis. In CHES 1999, LNCS, Springer, vol. 1717,

pp. 158–172, Worcester, MA, USA.

Kocher, P. C.. 1996. Timing attacks on implementations

of Diffie-Hellman. In CRYPTO ‘96, 16th Annual

International Cryptology Conference, Santa Barbara,

CA, USA.

Kocher, P. C.; Jaffe J.; Jun B.; 1999. Differential Power

Analysis. In CRYPTO ’99, 19

Annual International

Cryptology Conference, Santa Barbara, CA, USA.

Kulikowski, K. J.; Karpovsky, M. G.; Taubin, A.; 2006.

Power Attacks on Secure Hardware Based on Early

Propagation of Data. In IOLTS 2006, 12th IEEE

International On-Line Testing Symposium. IEEE

Computer Society, Como, Italy, 2006.

Mateos, E.; Gebotys, C., H.; 2010. A new correlation

frequency analysis of the side channel. In WESS '10,

5th Workshop on Embedded Systems Security,

Scottsdale, AZ, USA.

May, D.; Muller, H.; Smart, N.; 2001. Randomized

LNCS, Springer-Verlag,vol 2162, pp 28–38, Paris,

France.

Popp, T.; Kirschbaum, M.; Zefferer, T.; Mangard, S.;

2007. Evaluation of the masked logic style MDPL on

a prototype chip. In CHES 2007. LNCS, Springer, pp.

81–94, 2007.

Popp, T.; Mangard, S.; 2005. Masked dual-rail pre-charge

logic: DPA-resistance without routing constraints. In

CHES 2005. LNCS, pp. 172–186.

Rabaey, J. M.; Chandrakasan; A. P.; Nikolic, B.; 2003.

Digital Integrated Circuits: a Design Perspective.

Prentice Hall electronics and VLSI series, Pearson

Education 2003, 2

edition.

Saeki, M.; Suzuki, D.; 2008. Security Evaluations of

MRSL and DRSL Considering Signal Delays. In

IEICE Transactions on Fundamentals of Electonics,

Communications and Computer Sc.

Schimmel, O.; Duplys, P.; Boehl, E.; Hayek, J.; Bosch, R.;

Rosenstiel, W.; 2010. Correlation power analysis in

frequency domain. In COSADE 2010, 1st

International Workshop on Constructive Side-Channel

Analysis and Secure Design, Darmstadt, Germany.

Shamir, A.; 2000. Protecting Smart Cards from Passive

Power Analysis with Detached Power Supplies. In

CHES 2000. LNCS, Springer, vol 1965, pp 238–251,

Worcester, MA, USA.

Suzuki, D.; Saeki, M.; 2006. Security Evaluation of DPA

Countermeasures Using Dual-Rail Pre-Charge Logic

Style. In CHES 2006. LNCS, Springer, Yokohama,

Japan.

Suzuki, D.; Saeki, M.; 2008. An Analysis of Leakage

Factors for Dual-Rail Pre-Charge Logics Style. In

IEICE Transactions on Fundamental of Electronics,

Communications and Computer Sciences.

Tiri, K.; Akmal, M.; Verbauwhede, I.; 2002. A dynamic

and differential CMOS logic with signal independent

power consumption to withstand differential power

analysis on smart card. In ESSCIRC 2002, 28th

European Solid-State Circuits Conference. IEEE

Solid-State Circuits Conference, 2002, pp. 403–406.

Tiri, K.; Verbauwhede, I.; 2004. A logic design

methodology for a secure DPA resistant ASIC or

FPGA implementation. In DATE 2004, Conference on

Design, Automation and Test in Europe. Proceedings,

pp. 246–251.

Tiri, K.; Verbauwhede, I.; 2004. Place and route for secure

standard cell design. In CARDIS 2004, 6th Smart Card

Research and Advanced Application IFIP Conference.

Proceedings, pp. 143–158, Tolouse, France.

Tiri, K.; Verbauwhede, I.; 2005. Design Method for

Constant Power Consumption of Differential Logic

Circuit. In Date 2005. IEEE Computer Society 2005.

Tuyls, P.; Schrijen, G., J.; Skoric, B.; Van Geloven, J.;

Verhaegh, N.; Wolters, R.; 2006. Read-Proof

Hardware from Protective Coatings. In CHES 2006.

LNCS, Springer, vol 4249, pp 369–383, Yokohama,

Japan.

SECRYPT2013-InternationalConferenceonSecurityandCryptography

194