
Related-key Impossible Differential Cryptanalysis of Full-round HIGHT
Saeed Rostami
1
, Sadegh Bamohabbat Chafjiri
2
and Seyed Amir Hossein Tabatabaei
3
1
R&D Department, Tehran, Iran
2
Information Systems and Security Lab, Sharif University of Technology, Tehran, Iran
3
Chair for Data Communications Systems, University of Siegen, Siegen, Germany
sae.rostami@gmail.com, bamohabbat@ieee.org, amir.tabatabaei@uni-siegen.de
Keywords:
HIGHT, Lightweight Block Cipher, Related-key, Impossible Differential, Cryptanalysis.
Abstract:
The HIGHT algorithm is a 64-bit block cipher with 128-bit key length, at CHES’06 as a lightweight crypto-
graphic algorithm. In this paper, a new related-key impossible differential attack on the full-round algorithm
is introduced. Our cryptanalysis requires time complexity of 2
127.276
HIGHT evaluations which is slightly
faster than exhaustive search attack. This is the first related-key impossible differential cryptanalysis on the
full-round HIGHT block cipher.
1 INTRODUCTION
Nowadays using cryptographic primitives engaging
lightweight technology is in the point of interest for
the sake of efficiency. The most important applica-
tions lie in smart cards, sensors and, RFIDs where the
processing and memory resources are limited. By us-
ing lightweight technology, it is tried to remove the
problems which are arising from conditions imposed
on the available resources by using low-cost complex-
ity operations. On the other hand, when computa-
tional efficiency is increased security issues should be
taken into account. So, considering a concrete secu-
rity analysis is important in the design process of a
lightweight cryptographic primitive to avoid endan-
gering the desired security level.
The Block cipher HIGHT (high security and light
weight) with 64-block length and 128-key length has
been proposed by Hong et al. for low-cost, low-
power, and, ultra-light implementation (Hong and
et al., 2006). It is an iterative 32-round block cipher
in the shape of generalized Feistel network which is
used as a standard block cipher in South Korea. Sev-
eral attacks on the HIGHT have shown some potential
weaknesses of the reduced-round algorithm. The se-
curity strength of the algorithm against linear attack
(Matsui, 1994) and differential cryptanalysis (Biham
and Shamir, 1991) has been considered by its design-
ers (Hong and et al., 2006). In (Ozen et al., 2009)
the saturation attack (Lucks, 2002) on 16-round al-
gorithm using 12-round characteristic was presented
which has been improved in (Zhang et al., 2009) to
target 22-round HIGHT. Impossible differential and
related-key impossible differential attacks (Biham
et al., 2005; Biham et al., 1999) on the HIGHT are
covering more rounds (Hong and et al., 2006; Lu,
2007; Ozen et al., 2009). Till now with the best
knowledge of the authors, the only attacks which tar-
get the full-round HIGHT are related-key rectangle
attack (Hong et al., 2011) and biclique cryptanalysis
(Hong et al., 2012). Although their time complexity
(Hong et al., 2011) is almost the the same as com-
plexity of our attack, our attack is the first related-
key impossible differential attack on the full round
HIGHT so far. In this paper, we propose a related-
key impossible differential cryptanalysis on the full-
round HIGHT with the complexity less than exhaus-
tive search attack. A comparison between the re-
sult of our proposed attack and previously introduced
related-key impossible differential attacks is provided
in Table 1.
We mount our attack on the full-round algorithm
by using a 24-round impossible differential character-
istic. The main advantage of our approach in compar-
ison with attacks proposed in (Lu, 2007) and (Ozen
et al., 2009) is to use different differential characteris-
tics which enables us to attack on the algorithm with
one more round. The rest of this paper is organized
as follows. In Section 2, the block cipher HIGHT is
described. Extracting a new 24-round impossible dif-
ferential characteristic will be given in Section 3. In
Section 4, the full-round attack scenario and the com-
plexity discussion will be given which concludes the
paper.
537
Rostami S., Bamohabbat Chafjiri S. and Amir Hossein Tabatabaei S..
Related-key Impossible Differential Cryptanalysis of Full-round HIGHT.
DOI: 10.5220/0004528805370542
In Proceedings of the 10th International Conference on Security and Cryptography (SECRYPT-2013), pages 537-542
ISBN: 978-989-8565-73-0
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

Table 1: Summarized results of previous well-known attacks and our proposed attack.
Number Key Attack Data Time
of rounds size (bit) complexity complexity
28 128 related-key 2
60
2
125.54
impossible differential [8]
31 128 related-key 2
64
2
127.28
impossible differential [11]
full round 128 related-key 2
64
2
127.28
impossible differential
(this paper)
2 SPECIFICATION OF
ALGORITHM
2.1 Notations
The following notations and operations are used to de-
scribe the algorithm and its cryptanalysis.
⊕: XOR
⊞: addition mod 2
8|
≪ i: i−bit left rotation
M
i
: i
th
byte of master key
M
j
i
: j
th
bit of i
th
byte of master key
X
i
: variable of round i
X
i, j
: the j
th
byte of X
i
K
i
: the i
th
subkey
W
i
: the i
th
byte of whitening key
△M
i
: differential in byte i of master key
e
i, j,k
: indicating nonzero differential in
bit positions i, j and k of a byte and
zero differential for the rest
e
i∼
: zero differential in bit positions 0
till i − 1 and nonzero differential in
bit position i and unknown differen-
tial for the rest
z
i∼
: zero differential in bit positions 0
till i − 1 and unknown differential
for the rest
?: an arbitrary bit or byte value
2.2 The Description of HIGHT
Hight is a 32-round block cipher with 64-bit block
size and 128-bit master key which uses an unbalanced
Feistel network as its building blocks (Hong and
et al., 2006). An Initial Transformation (IT) together
with input whitening keys and a Final Transformation
(FT) together with output whitening keys are applied
to plaintext and output of the last round respectively.
The encryption process of the HIGHT consists of fol-
lowing steps in turn: key schedule, initial transform,
round function and, final transformation. The expla-
nation of decryption process is left out because of its
similarity to encryption process.
2.2.1 Key Schedule
The key schedule of the HIGHT consists of two
subroutines for generating 8 whitening key bytes
W
0
, ..., W
7
, and 128 subkey bytes K
0
, ..., K
127
. It uses
the bytes of master key based on the Table 2. The
detail of the key schedule of the HIGHT is found in
(Hong and et al., 2006).
2.2.2 Initial Transformation
In initial transformation four whitening keys
W
0
, ..., W
3
are used to map a plaintext P to the input
of the first round function.
Initial Transformation(P, X
0
, W
3
, W
2
, W
1
, W
0
)
{
X
0,0
← P
0
⊞W
0
;X
0,1
← P
1
;X
0,2
← P
2
⊞W
1
;X
0,3
← P
3
;
X
0,4
← P
4
⊞W
2
;X
0,5
← P
5
;X
0,6
← P
6
⊞W
3
;X
0,7
← P
7
}
2.2.3 Round Function
One round of the HIGHT is shown in Figure 1.
The equations of the round function are as follow.
Round Function(X
i
, X
i+1
, K
4i+3
, K
4i+2
, K
4i+1
, K
4i
)
{
X
i+1,1
← X
i,0
;X
i+1,3
← X
i,2
;X
i+1,5
← X
i,4
;X
i+1,7
← X
i,6
;
X
i+1,0
= X
i,7
⊕ (F
0
(X
i,6
)) ⊞ K
4i+3
X
i+1,2
= X
i,1
⊕ (F
1
(X
i,0
)) ⊞ K
4i+2
X
i+1,4
= X
i,3
⊕ (F
0
(X
i,2
)) ⊞ K
4i+1
X
i+1,6
= X
i,5
⊕ (F
1
(X
i,4
)) ⊞ K
4i
}
Round function of the HIGHT uses two building
block functions F
0
and F
1
:
SECRYPT2013-InternationalConferenceonSecurityandCryptography
538
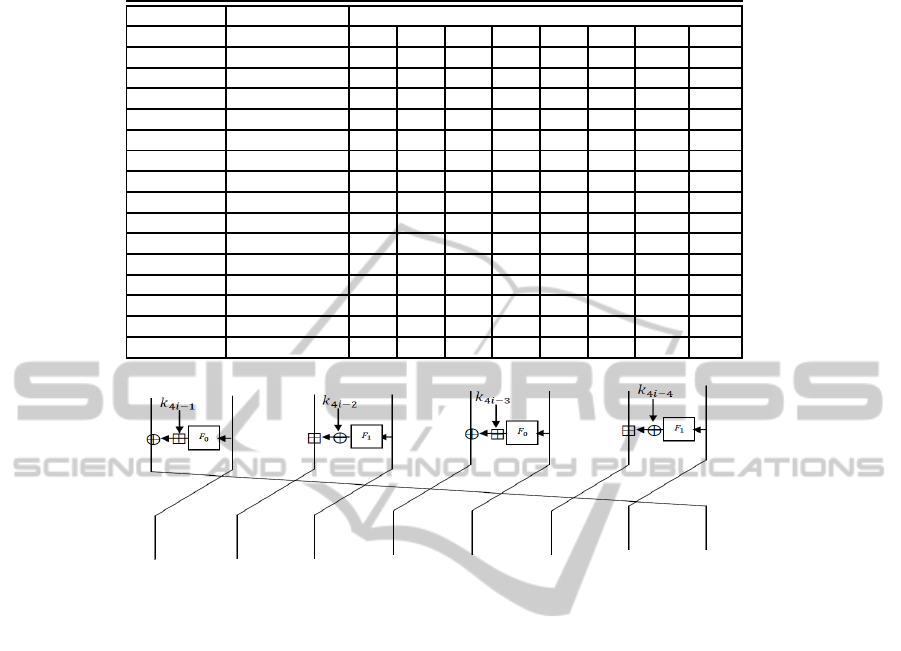
Table 2: Relationships between master key and subkeys.
Master key Whitening key Subkeys
M
15
W
3
K
15
K
24
K
41
K
58
K
75
K
92
K
109
K
126
M
14
W
2
K
14
K
31
K
40
K
57
K
74
K
91
K
108
K
125
M
13
W
1
K
13
K
30
K
47
K
56
K
73
K
90
K
107
K
124
M
12
W
0
K
12
K
29
K
46
K
63
K
72
K
89
K
106
K
123
M
11
- K
11
K
28
K
45
K
62
K
79
K
88
K
105
K
122
M
10
- K
10
K
27
K
44
K
61
K
78
K
95
K
104
K
121
M
9
- K
9
K
26
K
43
K
60
K
77
K
94
K
111
K
120
M
8
- K
8
K
25
K
42
K
59
K
76
K
93
K
110
K
127
M
7
- K
7
K
16
K
33
K
50
K
67
K
84
K
101
K
118
M
6
- K
6
K
23
K
32
K
49
K
66
K
83
K
100
K
117
M
5
- K
5
K
22
K
39
K
48
K
65
K
82
K
99
K
116
M
4
- K
4
K
21
K
38
K
55
K
64
K
81
K
98
K
115
M
3
W
7
K
3
K
20
K
37
K
54
K
71
K
80
K
97
K
114
M
2
W
6
K
2
K
19
K
36
K
53
K
70
K
87
K
96
K
113
M
1
W
5
K
1
K
18
K
35
K
52
K
69
K
86
K
103
K
112
M
0
W
4
K
0
K
17
K
34
K
51
K
68
K
85
K
102
K
119
Figure 1: One encryption round of the HIGHT.
F
0
(x) = x ≪ 1⊕ x ≪ 2⊕ x ≪ 7,
F
1
(x) = x ≪ 3⊕ x ≪ 4⊕ x ≪ 6.
2.2.4 Final Transformation
The final transformation applies four whitening key
bytes W
4
, W
5
, W
6
, W
7
and mixing operation on output
of the last round to produce ciphertext.
Final Transformation(X
32
, C, W
7
, W
6
, W
5
, W
4
)
{
C
0
← X
32,1
⊞ W
4
;C
1
← X
32,2
;
C
2
← X
32,2
⊕W
5
;C
3
← X
32,4
;
C
4
← X
32,5
⊞ W
6
;C
5
← X
32,6
;
C
6
← X
32,7
⊕W
7
;C
7
← X
32,0
}
3 CONDITIONAL ATTACK ON
THE FULL-ROUND HIGHT
In this section, an improved related-key impossible
differential attack on full-round algorithm is intro-
duced. The attack is mounted on a specific 24-round
differential characteristic used for filtering the wrong
subkeys. The details of the mentioned differential
characteristic is depicted in Tables 3 to 6.
3.1 24-round Characteristic
The 24-round characteristic is derived by imposing a
condition on 3 key bits of M
4
: M
0
4
= M
1
4
= M
6
4
= 0.
Imposing this condition causes that the differentials
in byte positions 1 and 7 in round 29 of Table 5 re-
sults byte differential at position 6 in round 28 in the
same table with probability one (using inverse char-
acteristic). Introducing this condition with the proba-
bility of 2
−3
has no impact on the 24-round key dif-
ferential characteristic which means that the 23-round
impossible differential path in (Ozen et al., 2009)
is increased by one round. In this case 125 key bits
must be recovered and the corresponding related-key
impossible differential characteristic under key differ-
ential (δM
15
, δM
14
, ..., δM
8
= 80
x
, ...δM
0
) is covering
rounds 6-29 of the HIGHT:
(0, 0, 0, 0, 80
x
, 0, 0, 0) 9 (80
x
, 0, 0, 0, 0, 0, 0, e
1,2,7∼
)
Forward and backward differential characteristic
paths are shown in Tables 4 and 5 and impossible dif-
ferential is occurred at the 17
th
round of the algorithm.
Related-keyImpossibleDifferentialCryptanalysisofFull-roundHIGHT
539
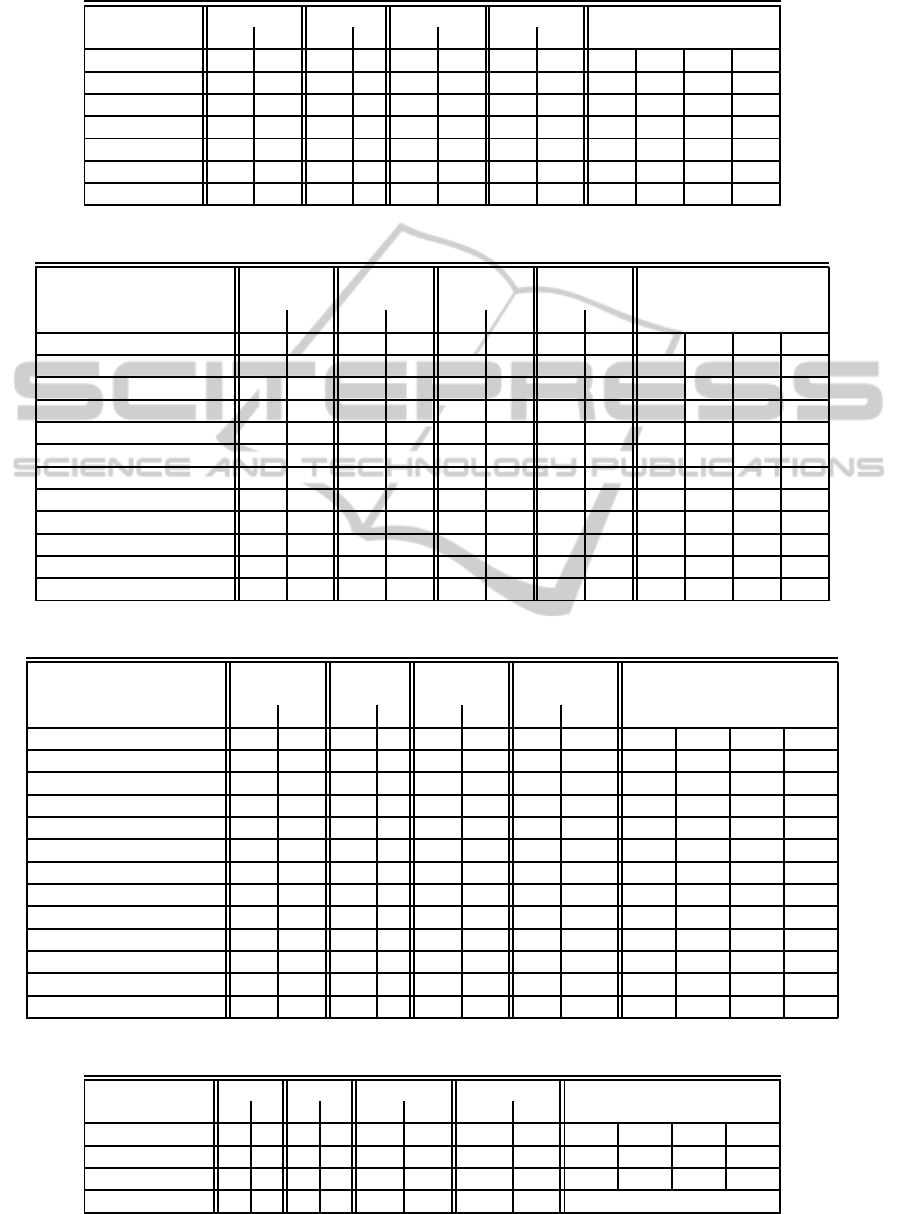
Table 3: Forward path of plaintexts satisfying the conditions of impossible differential characteristic.
Forward filter B
3
B
2
B
1
B
0
Subkeys
7 6 5 4 3 2 1 0
IT ? e
0∼
80
x
0 ? ? ? ? W
3
W
2
W
1
W
0
0 ? e
0∼
80
x
0 ? ? ? ? K
3
K
2
K
1
K
0
1 ? e
0∼
80
x
0 ? ? ? ? K
7
K
6
K
5
K
4
2 80
x
0 0 0 ? ? ? z
1∼
K
11
K
10
K
9
K
8
3 0 0 0 0 ? ? z
1∼
80
x
K
15
K
14
K
13
K
12
4 0 0 0 0 ? e
1∼
80
x
0 K
19
K
18
K
17
K
16
5 0 0 0 0 e
1∼
80
x
0 0 K
23
K
22
K
21
K
20
Table 4: Forward path of impossible differential characteristic.
Forward impossible dif-
ferential characteristic
B
3
B
2
B
1
B
0
Subkeys
7 6 5 4 3 2 1 0
6 0 0 0 0 80
x
0 0 0 K
27
K
26
K
25
K
24
7 0 0 0 0 0 0 0 0 K
31
K
30
K
29
K
28
8 0 0 0 0 0 0 0 0 K
35
K
34
K
33
K
32
9 0 0 0 0 0 0 0 0 K
39
K
38
K
37
K
36
10 0 0 0 0 0 0 0 0 K
43
K
42
K
41
K
40
11 0 80
x
0 0 0 0 0 0 K
47
K
46
K
45
K
44
12 80
x
0 0 0 0 0 0 e
0∼
K
51
K
50
K
49
K
48
13 0 0 0 0 0 ? e
0∼
80
x
K
55
K
54
K
53
K
52
14 0 0 0 ? ? e
0∼
80
x
0 K
59
K
58
K
57
K
56
15 0 ? ? ? e
0∼
80
x
0 80
x
K
63
K
62
K
61
K
60
16 ? ? ? e
0∼
80
x
e
0∼
80
x
? K
67
K
66
K
65
K
64
17 ? ? e
0∼
? e
0∼
? ? ? K
71
K
70
K
69
K
68
Table 5: Backward path of impossible differential characteristic.
Backward impossible dif-
ferential characteristic
B
3
B
2
B
1
B
0
Subkeys
7 6 5 4 3 2 1 0
17 ? e
0∼
80
x
0 ? ? ? ? K
71
K
70
K
69
K
68
18 e
0∼
80
x
0 0 ? ? ? ? K
75
K
74
K
73
K
72
19 80
x
0 0 0 ? ? ? e
0∼
K
79
K
78
K
77
K
76
20 0 0 0 0 ? ? e
0∼
80
x
K
83
K
82
K
81
K
80
21 0 0 0 0 ? e
0∼
80
x
0 K
87
K
86
K
85
K
84
22 0 0 0 0 e
0∼
80
x
0 0 K
91
K
90
K
89
K
88
23 0 0 0 0 80
x
0 0 0 K
95
K
94
K
93
K
22
24 0 0 0 0 0 0 0 0 K
99
K
98
K
97
K
96
25 0 0 0 0 0 0 0 0 K
103
K
102
K
101
K
100
26 0 0 0 0 0 0 0 0 K
107
K
106
K
105
K
104
27 0 0 0 0 0 0 0 0 K
111
K
110
K
109
K
108
28 0 80
x
0 0 0 0 0 0 K
115
K
114
K
113
K
112
29 80
x
0 0 0 0 0 0 e
0,1,6
K
119
K
118
K
117
K
116
Table 6: Backward path of ciphertexts satisfying the conditions of impossible differential characteristic.
Backward filter B
3
B
2
B
1
B
0
Subkeys
7 6 5 4 3 2 1 0
30 0 0 0 0 0 e
1∼
e
0,1,6
80
x
K
123
K
122
K
121
K
120
31 0 0 0 ? e
1∼
e
0∼
80
x
0 K
127
K
126
K
125
K
124
FT 0 ? ? ? e
0∼
80
x
0 0 W
7
W
6
W
5
W
4
C 0 0 ? ? ? e
0∼
80
x
0
SECRYPT2013-InternationalConferenceonSecurityandCryptography
540
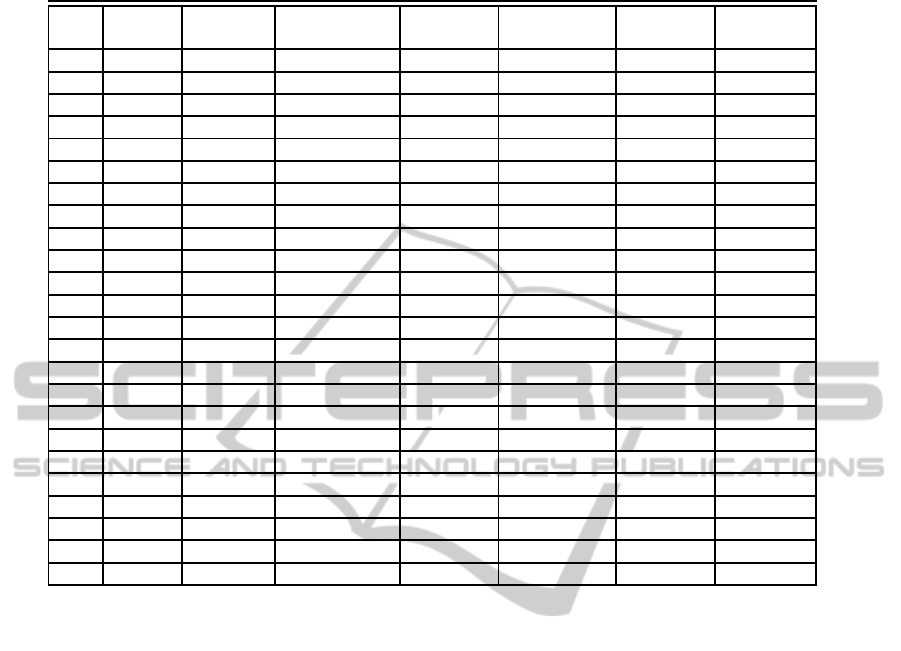
Table 7: Key filtering process-in this table by imposing conditions on M
4
all subkeys will be involved together.
Step Guess Subkeys Bytes Check No. of Remaining Time
to be used to be extracted (bitwise) bit conditions efforts complexity
1 M
13
, M
1
W
1
, K
1
3,4 of X
1
(?, 0) 8 2
69
2
87
2 M
0
, M
12
W
0
, K
0
1,2 of X
1
- - 2
69
2
79
3 M
5
K
5
3,4 of X
2
(?, 0) 8 2
61
2
95
4 M
2
, M
15
W
6
, K
126
4, 5 of X
31
(?, 0) 8 2
53
2
71
5 M
14
W
5
, K
125
2, 3 of X
31
(e
0∼
, e
1∼
) 2 2
51
2
63
6 M
10
K
121
2, 3 of X
30
(e
0∼
, 0) 8 2
43
2
77
7 M
3
W
3
, K
3
0, 7 of X
1
- - - 2
63
8 M
4
K
4
1, 2 of X
2
- - - 2
66
9 M
9
K
9
3, 4 of X
3
(?, 0) 8 2
35
2
82
10 - W
49
, K
124
0, 1 of X
31
- - - 2
47
11 - K
120
0, 1 of X
30
(80
x
, e
0,1,6
) 7 2
28
2
61
12 - K
116
0, 1 of X
29
(0, e
0,1,6
) 6 2
22
2
70
13 - W
2
, K
2
5, 6 of X
1
- - - 2
32
14 M
7
K
7
0, 7 of X
2
- - - 2
48
15 M
8
K
8
1, 2 of X
3
- - - 2
64
16 - K
13
3, 4 of X
4
(?, 0) 8 2
14
2
85
17 M
6
K
6
2, 6 of X
2
- - - 2
40
18 M
11
K
11
0, 7 of X
3
- - - 2
56
19 - K
12
1, 2 of X
4
- - - 2
80
20 - K
17
3, 4 of X
5
(e
1∼
, 0) 8 2
6
2
104
21 - K
10
5, 6 of X
3
- - - 2
48
22 - K
15
0, 7 of X
4
- - - 2
72
23 - K
16
1, 2 of X
5
- - - 2
96
24 - K
21
3, 4 of X
6
(80
X
, 0) 7 - 2
101
3.2 Key Filtration
In this section, the key filtering procedure is ex-
plained. Removing impossible keys procedureis done
in two steps. At first the required number of chosen
plaintexts are produced to encrypt and then the wrong
keys are discarded by guessing the key bits based on
the texts.
The structure of required plaintext has been shown
in Table 3. Required conditions are imposed on the
plaintext to fulfill 24-round related-key impossible
differential characteristic and the corresponding keys
will be eliminated from whole key space. Similarly in
Table 6 by choosing ciphertexts we discard those keys
that will satisfy in the second portion of the impossi-
ble differential characteristic as well as the right keys
in this process. This procedure is operated as follows.
3.2.1 Step 1
2
17
plaintext structures are selected where each con-
tains 2
47
texts: The fourth and fifth byte and the first
bit of the sixth byte of each structure are assigned to
constant values. The other bit positions get all pos-
sible values to satisfy the conditions of the first row
of Table 3. Number of all possible plaintext pairs for
encryption is evaluated as the following:
2
47
2
2
17
≈ 2
110
(1)
3.2.2 Step 2
Encrypt all plaintexts P
i
(P
′
i
) under key
K(K
′
i
) to get ciphertexts C
i
(C
′
i) in which
K ⊕ K
′
= (0, 0, ..., 0, 80
x
, 0, ..., 0) and C ⊕ C
′
=
(0, 0, ∗, ∗, ∗, e
0∼
, 80
x
, 0) (see differentials in row FT
of Table 6). In this step 33 bits are filtered and 2
77
plaintext pairs are left.
3.2.3 Step 3
The procedure of filtering the wrong keys is shown
step by step in Table 7. In step 24 from Table 7, a
guessed related key is discarded if a pair satisfies the
related-key impossible differential characteristic. As
there is a condition on 7 bits in step 24, each plain-
text pair will suggest 2
−7
wrong keys and at the end
2
125
(1 − 2
−7
)
2
6
= 2
124.276
keys are remained. Time
and memory complexities of this scenario is about
2
104.177
and 2
101
respectivelyand it requires data com-
plexity corresponding to block size i.e., 2
64
. This can
Related-keyImpossibleDifferentialCryptanalysisofFull-roundHIGHT
541

be derived simply by calculating the required com-
plexity for each of 24 steps.
4 EXTENSION OF THE ATTACK
AND CONCLUSIONS
In 3, all of the impossible keys of the attack
has been suggested based on the assumption K
4
=
(?0????00) which forces 3 bits of K
4
to be zero.
Now we remove this condition and extend the at-
tack. In the new scenario, we guess a differential
α = (0, 0, ..., (0z0000yx), ...0) and we assign it to two
chosen keys K and K
′
with non-zero common bits (in
positions 0, 1 and, 6 of K
4
). By guessing 2
3
bits
from α the corresponding space of rejected keys is
mapped to the one of 3 so that K ⊕ α = (?, ?, ..., K
4
=
(?0????00), ..., ?) and (K ⊕ α ⊕ β = (?, ?, ..., K
′
4
=
(?0????00), ..., ?). By trying all possible values of
α , the 24-step process of Section 3 is repeated to
discard 2
3
2
125
(1− 2
−7
)
2
6
= 2
127.276
number of keys.
Regarding to the discussions in Section 3, the whole
exhaustive search space of key is reduced to 2
127.276
which means the reduction in the entropy by 0.724.
The computational complexity of the key filtering is
around 2
3
2
104.177
= 2
107.177
. Also it requires data
complexity around 2
64
and memory complexity about
2
3
2
101
= 2
104
.
REFERENCES
Biham, E., Biryukov, A., and Shamir, A. (1999). Miss in
the middle attacks on idea and khufu. In FSE 1999,
LNCS, vol. 1636. Springer, Heidelberg.
Biham, E., Biryukov, A., and Shamir, A. (2005). Crypt-
analysis of skipjack reduced to 31 rounds using im-
possible differentials. In Journal of Cryptology 18(4).
Springer, Heidelberg.
Biham, E. and Shamir, A. (1991). Differential cryptanalysis
of des-like cryptosystems. In CRYPTO 1990, LNCS,
vol. 537. Springer, Heidelberg.
Hong, D. and et al. (2006). Hight: A new block cipher suit-
able for low-resource device. In CHES 2006, LNCS,
vol. 4249. Springer, Heidelberg.
Hong, D., Koo, B., and kwon, D. (2011). Related-key at-
tack on the full hight. In ICISC 2010, LNCS 6829.
Springer, Heidelberg.
Hong, D., Koo, B., and kwon, D. (2012). Biclique attack
on the full hight. In ICISC 2011, LNCS, vol. 7259.
Springer, Heidelberg.
Lu, J. (2007). Cryptanalysis of reduced versions of the hight
block cipher from ches 2006. In ICISC 2007, LNCS,
vol. 4817. Springer, Heidelberg.
Lucks, S. (2002). The saturation attacka bait for twofish. In
FSE 2001, LNCS, vol. 2355. Springer, Heidelberg.
Matsui, M. (1994). Linear cryptanalysis method for des
cipher. In EUROCRYPT 1993, LNCS, vol. 765.
Springer, Heidelberg.
Ozen, O., Vaici, K., Tezcan, C., and Kocair, C. (2009).
Lightweight block cipher revisited: Cryptanalysis of
reduced round present and hight. In CANS 2009,
LNCS, vol. 5888. Springer, Heidelberg.
Zhang, P., Sun, B., and Li, C. (2009). Saturation attack on
the block cipher hight. In ACISP 2009, LNCS, vol.
5594. Springer, Heidelberg.
SECRYPT2013-InternationalConferenceonSecurityandCryptography
542
