
An Efficient Approach to Assessing the Risk of Zero-Day Vulnerabilities
∗
Massimiliano Albanese
1
, Sushil Jajodia
1,2
, Anoop Singhal
3
and Lingyu Wang
4
1
Center for Secure Information Systems, George Mason University, 4400 University Dr, Fairfax, VA 22030, U.S.A.
2
The MITRE Corporation, 7515 Colshire Drive, McLean, VA 22102, U.S.A.
3
Computer Security Division, NIST, 100 Bureau Dr, Gaithersburg, MD 20899, U.S.A.
4
Concordia Institute for Information Systems Engineering, Concordia University,
1515 Sainte-Catherine St W, Montreal, QC H3G 2W1, Canada
Keywords:
Zero-Day Vulnerabilities, Vulnerability Analysis, Attack Graphs.
Abstract:
Computer systems are vulnerable to both known and zero-day attacks. Although known attack patterns can
be easily modeled, thus enabling the development of suitable hardening strategies, handling zero-day vulner-
abilities is inherently difficult due to their unpredictable nature. Previous research has attempted to assess the
risk associated with unknown attack patterns, and a suitable metric to quantify such risk, the k-zero-day safety
metric, has been defined. However, existing algorithms for computing this metric are not scalable, and as-
sume that complete zero-day attack graphs have been generated, which may be unfeasible in practice for large
networks. In this paper, we propose a set of polynomial algorithms for estimating the k-zero-day safety of
possibly large networks efficiently, without pre-computing the entire attack graph. We validate our approach
through experiments, and show that the proposed algorithms are computationally efficient and accurate.
1 INTRODUCTION
In today’s networked systems, attackers can lever-
age complex interdependencies among network con-
figurations and vulnerabilities to penetrate seemingly
well-guarded networks. Besides well-known weak-
nesses, attackers may leverage unknown (zero-day)
vulnerabilities, which even developers are not aware
of. In-depth analysis of network vulnerabilities must
consider attacker exploits not merely in isolation, but
in combination. Attack graphs reveal such threats by
enumerating potential paths that attackers can take to
penetrate networks (Sheyner et al., 2002; Ammann
et al., 2002). This helps determine whether a given
set of network hardening measures provides safety
of given critical assets. However, attack graphs can
only provide qualitative results (i.e., secure or inse-
cure), and this rendersresulting hardening recommen-
dations ineffective or far from optimal, as illustrated
by the example discussed in Section 3.1.
∗
The work presented in this paper is supported in part
by the National Institutes of Standard and Technology un-
der grant number 70NANB12H236, by the Army Research
Office under MURI award number W911NF-09-1-0525,
and by the Office of Naval Research under award number
N000141210461.
To address these limitations, traditional efforts
on network security metrics typically assign numeric
scores to vulnerabilities as their relative exploitabil-
ity or likelihood, based on known facts about each
vulnerability. However, this approach is clearly not
applicable to zero-day vulnerabilities due to the lack
of prior knowledge or experience. In fact, a major
criticism of existing efforts on security metrics is that
zero-day vulnerabilities are unmeasurable due to the
less predictablenature of both the process of introduc-
ing software flaws and that of discoveringand exploit-
ing vulnerabilities (McHugh, 2006). Recent work ad-
dresses the above limitations by proposing a security
metric for zero-day vulnerabilities, namely, k-zero-
day safety (Wang et al., 2010). Intuitively, the metric
is based on the number of distinct zero-day vulner-
abilities that are needed to compromise a given net-
work asset. A larger such number indicates relatively
more security, because it will be less likely to have
a larger number of different unknown vulnerabilities
all available at the same time, applicable to the same
network, and exploitable by the same attacker. How-
ever, as shown in (Wang et al., 2010), the problem of
computing the exact value of k is intractable. More-
over, (Wang et al., 2010) assumes the existence of a
complete attack graph, but, unfortunately, generating
207
Albanese M., Jajodia S., Singhal A. and Wang L..
An Efficient Approach to Assessing the Risk of Zero-Day Vulnerabilities.
DOI: 10.5220/0004530602070218
In Proceedings of the 10th International Conference on Security and Cryptography (SECRYPT-2013), pages 207-218
ISBN: 978-989-8565-73-0
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

attack graphs for large networks is usually infeasible
in practice (Noel and Jajodia, 2004). These facts com-
prise a major limitation in applying this metric or any
other similar metric based on attack graphs.
In this paper, we propose a set of efficient solu-
tions to address this limitation and thus enable zero-
day analysis of practical importance to be applied to
networks of realistic sizes. Therefore, the major con-
tribution of this work is to provide a practical solution
to a problem which was previously considered impos-
sible. We start from the problem of deciding whether
a given network asset is at least k-zero-day safe for a
given value of k (Wang et al., 2010), but then we go
beyond this basic problem and provide a more com-
plete analysis. First, we drop the assumption that the
zero-day vulnerability graph has been precomputed,
and combine on-demand attack graph generation with
the evaluation of k-zero-day safety. Second, we iden-
tify an upper bound on the value of k using a heuristic
algorithm that integrates attack graph generation and
zero-day analysis. Third, when the upper bound on
k is below an admissible threshold, we compute the
exact value of k by reusing the computed partial at-
tack graph. Section 4 formally states the three related
problems we are addressing in this paper, and shows
their role in the overall process of assessing the risk
of zero-day vulnerabilities. To the best of our knowl-
edge, this is the first attempt to define a comprehen-
sive and efficient approach to zero-day analysis.
The paper is organized as follows. Section 2 dis-
cusses related work. Section 3 recalls some prelim-
inary definitions and provides a motivating example.
Then Section 4 discusses the limitations of previous
approaches and provides a formal statement of the
problems addressed in our work. Section 5 describes
in detail our approach to efficient evaluation of k zero-
day safety. Finally, Section 6 reports experimental re-
sults, and Section 7 gives some concluding remarks
and indicates further research directions.
2 RELATED WORK
Existing standardization efforts, such as the Common
Vulnerability Scoring System (CVSS) (Mell et al.,
2006) and the Common Weakness Scoring System
(CWSS) (The MITRE Corporation, 2011), provide
standard ways for security analysts and vendors to
rank known vulnerabilities or software weaknesses
using numerical scores. These efforts provide a
practical foundation for research on security met-
rics, but are designed for individual vulnerabilities
and do not address the combined effect of multiple
vulnerabilities. Early work on security metrics in-
clude a Markov model-based metric for estimating
the time and efforts required by adversaries (Dacier,
1994), and a metric based on lengths of shortest at-
tack paths (Phillips and Swiler, 1998). The main lim-
itation of these approaches is that they do not consider
the relative severity or likelihood of different vulner-
abilities. Anther line of work adapts the PageRank al-
gorithm to rank states in an attack graph based on the
relative likelihood of attackers’ reaching these states
when they progress along different paths in a random
fashion (Mehta et al., 2006). Other recent work uses
specially marked attack trees (Balzarotti et al., 2005)
or more expressive attack graphs (Pamula et al., 2006)
in order to find the easiest attack paths. A Mean
Time-to-Compromise metric based on the predator
state-space model (SSM) captures the average time
required to compromise network assets (Leversage
and Byres, 2008). A probabilistic approach defines
a network security metric as attack probabilities and
derives such probabilities from CVSS scores (Wang
et al., 2008). Several important issues in calculating
probabilistic security metrics, such as dependencies
between attack sequences and cyclic structures, are
addressed in (Homer et al., 2009).
Most existing work on network security met-
rics has focused on previously known vulnerabilities
(McHugh, 2006). A few exceptions include an em-
pirical study on the total number of zero-day vulner-
abilities available on a single day (McQueen et al.,
2009), a study on the popularity of zero-day vulnera-
bilities (Greenberg, 2012), and an empirical study on
software vulnerabilities’ life cycles (Shahzad et al.,
2012). Another recent effort ranks different applica-
tions by the relative severity of having one zero-day
vulnerability in each application (Ingols et al., 2009),
which has a different focus than our work. Closest
to our work, recent work on k-zero-day safety defines
a metric based on the number of potential unknown
vulnerabilities in a network (Wang et al., 2010).
In this paper, we address the complexity issues
associated with the metric proposed in (Wang et al.,
2010), and propose a set of polynomial algorithms for
estimating the k-zero-day safety of possibly large net-
works efficiently. The proposed zero-day attack graph
model borrowsthe compact model given in (Ammann
et al., 2002) – based on the monotonicity assumption
– while incorporating zero-day vulnerabilities.
3 PRELIMINARIES
Attack graphs represent prior knowledge about vul-
nerabilities, their dependencies, and network connec-
tivity. With a monotonicity assumption, an attack
SECRYPT2013-InternationalConferenceonSecurityandCryptography
208

graph can record the dependencies among vulnerabil-
ities and keep attack paths implicitly without losing
any information. The resulting attack graph has no
duplicate vertices and hence has a polynomial size in
the number of vulnerabilities multiplied by the num-
ber of connected pairs of hosts.
Definition 1 (Attack Graph). Given a set of exploits
E, a set of security conditions C, a require relation
R
r
⊆ C× E, and an imply relation R
i
⊆ E ×C, an at-
tack graph G is the directed graph G = (E ∪C, R
r
∪
R
i
), where E ∪C is the vertex set and R
r
∪ R
i
the edge
set. For an exploit e, we call the conditions related
to e by R
r
and R
i
as its pre- and post-conditions, de-
noted using functions pre : E → 2
C
and post : E → 2
C
,
respectively.
We denote an exploit as a triple hv,h
s
,h
d
i, indi-
cating an exploitation of vulnerability v on the desti-
nation host h
d
, initiated from the source host h
s
. A
security condition is a pair hc,h
d
i – that indicates a
satisfied security-related condition c on host h
d
, such
as the existence of a vulnerability – or a pair hh
s
,h
d
i
– that indicates connectivity between hosts h
s
and h
d
.
Initial conditions are a special subset of security con-
ditions that are initially satisfied, whereas intermedi-
ate conditions are those that can only be satisfied as
post-conditions of some exploits.
Definition 2 (Initial Conditions). Given an attack
graph G = (E ∪ C,R
r
∪ R
i
), initial conditions refer
to the subset of conditions C
i
= {c ∈ C|∄e ∈ E s.t.
(e,c) ∈ R
i
}, whereas intermediate conditions refer to
the subset C\C
i
.
3.1 Zero-Day Attack Model
The very notion of unknown zero-day vulnerability
means we cannot assume any vulnerability-specific
property, such as the likelihood or severity. There-
fore, our zero-day vulnerability model is based on fol-
lowing generic properties that are common to most
vulnerabilities. Specifically, a zero-day vulnerability
is a vulnerability whose details are unknown except
that its exploitation requires a network connection be-
tween the source and destination hosts, a remotely ac-
cessible service on the destination host, and that the
attacker already has a privilege on the source host.
In addition, we assume that the exploitation can po-
tentially yield any privilege on the destination host.
These assumptions intend to depict a worst-case sce-
nario about the pre- and post-conditions of a zero-day
exploit, and are formalized as the first type of zero-
day exploit in Definition 3, whereas the second type
represents subsequent privilege escalation.
Definition 3 (Zero-Day Exploit). We define two types
of zero-day exploits,
• for each remote service s, we define a zero-day
vulnerability v
s
such that the zero-day exploit
hv
s
,h,h
′
i has three pre-conditions, hs,h
′
i (exis-
tence of service), hh, h
′
i (connectivity), and hp,hi
(attacker’s existing privilege); this zero-day ex-
ploit has one post-condition hp
′
,h
′
i where p
′
is
the privilege of service s on h
′
.
• for each privilege p, we define a zero-day vulner-
ability v
p
such that the zero-day exploit hv
p
,h,hi
has its pre-conditions to include all privileges of
remote services on h, and its post-condition to be
p on h.
We use E
0
and C
0
to denote the set of all zero-day ex-
ploits and the set of all their pre- and post-conditions
respectively, and we extend the functions pre() and
post() accordingly.
We are now ready to assemble all known and
zero-day exploits via their common pre- and post-
conditions into a zero-day attack graph.
Definition 4 (Zero-Day Attack Graph). Given an at-
tack graph G = (E ∪C,R
r
∪ R
i
), a set E
0
of zero-day
exploits, a set C
0
of pre and post-conditions of ex-
ploits in E
0
, a zero-day attack graph G
∗
is the directed
graph G
∗
= (E
∗
∪C
∗
,R
∗
r
∪ R
∗
i
), where E
∗
= E ∪ E
0
,
C
∗
= C ∪C
0
, R
∗
r
= R
r
∪ {(c,e) | e ∈ E
0
∧ c ∈ pre(e)},
and R
∗
i
= R
i
∪ {(e,c) | e ∈ E
0
∧ c ∈ post(e)}.
Figure 1 shows a simple network configuration in-
cluding three hosts. Host 0 is the user’s machine used
to launch attacks, whereas host 1 and host 2 are ma-
chines within the perimeter of the enterprise network
we are seeking to protect. Host 1 provides an HTTP
service (http) and a secure shell service (ssh), whereas
host 2 provides only ssh. The firewall allows traffic to
and from host 1, but only connections originated from
host 2. In this example, we assume the main security
concern is over the root privilege on host 2. Clearly,
if all the services are free of known vulnerabilities,
a vulnerability scanner or attack graph will both lead
to the same conclusion, that is, the network is secure
(an attacker on host 0 can never obtain the root privi-
lege on host 2), and no additional network hardening
effort is necessary. However, we may reach a differ-
ent conclusion by hypothesizing the presence of zero-
day vulnerabilities and considering how many distinct
zero-day exploits the network can resist.
Specifically, the zero-day attack graph of this ex-
ample is depicted in Figure 2, where each triple in-
side an oval denotes a zero-day exploit and a pair de-
notes a condition. In this attack graph, we can ob-
serve three sequences of zero-day exploits leading to
root(2). First, an attacker on host 0 can exploit a zero-
day vulnerability in the firewall (e.g., a weak pass-
word in its Web-base remote administration interface)
AnEfficientApproachtoAssessingtheRiskofZero-DayVulnerabilities
209

host 0
host 1
http
ssh
host 2
ssh
Figure 1: Example of network configuration.
<user,0>
<v_firewall,0,F> <v_http,0,1> <v_ssh,0,1>
<v_ssh,0,2>
<firewall,F> <0,F> <0,1> <ssh,1>
<user,1>
<v_root,1,1><v_ssh,1,2>
<root,1>
<root,F> <0,2>
<http,1>
<ssh,2> <1,2>
<user,2>
<v_root,2,2>
<root,2>
Figure 2: Example of zero-day attack graph.
to re-establish the blocked connection to host 2 and
then exploit ssh on host 2, or the attacker can exploit
a zero-day vulnerability in either http or ssh on host 1
to obtain the user privilege and then, using host 1 as a
stepping stone, the attacker can further exploit a zero-
day vulnerability in ssh on host 2 to reach root(2).
Since this last sequence (ssh on host 1 and then ssh on
host 2) involves one zero-day vulnerability in the ssh
service on both hosts, this network can resist at most
one zero-day attack. Contrary to the previous belief
that further hardening this network is not necessary,
this zero-day attack graph shows that further harden-
ing may indeed improve the security. For example,
suppose we limit accesses to the ssh service on host 1
using a personal firewall or iptables rules, such that an
arbitrary host 0 cannot reach this service from the In-
ternet. We can then imagine that the new attack graph
will only include sequences of at least two different
zero-day vulnerabilities (e.g., the attacker must first
exploit the personal firewall or iptables rules before
exploiting ssh on host 1). This seemingly unneces-
sary hardening effort thus can help the network resist
one more zero-day attack.
4 PROBLEM STATEMENT
The exact algorithm for computing the k-zero-day
safety metric presented in (Wang et al., 2010) first
derives a logic proposition of each asset in terms of
exploits by traversing the attack graph backwards.
Each conjunctive clause in the disjunctive normal
form (DNF) of the derived proposition corresponds
to a minimal set of exploits that jointly compromise
the asset. The value of k can then be decided by ap-
plying the metric k0d() – which counts the number of
distinct zero-day vulnerabilities – to each such con-
junctive clause. Although the logic proposition can
be derived efficiently, converting it to its DNF may
incur an exponential explosion. In fact, the authors of
(Wang et al., 2010) show that the problem of comput-
ing the k-zero day safety metrics is NP-hard in gen-
eral, and then focus on the solution of a more prac-
tical problem. They claim that, for many practical
purposes, it may suffice to know that every asset in a
network is k-zero-day safe for a given value of k, even
though the network may in reality be k
′
-zero-day safe
for some unknown k
′
> k (note that determining k
′
is intractable). Then, they describe a solution whose
complexity is polynomial in the size of a zero-day at-
tack graph if k is a constant compared to this size.
However, there are cases in which it is not satisfac-
tory to just know k
′
> k, but more accurate estima-
tions or exact calculation of the value of k is desired.
Moreover, those analyses are all based on complete
zero-day attack graphs, but for really large networks,
it may even be infeasible to generate the zero-day at-
tack graph in the first place. The metric then becomes
impractical in such cases since there is little we can
say about the value of k.
The aforementioned intractability result means no
polynomial algorithm will likely exist for computing
the exact value of k. However, in this section we
show that a decision process may still allow secu-
rity administrators to obtain good estimations about
k, and to calculate the exact value of k when it is
practically feasible. Our main objectives are three-
fold. First, all the algorithms involved in the decision
process will be efficient and have polynomial com-
plexity. Second, all the algorithms will adopt an on-
demand approach to attack graph generation, which
will only generate partial attack graphs necessary for
the analysis. Third, subsequent algorithms will reuse
the partial attack graph already generated earlier in
the decision process, thus further improving the over-
all efficiency. With those optimizations, we can pro-
vide a better understanding of zero-day vulnerabili-
ties even for relatively large networks. Specifically, in
most practical scenarios, security administrators may
simply want to assess whether the network or specific
assets are secure enough. In such cases, knowing that
k is larger than or equal to a given lower bound l may
be sufficient. However, once it has been confirmed
that k > l, a security administrator may want to know
whether it is possible to compute the exact value of k.
Since the problem of computing the exact value of k
is intractable, this may only be possible for relatively
small values of k. Therefore, we need to estimate
whether k is less than a practical upper bound that
SECRYPT2013-InternationalConferenceonSecurityandCryptography
210

! "
Insufficient Security
Harden Network
# $ # $
%
Yes
I
nsu
f
f
icien
t
yes
Find exact
No
Start
End
Figure 3: Flowchart of the decision process.
represents available computational power. Finally, if
this is true, then we can proceed to calculate the ac-
tual value of k in an efficient way. In the following,
we formalize the three related problems that form the
basis of the above decision process. We describe a
solution to each of these problem in the next section.
Problem 1 (Lower Bound). Given a network N, a
goal condition c
g
, and a small integer l, determine
whether k ≥ l is true for N with respect to c
g
.
Our goal is to identify a lower bound on the value
of k. This problem is analogous to the practical prob-
lem addressed in (Wang et al., 2010), but we do not
assume the entire attack graph is available. We simply
assume that the network is defined in terms of initial
conditions C
i
and known and unknown exploits E
∗
.
Problem 2 (Upper Bound). Given a network N, a
goal condition c
g
, and an integer u, find an upper
bound u on the value of k with respect to c
g
.
Our goal is to identify an upper bound on the value
of k. We show that, using a heuristic approach, it is
feasible to compute a good upper bound in polyno-
mial time. If the value of u is below a threshold u
∗
, it
may then be feasible to compute the exact value of k.
Problem 3 (Exact Value). Given a network N, and a
goal condition c
g
such that l ≤ k ≤ u ≤ u
∗
is true for
N with respect to c
g
, find the exact value of k.
In other words, when the value of k is known to
be bounded and the upper bound is small enough, we
will compute the exact value of k, leveraging the up-
per bound u for pruning, and reusing the partial attack
graph generated during previous steps of the decision
process. Figure 3 shows the role of these three prob-
lems in the overall decision process.
5 PROPOSED SOLUTION
5.1 Solution for Problem 1
The existing solution for this problem assumes that
the entire zero-day attack graph is available (Wang
et al., 2010), which is impractical since generating
such an attack graph may be infeasible for large net-
works. The idea behind our solution is to combine an
exhaustive forward search of limited depth with par-
tial attack graph generation, so that only attack paths
with up to l zero-day vulnerabilities are generated and
evaluated using the metric. We use connectivity infor-
mation to hypothesize zero-day exploits (see Defini-
tion 3) and guide the generation of the graph.
Algorithm k0dLowerBound (Algorithm 1) takes
as input a set C
i
of initial conditions on hosts, the set
E
∗
of known and zero-day exploits, an integer l ∈ N
representing the desired lower bound on the value of
k, and a goal condition c
g
∈ C
∗
. It returns a partial
zero-day attack graph G = (E ∪C,R
r
∪R
i
), and a truth
value indicating whether k ≥ l.
For ease of presentation, we consider problems
with a single goal condition. The generalization to
the case where multiple target conditions need to be
considered at the same time is straightforward and is
discussed below. Given a set C
g
of goal conditions,
we can add a dummy exploit e
g
, such that e
g
has each
c
i
∈ C
g
as a precondition. Then, we can add a dummy
goal condition c
g
as the only postcondition of e
g
. It is
clear that the minimum number of zero-day exploits
needed to reach all the conditions in C
g
corresponds
to the minimum number of zero-day exploits needed
to reach the dummy goal condition c
g
. In fact, as c
g
is reachable only from the dummy exploit e
g
, all the
preconditions of e
g
must be satisfied, therefore all the
actual goal conditions in C
g
must be reached.
Lines 1-6 of algorithm k0dLowerBound simply
initialize the sets of conditions and exploits in the
partial attack graph, the set C
new
of newly satisfied
conditions, and the mapping π : E ∪ C → 2
2
E
which
associates each exploit or condition with a set of at-
tack paths leading to it, where an attack path is a set
of exploits. By default, π(c) =
/
0 for all c ∈ C
i
. The
set C
new
will initially contain all the initial conditions,
whereas in each subsequent iteration of the algorithm
it will contain the conditions implied by exploit vis-
ited in that iteration. The main loop at Lines 7-30
iterates until the goal condition is reached (Lines 22-
24) or the set of newly satisfied conditions becomes
empty – which means that no path with fewer than
l distinct zero-day vulnerabilities can reach the goal
condition. In the first case the algorithm returns false
(i.e., k < l), otherwise it returns true (i.e., k ≥ l).
Line 8 defines the set E
new
of unvisited exploits
reachable from C. An exploit is unvisited if at least
one of its preconditions is in C
new
. For each e ∈ E
new
,
Lines 10-12 add edges from all preconditions of e to
e itself, and Lines 13-14 compute partial attack paths
leading to and including e. Finally, Line 15 prunes all
attack paths with l or more distinct zero-day vulnerab-
AnEfficientApproachtoAssessingtheRiskofZero-DayVulnerabilities
211

Algorithm 1: k0dLowerBound(C
i
,E
∗
,l,c
g
).
Input: Set C
i
of initial conditions, set E
∗
of known and zero-day exploits, integer l ∈ N representing the desired lower bound on k, and goal condition c
g
∈ C
∗
.
Output: Partial zero-day attack graph G = (E ∪C, R
r
∪ R
i
), and a truth value indicating whether k ≥ l.
1: C ← C
i
2: E ←
/
0
3: C
new
← C
i
4: for all c ∈ C
i
do
5: π(c) ←
/
0
6: end for
7: while C
new
6=
/
0 do
8: E
new
← {e ∈ E | pre(e) ⊆ C∧ pre(e) ∩C
new
6=
/
0} // Unvisited exploits reachable from C
9: for all e ∈ E
new
do
10: for all c ∈ pre(e) do
11: R
r
← R
r
∪ {(c,e)} // Add an edge from c to e
12: end for
13: {c
1
,...,c
m
} ← {c ∈ C | (c,e) ∈ R
r
}
14: π(e) ← {P
1
∪ . . . ∪ P
m
∪ {e} | P
i
∈ π(c
i
)}
15: π(e) ← {P ∈ π(e) | k0d(P) < l) // Prune paths with l or more zero-day vulnerabilities
16: end for
17: C
new
←
/
0
18: for all e ∈ E
new
s.t. π(e) 6=
/
0 do
19: for all c ∈ post(e) do
20: R
i
← R
i
∪ {(e,c)} // Add an edge from e to c
21: C
new
← C
new
∪ {c}
22: if c ≡ c
g
then
23: return G, false
24: end if
25: π(c) ←
S
e∈E|(e,c)∈R
i
π(e)
26: end for
27: end for
28: C ← C∪C
new
29: E ← E ∪E
new
30: end while
31: return G,true
ilities. As an exploit needs all the preconditions to be
satisfied, an attack path for e is constructed by com-
bining an attack path to each precondition.
Once all the newly visited exploits have been pro-
cessed and added to the attack graph, the algorithm
considers the new conditions that are implied by such
exploits. For each e ∈ E
new
such that at least one par-
tial path reaching e has k0d(P) < l, and each condi-
tion c in post(e), Lines 20-21 add an edge from e to
c to the graph and update C
new
(which was reset on
Line 17), and Line 25 computes the set π(c) of attack
paths leading to c as the union of the sets of attack
paths leading to each of the exploit implying c, unless
c is the goal condition, in which case the algorithm
terminates.
Example 1. When applied to the example shown in
Figure 2, Algorithm k0dLowerBound (Algorithm 1)
will basically proceed by each horizontal level of
conditions and exploits, from top to bottom, until it
reaches the second level of exploits (i.e., hv
ssh
,0,2i,
hv
ssh
,1,2i, and hv
root
,1,1i). Suppose l is given to
be 2, then obviously all the paths up to now will be
pruned by Line 15 (since each of them includes two
distinct zero-day vulnerabilities, failing the condition
k0d(P) < l), except the path hv
ssh
,0,1i, hv
ssh
,1,2i
(which includes only one vulnerability v
ssh
). There-
fore, the next loop on Lines 18-27 will be skipped for
exploit hv
ssh
,0,2i and hv
root
,1,1i (meaning the par-
tial attack graph generation stops at those exploits),
but it continues from exploit hv
ssh
,1,2i (the final result
will depend on whether we assume hv
ssh
,1,2i directly
yields hroot,2i).
The complexity of Algorithm k0dLowerBound
(Algorithm 1) is clearly dominated by the steps for
extending the paths on Lines 13-15. Specifically, the
loop at Line 7 will run at most | C | times; the nested
loop at Line 9 will run | E | times; steps 13-15 will in-
volve at most | E |
l
paths each of which has maximum
possible length of | E |. Therefore, the overall com-
plexity is O(| C | · | E | · | E |
l
· | E |) = O(| C | · | E |
l
),
which is polynomial when l is given as a constant
(compared to attack graph size).
5.2 Solution for Problem 2
In this section, we propose a solution to Problem 2.
SECRYPT2013-InternationalConferenceonSecurityandCryptography
212

As we did for the previous algorithm, instead of build-
ing the entire attack graph, we only build the portions
of the attack graph that are most promising for find-
ing an upper bound on the value of k. In order to
avoid the exponential explosion of the search space –
which includes all the sets of exploits leading to the
goal condition – we design an heuristic algorithm that
maintains only the best partial paths with respect to
the k0d metric.
Algorithm k0dU pperBound (Algorithm 2) builds
the attack graph forward, starting from initial con-
ditions. A key advantage of building the attack
graph forward is that intermediate solutions are in-
deed estimates of the upper bound on k for interme-
diate conditions. In fact, in a single pass, algorithm
k0dUpperBound can estimate an upper bound on k
with respect to any condition in C. To limit the ex-
ponential explosion of the search space, intermedi-
ate solutions can be pruned – based on some pruning
strategy – whereas this would not be possible for an
algorithm building the attack graph backwards.
The algorithm takes as input the set C
i
of initial
conditions on hosts, the set E
∗
of known and zero-
day exploits, and a goal condition c
g
∈ C
∗
. The al-
gorithm returns an upper bound u on the value of
k, and also computes a partial zero-day attack graph
G = (E ∪C,R
r
∪R
i
), a mapping π :C∪E → 2
2
E
which
associates each node in the partial attack graph with
attack paths leading to it, and a mapping zdu : C → N
which associates each node in the partial attack graph
with an estimate of the upper bound on k. In this sec-
tion, we assume that Algorithm 2 starts from initial
conditions, but modifying the algorithm to reuse par-
tial attack graphs generated by previous execution of
Algorithm 1 is straightforward, and can be done as
shown for algorithm k0dValue (Algorithm 5).
Lines 1-8 simply initialize all the components of
the partial attack graph. Line 1 adds the initial condi-
tions to the set C of security conditions in the partial
attack graph. As the algorithm builds the attack graph,
new conditions will be added to C. Lines 2-3 initial-
ize the require and imply relationships as empty sets.
For each c ∈ C
i
, Lines 5-6 set π(c) to
/
0 – meaning
that no exploit is needed to reach initial conditions,
as they are satisfied by default – and zdu(c) to 0 –
meaning that no zero-day exploit is needed to reach
initial conditions. Finally, Line 8 sets E to the set of
exploits reachable from conditions in C. For each ex-
ploit e ∈ E, Lines 10-12 add edges to e from each of
its preconditions, Line 13 associates e with the only
set of exploits leading to it, that is {e}, and Line 14
computes zdu(e) as the number of distinct zero-day
vulnerabilities in {e}, that is k0d({e})
2
.
2
For exploits directly reachable from initial conditions,
Line 16-21 try to find an attack path reaching
the goal condition with the lowest possible number
of distinct zero-day vulnerabilities. Since we use an
heuristic approach to prune the search space, the num-
ber of distinct zero-day vulnerabilities in such path
is naturally an upper bound on the minimum num-
ber k of zero-day vulnerabilities needed to reach the
goal. Line 16 uses Algorithm rankedPartition (Algo-
rithm 3) to rank exploits in E by increasing value of
zdu(e) and partition the set into ranked subsets. Then,
Lines 18-21 iteratively explore the partial attack graph
in a depth-first manner, by using the recursive algo-
rithm DFS (Algorithm 4), starting from the set of ex-
ploits E
1
with the smallest values of zdu().
Algorithm rankedPartition (Algorithm 3) takes as
input a set of exploits E
′
and returns a partition P
E
of E. Line 1 sorts exploits in E by increasing value
of zdu(e). Then, Line 2 partitions E into an ordered
set of sets E
1
,... ,E
n
, such that for each i ≤ j ≤ n all
exploits in E
i
have smaller values of zdu() than any
exploit in E
j
.
Algorithm DFS (Algorithm 4) takes as input a set
E
start
of exploits and a goal condition c
g
∈ C
∗
, and re-
turns an upper bound u on the value of k. We assume
that the partial attack graph and the two mappings π()
and zdu() are global variables.
For each e ∈ E
start
and each c ∈ post(e), (i)
Lines 4-5 add an edge from e to c, and update the
set C
new
of newly reached conditions, (ii) Line 6 com-
putes the set π(c) of attack paths leading to c as the
union of the sets of attack paths leading to each ex-
ploit implying it, and (iii) Line 7 computes an esti-
mate zdu(c) of the upper bound on k with respect to c
as the smallest zdu(P) over all paths P in π(c). If c is
the goal condition, then the algorithm returns zdu(c).
If none of the conditions in C
new
is the goal condi-
tion, then Line 14 defines a new set E
new
of unvisited
exploits reachable from C, which has been updated to
include all conditions reached from E
start
. An exploit
is unvisited if at least one of its preconditions is in
C
new
. If no new exploit is enabled, then the algorithm
return +∞ (Line 16), meaning that the goal condition
cannot be reached from the branch of the attack graph
explored in the current iteration of the algorithm. Oth-
erwise, for each e ∈ E
new
, (i) Lines 19-22 add e and
edges to e from each of its preconditions to the partial
attack graph, (ii) Lines 23-24 compute the set π(e) of
partial attack paths ending with e in the same way we
have described for algorithm k0dLowerBound, (iii)
Line 25 prunes π(e) by maintaining only the top b
partial attack paths with respect to the k0d() metric,
and (iv) Line 26 computes an estimate zdu(e) of the
upper bound on k with respect to e as the smallest
zdu(e) is either 1, if e is a zero-day exploit, or 0, otherwise.
AnEfficientApproachtoAssessingtheRiskofZero-DayVulnerabilities
213

Algorithm 2: k0dU pperBound(C
i
,E
∗
,c
g
).
Input: Set C
i
of initial conditions, set E
∗
of known and zero-day exploits, and goal condition c
g
∈ C
∗
.
Output: Partial zero-day attack graph G = (E ∪C,R
r
∪ R
i
), mapping π :C ∪ E → 2
2
E
, mapping zdu :C → N, and upper bound u on the value of k.
1: C ← C
i
2: R
r
←
/
0
3: R
i
←
/
0
4: for all c ∈ C
i
do
5: π(c) ←
/
0
6: zdu(c) ← 0
7: end for
8: E ← {e ∈ E
∗
| pre(e) ⊆ C}
9: for all e ∈ E do
10: for all c ∈ pre(e) do
11: R
r
← R
r
∪ {(c,e)}
12: end for
13: π(e) ← {{e}}
14: zdu(e) ← k0d({e})
15: end for
16: hE
1
,...,E
n
i ← rankedPartition(E)
17: i ← 0
18: while c
g
/∈ C ∧ i ≤ n do
19: i ← i+ 1
20: u ← DFS(E
i
)
21: end while
22: return G,π(),zdu(), u
Algorithm 3: rankedPartition(E
′
).
Input: Set E
′
of exploits.
Output: Partition P
E
of E
1: E
r
← he
1
,...,e
|E
′
|
i s.t. (∀i, j ∈ [1,|E
′
|])(i ≤ j ⇒ zdu(e
i
) ≤ zdu(e
j
))
2: P
E
← hE
1
,... , E
n
i s.t. (∀i, j ∈ [1,n])(i ≤ j ⇒ (∀e
′
∈ E
i
,e
′′
∈ E
j
)(zdu(e
′
) ≤ zdu(e
′′
)))
3: return P
E
zdu(P) over all paths P in π(e).
Finally, Line 28 uses algorithm rankedPartition
(Algorithm 3) to rank exploits in E by increasing
value of zdu(e) and partition the set. Then, Lines 30-
33 iteratively explore the partial attack graph in a
depth-first manner, by recursively calling algorithm
DFS, starting from the set of exploits E
1
with the
smallest values of zdu().
Example 2. When applied to the example shown in
Figure 2, algorithm k0dU pperBound (Algorithm 2)
will first consider exploits E reachable from the ini-
tial conditions (i.e., the first level of exploits, namely
hv
firewall
,0,Fi, hv
http
,0,1i, hv
ssh
,0,1i), and will rank
them by increasing value of zdu(). Then, assume
that algorithm rankedPartition (Algorithm 3) parti-
tions the set of exploits into subsets of size 1. As
each exploit e on the first level has zdu(e) = 1, al-
gorithm k0dU pperBound will continue building the
graph starting from any such exploit. If we assume it
will start from hv
firewall
,0,Fi, then its post-condition
h0,2i will be added to the graph. Subsequent re-
cursive calls of algorithm DFS will add hv
ssh
,0,1i,
huser,2i, hv
root
,2,2i, and hroot, 2i, thus reaching the
goal condition and returning u = 2. As seen in the
previous example, the actual value of k in this sce-
nario is 1, so u = 2 is a reasonable upper bound,
which we were able to compute efficiently by build-
ing only a partial attack graph.
The complexity of Algorithm k0dU pperBound
(Algorithm 2) is clearly dominated by the recursive
execution of algorithm DFS (Algorithm 4), which in
the worst case – due to the adopted pruning strategy
– has to process t partial attack paths for each node in
the partial attack graph. Therefore, the complexity is
O(t · (| C | + | E |)), which is linear in the size of the
graph when t is constant.
5.3 Solution for Problem 3
When the upper bound on the value of k is below a
practical threshold u
∗
, we would like to compute the
exact value of k, which is intractable in general. Our
solution consists in performing a forward search, sim-
ilarly to algorithm k0dLowerBound, starting from the
partial attack graphs computed in previous steps of
the decision process discussed in Section 4. To limit
SECRYPT2013-InternationalConferenceonSecurityandCryptography
214

Algorithm 4: DFS(E
start
,c
g
).
Input: Set E
start
of exploits and goal condition c
g
∈ C
∗
Output: Upper bound u on the value of k.
1: C
new
←
/
0
2: for all e ∈ E
start
do
3: for all c ∈ post(e) do
4: R
i
← R
i
∪ {(e,c)}
5: C
new
← C
new
∪ {c}
6: π(c) ←
S
e∈E|(e,c)∈R
i
π(e)
7: zdu(c) ← min
P∈π(c)
k0d(P)
8: if c = c
g
then
9: return zdu(c)
10: end if
11: end for
12: end for
13: C ← C ∪ C
new
14: E
new
← {e ∈ E | pre(e) ⊆ C ∧ pre(e) ∩ C
new
6=
/
0}
15: if E
new
=
/
0 then
16: return +∞
17: end if
18: for all e ∈ E
new
do
19: E ← E ∪ {e}
20: for all c ∈ pre(e) do
21: R
r
← R
r
∪ {(c,e)}
22: end for
23: {c
1
,... ,c
m
} ← {c ∈ C | (c, e) ∈ R
r
}
24: π(e) ← {P
1
∪ .. . ∪ P
m
∪ {e} | P
i
∈ π(c
i
)}
25: π(e) ← top(π(e),t)
26: zdu(e) ← min
P∈π(e)
k0d(P)
27: end for
28: hE
1
,... ,E
n
i ← rankedPartition(E
new
)
29: i ← 0
30: while c
g
/∈ C ∧ i ≤ n do
31: i ← i + 1
32: u ← DFS(E
i
)
33: end while
34: return u
the search space, compared to a traditional forward
search, and avoid the generation of the entire attack
graph, we leverage the upper bound computed by al-
gorithm k0dUpperBound to prune paths not lead-
ing to the solution. In fact, although the value of k
is known to be no larger than u, there still may be
many paths with more the u distinct zero-day vulner-
abilities, and we want to avoid adding such paths to
the attack graph. Algorithm k0dValue (Algorithm 5)
is indeed very similar to algorithm k0dLowerBound.
Therefore, for reasons of space, we only highlight the
main differences in our discussion. First, the algo-
rithm takes as input partial attack graphs, instead of
starting from initial conditions. Thus, Line 1 com-
putesC
new
as the set of pre-conditions of unvisited ex-
ploits (i.e., exploits not added yet to the attack graph).
Second, Line 10 prunes all attack paths with more
than u distinct zero-day vulnerabilities. Finally, when
the goal condition is reached, the algorithm computes
the exact value of k as the smallest k0d(P) over all
paths P in π(c
g
).
6 EXPERIMENTAL RESULTS
In this section, we present the results of experiments
we conducted to validate our approach. Specifically,
our objective is three-fold. First, we evaluated the
performance of the proposed algorithms in terms of
processing time in order to confirm that they are effi-
cient enoughto be practical. Second, we evaluated the
percentage of nodes included in the generated partial
attack graph compared to the full attack graph, which
shows the degree of savings, in terms of both time and
storage, that may be achieved through our on-demand
generation of attack graphs. Third, we also evaluated
the accuracy of estimations made using algorithm
k0dUpperBound compared to the real results ob-
tained using a brute force approach.
First, we show that, as expected, algorithm
k0dLowerBound is polynomial for given small
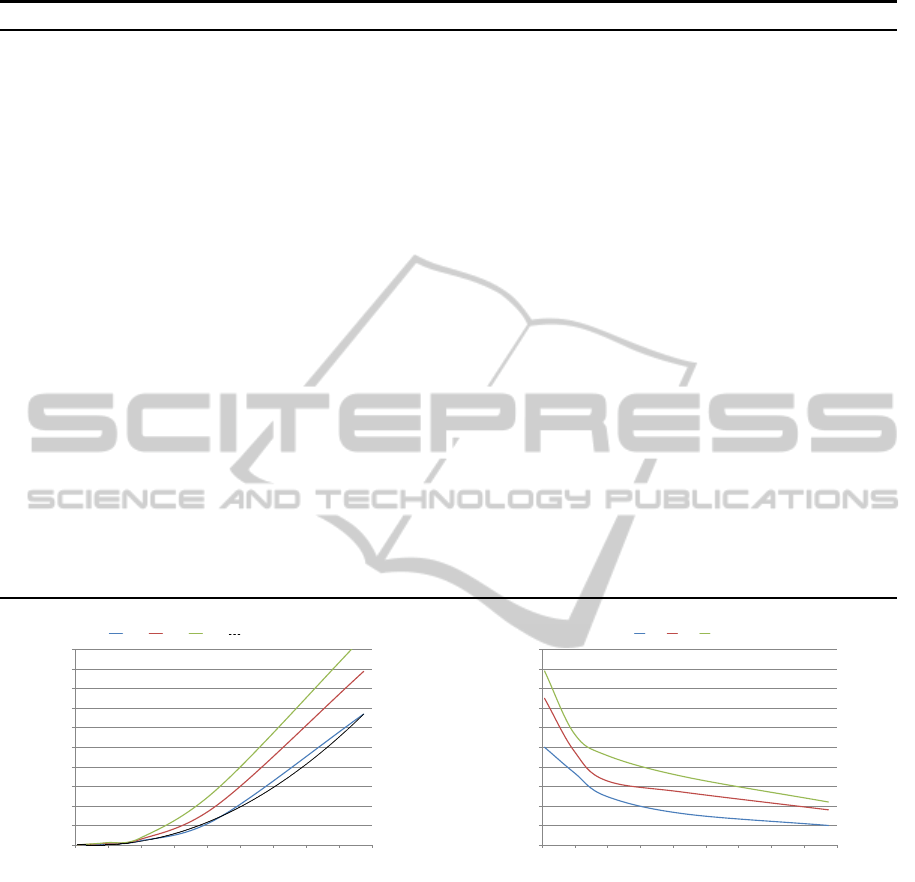
values of l. Specifically, Figure 4 (a) shows that the
running time of algorithm k0dLowerBound grows
almost quadratically in the size of attack graphs. It
AnEfficientApproachtoAssessingtheRiskofZero-DayVulnerabilities
215
Algorithm 5: k0dValue(G, E
∗
,u, c
g
).
Input: Partial zero-day attack graph G = (E ∪C, R
r
∪ R
i
), set E
∗
of known and zero-day exploits, integer u ∈ N representing the upper bound on the value of k
computed by algorithm k0dU pperBound, and goal condition c
g
∈ C
∗
.
Output: Updated Partial zero-day attack graph G = (E ∪C, R
r
∪ R
i
), and the exact value of k.
1: C
new
← {c ∈ C | ∄e ∈ E,(c,e) ∈ R
r
}
2: while C
new
6=
/
0 do
3: E
new
← {e ∈ E | pre(e) ⊆ C ∧ pre(e) ∩C
new
6=
/
0} // Unvisited exploits reachable from C
4: for all e ∈ E
new
do
5: for all c ∈ pre(e) do
6: R
r
← R
r
∪ {(c,e)} // Add an edge from c to e
7: end for
8: {c
1
,...,c
m
} ← {c ∈ C | (c,e) ∈ R
r
}
9: π(e) ← {P
1
∪ . . . ∪ P
m
∪ {e} | P
i
∈ π(c
i
)}
10: π(e) ← {P ∈ π(e) | k0d(P) ≤ u) // Prune paths with more than u zero-day vulnerabilities
11: end for
12: C
new
←
/
0
13: for all e ∈ E
new
s.t. π(e) 6=
/
0 do
14: for all c ∈ post(e) do
15: R
i
← R
i
∪ {(e,c)} // Add an edge from e to c
16: C
new
← C
new
∪ {c}
17: π(c) ←
S
e∈E|(e,c)∈R
i
π(e)
18: if c ≡ c
g
then
19: return G, min
P∈π(c)
k0d(P)
20: end if
21: end for
22: end for
23: C ← C ∪C
new
24: E ← E ∪ E
new
25: end while
R² = 0.9999
0
2
4
6
8
10
12
14
16
18
20
- 10,000 20,000 30,000 40,000 50,000 60,000 70,000 80,000 90,000
Processing time (seconds)
Number of nodes
l = 1 l = 2 l = 3 Quadratic regression
(a) Processing time
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
- 10,000 20,000 30,000 40,000 50,000 60,000 70,000 80,000 90,000
Percentage of visited nodes
Number of nodes
l = 1 l = 2 l = 3
(b) Percentage of nodes in the partial attack graph
Figure 4: Processing time and percentage of nodes for algorithm k0dLowerBound vs. number of nodes in the full attack graph
for different values of l.
is also clear that the actual running time is quite
reasonable even for relatively large graphs (e.g., it
only takes about 20 seconds to determine k > 3 for a
graph with 80,000 nodes). We can also observe that,
although the value of l affects the average running
time of the algorithm, such effect is not dramatic for
such small values of l (which may be sufficient in
most practical cases). This experiment confirms that
algorithm k0dLowerBound is efficient enough for
realistic applications. Next, we show how generating
partial attack graphs may lead to savings in both time
and storage cost. Specifically, Figure 4 (b) shows
the percentage of nodes that are generated by algo-
rithm k0dLowerBound in performing the analysis.
We can see that such a percentage will decrease while
the size of attack graphs increases, which is desirable
since this reflects higher amount of savings for larger
graphs. It is also clear that although a higher value
of l will imply less savings (more nodes need to be
generated), in most cases the savings are significant
(e.g., less than half of the nodes are generated in most
cases). This experiment confirms the effectiveness of
our on-demand approach to generating attack graphs.
Similarly, we now show that algorithm
SECRYPT2013-InternationalConferenceonSecurityandCryptography
216
0
20
40
60
80
100
120
140
160
180
200
- 10,000 20,000 30,000 40,000 50,000 60,000 70,000 80,000 90,000
Processing time (seconds)
Number of nodes
t = 1 t = 2 t = 5
(a) Processing time
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
- 10,000 20,000 30,000 40,000 50,000 60,000 70,000 80,000 90,000
Percentage of visited nodes
Number of nodes
t = 1 t = 2 t = 3
(b) Percentage of nodes in the partial attack graph
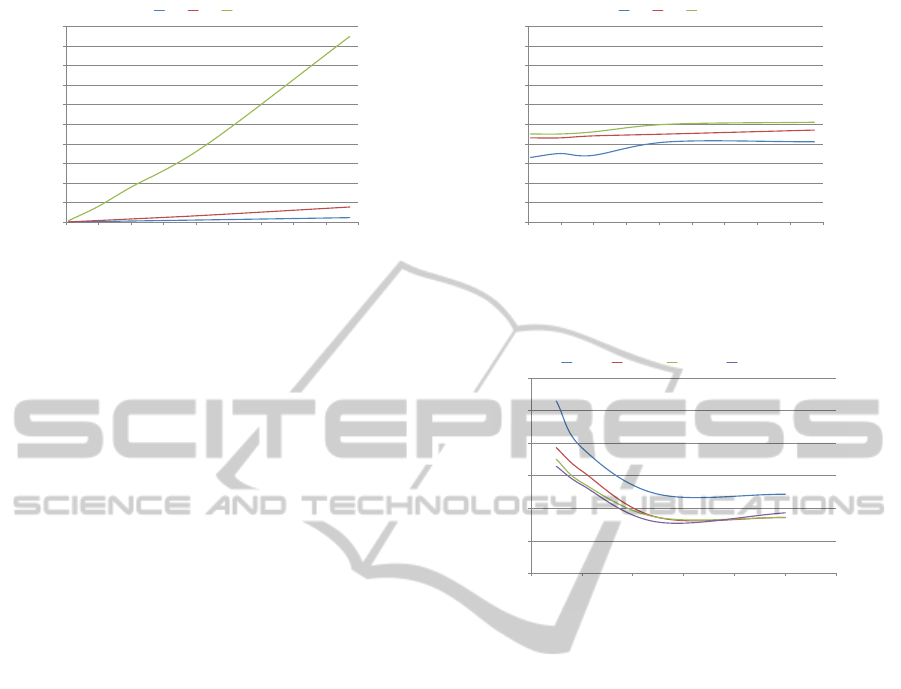
Figure 5: Processing time and percentage of nodes for algorithm k0dU pperBound vs. number of nodes in the full attack
graph for different values of t.
k0dUpperBound is polynomial for given small
parameters. Specifically, Figure 5 (a) shows that the
running time of algorithm k0dU pperBound grows
linearly in the size of attack graphs.
The value of t represents the number of partial so-
lutions maintained at each step (i.e., the degree of
approximation). It is clear that the actual running
time is very reasonable even for large graphs (e.g.,
it only takes less than 20 seconds for a graph with
almost 90,000 nodes). However, we can also ob-
serve that the degree of approximation (the value of
t) will significantly affect the growth of the average
running time of the algorithm, which shows a natu-
ral trade-off between accuracy and cost. Next, we
also show how generating partial attack graphs may
lead to savings for this algorithm. Specifically, Fig-
ure 5 (b) shows the percentage of nodes that are gen-
erated by algorithm k0dU pperBound in performing
the analysis. We can see that such a percentage re-
mains relatively stable across different graph sizes.
That is, although the absolute number of generated
nodes increases for larger graphs, the ratio remains al-
most constant, which partially justifies the linear run-
ning time of the algorithm. It is also clear that in most
cases the savings are significant (less than half of the
nodes are generated in most cases). This experiment
again confirms the effectiveness of our on-demand at-
tack graph generation.
Finally, we show the accuracy of algorithm
k0dUpperBound. Specifically, Figure 6 shows the
approximation ratio (i.e., the result u obtained using
the algorithm divided by the real value of k obtained
using a brute force method) in the approximation pa-
rameter t. We can see that, as expected, such a ratio
decreases when more partial results are kept at each
step, resulting in higher accuracy (and higher cost as
well). Overall, the approximation ratio is acceptably
low even for a small t (e.g., the result is only about
1.4 times the real value of k when t = 1). We can
0.9
1
1.1
1.2
1.3
1.4
1.5
0 2 4 6 8 10 12
Approximation ratio
t
7 nodes 21 nodes 121 nodes 341 nodes
Figure 6: Approximation ratio of k0dU pperBound vs. t.
also observe that larger graphs tend to have more ac-
curate results, which is desirable since the analysis
actually becomes relevant for larger graphs. Since
algorithm k0dValue(G,E
∗
,u,c
g
) is similar to algo-
rithm k0dLowerBound except that it reuses, instead of
generating, attack graphs, we expect its running time
to be similar to (lower than) that of the latter and thus
experiments are omitted here for reasons of space.
7 CONCLUSIONS
In this paper, we have studied the problem of ef-
ficiently estimating and calculating the k-zero-day
safety of networks. We presented a decision process
consisting of three polynomial algorithms for estab-
lishing lower and upper bounds of k and for calculat-
ing the actual value of k, while generating only partial
attack graphs in an on-demand manner. Experimental
results confirm the efficiency and effectiveness of our
algorithms. Although we have focused on the k-zero-
day safety metric in this paper, we believe our tech-
niques can be easily extended to other useful analyses
related to attack graphs. Other future work include
fine-tuning the approximation algorithm through var-
AnEfficientApproachtoAssessingtheRiskofZero-DayVulnerabilities
217

ious ways for ranking the partial solutions and evalu-
ating the solution on diverse network scenarios.
REFERENCES
Ammann, P., Wijesekera, D., and Kaushik, S. (2002).
Scalable, graph-based network vulnerability analy-
sis. In Proceedings of the 9th ACM Conference on
Computer and Communications Security (CCS 2002),
pages 217–224, Washington, DC, USA.
Balzarotti, D., Monga, M., and Sicari, S. (2005). Assessing
the risk of using vulnerable components. In Proceed-
ings of the 1st ACM Workshop on Quality of Protec-
tion (QoP 2005), volume 23 of Advances in Informa-
tion Security, pages 65–77. Springer.
Dacier, M. (1994). Towards quantitative evaluation of com-
puter security. PhD thesis, Institut National Polytech-
nique de Toulouse.
Greenberg, A. (2012). Shopping for zero-days: A price list
for hackers’ secret software exploits. Forbes.
Homer, J., Ou, X., and Schmidt, D. (2009). A sound and
practical approach to quantifying security risk in en-
terprise networks. Technical report, Kansas State Uni-
versity.
Ingols, K., Chu, M., Lippmann, R., Webster, S., and Boyer,
S. (2009). Modeling modern network attacks and
countermeasures using attack graphs. In Proceedings
of the Annual Computer Security Applications Con-
ference (ACSAC 2009), pages 117–126, Honolulu, HI,
USA.
Leversage, D. J. and Byres, E. J. (2008). Estimating a sys-
tem’s mean time-to-compromise. IEEE Security &
Privacy, 6(1):52–60.
McHugh, J. (2006). Quality of protection: Measuring the
unmeasurable? In Proceedings of the 2nd ACM Work-
shop on Quality of Protection (QoP 2006), pages 1–2,
Alexandria, VA, USA. ACM.
McQueen, M. A., McQueen, T. A., Boyer, W. F., and Chaf-
fin, M. R. (2009). Empirical estimates and observa-
tions of 0day vulnerabilities. In Proceedings of the
42nd Hawaii International Conference on System Sci-
ences (HICSS 2009), Waikoloa, Big Island, HI, USA.
Mehta, V., Bartzis, C., Zhu, H., Clarke, E., and Wing, J.
(2006). Ranking attack graphs. In Proceedings of
the 9th International Symposium On Recent Advances
In Intrusion Detection (RAID 2006), volume 4219 of
Lecture Notes in Computer Science, pages 127–144,
Hamburg, Germany.
Mell, P., Scarfone, K., and Romanosky, S. (2006). Com-
mon vulnerability scoring system. IEEE Security &
Privacy, 4(6):85–89.
Noel, S. and Jajodia, S. (2004). Managing attack graph
complexity through visual hierarchical aggregation.
In Proceedings of the ACM CCS Workshop on Vi-
sualization and Data Mining for Computer Security
(VizSEC/DMSEC 2004), pages 109–118, Fairfax, VA,
USA. ACM.
Pamula, J., Jajodia, S., Ammann, P., and Swarup, V. (2006).
A weakest-adversary security metric for network con-
figuration security analysis. In Proceedings of the 2nd
ACM Workshop on Quality of Protection (QoP 2006),
volume 23 of Advances in Information Security, pages
31–68, Alexandria, VA, USA. Springer.
Phillips, C. and Swiler, L. P. (1998). A graph-based system
for network-vulnerability analysis. In Proceedings of
the New Security Paradigms Workshop (NSPW 1998),
pages 71–79, Charlottesville, VA, USA.
Shahzad, M., Shafiq, M. Z., and Liu, A. X. (2012). A
large scale exploratory analysis of software vulnera-
bility life cycles. In Proceedings of the 34th Inter-
national Conference on Software Engineering (ICSE
2012), pages 771–781, Zurich, Switzerland.
Sheyner, O., Haines, J., Jha, S., Lippmann, R., and Wing,
J. M. (2002). Automated generation and analysis of
attack graphs. In Proceedings of the 2002 IEEE Sym-
posium on Security and Privacy (S&P 2002), pages
273–284, Berkeley, CA, USA.
The MITRE Corporation (2011). Common Weakness Scor-
ing System (CWSS
TM
). http://cwe.mitre.org/cwss/.
Version 0.8.
Wang, L., Islam, T., Long, T., Singhal, A., and Jajodia, S.
(2008). An attack graph-based probabilistic security
metric. In Atluri, V., editor, Proceedings of the 22nd
Annual IFIP WG 11.3 Working Conference on Data
and Applications Security, volume 5094 of Lecture
Notes in Computer Science, pages 283–296, London,
United Kingdom. Springer.
Wang, L., Jajodia, S., Singhal, A., and Noel, S. (2010). k-
zero day safety: Measuring the security risk of net-
works against unknown attacks. In Gritzalis, D.,
Preneel, B., and Theoharidou, M., editors, Proceed-
ings of the 15th European Symposium on Research in
Computer Security (ESORICS 2011), volume 6345 of
Lecture Notes in Computer Science, pages 573–587,
Athens, Greece. Springer.
SECRYPT2013-InternationalConferenceonSecurityandCryptography
218
