
Differential Power Analysis of HMAC SHA-2
in the Hamming Weight Model
Sonia Bela¨ıd
1,2∗
, Luk Bettale
3
, Emmanuelle Dottax
3
, Laurie Genelle
3
and Franck Rondepierre
3
1
´
Ecole Normale Sup´erieure, 45 rue d’Ulm, 75005 Paris, France
2
Thales Communications & Security, 4 Avenue des Louvresses, 92230 Gennevilliers, France
3
Oberthur Technologies, Cryptography Group, 420 rue d’Estienne d’Orves, 92700 Colombes, France
Keywords:
Side Channel Analysis, Differential Power Analysis, Hamming Weight, HMAC, SHA-2.
Abstract:
As any algorithm manipulating secret data, HMAC is potentially vulnerable to side channel attacks. In 2007,
McEvoy et al. proposed a differential power analysis attack against HMAC instantiated with hash functions
from the SHA-2 family. Their attack works in the Hamming distance leakage model and makes strong as-
sumptions on the target implementation. In this paper, we present an attack on HMAC SHA-2 in the Hamming
weight leakage model, which advantageously can be used when no information is available on the targeted
implementation. Furthermore, our attack can be adapted to the Hamming distance model with weaker assump-
tions on the implementation. We show the feasibility of our attack on simulations, and we study its overall cost
and success rate. We also provide an evaluation of the performance overhead induced by the countermeasures
necessary to avoid the attack.
1 INTRODUCTION
With the expansion of internet communications, on-
line transactions and the transfer of confidential data
in general, ensuring the integrity and the authenticity
of transmitted information is a prime necessity. To
this end, a Message Authentication Code (MAC) is
generally used. A MAC algorithm accepts as input a
secret key – shared between senders and receivers –
and an arbitrarily long message. The output is a short
bit-string which is jointly transmitted with the mes-
sage. It allows the receiver to verify that the message
has not been altered by an attacker.
Several MAC constructions exist, and the most
common ones are based on block-ciphers or on hash
functions. Among the hash-based MAC algorithms,
HMAC (Bellare et al., 1996) is the most widely used.
Today it is a standardized algorithm (FIPS 198-1,
2008) and it is used by several protocols running on
embedded devices (Haverinen and Salowey, 2006;
Arkko and Haverinen, 2006). The use of HMAC
in such a context leads the research community to
study its vulnerability against Side Channel Analysis
∗
This work was essentially done while this author was a
member of the Cryptography Group of Oberthur Technolo-
gies.
(SCA) attacks. Those attacks take advantage of statis-
tical dependencies that exist between a physical leak-
age (e.g., the power consumption, the electromagnetic
emanations) produced during the execution of a cryp-
tographic algorithm and the intermediate values ma-
nipulated. In the family of side channel analyses, Dif-
ferential Power Analysis (DPA) is of particular inter-
est (Kocher et al., 1999). The principle is the fol-
lowing. The attacker executes the cryptographic al-
gorithm several times with different inputs and gets a
set of power consumption traces, each trace being as-
sociated to one value known by the attacker. At some
points in the algorithm execution, sensitive variables
are manipulated, i.e., variables that can be expressed
as a function of the secret key and the known value.
These sensitive values are targeted as follows: the
attacker makes hypotheses about the secret key and
predicts the sensitive values and the corresponding
leakages. Then, a statistical tool is used to compute
the correlation between these predictions and the ac-
quired power consumption traces. The obtained cor-
relation values allow the attacker to (in)validate some
hypotheses. In order to map the hypothetical sensitive
value towards an estimated leakage, a model function
must be chosen. The Hamming Distance (HD) and
the Hamming Weight (HW) models are the most com-
monly used by attackers to simulate the power con-
230
Belaïd S., Bettale L., Dottax E., Genelle L. and Rondepierre F..
Differential Power Analysis of HMAC SHA-2 in the Hamming Weight Model.
DOI: 10.5220/0004532702300241
In Proceedings of the 10th International Conference on Security and Cryptography (SECRYPT-2013), pages 230-241
ISBN: 978-989-8565-73-0
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

sumption of an embedded device. In the HW model,
the leakage is assumed to rely on the number of bits
that are set in the handled data. It is considered as a
special case of the HD model, which assumes that the
leakage depends on the bits switching from one state
to the next one. The latter is usually considered to bet-
ter integrate the behavior of CMOS circuits, however
it requires significant knowledge of the implementa-
tion. As for the HW model, it can always be used
and gives valid results for a large number of devices
(Kocher et al., 1999; Messerges, 2000; Mangard et al.,
2007).
Related Works. Several DPA scenarios have been
proposed in the literature to attack the HMAC al-
gorithm. Okeya et al. addressed in several papers
(Okeya, 2006; Gauravaram and Okeya, 2007; Gau-
ravaram and Okeya, 2008) the question of protect-
ing HMAC against DPA. They focused their study on
block-cipher based hash functions. As well, (Zhang
and Shi, 2011) dealt with HMAC based on Whirlpool.
In (Lemke et al., 2004), Lemke et al. described a the-
oretical attack on HMAC based on the hash func-
tions RIPEMD-160 and SHA-1 in the HW model.
McEvoy et al. (McEvoy et al., 2008) proposed an at-
tack against HMAC based on SHA-2 functions. They
chose the HD model to characterize the physical leak-
age of the device. The paper (Fouque et al., 2009)
presents a template attack on HMAC SHA-1, which
implies a more powerful adversary than DPA (Chari
et al., 2002). More recently, DPA on keyed versions
of KECCAK have been explored in (Zohner et al.,
2012; Bertoni et al., 2013).
Contributions. In this paper, we improve the state
of the art on the security of HMAC against DPA by
proposing an attack in the HW model. Contrary to
(McEvoy et al., 2008), our attack can be used even
when no information about the HMAC implemen-
tation is available. Moreover, our attack can easily
be adapted to the HD model, and it turns out that
the resulting attack requires weaker assumptions on
the HMAC implementation than the ones made in
(McEvoy et al., 2008). Indeed, the attack by McEvoy
et al. relies on a constraining HMAC implementation,
which reduces the scope of their attack. We also study
the cost and the success rate of the attack, that leads to
the first complete study of a full DPA attack complex-
ity on HMAC. We focus our study on HMAC based
on SHA-256, however our work can be straightfor-
wardly adapted to all SHA-2 family functions, and to
RIPEMD-160, MD5 and SHA-1 with small modifica-
tions.
Paper Organisation. The rest of the paper is or-
ganized as follows. Section2 introduces the neces-
sary backgroundon HMAC and SHA-256 algorithms.
Section3 discusses the interest of our attack and de-
scribes the details. Section 4 exhibits the results of
simulations and evaluates the efficiency of the new
attack on unprotected implementations. Eventually,
Sect. 5 deals with the protections required to secure
a HMAC implementation against our attack, and no-
tably it evaluates the impact on performances.
2 TECHNICAL BACKGROUND
2.1 The HMAC Construction
The HMAC cryptographic algorithm involves a hash
function H in combination with a secret key k. Ac-
cording to (FIPS 198-1, 2008), it is defined as follows:
HMAC
k
:
{0,1}
∗
−→ {0,1}
h
m 7−→ H((k⊕ opad) k H((k⊕ ipad) k m)) ,
where ⊕ denotes the bitwise exclusive or, k denotes
the concatenation, and opad and ipad are two pub-
lic fixed constant. We call inner hash the first hash
computation H((k⊕ ipad) k m) and the second one is
referred to as the outer hash.
In this paper, we focus on HMAC instantiated
with a hash function H based on the Merkle-Damg˚ard
construction (Merkle, 1989; Damg˚ard, 1989) (MD5,
SHA-1 and SHA-2 are among the most widely used).
An overview of this construction is given in Fig. 1.
The input message m is first padded using a specific
procedure to obtain N blocks of bit-length n denoted
by m
1
,... ,m
N
. Then each block m
i
is processed with
a h-bit chaining value CV
i−1
through a one-way com-
pression function F that outputs a new h-bit chaining
value CV
i
. The chaining value CV
0
, also denoted by
k
1
, is fixed and depends only on the secret key k. It is
computed as F(IV, k⊕ ipad), with IV being the pub-
lic Initial Value of the hash function. The final chain-
ing value CV
N
, also denoted by z, is the input of the
outer hash. It is processed with a second fixed key-
dependent value k
0
= F(IV, k⊕ opad) in the last call
of the compression function that outputs the MAC. So
we rewrite the HMAC procedure as follows:
HMAC
k
(m) =
F(k
0
,F(... F(F(k
1
,m
1
),m
2
), ... ,m
N
) k pad) ,
where pad is the bit-string used to pad the input of
the outer hash. For the sake of simplicity and without
loss of generality, we omit this value in the following.
In the rest of the paper we make our analysis on
the HMAC algorithm based on SHA-256. We assume
F to be the SHA-256 compression function. A brief
description is given in the next section.
DifferentialPowerAnalysisofHMACSHA-2intheHammingWeightModel
231
k⊕ ipad m
1
...
m
N
IV
F F
...
F
F
MAC
IV
k⊕ opad
F
k
1
k
0
CV
1
CV
N−1
CV
N
= z
inner hash
outer hash
Figure 1: HMAC using a Merkle-Damg˚ard hash function.
2.2 The SHA-256 Compression
Function
The SHA-256 compression function F is described in
Alg. 1. It accepts as input a 512-bit message block M
and a 256-bit chaining value V (i.e., parameters n and
h in Sect. 2.1 equal 512 and 256 respectively). The
function iterates 64 times the same round transforma-
tion on an internal state. The state is represented by
eight 32-bit words A,B,C,D,E,F,G and H initially
filled with V = (V
1
,... ,V
8
). The round is a composi-
tion of 32-bit modular additions, denoted by ⊞, with
boolean operations which are defined on 32-bit words
u, v and w as follows:
Ch(u, v,w) = (u∧ v) ⊕ (¬u∧ w) ,
Maj(u, v,w) = (u∧ v) ⊕ (u∧ w) ⊕ (v∧ w),
Σ
0
(u) = (u ≫ 2) ⊕ (u ≫ 13) ⊕ (u ≫ 22) ,
Σ
1
(u) = (u ≫ 6) ⊕ (u ≫ 11) ⊕ (u ≫ 25) ,
where ∧ denotes the bitwise and, ¬ denotes the bit-
wise complement and x ≫ j denotes a rotation of j
bits to the right on x.
The message expansion splits the message block
M into 32-bit words M
1
,... ,M
16
, and expands it into
64 words W
t
by using the following additional 32-bit
words operations:
σ
0
(u) = (u ≫ 7) ⊕ (u ≫ 18) ⊕ (u ≫ 3) ,
σ
1
(u) = (u ≫ 17) ⊕ (u ≫ 19) ⊕ (u ≫ 10) ,
where x ≫ j denotes a shift of j bits to the right on x.
In Alg.1, the values K
1
,... ,K
64
are public constants.
3 DPA ON HMAC SHA-256
3.1 Related Work and Contribution
In (McEvoy et al., 2008), the authors proposeto attack
the SHA-256 compression function to recover k
0
and
k
1
. The authors mount their attack in the HD leakage
Algorithm 1: SHA-256 Compression Function.
Inputs: the data block M = (M
1
,... ,M
16
),
the chaining value V = (V
1
,... ,V
8
)
Output: the chaining value F(V,M)
1: (W
1
,... ,W
16
) ← (M
1
,... ,M
16
)
2: for t = 17 to 64 do ⊲ Message Expansion
3: W
t
← σ
1
(W
t−2
) ⊞ W
t−7
⊞ σ
0
(W
t−15
) ⊞W
t−16
4: end for
5: (A,B,C, D,E,F,G, H) ← (V
1
,... ,V
8
)
6: for t = 1 to 64 do ⊲ Main Loop
7: T
1
← H ⊞ Σ
1
(E) ⊞ Ch(E,F,G) ⊞ K
t
⊞W
t
8: T
2
← Σ
0
(A) ⊞ Maj(A, B,C)
9: H ← G
10: G ← F
11: F ← E
12: E ← D⊞ T
1
13: D ← C
14: C ← B
15: B ← A
16: A ← T
1
⊞ T
2
17: end for
18: return (V
1
⊞ A, .. ., V
8
⊞ H) ⊲ Final Addition
model, and they assume to have knowledge (only) of
the input messages. They consider an implementa-
tion that strictly follows Alg.1, and in particular they
make the following assumptions. Firstly, the vari-
ables A, B,.. ., H are initialized with the input chain-
ing value and T
1
is initialized with an unknown but
constant value. Secondly, each one of the variables
T
1
,T
2
,A, B,.. .,H is updated with its value at the next
round. It means that for each of these variables, the
HD between its value at round t − 1 and its value at
round t is leaked at each round t, for t = 1,. .. ,64.
Under these assumptions, the authors present an at-
tack wich consists in a succession of DPAs. Each one
allows the attacker to recover either a part of the se-
cret key or an intermediate result, and these results are
re-used in the following DPAs to recover the remain-
ing secrets. It is worth noticing that these assumptions
are quite strong and could prevent applying the attack
on some implementations. For instance, a software
implementation would probably avoid updating reg-
isters value (steps 9 to 16 of Alg. 1) and rather choose
to directly update the pointers, which would clearly
be more efficient.
In this paper, we propose an attack on the com-
pression function that targets different steps in the al-
gorithm compared to (McEvoy et al., 2008). This new
method brings two main advantages. First, our new
attack benefits from the feature to work in the HW
model in which the power consumption is assumed to
be proportional to the number of non-zero bits of the
processed values. Therefore our proposal can be ap-
SECRYPT2013-InternationalConferenceonSecurityandCryptography
232

plied on devices that leak in this model, and also when
the attacker has no information about the implementa-
tion, as stated in (Mangard et al., 2007). Secondly, we
show in Sect. 3.3 that our proposal can also be turned
into an attack in the HD model but with less restric-
tive assumptions than (McEvoy et al., 2008), which
advantageously extends the scope of the attack.
3.2 New Attack in the Hamming Weight
Model
To forge MACs for arbitrary messages, the attacker
needs either to recover the secret key k or both val-
ues k
0
and k
1
. As seen in Fig. 1, the attacker can-
not target directly the secret key k since it is never
combined with variable and known data. On the con-
trary, k
0
and k
1
may potentially be recovered by the
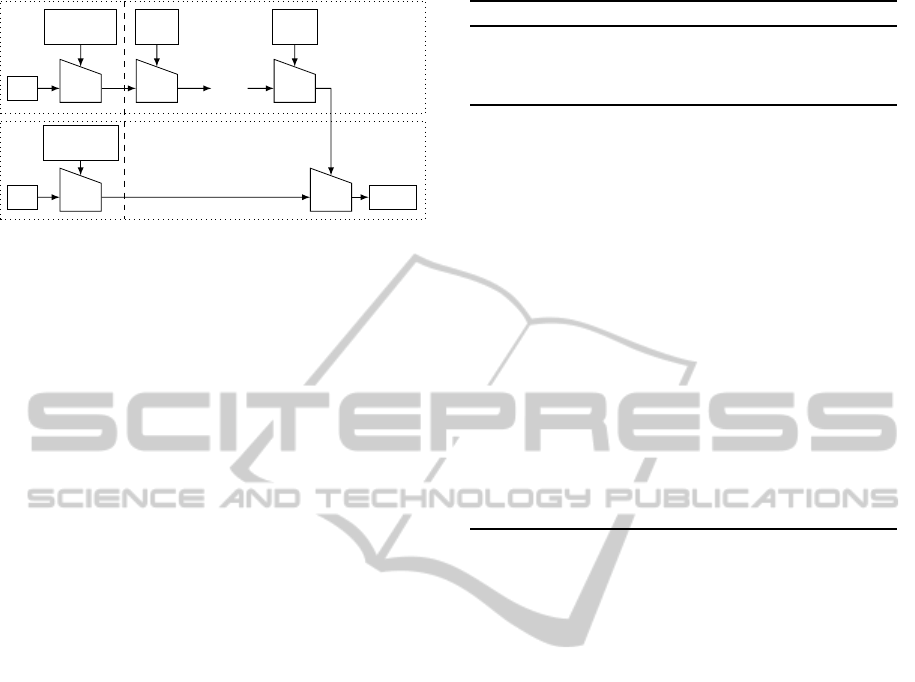
attacker. In the following, we define the three paths
the attacker can follow to recover k
1
and k
0
(they are
shown by Fig. 2). Then, Sect. 3.2.1, 3.2.2 and 3.2.3
give the detailed steps of the attacks following respec-
tively Path1, 2 and 3.
k⊕ ipad m
1
...
m
N
IV
F F
...
F
F
MAC
IV
k⊕ opad
F
k
1
k
0
CV
1
CV
N−1
CV
N
= z
E
Path 1
E
Path 2
E
Path 3
inner hash
outer hash
Figure 2: Attack paths on HMAC.
As already noted, the value k
1
may be obtained
when it is combined with the known and variable data
m
1
in the compression function. This attack path is
referred to as Path1.
Definition 1 (Path1: Inner hash - DPA with known
input.). The attacker targets the compression function
whose input is the first message block m
1
to recover
the secret value k
1
.
Once k
1
is known, the attacker is able to compute
the inner hash result z = H(k
1
||m) for all input mes-
sages m. She can thus mount a DPA on the outer hash
compression function execution whose input is z to
recover the constant value k
0
. This path is denoted by
Path2.
Definition 2 (Path2: Outer hash - DPA with known
input.). The attacker targets the last call of the com-
pression function whose input is the known and vari-
able value z.
Another way for the attacker to obtain the secret
value k
0
is to target the last call of the compression
function focussing on the MAC value which is known
and variable. We refer to this attack path as Path3.
Definition 3 (Path3: Outer hash - DPA with known
output.). The attacker targets the last compression
function execution whose output is the known and
variable MAC.
3.2.1 Path 1
We depict here the attack following Path 1, i.e., on the
computation F(k
1
,m
1
). In this context, the attacker
aims at recovering the secret value k
1
. We completely
develop this attack in Table 1. The notation X
(i)
refers to a given intermediate variable X computed
at round i. Variables denoted by X
(0)
correspond
to the input chaining value of the compression func-
tion. For the sake of simplicity, δ
(i)
denotes the sum
H
(i)
⊞ Σ
1
E
(i)
⊞ Ch
E
(i)
,F
(i)
,G
(i)
⊞ K
i+1
. Even-
tually,
b
X denotes a variable controlled by the attacker,
meaning that she can predict its value when the mes-
sage changes.
Each line of the table describes a DPA attack. The
column Hyp indicates the secret value which is the
target of the attack Attack in the operation Targeted
Operation. In each targeted operation, the hat indi-
cates the variable that is controlled (modified) by the
attacker. The column Result lists the useful variables
on which the attacker gains control after the attack (it
includes, but is not limited to, the target secret vari-
ables). Eventually, the double line separates the at-
tacks executed in Round 1 from the ones processed in
Round 2.
The attacker progresses line after line and fi-
nally recovers the following parts of the secret:
A
(0)
,B
(0)
,D
(0)
,E
(0)
,F
(0)
,G
(0)
. The last remaining
parts H
(0)
and C
(0)
can be recovered by making sub-
stitutions in Alg. 1: in Step 7 of round1, where H
(0)
is the only unknown variable, and similarly in Step 8
of round1 where C
(0)
is the only unknown variable.
Remark. DPA8 involves the message block W
2
.
The attacker has two possibilities to mount this attack:
1. She can fix the first message block W
1
and thus
makes hypotheses on the whole constant sum δ
(1)
,
while modifyingW
2
. She obtains the value of δ
(1)
and deduces the secret H
(1)
from the knowledge
of the other values.
2. W
1
is not fixed, but rather changes together with
W
2
. She then considers the sum Σ
1
E
(1)
⊞
Ch
E
(1)
,F
(1)
,G
(1)
⊞ K
2
⊞W
2
as the variable to
DifferentialPowerAnalysisofHMACSHA-2intheHammingWeightModel
233

Table 1: DPA attack on SHA-256 compression function us-
ing HW leakage model.
Attack Targeted Operation Hyp Result
DPA 1 T
(1)
1
← δ
(0)
⊞
b
W
1
δ
(0)
b
T
(1)
1
,δ
(0)
DPA 2 E
(1)
← D
(0)
⊞
b
T
(1)
1
D
(0)
b
E
(1)
,
D
(0)
DPA 3 A
(1)
←
b
T
(1)
1
⊞ T
(1)
2
T
(1)
2
b
A
(1)
,T
(1)
2
DPA 4
b
E
(1)
∧
F
(1)
in Ch F
(1)
F
(1)
=
E
(0)
DPA 5
b
E
(1)
∧
G
(1)
in Ch G
(1)
G
(1)
=
F
(0)
DPA 6
b
A
(1)
∧
B
(1)
in Maj B
(1)
B
(1)
=
A
(0)
DPA 7
b
A
(1)
∧
C
(1)
in Maj C
(1)
C
(1)
=
B
(0)
DPA 8
T
(2)
1
←
H
(1)
⊞ Σ
1
E
(1)
⊞
Ch⊞K
2
⊞
b
W
2
H
(1)
H
(1)
=
G
(0)
mount the DPA. Knowing the values taken by
the variable and making hypotheses on the secret
H
(1)
, she obtains as well the targeted value.
Both methods require the same number of traces and
are applicable with respect to the attack model. How-
ever, note that fixing W
1
may be more convenient
since there is no need to compute E
(1)
for each ex-
ecution.
The combination of these eight DPAs allows an
attacker to recover the input chaining value k
1
from
the observation of the first two rounds of F only.
3.2.2 Path 2
The attack related to Path 2 to recover k
0
follows the
same outline as the one associated to Path1. Indeed,
it targets the computation F(k
0
,z) in the outer hash,
whose input is z. However, in this context the value
z is known for any input message but not chosen. As
a consequence, the attacker cannot easily fix the first
message block and would probably choose the second
alternative to mount DPA 8 in Table1.
3.2.3 Path 3
The attack related to Path 3 targets the same compres-
sion function execution as Path 2. It also aims at re-
covering the same secret value k
0
but focuses on the
output of the compression function. Indeed in the
HMAC algorithm, the last call to the compression
function outputs the MAC value R. This final value is
obtained by performing a final addition between the
secret chaining input V = k
0
and the output of a 64-
round process. Thus we have:
A
(64)
= R
1
⊟V
1
,
B
(64)
= R
2
⊟V
2
,
...
H
(64)
= R
8
⊟V
8
,
where ⊟ is the modular subtraction on 32 bits. In
these final operations, the (R
i
)
16i68
are known and
variable and the (V
i
)
16i68
are constant parts of the
secret k
0
, thus the values A
(64)
, .. ., H
(64)
are sensitive.
Eight DPA attacks can thus be mounted to recover the
eight 32-bit parts (V
i
)
16i68
of the secret k
0
.
3.2.4 Full Attack
To conclude, the attacker can follow either Paths1 and
2 or Paths 1 and 3 to recover the secret values required
to forge MACs. In both cases, she needs to mount six-
teen DPAs on 32-bit words. As mentioned above, the
attack can be generalized on HMAC instantiated with
any of the SHA-2 family hash function with few adap-
tations. Indeed, the other SHA-2 hash functions differ
either in the size of the internal variables (32 bits or 64
bits), or in the length of the final output. For the DPAs
to be computationally practical when mounted on 32-
bit or 64-bit values, one can use partial DPAs (Lemke
et al., 2004) as explained in Sect. 4.1.2. For HMAC
implementations whose final output is truncated, the
attacker cannot directly follow Path3 to recover k
0
but
is still able to use Path2.
3.3 New Attack in the Hamming
Distance Model
If the device attacked is known to leak in the HD
model, our proposal can be adjusted into an attack in
the HD leakage model. To do so, we make the as-
sumption that the variables T
1
,T
2
,A, B,.. .,H are ini-
tialized with unknown but constant values. Then, the
DPA attack can be mounted provided that we make
additional hypotheses on these initial values. This im-
plies making 64-bit hypotheses, which can be handled
using partial DPA as done in (McEvoy et al., 2008).
Our new attack benefits from the feature to require
less restrictive assumptions on the implementation.
Indeed, contrary to (McEvoy et al., 2008), our pro-
posal does not expect the initial values to be equal to
the input chaining value. It also removes the require-
ment for the variables T
1
,T
2
,A, B,.. .,H to be updated
with their next values.
Eventually our attack in the HD model is as effi-
cient as the attack in (McEvoy et al., 2008) in terms of
SECRYPT2013-InternationalConferenceonSecurityandCryptography
234

number of DPAs. However, the scope of our proposal
is definitely larger than the existing attack.
4 ATTACK COST EVALUATION
In this section, we focus on evaluating the cost of the
attack paths described in Sect. 3. To achieve it, first
we give some background on DPA and in particular
on so-called partial DPA (Lemke et al., 2004; Tun-
stall et al., 2007). Then we explain how to apply it
in the particular case of an unprotected HMAC im-
plementation. Eventually we give an overview of the
total cost of the full attack to retrieve the two secret
keys k
0
and k
1
.
4.1 DPA Background
4.1.1 DPA Process
As already mentioned, a DPA exploits the statistical
dependencybetween the secret key and physical leak-
ages. This dependency results from the manipulation
of sensitive variables during the algorithm execution.
Instead of observing values related to the whole se-
cret key (for which brute-force attack is infeasible),
DPA focuses on sensitive values linked to a relatively
small part K of the secret. The size of K depends
on the processed algorithm and the chip architecture.
For instance, on 32-bit processors, data are manipu-
lated by 32-bit chunks. We express a sensitive vari-
able as a function g of K and a known value M. An
attacker can then test hypotheses
b
K by comparing the
predicted leakage to the measured leakage. We sum-
up hereafter the different steps:
1. Measure the leakage (l
i
)
i
produced by the N cal-
culations of g(K,M
i
) using a sample (M
i
)
i
of N
values. If L denotes the leakage of a physical de-
vice then l
i
= L ◦ g(K,M
i
).
2. Select a prediction function P that approximates
the leakage function L.
3. For each hypothesis
b
K, compute the correlation
between the predicted leakage (P◦ g(
b
K,M
i
))
i
and
the observed leakage (l
i
)
i
. In this paper we eval-
uate the correlation by using Pearson’s coefficient
(Brier et al., 2004).
4. The hypothesis
b
K maximizing this correlation is
assumed to be the secret part K.
4.1.2 Partial DPA
In practice, the value K may remaintoo large to mount
a DPA. However, for some functions g, it is possible
to predict some bits of g(K,M
i
) with assumptions on
only few bits (say ℓ) of K. This property enables to
use partial DPA in order to guess the whole secret K
by blocks of ℓ bits. If we assume that K is split such
that K =
∑
j
K
j
· 2
jℓ
, then a partial DPA follows the
same steps as described above but it targets the pro-
cessing of g related to the j
th
ℓ-bit block of K (denoted
g
ℓ
(K,M
i
, j) for a given message M
i
). We denote by
partial DPA the process of recovering the whole se-
cret K with several ℓ-bit DPAs.
Partial DPA is a useful tool to limit the attack
cost. Indeed, if we denote by O(N) the number of
operations required to compute one correlation coef-
ficient for N messages/leakages, a classical DPA on
N messages needs 2
w
O(N) operations to recover a
w-bit secret, whereas a partial DPA requires a total
of
w
ℓ
· 2
ℓ
O(N) operations (
w
ℓ
ℓ-bit DPA). The main
drawback is that the measured leakage depends on w
bits, but the correlation is performed only on ℓ bits.
This means that the w − ℓ other bits are assimilated
to noise in the DPA correlation computation. More
precisely if ρ is the Pearson correlation coefficient of
the leakage of the ℓ-bit useful data taken separately,
the total correlation coefficient of the w-bit data is in
average
q
ℓ
w
ρ (see for instance (Brier et al., 2004;
Tunstall et al., 2007)).
4.2 Partial DPAs on HMAC Operations
In the following, we consider the leakage L result-
ing from the manipulation of a sensitive variable x as
the sum of two terms: the information expressed as
the Hamming weight of x and an independent noise
denoted by ε. We assume that the noise follows a
Gaussian distribution with a null mean and a standard
deviation σ (denoted by N (0,σ)):
L(x) = HW(x) + ε, ε ∼ N (0,σ) .
As already seen in Table 1, only two elementary oper-
ations are involved: the 32-bit modular addition (⊞)
and the 32-bit bitwise and (∧). Hence the function g
introduced in the previous section is either the prim-
itive operation ⊞ or ∧, and the length of the data
equals 32 bits. Let us introduce the prediction func-
tion used to approximate the leakage related to the
j
th
ℓ-bit block. In the case of modular addition, the
value of the first j − 1 blocks has an impact on the
value of the j
th
block because of the carry propaga-
tion. Thus, when starting the attack from the least sig-
nificant block, the first j−1 guessed blocks haveto be
reused to approximate the leakage of the j
th
block. A
similar process can be used for the bitwise and. Our
prediction function for both operations is
P(g
ℓ
(
b
K,M
i
, j)) =
DifferentialPowerAnalysisofHMACSHA-2intheHammingWeightModel
235
HW
g
c
K
j
· 2
jℓ
+
j−1
∑
k=0
K
k
· 2
kℓ
,M
i
!
mod 2
( j+1)·ℓ
!
,
for each j, 0 6 j <
32
ℓ
. Eventually, we assume that
HMAC is processed on a 32-bit processor (i.e., nowa-
days the largest size for embedded devices). This is
the worst case for an attacker to mountpartialDPAs as
the leakage of 32− ℓ bits will be assimilated to noise.
It has to be noted that with modular addition, it is
not possible to perform 1-bit partial DPA. Indeed, if
ℓ = 1, a modular addition is an exclusive or operation.
The hypothesis K = 0 cannot be distinguished from
K = 1 (see for instance (Lemke et al., 2004)). As for
the bitwise and, the hypothesis K = 0 does not bring
any information. As M
i
∧ K = 0 for any message M
i
the leakage is just a measurement of noise. While
the zero key case is very unlikely for large values of
ℓ, it becomes a problem for small values. It is even
impossible to perform a partial DPA on bitwise and
for ℓ = 1. In what follows, we consider only partial
DPA on ℓ > 1 bits.
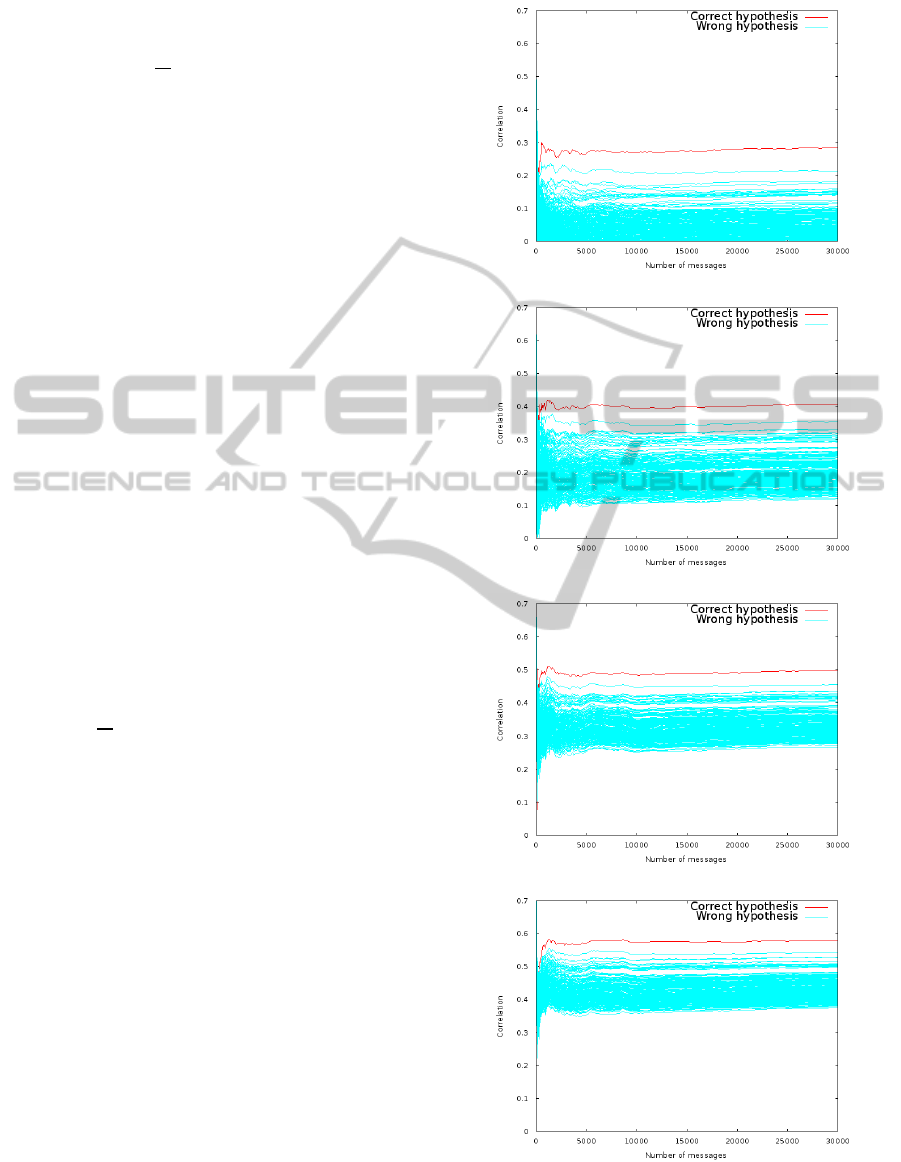
4.2.1 Simulations
Now let us compare the results of the partial DPA
applied on the two operations. We consider partial
DPA on 8-bit words (i.e., ℓ = 8). We depict in Fig. 3
(resp. Fig. 4) the correlation progression according to
the number of messages used to attack the modular
addition (resp. bitwise and). We say that the DPA
converges when one hypothesis remains above the
other as the number of messages grows. Each figure is
composed of
32
ℓ
= 4 graphs from top to bottom. The
graphs on the top show the correlation for the eight
least significant bits. The most correlated hypothe-
sis is then reused in the guess of the eight next bits,
and so on until the eight most significant bits (bottom
graphs) are guessed.
As expected, the value of the correlation is lesser
for the least significant bits because the other bits
are not used in the leakage prediction function g
ℓ
.
When comparing attacks on both operations, we ob-
serve that more messages are required in the bitwise
and case for the DPA to converge. Moreover we
notice that the correlation is lower and that the cor-
relation of the second most correlated hypothesis is
closer to the correct one. This can be explained by
the characteristic of the bitwise and. For instance,
consider one key hypothesis K
1
and the key hypothe-
sis K
2
= K
1
⊕ 1. Then, for all message M
i
such that
M
i
∧ 1 = 0, HW(K
1
∧ M
i
) = HW(K
2
∧ M
i
), and the
difference will be only 1 for the other messages. Both
hypotheses have similar correlation coefficients.
Partial DPA on modular addition, byte 0 (least significant)
Partial DPA on modular addition, byte 1
Partial DPA on modular addition, byte 2
Partial DPA on modular addition, byte 3 (most significant)
Figure 3: Attack on 32-bit addition with ℓ = 8 bits partial
DPA based on simulated curves with σ = 4. Top-most graph
shows the partial DPA on the least significant byte.
SECRYPT2013-InternationalConferenceonSecurityandCryptography
236

Partial DPA on bitwise and, byte 0 (least significant)
Partial DPA on bitwise and, byte 1
Partial DPA on bitwise and, byte 2
Partial DPA on bitwise and, byte 3 (most significant)
Figure 4: Attack on 32-bit logical AND with ℓ = 8 bits par-
tial DPA based on simulated curves with σ = 4. Top-most
graph shows the partial DPA on the least significant byte.
Figure 5: Success rate of partial DPA when attacking a bit-
wise and when the special case 0 is not taken into account.
The success rate is the same for any value ℓ.
Figure 6: Success rate of partial DPA when attacking a
modular addition. The success rate is always greater than
the one of bitwise and.
4.3 Full HMAC Attack
We focus on the cost and the success rate of an attack
on the full HMAC using ℓ-bit partial DPA. The suc-
cess rate is the probability that the best key hypothesis
revealed by the partial DPA is the correct key. We de-
note by P
⊞,ℓ
(N) (resp. P
∧,ℓ
(N)) the success rate of
an ℓ-bit DPA for ⊞ (resp. ∧) with N messages. Note
that the case of full length DPA is covered by taking
ℓ = 32. We simulated this success rate on ⊞ and ∧
with different noises σ ∈ {0,2,4,8} for an ℓ-bit par-
tial DPA with ℓ ∈ {4,8} (Fig. 5 and 6). Note that these
success rates can be computed on a copy of the target
device independently of the HMAC algorithm. These
success rates will serve to compute the success rate of
the whole attack. It can be observed that the curves
in Fig. 5 are gathered by noise level. This means that
the success rate seems not to depend on the size ℓ of
the partial DPA, but only on the amount of noise and
DifferentialPowerAnalysisofHMACSHA-2intheHammingWeightModel
237

the number of messages. In Fig. 5 the special case of
the 0 key has not been taken into account. We assume
that the partial DPA fails when at least one of the ℓ-bit
chunks of the key is zero. The success rate has then
to be multiplied by the probability of not having a 0
subkey which is
2
ℓ
−1
2
ℓ
N
ℓ
. In regards of our experi-
mental results, we can write
P
∧,ℓ
(N) =
2
ℓ
− 1
2
ℓ
32
ℓ
· P
∧
(N) , (1)
where P
∧
(N) denotes the success rate of a partial DPA
with N messages for any value ℓ without 0 subkey.
Moreover, for a same number of messages, the suc-
cess rate of modular addition is always greater than
the one of the bitwise and for any value of ℓ. In our
success rate evaluation, we may then use the follow-
ing assumption:
P
⊞,ℓ
(N) = P
⊞
(N) > P
∧
(N) . (2)
These values are enough to determine the success
rate of the whole attack presented in Sect. 3.
4.3.1 Attack Cost and Success Rate
The only way to verify that a key is correct is to com-
pute the HMAC of a message with the whole 2× 256-
bit keys k
0
and k
1
. This means that one cannot tell
that a partial DPA has failed until the whole keys have
been tested. According to the attack paths described
in Sect. 3, eight 32-bit DPAs are needed for each 256-
bit. In Paths 1 and 2, four of them are DPAs on ⊞ and
the other four are DPAs on ∧ operation. In Path 3,
the eight DPAs are on ⊞. All in all, when consid-
ering ℓ-bit partial DPA, one needs to perform a total
of
512
ℓ
DPAs on ℓ bits. The total cost of an attack is
512
ℓ
· 2
ℓ
O(N).
The total success probability of the whole attack is
the combined success probability of each DPA taken
independently. Using the success rates for partial
DPA defined in (2) and (1), the success rate of Paths 1
or 2 is
(P
⊞
(N))
4
·
2
ℓ
− 1
2
ℓ
32
ℓ
· P
∧
(N)
4
,
and the success rate of Path 3 is
(P
⊞
(N))
8
.
Provided that she has access to the HMAC results, an
attacker is then more likely to choose to attack HMAC
using Path 1 to recover k
1
and then Path 3 rather than
Path 2 to recover k
0
to maximize his success rate.
To minimize the complexity of the attack while
keeping a good success rate, the attacker has to de-
fine the appropriate parameters ℓ and N. For instance
we compute the total success rate of an attack (Path 1,
Path 3) using N = 2600 messages, for ℓ = 8-bit par-
tial DPA in a setting with a standard noise of deviation
σ = 4. According to our simulations, we obtain a suc-
cess rate P
⊞
(2600) = 1.00 for modular addition and
P
∧
(2600) = 0.92 for bitwise and. An attacker can
mount an attack of complexity
Path 1
z
}| {
4·
32
8
· 2
8
|
{z }
4 ⊞ operations
+ 4·
32
8
· 2
8
|
{z }
4 ∧ operations
+
Path 3
z
}| {
8·
32
8
· 2
8
|
{z }
4 ⊞ operations
O(N)
that is, 2
14
correlation computations on N mes-
sages/leakages. The success probability of this attack
is
Path 1
z
}| {
1.00
4
|
{z}
4 ⊞ operations
×
2
8
− 1
2
8
32
8
× 0.92
4
|
{z }
4 ∧ operations
×
Path 3
z
}|{
1.00
8
|
{z}
4 ⊞ ops.
= 0.71.
Our estimations allow an attacker to quickly evaluate
the total cost and success rate of a full DPA attack
on HMAC SHA-256 according to his settings and the
number of available messages. Then he can adjust
the parameter ℓ of the partial DPA to achieve the best
trade-off between attack cost and success rate.
5 PROTECTED
IMPLEMENTATION
In the previous section, it has been demonstrated that
the theoretical attack paths presented in Sect.3 are
sound. In order to secure a HMAC implementation
against this attack – and the one in (McEvoy et al.,
2008) – adequate countermeasures must be applied.
In software, the main techniques used to thwart such
SCA are masking and shuffling, as well as combina-
tion of both (Rivain et al., 2009). The principle is to
inject some randomness in the algorithm execution, in
order to reduce the amount of information that leaks
on sensitive intermediate variables during the execu-
tion. In the rest of this section, we examine how
to prevent attacks that use the previously presented
paths, and we provide an evaluation of the perfor-
mance overhead, independently of the technique ac-
tually used to implement the countermeasures.
SECRYPT2013-InternationalConferenceonSecurityandCryptography
238

5.1 Preventing Paths1 and 2
To mount an attack via Path2, we recall that the at-
tacker must be able to compute the intermediate value
z for various messages. As shown in Sect.3.2, this
ability can be gained after recovering the value k
1
by
an attack following Path1, i.e., during the first com-
pression function call F(k
1
,m
1
) in the inner hash.
However, preventing the recovery of k
1
is not suf-
ficient to completely annihilate Path2. Indeed, the
knowledge of any of the chaining values CV
i
in the
inner hash still allows the attacker to compute the in-
termediate result z for fixed-prefix messages, and to
mount an attack with Path2. As every CV
i
can be re-
covered by applying the attack following Path1 to the
corresponding compression function call, we deduce
that every execution of the compression function in
the inner hash has to be protected from attacks using
Path1. This is sufficient to prevent attacks via Path2
as well.
Let us now see how to prevent the attack follow-
ing Path1. They rely on the observation of the first
two roundsof the compression function, where the in-
put message block m
i
is manipulatedtogether with the
targeted secret values. It is thus necessary to protect
the sensitive variables of the first two rounds. Fur-
thermore, as we can see in Alg. 1, parts of the input
message block are also involved in each one of the 64
rounds, via the message expansion output W
t
. Thus,
we have to check the feasibility of the attack on later
rounds. We assume that the attacker adapts the attack
described by Table 1 to rounds t and t + 1, with t ≥ 2.
The first attack DPA 1 now relies on the variable W
t
.
The attacker can perform this attack and gain control
on T
(t)
1
when the values involved in δ
(t−1)
(namely
E
(t−1)
,F
(t−1)
,G
(t−1)
and H
(t−1)
) are constant. Af-
terwards, an adaptation of DPA 2 can be performed
provided that D
(t−1)
is constant as well, and DPA 3
can be performed if A
(t−1)
,B
(t−1)
and C
(t−1)
are con-
stant. Remaining DPAs can then be performed, and
the full internal state (A
(t−1)
,B
(t−1)
,... ,H
(t−1)
) can
be finally recovered. The attacker subsequently re-
covers previous states by inverting the round func-
tion, until she recovers the secret input chaining value
V = (A
(0)
,B
(0)
,... ,H
(0)
).
Coming back to the above described adaptation of
DPA 1, the following two conditions must thus be ful-
filled:
• values E
(t−1)
,F
(t−1)
,G
(t−1)
,H
(t−1)
must be fixed,
• the value W
t
must be variable.
To achieve the first condition, variables associated to
the previous rounds(W
1
,... ,W
t−1
) must all be fixed as
well. Yet, as soon as t > 16, the message expansion
is such that constant values forW
1
,... ,W
t−1
implies a
constant value for W
t
too, which contradicts the sec-
ond condition. Hence, these two requirements can be
fulfiled only for t 6 16.
We conclude that the attack from Path 1 presented
in Sect. 3.2.1 can be extended to any rounds among
the first 16 rounds. Moreover, due to the structure of
the compression function, some of the sensitive vari-
ables produced at round 16 remain available in rounds
17 to 20. Consequently, it is necessary to protect the
sensitive variables until the 20th round.
5.2 Preventing Path3
Section 3.2.3 describes an attack on the outer hash
computation that targets the final addition of the last
compression function call F(k
0
,z). We recall that the
sensitive variables targeted by the attack are:
A
(64)
= R
1
⊟V
1
,
B
(64)
= R
2
⊟V
2
,
...
H
(64)
= R
8
⊟V
8
,
where the R
i
’s are known outputs, and the V
i
’s con-
stitute the secret chaining input k
0
. An attack can
be mounted as soon as these sensitive values are ma-
nipulated. Rolling back the rounds of the compres-
sion function, we track these sensitive variables and
present them in bold in Table 2. This shows that sen-
sitive variables are produced from round 61 and that
protection is required from round 61 to round 64, on
top of the final addition.
Remark. One has to recall that for 1 6 i 6 64:
T
(i)
1
← H
(i−1)
+ Σ
1
E
(i−1)
+Ch
E
(i−1)
,F
(i−1)
,G
(i−1)
+ K
i
+W
i
,
T
(i)
2
← Σ
0
A
i−1
+ Maj
A
(i−1)
,B
(i−1)
,C
(i−1)
.
Hence, evenif the values of T
(i)
1
and T
(i)
2
are not sensi-
tive, sensitive variables may be involved in their com-
putations. For instance, the computation of T
(64)
1
in-
volves the sensitive variables E
(63)
,F
(63)
, and G
(63)
.
A careful implementation is thus needed to avoid
leakage from intermediate results.
5.3 Performance Overhead Evaluation
First, the two calls to the compression function ded-
icated to k
0
and k
1
computations need no security
against DPA, so they can be omitted. Then, following
DifferentialPowerAnalysisofHMACSHA-2intheHammingWeightModel
239

Table 2: Sensitive variables in last rounds.
Round 64 Round 63
A
(64)
← T
(64)
1
⊞ T
(64)
2
A
(63)
← T
(63)
1
⊞ T
(63)
2
B
(64)
← A
(63)
B
(63)
← A
(62)
C
(64)
← B
(63)
C
(63)
← B
(62)
D
(64)
← C
(63)
D
(63)
← C
(62)
E
(64)
← D
(63)
⊞ T
(64)
1
E
(63)
← D
(62)
⊞ T
(63)
1
F
(64)
← E
(63)
F
(63)
← E
(62)
G
(64)
← F
(63)
G
(63)
← F
(62)
H
(64)
← G
(63)
H
(63)
← G
(62)
Round 62 Round 61
A
(62)
← T
(62)
1
⊞ T
(62)
2
A
(61)
← T
(61)
1
⊞ T
(61)
2
B
(62)
← A
(61)
B
(61)
← A
(60)
C
(62)
← B
(61)
C
(61)
← B
(60)
D
(62)
← C
(61)
D
(61)
← C
(60)
E
(62)
← D
(61)
⊞ T
(62)
1
E
(61)
← D
(60)
⊞ T
(61)
1
F
(62)
← E
(61)
F
(61)
← E
(60)
G
(62)
← F
(61)
G
(61)
← F
(60)
H
(62)
← G
(61)
H
(61)
← G
(60)
the results exposed above, preventing the attack pre-
sented in this paper requires countermeasures to pro-
tect the intermediate variables of at least the first 20
rounds of each call to the compression function in the
inner hash, and of the last 4 rounds of the final call to
the compression function in the outer hash. In a first
approximation, we leave the details of the implemen-
tation for a secure round and simply consider it is k
times slower than a non-secure round. In that case, the
execution time of an implementation where sensitive
rounds of the compression function are protected is
approximately (20k + 44)/64 ≈ 0,31k times slower
than an unprotected implementation. Additional work
is required to precisely evaluate k, however we expect
it to be relatively large. Indeed, if masking is cho-
sen as a countermeasure, switching from arithmetic to
boolean masks and backwards (wich is required when
arithmetic and boolean operations are mixed, as it is
the case for all SHA-1/SHA-2 functions) is usually
costly (Mangard et al., 2007).
6 CONCLUSIONS
We have presented in this paper a side channel attack
on HMAC SHA-256 in the Hamming weight model,
which requires no assumption on the implementation.
Furthermore, it has been seen that this attack can be
easily adapted to the Hamming distance model, with
less assumptions on the implementation than previous
existing attacks. To ensure its feasibility and measure
its efficiency, we have simulated the attack. The tech-
nique of partial DPA has been used for different op-
erations, and we have estimated the cost of the com-
plete attack depending on the efficiency of the partial
attacks. Then, we haveanalysed the attacks and corre-
sponding protections, and evaluated the performance
overhead for software implementations. Further work
has to be done to focus on the details of the counter-
measures.
ACKNOWLEDGEMENTS
The authors wish to thank Christophe Giraud for help-
ful discussions, and anonymous referees of a previous
version of this work for their valuable comments.
REFERENCES
Arkko, J. and Haverinen, H. (2006). RFC 4187: Extensi-
ble Authentication Protocol Method for 3rd Genera-
tion Authentication and Key Agreement (EAP-AKA).
Bellare, M., Canetti, R., and Krawczyk, H. (1996).
Keying Hash Functions for Message Authentication.
In Koblitz, N., editor, Advances in Cryptology –
CRYPTO ’96, volume 1109 of LNCS, pages 1–15.
Springer.
Bertoni, G., Daemen, J., Debande, N., Le, T.-H., Peeters,
M., and Van Assche, G. (2013). Power Analysis
of Hardware Implementations Protected with Secret
Sharing. IACR Cryptology ePrint Archive Report
2013/67.
Brassard, G., editor (1989). Advances in Cryptology –
CRYPTO ’89, volume 435 of LNCS. Springer.
Brier, E., Clavier, C., and Olivier, F. (2004). Correlation
Power Analysis with a Leakage Model. In (Joye and
Quisquater, 2004), pages 16–29.
Chari, S., Rao, J., and Rohatgi, P. (2002). Template Attacks.
In Kaliski Jr., B., Koc¸, C¸., and Paar, C., editors, Cryp-
tographic Hardware and Embedded Systems – CHES
2002, volume 2523 of LNCS, pages 13–29. Springer.
Clavier, C. and Gaj, K., editors (2009). Cryptographic
Hardware and Embedded Systems – CHES 2009, vol-
ume 5747 of LNCS. Springer.
Damg˚ard, I. (1989). A Design Principle for Hash Functions.
In (Brassard, 1989), pages 416–427.
FIPS 198-1 (2008). The Keyed-Hash Message Authentica-
tion Code (HMAC). National Institute of Standards
and Technology.
Fouque, P.-A., Leurent, G., R´eal, D., and Valette, F. (2009).
Pratical Electromgnetic Template Attack on HMAC.
In (Clavier and Gaj, 2009), pages 66–80.
SECRYPT2013-InternationalConferenceonSecurityandCryptography
240

Gauravaram, P. and Okeya, K. (2007). An Update on the
Side Channel Cryptanalysis of MACs Based on Cryp-
tographic Hash Functions. In Srinathan, K., Rangan,
C. P., and Yung, M., editors, Progress in Cryptology
– INDOCRYPT 2007, volume 4859 of LNCS, pages
393–403. SV.
Gauravaram, P. and Okeya, K. (2008). Side Channel Analy-
sis of Some Hash Based MACs: A Response to SHA-
3 Requirements. In Chen, L., Ryan, M. D., and Wang,
G., editors, Information and Communications Secu-
rity – ICISC 2008, volume 5308 of LNCS, pages 111–
127. Springer.
Haverinen, H. and Salowey, J. (2006). RFC 4186: Exten-
sible Authentication Protocol Method for Global Sys-
tem for Mobile Communications (GSM) Subscriber
Identity Modules (EAP-SIM).
Joye, M. and Quisquater, J.-J., editors (2004). Crypto-
graphic Hardware and Embedded Systems – CHES
2004, volume 3156 of LNCS. Springer.
Kocher, P., Jaffe, J., and Jun, B. (1999). Differential Power
Analysis. In Wiener, M., editor, Advances in Cryp-
tology – CRYPTO ’99, volume 1666 of LNCS, pages
388–397. Springer.
Lemke, K., Schramm, K., and Paar, C. (2004). DPA
on n-Bit sized Boolean and Arithmetic Operations
and its Application to IDEA, RC6, and the HMAC-
Construction. In (Joye and Quisquater, 2004), pages
205–219.
Mangard, S., Oswald, E., and Popp, T. (2007). Power Anal-
ysis Attacks – Revealing the Secrets of Smartcards.
Springer.
McEvoy, R., Tunstall, M., Murphy, C. C., and Marnane,
W. P. (2008). Differential Power Analysis of HMAC
based on SHA-2, and Countermeasures. In Kim, S.,
Yung, M., and Lee, H.-W., editors, WISA 2007, vol-
ume 4867 of LNCS, pages 317–332. Springer.
Merkle, R. C. (1989). A Certified Digital Signature. In
(Brassard, 1989), pages 218–238.
Messerges, T. (2000). Using Second-order Power Analy-
sis to Attack DPA Resistant Software. In Koc¸, C¸ . and
Paar, C., editors, Cryptographic Hardware and Em-
bedded Systems – CHES 2000, volume 1965 of LNCS,
pages 238–251. Springer.
Okeya, K. (2006). Side Channel Attacks Against HMACs
Based on Block-Cipher Based Hash Functions. In
Batten, L. M. and Safavi-Naini, R., editors, ACISP,
volume 4058 of LNCS, pages 432–443. Springer.
Rivain, M., Prouff, E., and Doget, J. (2009). Higher-Order
Masking and Shuffling for Software Implementations
of Block Ciphers. In (Clavier and Gaj, 2009), pages
171–188.
Tunstall, M., Hanley, N., McEvoy, R., Whelan, C., Murphy,
C., and Marnane, W. (2007). Correlation Power Anal-
ysis of Large Word Sizes. In IET Irish Signals and
System Conference – ISSC 2007, pages 145–150.
Zhang, F. and Shi, Z. J. (2011). Differential and Corre-
lation Power Analysis Attacks on HMAC-Whirlpool.
In ITNG’11, pages 359–365. IEEE Computer Society.
Zohner, M., Kasper, M., St¨ottinger, M., and Huss, S. A.
(2012). Side Channel Analysis of the SHA-3 Final-
ists. In Rosenstiel, W. and Thiele, L., editors, Design,
Automation & Test in Europe Conference & Exhibi-
tion, DATE 2012, pages 1012–1017. IEEE Computer
Society.
DifferentialPowerAnalysisofHMACSHA-2intheHammingWeightModel
241
