
Protein Secondary Structure Prediction using an Optimised Bayesian
Classification Neural Network
Son T. Nguyen and Colin G. Johnson
School of Computing, University of Kent, Canterbury, Kent, U.K.
Keywords: Protein Secondary Structure Prediction, Classification Bayesian Neural Network, Optimised Network
Architecture.
Abstract: The prediction of protein secondary structure is a topic that has been tackled by many researchers in the
field of bioinformatics. In previous work, this problem has been solved by various methods including the
use of traditional classification neural networks with the standard error back-propagation training algorithm.
Since the traditional neural network may have a poor generalisation, the Bayesian technique has been used
to improve the generalisation and the robustness of these networks. This paper describes the use of
optimised classification Bayesian neural networks for the prediction of protein secondary structure. The
well-known RS126 dataset was used for network training and testing. The experimental results show that
the optimised classification Bayesian neural network can reach an accuracy greater than 75%.
1 INTRODUCTION
The accurate prediction of protein secondary
structure is an important step to understand protein
folding. A large number of papers have tackled this
problem, with the most common approach being the
use of various machine learning methods to learn the
connection between amino acid sequences and
secondary structure. Some of these approaches use
the amino acid states directly as the input data to
learning, whereas other methods have used the
biophysical features of amino acids, sequence
homology, pattern matching and statistical analyses
of proteins of known structures (Rost and Sander,
1993a), (Rost and Sander, 1993b).
The standard way of presenting this task as a
machine learning problem is as a classification
problem, where each data instance consists of a
number of predictor features (e.g. the neighbouring
amino acid values) and a class drawn from the set
{helix, strand, coil}. The aim of the learned model is
to be able to predict this class for examples not seen
during training.
According to (Holley and Karpus, 1989), the
maximum accuracy of predicting three states
(helices, strands and coils) has a limit, due to the
amount of data available and/or that the secondary
structure is determined by tertiary interactions not
included in the local sequence. Nonetheless, models
have been learned that can predict the class with
reasonable accuracy (65% for simple methods, rising
to around 92% for more sophisticated methods that
use additional data about similar proteins) (Lee et
al., 2012)
This paper describes the use of classification
Bayesian neural networks for the prediction of
protein secondary structure. In the past,
classification Bayesian neural networks have been
proven to be useful for several classification tasks
(Nguyen et al., 2004), (Nguyen et al., 2006), (Penny
and Roberts, 1999) and (Thodberg, 1996). Unlike
the traditional neural network training, the Bayesian
neural network training does not require a validation
set separated from the training subset. As a result, all
of the available data set can be divided into only two
subsets: the training subset and the test subset
(Mackay, 1992a), (Mackay, 1992b). The Bayesian
neural network training also encourages
generalisation as the values of the weight decay
parameters, sometimes known hyper-parameters,
can be well adjusted during the network training
phase. Moreover, Bayesian neural networks allow
users to rank and compare different networks with
different architectures. Therefore, the optimal
network architecture can be easily found based on
evaluating the log evidence of candidate networks
with the Bayesian framework (Penny and Roberts,
1999), (Mackay, 1992b).
451
T. Nguyen S. and G. Johnson C..
Protein Secondary Structure Prediction using an Optimised Bayesian Classification Neural Network.
DOI: 10.5220/0004538604510457
In Proceedings of the 5th International Joint Conference on Computational Intelligence (NCTA-2013), pages 451-457
ISBN: 978-989-8565-77-8
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

The structure of the paper is organised as
follows. Section II provides an overview of protein
secondary structure prediction and classification
neural networks. In Section III, the formulation of
classification Bayesian neural networks is briefly
described. In Section IV, the paper gives the
assessment methods for the obtained results. Section
V presents how to train and optimise classification
Bayesian neural networks for predicting three states:
helices, strands and coils. Finally, Section VI
provides a conclusion.
2 PROTEIN SECONDARY
STRUCTURE PREDICTION
AND CLASSIFICATION
NEURAL NETWORKS
Protein structure prediction is the foundation of
protein structure biology. Proteins are
macromolecules made of chains of 20 different
amino acids, which fold into a particular three-
dimensional structure that is distinctive to that
protein. This three-dimensional structure is what
determines the function of a protein. The ultimate
goal is to understand the function of proteins, and
therefore an important step towards this
understanding is to understand the protein structure
and how this relates to its sequence. Biochemists
distinguish four distinct aspects of a protein’s
structure: Primary structure, Secondary structure,
Tertiary structure and Quaternary structure. Protein
Secondary Structure Prediction (PSSP) means
predicting which parts of a protein will form the
large-scale structures known as α-helix, β-strand and
coils, based on the amino acid sequence of a protein
(Mottalib et al., 2010).
In the last two decades, a huge number of
approaches have been taken to the PSSP. In these
works, the probabilistic approaches were the first to
be used. The first attempt at using neural networks
for PSSP was done by Qian and Sejnowski in 1988,
and they obtained an accuracy of 64.3% (Qian and
Sejnowski, 1988). More recent neural network based
approaches have achieved accuracies greater than
70% (Rost and Sander, 1993a), (Jones, 1999). The
most important improvement in these approaches is
to modify the input set to the neural network by
finding similar proteins from a large database, and
forming an input based on the proportion of amino
acid values at each position in the sequence. The aim
of this is to provide more information to the network
about the kind of protein, and to eliminate the
influence of an uncharacteristic amino acid at a
particular position.
This part of the paper will describe how
classification neural networks are used for PSSP.
The primary sequences are used as the network
input. In order to read the input, a moving window
through the sequences needs to be created.
According to (Qian and Sejnowski, 1988), the size
of the moving window should be chosen to be 13 as
this window size has given the best performances
when testing the trained network on the test subset—
this window size has also been found in many
subsequent papers.
In this work, the define secondary structure of
proteins (DSSP) method is used. According to this
method, the secondary structure of each residue
classifies into 8 classes, namely H (α-helix), G (310-
helix), I (π-helix), B (isolated β-bridge), E (extended
β-strand), T (hydrogen bonded turn), S (bend), and
C (not HBEGIT or S). The prediction methods are
assessed for only 3 standard classes associated with
α helices (H), β-strands (E) and coils (C). Hence, 8
classes are reduced to 3. In the literature, there are
four main mappings to perform the reduction
process (Sepideh et al., 2008). These are:
1. H,G H
E E
S,T,B,I,C C
2. H H
E E
G,S,T,B,I,C C
3.
H,G,I H
E,B E
S,T,C C
4. H,G H
E,B E
S,T,I,C C
Here, the method 2 is adopted in this research as
it is considered as the strictest criterion. In order to
encode the secondary structure classes for the
classification, three output units are assigned in our
neural network as binary values as follows
H=[1,0,0], E=[0,1,0], and C=[0,0,1]
The prediction of protein secondary structure
based on a multiple alignment profile of protein
instead of a single sequence has been adopted as a
way to improve the prediction accuracy in several
papers (Rost and Sander, 1993a), (Rost and Sander,
1993b). The aim of this is to improve predictive
power by finding proteins that are similar to the
protein being examined, and modifying the input to
be a mixture of the original protein information and
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
452

(a)
(b)
Figure 1: The PSSM matrix: (a) the raw matrix values, (b)
the matrix values normalised with the standard logistic
function.
that of these similar proteins.
There are two kinds of multiple alignment
profiles: 1) the multiple sequence alignment profiles
(MSAP), 2) the position-specific score matrices
(PSSM) (Sepideh et al., 2008). In this research, the
PSSMs for the RS126 dataset are used and they can
be easily obtained from (Jpred 3), which is a simple
and accurate protein secondary structure prediction
method incorporating two feed-forward neural
networks. The profile matrix has 20xL elements,
where L is the length of the target sequence as
shown in Figure.1. As the values of the feed-
forward neural network inputs can only accept 0 to
1, the raw PSSM needs to be normalised using the
logistic function as shown in equation (1).
1
1
x
fx
e
(1)
where
x
is the raw matrix value.
As the window size is 13 with 20 amino acids,
there are 13x20 + 1 = 261 neural network inputs (the
last input for the bias term). There are three output
units corresponding to three states (helix, strand and
other structures (sometimes known as loops or
coils)). The network has a single hidden layer, as
one hidden layer is sufficient to solve every problem
including regression and classification (Bishop,
1995). The optimal number of hidden nodes is
theoretically determined based on the Bayesian
inference discussed in details in Section III.
3 CLASSIFICATION BAYESIAN
NEURAL NETWORKS
Bayesian learning of multi-layer perceptron neural
networks is performed by considering Gaussian
probability distributions of the weights which give
the best generalization (Mackay, 1992a), (Mackay,
1992b). In particular, the weights
w
in network
X
are adjusted to their most probable values given the
training data
D
. Specifically, the posterior
distribution of the weights can be computed using
Bayes’ rule as follows
XDp
XwpXwDp
XDwp
|
|,|
,|
(2)
where
XwDp ,| is the likelihood function, which
contains information about the weights from
observations, and the prior distribution
Xwp |
contains information about the weights from
background knowledge. The denominator,
XDp | ,
is known as the evidence for network X given data-
set D.
Given a set of candidate networks
i
X having
different numbers of hidden nodes, the posterior
probability of each network can be expressed as
Dp
XpXDp
DXp
ii
i
|
|
(3)
If the networks are assumed to be equally probable
before any data is observed, then
i
Xp is the same
for all networks. Since
Dp does not depend on the
network, then the probable network is the one with
the highest evidence
i
XDp | . Therefore, the
evidence can be used to compare and rank different
candidate networks.
The weights and biases of the Bayesian neural
network are grouped into a single vector and
determined as follows
1mmmm
ww d
(4)
where
1m
w
is the weight vector at the training
iteration
1m
,
m
w
is the weight vector at the
training iteration
m
,
m
is the adaptive learning rate
at the training iteration
m
and
m
d
is the search
direction at the training iteration
m
. The adaptive
learning rate is adjusted during the training phase
based on the Scaled Conjugate Gradient method
(Moller, 1993). In this research, the search direction
ProteinSecondaryStructurePredictionusinganOptimisedBayesianClassificationNeuralNetwork
453

is predefined to be the negative gradient
m
g
.
Regularisation is used to prevent any weights
becoming excessively large, which can lead to poor
generalisation. For a multi-layer perceptron neural
network classifier with
G
groups of weights and
biases, a weight decay penalty term proportional to
the sum of squares of the weights and biases is
added to the data error function
D
E to obtain the
cost function
g
W
G
g
gD
EES
1
(5)
2
2
1
gW
wE
g
),...,1( Gg
(6)
where
S
is called the cost function,
g
is a non-
negative scalar, sometimes known as a
hyperparameter, ensuring the distribution of weights
and biases in group
g
and
g
w
is the vector of
weights and biases in group
g
.
In network training, the hyperparameters are
initialised to be arbitrary small values. The cost
function is then minimised using the Scaled
Conjugate Gradient method. When the cost function
has reached a local minimum, the hyperparameter
g
( Gg ,...,1 ) is re-estimated. This task requires
computing the Hessian matrix of the cost function:
g
G
g
g
IHA
1
(7)
where
H
is the Hessian matrix of
D
E and
g
I
is
the identity matrix, which selects weights in the
g
th
group. The number of ‘well-determined’ weights
g
in group
g
is calculated based on the old value of
g
as follows:
1
ggg g
WtrAI
),...,1( Gg
(8)
The new value of the hyperparameter
g
is then re-
estimated as
g
W
g
g
E2
),...,1( Gg
(9)
The hyperparameters need to be re-estimated several
times until the cost function value ceases to change
significantly between consecutive re-estimation
periods. After the network training is completed, the
values of parameters
g
and
g
are then used to
compute the log evidence of network
i
X having
M
hidden nodes as follows (Penny and Robert, 1999):
lnln
4
2
1
2ln!lnln
2
1
ln
2
ln
1
1
G
MMA
W
SXEv
g
G
g
g
G
g
g
i
(10)
where
g
W
is the number of weights and biases in
group
g
, and
is set to be
3
10 (Thodberg, 1996).
However,
is a minor factor because it is the same
for all models and therefore does not effect to the
relative comparison of log evidence of different
network architectures. Equation (10) is used to
compare different networks having different
numbers of hidden nodes. The best network will be
selected with the highest log evidence.
4 EVALUATION METHODS
A useful accuracy evaluation for classification
neural networks is well-known three state overall
residue accuracy percentage defined as follows
3
100
loop
PPP
Q
N
(11)
where
P
,
P
and
loop
P
are the number of correctly
predicted
-helix,
-sheet and loop, respectively.
N
is the total number of residues in a given protein
sequence.
Another widely used accuracy measurement is
the Matthew’s correlation coefficients. In the case of
P
helix, this coefficient is determined as follows
pn uo
C
nuno pu po
(12)
where
p
is the number of correctly predicted
positive cases,
n
is the number of correctly
rejected negative cases,
o
is the number of over-
predicted cases (false positives), and
u
is the
number of under-predicted cases (misses). Similarly,
C
and
loop
C
can be also defined for
-sheet and
loop, respectively. If the coefficients are equal to 1,
the model predictions are 100% correct. Whereas, if
the coefficients are equal to -1, the model
predictions are 100% incorrect.
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
454
5 EXPERIMENTS AND RESULTS
The RS126 dataset was used for training and testing
the networks (Rost and Sander, 1993a). All of the
dataset was randomly divided into seven subsets. A
seven fold cross-validation technique was applied to
determine the prediction accuracy. In particular, six
subsets were used for training networks and the
remaining subset was used for testing networks. This
procedure was repeated for the different test subsets.
Bayesian neural networks with different numbers of
hidden nodes were trained to select the optimal
network architecture. These networks have the
following specification, as discussed in detail earlier
in the paper:
four hyperparameters
1
,
2
,
3
and
4
to
constrain the magnitudes of the weights on the
connection from the input nodes to the hidden
nodes, the biases of the hidden nodes, the weights
on the connection from the hidden nodes to the
output nodes, and the biases of the output nodes;
261 inputs, corresponding to 20 inputs for each
letter in the moving with the size is 13 and one
bias term with a constant value of 1;
three outputs, each corresponding to one of the
states: helix, strand and other structures.
For a given number of hidden nodes, five
networks with different initial values of the weights
and biases were trained. The training procedure was
implemented as follows:
1. The weights and biases in four different groups
were initialised by random selections from zero-
mean, unit variance Gaussians and the initial
hyperparameters were chosen to be small values.
2. The network was trained to minimise the cost
function
S
using Scaled Conjugate Gradient
training algorithm.
3. When the network training had reached a local
minimum, the values of the hyperparameters
were re-estimated according to equation (8) and
(9).
4. Steps 2 and 3 were repeated until the cost
function value was smaller than a pre-determined
value and did not change significantly in
subsequent re-estimations.
The performances of the trained networks were
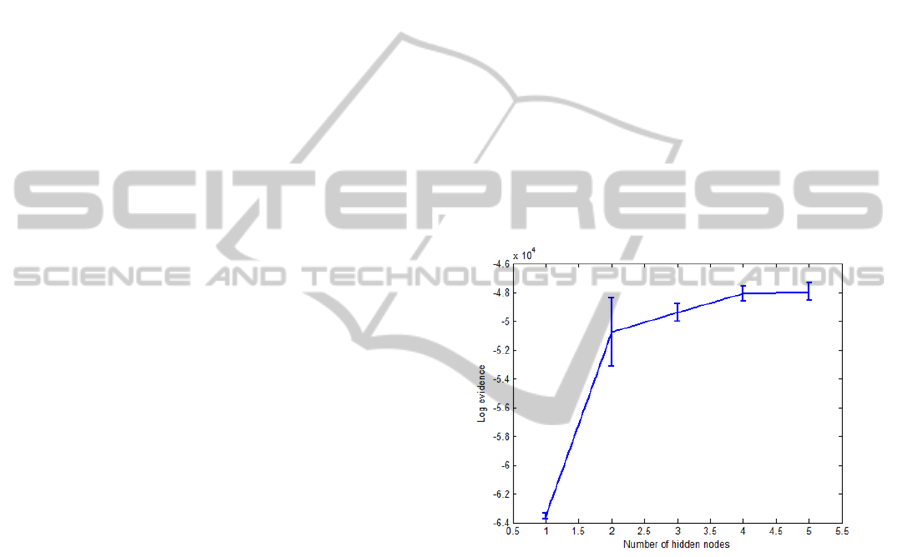
tested on the seventh subset. As shown in Figure 2,
the networks having four hidden nodes is the last
increase that produces a meaningful increase in log
evidence. This means that four hidden nodes are
sufficient to solve the problem. Table 1 shows the
change of hyperparameters according to the periods
of re-estimation of a specific network training run.
For each period, there are 100 predefined
trainingiterations.
Table 2 shows the prediction accuracy and the
Matthew’s correlation coefficients on three states
from the classification Bayesian neural network. We
can see that the accuracy is 75.77%. Next, a standard
classification neural network that has the same
structure with the classification Bayesian neural
network was trained to obtain the three-state
prediction accuracy. However, the prediction
accuracy of the trained classification standard neural
network 74.97% and the Matthew’s correlation
coefficients, shown in Table 3, are also smaller than
those of the trained classification Bayesian neural
network shown in Table 2. Whilst this increase is
small, progress in this area has typically come from
the accumulation of small improvements, which can
be combined together to make a larger improvement.
Figure 2: Log evidence versus number of hidden nodes:
The solid curve shows the evidence averaged over the five
networks.
6 CONCLUSIONS
The results obtained show that Bayesian neural
networks can be used to predict the protein
secondary structure with the maximum accuracy of
75.77%. This is better than the traditional neural
network training methods. According to the obtained
results, the use of four hidden nodes is an optimal
choice for the network architecture. This number of
hidden nodes can give the best generalisation of the
trained network without the use of a validation set.
Therefore, the available data was only divided into
two subsets: one for training and another for testing.
Moreover, Bayesian training for neural network can
ProteinSecondaryStructurePredictionusinganOptimisedBayesianClassificationNeuralNetwork
455
automatically adjust the hyperparameters during the
training phase.
The procedure for determining the optimal
structure of the classification standard neural
network (the growing and pruning technique) has
not been mentioned in this paper as this approach
requires a lot of statistical tasks. The main
disadvantage of the Bayesian learning for feed-
forward neural networks is that it takes a quite long
time on evaluating the Hessian matrix, especially
when the number of network parameters (weights
and biases) is relatively large.
Table 1: The change of hyperparameters according to the
periods of re-estimation.
Periods
1
2
3
4
1 31.392 1.371 0.529 0.775
2 99.919 2.389 0.334 2.432
3 198.498 4.055 0.231 3.949
Table 2: The three-state prediction accuracy and
Matthew’s correlation coefficients of classification
Bayesian neural network.
Matthew’s Correlation
Coefficients
Fold
3
(%)Q C
C
loo
p
C
A 75.840 0.699 0.531 0.565
B 78.187 0.728 0.607 0.604
C 72.422 0.635 0.510 0.524
D 75.319 0.658 0.550 0.540
E 74.826 0.641 0.580 0.542
F 76.362 0.697 0.598 0.569
G 77.462 0.696 0.578 0.604
Average 75.774 0.679 0.565 0.564
Table 3: The three-state prediction accuracy and
Matthew’s correlation coefficients of standard
classification Bayesian neural network.
Matthew’s Correlation
Coefficients
Fold
3
(%)Q C
C
loo
p
C
A 75.927 0.689 0.543 0.565
B 77.347 0.725 0.583 0.587
C 71.321 0.619 0.496 0.502
D 74.826 0.646 0.551 0.536
E 73.812 0.622 0.571 0.521
F 74.739 0.669 0.572 0.548
G 76.796 0.669 0.568 0.604
Average 74.967 0.663 0.555 0.552
REFERENCES
B. Rost and C. Sander, "Prediction of protein secondary
structure at better than 70% accuracy," J.Mol.Biol.,vol.
232, pp. 584-599, 1993a.
B. Rost and C. Sander, "Improved prediction of protein
secondary structure by use of sequence profiles and
neural networks.," Proc, Natl, Acad, Sci, Biophysics,
USA, pp. 7558 - 7562, 1993b.
L. H. Holley and M. Karpus, "Protein secondary structure
prediction with a neural network," Proc, Natl, Acad,
Sci, Biophysics, USA, vol. 86, pp. 152 - 156, 1989.
L. Lee, J. L. Leopold, and R. L. Frank, "Protein secondary
structure prediction using BLAST and exhaustive RT-
RICO, the search for optimal segment length and
threshold," 2012 IEEE Symposium on Computational
Intelligence in Bioinformatics and Computational
Biology (CIBCB), pp. 35 – 42, 2012.
S. T. Nguyen, H. T. Nguyen, and P. Taylor, "Hands-Free
Control of Power Wheelchairs using Bayesian Neural
Networks," Proceedings of IEEE Conference on
Cybernetics and Intelligent Systems, Singapore, 2004,
pp. 745 - 749, 2004.
S. T. Nguyen, H.T.Nguyen, P. Taylor, and J. Middleton,
"Improved Head Direction Command Classification
using an Optimised Bayesian Neural Network,"
Proceedings of IEEE International Conference of the
Engineering in Medicine and Biology Society, New
York City, New York, USA, August 30-Sept. 3, 2006.
W.D. Penny and S. J. Roberts, "Bayesian neural networks
for classification: how useful is the evidence
framework," Neural Networks, vol. 12, pp. 877 - 892,
1999.
H. H. Thodberg, "A review of Bayesian neural networks
with an application to near infrared spectroscopy,"
IEEE Transactions on Neural Networks, vol. 7, pp. 56
- 72, 1996.
D. MacKay, "A practical Bayesian Framework for
Backpropagation Networks," Computation and Neural
Systems, vol. 4, pp. 448-472, 1992a.
D. MacKay, "The Evidence Framework Applied to
Classification Networks," Neural Computation, vol. 4,
pp. 720 -736, 1992b.
C. M. Bishop, "Neural networks for pattern recognition,"
Oxford: Clarendon Press; New York: Oxford
University Press, 1995.
M. A. Mottalib, M. S. R. Mahdi, A. B. M. Z. Haque, S. M.
A. Mamun, and H. A. Al-Mamun, "Protein Secondary
Structure Prediction using Feed-Forward Neural
Network," JCIT, vol. 1, pp. 64 - 68, 2010.
N. Qian and T. J. Sejnowski, "Predicting the Secondary
Structure of Globular Proteins Using Neural Network
Models," J. Mol. Biol. 202, pp. 865 - 884, 1988.
M. F. Moller, "A Scaled Conjugate Gradient Algorithm
for Fast Supervised Learning," Neural Networks, vol.
6, pp. 525 - 533, 1993.
Jpred 3, http://www.compbio.dundee.ac.uk/www-jpred/
David T. Jones, "Protein Secondary Structure Prediction
Based on Position-specific Scoring Matrices,"
J.Mol.Biol.,vol.292, pp.195-202, 1999.
IJCCI2013-InternationalJointConferenceonComputationalIntelligence
456

B. Sepideh, S. S. Ali, and G. A. R, "Pruning neural
networks for protein secondary structure prediction,"
8th IEEE International Conference on BioInformatics
and BioEngineering, 2008. BIBE 2008, pp. 1 - 6,
2008.
K. Rajasekhar, D. V. Kumar, and O. O. Ahmad, " A two-
stage neural network based technique for protein
secondary structure prediction " The 2nd International
Conference on Bioinformatics and Biomedical
Engineering, 2008. ICBBE 2008, pp. 1355 - 1358
2008.
ProteinSecondaryStructurePredictionusinganOptimisedBayesianClassificationNeuralNetwork
457
